Planning, Control and Sensing for Contact-rich Robotic Manipulation
Tao Pang
Oct 2022


Why contact-rich?

Collision-free Motion Planning
Interact with the world



Smaller
What about RL (reinforcement learning)?

- RL generates robust policies for specific tasks, but...
- RL requires heavy offline computation,
- the learned policy does not generalize (e.g. to opening a door).
We believe that understanding in model-based methods can lead to insights in RL, and vice versa.
- (OpenAI) Andrychowicz et al. "Learning dexterous in-hand manipulation." The International Journal of Robotics Research, 2020.
- (Nvidia) Handa et al. "DeXtreme: Transfer of Agile In-hand Manipulation from Simulation to Reality", arXiv preprint, 2022.
[1] OpenAI.
[2] Nvidia.

Why is contact-rich planning hard?
Contact dynamics is non-smooth!
Two solutions
Descend with gradients of smoothed dynamics
Reason explicitly about contact mode transitions
Contact
No Contact
- But descent methods get stuck in local minima.
- Therefore they need non-trivial initialization.
- Good at escaping local minima,
- But mode enumeration scales poorly (exponentially) with the number of contacts.
smoothed dynamics
original dynamics
\(u = 0\)
Model-based Planning through Contact: a Quick Review
- Trajectory Optimization through Contact
- Mordatch, Igor, Emanuel Todorov, and Zoran Popović. "Discovery of complex behaviors through contact-invariant optimization." ACM Transactions on Graphics (TOG), 2012.
- Hogan, François Robert, and Alberto Rodriguez. "Feedback control of the pusher-slider system: A story of hybrid and underactuated contact dynamics." arXiv preprint arXiv:1611.08268, 2016.
- Posa, Michael, Cecilia Cantu, and Russ Tedrake. "A direct method for trajectory optimization of rigid bodies through contact." The International Journal of Robotics Research, 2014.
- Aydinoglu, Alp, and Michael Posa. "Real-time multi-contact model predictive control via admm." 2022 International Conference on Robotics and Automation (ICRA), 2022.
- Cheng, Xianyi, et al. "Contact mode guided motion planning for quasidynamic dexterous manipulation in 3d." 2022 International Conference on Robotics and Automation (ICRA), 2022.
- Marcucci, Tobia, et al. "Approximate hybrid model predictive control for multi-contact push recovery in complex environments." 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), 2017.
- Enumerate mode switches locally
- Enumerate Mode Switches
- Sampling mode switches
Good
Scalability
Bad Scalability
Local Planning
Global Planning
Global planning + Smoothed dynamics?
[1] Mordatch et al.

[3] Posa et al.
[5] Cheng et al.
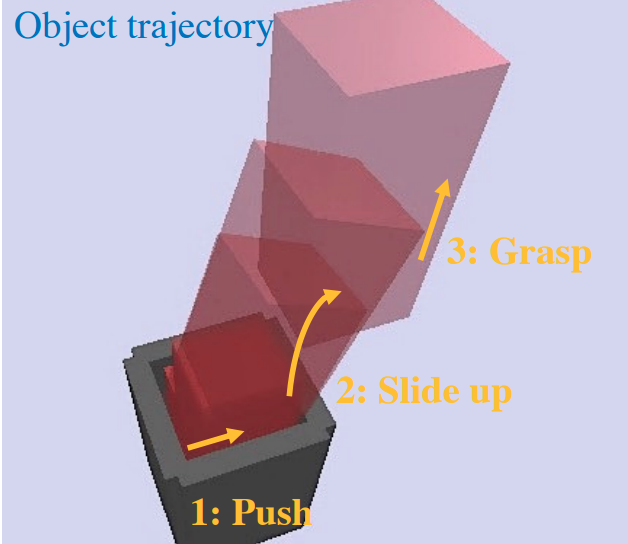
[6] Marcucci et al.
[4] Aydinoglu and Posa.

[2] Hogan and Rogriguez.
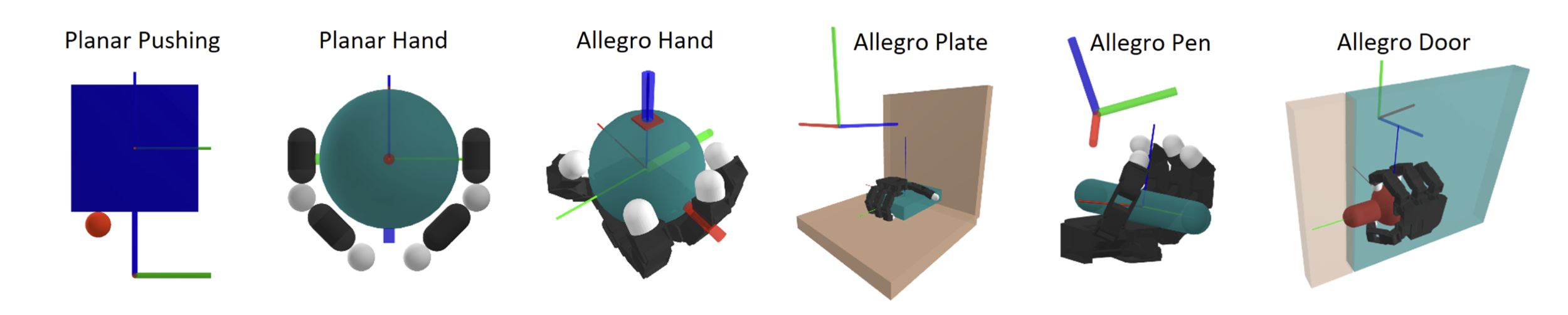
Our Method: Sim and Hardware Demos.
- Our planner combines sampling-based global search and smoothed contact dynamics.
- Our planner takes less than a minute to find most plans shown above.
Open-loop execution of contact-rich plans on hardware:
Our method: Kino-dynamic RRT through contact
- We leverage the sampling-based nature of RRT to globally explore the state space.
- We abstract modes away using smoothed linearization of the contact dynamics.
- RRT is powered by a Convex, Quasi-static, Differentiable contact dynamics model.
- Convex: the discrete-time dynamics \(x_+ = f(x, u)\) can be evaluated by solving a convex program.
-
Quasi-static:
- Valid for many manipulation tasks.
- Smaller state space,
- Fewer planning steps.
- The dynamics model can be easily smoothed.
- Differentiable: the smoothed linearization provides an effective distance metric.
How does RL power through non-smooth contact dynamics? [1][2]
- RL minimizes a stochastic objective via sampling.
- Sampling has a smoothing effect on the objective's landscape.
We can smooth contact dynamics, but without using samples (faster).

Terry Suh
-
H.J. Terry Suh*, Tao Pang*, Russ Tedrake, “Bundled Gradients through Contact via Randomized Smoothing”, RA-L, 2022.
-
Tao Pang*, H.J. Terry Suh*, Lujie Yang, Russ Tedrake, "Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models", under review.
Contact-rich manipulation also needs control and sensing
A QP controller that bounds contact forces while tracking a trajectory. [1]
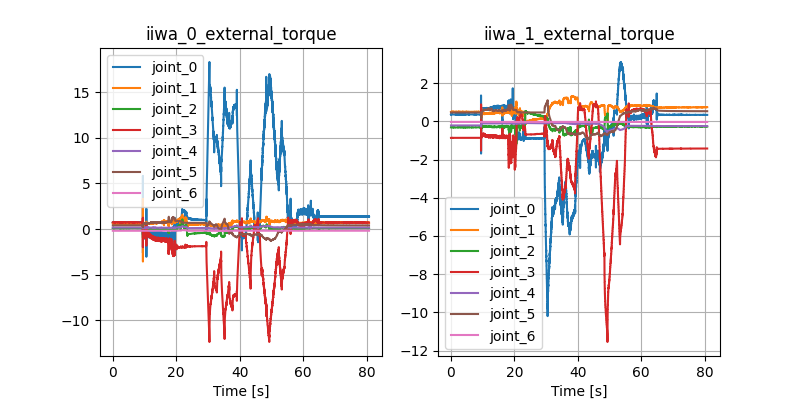
Detecting contact forces from joint torques is tricky and unreliable.[2]
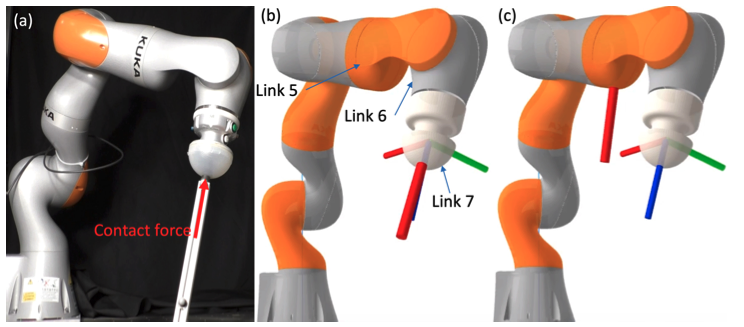
-
Tao Pang, Russ Tedrake, "Easing Reliance on Collision-free Planning with Contact-aware Control", ICRA, 2022.
-
Tao Pang, Jack Umenberger, Russ Tedrake, "Identifying external contacts from joint torque measurements on serial robotic arms and its limitations", ICRA,2021.
Presented Works
Collaborators

-
Tao Pang*, H.J. Terry Suh*, Lujie Yang, Russ Tedrake, "Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models", under review.
-
H.J. Terry Suh*, Tao Pang*, Russ Tedrake, "Bundled Gradients through Contact via Randomized Smoothing", RA-L, 2022.
-
Tao Pang, Russ Tedrake, "A Convex Quasistatic Time-stepping Scheme for Rigid Multibody Systems with Contact and Friction", ICRA, 2021.
-
Tao Pang, Russ Tedrake, "Easing Reliance on Collision-free Planning with Contact-aware Control", ICRA, 2022.
-
Tao Pang, Jack Umenberger, Russ Tedrake, "Identifying external contacts from joint torque measurements on serial robotic arms and its limitations", ICRA,2021.



Terry Suh
Lujie Yang
Russ Tedrake

Jack Umenberger
Opinion: we need robots designed for contact-rich interactions
- Hogan, Francois R., et al. "Tactile dexterity: Manipulation primitives with tactile feedback." 2020 IEEE international conference on robotics and automation (ICRA). IEEE, 2020.
- Suh, H. J., et al. "SEED: Series Elastic End Effectors in 6D for Visuotactile Tool Use." arXiv preprint arXiv:2111.01376, 2021.
- Luo, Yiyue, et al. "Learning human–environment interactions using conformal tactile textiles." Nature Electronics, 2021.

Human


OpenAI
Nvidia
This robot needs full-body tactile sensing, ...


Joint torque

Hogan et al.

Hogan et al.[1]
Suh et al.[2]
"Camera under the fingertip"

Luo et al.[3]
Tactile skin
Opinion: we need robots designed for contact-rich interactions
- Hwangbo, Jemin, et al. "Learning agile and dynamic motor skills for legged robots." Science Robotics 4.26 (2019): eaau5872.
- Salisbury, Kenneth, et al. "Preliminary design of a whole-arm manipulation system (WAMS)." Proceedings. 1988 IEEE International Conference on Robotics and Automation. IEEE, 1988.
"Probably of highest importance has been a focus on force control. Since the system is intended to contact objects, sometimes unpredictably, with any part of its mechanism, it is important that forces anywhere along the links be controllable." -- Ken Salisbury on whole-arm manipulation, 1988 [2].
This robot also needs precisely-modeled compliance.


Other interesting things I did
- Take-off weight: 10kg.
- Maximum endurance: 3 hours.
Gasoline-engine-powered Quadcopter

3D Geometry from NeRF

I wrote the code that rendered this image.
Active SLAM of a planar robot
Why the AI Institute?
My goals
the AI Institute's goals
Goal: a robot that can interact with anything using any part of its body.
- Robust planning and control for contact-rich manipulation.
- Human-level dexterity? Seems very natural after human-level locomotion!
- Working with hardware team to design next-gen robots for contact-rich interactions.
- Athletic intelligence + organic hardware design.
- Components of the contact-rich planning pipeline can benefit from learning.
- Improving model-based methods by learning and vice versa.
- Athletic intelligence + Cognitive intelligence.
Why is contact-rich planning hard?

Contact dynamics is non-smooth!
Contact
No Contact
Smoothing
What is quasi-static dynamics?
- Quasi-static: velocity is small so that inertial and Coriolis forces are negligible.
- \(x \coloneqq q \coloneqq [q^\mathrm{u}, q^\mathrm{a}]\): system configuration.
- \(q^\mathrm{a}\): actuated, imepdance-controlled robots
- \(q^\mathrm{u}\): un-actuated objects.
- \( u \):
robot velocitiesposition command to the stiffness-controlled robots [1]. - \(\delta q \coloneqq q_+ - q\)
- \(h\): step size in seconds.
\( x_{+} = f(x, u)\)
- \(\lambda_i\): contact forces/impulses
- \(\phi_i \): signed distances
(KKT)
- A convex quadratic program (QP), after linearizing \(\phi_i\).
- "Minimizing potential energy, subject to non-penetration constraints."
Force balance of the robot.
Force balance of the object.
Non-penetration.
"Contact forces cannot pull."
"Contact force needs contact."
-
Tao Pang, Russ Tedrake, "A Convex Quasistatic Time-stepping Scheme for Rigid Multibody Systems with Contact and Friction", ICRA, 2021.
Quasi-static dynamics is good for manipulation planning!
- Many manipulation tasks are quasi-static.
- Spatial benefit: Smaller state space (\([q, v]\) vs. only \(q\)).
-
Temporal benefit: Ignoring transients => looking into the future with fewer steps.
-
Tao Pang, Russ Tedrake, "A Convex Quasistatic Time-stepping Scheme for Rigid Multibody Systems with Contact and Friction", ICRA, 2021.
Second-order Dynamics
Quasi-static Dynamics
Quasi-static Dynamics Needs Regularization
Quasi-static Dynamics
- The quadratic cost is positive semi-definite.
- The object can be anywhere between the robot and the wall, similar to having a null space.
Regularized least squares
Regularized Quasi-static Dynamics
- The quadratic cost is now positive definite.
- "Among all possible object motions, give me the one that moves the least."
- Picking \(\epsilon = m^\mathrm{u} / h\) gives Mason's definition of quasi-dynamic dynamics.
What about friction?
- For a frictionless multi-body system with \(n_\mathrm{c}\) contacts, the dynamics can be solved as a QP:
- \(\mathcal{K}^\star_i\) is the dual of the \(i\)-th friction cone.
- Still convex! Convexity is achieved at the expense of "hydroplaning" between relatively-sliding objects.
- But hydroplaning disappears as \(h \rightarrow 0\).
- Anitescu [1] has a nice convex approximation of Coulomb friction constraints, allowing us to write down the dynamics as a Second-Order Cone Program (SOCP):
Tangential displacements
Dynamics of the Toy Problem
- Anitescu, Mihai. "Optimization-based simulation of nonsmooth rigid multibody dynamics." Mathematical Programming 105.1 (2006): 113-143.
Differentiability
Convex, Quasi-Static, Differentiable Dynamics (an SOCP)
- The KKT optimality condition of the dynamics SOCP defines equality constraints (including active contact constraints), from which the derivatives of \(\delta q^\star\) w.r.t. \((\mathbf{Q}, b, \phi_i, \mathbf{J}_{\mathrm{n}_i}, \mathbf{J}_{\mathrm{t}_i})\) can be computed using the Implicit Function Theorem (IFT).
- \(\mathbf{A}, \mathbf{B}\) can then be computed using the gradients from IFT and the chain rule.
- Standard practice for many differentiable simulators, even though many of them do not find the active constraints by solving convex programs.



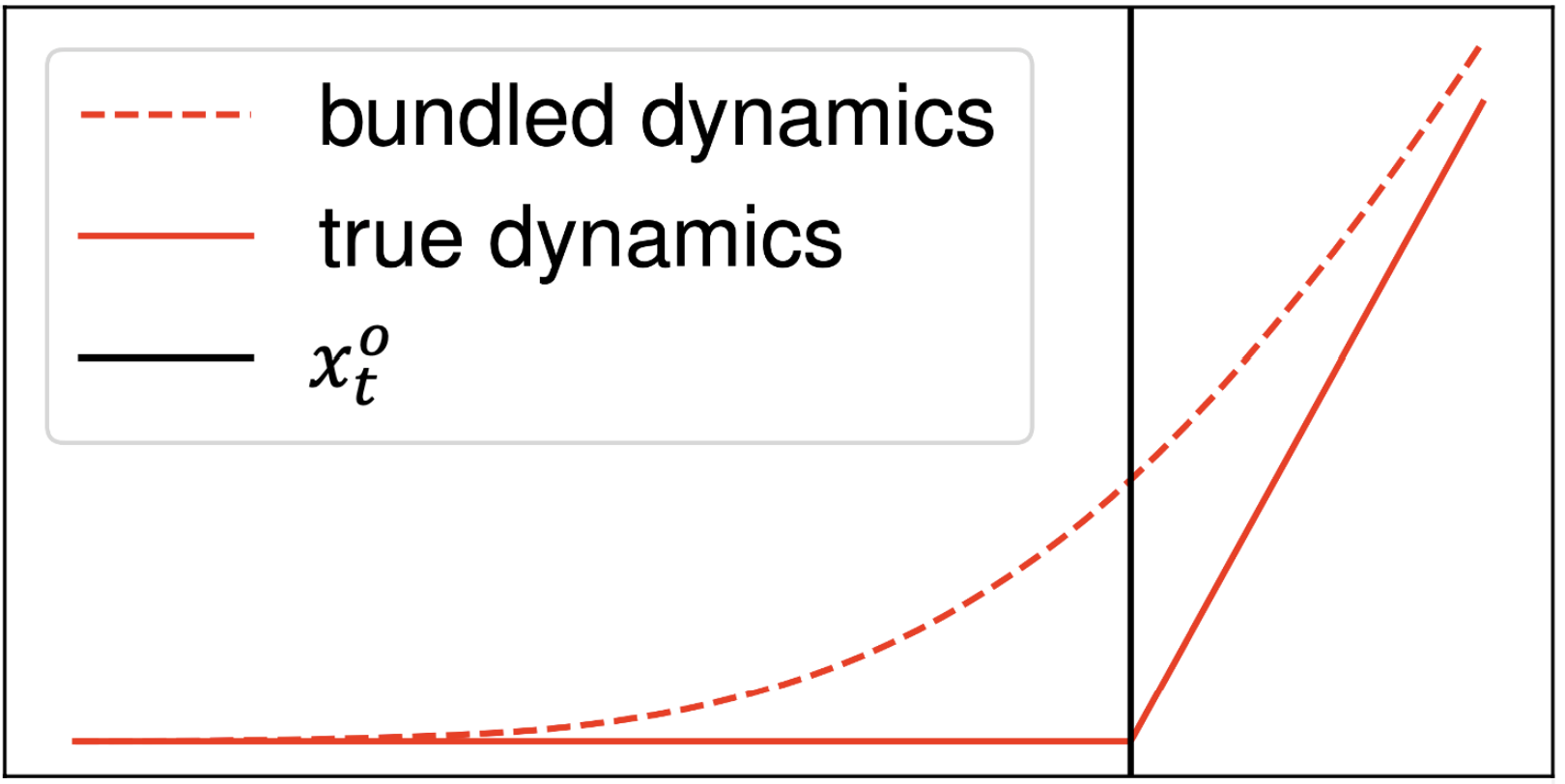
Smoothing
- The contact dynamics \(f(q, u) \in C^0\) has discontinuous gradients, which are bad for planning methods that use gradients.
- Smoothing with "force at a distance" is a common method to alleviate this problem.
Optimality Condition
KKT
Original Dynamics
Smoothed Dynamics
Smoothing, the general case.
Put constraints in a generalized log for \(\mathcal{\kappa}_i^\star\)
- An unconstrained convex program.
- Can be solved with Newton's method.
- Also differentiable.
Convex, Quasi-Dynamic, Differentiable Dynamics (an SOCP)
Notation:
Original dynamics
Smoothed dynamics
Smoothed gradients enable trajectory optimization for dexterous hands, but...
Task: Turning the ball by 30 degrees.
What about 180 degrees?
Finding this trajectory requires powering through local minima!
Sampling-based Motion Planing is Great at Global Exploration, but...
- Rapidly-Exploring Random Tree (RRT): iteratively builds a tree that fills the state space. [1]
- Dynamic reachability is essential for efficient exploration. [2]
- Steven M. LaValle, "Planning Algorithms", Cambridge University Press , 2006.
-
H.J.T. Suh, J. Deacon, Q. Wang, "A Fast PRM Planner for Car-like Vehicles", self-hosted, 2018.
How do we think about reachability under the contact-dynamics constraint?
A distance metric that reflects reachability
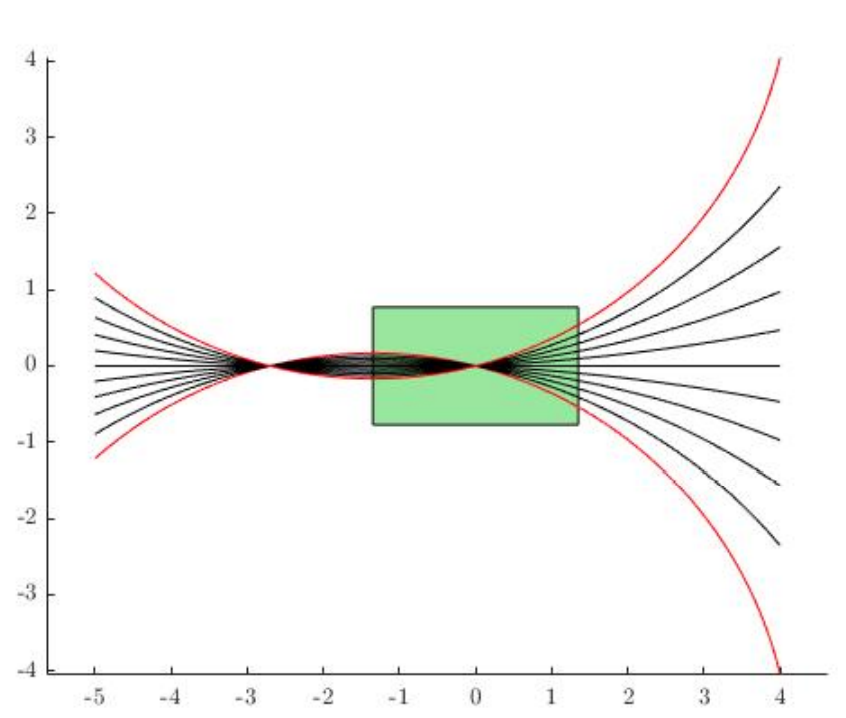
Smoothed Contact Dynamics
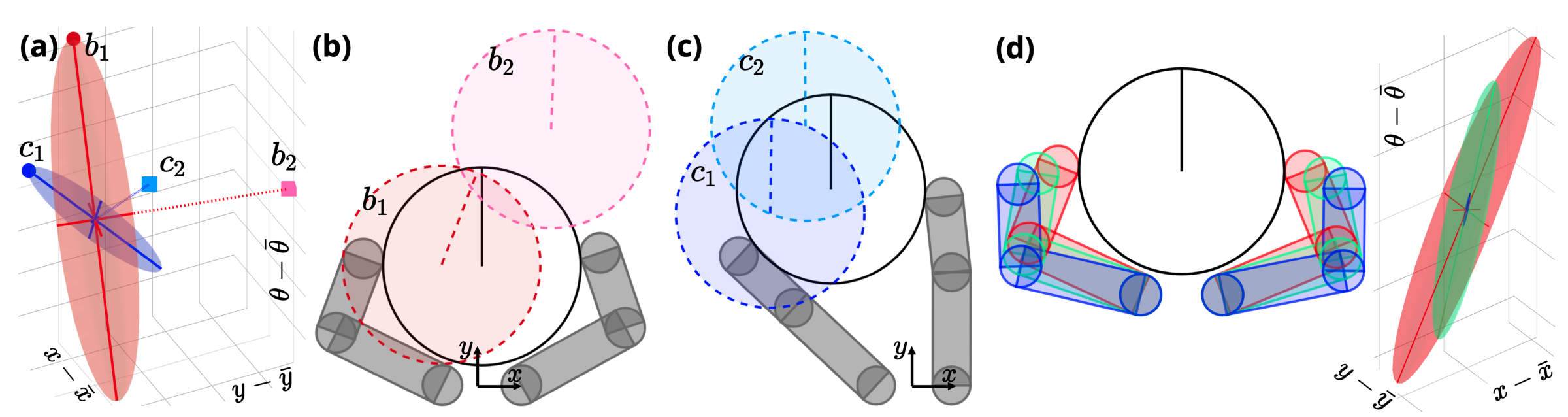
\(\varepsilon \) sub-level set
Nominal state
un-actauted(objects)
Smoothed
At state \(\bar{q}\), what doe an \(\varepsilon\)-ball in action space get transformed into under the smoothed dynamics?
RRT through contact
Three modifications to the vanilla RRT are made:
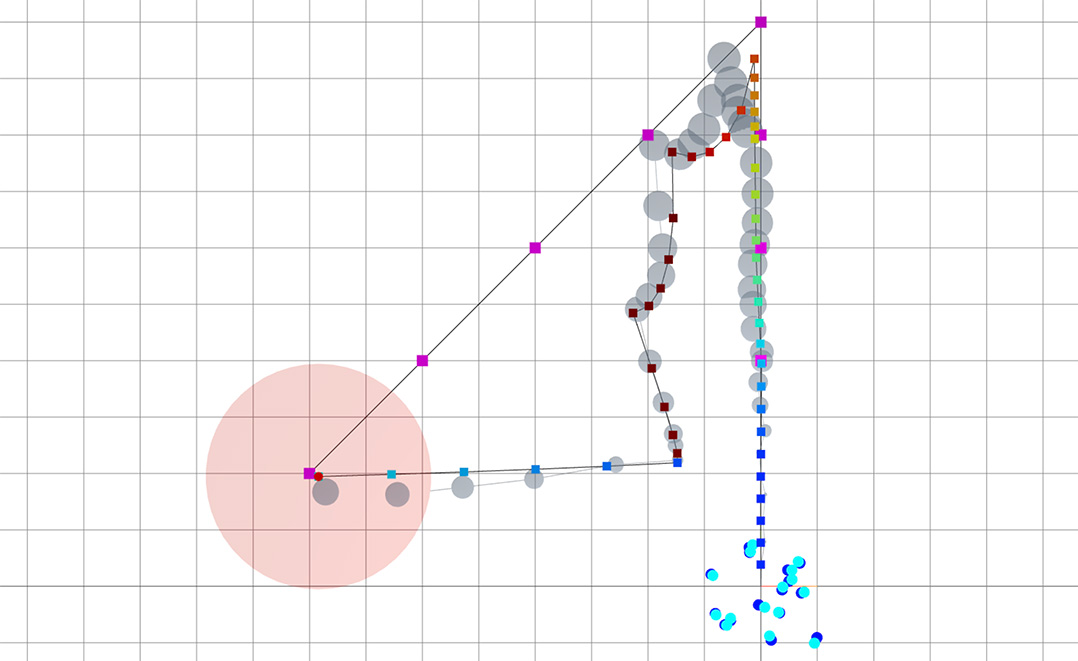
- Nearest node on tree is found using \( d^\mathrm{u}_{\rho}(q; \bar{q}) \).
- Contact sampling: robot configuration is occasionally reset to one that has a good distance metric, which typically corresponds to grasps.
- Dynamic-consistent extension: an action is computed using the smooth linearized dynamics to reach \(q\).
Distance Metric
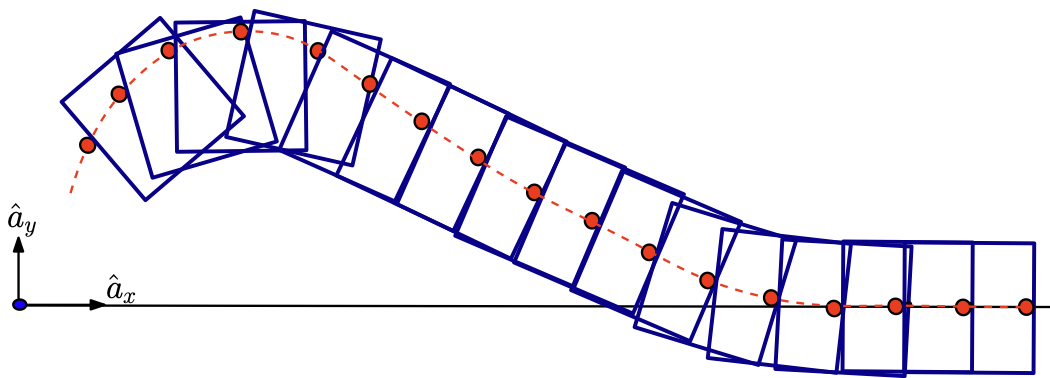
RRT tree for a simple system with contacts
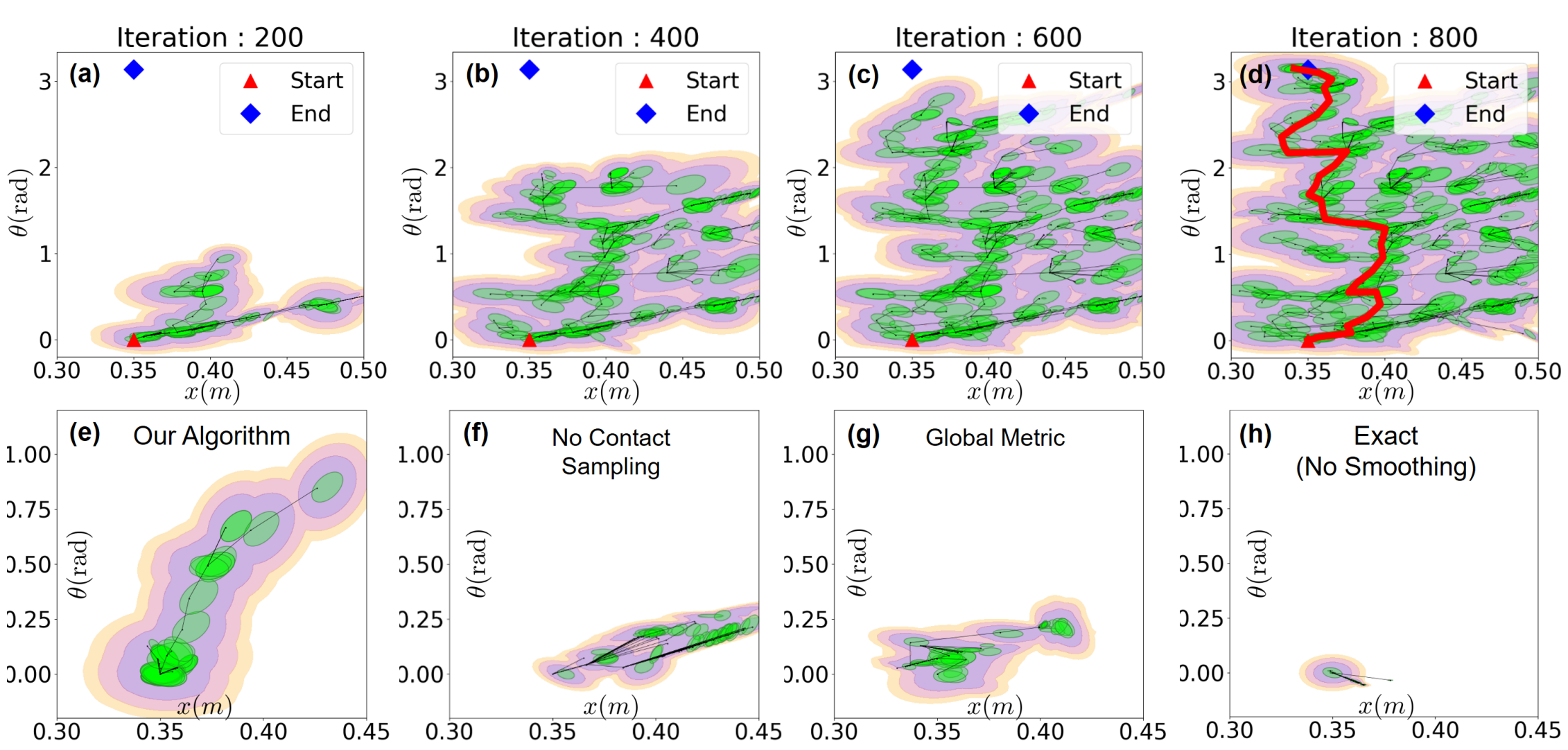

Ablation study: what trees look like after growing a fixed number of nodes.
The modified RRT works well for contact-rich tasks!


Planning wall-clock time (seconds)
RRT is good at escaping local minima, but...
- Kino-dynamic RRT needs a good distance metric! Think about the bycicle.
- A good metric from a queried state \(q\) to a nominal state \(\bar{q}\) can be derived based on the smoothed linearization at \(\bar{q}\):
Smoothed Contact Dynamics
- \(d^\mathrm{u}_{\rho}(q; \bar{q})\) reflects the reachability of \(q\) from \(\bar{q}\) under the smoothed linearization.

\(\varepsilon \) sub-level set
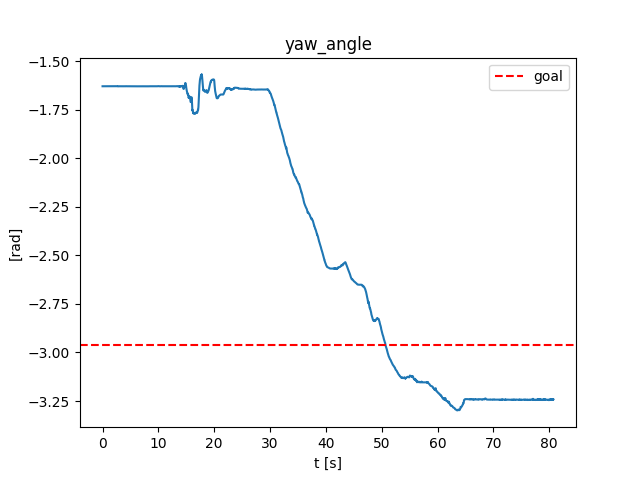
Preliminary: stabilizing contact-rich plans
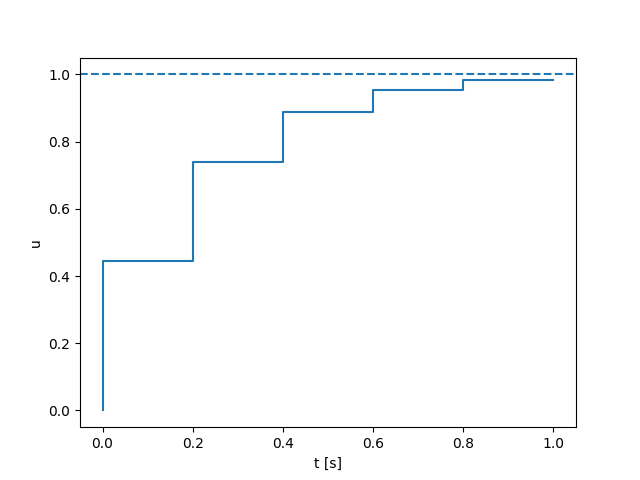
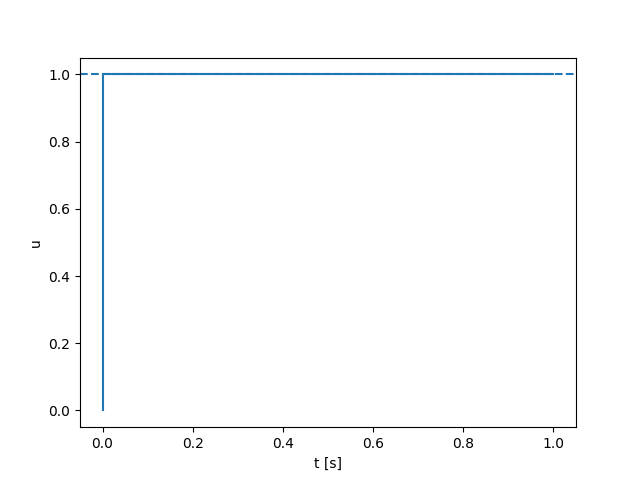
Open-loop
Closed-loop
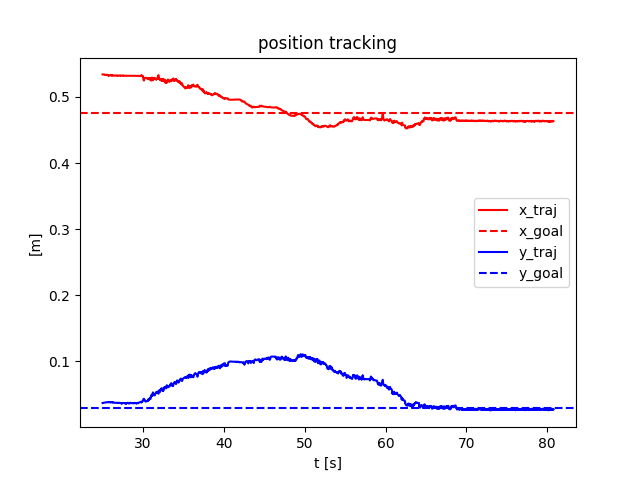

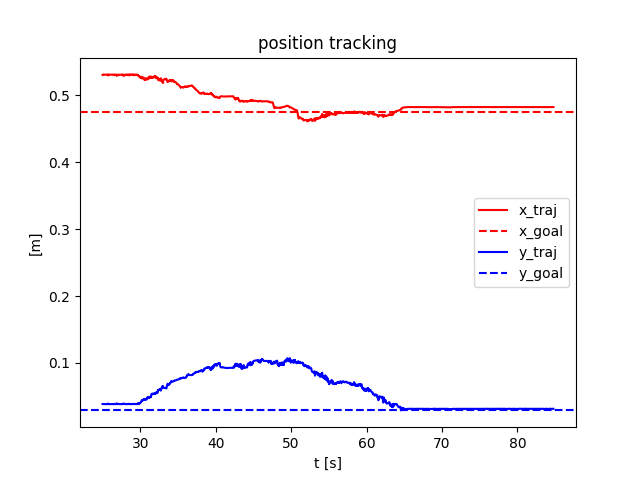
Naive QP controller based on smoothed linearization:
Quasi-static dynamical systems: how to fix it.
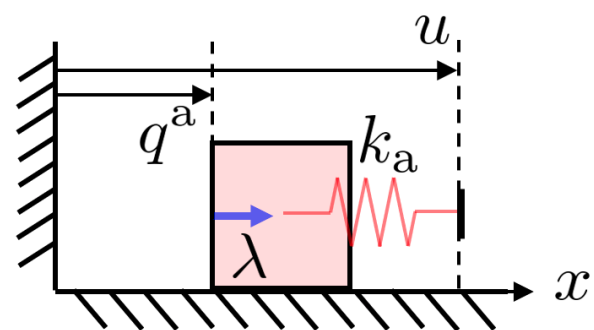
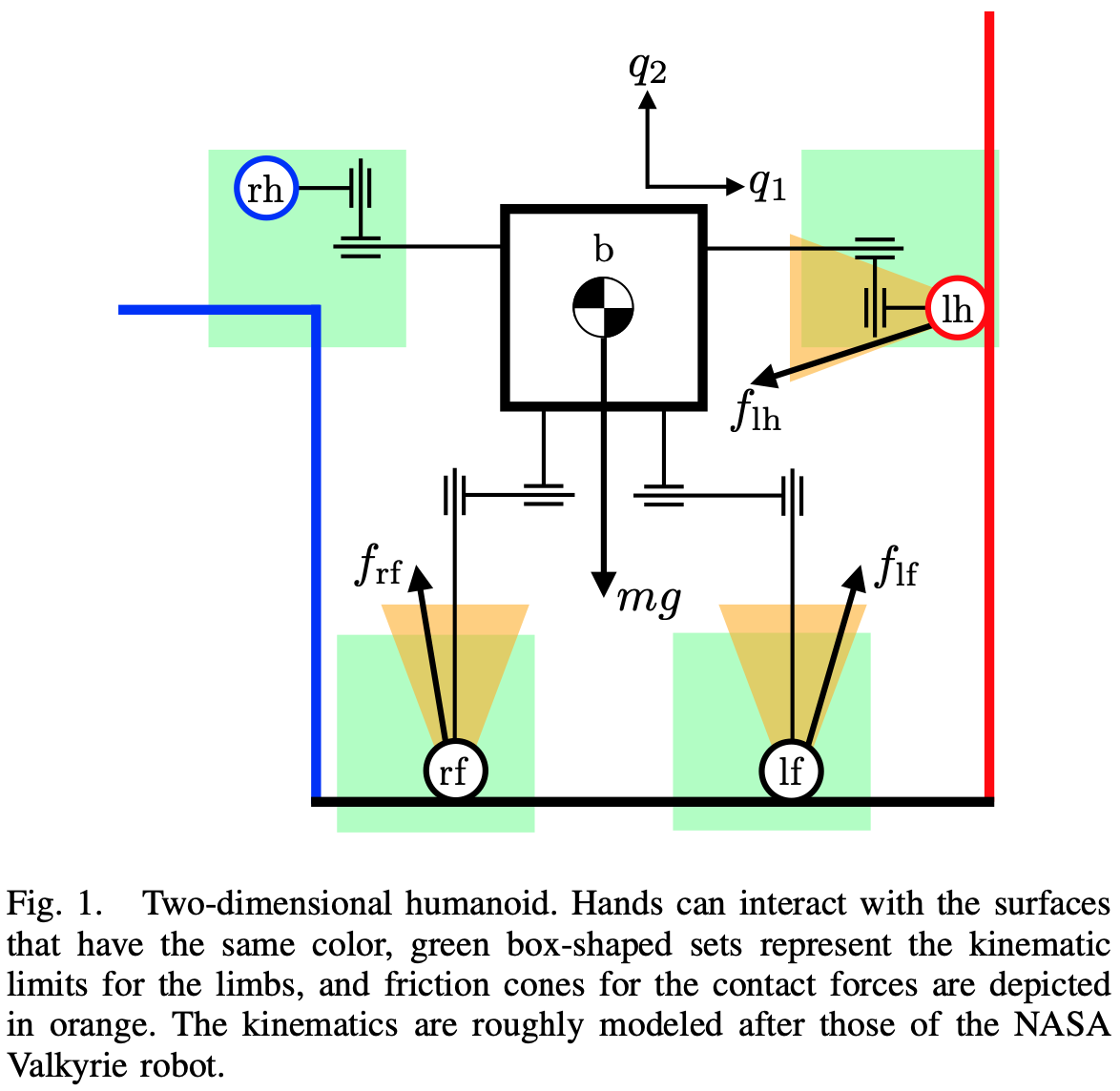
A Impedance-controlled 1D robot and an object.
- Pang, Tao, and Russ Tedrake. "A convex quasistatic time-stepping scheme for rigid multibody systems with contact and friction." 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021.
- Pang, Tao, and Russ Tedrake. "A robust time-stepping scheme for quasistatic rigid multibody systems." 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2018.
\( x_{+} = f(x, u)\)
- \(x \coloneqq q \coloneqq [q^\mathrm{u}, q^\mathrm{a}]\): system configuration.
- \(q^\mathrm{a}\): actuated, imepdance-controlled robots
- \(q^\mathrm{u}\): un-actuated objects.
- \( u \):
robot velocities.position command to the impedance-controlled robots.
Contact force and \(q_+\) can now be uniquely* determined from \(u\), even for grasping.
Force-acceleration vs. Impulse-Momentum
Force-acceleration
- Stewart, David E. "Rigid-body dynamics with friction and impact." SIAM review 42.1 (2000): 3-39.
Impulse-momentum
is the optimality condition of
But impacts can lead to infinite forces (e.g. Painleve's Paradox) [1].
Time step
Stabilizing contact-rich plans
Open-loop hardware
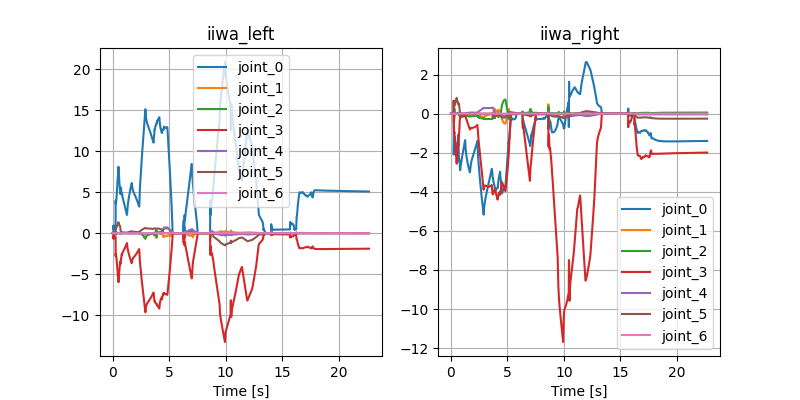
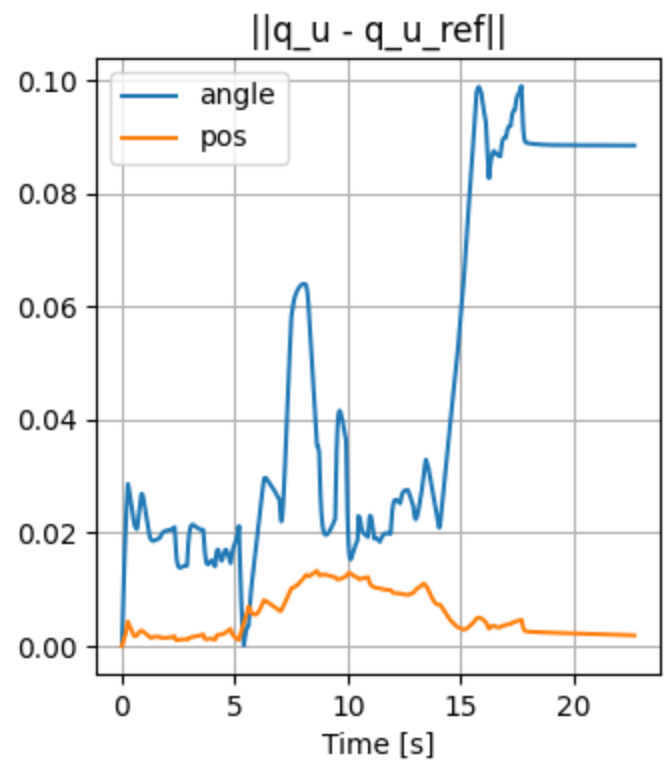
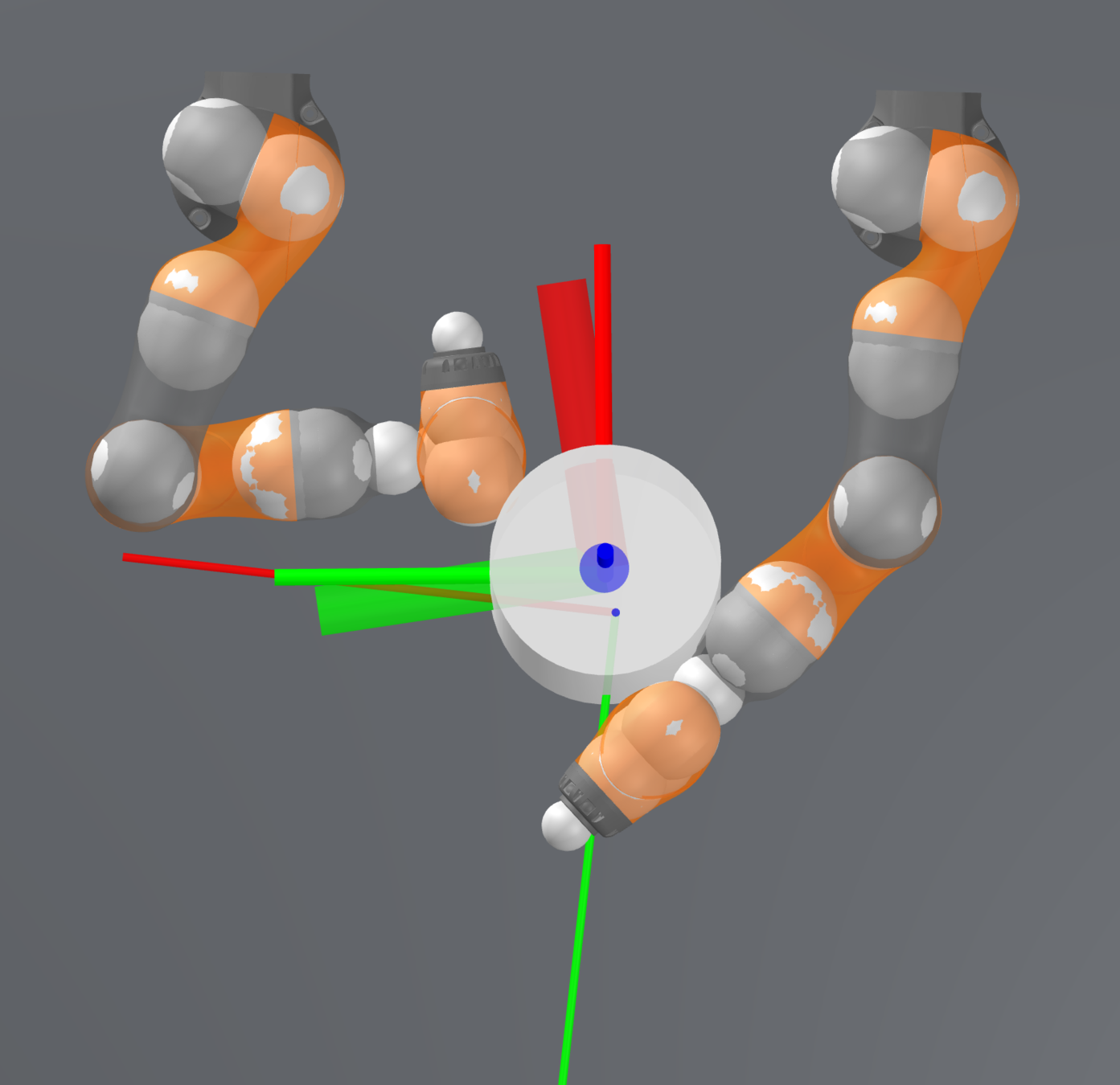
Open-loop Drake
Quasi-static dynamical systems: what it was.
\( x_{+} = f(x, u)\)
- \(x \coloneqq q \coloneqq [q^\mathrm{u}, q^\mathrm{a}]\): system configuration.
- \(q^\mathrm{a}\): actuated, imepdance-controlled robots
- \(q^\mathrm{u}\): un-actuated objects.
- \( u \): robot velocities.
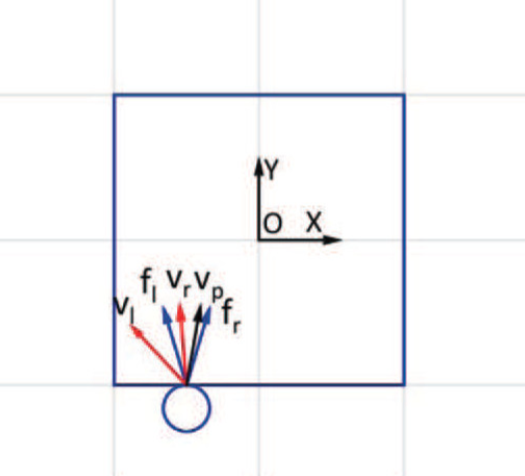
\(\mathrm{v}_p\): applied velocities by the manipulator end effector at the contact point. [1]
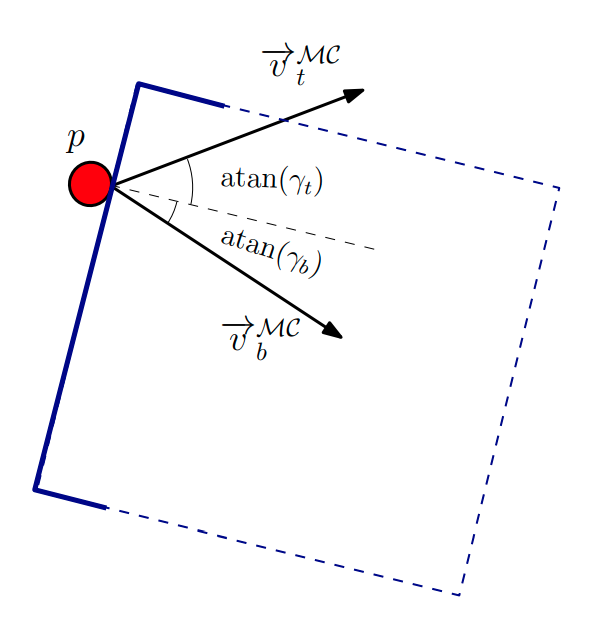
[3]
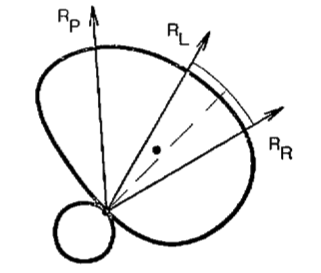
\(R_P\): "the ray of pushing". [2]
This is a good model for planar pushing:
- Contact force cannot be uniquely determined from \(u\) when there is contact.
- As a result, \(q_+\) cannot be determined from \(u\).
- Defining \(u\) as velocity leads to ill-posed dynamical systems (invalid Bond Graphs).
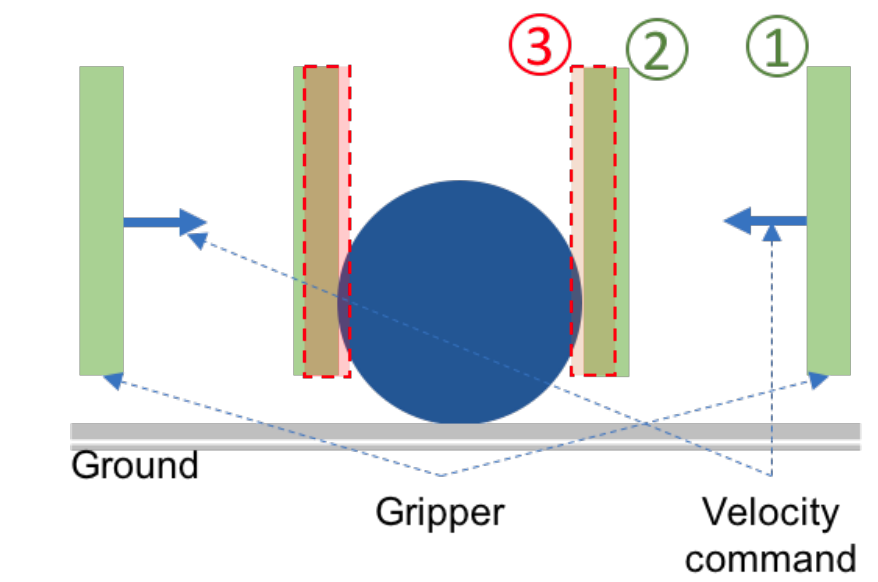
But what about grasping?
- Zhou, Jiaji, et al. "A convex polynomial model for planar sliding mechanics: theory, application, and experimental validation." The International Journal of Robotics Research, 2018.
- Mason, Matthew T. "Mechanics and planning of manipulator pushing operations." The International Journal of Robotics Research, 1986.
- Hogan, François Robert, and Alberto Rodriguez. "Feedback control of the pusher-slider system: A story of hybrid and underactuated contact dynamics." Algorithmic Foundations of Robotics XII, 2020.
What does quasi-dynamic mean?
- Quasi-static \(\Longleftrightarrow \Sigma F = 0\)
- Quasi-dynamic:
"Quasi-dynamic analysis is intermediate between quasi-static and dynamic. Suppose that a manipulation task involves occasional brief periods when there is no quasistatic balance. The task is then governed by Newton's laws. But in some instances, these periods are so brief that the accelerations do not integrate to significant velocities. Momentum and kinetic energy are negligible. Restitution in impact is negligible. It is as if a viscous ether is constantly damping all velocities and sucking the kinetic energy out of all moving bodies. We can analyze such a system by assuming it is at rest, calculating the total forces and body accelerations, then moving each body some short distance in the corresponding direction." -- Matt Mason <Dynamics of Robotic Manipulation>
-
But why is it a good idea?
-
Benefits of quasi-static dynamics for planning:
- Smaller state space (\([q, v]\) vs. only \(q\)).
Larger time steps.
Quasi-dynamic is quasi-static with regularization.
-
Second-order
mass matrix
Quasi-static
Coriolis Force
Torque (contact + actuation)
Quasi-dynamic
Before my PhD defense in December 2022...

- Stabilize this with MPC.
- Already done in Drake.
- Potential problems:
- Robustness.
- Shape variation.
- Coefficient of friction.
- etc.
- Robustness.
- Imperfect actuators.
- Poor tracking.
- Hysteresis.
Turning the ball by 30 degrees: open-loop
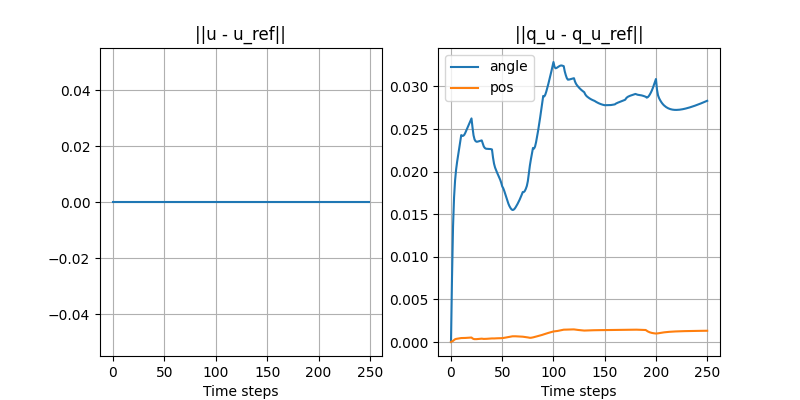
- Simulated in Drake with the same SDF as the quasi-dynamic model used for planning.
Turning the ball by 30 degrees: open-loop with disturbance
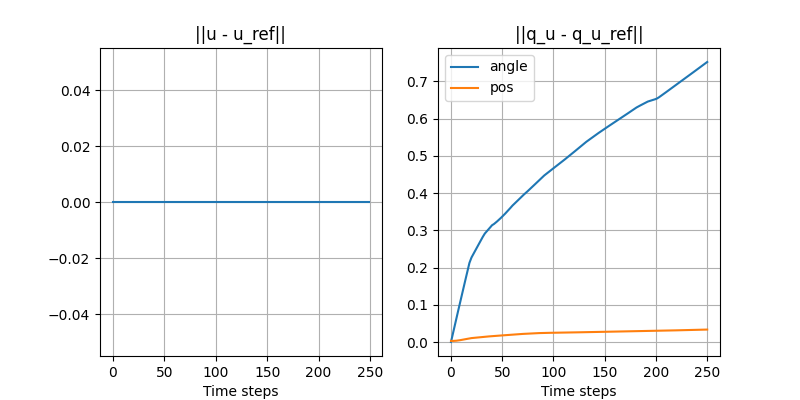
- Initial position of the ball is off by 3mm.
Turning the ball by 30 degrees: closed-loop with disturbance
- Initial position of the ball is off by 3mm.
- Simple controller:
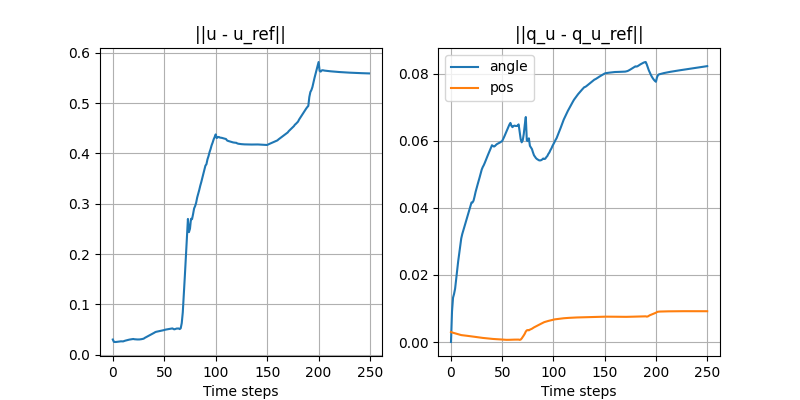
Smooth linearization
talk_30min
By Pang
talk_30min
- 186



