Low-dimensional linear programming
Reminder: what is linear programming?
Most generically, a linear program is a problem of the form
\text{min } \mathbf{c}^T \mathbf{x} \\
\text{s.t. } A \mathbf{x} \leq \mathbf{\beta}
c, x \in \mathbb{R}^n, \beta \in \mathbb{R}^m, A \in \mathbb{R}^{m \times n}
(n variables, m constraints)
Reminder: what is linear programming?
(Sometimes, we add another constraint.)
\text{min } \mathbf{c}^T \mathbf{x} \\
\text{s.t. } A \mathbf{x} \leq \mathbf{\beta} \\
\quad \mathbf{x} \geq 0
How are linear programs solved?
Simplex method (Dantzig, 1940s)
Basic idea: pivot around on the convex polytope of constraints
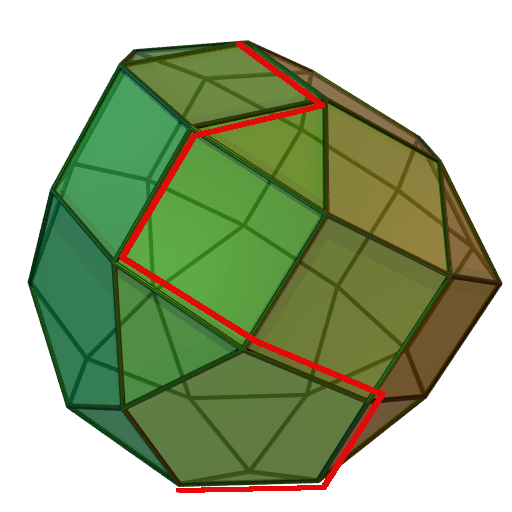
From User:Sdo (Wikimedia). CC BY-SA 3.0.
Works well in practice, but technically has exponential asymptotic complexity (Klee 1973)
How are linear programs solved?
Karmarkar's algorithm (1984)
Runs in polynomial time...
O(n^{3.5} L)
Complicated (relies on projective geometry)
Constraints on a plane
Two types (ignoring vertical constraints):
y \leq mx + b
y \geq mx + b
Constraints on a plane
Some constraints may be redundant.
Constraints on a plane
Ultimately, we are interested in the intersection of half-planes.
How many vertices can we have?
Counting vertices
By McMullen's upper-bound theorem, there are only O(n) vertices to consider for the intersection of half-spaces in and .
\mathbb{R}^2
\mathbb{R}^3
Counting vertices
In general, a convex hull of dimension d has facets, and a polytope with n facets can have vertices.
O(n^{\lfloor d/2 \rfloor})
O(n^{\lfloor d/2 \rfloor})
Thus, the (asymptotically) best methods for low-dimensional linear programming depend on dimension.
Half-plane intersection
Naive algorithm
Let the set of constraints be P. For every unique
, compute the intersection and check to see if the vertex satisfies all constraints.
(p_i, p_j) \in P
Runtime: O(n³)
Half-plane intersection
Divide-and-conquer (Shamos 1978)
Recursively merge half-planes until reaching a (potentially unbounded) convex hull.
D&C half-plane intersection
Need to deal with unboundedness (...but each chain can only have two rays)
D&C half-plane intersection
Runtime (Shamos 1978): O(n log n) — reduces to sorting
Can we do better?
Half-plane intersection
Duality — map constraints in the primal to points in the dual and take the convex hull; edges are intersections.
Requires taking the convex hull—O(n log n)
Incremental — merge in one half-plane at a time.
Still O(n²) or O(n log n) — where to merge?
Pruning (Megiddo 1983)
What if taking all the half-plane intersections is overkill?
Rewrite the LP.
\text{min } ax + by \\
\text{s.t. } a_i x + b_i y \leq \beta_i \quad \forall i \in \{1, \dots, m\} \\
\text{min } y \\
\text{s.t. } y \geq c_i x + d_i \quad \forall i \in I_1 \\
\text{ } \quad y \leq c_i x + d_i \quad \forall i \in I_2 \\
\text{ } \quad L \leq x \leq U
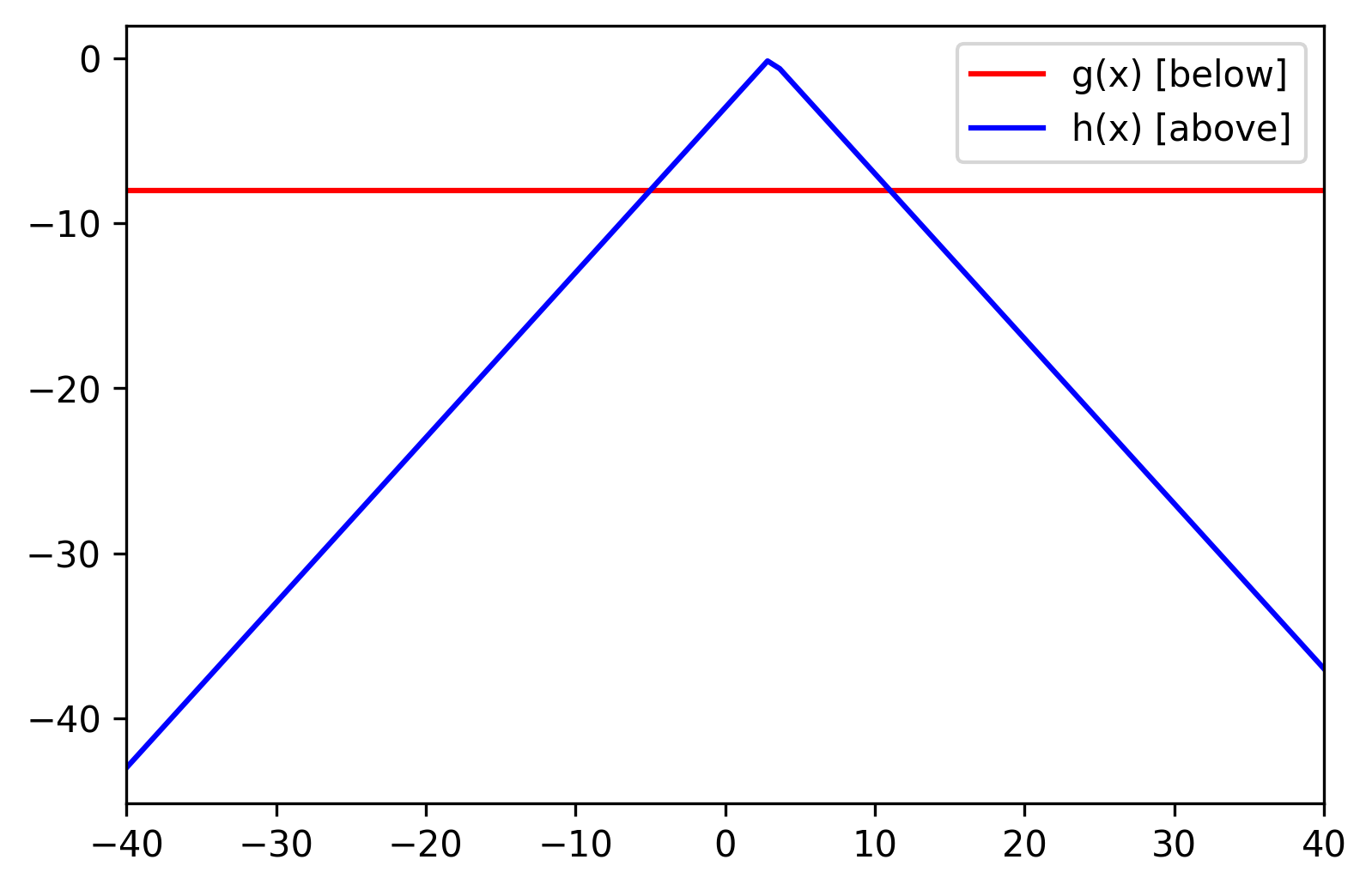
Pruning (Megiddo 1983)
What if taking all the half-plane intersections is overkill?
Now we're just looking for the x* that induces the minimum y-value.
\text{min } y \\
\text{s.t. } y \geq c_i x + d_i \quad \forall i \in I_1 \\
\text{ } \quad y \leq c_i x + d_i \quad \forall i \in I_2 \\
\text{ } \quad L \leq x \leq U
Observation: every x has a tightest upper and lower constraint.
Pruning (Megiddo 1983)
What if taking all the half-plane intersections is overkill?
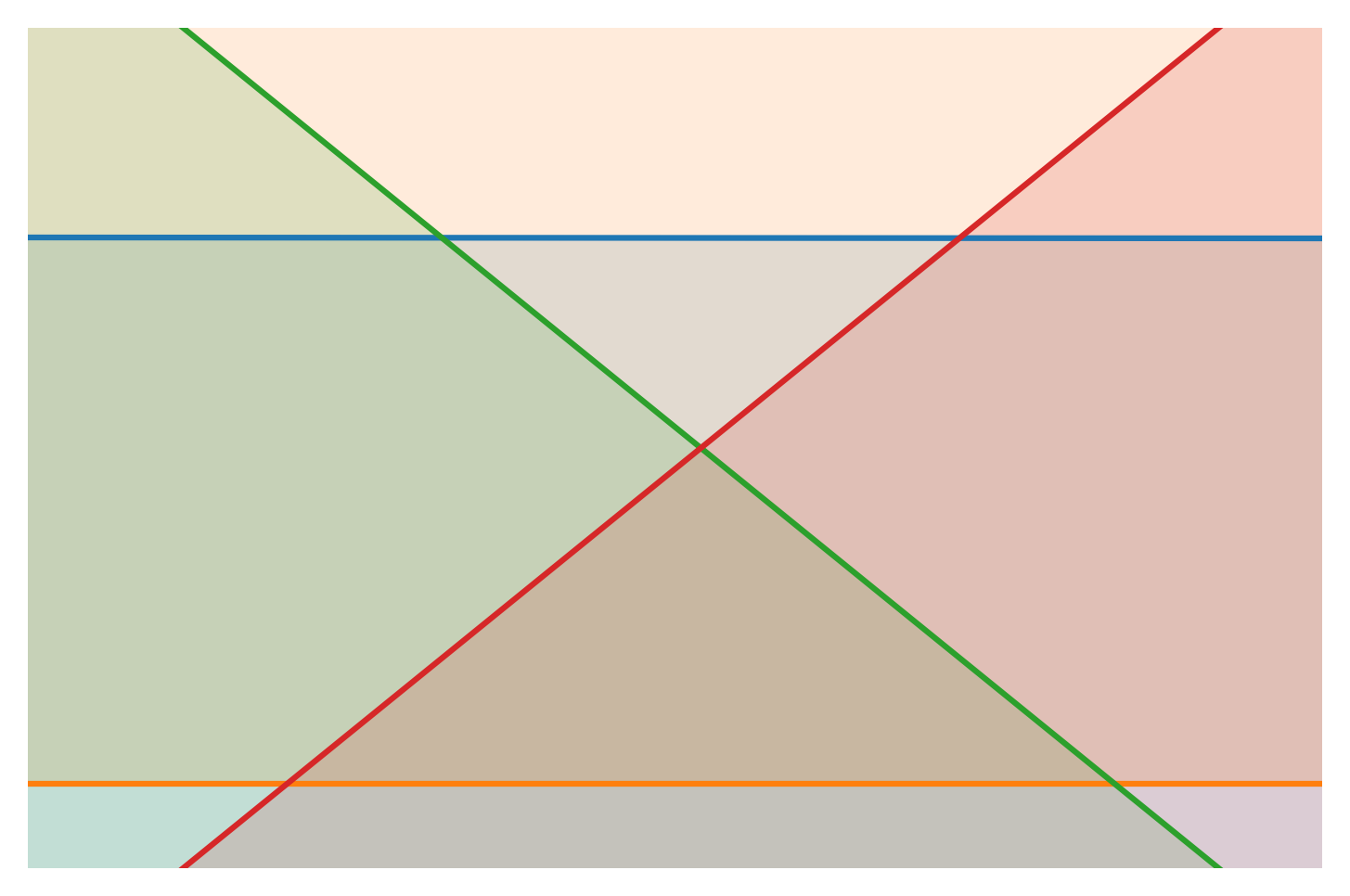
Merge constraints piecewise.
Eliminating constraints
Our goal is to narrow down the range of x-values. First we must find a feasible range; then we must find x* (or determine that the problem is infeasible).
We move along edges of the piecewise constraints and attempt narrow down the range of x-values. The more we narrow down the range, the more constraints we can eliminate.
The algorithm removes approximately n/4 points at each step, yielding an O(n) runtime.
The Megiddo paradigm
Megiddo 1983 solves several related problems in O(n), including the smallest enclosing circle problem. Shamos offers a O(n log n) algorithm for this problem (naively O(n⁴)) using farthest-point Voronoi diagrams.
Code
Low-dimensional linear programming
By Parker Rule
