High-Level GPU Programming with Julia
Peter
The CUDA approach
Introduction
What is GPU
Not for coin

What is GPU
- Graphics Processing Unit
- Designed to rapidly manipulate and alter memory to accelerate the creation of images
- Highly parallel structure
How CPU Draw

How GPU Draw

GPU programming concept
GPu programming concept
- Utilize the parallel structure
- Lots of threads running at the same time
work flow
- GPU memory allocation
- copy data to device
- call kernel
- copy data back to host
- free GPU memory
<- I'm parallel!
How gpu programming looks like in other language
CUDA C/c++
__global__ void vec_add(float *C, float *A, float *B)
{
int i = threadIdx.x;
if (i < N)
C[i] = A[i] + B[i];
}
int main(){
size_t size = N * sizeof(float);
float *dA;
cudaMalloc((void **)&dA, size);
float *dB;
cudaMalloc((void **)&dB, size);
float *dC;
cudaMalloc((void **)&dC, size);
cudaMemcpy(dA, hA, size, cudaMemcpyHostToDecvice);
cudaMemcpy(dB, hB, size, cudaMemcpyHostToDecvice);
vec_add<<<1, N>>>(dC, dA, dB);
cudaMemcpy(hC, dC, size, cudaMemcpyDeviceToHost);
cudaFree(dA);
cudaFree(dB);
cudaFree(dC);
return 0;
}Python
PyCUDA
import pycuda.autoinit
import pycuda.driver as drv
import numpy
from pycuda.compiler import SourceModule
mod = SourceModule("""
__global__ void vec_add(float *c, float *a, float *b)
{
const int i = threadIdx.x;
c[i] = a[i] * b[i];
}
""")
vec_add = mod.get_function("vec_add")
a = numpy.random.randn(400).astype(numpy.float32)
b = numpy.random.randn(400).astype(numpy.float32)
dest = numpy.zeros_like(a)
vec_add(
drv.Out(dest), drv.In(a), drv.In(b),
block=(400,1,1), grid=(1,1))
why Julia
why Julia
-
High-level programming language
with low-level performance -
Provides a first-class array implementation
-
Good compiler design
High-level programming language with low-level performance
No need to worry about the non-gpu part is too slow
Provides a first-class array implementation
No more reimplementation on array/tensor type
Good compiler design
Allow us to compile native julia code into gpu code
Julia over GPU
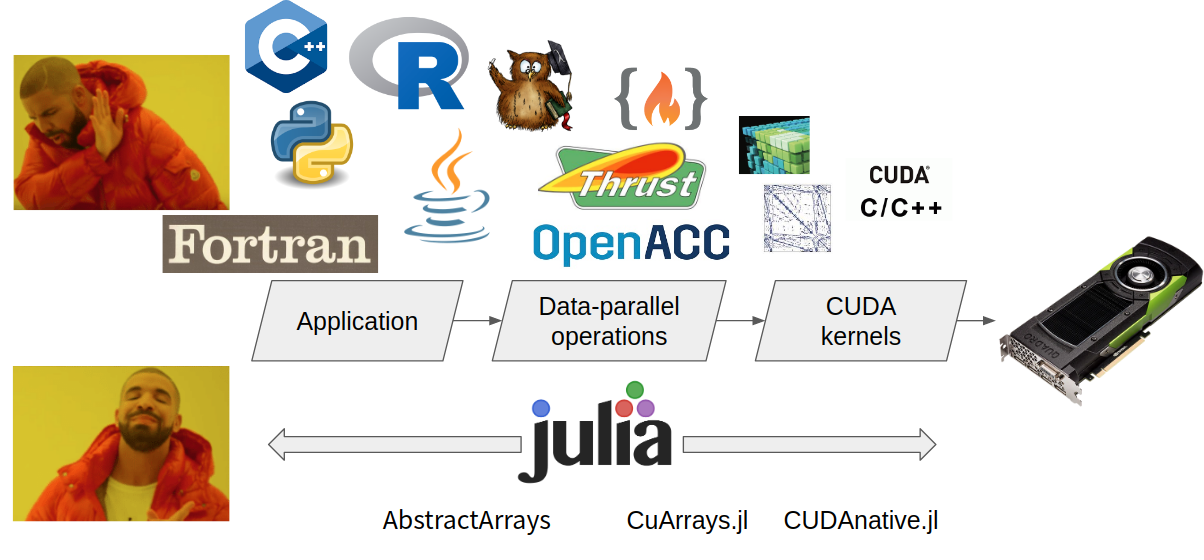
Basic gpu programming
Kernel
- Code that run on GPU
- Execute on multiple GPU threads
writing a kernel
- pick a function you want to parallelize
- Split the workload into several subset
- Let each thread do the subset
Example
function serial_vec_add(C, A, B)
for i ∈ 1:length(C)
C[i] = A[i] + B[i]
end
end
function parallel_vec_add(C, A, B)
i = threadIdx().x
C[i] = A[i] + B[i]
end
# or
function parallel_vec_add(C, A, B)
i = threadIdx().x + (blockIdx().x - 1) * blockDim().x
if i < length(C)
C[i] = A[i] + B[i]
end
end
threads & blocks

Threads & Blocks
- hardware dependent numbers of threads & blocks
-
each threads/blocks can be organized as 1/2/3 dimension grid
- e.g. 32 threads can be (4, 8) or (4,4,2)
gpu programming in julia
Packages
-
CUDAnative.jl
- Support for compiling and executing native Julia kernels on CUDA hardware.
-
CUDAdrv.jl
- wrapper for the CUDA driver API.
-
CuArrays.jl
- provides a fully-functional GPU array.
-
GPUArrays.jl
- AbstractArray API for GPU
- see https://github.com/JuliaGPU for other packages
GPU hello world
using CUDAnative
# hello world kernel
function greeting()
@cuprintf("This is block %ld, thread %d speaking: hello\n",
blockIdx().x, threadIdx().x)
return
end
function helloGPU(blocks::Int, threads::Int)
@cuda blocks=blocks threads=threads greeting()
return
end
# 2d block/thread version
function greeting2d()
@cuprintf("This is block (%ld, %ld), thread (%ld, %ld) speaking: hello\n",
blockIdx().x, blockIdx().y, threadIdx().x, threadIdx().y)
return
end
function helloGPU(blocks::Tuple, threads::Tuple)
@cuda blocks=blocks threads=threads greeting2d()
return
end
helloGPU(3, 5) #say hello to 3 blocks with 5 threads, total 15 hello
helloGPU((2,2), (3,3)) #say hello to 2x2 blocks with 3x3 threads, total 36 hello
High level gpu programming
- With CuArrays.jl we can really use GPU without any GPU knowledges.
- Also support custom type.
gpu unaware code on gpu
w = randn(5,5)
b = randn(5)
x = randn(5,3)
linear(w,x,b) = w * x .+ b
dw = cu(w)
dx = cu(x)
db = cu(b)
linear(w,x,b)
linear(dw,dx,db)
struct Point{T<:Number}
x::T
y::T
end
import Base: *, +, adjoint
function Base.:*(a::Point{T}, b::Point{T}) where T
Point{T}(a.x * b.y + a.y * b.x, a.x * b.x + a.y * b.y)
end
Base.:(+)(p1::Point, p2::Point) = Point(p1.x + p2.x, p1.y + p2.y)
adjoint(a::Point) = a
a = [Point(randn(2)...) for i = 1:10]
b = [Point(randn(2)...) for i = 1:10]
a * b'
cu(a) * cu(b)'gpu kernel example
- matmul
- conv
- gather
matmul
function cpu_matmul(C, A, B)
for i ∈ 1:size(A, 1)
for j ∈ 1:size(B, 2)
for k ∈ 1:size(A, 2)
C[i, j] += A[i, k] * B[k, j]
end
end
end
C
end
matmul
using CuArrays
function matmul_kernel(C, A, B)
i = threadIdx().x + (blockIdx().x - 1) * blockDim().x
j = threadIdx().y + (blockIdx().y - 1) * blockDim().y
if i <= size(A, 1) && j <= size(B, 2)
for k ∈ 1:size(A, 2)
C[i, j] += A[i, k] * B[k, j]
end
end
return
end
function gpu_matmul(C, A, B)
max_threads = 256
threads_x = min(max_threads, size(C,1))
threads_y = min(max_threads ÷ threads_x, size(C,2))
threads = (threads_x, threads_y)
blocks = ceil.(Int, (size(C,1), size(C,2)) ./ threads)
@cuda blocks=blocks threads=threads matmul_kernel(C, A, B)
C
end
a = cu(randn(3,5)); b = cu(randn(5,3); c = cu(zeros(3,3))
gpu_matmul(c, a, b)
#or @cuda threads=(3,3) matmul_kernel(c, a, b)
#or wasted ver.
# @cuda threads=(2,2) blocks=(2, 2) matmul_kernel(c, a, b)
Conv2d

Conv2d
function naive_conv2d_kernel(y, x, k)
i = threadIdx().x + (blockIdx().x - 1) * blockDim().x
j = threadIdx().y + (blockIdx().y - 1) * blockDim().y
if i <= size(y, 1) && j <= size(y, 2)
for k1 ∈ 1:size(k, 1)
if i + k1 - 1 <= size(x, 1)
for k2 ∈ 1:size(k, 2)
if j + k2 - 1 <= size(x, 2)
y[i,j] += x[i+k1-1, j+k2-1] * k[k1, k2]
end
end
end
end
end
end
function gpu_naive_conv2d(C, A, B)
max_threads = 256
threads_x = min(max_threads, size(C,1))
threads_y = min(max_threads ÷ threads_x, size(C,2))
threads = (threads_x, threads_y)
blocks = ceil.(Int, (size(C,1), size(C,2)) ./ threads)
@cuda blocks=blocks threads=threads naive_conv2d_kernel(C, A, B)
C
end
x = cu(reshape(collect(1:25), 5,5));
k = cu(reshape(collect(1:9), 3,3)) ;
y = cu(zeros(5,5))
gpu_naive_conv2d(cy, cx, ck) gather
function gather(w::CuMatrix{T}, xs::CuArray{Int}) where T
ys = CuArray{T}(undef, size(w, 1), size(xs)...)
function kernel!(ys::CuDeviceArray{T}, w::CuDeviceArray{T}, xs)
li = threadIdx().y + (blockIdx().y - 1) * blockDim().y
i = threadIdx().x + (blockIdx().x - 1) * blockDim().x
@inbounds if li <= length(xs)
ind = Tuple(CartesianIndices(xs)[li])
ys[i, ind...] = w[i, xs[li]]
end
return
end
max_threads = 256
threads_x = min(max_threads, size(ys,1))
threads_y = min(max_threads ÷ threads_x, length(xs))
threads = (threads_x, threads_y)
blocks = ceil.(Int, (size(ys,1), length(xs)) ./ threads)
CuArrays.@cuda blocks=blocks threads=threads kernel!(ys, w, xs)
return ys
end
w = cu(randn(10,10))
ind = CuArray(rand(1:10, 3,5))
gather(w, ind)Tools
profiling with nvprof
using CUDAdrv
x = cu(randn(3,5)); y = cu(randn(5,4)); z = cu(zeros(3,4))
CUDAdrv.@profile gpu_matmul(z, x, y)
#run with $ nvprof --profile-from-start off /path/to/julia file.jl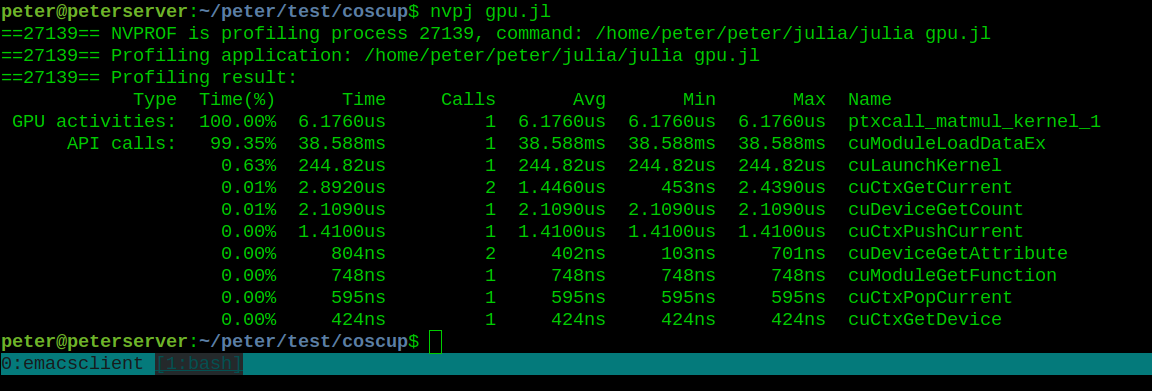
what get compiled
@device_code_typed @cuda matmul_kernal(z, x, y)
@device_code_llvm gpu_matmul(z, x, y)
@device_code_sass gpu_matmul(z, x, y)
@device_code_ptx @cuda greeting()
Conclusion
Reference
HIGH-LEVEL GPU PROGRAMMING WITH JULIA
By Peter Cheng
HIGH-LEVEL GPU PROGRAMMING WITH JULIA
The CUDA approach
- 2,056



