Intro to Zygote.jl

Peter

21st Century AD Technique

What is AD

Automatic/Algorithmic Differentiation

Automatic Differentiation

  • One way to compute derivative
  • Core technique of modern ML/DL optimization

How AD work

How AD work

  • Wengert List (Tape/Graph)
  • Derivative Definition
  • Chain Rules

Derivative Definition

Chain Rules

Wengert List

  • A list of expression/instruction
  • Transform the expression with derivative definition

Wengert List

f(x) = 5sin(log(x)) \\\\ \text{Wengert List of}\ f\\ y1 = log(x) \\ y2 = sin(y1) \\ y3 = 5 * y2 \\

Wengert List

f'(x) = \frac{d}{dx}f(x) = \frac{5\cos(\log(x))}{x}\\ \text{Wengert List of}\ f'\\ dy1 = 1 / x \\ dy2 = cos(y1) \\ dy3 = dy2 * dy1 \\ dy4 = 5 * dy3 \\

Wengert List

\frac{d}{dx}f(x) = \frac{5\cos(\log(x))}{x}\\ \text{Wengert List of}\ f'\\ dy1 = 1 / x \\ dy2 = cos(y1) \\ dy3 = dy2 * dy1 \\ dy4 = 5 * dy3 \\
f(x) = 5sin(log(x)) \\\\ \text{Wengert List of}\ f\\ y1 = log(x) \\ y2 = sin(y1) \\ y3 = 5 * y2 \\

How AD work

  1. Get the Wengert List of the given expression
  2. Transform each instruction in the Wengert List
  3. Apply Chain rule

Different Types of AD

Different Types of AD

  • Forward mode
  • Reverse mode
  • Mix mode
  • ...

Forward mode

  • Dual number
  • chain rule multiplication start from the input (dy1/dx * dy2/dy1)
  • computational efficiency on multivariable differentiation with more output than input

Reverse mode

  • Tracker
  • Chain rule multiplication start from the output (dy/dy2 * dy2/dy1)
  • computational efficiency on multivariable differentiation with more input than output

 DL situation!!

Dual Number

struct Dual{T<:Real} <: Real
  x::T
  ϵ::T
end

import Base: +, -, *, /
a::Dual + b::Dual = Dual(a.x + b.x, a.ϵ + b.ϵ)
a::Dual - b::Dual = Dual(a.x - b.x, a.ϵ - b.ϵ)
a::Dual * b::Dual = Dual(a.x * b.x, b.x * a.ϵ + a.x * b.ϵ)
a::Dual / b::Dual = Dual(a.x * b.x, b.x * a.ϵ - a.x * b.ϵ)

Base.sin(d::Dual) = Dual(sin(d.x), d.ϵ * cos(d.x))
Base.cos(d::Dual) = Dual(cos(d.x), - d.ϵ * sin(d.x))
Base.log(d::Dual) = Dual(log(d.x), d.ϵ / d.x)

Base.convert(::Type{Dual{T}}, x::Dual) where T = Dual(convert(T, x.x), convert(T, x.ϵ))
Base.convert(::Type{Dual{T}}, x::Real) where T = Dual(convert(T, x), zero(T))
Base.promote_rule(::Type{Dual{T}}, ::Type{R}) where {T,R} = Dual{promote_type(T,R)}

D(f, x) = f(Dual(x, one(x))).ϵ

f(x) = 5*sin(log(x))
df(x) = 5*cos(log(x))/x

D(f, 3.) == df(3.)

Tracker

  • Record every operation on variables to Wengert List
  • Derive the Wengert List w.r.t. given variable
  • Static graph -> build Wengert List one time
  • Dynamic graph -> build Wengert List every time

<- TensorFlow

Pytorch, ->

 eager mode

Where is the Wengert List in Forward mode?

Wengert underneath Dual Number

julia> @code_warntype f(3.)
Body::Float64
1 ─ %1 = invoke Main.log(_2::Float64)::Float64
│   %2 = invoke Main.sin(%1::Float64)::Float64
│   %3 = (Base.mul_float)(5.0, %2)::Float64
└──      return %3

julia> @code_warntype D(f, 3)
Body::Float64
1 ─ %1  = (Base.sitofp)(Float64, x)::Float64
│   %2  = invoke Base.Math.log(%1::Float64)::Float64
│   %3  = (Base.sitofp)(Float64, 1)::Float64
│   %4  = (Base.sitofp)(Float64, x)::Float64
│   %5  = (Base.div_float)(%3, %4)::Float64
│   %6  = invoke Main.sin(%2::Float64)::Float64
│   %7  = invoke Main.cos(%2::Float64)::Float64
│   %8  = (Base.mul_float)(%5, %7)::Float64
│   %9  = (Base.mul_float)(%6, 0.0)::Float64
│   %10 = (Base.mul_float)(5.0, %8)::Float64
│   %11 = (Base.add_float)(%9, %10)::Float64
└──       return %11

Wengert underneath Dual Number

julia> @code_warntype f(3.)
Body::Float64
1 ─ %1 = invoke Main.log(_2::Float64)::Float64
│   %2 = invoke Main.sin(%1::Float64)::Float64
│   %3 = (Base.mul_float)(5.0, %2)::Float64
└──      return %3

julia> @code_warntype D(f, 3)
Body::Float64
1 ─ %1  = (Base.sitofp)(Float64, x)::Float64
│   %2  = invoke Base.Math.log(%1::Float64)::Float64
│   %3  = (Base.sitofp)(Float64, 1)::Float64
│   %4  = (Base.sitofp)(Float64, x)::Float64
│   %5  = (Base.div_float)(%3, %4)::Float64
│   %6  = invoke Main.sin(%2::Float64)::Float64
│   %7  = invoke Main.cos(%2::Float64)::Float64
│   %8  = (Base.mul_float)(%5, %7)::Float64
│   %9  = (Base.mul_float)(%6, 0.0)::Float64
│   %10 = (Base.mul_float)(5.0, %8)::Float64
│   %11 = (Base.add_float)(%9, %10)::Float64
└──       return %11
\text{Wengert List of}\ f'\\ y1 = log(x) \\ dy1 = 1 / x \\ dy2 = cos(y1) \\ dy3 = dy2 * dy1 \\ dy4 = 5 * dy3 \\

Why Julia

Why Julia

  • Fast
  • really good compiler design

Zygote.jl

Zygote.jl

  • Source to source AD
  • support control flow, recursion, closures, structs, dictionaries, ...

Zygote.jl

julia> using Zygote

julia> f(x) = 5x + 3

julia> f(10), f'(10)
(53, 5)

julia> @code_llvm f'(10)
define i64 @"julia_#625_38792"(i64) {
top:
  ret i64 5
}

Zygote.jl

julia> f(x) = 5*sin(log(x))
f (generic function with 1 method)
                         
julia> f'                                              
#34 (generic function with 1 method)
                                         
julia> f'(3.)                  
0.7580540380443495                       
                                                           
julia> @code_llvm f'(3.)  
define double @"julia_#34_13685"(double) {
top:
  %1 = call double @julia_log_4663(double %0)
  %2 = call double @julia_sin_13686(double %1)
  %3 = call double @julia_cos_13689(double %1)
  %4 = fmul double %3, 5.000000e+00
  %5 = fdiv double 1.000000e+00, %0
  %6 = fmul double %5, %4
  ret double %6
}

julia> @code_native f'(3.)
...

Zygote.jl

julia> f(x) = 5*sin(log(x))
f (generic function with 1 method)
                         
julia> f'                                              
#34 (generic function with 1 method)
                                         
julia> f'(3.)                  
0.7580540380443495                       
                                                           
julia> ddf(x) = -(5(sin(log(x)) + cos(log(x))))/x^2
ddf (generic function with 1 method)

julia> ddf(3.)
-0.7474497024968649

julia> (f')'(3.)
-0.7474497024968648

Zygote.jl

julia> fs = Dict("sin" => sin, "cos" => cos, "tan" => tan);

julia> gradient(x -> fs[readline()](x), 1)
sin
0.5403023058681398

julia> function pow(x::T, n::Int) where T
           r = 1::T
           while n > 0
               n -= 1
               r *= x
           end
           return r
       end
pow (generic function with 1 method)

julia> g(x) = pow(x, 5)
g (generic function with 1 method)

julia> g'(2)
80

julia> gradient(pow, 2, 5)
(80, nothing)

Zygote.jl

julia> using Zygote: @adjoint

julia> add(a, b) = a + b

julia> @adjoint add(a, b) = add(a, b), Δ -> (Δ, Δ)

Source to Source AD

Source-to-source AD

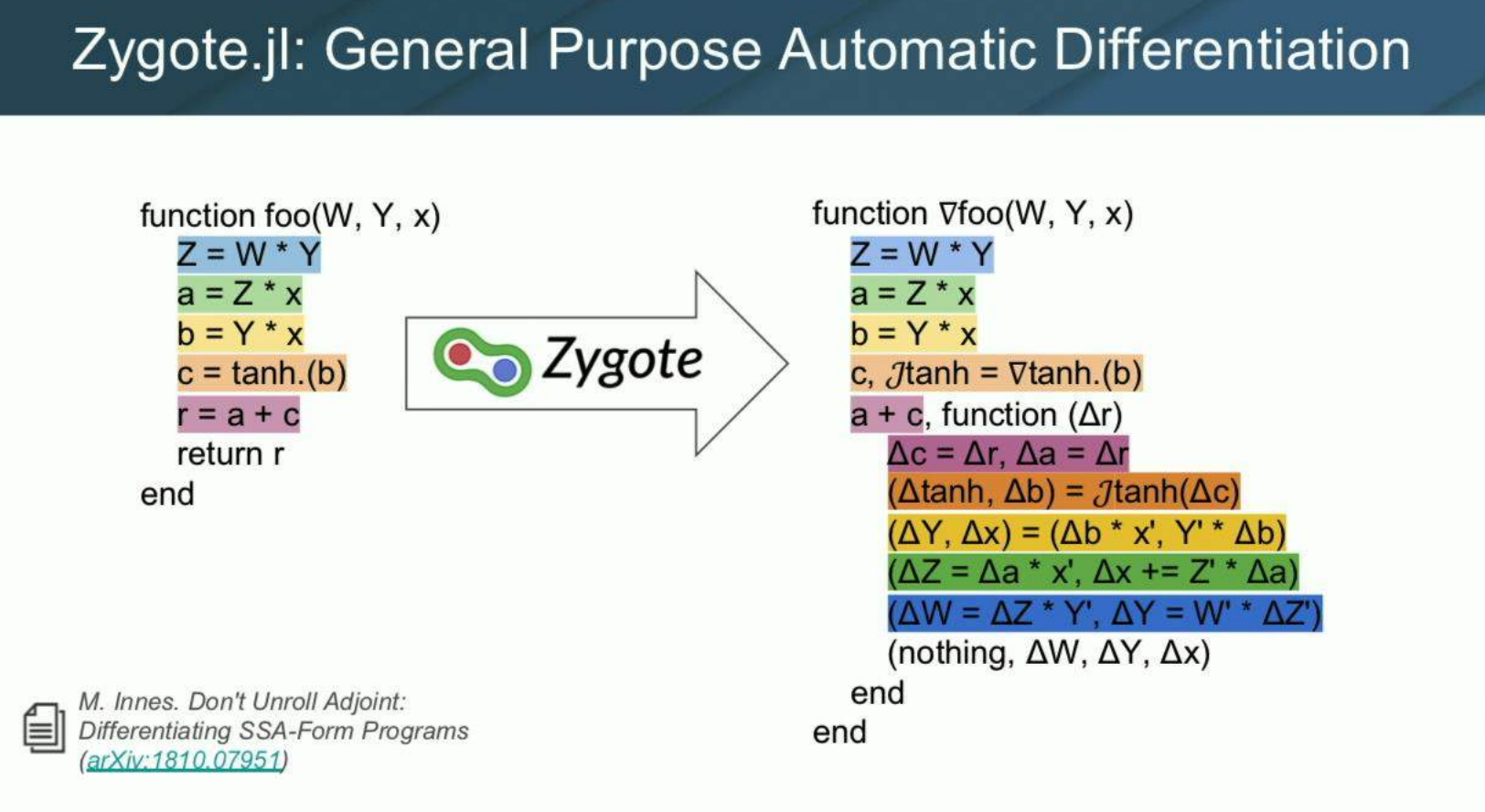
https://www.microsoft.com/en-us/research/uploads/prod/2019/06/Models-as-Code-Differentiable-Programming-with-Zygote-slides.pdf

Differentiate SSA Form

Julia Compile Process

http://blog.rogerluo.me/2019/07/27/yassad/

SSA From

  • Static Single Assignment Form
  • All the variable will only be assigned once
  • Most variable comes from function calls
  • All the control flows become branches

SSA Form

https://arxiv.org/pdf/1810.07951.pdf

Not just Unroll control flow

function grad_pow(x, n)
    r = 1
    Bs = Tuple{Int, Int}[]
    while n > 0
        push!(Bs, (r, x))
        r *= x
        n -= 1
    end
    dx = 0
    dr = 1
    for i = length(Bs):-1:1
        (r, x) = Bs[i]
        dx += dr*r
        dr = dr*x
    end
    return dx
end
function pow(x, n)
    r = 1
    while n > 0
        n -= 1
        r *= x
    end
    return r
end

Zygote

Zygote

  • Compile every Julia function into differentiable
  • Easy to add gradient hook
  • Differentiable Programming!!

Differentiable Programming

https://fluxml.ai/2019/03/05/dp-vs-rl.html

Zygote + Pytorch

https://www.youtube.com/watch?v=OcUXjk7DFvU&t=839s

Zygote + XLA.jl

https://arxiv.org/pdf/1810.09868.pdf

Conclusion

Reference

Intro to Zygote.jl

By Peter Cheng

Made with Slides.com

Intro to Zygote.jl

21st Century AD Technique

  • 1,912

More from Peter Cheng