Super-efficiency of automatic differentiation for functions defined as a minimum
Pierre Ablin\(^1\), Gabriel Peyré\(^1\), Thomas Moreau\(^2\)
1: ENS and CNRS, PSL university 2: Inria and CEA
Context
Context: computing the gradient of a minimum
- Let \(\mathcal{L}(z, x)\) a smooth function where \(z\in \mathbb{R}^m\) and \(x\in\mathbb{R}^n\), and
$$\boxed{\ell(x) = \min_z \mathcal{L}(z, x)}$$
- We want to compute \(\nabla \ell(x)\)
Examples: min-min optimization
- Dictionary learning
- Alternate optimization
- Frechet means
max-min optimization
- Game theory
- GANs
Technical assumptions
- \(\ell(x) = \min_z \mathcal{L}(z, x)\), we want to compute \(\nabla \ell(x)\)
We assume:
- For all \(x\), \(\mathcal{L}\) has a unique minimizer \(z^*(x)=\arg\min_z \mathcal{L}(z, x)\)
$$\ell(x) = \mathcal{L}(z^*(x), x)$$
- \(x\to z^*(x) \) is differentiable
Consequence (Danskin):
\nabla \ell(x) = \frac{\partial}{\partial x} \left[\mathcal{L}(z^*(x), x)\right]
\nabla \ell(x) = \frac{\partial z^*}{\partial x} \nabla_1\mathcal{L}(z^*(x), x) + \nabla_2 \mathcal{L}(z^*(x), x)
\boxed{\nabla \ell(x) = \nabla_2 \mathcal{L}(z^*(x), x)}
\nabla_1 \mathcal{L}(z^*(x), x) = 0
\nabla \ell(x) = \frac{\partial z^*}{\partial x} \underbrace{\nabla_1\mathcal{L}(z^*(x), x)}_{=0} + \nabla_2 \mathcal{L}(z^*(x), x)
Approximate optimization
- \(\ell(x) = \min_z \mathcal{L}(z, x)\), we want to compute \(\nabla \ell(x)\)
-No closed-form: We assume that we only have access to a sequence \(z_t\) such that \(z_t \to z^*\)
Example: \(z_t\) produced by gradient descent on \(\mathcal{L}\)
- \(z_0 = 0\)
- \(z_{t+1} = z_t - \rho \nabla_1 \mathcal{L}(z_t, x)\)
- \(z_t\) depends on \(x\): \(z_t(x)\)
How can we approximate \(\nabla \ell(x)\) using \(z_t(x)\) ? At which speed ?
The analytic estimator
g^1_t(x) = \nabla_2 \mathcal{L}(z_t(x), x)
Very simple to compute: simply plug \(z_t\) in \(\nabla_2 \mathcal{L}\) !
\nabla \ell(x) = \nabla_2 \mathcal{L}(z^*(x), x)
z_t(x) \to z^*(x)
The automatic estimator
g^2_t(x) = \frac{\partial}{\partial x}\left[\mathcal{L}(z_t(x), x)\right]
\(g^2_t\) is computed by automatic differentiation:
\nabla \ell(x) = \nabla_2 \mathcal{L}(z^*(x), x)
z_t(x) \to z^*(x)
g^2_t(x) = \frac{\partial z_t}{\partial x} \underbrace{\nabla_1\mathcal{L}(z_t(x), x)}_{\neq 0} + \nabla_2 \mathcal{L}(z_t(x), x)
- Easy to code (e.g. in Python, use pytorch, tensorflow, autograd...)
- \(\sim\) as costly to compute as \(z_t\)
- Memory cost linear with # iterations
The implicit estimator
\nabla \ell(x) = \nabla_2 \mathcal{L}(z^*(x), x)
z_t(x) \to z^*(x)
Implicit function theorem:
\frac{\partial z^*(x)}{\partial x} = \mathcal{J}(z^*(x), x)
\mathcal{J}(z, x) = - \nabla_{21} \mathcal{L}(z, x)\left[\nabla_{11}\mathcal{L}(z, x)\right]^{-1}
g^3_t(x) = \mathcal{J}(z_t(x), x) \nabla_1\mathcal{L}(z_t(x), x) + \nabla_2 \mathcal{L}(z_t(x), x)
- Need to invert a linear system: might be too costly to compute
Three gradient estimators
\nabla \ell(x) = \nabla_2 \mathcal{L}(z^*(x), x)
z_t(x) \to z^*(x)
- Analytic: \(g^1_t(x) = \nabla_2 \mathcal{L}(z_t(x), x)\)
- Automatic: \(g^2_t(x) = \frac{\partial z_t}{\partial x} \nabla_1\mathcal{L}(z_t(x), x) + \nabla_2 \mathcal{L}(z_t(x), x)\)
- Implicit: \(g^3_t(x) = \mathcal{J}(z_t(x), x) \nabla_1\mathcal{L}(z_t(x), x) + \nabla_2 \mathcal{L}(z_t(x), x)\)
These estimators are all "consistent":
If \(z_t(x)= z^*(x)\)
\boxed{g^1_t(x) = g^2_t(x) = g^3_t(x) = \nabla \ell(x)}
Convergence speed of the estimators
Toy example (regularized logistic regression)
- \(D\) rectangular matrix
- \(\mathcal{L}(z, x) = \sum_{i=1}^n\log\left(1 + \exp(-x_i[Dz]_i)\right) + \frac{\lambda}{2}\|z\|^2\)
- \(z_t\) produced by gradient descent
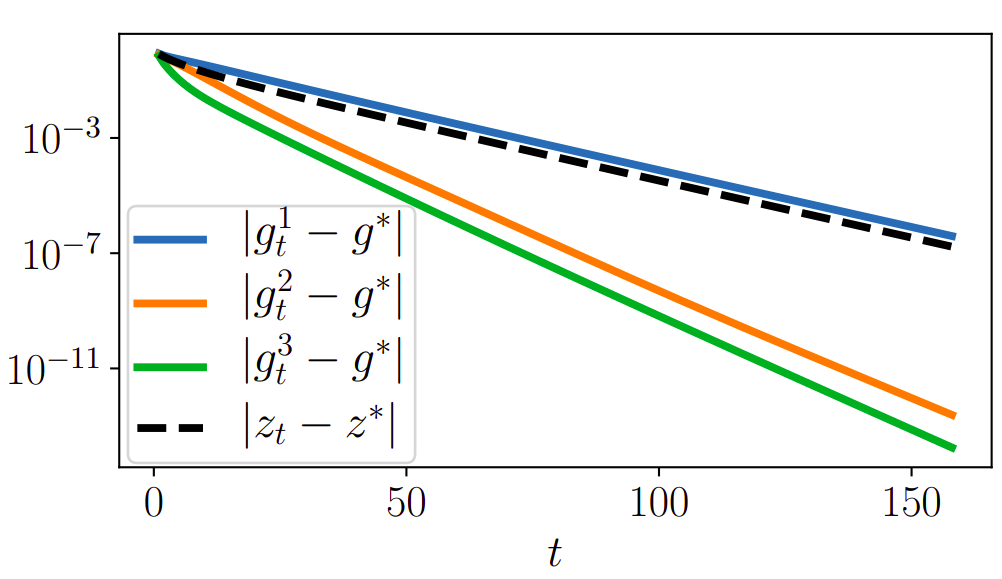
Implicit estimator
g^1_t(x) = \nabla_2 \mathcal{L}(z_t(x), x)
If \(\nabla_2 \mathcal{L} \) is \(L\)-Lipschitz:
|g^1_t(x) - \nabla \ell(x)| \leq L |z_t(x) - z^*(x)|
- The implicit estimator converges at the same speed as \(z_t\)
Automatic estimator
g^2_t(x) = \frac{\partial z_t}{\partial x} \nabla_1\mathcal{L}(z_t(x), x) + \nabla_2 \mathcal{L}(z_t(x), x)
It is of the form \(g^2_t(x) = J \nabla_1 \mathcal{L}(z_t, x) + \nabla_2 \mathcal{L}(z_t, x)\), \(J\) rectangular matrix
Taylor expansion around \(z^*\):
\nabla_1\mathcal{L}(z_t, x) = \underbrace{\nabla_1 \mathcal{L}(z^*, x)}_{=0} + \left[\nabla_{11}\mathcal{L}(z^*, x)\right](z_t - z^*) + \underbrace{R_{11}}_{O(|z_t-z^*|^2)}
\nabla_1\mathcal{L}(z_t, x) = \left[\nabla_{11}\mathcal{L}(z^*, x)\right](z_t - z^*) + R_{11}
\nabla_2\mathcal{L}(z_t, x) = \underbrace{\nabla_2 \mathcal{L}(z^*, x)}_{\nabla\ell(x)} + \left[\nabla_{21}\mathcal{L}(z^*, x)\right](z_t - z^*) + \underbrace{R_{21}}_{O(|z_t-z^*|^2)}
\nabla_2\mathcal{L}(z_t, x) = \nabla\ell(x) + \left[\nabla_{21}\mathcal{L}(z^*, x)\right](z_t - z^*) + R_{21}
g^2_t(x) = \nabla \ell(x) + \underbrace{\left(J \nabla_{11}\mathcal{L}(z^*, x) + \nabla_{21}\mathcal{L}(z^*, x)\right)}_{R(J)}(z_t -z^*) + R_{21} + JR_{11}
g^2_t(x) = \nabla \ell(x) + R(J)(z_t - z^*) + O(|z_t-z^*|^2)
Automatic estimator
g^2_t(x) = \nabla \ell(x) + R(J)(z_t - z^*) + O(|z_t-z^*|^2), \text{ where } J = \frac{\partial z_t}{\partial x}
Implicit function theorem: \(R(J) = J\nabla_{11}\mathcal{L}(z^*, x) + \nabla_{21}\mathcal{L}(z^*, x)\) cancels when \(J = \frac{\partial z^*}{\partial x}\)
If \(\frac{\partial z_t}{\partial x} \to \frac{\partial z^*}{\partial x}\):
|g^2_t(x) -\nabla \ell(x) | = o(|z_t - z^*|)
Super-efficiency: Stricly faster than \(g^1_t\) !
Implicit estimator
|g^3_t(x) -\nabla \ell(x) | =O(|z_t - z^*|^2)
Twice as fast as \(g^1_t\) !
g^3_t(x) = \nabla \ell(x) + R(J)(z_t - z^*) + O(|z_t-z^*|^2)
\text{with } J = \mathcal{J}(z_t, x)= - \nabla_{21}\mathcal{L}(z_t, x)\left[\nabla_{11}\mathcal{L}(z_t, x)\right]^{-1}
If \(\mathcal{J}\) is Lipschitz w.r.t. \(z\):
Example
Gradient descent in the strongly convex case
Assumptions and reminders
-We assume that \(\mathcal{L}\) is \(\mu\)-strongly convex and \(L\)-smooth w.r.t. \(z\) for all \(x\).
- \(z_t\) produced by gradient descent with step \(1/L\):
\(z_{t+1} = z_t - \frac1L \nabla_1\mathcal{L}(z_t, x)\)
Linear convergence:
\boxed{|z_t - z^*| \leq \kappa^t |z_0 - z^*|}\enspace, \enspace \kappa = (1 - \frac{\mu}{L})
Convergence of the jacobian
\(z_{t+1} = z_t - \frac1L \nabla_1\mathcal{L}(z_t, x)\)
Let \(J_t =\frac{\partial z_t}{\partial x}\) :
\(J_{t+1} =J_t - \frac1L \left(J_t\nabla_{11}\mathcal{L}(z_t, x) + \nabla_{21}\mathcal{L}(z_t, x)\right) \)
[Gilbert, 1992]:
\boxed{\|J_t - \frac{\partial z^*} {\partial x}\| = O(t\kappa^{t})}
Convergence speed of the estimators
\|J_t - \frac{\partial z^*} {\partial x}\| = O(t\kappa^{t})
|z_t - z^*\| = O(\kappa^{t})
|g^1_t(x)- \nabla\ell(x)| = O(\kappa^{t})
|g^2_t(x)- \nabla\ell(x)| = O(t\kappa^{2t})
|g^3_t(x)- \nabla\ell(x)| = O(\kappa^{2t})
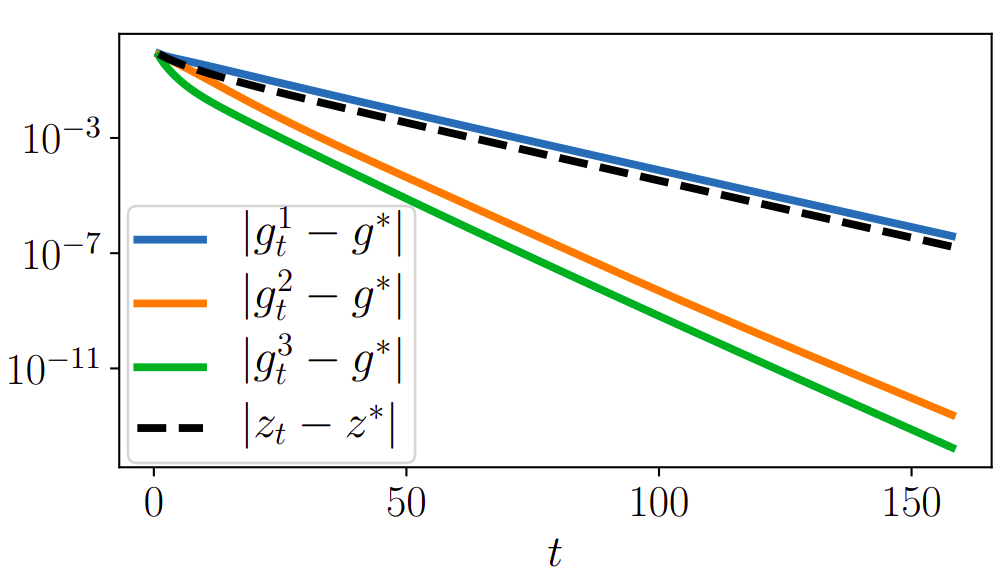
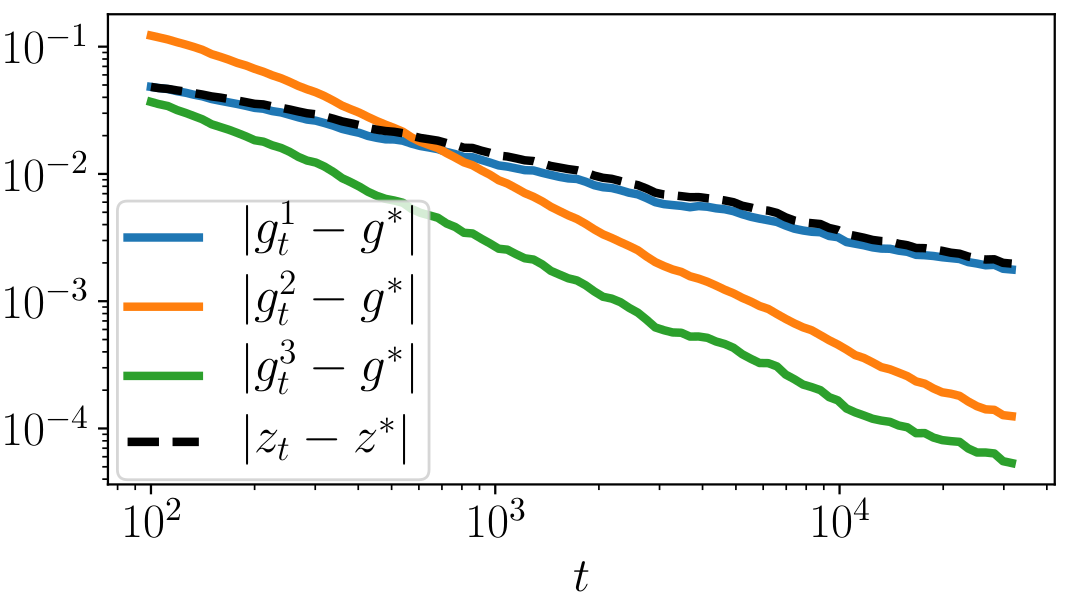
In the paper...
- Analysis in stochastic gradient descent case with step \(\propto t^{-\alpha}\):
\(|g^1_t - g^*| = O(t^{-\alpha})\), \(|g^2_t - g^*| = O(t^{-2\alpha})\), \(|g^3_t - g^*| = O(t^{-2\alpha})\)
- Consequences on optimization: gradients are wrong, so what?
- Practical guidelines taking time and memory into account
Thanks for you attention !
icml presentation
By Pierre Ablin
