Gravitational Lensing and the Most Powerful Explosions in the Space

Talk for The Astronomy Club, IISER Mohali

March 21, 2023

Kelly et al, 2015

Bending of light due to the gravitational field of massive objects.
Different forms
- Strong gravitational lensing
- Weak gravitational lensing
- Microlensing

Gravitational Lensing

JWST's First Deep Field Image

The Lensing Theory

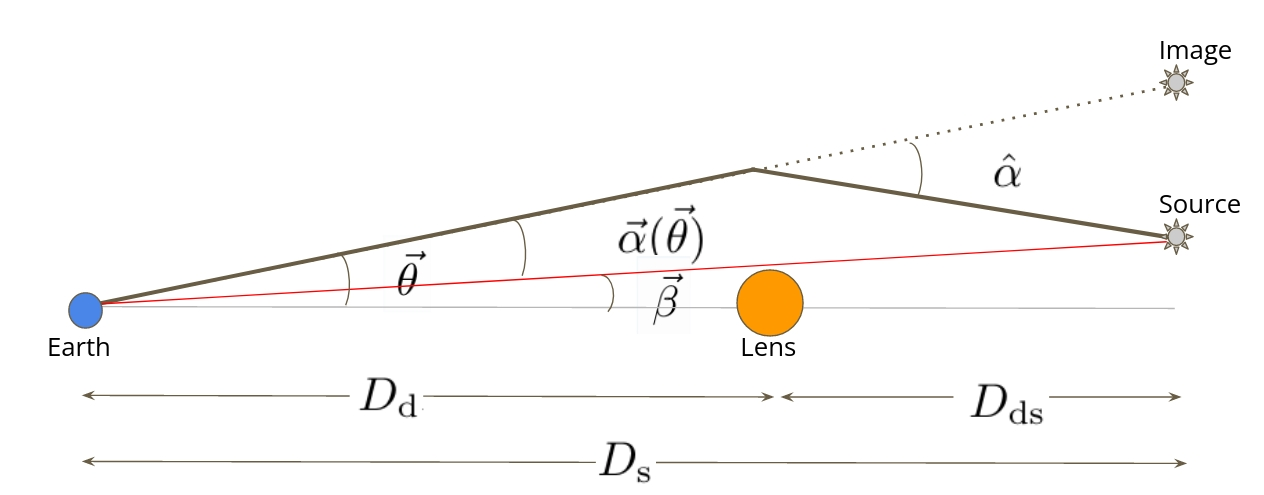
\boldsymbol{\beta} = \boldsymbol{\theta} - \boldsymbol{\alpha}(\boldsymbol{\theta})

Lens Equation

\boldsymbol{\alpha}(\boldsymbol{\theta}) = \frac{D_{ds}}{D_s} \hat{\boldsymbol{\alpha}}(\boldsymbol{\xi}) = \frac{D_{ds}}{D_s} \left[\frac{4G}{c^2}\int D^2_d d^2\boldsymbol{\theta'} \Sigma(D_d\boldsymbol{\theta'}) \frac{D_d (\boldsymbol{\theta}-\boldsymbol{\theta'})}{D^2_d |\boldsymbol{\theta}-\boldsymbol{\theta'}|^2}\right]

The Lensing Theory

\boldsymbol{\beta} = \boldsymbol{\theta} - \boldsymbol{\alpha}(\boldsymbol{\theta})

The Lens Equation

Deflection Angle

\boldsymbol{\alpha}(\boldsymbol{\theta}) = \frac{1}{\pi} \left[\int d^2\boldsymbol{\theta'} \kappa(\boldsymbol{\theta}) \frac{\boldsymbol{\theta}-\boldsymbol{\theta'}}{|\boldsymbol{\theta}-\boldsymbol{\theta'}|^2}\right]

\kappa = \frac{\Sigma}{\Sigma_{crit}}

\Sigma_{crit} = \frac{c^2}{4\pi G} \frac{D_s}{D_{ds}D_d}

where

\boldsymbol{\alpha}(\boldsymbol{\theta}) = \boldsymbol{\nabla}_{\boldsymbol{\theta}}\psi

\nabla^2_{\boldsymbol{\theta}}\psi = 2\kappa

Lensing/Deflection Potential and Fermat Potential

\psi(\boldsymbol{\theta}) = \frac{1}{\pi} \int d^2\boldsymbol{\theta'} \kappa(\boldsymbol{\theta'}) ln|\boldsymbol{\theta}-\boldsymbol{\theta'}|

where, lensing/deflection potential is given as,

\tau(\boldsymbol{\theta}, \boldsymbol{\beta}) = \frac{1}{2} (\boldsymbol{\theta} - \boldsymbol{\beta})^2 - \psi(\boldsymbol{\theta})

and Fermat Potential,

The Fermat principle: The physical light rays are those for which the light travel time is stationary.

\therefore \nabla \tau(\boldsymbol{\theta}, \boldsymbol{\beta}) = 0 \implies \boldsymbol{\beta} = \boldsymbol{\theta} - \boldsymbol{\alpha}(\boldsymbol{\theta})

Physical Interpretation

If the lens equation has more than one solutions for a single value of β then a source at β has images at multiple positions on the sky, leading to multiply lensed source.
This is satisfied if a mass distribution has κ ≥ 1 i.e., Σ ≥ Σcrit. Σcrit serves as characteristic value for the surface mass density that divides between the strong and the weak lenses.
This inversion of the lens equation, to obtain the image positions θ from source position β for multiple images, can be carried out analytically only for very simple mass models of the lens. As the number of images θ for a given source β is not known a priori, a numerical inversion is non-trivial in a general case.

Important Parameters in Lensing

1. Magnification

2. Distortion

Important Parameters in Lensing

1. Magnification

2. Distortion

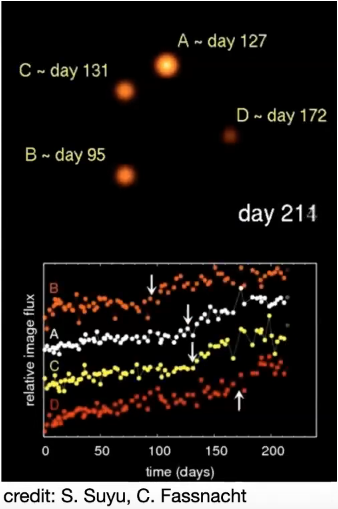
3. Time Delay

Magnification and Distortion

The magnification of each image is related to the Jacobian of the transformation equation.

M(\boldsymbol{\theta}) = |\mathcal{M}(\boldsymbol{\theta})| = \left|\frac{\partial\boldsymbol{\theta}}{\partial\boldsymbol{\beta}}\right|_{\boldsymbol{\theta}}

\mathcal{M}^{-1}(\boldsymbol{\theta}) = \mathcal{A}(\boldsymbol{\theta})= \left( {\begin{array}{cc} 1-\kappa-\gamma_1 & -\gamma_2 \\ -\gamma_2 & 1-\kappa+\gamma_1 \\ \end{array} } \right)

\gamma_1 = \frac{1}{2}(\psi_{11}-\psi_{22}), \gamma_2 = \psi_{12},\kappa = \frac{1}{2}(\psi_{11}+\psi_{22})

\mathcal{A}(\boldsymbol{\theta}) = \left( {\begin{array}{cc} 1-\kappa & 0 \\ 0 & 1-\kappa \\ \end{array} } \right) + \left( {\begin{array}{cc} -\gamma_1 & -\gamma_2 \\ -\gamma_2 & \gamma_1 \\ \end{array} } \right)

\mu = \det \mathcal{M} = \frac{1}{\det \mathcal{A}} = \frac{1}{(1-\kappa)^2 - |\gamma|^2}

where the magnification matrix is given as,

where the magnification matrix can also be written as,

combination of the symmetric magnification and the sheer

The magnification of each image is related to the Jacobian of the transformation equation.

µ = fluxes observed from image/fluxes observed from unlensed source

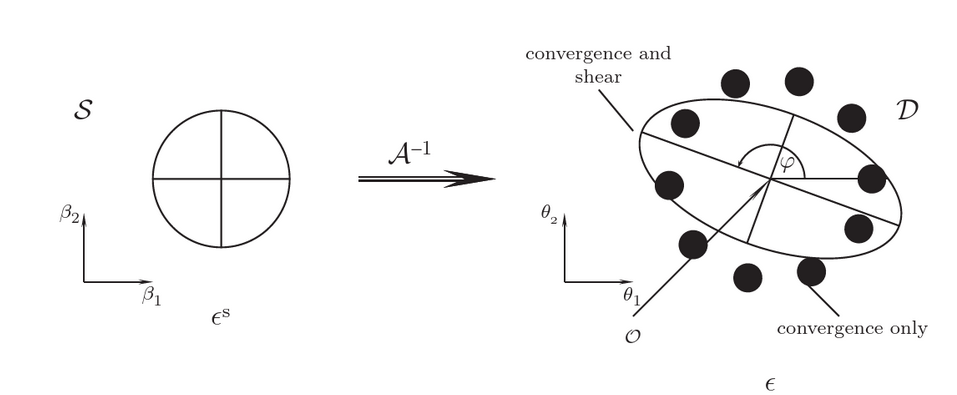
Magnification and Distortion

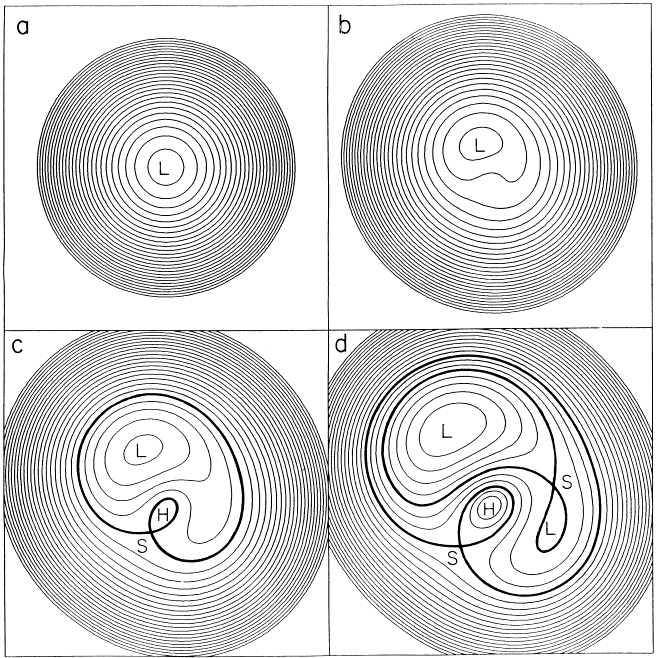
Predicting Multiplicity

Critical Curves in image plane

Extended, elliptical lens

Joachim Wambsganss, 1998 + Narayan and Bartelmann, 1998

Caustics in source plane

\det \mathcal{A}(\boldsymbol{\theta})= 0

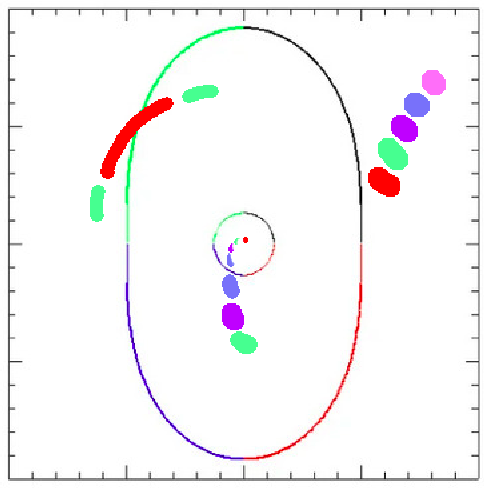
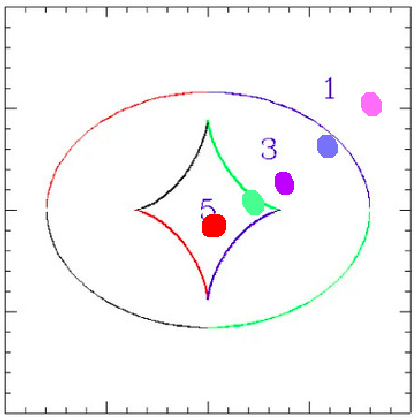
curves

When the source position crosses a caustic, a pair of images is either created or destroyed near the corresponding critical curve on the lens plane, depending on the direction of crossing.
The inner side of a caustic produces a pair of images with very high and nearly equal magnification on either side of the critical curve, in addition to any other images.
The magnification changes sign at the critical curve.

\nabla_{\tau}(\boldsymbol{\theta}, \boldsymbol{\beta}) = 0

Based on the eigenvalues of the Jacobian A, the lensed images can be divided into three types

contours

Blandford and Narayan, 1986

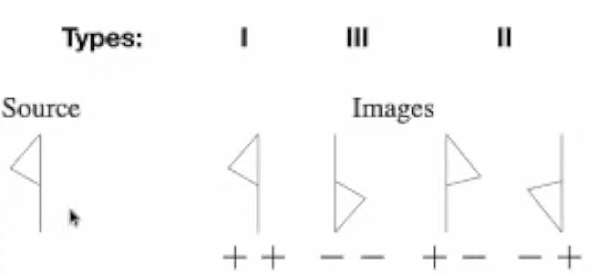
type I: forms at the minimum of τ, both the eigenvalues positive
type II: forms at the saddle point of τ, a set of differently signed eigenvalues
type III: forms at the maximum of the τ, both the eigenvalues negative.
The source flips its sign in the direction of the eigenvalues in the lens plane.

Time Delay

Two components

1. Geometrical Time Delay: the individual light rays get deflected at different angles, their geometrical lengths are different giving rise to the geometrical time delay.

2. Gravitational Time Delay: light rays propagate through a gravitational potential which retards them, resulting in the gravitational time delay.

Total time delay = geometrical time delay + gravitational time delay

\Delta t= \frac{1+z}{2c} (\boldsymbol{\theta} - \boldsymbol{\beta})^2 \frac{D_d D_s}{D_{ds}} + \frac{1+z}{c} \frac{D_d D_s}{D_{ds}} \psi(\boldsymbol{\theta}) = \frac{D_d D_s}{cD_{ds}}(1+z)\Delta\tau

A supernova is a transient astronomical event that occurs during the last evolutionary stages of a massive star or when a white dwarf is triggered into runaway nuclear fusion.
Is classified according to the light curves and the absorption lines of different chemical elements that appear in the spectra.
Type Ia supernovae occur in binary systems in which one of the stars is a white dwarf.
Have the light curves with a sharp maximum and gradual decline, producing a fairly consistent peak luminosity because of the fixed critical mass at which a white dwarf will explode.
Generally occur in all types of galaxies.

Supernova Type Ia

Why Lensed Type Ia Supernovae?

Cosmological parameters governing the evolution of the universe:

Parameters to be found observationally:

H(t), q_0, \rho_i, \omega_i

H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3} \rho + \frac{\Lambda}{3} - \frac{\kappa}{a^2}

∵ First Friedmann Equation

P = \omega \rho

∵ Equation of state

\frac{1}{a(t)} \approx 1 - H_0 (t-t_0) + \left(\frac{1+q_0}{2}\right) H_0^2 (t-t_0)^2

Taylor expanding a(t):

∵ Independent of cosmological

models

\text{where } q_0 = - \left( \frac{\ddot{a}}{a H^2}\right) = \frac{1}{2} \sum_{i}^{} \Omega_{i, 0} (1+3\omega_i)

∵ The Deceleration parameter

Standard Candles: Type Ia supernovae are the most useful, precise, and mature tools for determining astronomical distances and can provide constraints on value of the Hubble's constant.

D_L = \left(\frac{L}{4 \pi f}\right)^{\frac{1}{2}} \approx \frac{c}{H_0} z \left(1 + \frac{1-q_0}{2}z\right)

The luminosity distance DL is defined as,

L: Standardized luminosity
f: Flux of the standard candle measured on earth

z: Redshift of the standard candle, found from (1+z) = 1/a(t) relation

Collaborations like High-z supernova Search Team, PI: Perlmutter;

Supernova Cosmology Project, PI: Schmidt and Riess

H0 measurement from low-z supernovae,

q0 measurement from high-z supernovae

Dark Energy: Discovery and constraints

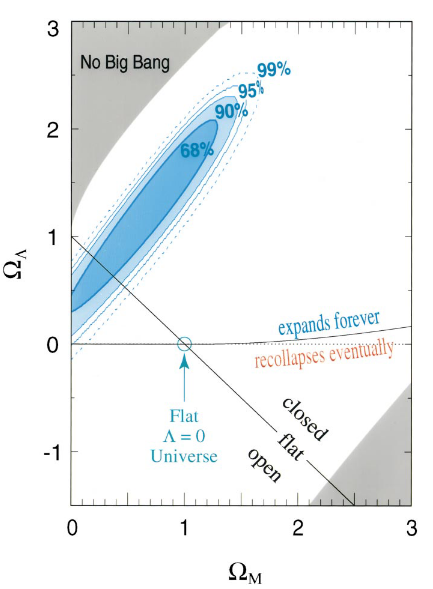
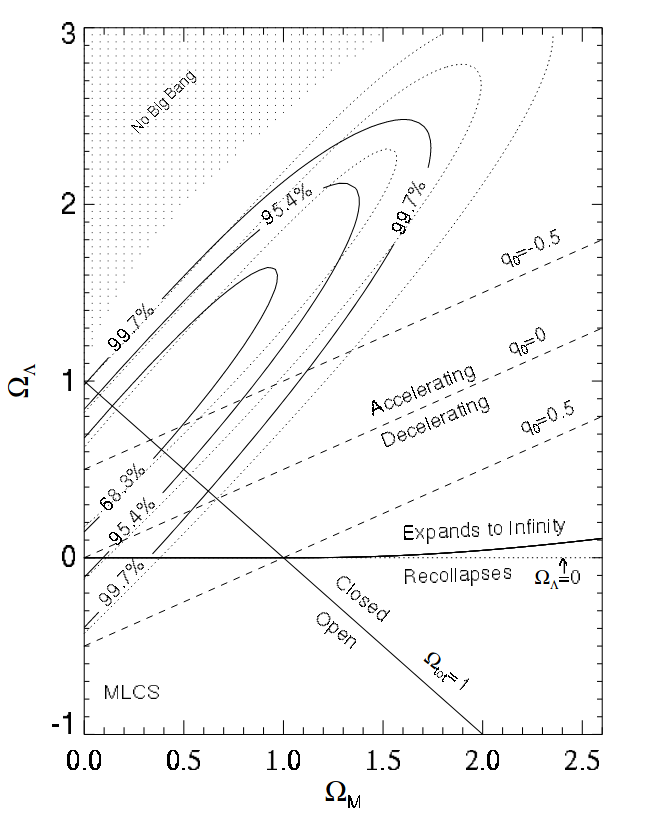
Riess et al, 1999

Permutter et al, 1999

Independent Method to Constrain the value of the Hubble's Constant: The time-delay measurements of the lensed, multiply imaged supernovae.

\Delta t = \frac{D_d D_s}{cD_{ds}}(1+z)\Delta\tau

\frac{D_d D_s}{D_{ds}} \alpha \frac{1}{H_0}

Collaborations like H0LiCoW, COSMOGRAIL, TDCOSMO

Vera Rubin observatory: Legacy Survey of Space and Time (LSST) Conduct a deep survey of sky for ten years to image about 20000 sq deg of sky in the optical wavelength every week.
Construct a pipeline to analyze the LSST data to identify the lensed Type Ia supernovae from the data within the LSST stack framework and to analyze the pipeline for its efficiency.