In by Out Again
Arbitrarily-Deep Zooming on Iterated Function Systems by 'Self-Similarity Jumping'
BSc Wiebe-Marten Wijnja

Summary
- Iterated Function Systems?
- Existing rendering methods
- New approach
- Results & Remarks
- Conclusion
What is an Iterated Function System?
- What: Mathematical concept, related to set theory and constructing fractals
- Why: physics, image compression, gene structures, beauty
- How:



What is an Iterated Function System?
- What: Mathematical concept, related to set theory and constructing fractals
- Why: physics, image compression, gene structures, beauty
- How:
"repeatedly apply the collection of mappings"



What is an Iterated Function System?
- What: Mathematical concept, related to set theory and constructing fractals
- Why: physics, image compression, gene structures, beauty
- How:
iterate
system
(transformation) functions
"repeatedly apply the collection of mappings"



Transformation function (mapping)
image \(\longrightarrow\) transformed image
image: Set of points
Transformation function (mapping)
System of functions

{
}
,

Iterate


Another example
Formally
-
IFS $$ \mathcal{F} = \{ f_i : \mathcal{M} \rightarrow \mathcal{M}\}_{i=1}^N, N \in \mathbb{N}$$(mappings are required to be contractive)
-
one iteration: $$ \mathcal{S}_{n + 1} = \bigcup_{i=1}^{N} f_i(\mathcal{S}_n), n \in \mathbb{N}$$
-
Attractor: $$\mathcal{A} = \lim_{n \rightarrow \infty} \mathcal{S}_n$$
(\(\mathcal{S}_0 \) can be an arbitrary non-empty set of points)
Formally
-
IFS $$ \mathcal{F} = \{ f_i : \mathcal{M} \rightarrow \mathcal{M}\}_{i=1}^N, N \in \mathbb{N}$$(mappings are required to be contractive)
-
one iteration: $$ \mathcal{S}_{n + 1} = \bigcup_{i=1}^{N} f_i(\mathcal{S}_n), n \in \mathbb{N}$$
-
Attractor: $$\mathcal{A} = \lim_{n \rightarrow \infty} \mathcal{S}_n$$
(\(\mathcal{S}_0 \) can be an arbitrary non-empty set of points)
!!
Formally
-
IFS $$ \mathcal{F} = \{ f_i : \mathcal{M} \rightarrow \mathcal{M}\}_{i=1}^N, N \in \mathbb{N}$$(mappings are required to be contractive)
-
one iteration: $$ \mathcal{S}_{n + 1} = \bigcup_{i=1}^{N} f_i(\mathcal{S}_n), n \in \mathbb{N}$$
-
Attractor: $$\mathcal{A} = \lim_{n \rightarrow \infty} \mathcal{S}_n$$
(\(\mathcal{S}_0 \) can be an arbitrary non-empty set of points)
!!
👌
Rendering an IFS's attractor

\(t(t(t(\mathcal{S}_0))) \cup t(t(l(\mathcal{S}_0))) \cup \ldots r(r(r(\mathcal{S}_0)))\)
how to find all transformation-sequences?
Transformation-sequences as trees

\(t(t(t(\mathcal{S}_0))) \cup t(t(l(\mathcal{S}_0))) \cup \ldots r(r(r(\mathcal{S}_0)))\)

Depth-First

Breadth-First

- Depth-First:
- \(\mathcal{O}\big(\log{P}\big)\) memory
- Breadth-First:
- \(\mathcal{O}\big(P\big)\) memory,
- but able to stop interactively
Can we do better?
- Both use quite a bit of memory
- Difficult to parallellize (reason: coordination)*
* There is one cool (but complex) implementation,
c.f. Orion Sky Lawlor. "GPU-accelerated rendering of unbounded nonlinear iterated function system fixed points"
\(t(t(t(\mathcal{S}_0))) \cup t(t(l(\mathcal{S}_0))) \cup \ldots r(r(r(\mathcal{S}_0)))\)
\(t(t(t(l(\mathcal{S}_0)))) \approx t(t(t(r(\mathcal{S}_0)))) \)
[
[
indistinguishable!
\( t(t(t(\ldots)))) \rightarrow r(t(t(t(\ldots))))) \rightarrow t(r(t(t(t(\ldots)))))) \rightarrow l(t(r(t(t(t(\ldots))))))) \) etc.
[
[
[
[
ttt, rtt, trt, ltr, etc.
Yes!
- \(\mathcal{O}(1)\) memory
- Simple implementation
- including a parallel one
-
but needs
- enough points
- fine-tuned probabilities


the chaos game
the chaos game
N: the number of mappings of the IFS;
z: a single arbitrary starting point;
v: the camera's view transformation;
m = 0;
for m ∈ [0..n + P) {
i: a random integer between 0 and N;
if(m >= n){
render(v(z)) cumulatively;
}
z = fᵢ(z);
}
But what about animations?
New Approach
- Use a point cloud
- moving the camera does not change points
-
'self-similarity jumping'
- Too little detail? (ab)use self-similarity to (re)use more points!
- Based on the Chaos Game
- Meant for animations/interaction
Self-Similarity Jumping

Self-Similarity Jumping

"inside", "outside", "overlapping"
n: the number of mappings the IFS consists of;
v: the current camera's view transformation;
s: a stack of jumps made so far;
for i <- [1, ..., n] {
if isInvertible(fᵢ) and isInside(v⁻¹, fᵢ) {
push(s, fᵢ);
v = fᵢ⁻¹ ◦ v;
break;
}
}
v: the current camera's view transformation;
s: a stack of jumps made until now;
if notEmpty(s) and isOutsideUnitSquare(v⁻¹) {
f = pop(s);
v = f ◦ v;
}
Jump 'up'
Jump 'down'
Implementation
- Haskell
- Accelerate library
- Haskell EDSL \(\rightarrow\) LLVM \(\rightarrow\) NVidia PTX ('GPU assembly')

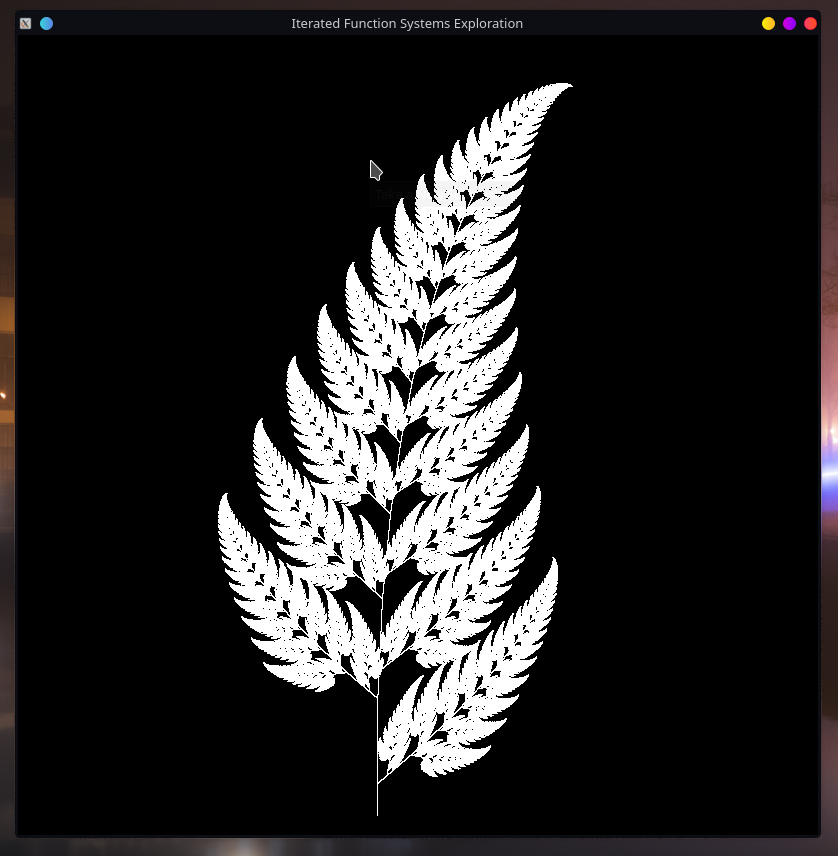
Results & Remarks
- Point clouds take a lot of GPU memory
- Self-similarity jumping has two restrictions

Cannot be used on 'borders'

Points of single subtransformation visible

Points of multiple subtransformations visible: problem
Both cases are unfortunately rather common
Conclusion
- The technique works, but has limited applicability
- point clouds take a lot of memory
- self-similarity jumping cannot be used everywhere
Summary
- Iterated Function Systems?
- Existing rendering methods
- New approach
- Results & Remarks
- Conclusion
Image Attribution
Thank you!
Thanks to
- Jiří Kosinka for answering all my questions, and sheer limitless patience
- Luc, Jeroen, Sietze and Michiel for kindling my love for computer graphics, visualization and clever algorithms
-
2D affine transformations (slide 7): Cmglee (https://commons.wikimedia.org/wiki/File:2D_affine_transformation_matrix.svg)
-
IFS construction (slide 8): Scott Draves (https://en.wikipedia.org/wiki/File:Ifs-construction.png)
Thank you!
Questions?



In by Out Again
By qqwy
In by Out Again
- 968



