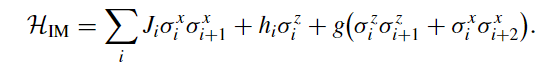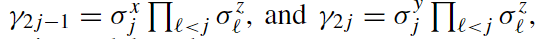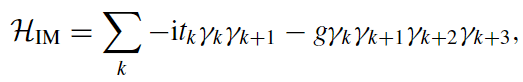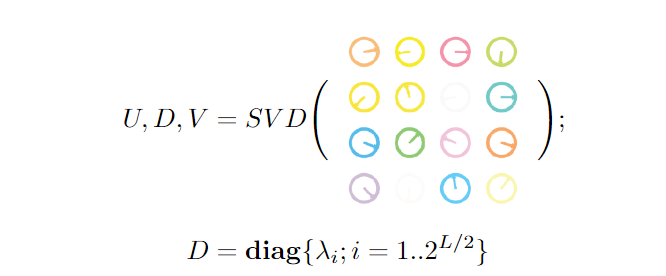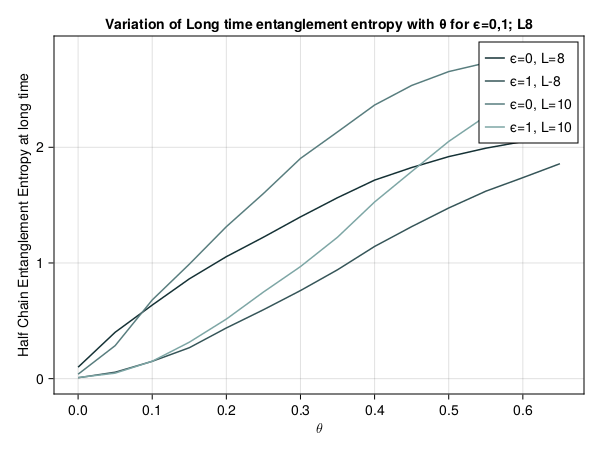A Hunt for
Phase Space

Sagnik Ghosh •Group Retreat• Die Ebernburg  •January 15, 2024

Order paramerters:

 

 

 

1. avg level spacing ratio

 

2. Envelope of Z_iZ_j

 

3. SFF

 

4. Statistics of Lazadires diagonals

 

5. Half chain entanglement entropy

Recall: Model

Parameter 1. Level spacing ratio:

Half chain EE: Motivation: PRR L032016

Model:
 

  • Z2 symmetric random interacting Majorana chains at high energies.
  • Note the NNN term.
  • Two topologically different distinct MBL phases. Consequence of avalanche theory.

Shift Invert ED:


Explored the infinite temp. phase diagram. Kramers-Wanier duality [31] leads to symmetric phase boundaries .

 

 

Consequences:

 

MBL-SG phase exhibits cat states for all energies with a global double degeneracy of the MBL spectrum in the two parity sectors.

 

Writing H as Majoranas:

The original Hamiltonian becomes:

Randomness: Assume Box distribution for both couplings J and fields h,

 

with          

Numerics: Shift invert ED of IM chains upto L=16.
 

Computed ~100 midspectrum eigenpairs of each parity sector for ~500-1000 independennt random samples.

Phase Diagram:

Algorithm:

Algorithm:

Algorithm:

Algorithm:

Algorithm:

SV_{L/2}= \sum_i -\lambda_i \log_e \lambda_i

The entanglement entropy is then computed as the Von-Neumann entropy of this matrix

Behaviour:

Scaling with size:

Behaviour in the pure MBL phases with θ

Finite size scaling:

Phase space:

Phase space:Till now

Questions!

Retreat! Retreat!

By Sagnik Ghosh

Made with Slides.com

Retreat! Retreat!

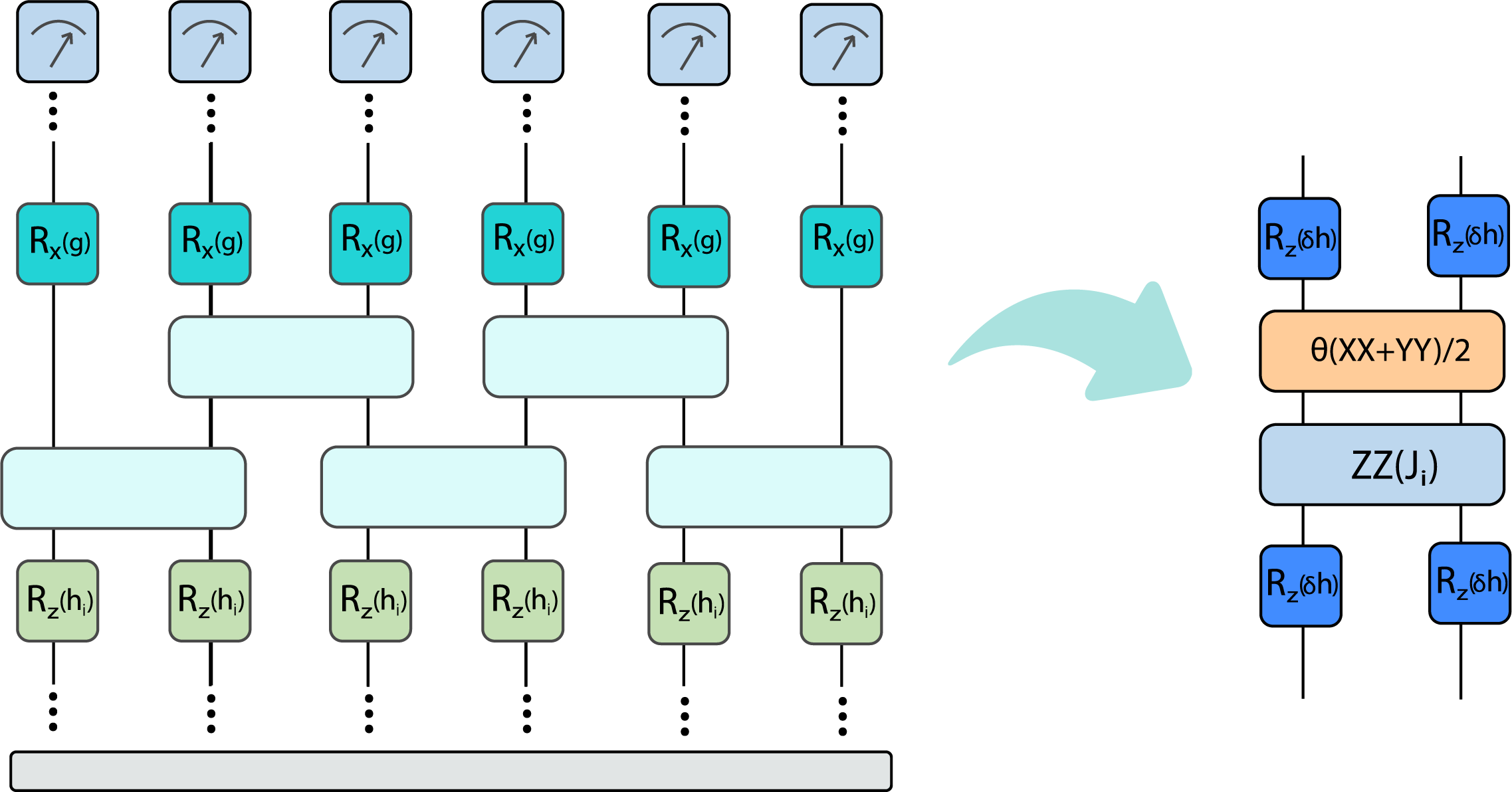
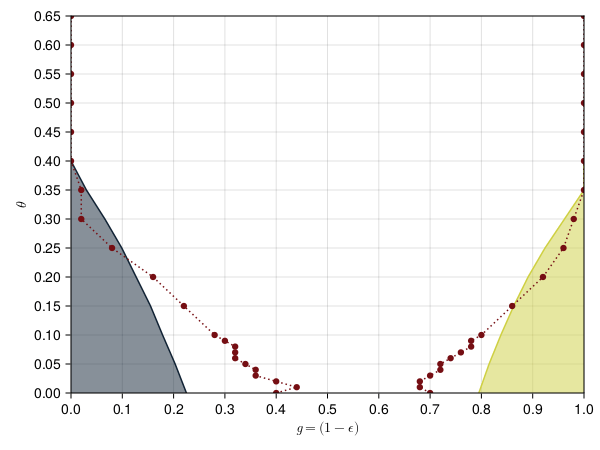
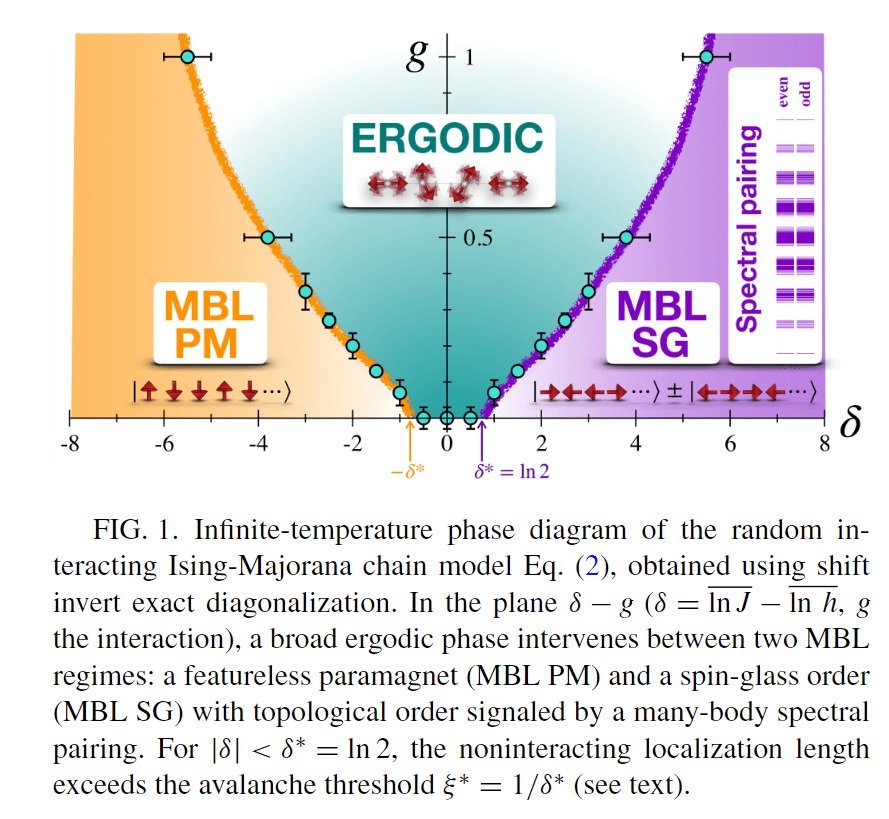
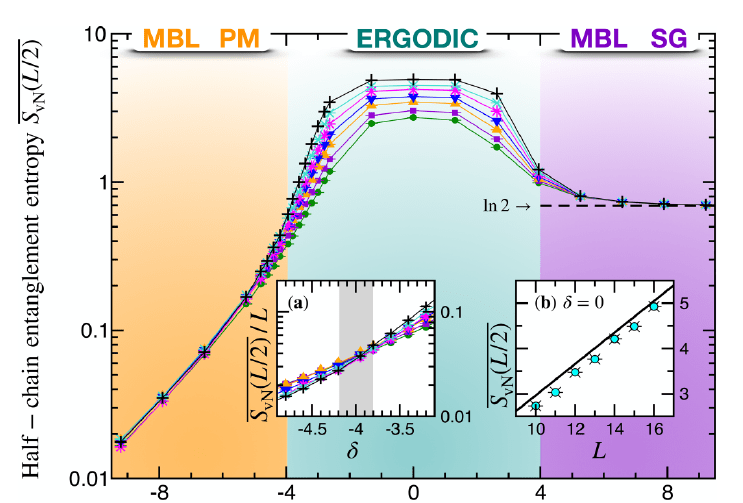
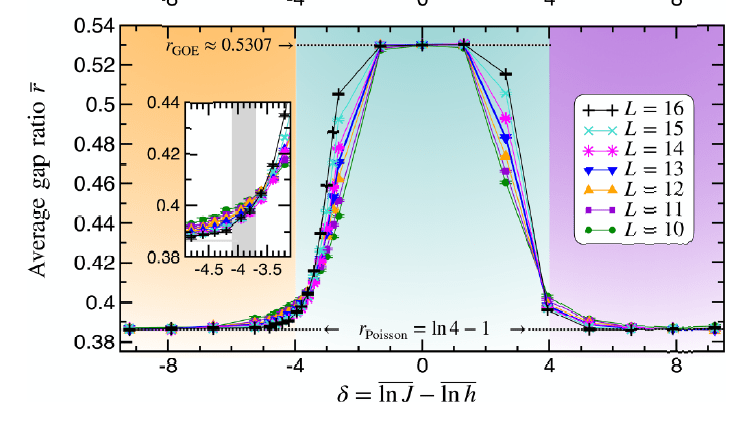
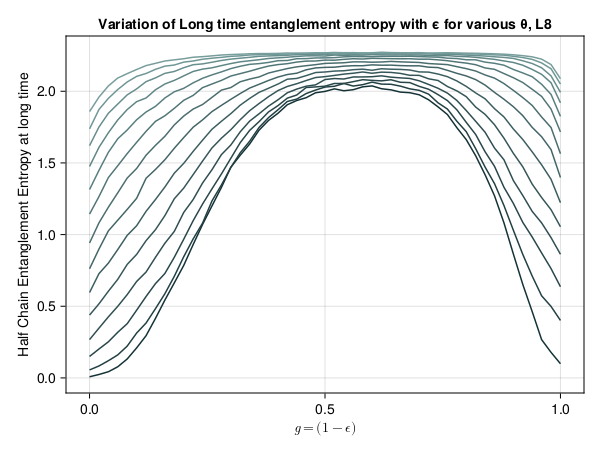
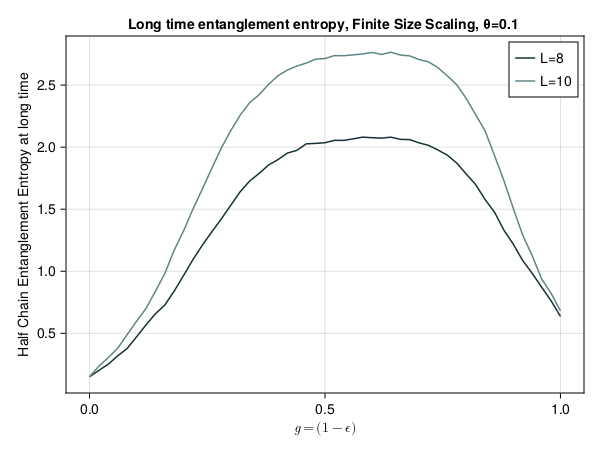
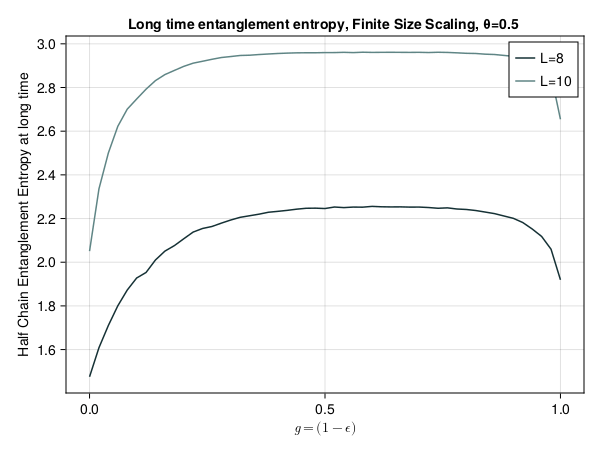
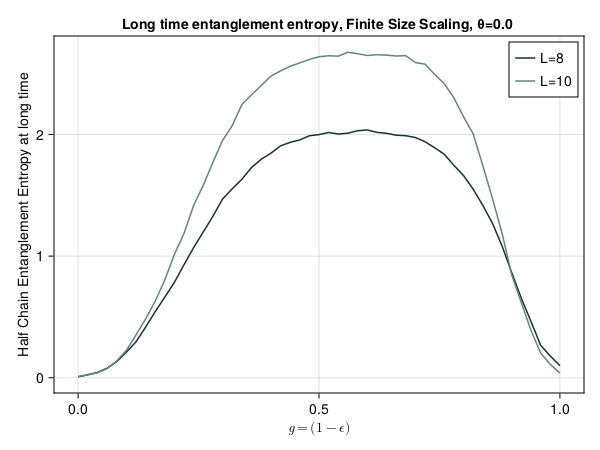
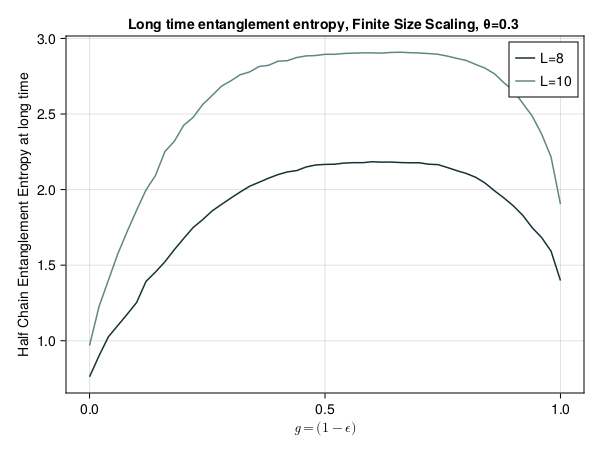
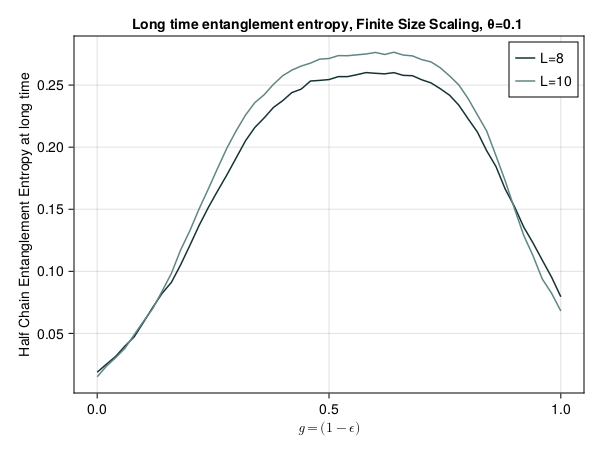
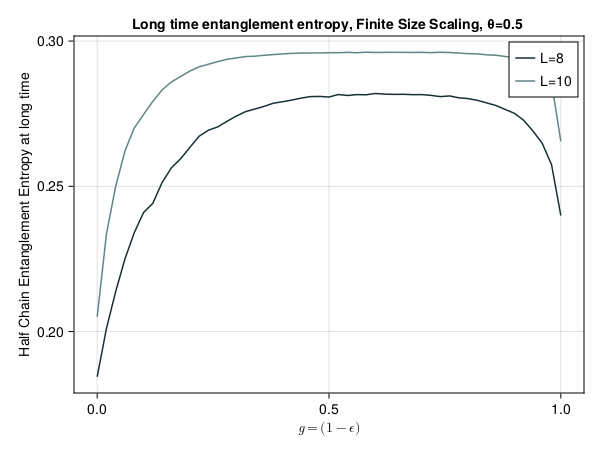
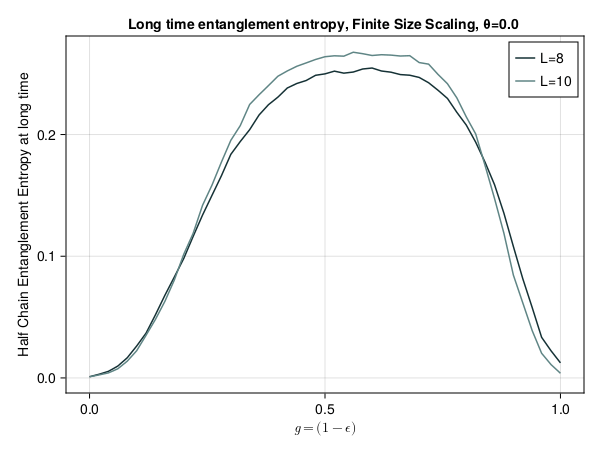
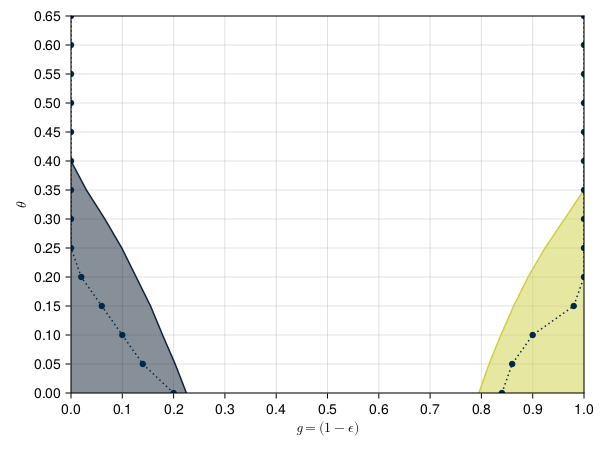
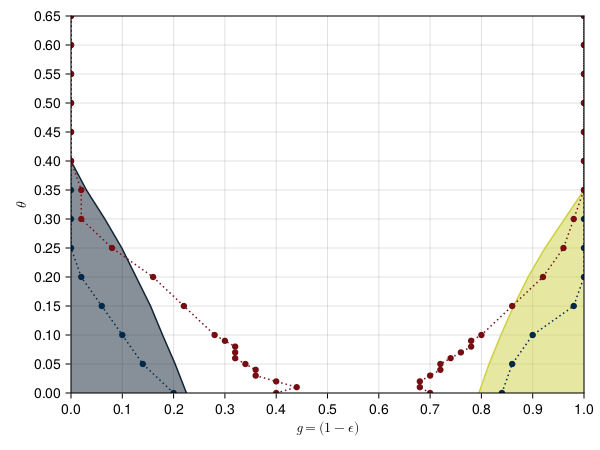
This presentation explores various order parameters in the hunt for phase space. Topics include average level spacing ratio, envelope of Z_iZ_j, SFF, statistics of Lazadires diagonals, and half chain entanglement entropy. The model discussed is Z2 symmetric random interacting Majorana chains at high energies.

  • 1

More from Sagnik Ghosh