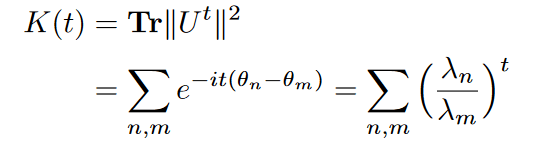Finite size scaling
the time crystalline criticality:
Spectral Form Factor
Sagnik Ghosh •Uni Bonn •ML4Q Retreat •July 30, 2024
Advertisement!
sghosh@uni-bonn.de
Summer School: (Bonn, Sept 23-27, 2024)
Defintions:
[Typical systems]
For systems that scrambles, any expectation value of local operator at infinite time under finite size scaling is always zero.
Defintions:
[Time Fluids]
Time fluids are systems, for which there exists local operators, whose expectation value at the thermodynamic limit, under long time dynamics is finite and non-zero.
Eg: MBL
\lim_{t\to\infty} \lim_{L\to\infty} \braket{\mathcal{O}(t)} \neq 0
Defintions:
[Time Crystals and Time Glasses]
Time crystals are time glasses where the time translation symmetry is spontaneously broken.
If at large times, at the thermodynamic limit, the expectation value is a periodic function of t then the system is a time crystal.
If <O>(t)is a non-periodic function of t then it is a time glass.
In these cases typically you would look at two time correalator of local operators under the defined limit.
Bar Lev, Lazadires (2024) arXiv:2403.01912
The Circuit: Ippoliti PRXQuantum030346.2021
DTC in chip
Features of DTC: (Ippoliti PRXQuantum030346.2021)
Dynamical
Signatures:
Features of DTC:
Eigenstate Signatures:
Spectral Form Factors of an Unitary
The SFF is defined as K(t)=|Tr(U(t))|^2.
Using the spectral decomposition, one can reduce it to a more familiar form.
SFF is the fourier transform of the two point correlator of the level density.
Motivation:
Motivation:
Behaviour of SFF around Thermal Point
Behaviour of SFF around Thermal Point
- Diagonal elements are exactly 1
- The ramp is a signature from Random Matrix Theory
Behaviour of SFF at PM-MBL ETH transition
- Diagonal elements are exactly 1
- Deep in MBL, the Poission statistics destroy the ramp
Behaviour of SFF at DTC transition
- Diagonal elements are still exactly 1.
- But now, there are also exactly -1 in the sum, which comes from the cat-states phase separated by pi.
Why?
- But now, there are also exactly -1 in the sum, which comes from the cat-states phase separated by pi. In the even periods they add up, in odd periods the cancels.
Hence oscillations between 0,2n.
SFF Undersampling
SFF Undersampling
SFF Undersampling
Polynomial filtering Exact Diagonalisation (PolFED)
David Luitz
Polynomial filtering Exact Diagonalisation (PolFED)
Accuracy of under sampling: comparison
Future plan:
- To show for a final detuning the envelope survives.
- Does this explain robustness from a "molecular picture"?
- Can the transfer matrix generating the SFF, explain the asymmetry of the transition?
Retreat2024
By Sagnik Ghosh
Retreat2024
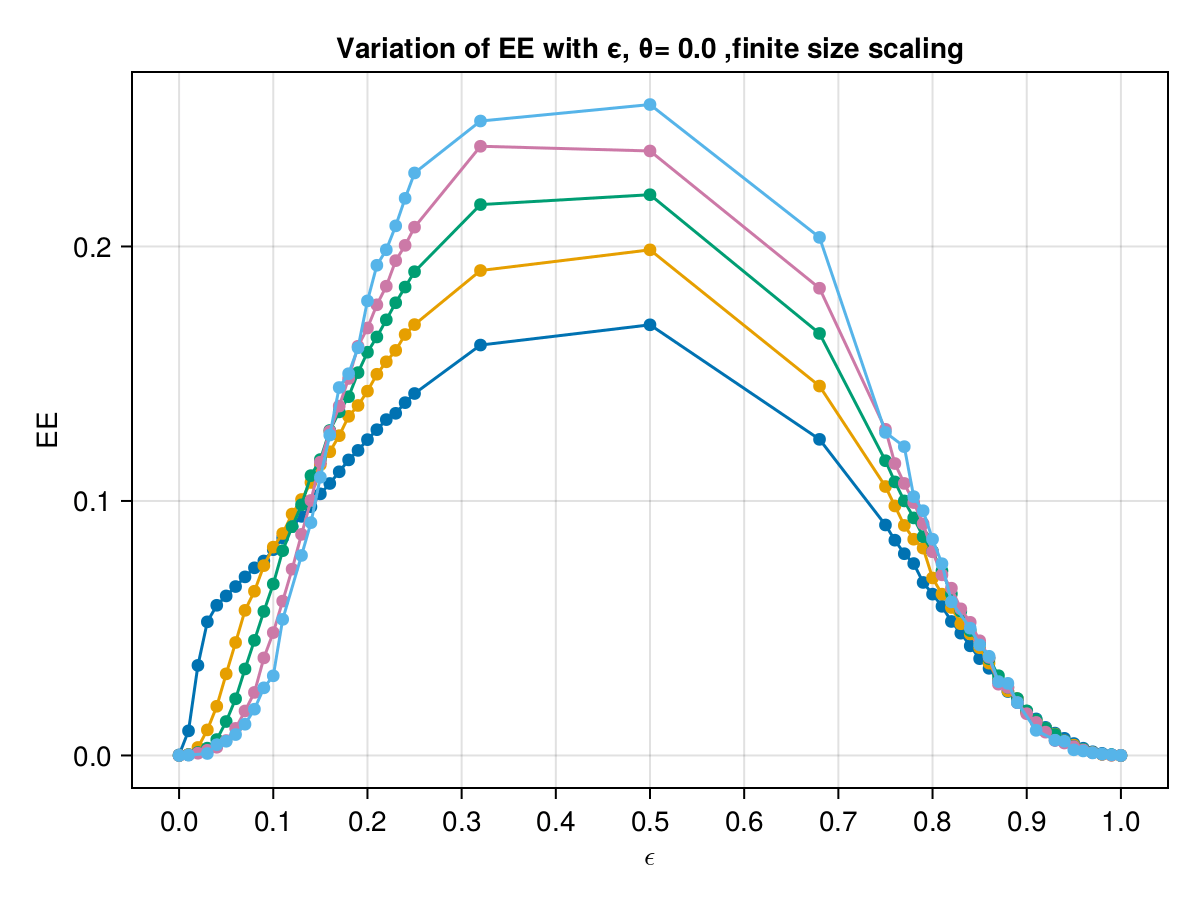
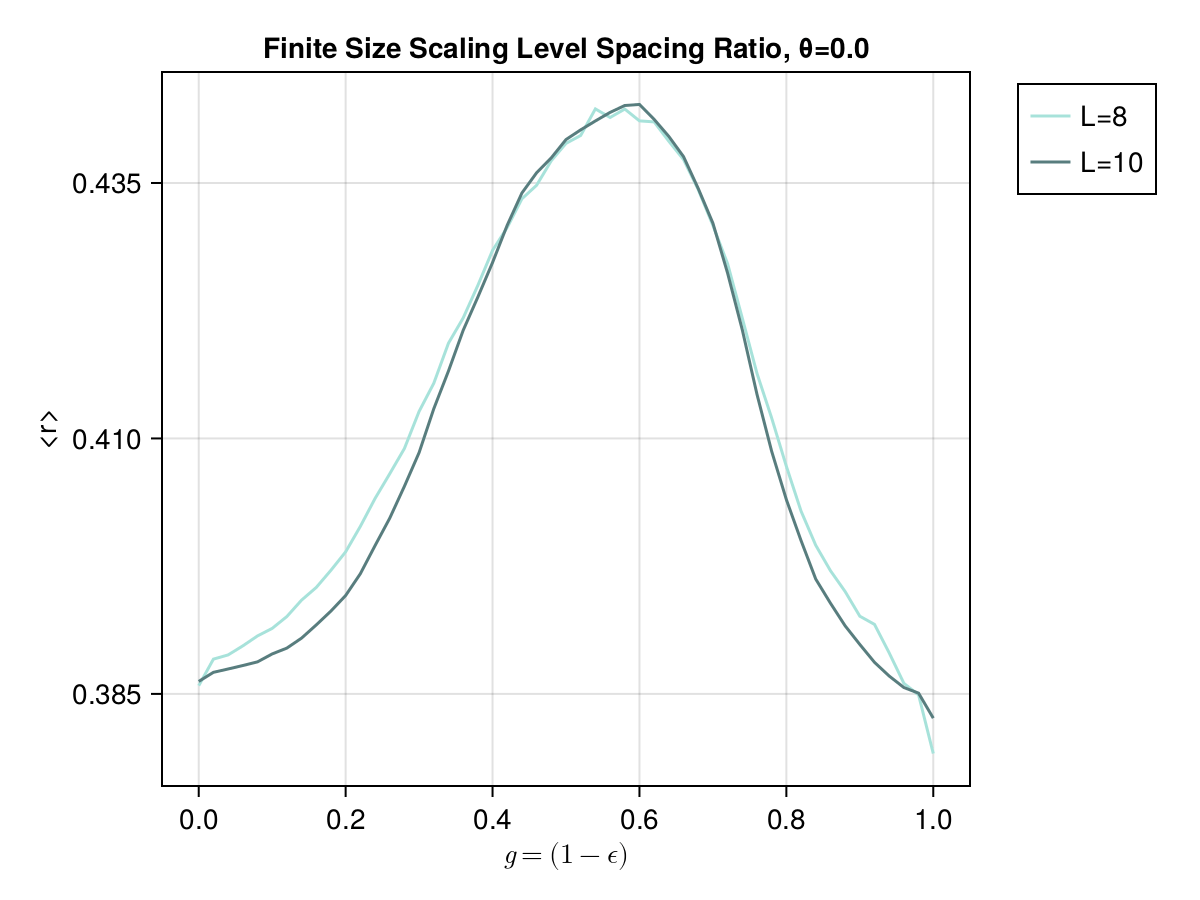
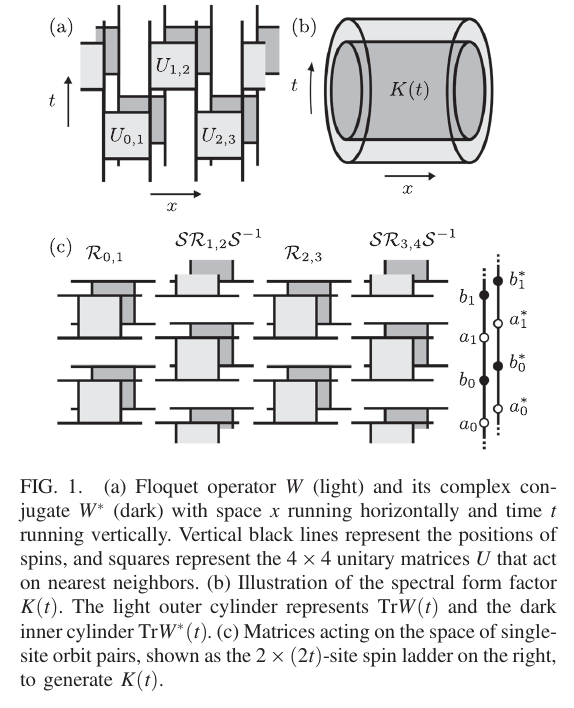
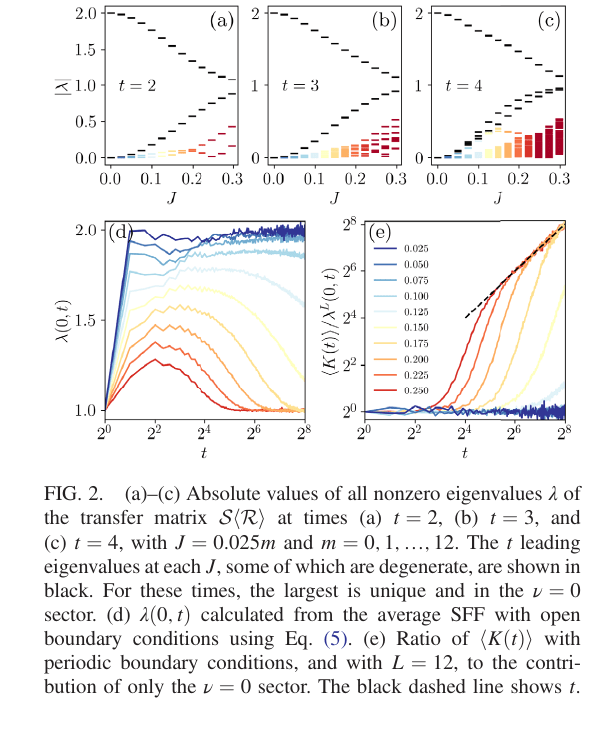
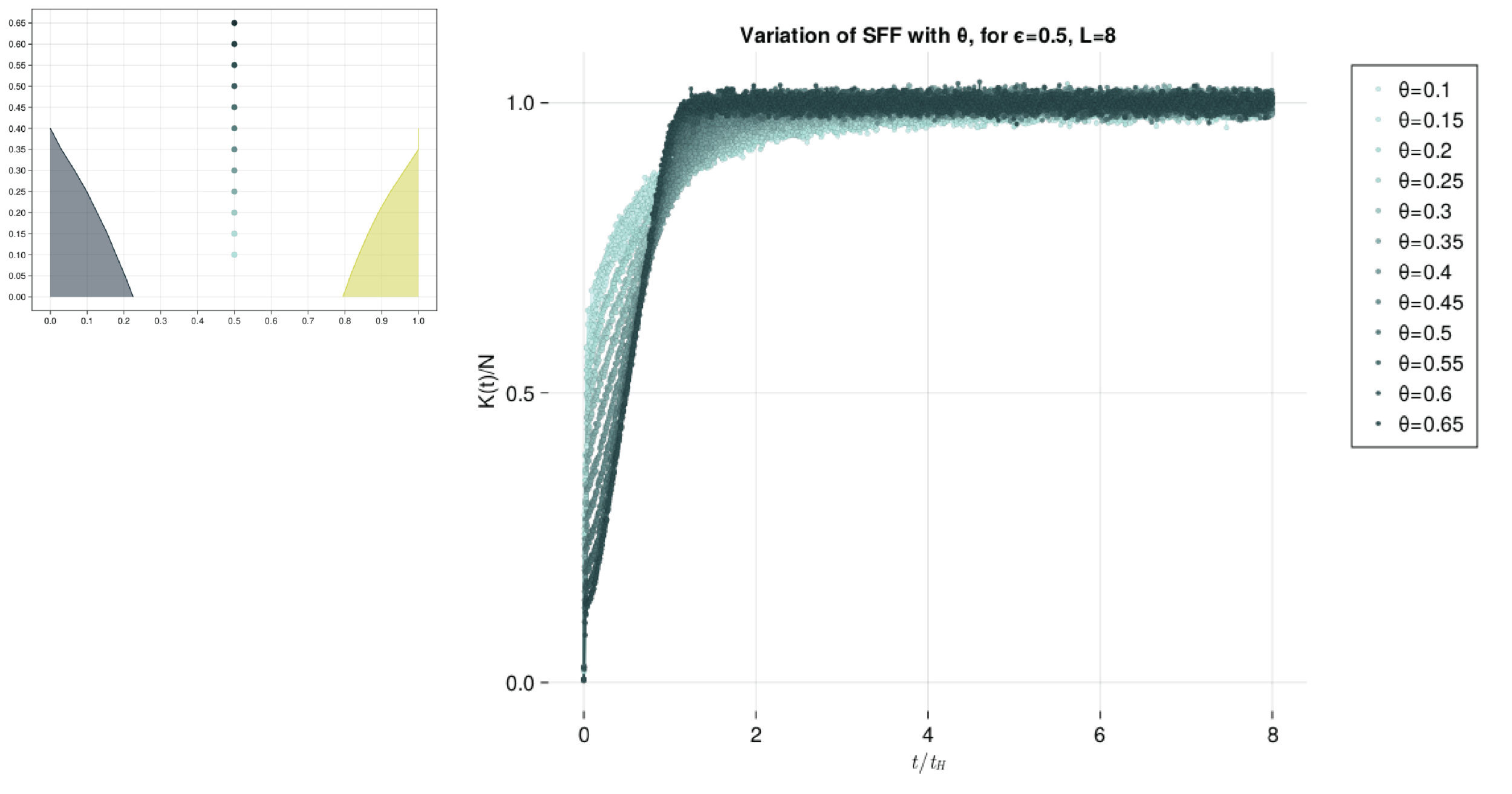
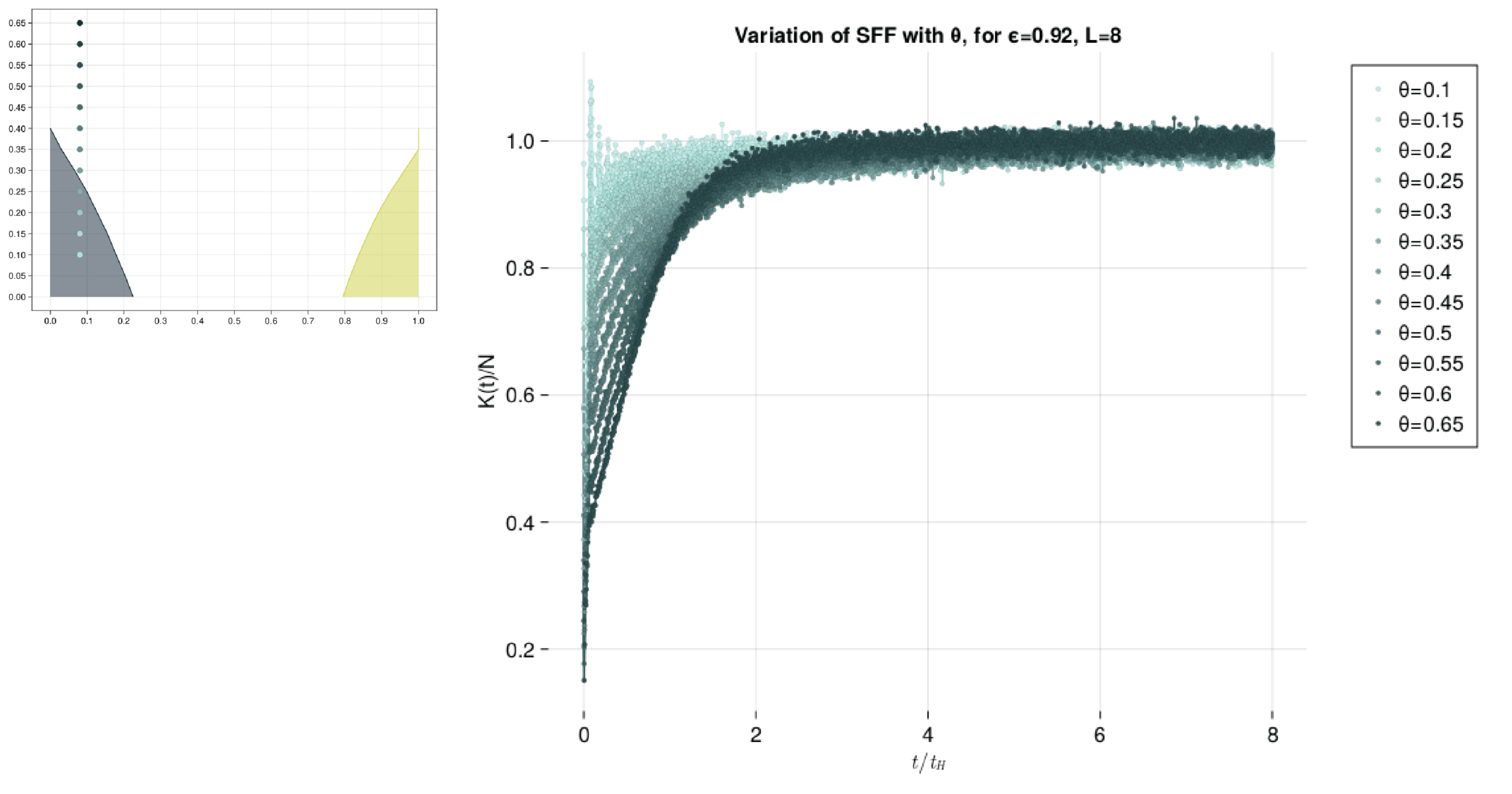
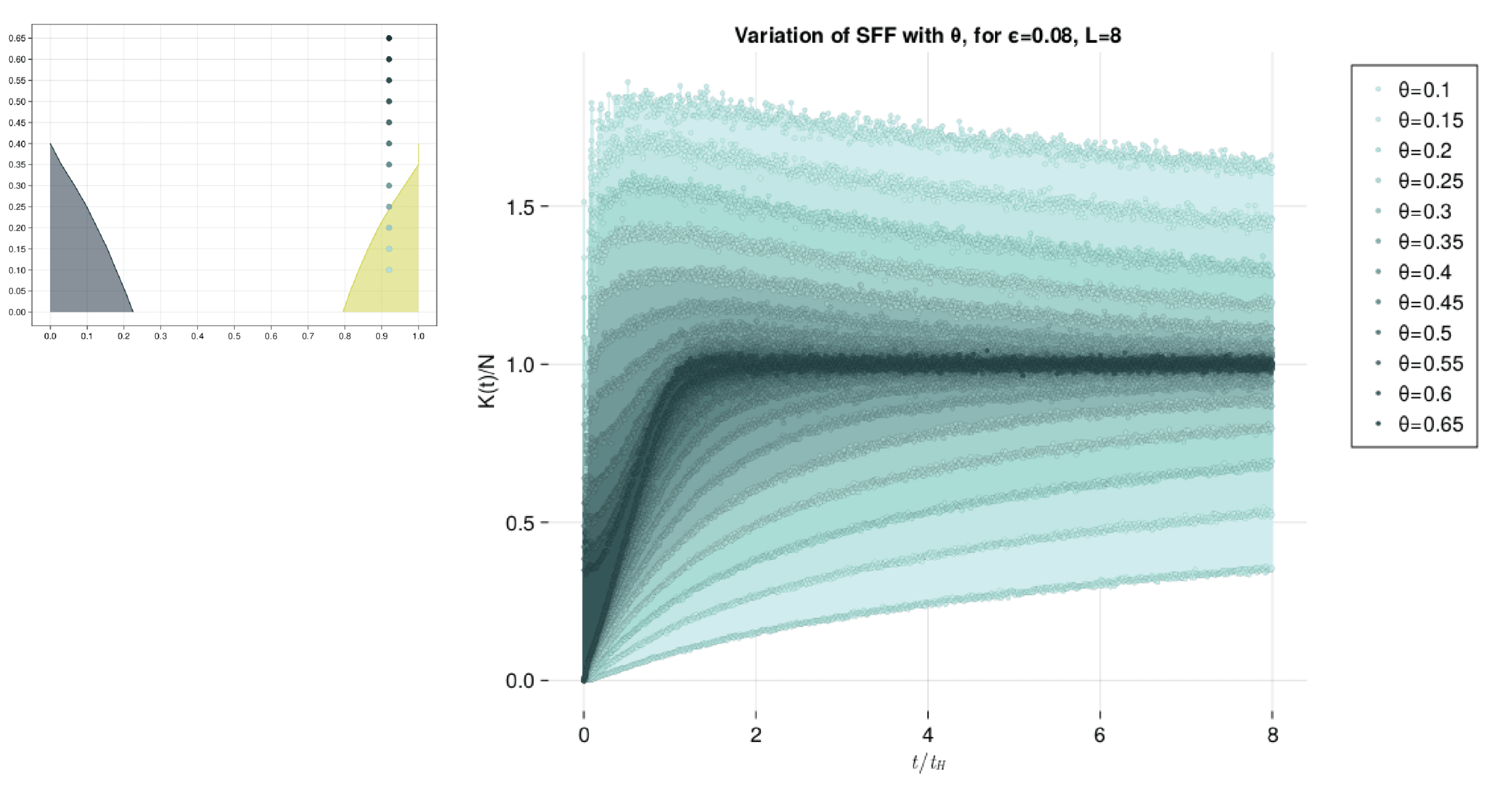
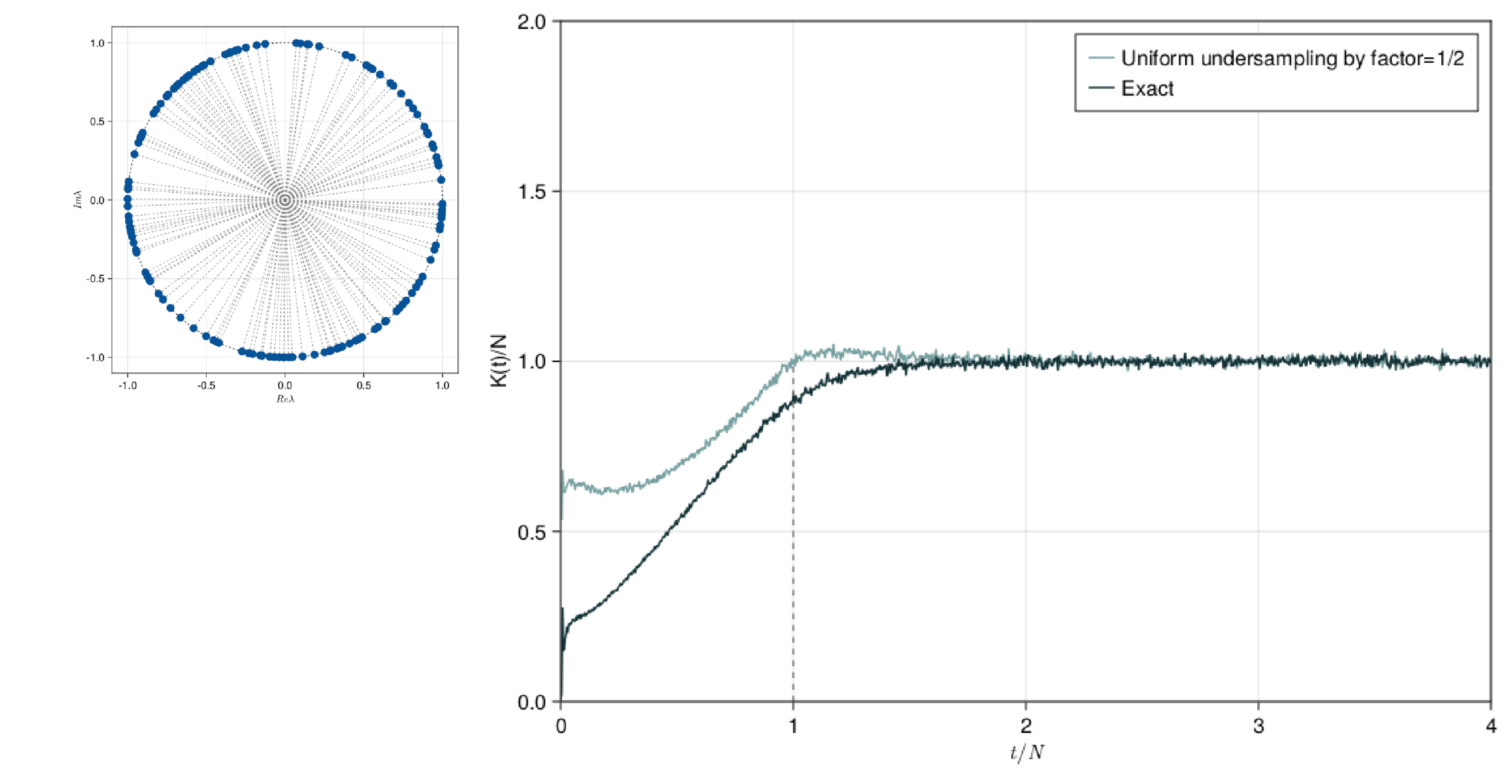
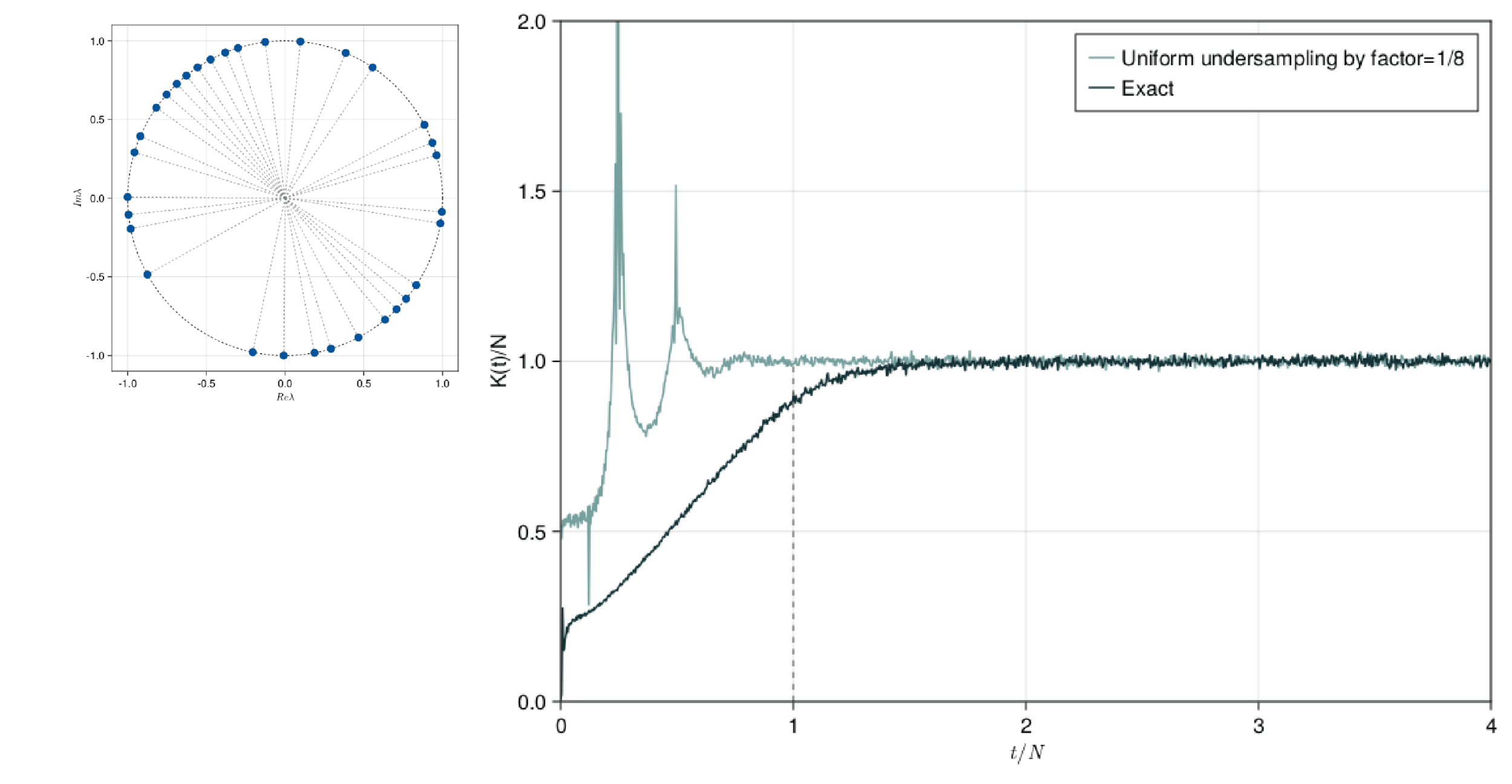
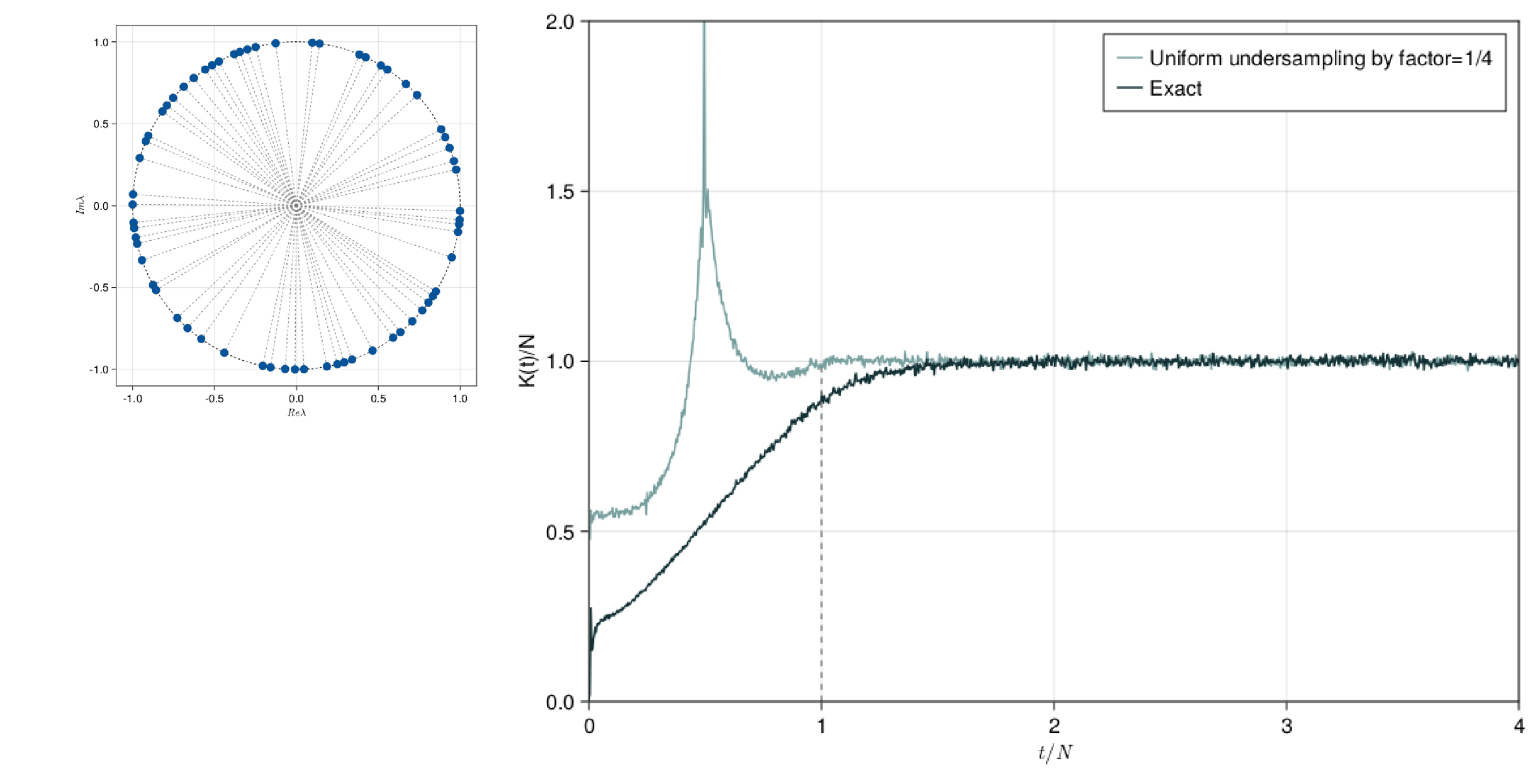
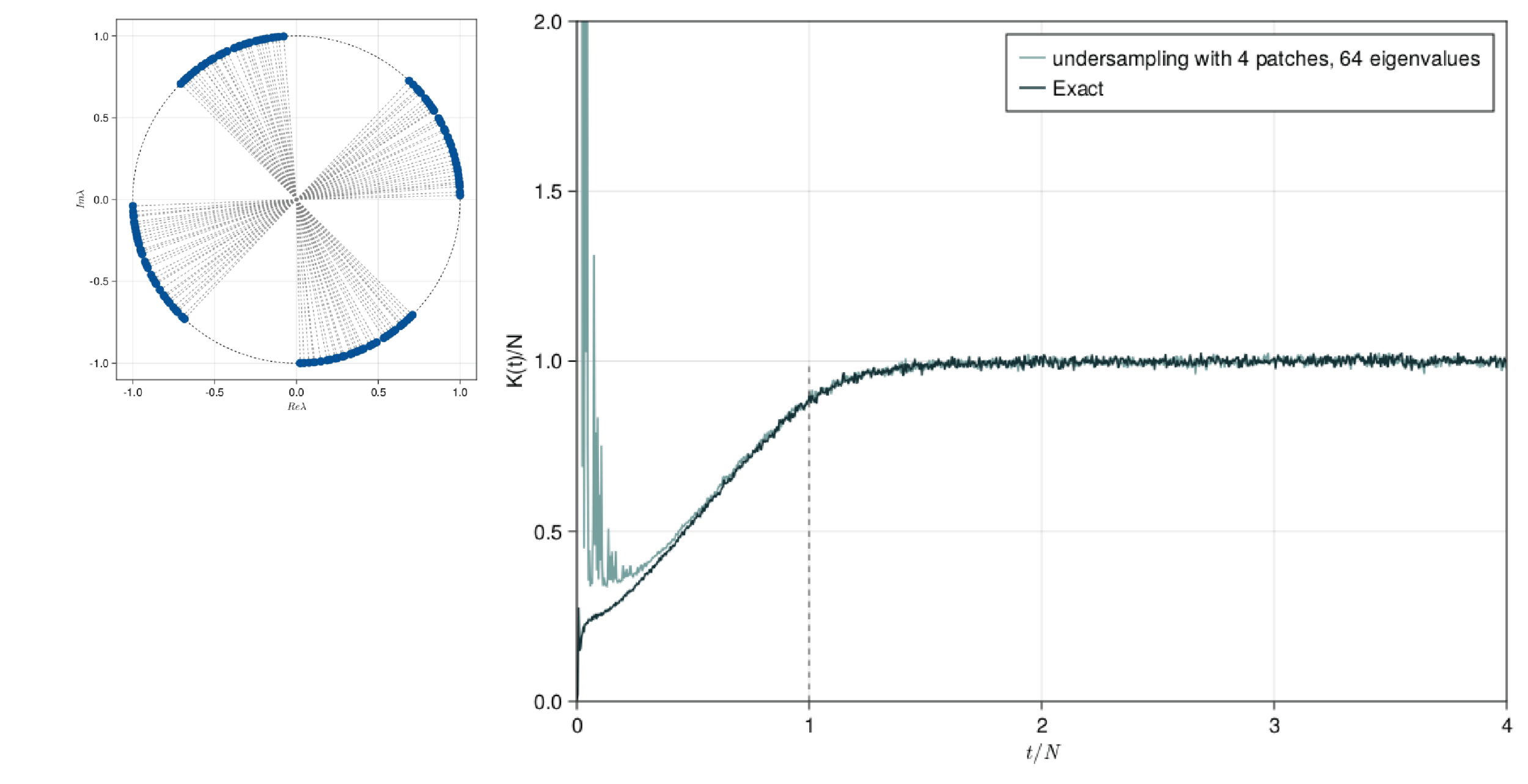
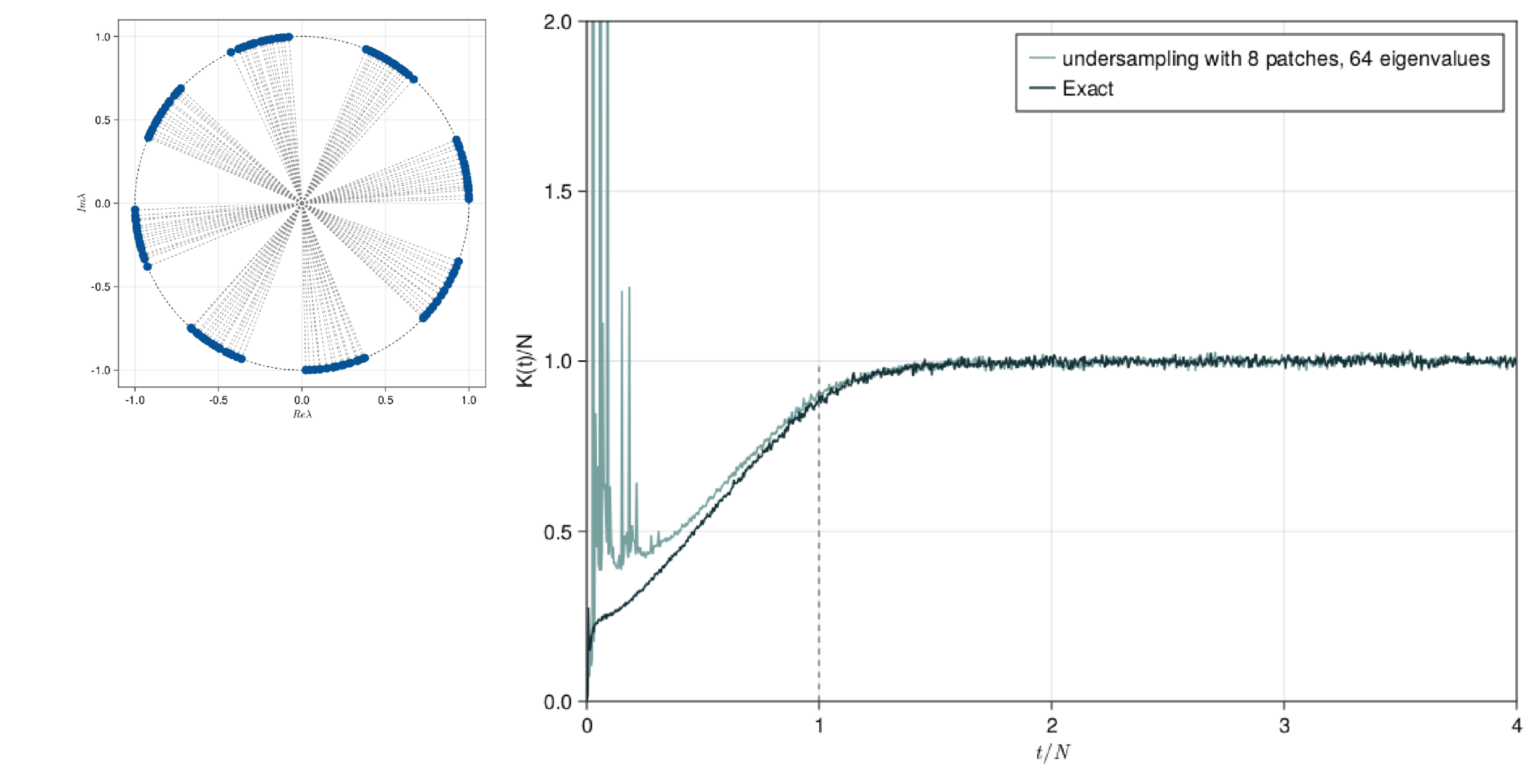
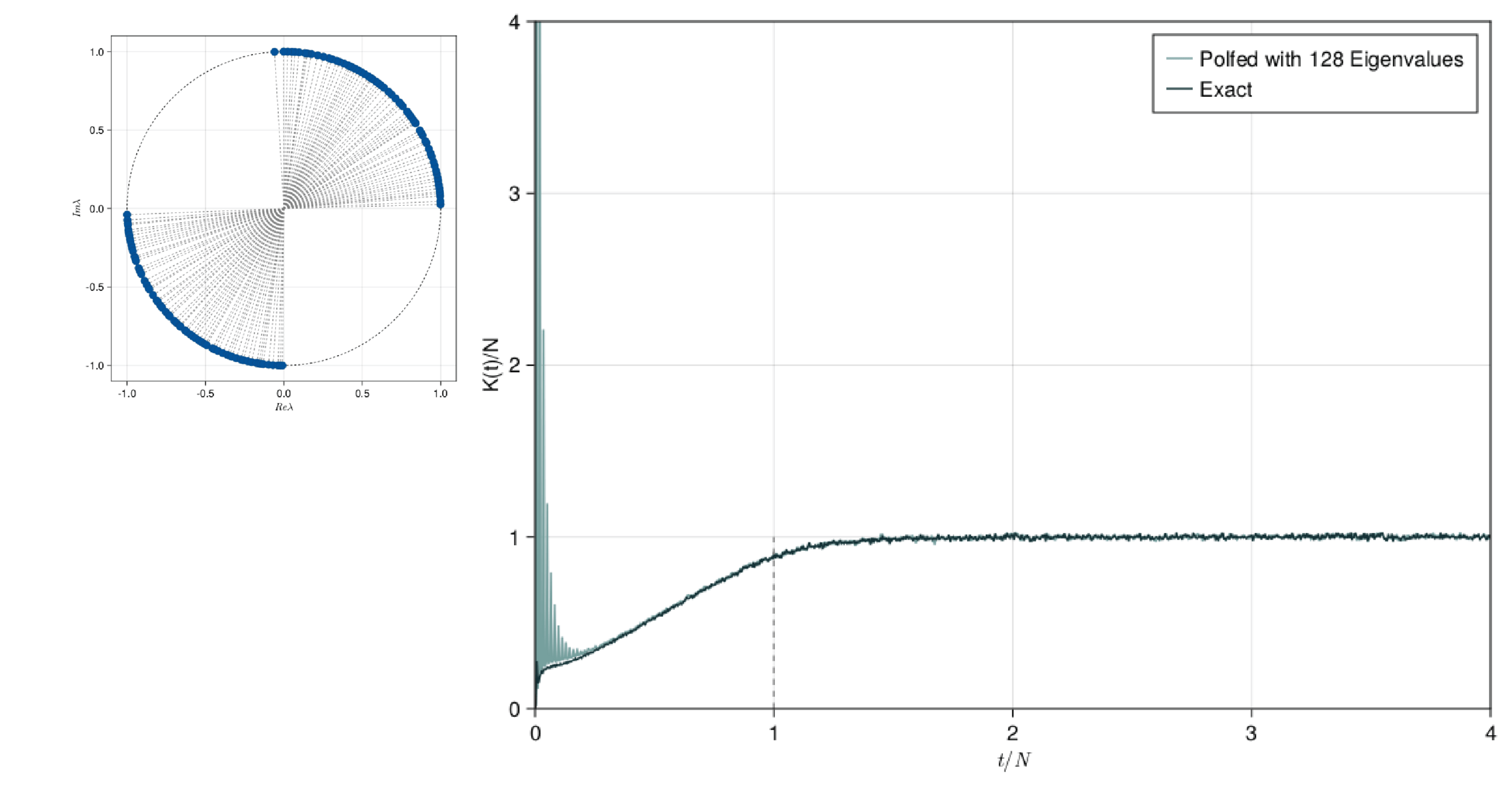
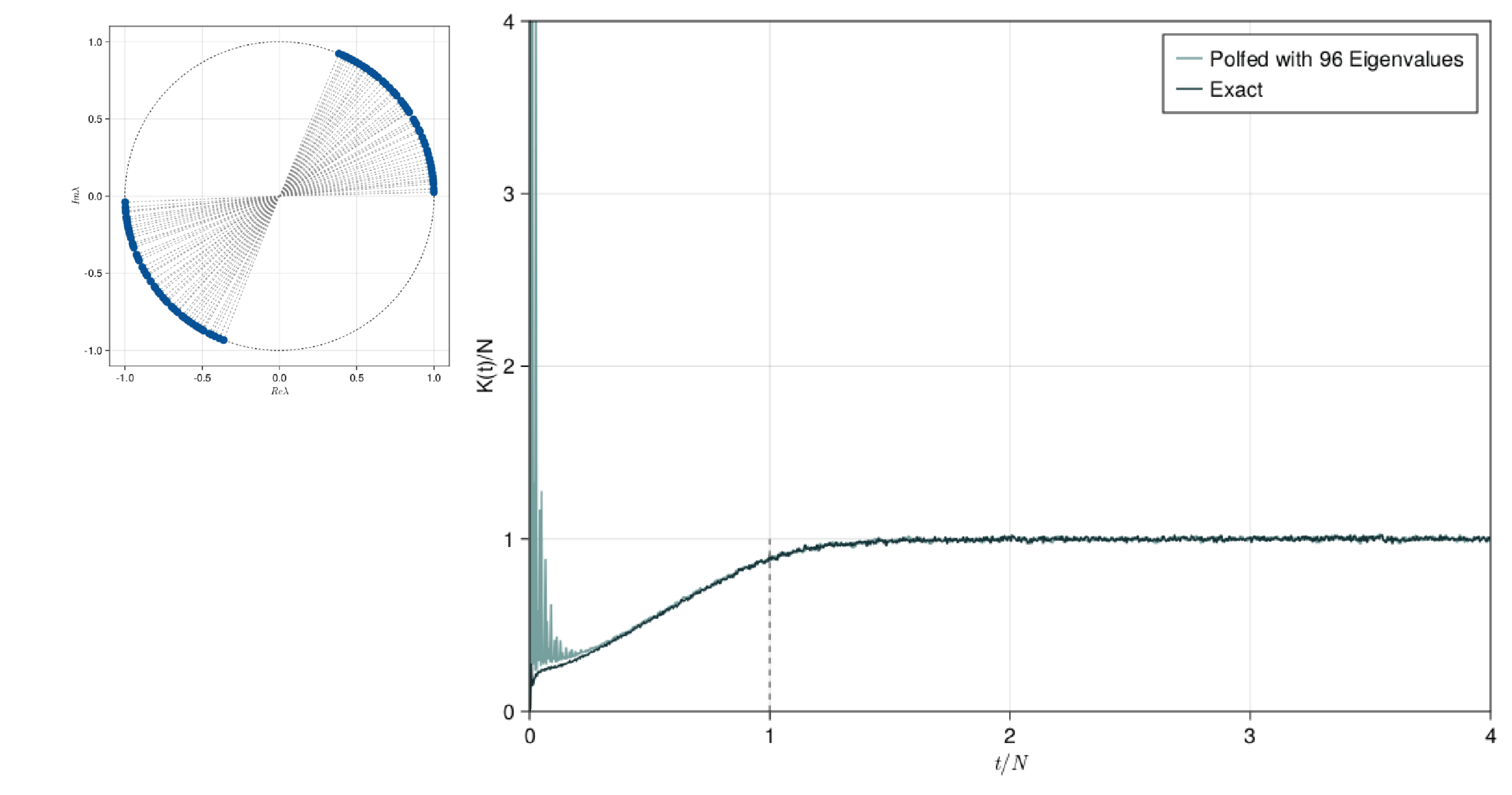
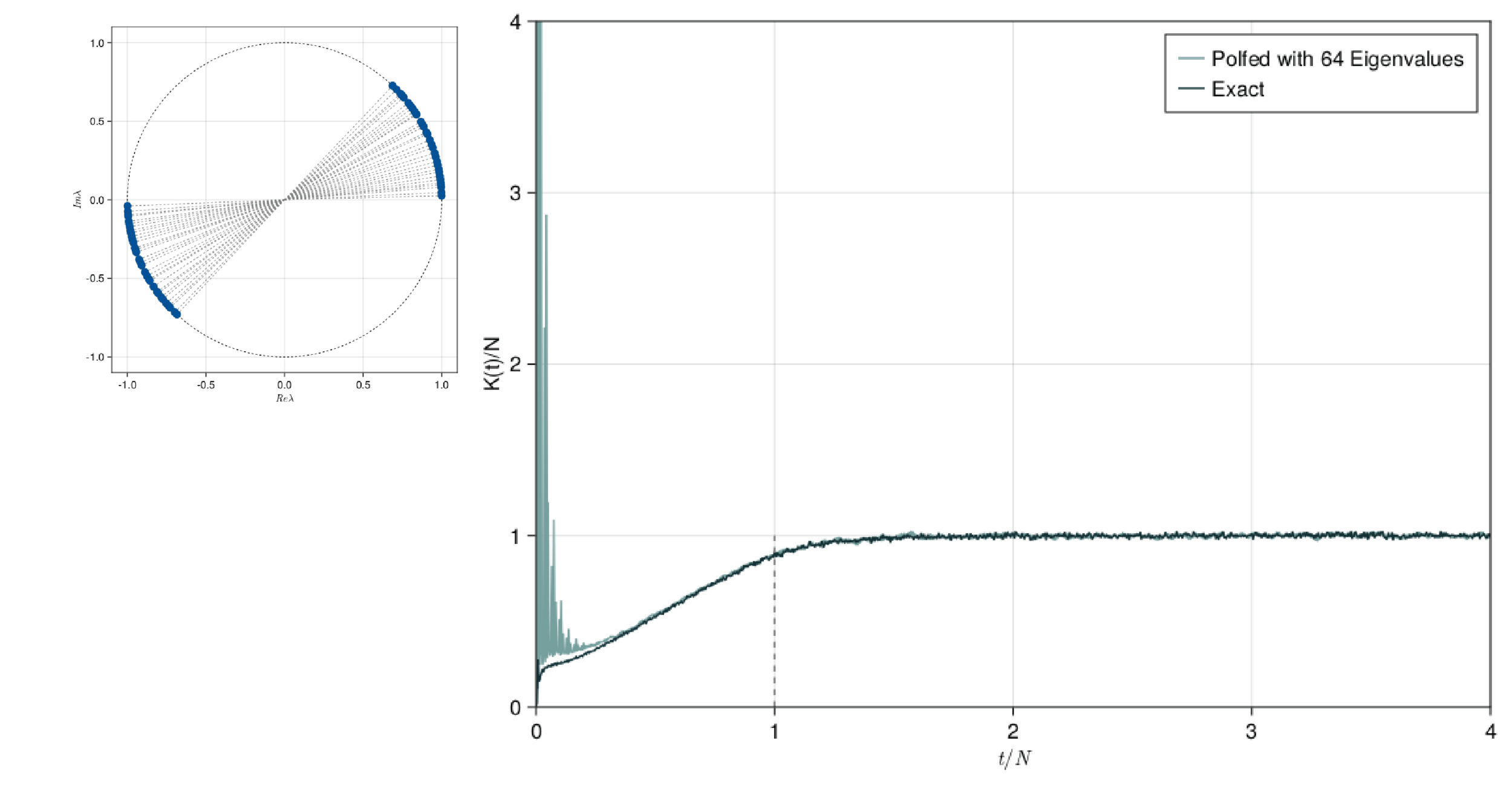
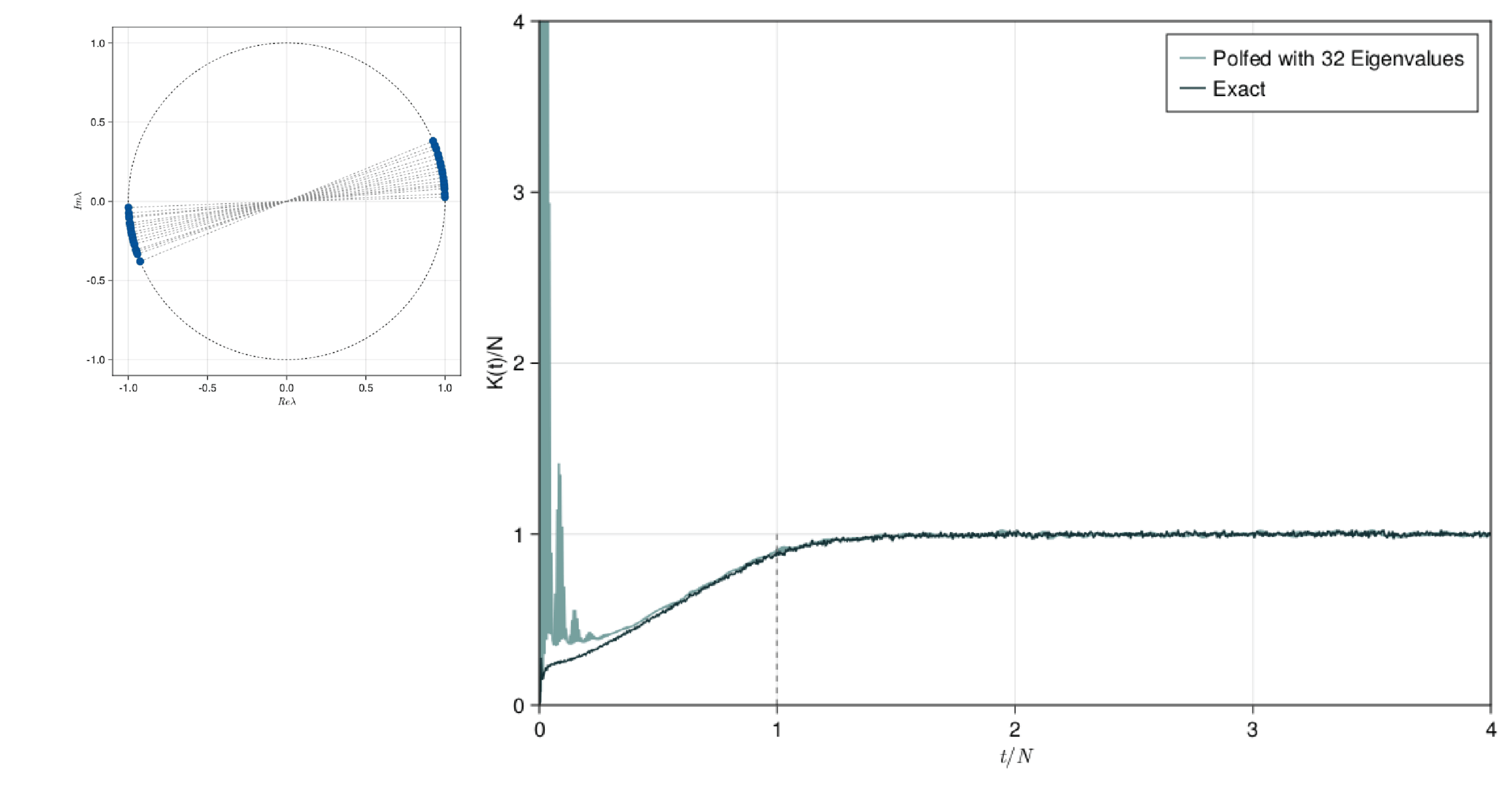
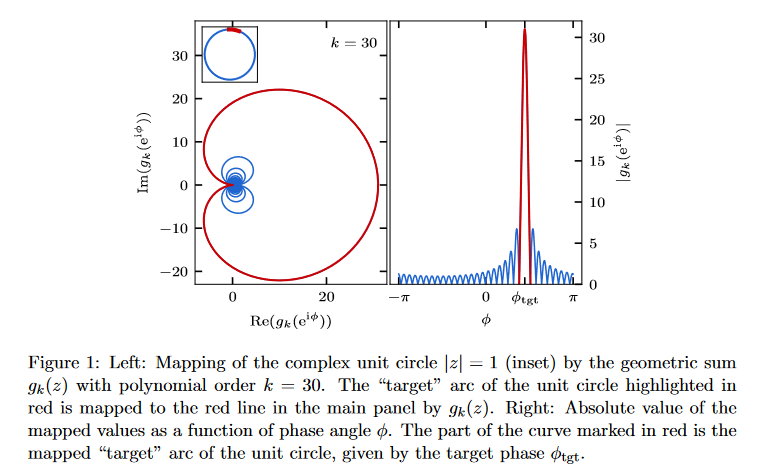
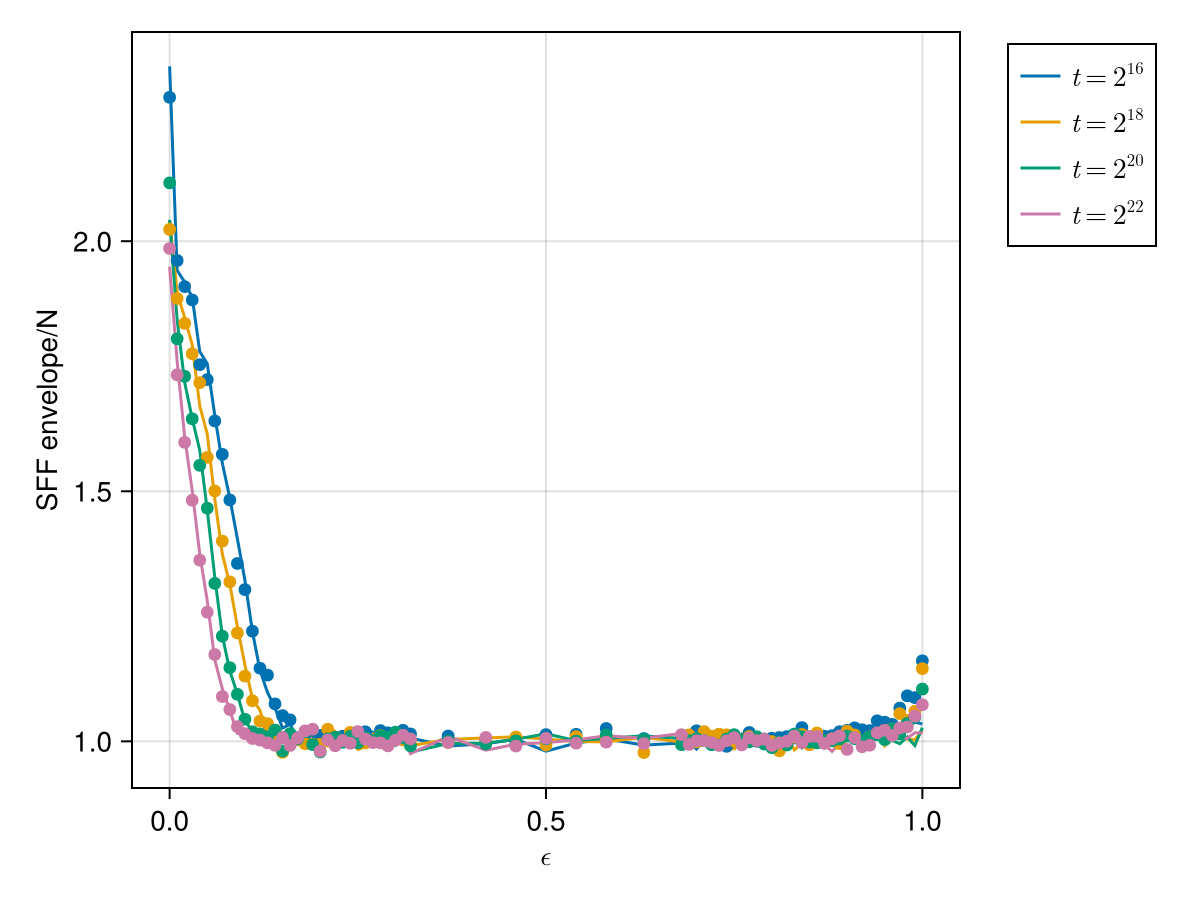
This presentation explores the Spectral Form Factors of an Unitary. It discusses the definition of SFF and how it can be reduced to a more familiar form using spectral decomposition. The presentation also mentions the connection between SFF and the two point correlator of the level density.
