Unitary Evolution of
Self-Dual Floquet Models
Jan-June 2020
Background:
Consider the Space-Time rotated Circuit.
Rotated Circuit is not in general Unitary
What are the conditions for it to be unitary (for d=2)?
Cause, if that's true, one can compute exactly the Dynamical Correlation
of all local observable by reducing them in the light cone!
Diagrammatic Notations:
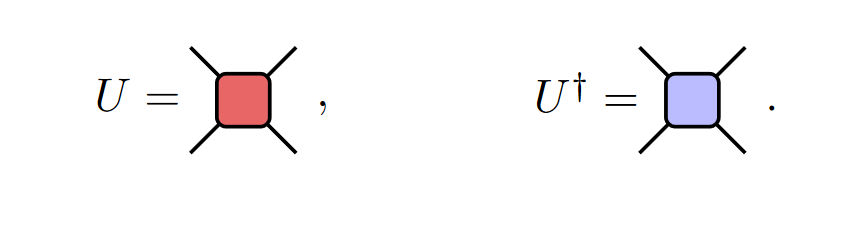
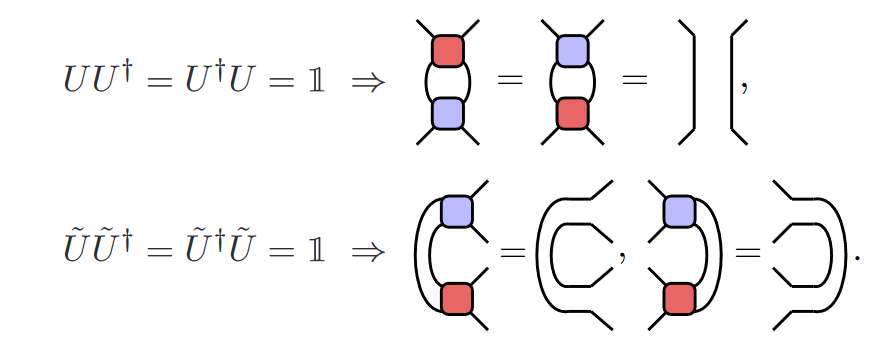
Duality conditions:
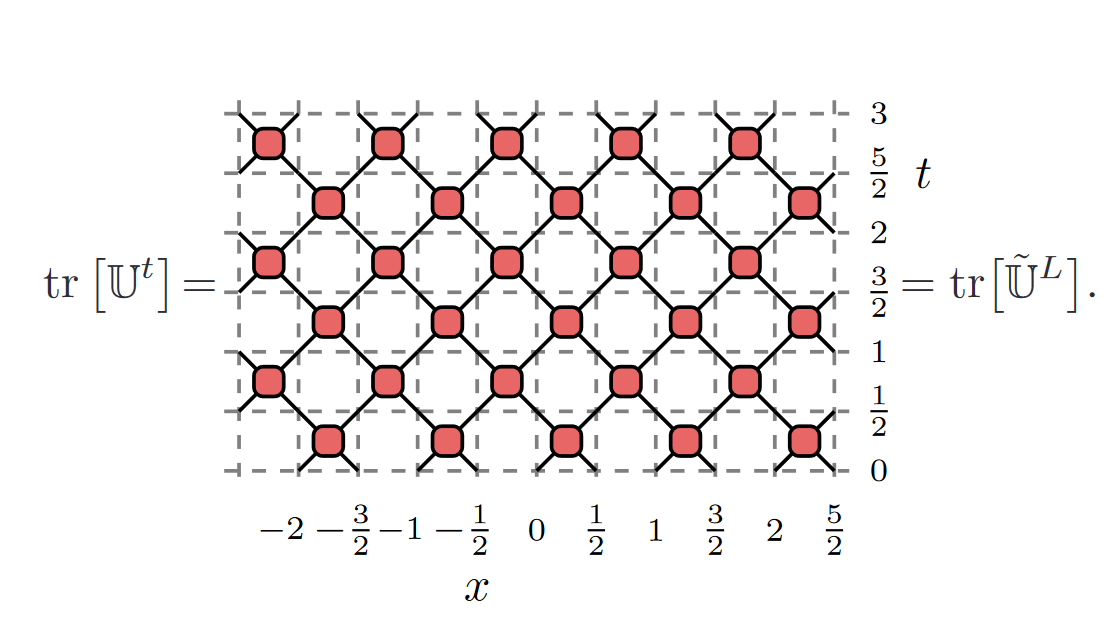
Trace:
Diagrammatic Notations:
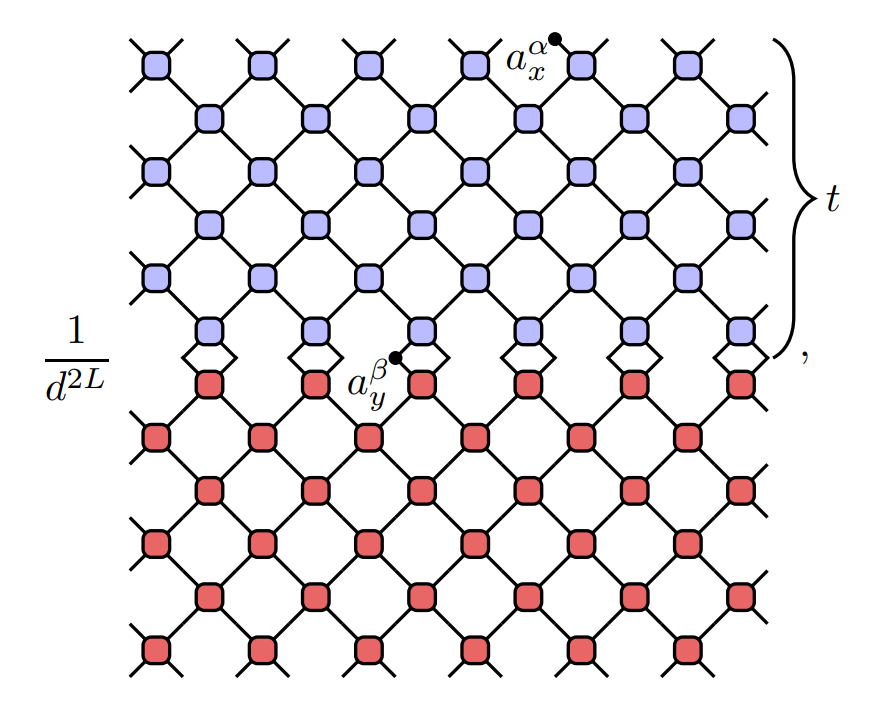
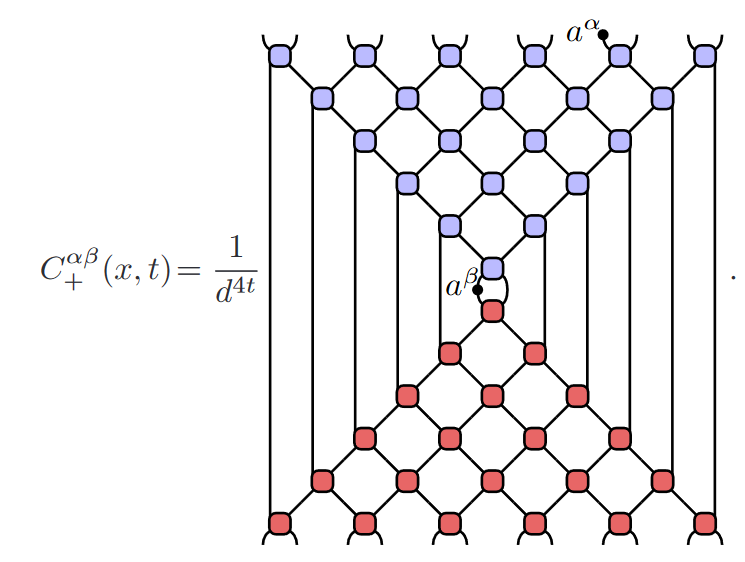
Correlations:
SU(2):
where, and,
Then, the dual is obtained as,
\tilde{U} = e^{i\phi}((v_2)^T \otimes u_2) \tilde{V}[J_1, J_2, J_3](v_1 \otimes (u_1)^T)
where everything other than is already Unitary.
\tilde{V}
U = e^{i\phi}(u_1 \otimes u_2) V[J_1, J_2, J_3](v_1 \otimes v_2)
a_1,a_2,a_3,\in \mathbb{R} \;\text{and}\; u_1,u_2,v_1,v_2 \in SU(2)
V[J_1, J_2, J_3]\exp \{ i (J_1\sigma_x \otimes \sigma_x + J_2 \sigma_y \otimes \sigma_y + J_3 \sigma_z \otimes \sigma_z)\}
SU(2):
\tilde{V}[J_1, J_2, J_3]=\begin{pmatrix}
e^{-iJ_3} \cos(J_1-J_2) & 0 & 0 & e^{iJ_3} \cos(J_1+J_2) \\
0 & -e^{-iJ_3} \sin(J_1-J_2) & -e^{iJ_3} \sin(J_1+J_2) & 0 \\
0 & -e^{iJ_3} \sin(J_1+J_2) & -e^{-iJ_3} \sin(J_1-J_2) & 0 \\
e^{iJ_3} \cos(J_1+J_2) & 0 & 0 & e^{-iJ_3} \cos(J_1-J_2) \\
\end{pmatrix}
Now has the parametrisation,
\tilde{V}
And the solution for unitarity is,
J_1= \frac{\pi}{4} + \frac{\pi}{2}n_1 \;\;,\;\; J_2= \frac{\pi}{4} + \frac{\pi}{2}n_2, \;\;,\;\; J_3 = J
One can show that the Kicked Ising Model,
is self-dual at
H_{KI}[t] = J\sum_j \sigma_j^z\sigma_{j+1}^z + h \sum_j \sigma_j^z + b \sum_j \sigma_j^x
|J|=|b|=\frac{\pi}{4}
Question to Ponder:
U = e^{i\phi}(u_1 \otimes u_2) V[\overline{J}](v_1 \otimes v_2)
where,
Can we write a similar decomposition for SU(3)?
\overline{J},\in \mathbb{R}^m \;\text{and}\; u_1,u_2,v_1,v_2 \in SU(3)
- If yes, then what is the structure of ?
V[\overline{J}]
- What are the duality conditions in terms of .
\overline{J}
A:
Such a decomposition is actually not possible to write for SU(3), in fact for any higher n.
Cartan Decomposition:
Let G be a group and K be a normal subgroup of G. Let g,k be their respective algebras. Let p be defined as,
\mathbf{g}=\mathbf{k}\oplus \mathbf{p}
Then if k,p satisfies,
[\mathbf{k},\mathbf{k}] \subset \mathbf{k}\\
[\mathbf{p},\mathbf{p}] \subset \mathbf{k}\\
[\mathbf{p},\mathbf{k}] \subset \mathbf{p}
Then at the level of groups,
where A is the maximal abbelian subalgebra contained in g
G=K e^{\mathbf{A}}K
Cartan Decomposition of SU(2):
\mathbf{k}=\{i \sigma_i \otimes \mathbf{I}, i \mathbf{I} \otimes\sigma_i \}\\
\mathbf{p}=\{i \sigma_i \otimes \sigma_j \}
It satisfies the Cartan Conditions. So,
and,
\mathbf{A}=\text{span}\{i \sigma_x \otimes \sigma_x, i \sigma_y \otimes \sigma_y, i \sigma_z \otimes \sigma_z\}
Same does not work for any higher dimensions
Let,
G=K e^{\mathbf{A}}K
Classification of Cartan Decomposition:
| Algebra | Universality Class |
|---|---|
| su(N) | AI,AII,AIII |
| so(N) | BI,BDI |
| sp(N) | CI,CII |
Upto conjugation, all cartan decompositions can be classified as,
Classification of Cartan Decomposition:
AI: Cartan Decomposition of su(N) into purely real and purely imaginary subspaces,
\mathbf{su}(N) =\mathbf{so}(N) \oplus \mathbf{so}(N)^{\perp}
AII:
\mathbf{su}(N) =\mathbf{sp}(N/2) \oplus \mathbf{sp}(N/2)^{\perp}
AIII:
\mathbf{su}(N) = r \oplus t
where r,t are respectively spanned by matrices of the form,
\sigma:=\begin{pmatrix}
A & 0 \\
0 & B \\
\end{pmatrix},
s:=\begin{pmatrix}
0 & C \\
-C^{\dagger} & 0 \\
\end{pmatrix}
SU(2) revisited:
For SU(4) it works because at the level of algebras so(4) is conjugate to su(2)xsu(2)
If the basis is chosen as,
Then, the real matrices forms the so(4) algebra, and the diagonals form the cartan subalgebra, a.
When rotated accordingly, a rotates into,
\mathbf{k}=\{i \sigma_i \otimes \mathbf{I}, i \mathbf{I} \otimes\sigma_i \}\\
\mathbf{p}=\{i \sigma_i \otimes \sigma_j \}
\mathbf{A}=\text{span}\{i \sigma_x \otimes \sigma_x, i \sigma_y \otimes \sigma_y, i \sigma_z \otimes \sigma_z\}
SU(3):
For SU(9), so(9) is not conjugate to su(3)xsu(3), so the program fails,
su(3)xsu(3) is a normal subalgebra, but If the basis is chosen as,
where the λ are Gellmann matrices, it does not satisfy the Cartan Conditions.
The subspace p is not even a subalgebra, and its dimension (48)> rank(8)
\mathbf{k}=\{i \lambda_i \otimes \mathbf{I}, i \mathbf{I} \otimes\lambda_i \}\\
\mathbf{p}=\{i \lambda_i \otimes \lambda_j \}
Can we find Abbelian subspaces within p?
Abbelian Subspace:
\mathbf{a_1}=\{i \lambda_1 \otimes \lambda_1 ,\;\;\;i \lambda_2 \otimes \lambda_2 , \;\;\;i \lambda_3 \otimes \lambda_3 , \;\;\;i \lambda_3 \otimes \lambda_8, \;\;\;i \lambda_8 \otimes \lambda_3 , \;\;\;i \lambda_8 \otimes \lambda_8 ,\\\lambda_4 \otimes \lambda_4 +i \lambda_5 \otimes \lambda_5 ,\;\;\;i \lambda_6 \otimes \lambda_6 +i \lambda_7 \otimes \lambda7 \}
\mathbf{a_2}=\{i \lambda_1 \otimes \lambda_2+i \lambda_2 \otimes \lambda_1 ,\;\;\; i \lambda_1 \otimes \lambda_2 -i \lambda_2 \otimes \lambda_1, \;\;\;i \lambda_3 \otimes \lambda_3 ,\;\;\; i \lambda_8 \otimes \lambda_8 ,\\ i \lambda_4 \otimes \lambda_5 -i \lambda_5 \otimes \lambda_4 ,\;\;\;i \lambda_6 \otimes \lambda_6 -i \lambda_7 \otimes \lambda6 \}
\lambda_1=
\begin{pmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
,\lambda_2=
\begin{pmatrix}
0 & -i & 0 \\
i & 0 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
,\lambda_3=
\begin{pmatrix}
1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
,\lambda_4=
\begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
1 & 0 & 0 \\
\end{pmatrix}
\lambda_5=\begin{pmatrix}
0 & 0 & -i \\
0 & 0 & 0 \\
i & 0 & 0 \\
\end{pmatrix}
,\lambda_6=
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{pmatrix}
,\lambda_7=
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -i \\
0 & i & 0 \\
\end{pmatrix}
,\lambda_8= \frac{1}{\sqrt{3}}
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -2 \\
\end{pmatrix}
where the Gellmann Matrices are,
Abbelian Subspace 1:
\left(
\begin{array}{ccccccccc}
e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \cos \left(a_1-a_2\right) & 0 & 0 & 0 & e^{\frac{1}{3} i \left(3 a_3-a_4\right)} \cos \left(a_1+a_2\right) & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \cos \left(2 a_5\right) \\
0 & -i e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \sin \left(a_1-a_2\right) & 0 & -i e^{\frac{1}{3} i \left(3 a_3-a_4\right)} \sin \left(a_1+a_2\right) & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & -i e^{\frac{2 i a_4}{3}} \sin \left(2 a_5\right) & 0 & 0 \\
0 & -i e^{\frac{1}{3} i \left(3 a_3-a_4\right)} \sin \left(a_1+a_2\right) & 0 & -i e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \sin \left(a_1-a_2\right) & 0 & 0 & 0 & 0 & 0 \\
e^{\frac{1}{3} i \left(3 a_3-a_4\right)} \cos \left(a_1+a_2\right) & 0 & 0 & 0 & e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \cos \left(a_1-a_2\right) & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \cos \left(2 a_6\right) \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & -i e^{\frac{2 i a_4}{3}} \sin \left(2 a_6\right) & 0 \\
0 & 0 & -i e^{\frac{2 i a_4}{3}} \sin \left(2 a_5\right) & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & -i e^{\frac{2 i a_4}{3}} \sin \left(2 a_6\right) & 0 & 0 & 0 \\
e^{\frac{2 i a_4}{3}} \cos \left(2 a_5\right) & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \cos \left(2 a_6\right) & 0 & 0 & 0 & e^{-\frac{1}{3} \left(4 i a_4\right)} \\
\end{array}
\right)
The structure of the dual sub-space:
The solution to the unitarity conditions are
a_1 = a_2 = a_5 = a_6= \frac{\pi}{4} \;\;\; a_3, a_4 \in \mathbb{R}
Abbelian Subspace 2:
\left(
\begin{array}{ccccccccc}
e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \cos \left(2 a_1\right) & 0 & 0 & 0 & e^{i a_3-\frac{i a_4}{3}} \cos \left(2 a_2\right) & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \cos \left(2 a_5\right) \\
0 & -e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \sin \left(2 a_1\right) & 0 & e^{i a_3-\frac{i a_4}{3}} \sin \left(2 a_2\right) & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \sin \left(2 a_5\right) & 0 & 0 \\
0 & -e^{i a_3-\frac{i a_4}{3}} \sin \left(2 a_2\right) & 0 & e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \sin \left(2 a_1\right) & 0 & 0 & 0 & 0 & 0 \\
e^{i a_3-\frac{i a_4}{3}} \cos \left(2 a_2\right) & 0 & 0 & 0 & e^{-\frac{1}{3} i \left(3 a_3+a_4\right)} \cos \left(2 a_1\right) & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \cos \left(2 a_6\right) \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \sin \left(2 a_6\right) & 0 \\
0 & 0 & -e^{\frac{2 i a_4}{3}} \sin \left(2 a_5\right) & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & -e^{\frac{2 i a_4}{3}} \sin \left(2 a_6\right) & 0 & 0 & 0 \\
e^{\frac{2 i a_4}{3}} \cos \left(2 a_5\right) & 0 & 0 & 0 & e^{\frac{2 i a_4}{3}} \cos \left(2 a_6\right) & 0 & 0 & 0 & e^{-\frac{1}{3} \left(4 i a_4\right)} \\
\end{array}
\right)
a_5= \frac{3\pi}{4},\;\; a_1= a_6= \frac{\pi}{4}, \;\;a_2=a_3=\frac{\pi}{2}, \;\; a_4 \in \mathbb{R}
The structure of the dual sub-space:
The solution to the unitarity conditions are
Further:
- Can we construct a "representation" of SU(9)/SU(3)xSU(3) in terms of the abbelian patches?
- How many such subalgebras exists? Do the set containing all of them spans the entire subspace?
- How many types of the abbelian sub-algebras are there?
- How do the structure generalises to SU(N^2)/SU(N)xSU(N)
- In the current patches? Can we map any physical model? (3-level Potts)
Unitary Evolution
By Sagnik Ghosh
