賽局理論

(Game Theory)

賽局 DP

(Game DP)

來看一個超級經典的題目吧

CSES - Removal Game

現在，在桌子上有 $N$ 顆石頭排成一排，每顆石頭上分別都寫著一個數字 $a_i$。Alice 和 Bob 在玩一個遊戲，他們只能從最左邊和最右邊的石頭開始拿，兩個人都以最佳的走法去玩遊戲，請問 Alice 最多可以拿到多少石頭?

狀態: 令 $dp[l][r]$ 表示先手在區間 $[l,r]$ 內所能拿到的最多石頭

轉移式: $dp[l][r] = \max(sum(l,r) - dp[l+1][r], sum(l,r) - dp[l][r-1])$

Base Case: $dp[i][i] = a_i$

相信大家都已經很熟悉這個做法了！

這種題目特別的點在於，當先手做完操作之後，後手就會變成下一回合的先手。而我們靠著這一點去設計了我們的狀態以及轉移式。

而這題其實也有另外一種狀態的假設方法

令 $dp[l][r]$ 表示先手與後手在區間 $[l,r]$ 內的分數差

而在這樣的假設方法當中，先手會去最大化分數差，而後手會去最小化分數差

ABC201D - Game in Momotetsu World

現在有一張 $H \times W$ 的網格圖，而 Takahashi 和 Aoki 兩個人在玩遊戲。在每一個格子上，都被塗上了紅色與藍色兩種顏色。兩個人輪流移動這個棋子，玩家可以選擇將棋子往右或往下移動，如果將棋子移動到了紅色的格子上，分數就會 $-1$，否則玩家的分數就會 $+1$，請問在兩個人皆以最佳策略玩遊戲時，誰會贏?

這題基本上可以滿輕易地列出狀態

令 $dp[i][j]$ 表示棋子走到 $(i,j)$ 時的分數差

當輪到 Takahashi 時，會是最大分數差

當輪到 Aoki 時，會是最小分數差

轉移式的話應該也算好想到

不過這裏特別的點是，你可能會列出一個

$dp[i][j]$ 是從 $dp[i-1][j]$ 與 $dp[i][j-1]$ 所轉移而來的轉移式

但你仔細想想，會發現我們從前面開始轉移會有很大的問題

你在 $(i,j)$ 時讓自己照著規則這樣去移動的話

真的會是最佳的走法嗎?

這裡的解決方式會是將順序反過來思考

從 $(n,m)$ 開始轉移回到 $(1,1)$

照著這樣的方式，就可以正確得到答案了！

參考程式碼

組合賽局

(Combinatorial Game Theory)

接下來所提到的所有賽局都會是組合賽局

組合賽局?

說到賽局理論，這個東西其實有很多不同種類

而在競程上，我們主要會討論的

則是所謂的組合賽局

組合賽局

由兩人進行對戰，並且輪流進行操作
資訊是公開的，兩人都可以知道賽局的完整盤面
遊戲不受任何機率所影響，在同個盤面下的操作會有相同結果
賽局的結果會是一贏一輸，或者是平手

來看一個經典的小例題吧!

Subtraction Game

Alice 和 Bob 在玩遊戲，現在，在桌子上有 $n$ 顆石頭，輪到該玩家的回合時，可以選擇拿取 $1 \sim 3$ 顆石頭，拿不了石頭的人就輸了。Alice 先拿，問你如果雙方都以最佳策略在玩遊戲，Alice 和 Bob 誰會贏？

我們可以來分析一下 $n$ 很小的 case

當 $n \le 3$ 時，只要先手把石頭都拿完就贏了
當 $n=4$ 呢? 會發現不管怎麼拿，都會導致後手贏！
當 $n=5$ 呢? 只要先手把石頭拿成 $n=4$ 就會贏了！

我們可以把這個畫成一個表格

0	1	2	3	4	5	6	7	8	9
Bob	Alice	Alice	Alice	Bob	Alice	Alice	Alice	Bob	Alice

在 $n \bmod 4 = 0$ 的時候，後手贏，否則先手會贏！

遊戲圖

(Game Graph)

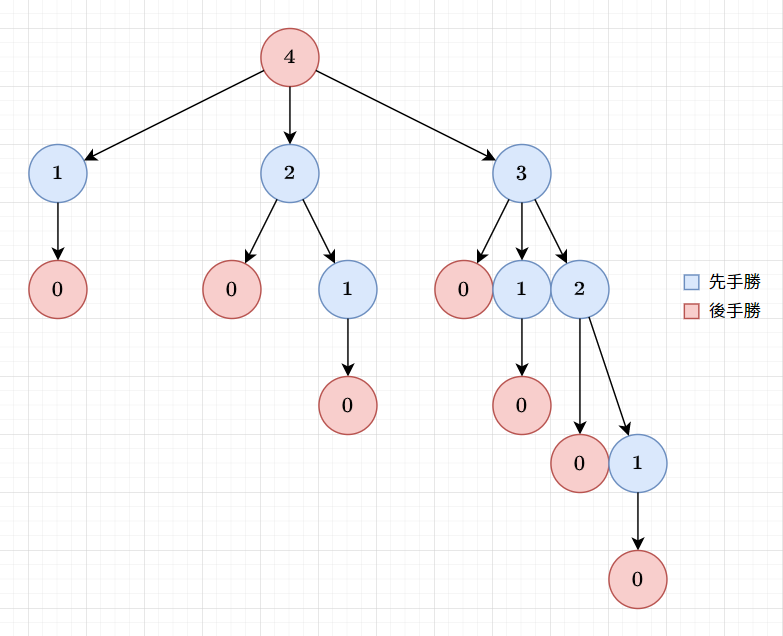
剛剛的 Subtraction Game 的遊戲圖

會發現到

一個狀態是先手勝，倘若可以走到一個後手勝的狀態

一個狀態是後手勝，倘若所有可以走到的狀態皆為先手勝

因此，如果今天遊戲圖是一張 DAG

就可以在上面做拓樸排序 + DP 去找到一個狀態的勝負了！

同時也可以想成是兩個人在一張有向圖上玩遊戲

ABC209E - Shiritori

現在，Takahashi 和 Aoki 在玩三個字母的接龍，而他們可以說 $n$ 種不同的字串。同一個字可以重複使用，但沒有辦法接下去的人就輸了，請問雙方都以最佳策略下去玩的時候，假設 Takahashi 從第 $i$ 個字串開始說，誰會贏?

(看原題敘可能會好懂很多)

我們可以將題目轉換一下

其實每個 word 代表的意義可以變成是一條邊

而這條邊是從前三個字母 $\rightarrow$ 後三個字母

因此，這個題目就被轉換成了有 $52^3$ 個狀態與 $n$ 條邊的遊戲圖了

用拓樸排序就可以計算出每個狀態的答案了！

參考程式碼

賽局的分類

對於每一個組合賽局，我們可以將其分類為以下幾種

無偏 (Impartial)	有偏 (Partisan)
無環 (Loopfree)	有環 (Loopy)
有限 (Finite)	超限 (Transfinite)

不過這裡我們只介紹無偏和有偏賽局

無偏 (Impartial)：對於同一個盤面，雙方可做的操作皆相同

有偏 (Partisan)：對於同一個盤面，雙方可做的操作可不同

簡單來說，例如西洋棋、象棋、圈圈叉叉等都是有偏賽局

而剛剛所介紹的 Subtraction Game 則是無偏賽局

照遊戲決定勝負的方式也被分為以下兩種

標準 (Standard)：無法移動的玩家被判輸

匱乏 (Misere)：無法移動的玩家被判贏

而我們會講的基本上都是標準無偏賽局

並且這些賽局皆只有輸贏沒有平手

而對於標準無偏賽局，每個賽局有兩種型別

$N$：先手勝

$P$：後手勝

也就是當雙方都以最佳策略下去玩的時候

每個賽局只會有這兩種可能性

賽局和

(Disjuntive Sum)

再來要介紹的東西會有點抽象

定義

對於兩個賽局 $G_1, G_2$，定義他們的賽局和 $G_1+G_2$ 為將兩個賽局放在同一個盤面上，每一次要選擇 $G_1,G_2$ 其中一個賽局進行操作所產生的賽局

簡單來說，例如 $G_1$ 是西洋棋，$G_2$ 是圍棋

那把西洋棋和圍棋同時擺在桌上就是 $G_1+G_2$

定義

對於兩個賽局 $G_1, G_2$，如果所有賽局 $H$ 都可以使得 $G_1+H = G_2 + H$，則我們說兩個賽局等價

這裡可能有點難懂，但可以想成如果我們對兩個盤面做任意相同的操作，都可以使得他們的勝負關係是相同的，那他們就是等價的

而其實後面的很多東西都可以利用這兩點去證明

不過我們接下來會省略證明的部分

主要是想介紹一下名詞

Nim Game

這是整個無偏賽局中最重要的遊戲喔！

CSES - Nim Game I

在桌上有 $n$ 堆石頭，每堆分別有 $a_i$ 顆石頭，有兩個人輪流拿石頭，每次可以選擇一堆，拿取數量非 $0$ 的石頭，沒有辦法取石頭的人就輸了。請問在雙方都以最佳策略玩遊戲時，先手還是後手必勝?

我們直接來講結論

令 $X = a_1 \oplus a_2 \oplus \cdots \oplus a_n$

當 $X = 0$ 時，後手必勝

當 $X \ne 0$ 時，先手必勝

($\oplus$ 是指 XOR)

至於為什麼是這樣呢?

可以嘗試證明看看以下這兩點

1. 對於 $X=0$ 的狀態，只能走到 $X \ne 0$ 的狀態或無法操作

2. 對於 $X \ne 0$ 的狀態，至少有一個方法可以走到 $X = 0$

證明完這兩點，其實概念就跟剛剛講的遊戲圖差不多

而每個盤面，其實都等價於只有一堆 $X$ 顆石頭的 Nim

然後為了等一下要講的 SG Theorem

這裡我們來看一下一個小小的變化

Nim With Increases

現在桌上有 $n$ 堆石頭，每次玩家可以選擇一堆石頭拿取或增加石頭 (不可以不做事情)，但是當每一堆的石頭數量都是 $0$ 時，遊戲就結束了，假設遊戲一定會結束。請問先手會贏還是後手會贏。

會發現其實這個跟原本的 Nim 一模一樣

假設當前的玩家將某一堆的石頭增加 $a$ 顆

那下一位玩家只要把那 $a$ 顆都拿走就好了

所以其實這個遊戲還是等價於一堆有 $X$ 顆石頭的 Nim

CSES - Stair Game

現在有一個 $n$ 階的階梯，在每一階上面都放了 $a_i$ 個石頭

每一次可以選擇任意數量在第 $k$ 階的石頭 $(k > 0)$

並將這些石頭移到 $k-1$ 階

兩個人輪流進行操作，無法移動的人就輸了

請問先手勝還是後手勝

其實這題就是在奇數階的石頭上玩遊戲而已

所以答案就是等價於一堆有 $a_1 \oplus a_3 \oplus ...$ 的 Nim！

仔細想想，你會發現先手其實不必去碰偶數階梯上的石頭！

因為如果先手將第 $i$ 階上的石頭移下來

那麼後手一定可以將同樣數量的石頭從 $i-1$ 階移到 $i-2$ 階

讓奇數階的石頭數量維持一樣

所以跟 Nim with Increases 的概念一模一樣

而且當奇數階沒有石頭的時候，先手必敗

因為當先手移動偶數階時，後手只要照我們剛剛講的

進行對應的操作

則後手必勝，因此會發現這個遊戲只與奇數階有關

Sprague-Grundy Theorem

任一個無偏賽局都等價於一堆有 $X$ 顆石頭的 Nim

而這個 $X$ 我們稱其為這個賽局的 SG Value (或 Grundy Number, Nimber, ...)

Sprague-Grundy Theorem

不過在我們講要怎麼找到一個賽局的 SG Value 之前

我們再來看看另外一個例子吧

Choose Nim

現在有 $n$ 堆石頭，石頭的數量分別是 $\{a_1,a_2,\cdots,a_n\}$，先手可以選擇任何一堆，接著兩人就按照 Nim 的規則對那堆石頭玩遊戲。

這個遊戲可能還滿廢的，畢竟只要有任何一堆的石頭數量是 $0$ 就是先手獲勝，不過，我們這裡想要討論的是，對於這個賽局，他其實等價於一堆數量有 $X$ 的 Nim With Increases。而我們要怎麼找到這個 $X$ 呢?

事實上，這個 $X$ 的值會是

$$\text{mex}(\{a_1,a_2,\cdots,a_n\})$$

而這裡的 mex 指的是這些數字當中，最小沒有出現過的正整數 (Minimum Excluded)

比較好的思考方式是，如果先手選擇了小於 $X$ 的一堆 $a$

那後手一定可以將 $a$ 增加到 $X$ 顆

而如果先手選擇了大於 $X$ 的一堆，後手也可以把它減少回到 $X$

因此兩個遊戲其實是等價的

而我們剛剛也看過了，Nim With Increases 其實等價於 Nim

所以這個遊戲等價於 $X$ 顆石頭的 Nim

因此，根據這個定理，我們會發現

$SG(A+B) = SG(A) \oplus SG(B)$

還有

$SG(A) = \text{mex}(\{SG(C)\}), \forall C \text{ where } A \rightarrow C$

用遊戲圖來理解 SG Theorem

有了 Sprague-Grundy Theorem 之後

對於每一個無偏賽局的狀態

我們都可以用一個 SG Value 來表示這些狀態

而 $n$ 堆石頭的 Nim Game

可以把它看成是 $n$ 個一堆的 Nim 加在一起所得到的遊戲

因此當我們把不同的賽局作賽局和時

其實就只要將他們的 SG Value 給 XOR 起來就可以找到新的 SG 了

感覺很難理解對吧！那我們實際來看看例子吧

我們用前面講過的 Subtraction Game 來作為例子

對於 $N$ 顆石頭的狀態

$SG(N) = \text{mex}(SG(N-1),SG(N-2),SG(N-3))$

而當 $N=0$ 時，由於後手必勝，$SG(0) = 0$

我們可以將圖畫出來，會得到下面這樣的圖

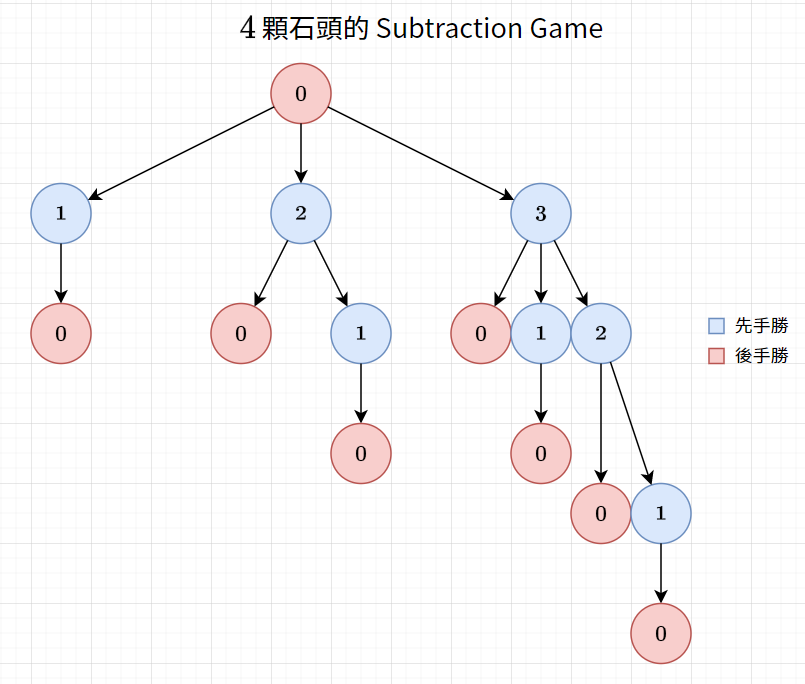
因此，其實會發現，$SG(X) = X \bmod 4$

也就是說，有 $X$ 顆石頭的 Subtraction Game

等價於一堆有 $X \bmod 4$ 顆石頭的 Nim

CSES - Nim Game II

Alice 和 Bob 在玩遊戲，現在，在桌子上有 $n$ 堆石頭，輪到該玩家的回合時，選擇任何一堆拿取 $1 \sim 3$ 顆石頭，拿不了石頭的人就輸了。Alice 先拿，問你如果雙方都以最佳策略在玩遊戲，Alice 和 Bob 誰會贏？

對於一堆有 $X$ 顆石頭的 Subtraction Game

我們知道他的 $SG(X) = X \bmod 4$

因此對於 $n$ 堆，其實整個賽局的 SG Value 會是

$(a_1 \bmod 4) \oplus \cdots \oplus (a_n \bmod 4)$

CSES - Grundy's Game

桌上一堆 $n$ 個硬幣的堆，以及兩個玩家在玩遊戲

兩個玩家輪流進行操作

每次可以選擇一堆，將這堆分成兩堆大小不同的硬幣堆

移動不了的人就輸了

請問先手必勝還是後手必勝

當我們遇到一題賽局時，我們要想辦法算出每個狀態的 SG Value

那現在假設有一堆的石頭數量是 $x$ 呢

他的 SG Value 會是多少?

我們可以列出下面的轉移式

$SG(x) = \text{mex}(\{SG(a) \oplus SG(b)\}) , \text{where } a+b = x \text{ and } a \ne b$

舉例來說，對於 $5$ 顆石頭，我們有底下幾種分法

$1+4, 2+3, 3+2, 4+1$

而分成兩堆之後，這兩堆放在一起的 SG Value 可以 XOR 計算

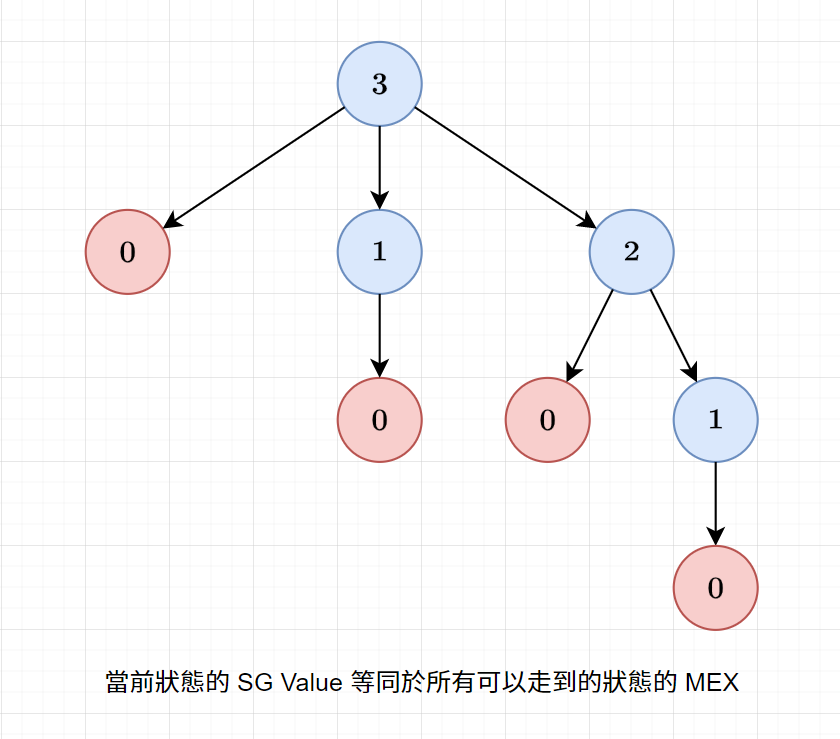
並且當前狀態的 SG Value 會是所有可以走到的狀態的 MEX

參考程式碼

int mex(vector<int> v){
    set<int> s;
    for(int i = 0;i < v.size();i++) s.insert(v[i]);
    for(int i = 0;i < N;i++) if(s.find(i)==s.end()) return i;
}
 
void init(){
    for(int i = 3;i <= MAXV;i++){
        vector<int> v;
        for(int j = 1;j < (i+1)/2;j++){
            v.push_back(dp[j]^dp[i-j]);
        }
        dp[i] = mex(v);
    }
}

不過我們可以來想一下這樣的時間複雜度

對於 $SG(x)$，可以在 $O(x^2)$ 的時間內得到所有的狀態的 SG

然後再用 $O(x)$ 的時間計算出 MEX

因此總共的時間複雜度是 $O(x^3)$！

欸？等等，可是最大的石頭數量可以到 $10^6$ 欸

實際上，如果實際去跑過這個程式之後

會發現當 $x$ 超過一定的數字 (一千多) 之後

SG Value 都不會是 $0$！

因此，我們可以多判斷這件事

完整程式碼

Codeforces 603C - Lieges of legendre

雖然現在有 $n$ 堆，但是其實我們可以分開來看

先將每一堆各自的 SG Value 計算出來之後

最後再將它們 XOR 起來就好了

照著同樣的概念，我們其實可以很輕易地列出這樣的轉移式

SG(X) = \begin{cases} \text{mex}(\{SG(X-1)\}) &, \text{if } x \bmod 2 = 1 \\ \text{mex}(\{SG(X-1),SG(x/2) \cdot (k \bmod 2)\}) &, \text{if } x \bmod 2 = 0 \\ 0 &, \text{if } x = 0 \end{cases}

因此只要照著這個轉移式去計算即可！

不過會發現一件事情，$a_i$ 的數量可以到 $10^9$ 欸！

因此我們其實可以嘗試將 SG 的表格印出來看看

#include <bits/stdc++.h>
 
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
 
using namespace std;
 
int mex(vector<int> v){
    set<int> s;
    for(int i = 0;i < v.size();i++) s.insert(v[i]);
    for(int i = 0;i < N;i++) if(s.find(i)==s.end()) return i;
}
 
int k;

int SG(int x){
	if(x == 0) return 0;
	else if(x % 2 == 1) return mex({SG(x-1)});
	else return mex({SG(x-1),SG(x/2)*(k%2)});
}
 
signed main(){
    fastio
    int n;
    cin >> n;

    k = 0;

    for(int i = 0; i <= n; i++){
    	cout << SG(i) << " ";
    }
}

會發現當 $k$ 是偶數時，表格長這樣

i	0	1	2	3	4	5	6	7	8
SG(i)	0	1	2	0	1	0	1	0	1

會發現當 $i \ge 3$ 的時候

如果 $i$ 是偶數，$SG(i) = 1$

如果 $i$ 是奇數，$SG(i) = 0$

會發現當 $k$ 是奇數時，表格長這樣

i	0	1	2	3	4	5	6	7	8
SG(i)	0	1	0	1	2	0	2	0	1

會發現當 $i > 4$ 的時候

如果 $i$ 是奇數，答案就是 $0$

否則可能是 $1$ 或 $2$

i	9	10	11	12	13	14	15	16	17
SG(i)	0	1	0	1	0	1	0	2	0

那我們要怎麼知道他是 $1$ 還是 $2$ 呢?

我們其實可以直接從轉移式去思考

當 $k$ 是奇數且 $X$ 是偶數時，會有

SG(X) = \text{mex}(\{SG(X-1),SG(x/2)\})

而我們知道當 $X > 4$ 時，奇數答案都是 $0$

所以其實轉移式變成

SG(X) = \begin{cases} 2 &, \text{ if } SG(x/2) = 1 \\ 1 &, \text{ if } otherwise \end{cases}

可以在 $O(\log x)$ 的時間算完

所以對於每堆，我們可以在 $O(1)$ 或 $O(\log a_i)$ 的時間算完

因此只要算出每堆的 SG Value 之後

將他們 XOR 起來就是答案了！

參考程式碼

SG Value 的循環

通常，對於一個賽局，SG Value 常常會出現規律

而最常出現的可能性就是循環！

Kayles

有 $n$ 堆石頭，每堆有 $a_i$ 顆石頭

每次可以選擇一堆，並且對他進行以下操作

拿取 $1$ 或 $2$ 顆
將剩下來的石頭分成兩堆 (大小可以是 $0$ 也可以大小相同)

請問當兩人都以最佳策略在玩的時候，先手還是後手必勝?

同樣的，會發現其實我們可以把 $n$ 堆看成很多個一堆

因此我們只需要去找出每堆的 SG Value 即可

對於一堆有 $x$ 顆的石頭，SG Value 可以靠以下轉移式計算

SG(x) = \text{mex}(\{SG(a) \oplus SG(b)\}), \text{where } a+b = x-1 \text{ or } a+b = x-2

不過如果這個轉移式的複雜度會是 $O(x^2)$ 欸！

如果石頭的數量很大，就沒辦法用這個方式計算了

所以我們一樣來看看規律！

#include <bits/stdc++.h>
 
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
 
using namespace std;

const int N = 1e6+5;
int dp[N];

int mex(vector<int> v){
    set<int> s;
    for(int i = 0;i < v.size();i++) s.insert(v[i]);
    for(int i = 0;;i++) if(s.find(i)==s.end()) return i;
}

int SG(int x){
	if(dp[x]) return dp[x];
	vector<int> v;
	for(int a = 0; a <= x; a++){
		int b = x-1-a, b2 = x-2-a;
		if(b >= 0) v.push_back(SG(a)^SG(b));
		if(b2 >= 0) v.push_back(SG(a)^SG(b2));
	}
	return dp[x] = mex(v);
}
 
signed main(){
    fastio
    int n;
    cin >> n;

    for(int i = 0; i <= n; i++){
    	cout << SG(i) << " ";
    }
}

最後會發現其實當 $x \ge 72$ 的時候

每 $12$ 個數字會產生循環！

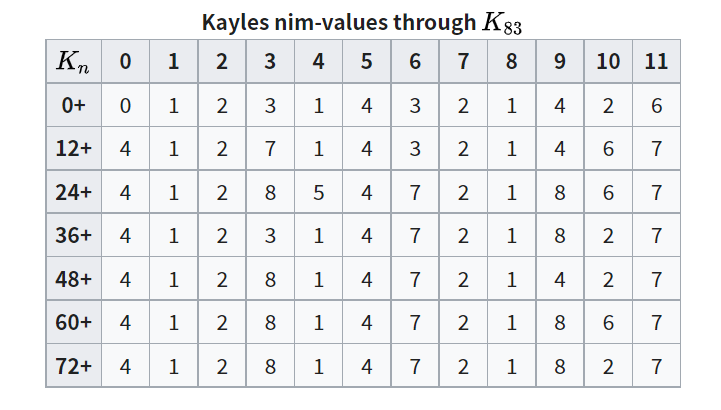
所以其實只要暴力計算出前 $72$ 個 SG Value

剩下的用規律就可以知道答案了

練習題

CSES Mathematics 所有的 Game

TIOJ 1123 - 辣椒醬蛋糕問題

Codeforces 1451F - Nullify the Matrix

ARC151C - 01 Game

Codeforces 1407F - Colouring Game

ABC278G - Generalized Subtraction Game

ABC255G - Constrained Nim

賽局理論

By sam571128

賽局理論

賽局 DP

來看一個超級經典的題目吧

組合賽局

組合賽局?

組合賽局

來看一個經典的小例題吧!

Subtraction Game

遊戲圖

賽局的分類

賽局和

再來要介紹的東西會有點抽象

定義

定義

Nim Game

Sprague-Grundy Theorem

Sprague-Grundy Theorem

Choose Nim

用遊戲圖來理解 SG Theorem

更多例題

SG Value 的循環

Kayles

賽局理論

More from sam571128