Dynamic
Programming
UMD Competitive Programming Club Week 4
What is Dynamic Programming
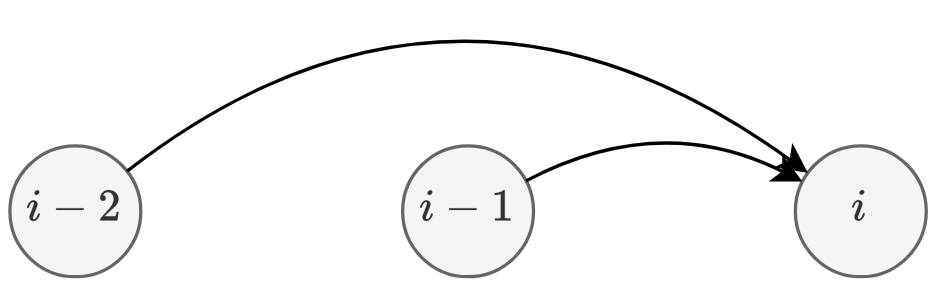
1. Overlapping Subproblems
What is Dynamic Programming
1. Overlapping Subproblems
What is Dynamic Programming
f_n = f_{n-1} + f_{n-2}
1. Overlapping Subproblems
What is Dynamic Programming
f_n
f_{n-1}
f_{n-2}
f_{n-2}
f_{n-3}
1. Overlapping Subproblems
What is Dynamic Programming
f_n
f_{n-1}
f_{n-2}
f_{n-2}
f_{n-3}
They are same!
1. Overlapping Subproblems
What is Dynamic Programming
int f(int n) {
if (n <= 1) return 1;
else return f(n-1) + f(n-2);
}You will compute some states more than once!!
\mathcal{O}(\phi^n)
1. Overlapping Subproblems
What is Dynamic Programming
int dp[MAXN];
int f(int n) {
if (dp[n]) return dp[n];
else if (n <= 1) return dp[n] = 1;
else return dp[n] = f(n-1) + f(n-2);
}Every state will now only be compute once
This is called Memoization
\mathcal{O}(n)
2. Optimal Substructures
What is Dynamic Programming
2. Optimal Substructures
What is Dynamic Programming
There is a stairs with \(n\) levels, there are \(a_i\) coins on each level, you can walk \(1\) or \(2\) steps each time. What is the maximum coins you can get?
f(n) = \max(f(n-1),f(n-2)) + a_i
Let \(f(n)\) be the maximum coins you get when you get to \(n\)
Two Different Ways
Two Different Ways
Top-Down Approach (Recursion)
Bottom-Up Approach (For Loop)
Two Different Ways
Let's look at Fibonacci again!!!
Two Different Ways
Top-Down (Recursion with Memoization)
int dp[MAXN];
int f(int n) {
if (dp[n]) return dp[n];
else if (n <= 1) return dp[n] = 1;
else return dp[n] = f(n-1) + f(n-2);
}Two Different Ways
Bottom-Up (For Loop)
int dp[MAXN];
dp[0] = dp[1] = 1;
for (int i = 2; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}We prefer Bottom-Up since the constant is smaller than recursion
How to Solve DP Problems
How to Solve DP Problems
Define States \(\Rightarrow\) Find The Transition \(\Rightarrow\) Handle Base Cases
The concept is abtract
Let's look at the problems!
Classic DP Problems
Classic DP Problems 1 - Frogs 1
Classic DP Problems 1 - Frogs 1
\text{Let } dp[i] \text{ be the minimum cost for the frog to jump to stone } i
Define The States
Classic DP Problems 1 - Frogs 1
Find The Transition
dp[i] = \min(dp[i-1] + |h_i - h_{i-1}|, dp[i-2] + |h_i - h_{i-2}|)
Classic DP Problems 1 - Frogs 1
Base Case
There is no cost for Frog to be at stone \(1\)
\Rightarrow dp[1] = 0
Classic DP Problems 1 - Frogs 1
Time complexity
\mathcal{O}(n)
Classic DP Problems 2 - Frogs 2
What if now a frog can jump at most \(k\) step forward?
\displaystyle dp[i] = \max_{1 \le j \le k} (dp[i-j] + |h_i - h_{i-j}|)
Each transition is \(\mathcal{O}(k)\)
\(\Rightarrow \mathcal{O}(nk)\)
Classic DP Problems 3 - Vacation
You are on a vacation for \(n\) days,
each day, you can do three activities
- Swim in the sea, and get \(a_i\) happiness
- Catch bugs, and get \(b_i\) happiness
- Do homework, and get \(c_i\) happiness
However, you cannot do same activities on consecutive days
What is the maximum happiness you can have?
Classic DP Problems 3 - Vacation
Define the state!
\text{ Let } dp[i] \text{ be the maximum happiness for the first } i \text{ days }
You want the state to be easy to do transition!
\text{ Let } dp[i][j] \text{ be the maximum happiness for the first } i \text{ days} \\
\text{where you do } jth \text{ activity on } ith \text{ day}
The answer is
\max(dp[n][0], dp[n][1], dp[n][2])
Classic DP Problems 3 - Vacation
Find The Transition!
dp[i][0] = \max(dp[i-1][1], \ dp[i-1][2]) + a_i \\
dp[i][1] = \max(dp[i-1][0], \ dp[i-1][2]) + b_i \\
dp[i][2] = \max(dp[i-1][0], \ dp[i-1][1]) + c_i
Each transition is \(\mathcal{O}(1)\)
Classic DP Problems 3 - Vacation
Base Case
dp[0][0] = dp[0][1] = dp[0][2] = 0
\mathcal{O}(n)
Time
Classic DP Problems 4 - LCS
You are given two strings \(s,t\)
Output their Longest Common Subsequence (LCS)
Classic DP Problems 4 - LCS
Define the states
\text{ Let } dp[i][j] \text{ be the LCS of } s_{0..i-1} \text{ and } t_{0..j-1}
You can also think of \(i,j\) as lengths
You can also think of \(i,j\) as lengths
Classic DP Problems 4 - LCS
Find The Transition
dp[i][j] =
\max \begin{cases}
dp[i-1][j-1] + 1 &, \text{ if } s[i-1] = t[j-1] \\
dp[i-1][j-1] \\
dp[i][j-1]
\end{cases}
Each Transition is \(\mathcal{O}(1)\)
Classic DP Problems 4 - LCS
Base Case
dp[0][i] = dp[i][0] = 0
Time
\mathcal{O}(nm)
Classic DP Problems 4 - LCS
How to construct answer?
Classic DP Problems 4 - LCS
How to construct answer?
Let \(from[i][j]\) be \(\{x,y\}\) where the value of \(dp[i][j]\) is from
Classic DP Problems 4 - LCS
How to construct answer?
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (s[i-1] == s[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
from[i][j] = {i-1, j-1};
}
if (dp[i-1][j] > dp[i][j]) {
dp[i][j] = dp[i-1][j];
from[i][j] = dp[i-1][j];
}
if (dp[i][j-1] > dp[i][j]) {
dp[i][j] = dp[i][j-1];
from[i][j] = dp[i][j-1];
}
}
}Classic DP Problems 5 - MCS
You are given an array with \(n\) integers
Find the maximum sum over all continuous subarray
Classic DP Problems 5 - MCS
Define the states
\text{Let } dp[i] \text{ be the maximum subarray sum ending at } i
The answer will be \(\max(dp[i])\) over all \(i\)
Classic DP Problems 5 - MCS
Find The Transitions
dp[i] = \max(dp[i-1] + a[i], a[i])
Either continue the previous sum, or start a new one
Classic DP Problems 5 - MCS
Base Case
dp[0] = 1
Classic DP Problems 6 - LIS
You are given an array of \(n\) numbers
Find the Longest Increasing Subsequence
Classic DP Problems 6 - LIS
Define The States
\text{Let } dp[i] \text{ be the length of LIS ends with } a_i
Classic DP Problems 6 - LIS
Find Transition
\displaystyle dp[i] = \max_{j \le i, \ a_j < a_i}(dp[j] + 1)
Classic DP Problems 6 - LIS
Base Case
dp[i] = 1
Time
\mathcal{O}(n^2)
Classic DP Problems 6 - LIS
Can we do better?
Classic DP Problems 6 - LIS
There are two ways to speed this up
- RMQ + Point Update
- Binary Search
We will only talk about 2. here
Classic DP Problems 6 - LIS
Consider the sequence
1, \ 3, \ 7, \ 5, \ 2, \ 6, \ 1
Let's look at it's DP Table
Classic DP Problems 6 - LIS
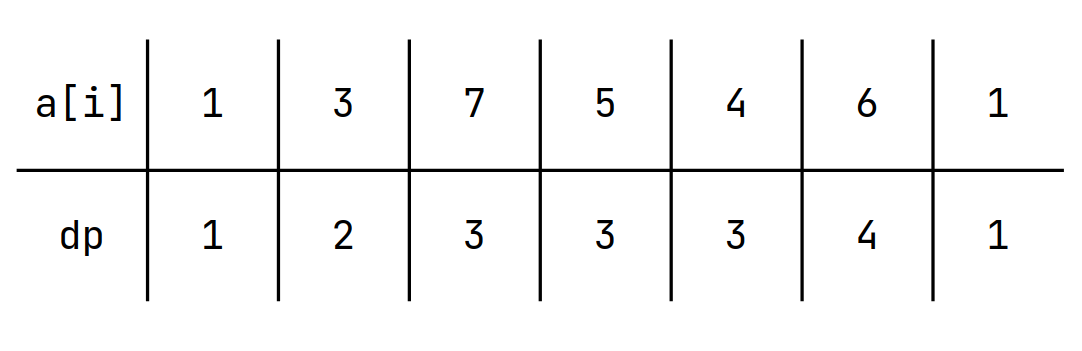
Let's define \(v[j]\) as the Minimum Value \(a_i\) such that \(dp[i] = j\)
Classic DP Problems 6 - LIS
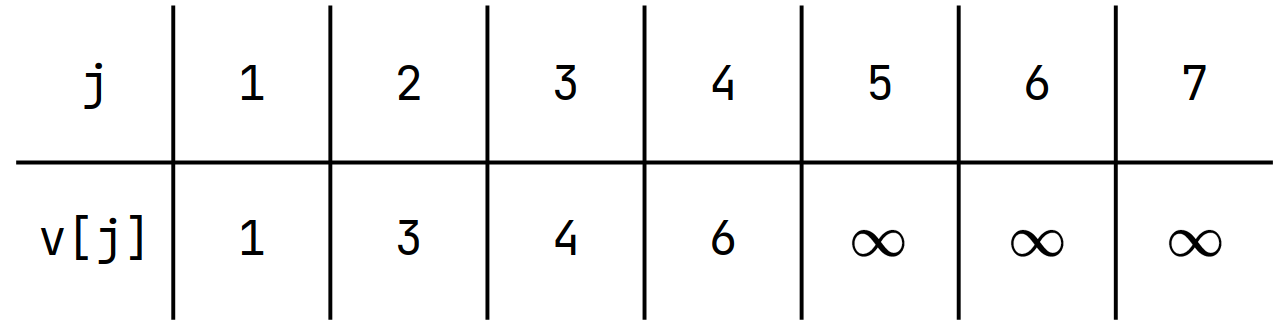
Classic DP Problems 6 - LIS
You can easily prove that \(v\) is increasing
Find the largest number less than \(a_i\)
Binary Search!!
Classic DP Problems 6 - LIS
1
1
Classic DP Problems 6 - LIS
1
1
2
3
Classic DP Problems 6 - LIS
1
1
2
3
3
7
Classic DP Problems 6 - LIS
1
1
2
3
3
5
3
Classic DP Problems 6 - LIS
1
1
2
3
3
4
3
3
Classic DP Problems 6 - LIS
1
1
2
3
3
4
3
3
4
6
Classic DP Problems 6 - LIS
1
1
2
3
3
4
3
3
4
6
1
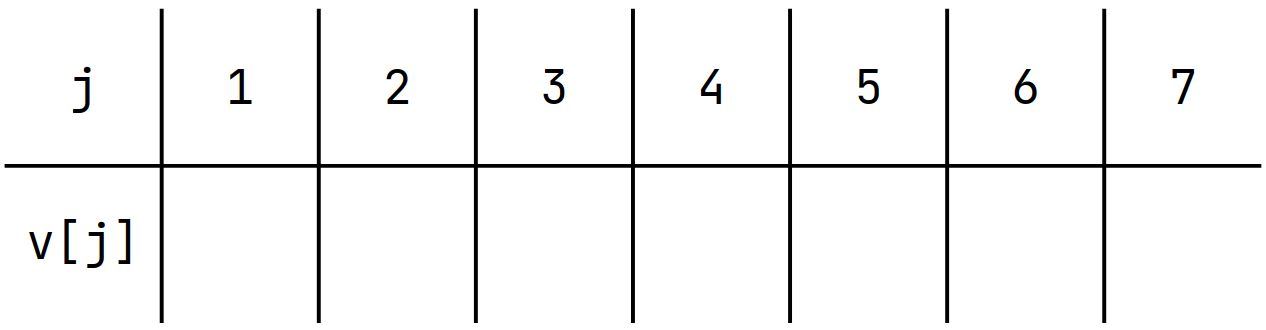
Classic DP Problems 6 - LIS
Code
int dp[n];
vector<int> v;
for(int i = 0; i < n; i++){
int idx = lower_bound(v.begin(), v.end(), a[i]) - v.begin();
if(idx == v.size()) v.push_back(a[i]);
else v[idx] = a[i];
dp[i] = idx + 1;
}
cout << v.size() << "\n";\mathcal{O}(n \log n)
Knapsack Problem
There are \(n\) items, each has weight \(w_i\) and value \(v_i\)
Now, you have a knapsack with capacity \(C\), find the maximum sum of values of items you can put in the knapsack
Define The States
\text{Let } dp[i][j] \text{ be the sum of value such that} \\
\text{The first } i \text{ items has sum of weight } j
Answer would be \(dp[n][W]\)
Find The Transition
For each item, you can choose to take or not take
Therefore, we can derive the transition as
dp[i][j] = \max(dp[i-1][j], dp[i-1][j-w[i]] +v[i])
Base Case
dp[0][j] = 0
(This can prevent some border cases)
Do we really need 2D?
NO!
There is a trick called Rolling DP
There is a trick called Rolling DP
dp[i\bmod 2][j]
We can define the states as this
since every time we do transition from \(i-1\)
dp[i\bmod 2][j] = \max(dp[(i-1) \mod 2][j], dp[(i-1) \mod 2][j - W] + v[i])
Transition becomes
dp[i\bmod 2][j] = \max(dp[(i-1) \mod 2][j], dp[(i-1) \mod 2][j - W] + v[i])
Transition becomes
Actually, we can even get rid of the first dimension!
for(int i = 1; i <= n; i++){
for(int j = W; j >= 0; j--){
if(j >= w[i])
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
}
}1D Version!
You may ask "Why is \(j\) from \(W\) to \(0\)?"
This is the original transition
You want the arrows to be exactly once
What if every item has infinitely many?
\(k\) from \(0\) to \(W\)!
for(int i = 1; i <= n; i++){
for(int j = 0; j <= W; j++){
if(j >= w[i])
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
}
}for(int i = 1; i <= n; i++){
for(int j = 0; j <= W; j++){
if(j >= w[i])
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
}
}O(nW)
for(int i = 1; i <= n; i++){
for(int k = 0; k < num[i]; k++){
for(int j = W; j >= 0; j--){
if(j >= w[i])
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
}
}
}O(W\sum k)
Can we do better?
Can we do better?
Do we really need to go through \(k\) for each item?
There is actually a faster way in
O(W\sum \lg k)
Range DP
Range DP
There are \(n\) slimes in a line each with a size \(a_i\), every time, you can choose \(2\) adjacent slimes with size \(a,b\) , and combine them into a slime with size \(a+b\), creating a cost of \(a+b\). What is the minimum cost required to combine all slimes?
Range DP
How should we define the state?
Range DP
Let \(dp[i]\) be the minimum cost to combine the first \(i\) slimes?
This will not work!!
Range DP
Define the states
\text{Let } dp[l][r] \text{ be the minimum cost to combine all simes in } [l,r]
Answer will be \(dp[1][n]\)
Range DP
Find The Transition
\displaystyle dp[l][r] = \min_{l \le k \le r}(dp[l][k] + dp[k][r] + \text{sum}(l,r))
Range DP
Find The Transition
\displaystyle dp[l][r] = \min_{l \le k \le r}(dp[l][k] + dp[k][r] + \text{sum}(l,r))
Consider this range
Range DP
Either \(10 + 3\) or \(4 + 9\) is possible
Combining \(6+3\), then combine \(4+9\) gives smaller cost!
Range DP
Base Case
dp[i][i] = 0
(No cost)
Range DP
Runtime
\displaystyle dp[l][r] = \min_{l \le k \le r}(dp[l][k] + dp[k][r] + \text{sum}(l,r))
The transition takes \(O(n)\) if you precompute the prefix sum
Therefore, the total time is \(O(n^3)\)
Range DP
Important thing about Range DP!
Let's look at two different codes, and let's vote on which one is correct!
Range DP
for (int l = 1; l <= n; l++) {
for(int r = 1; r <= n; r++) {
for (int k = l; k <= r; k++) {
dp[l][r] = min(dp[l][k] + dp[k][r] + sum(l, r));
}
}
}for (int l = n; l >= 1; l--) {
for(int r = l; r <= n; r++) {
for (int k = l; k <= r; k++) {
dp[l][r] = min(dp[l][k] + dp[k][r] + sum(l, r));
}
}
}Range DP
Why is the first one incorrect?
for (int l = 1; l <= n; l++) {
for(int r = 1; r <= n; r++) {
for (int k = l; k <= r; k++) {
dp[l][r] = min(dp[l][k] + dp[k][r] + sum(l, r));
}
}
}It is possible to use the data from ranges that we have not computed!
Range DP
The order of transition is important for Range DP!
Range DP
The order of transition is important for Range DP!
Range DP
Range DP
Define the states
\text{Let } dp[l][r] \text{ be the maximum score the first player can get in } [l,r]
Range DP
Find The Transition
dp[l][r] = \max \begin{cases}arr[l] + (\text{sum}(l+1,r) - dp[l+1][r]) \\
(\text{sum}(l,r-1) - dp[l][r-1]) + arr[r]
\end{cases}
This is because second player becomes first after first player's operation!
Range DP
Find The Transition
dp[l][r] = \text{sum}(l,r) - \min(dp[l+1][r],dp[l][r-1])
This is because second player becomes first after first player's operation!
Range DP
Base Case
dp[i][i] = a[i]
If there is only one stone, then first player takes the stone!
\mathcal{O}(n^2)
Bitmask DP
Bitmask DP
Travelling Salesman Problem
You are given a weighted graph with \(n\) vertices and \(m\) directed edges. You want to know the minimum sum of weights to start from \(s\), going through all vertices exactly once, then return to \(s\)
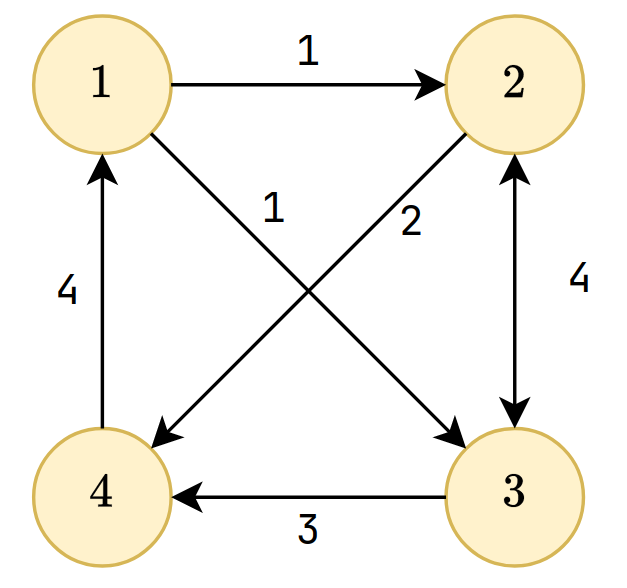
Bitmask DP
Travelling Salesman Problem
Define the states
\text{Let } dp[i][0/1]\ldots[0/1] \text{ be the minimum sum to visit the cities and ends at } i
If there are \(20\) vertices, then it means you have to do 20D DP!
Bitmask DP
Travelling Salesman Problem
Define the states
\text{Let } dp[i][mask] \text{ be the minimum sum to visit the cities and ends at } i
Compress the \(n\)D into a single integer!
Then answer will be \(\min(dp[i][2^n-1] + dis[i][s])\)
Bitmask DP
Travelling Salesman Problem
Find the transitions
dp[i][mask] = \min_{j \not \in mask}(dp[j][mask \oplus 2^j] + dis[j][i])
We go through all pairs of vertices for each mask!
Bitmask DP
Travelling Salesman Problem
Base Case
dp[s][2^s] = 0
Bitmask DP
Travelling Salesman Problem
Base Case
dp[s][2^s] = 0
Bitmask DP
for(int mask = 0;mask < (1<<n);mask++){
for(int u = 0;u < n;u++){
if(mask&(1<<u)){
for(int v = 0;v < n;v++){
if(mask&(1<<v)) continue;
dp[v][mask^(1<<v)] = min(dp[v][mask^(1<<v)], dp[u][mask] + dis[u][v]);
}
}
}
}\mathcal{O}(n^2 2^n)
Some Cool Problems
UMD CP Club - Dynamic Programming
By sam571128
