Inventory management of a scarce vaccine for epidemic control: Uncertainty quantification of time for deliveries and order sizes based on a model of sequential decisions
Towards Reinforcement learning
SEMINARIO SOBRE MÉTODOS MATEMÁTICOS Y ALGORITMOS.


Yofre H. Garcia
Saúl Diaz-Infante Velasco
Jesús Adolfo Minjárez Sosa
sauldiazinfante@gmail.com

October 02, 2024


When a vaccine is in short supply, sometimes refraining from vaccination is the best response—at least for a while.

On October 13, 2020, the Mexican government announced a vaccine delivery plan by Pfizer-BioNTech and other firms as part of the COVID-19 vaccination campaign.

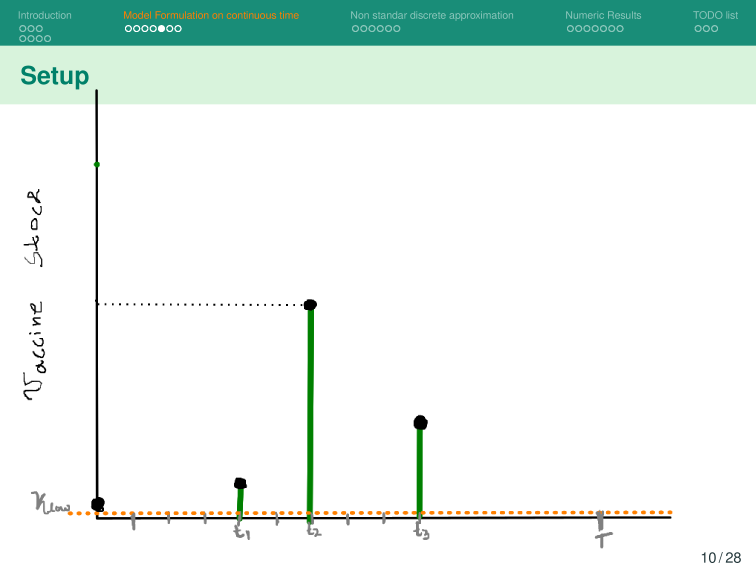
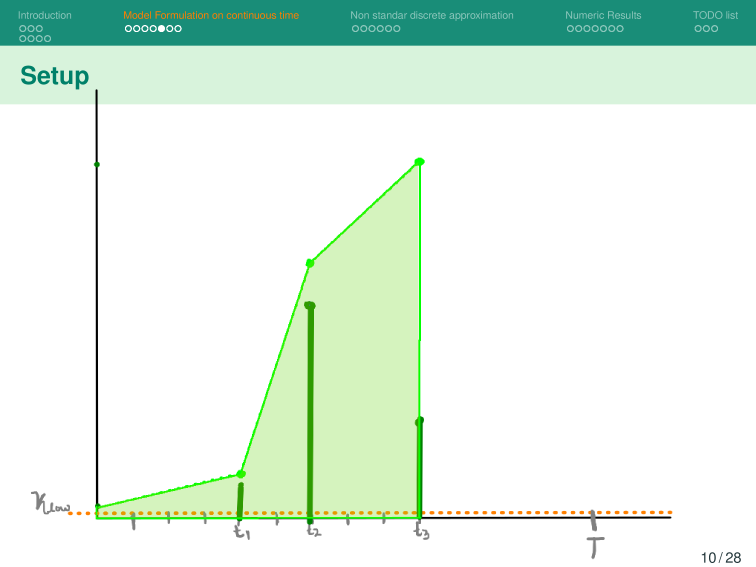
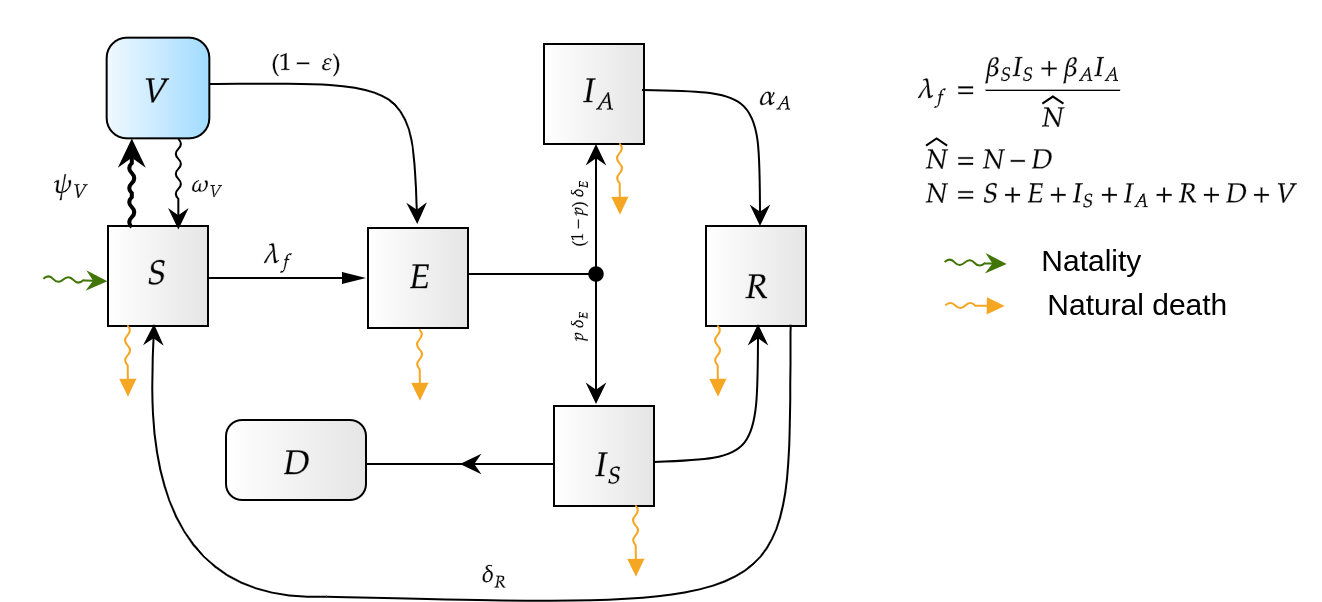
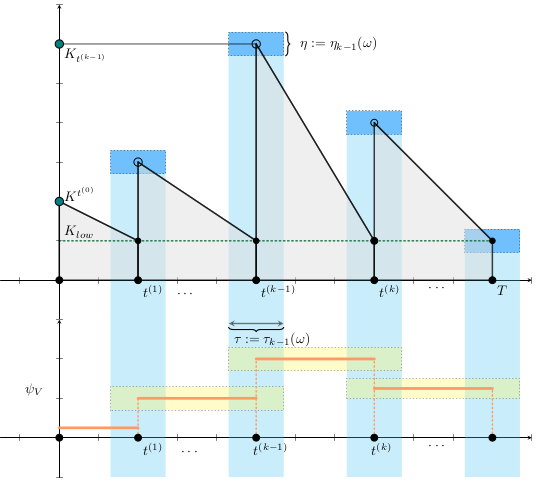
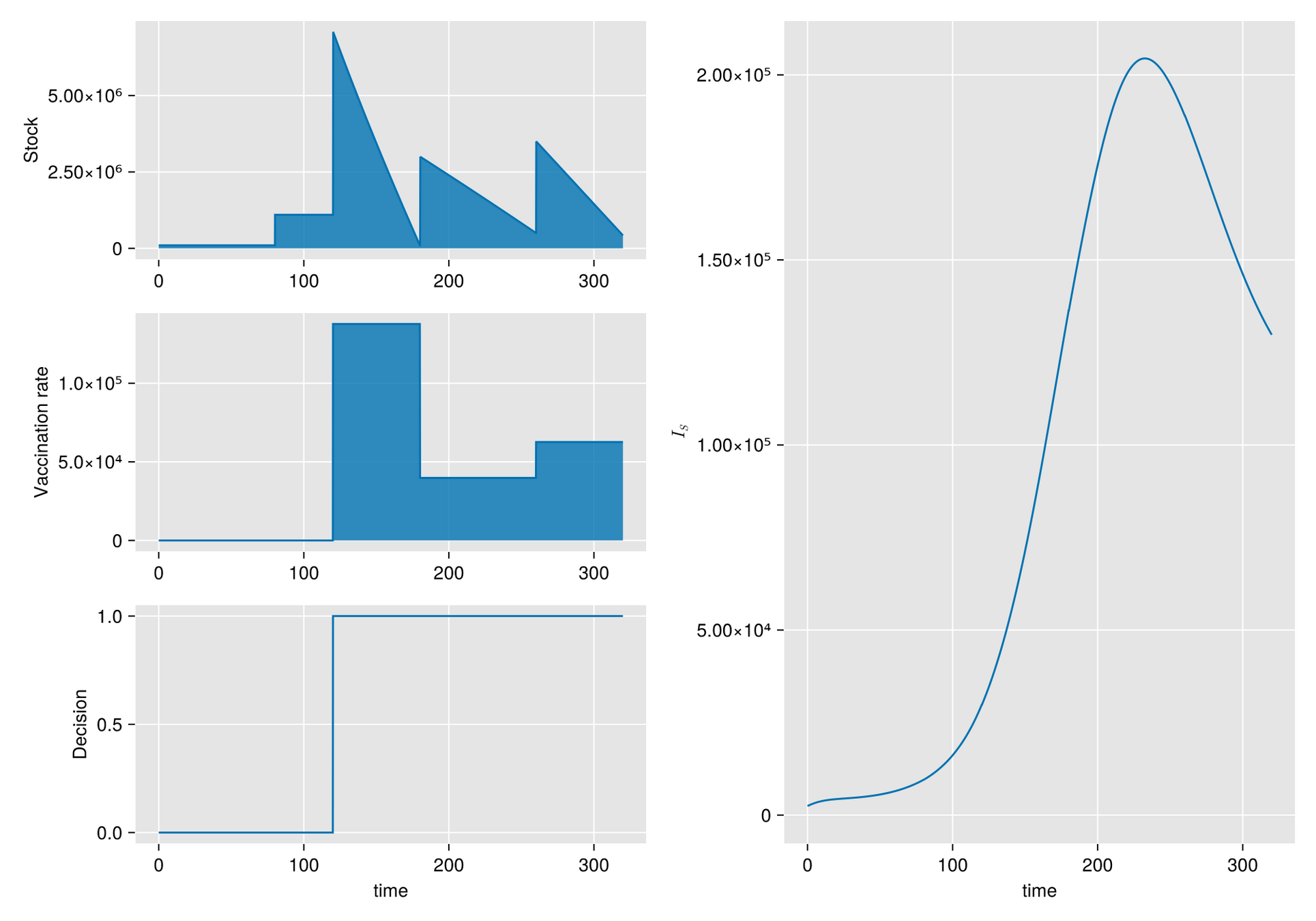
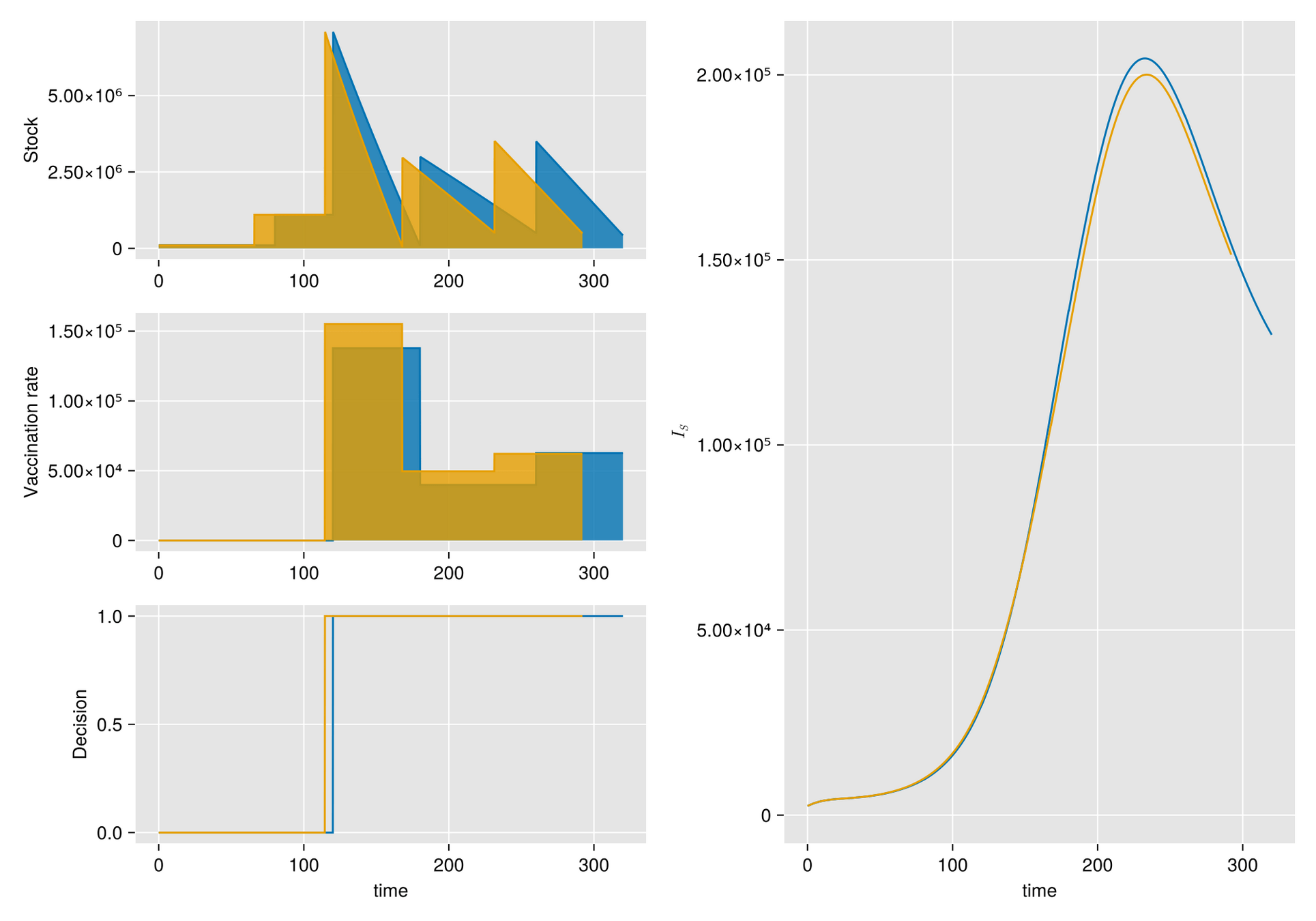
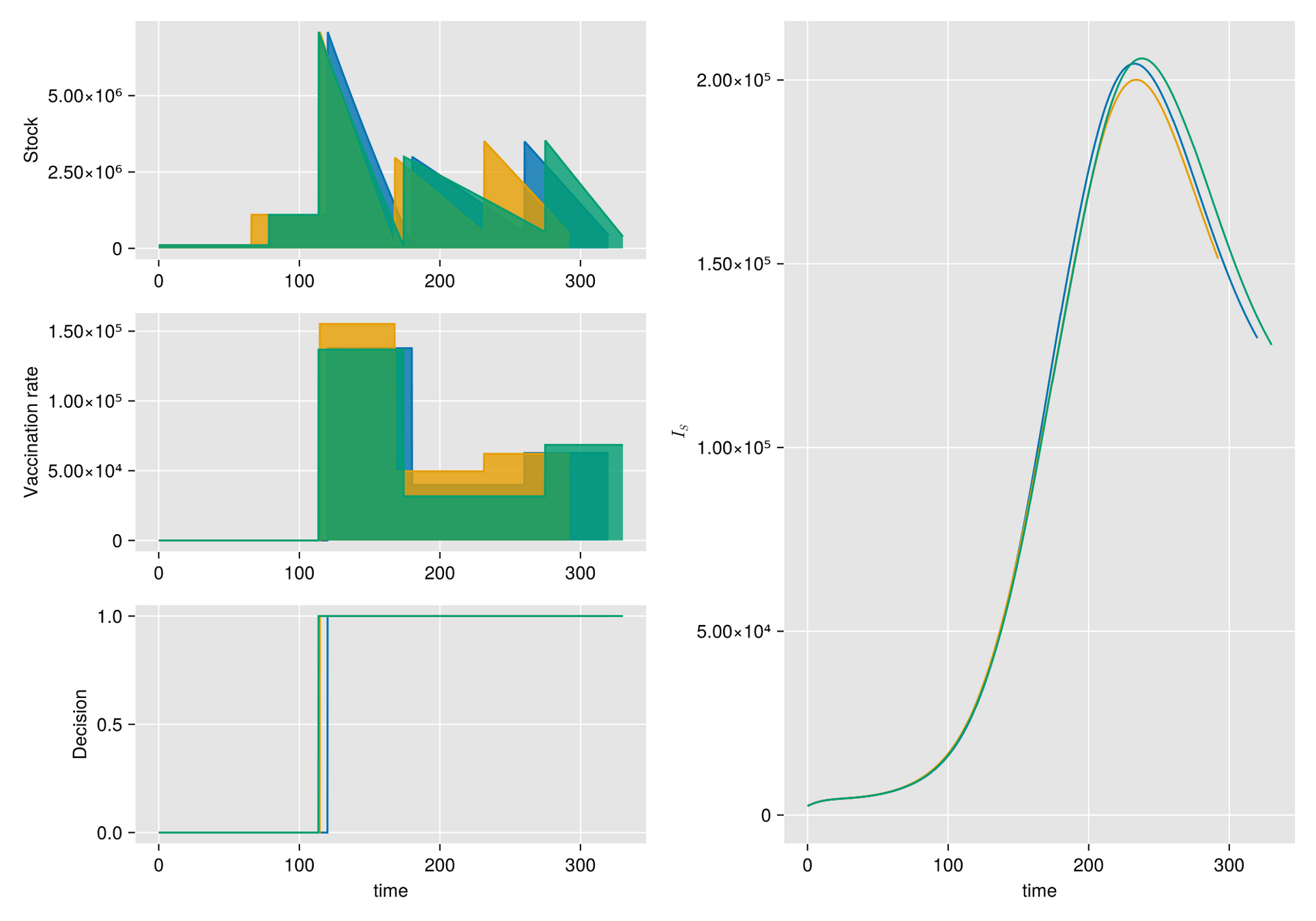
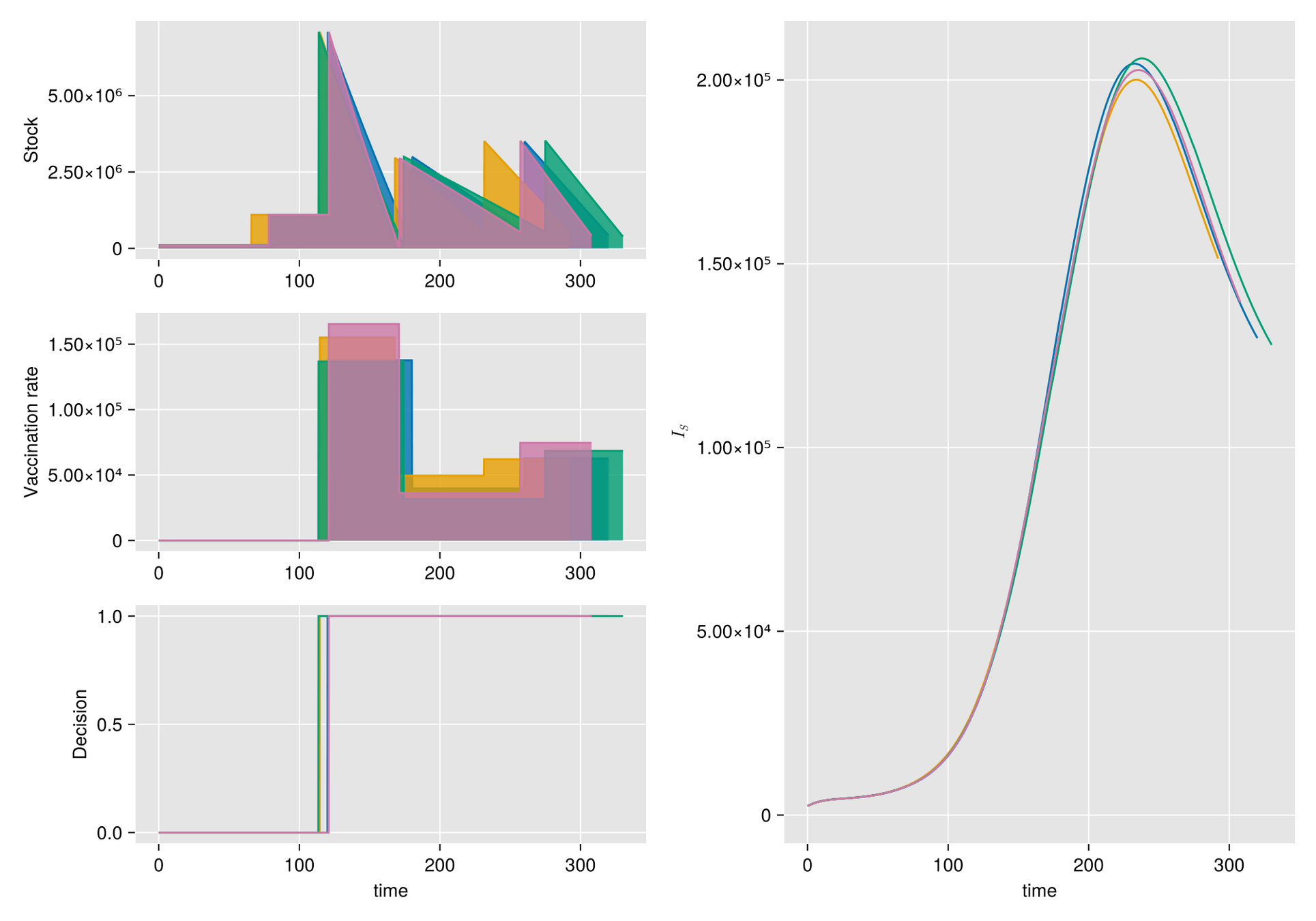
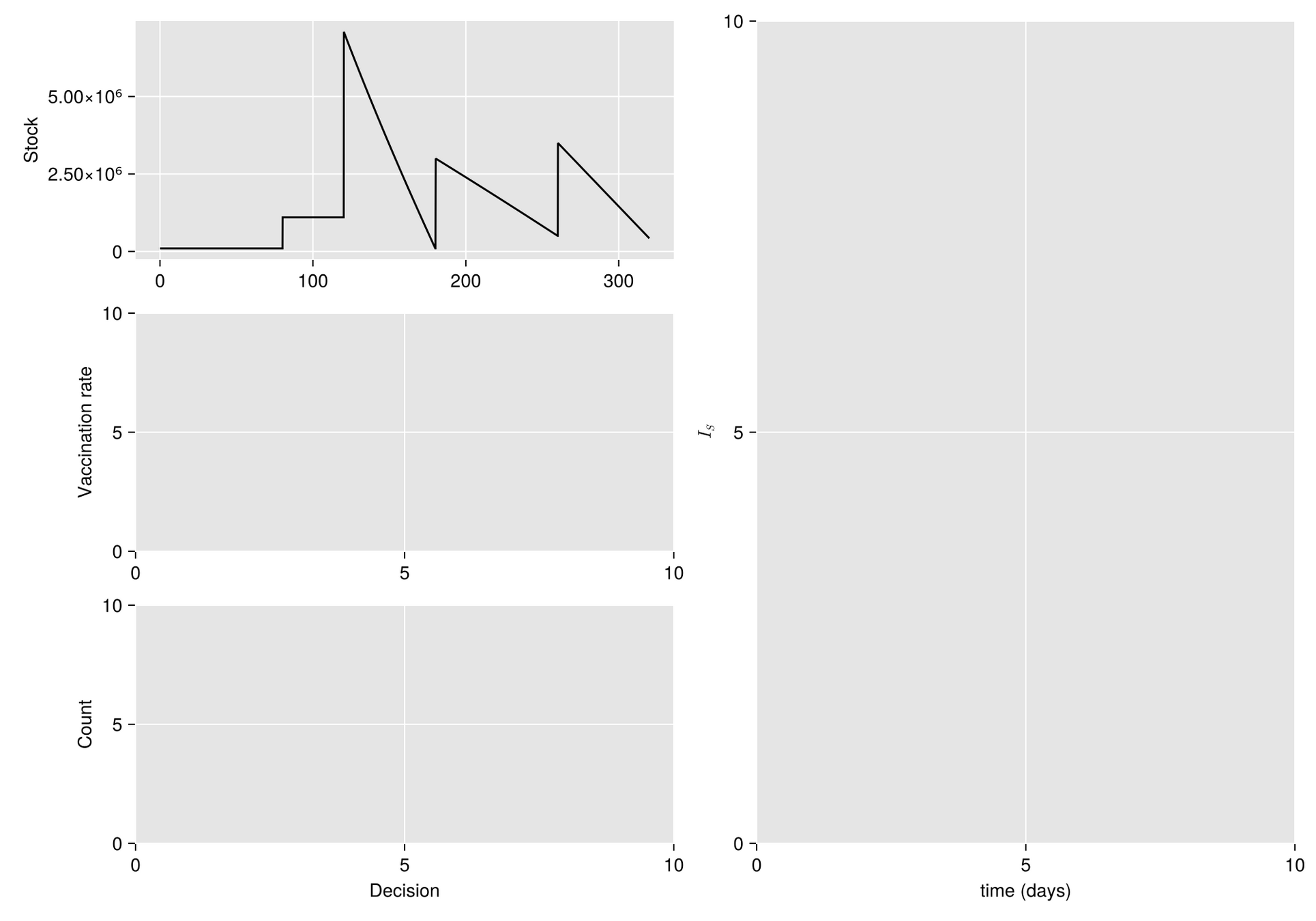
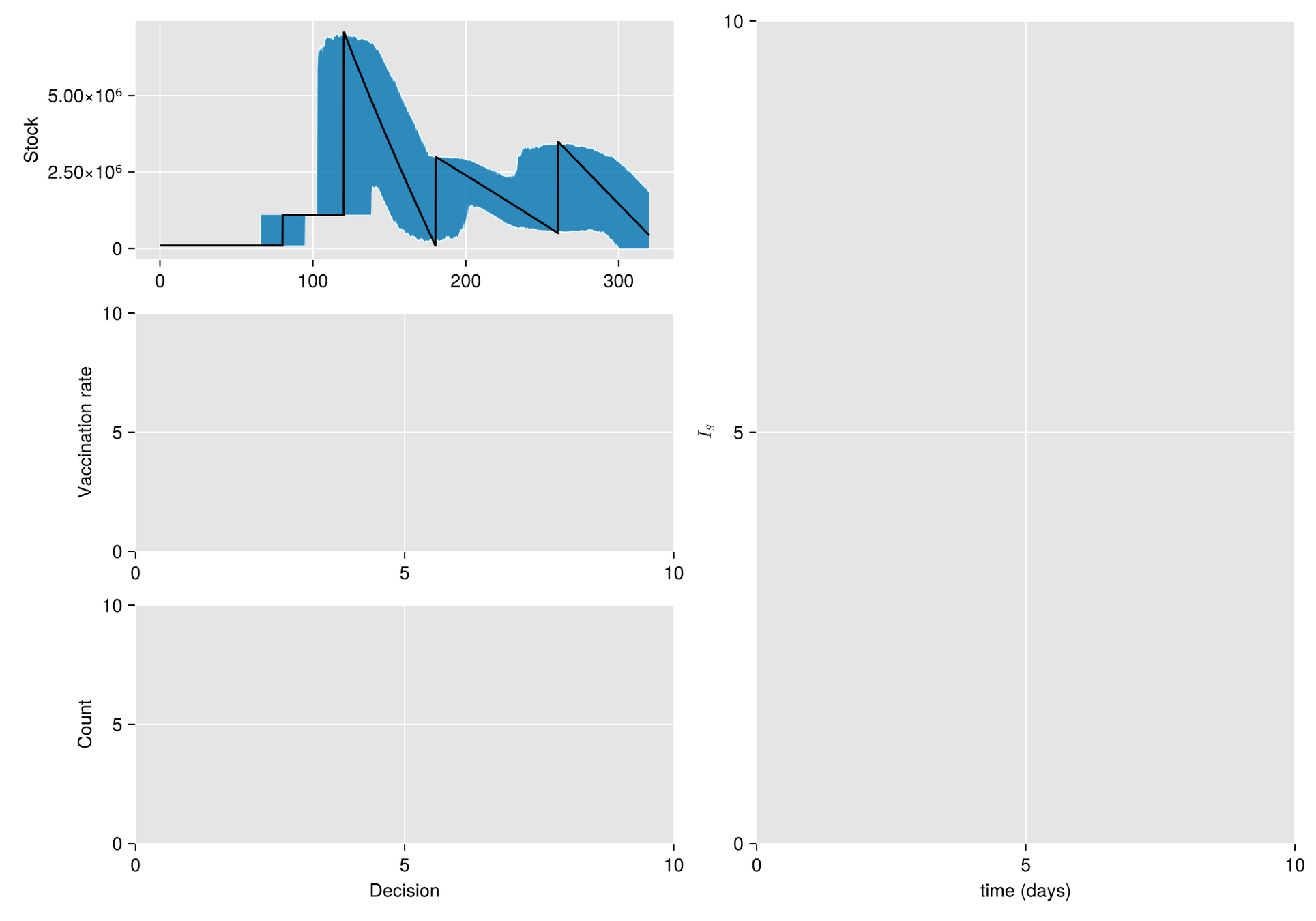
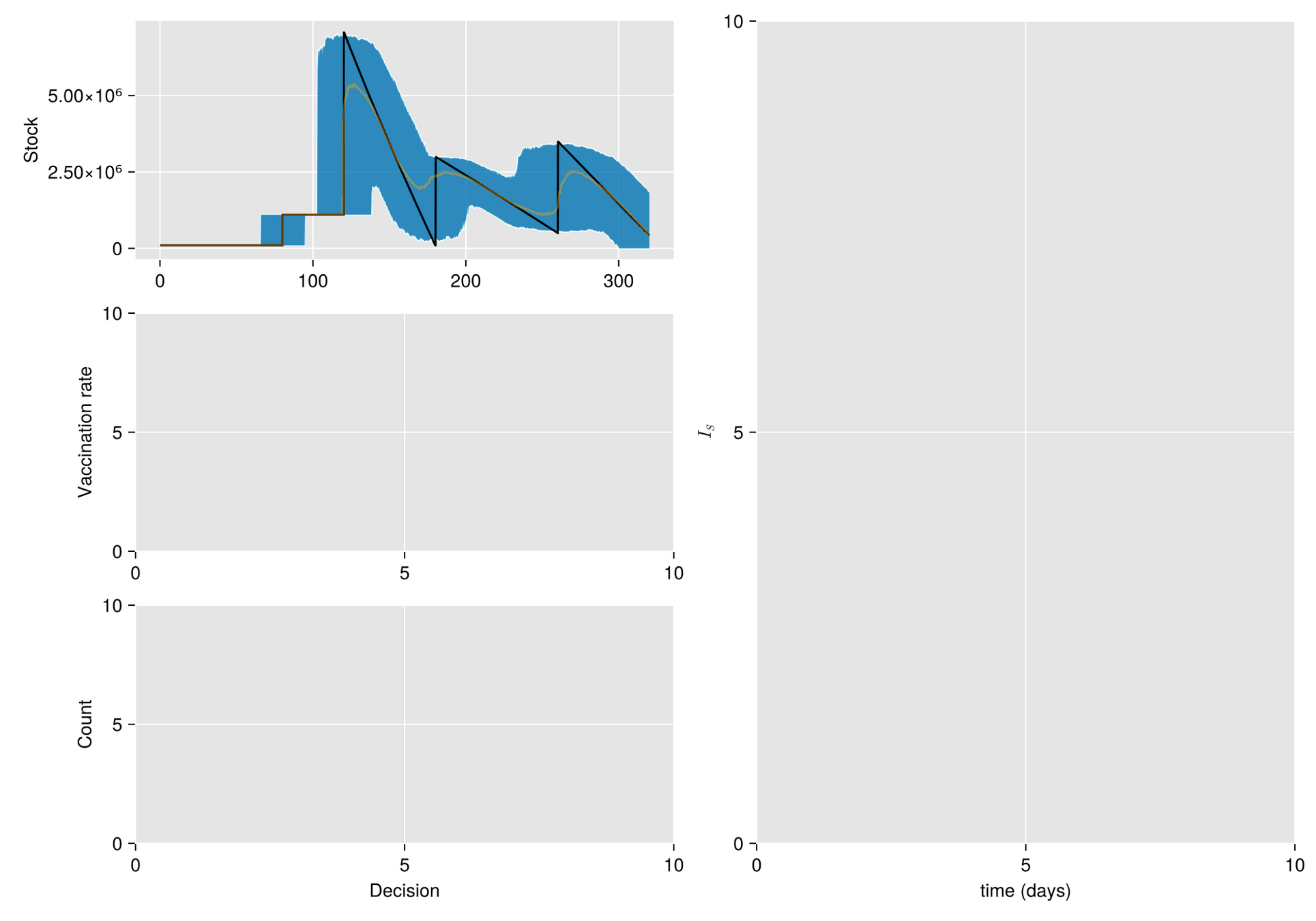
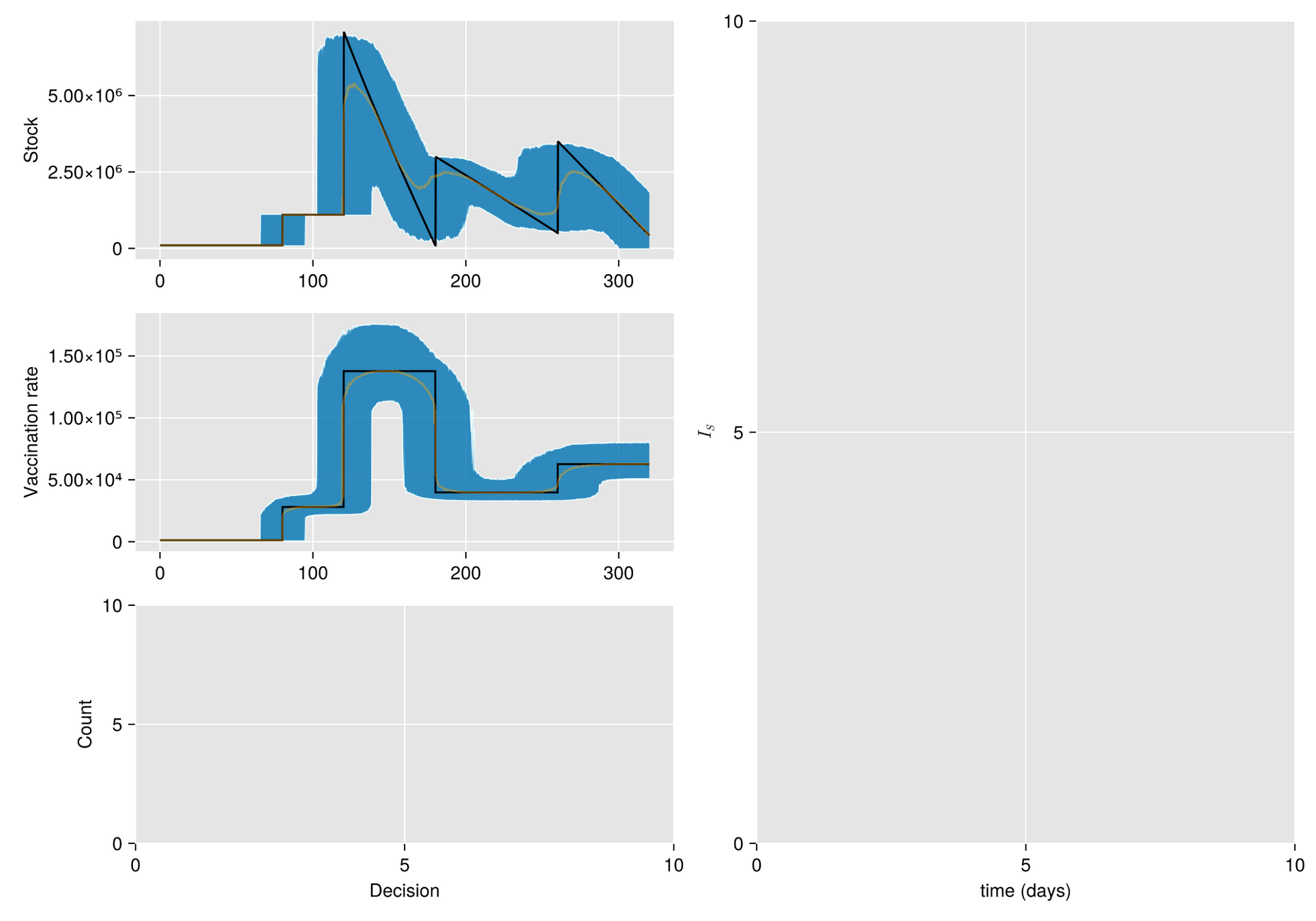
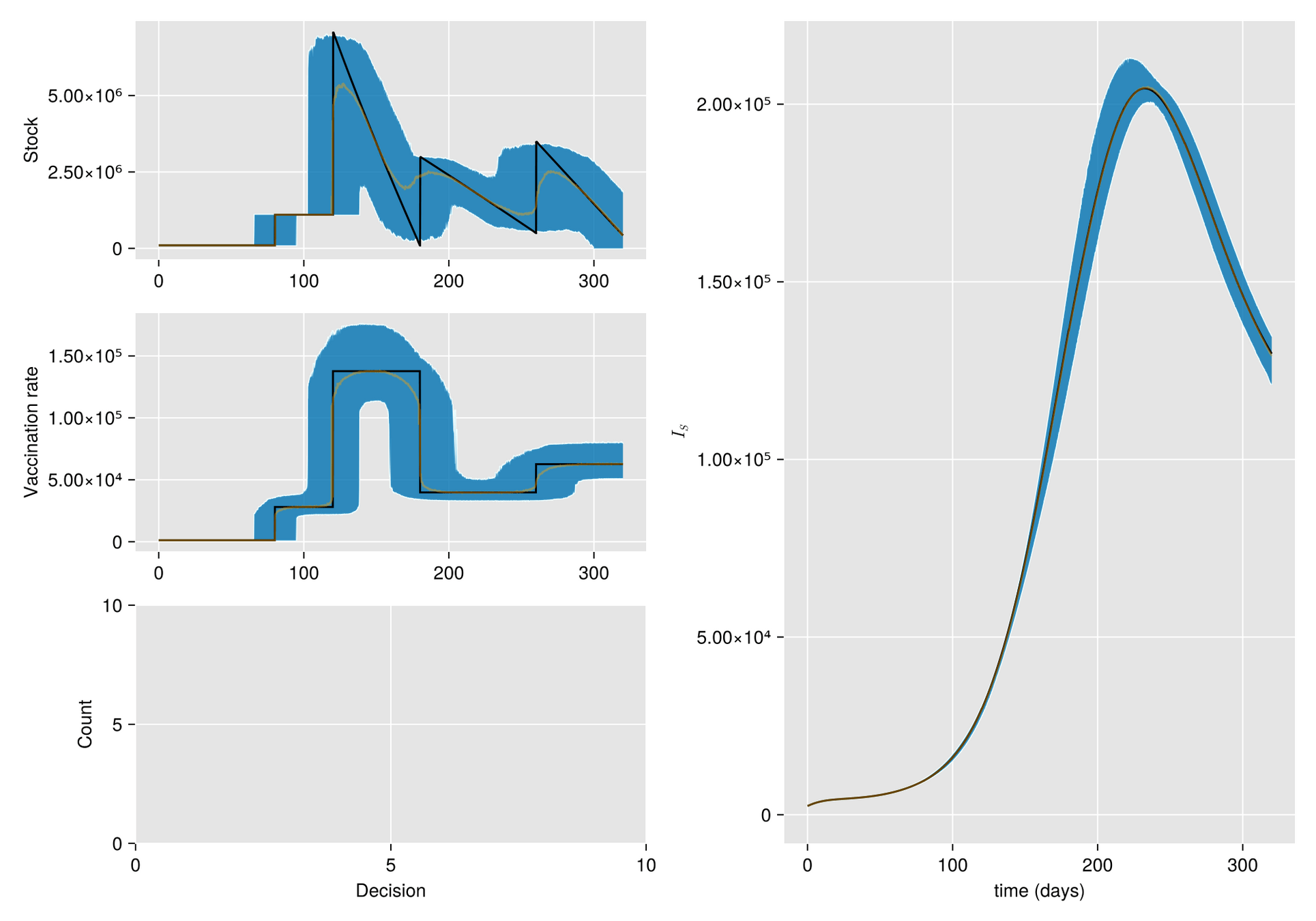
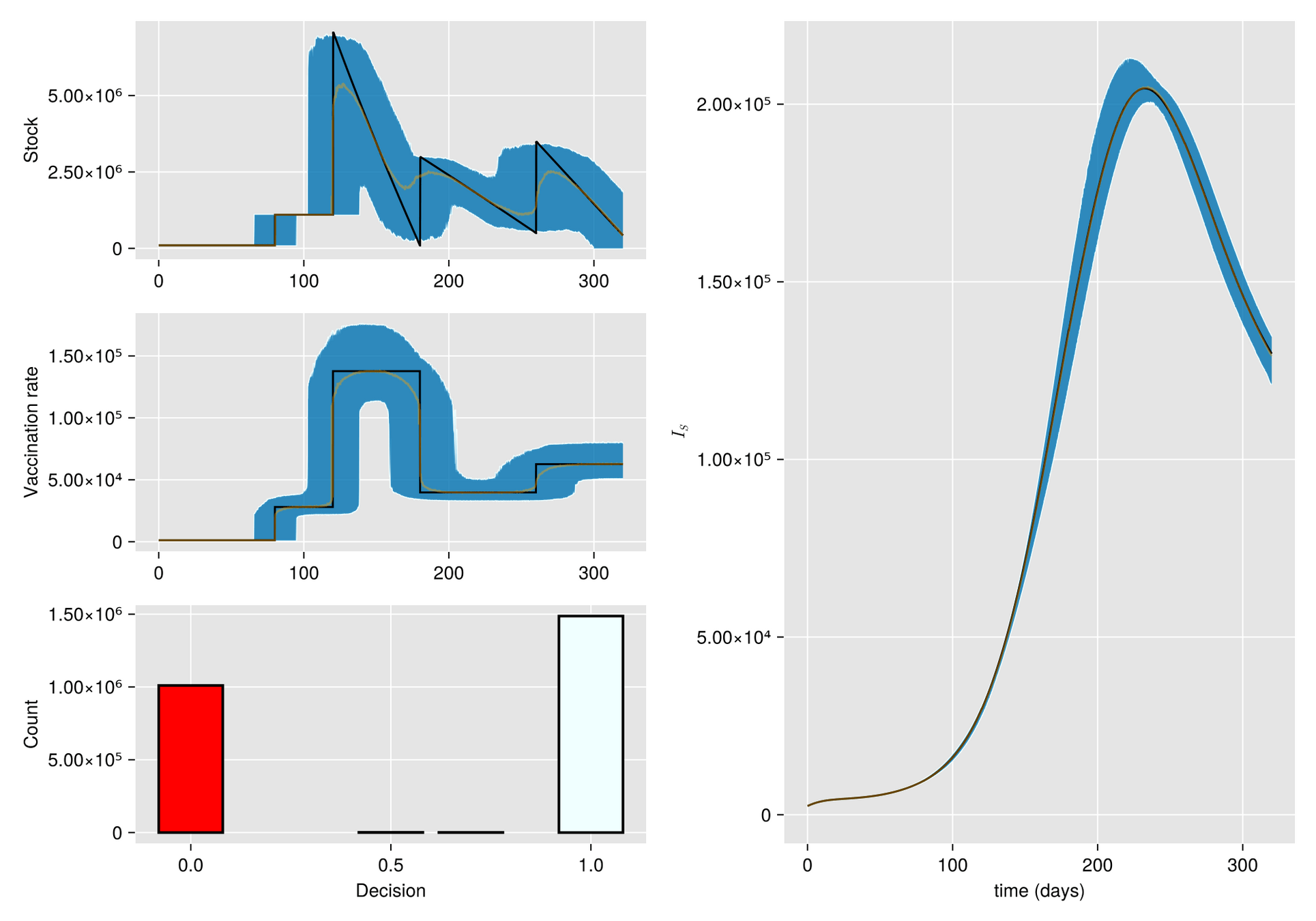
Given a shipment of vaccines calendar, describe the stock management with backup protocol and quantify random fluctuations
due to schedule or quantity.
Then, incorporate this dynamic into an ODE system that describes the disease and evaluates its response accordingly.
Text
Nonlinear control: HJB and DP
Given
Goal:
Desing
to follow
s. t. optimize cost
Agent




















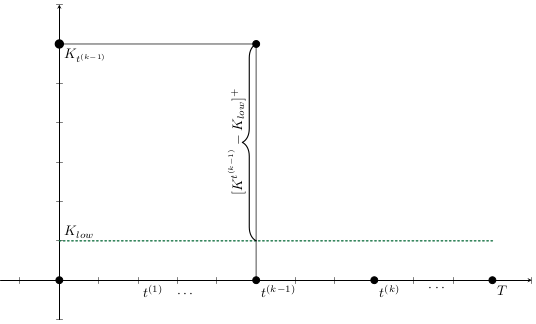
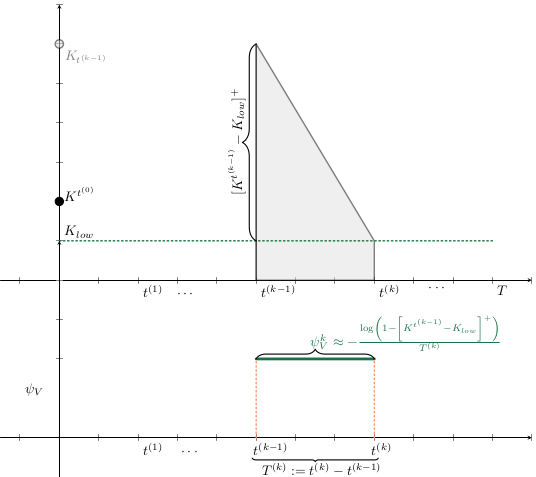
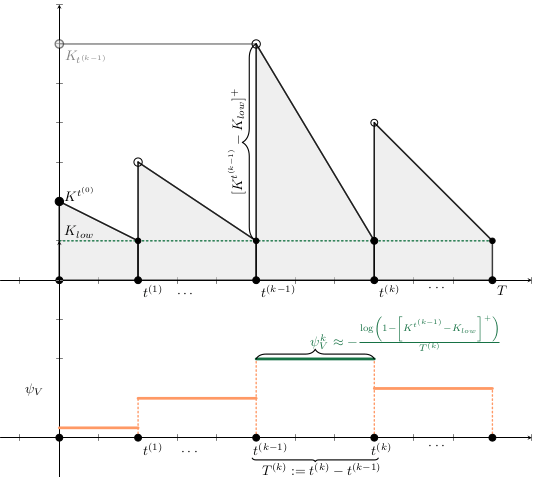
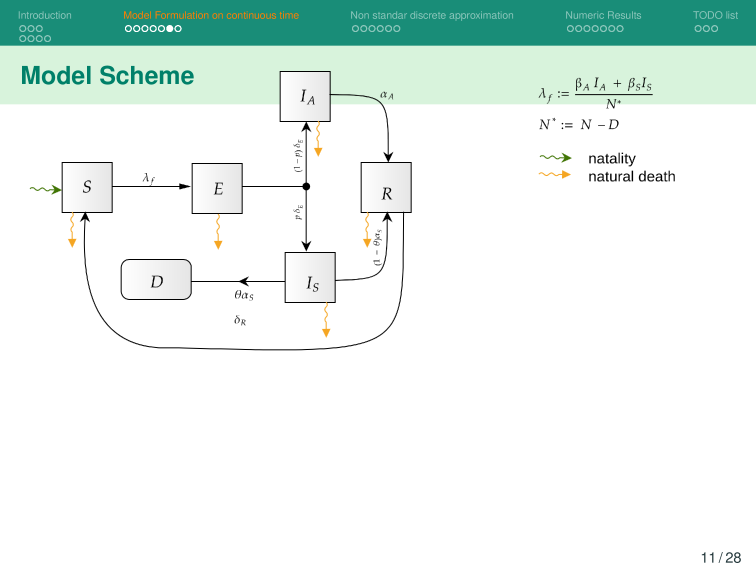







Agent
action
state
reward
Discounted return
Total return
Dopamine Reward




Agent
Deterministic Control


https://slides.com/sauldiazinfantevelasco/cinvestav-smma-oct-02-2024
Gracias!!

CINVESTAV-SeminarioSobreMetodosMatematicosAlgoritmos
By Saul Diaz Infante Velasco
CINVESTAV-SeminarioSobreMetodosMatematicosAlgoritmos
Explore innovative strategies for managing scarce vaccines in inventory! See how uncertainty in delivery times and order sizes impacts epidemic control efforts.
- 183



