Reinforcement learning and epidemiology: an invitation to the applications of Markov decision processes in Data Science
Latin American Congress of Mathematical Biology SOLABIMA XIII
Yofre H. Garcia
Saúl Diaz-Infante Velasco
Jesús Adolfo Minjárez Sosa
sauldiazinfante@gmail.com
November 15, 2024
Inventory management of a scarce vaccine for epidemic control: Uncertainty quantification of time for deliveries and order sizes based on a model of sequential decisions
Argument. When there is a shortage of vaccines, sometimes the best response is to refrain from vaccination, at least for a while.
Hypothesis. Under these conditions, inventory management suffers significant random fluctuations
Objective. Optimize the management of vaccine inventory and its effect on a vaccination campaign
On October 13 2020, the Mexican government announced a vaccine delivery plan from Pfizer-BioNTech and other companies as part of the COVID-19 vaccination campaign.
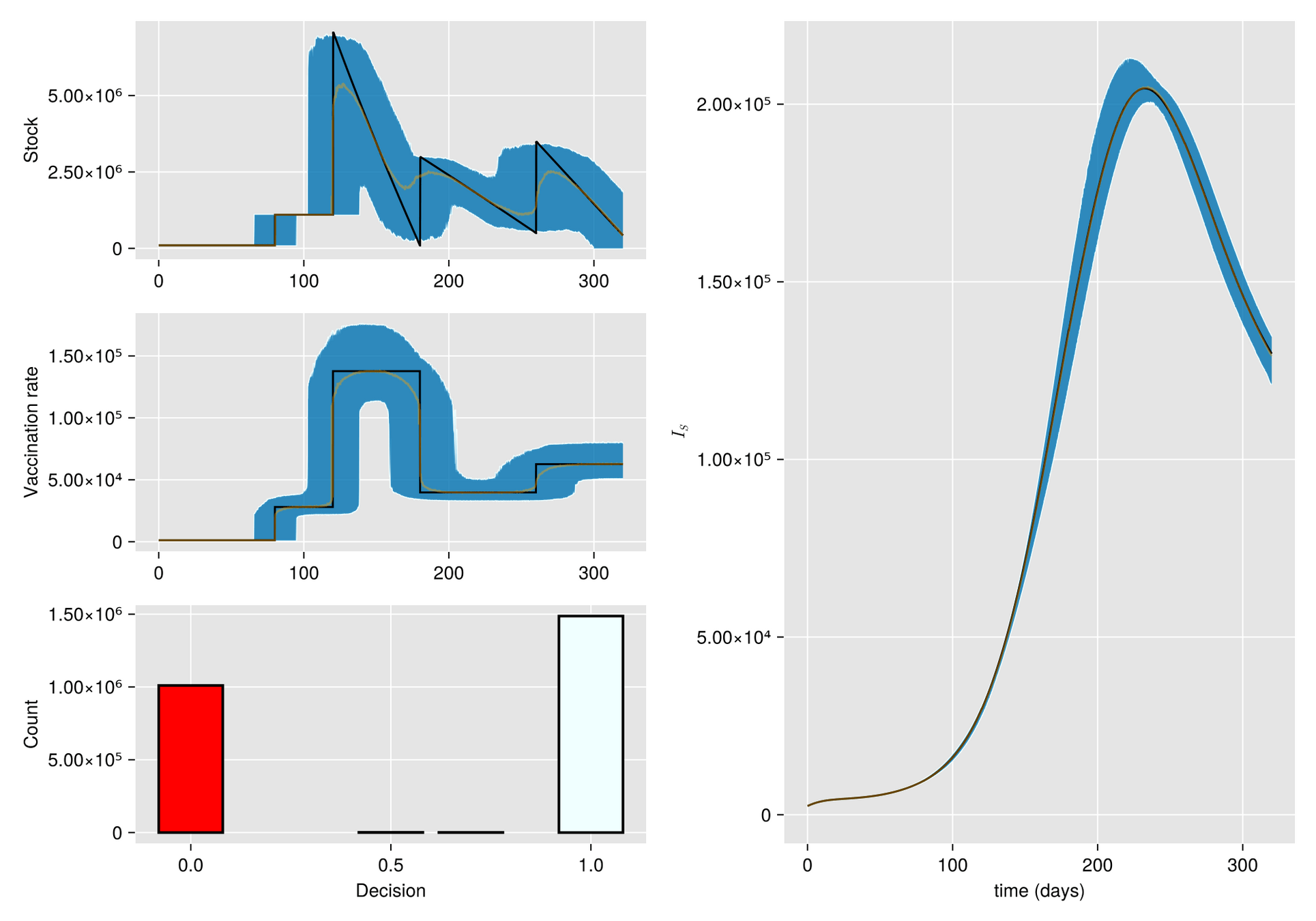
Methods. Given a vaccine shipping schedule, we describe stock management with a backup protocol and quantify the random fluctuations due to a program under high uncertainty.
Then, we incorporate this dynamic into a system of ODE that describes the disease and evaluate its response.
Nonlinear control: HJB and DP
Given
\frac{dx}{dt} = f(x(t))
\frac{dx_{t}}{dt} =f(x_{t} ,a_{t})
Agent
a_t\in \mathcal{A}
x_t
J(x_t, a_t, 0, T) = Q(x_T, T)
+ \int_0^T \mathcal{L}(x_{\tau}, a_{\tau}) d_{\tau}
Objective:
Design
to follow
t. q. optimize cost
\text{action } a_t\in \mathcal{A},
\text{state } x_t
J(x_t, a_t, 0, T) .
To set ideas: A model of exponentially growing population.
J(P_t, a_t, 0, T) =
Q(P_T, T)
+ \int_0^T \mathcal{L}(P_{\tau}, a_{\tau}) d_{\tau}
Objective:
Design
to direct
t. q. optimize cost
\text{accion } a_t\in \mathcal{A},
\text{estado } P_t
J(P_t, a_t, 0, T) .
J(P_t, a_t, 0, T) =
Q(P_T, T)
+ \int_0^T
\underbrace{\mathcal{L}(P_{\tau}, a_{\tau})}_{\frac{1}{2} (w_1 P_{\tau} + a_{\tau}^ 2)} d_{\tau}
\begin{aligned}
\dfrac{dP_t}{dt}
& = (k + a_t) P_t , \qquad t \in [0,T]
\\
P_0 &= p_0
\end{aligned}
\begin{aligned}
\dfrac{dP_t}{dt}
& = kP_t, \qquad t \in [0,T]
\\
P_0 &= p_0
\end{aligned}
\begin{aligned}
\dfrac{dP_t}{P_t}
&= k \, dt
\\
\int \frac{1}{P_t} \, dP_t
&= \int k \, dt
\\
\ln |P_t|
&= kt + C
\\
|P_t|
&= e^{kt + C}
\\
|P_t|
&= C_1 e^{kt}
\\
P_t
&= P_0 e^{kt}
\end{aligned}
\begin{aligned}
\dfrac{dP_t}{dt}
& = kP_t, \qquad t \in [0,T]
\\
P_0 &= p_0
\end{aligned}
Nonlinear control: HJB and DP
V(x_0, 0, T):=
\min_{a_t \in \mathcal{A}} J(x_t, a_t, 0, T)
V(x_0, 0, T) = V(x_0, 0, t) + V(x_0, t, T)
Bellman optimality principle
Control Problem
\frac{dx_t}{dt} = f(x_t, a_t)
\min_{a_t\in \mathcal{A}} J(x_t, a_t, 0, T) = Q(x_T, T)
+ \int_0^T \mathcal{L}(x_{\tau}, a_{\tau}) d_{\tau}
t.q-
x_T
x_t
x_0
\frac{\partial V}{\partial t} =
\min_{a_t\in \mathcal{A}}
\left[
\left(
\frac{\partial V}{\partial x}
\right)^{\top}
f(x,a) +
\mathcal{L}(x,a)
\right]
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
& S(0) = S_0, I(0)=I_0, R(0)=0
\\
& S(t) + I(t) + R(t )= 1
\end{aligned}
\end{equation*}
S+I+R = \underbrace{1}_{\leftrightarrow N }
\begin{aligned}
S'(t) &= -\beta IS
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
& S(0) = S_0, I(0)=I_0, R(0)=0
\\
& S(t) + I(t) + R(t )= 1
\end{aligned}
\dfrac{d(S+I+R)}{dt} = 0
\to {\text{población cte.}}
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
& S(0) = S_0, I(0)=I_0, R(0)=0
\\
& S(t) + I(t) + R(t )= 1
\end{aligned}
\end{equation*}
\lambda_V:=
\underbrace{ \textcolor{orange}{\xi}}_{cte.}
\cdot \ S(t)
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS - \textcolor{red}{\lambda_V(t)}
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
V'(t) & = \textcolor{red}{\lambda_V(t)}
\\
& S(0) = S_0, I(0)=I_0,
\\
&R(0)=0, V(0) = 0
\\
& S(t) + I(t) + R(t) + V(t)= 1
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS - \textcolor{red}{\lambda_V(x, t)}
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
V'(t) & = \textcolor{red}{\lambda_V(x,t)}
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS - \textcolor{red}{\lambda_V(x, t)}
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
V'(t) & = \textcolor{red}{\lambda_V(x,t)}
\end{aligned}
\end{equation*}
\lambda_V:=
\underbrace{ \textcolor{orange}{\Psi_V}}_{cte.}
\cdot \ S(t)
\begin{aligned}
S'(t) &= \cancel{-\beta IS} - \underbrace{\textcolor{red}{\lambda_V(x, t)}}_{=\Psi_V S(t)}
\\
I'(t) &= \cancel{\beta IS} - \cancel{\gamma I}
\\
{R'(t)} & = \cancel{\gamma I}
\\
V'(t) & = \underbrace{\textcolor{red}{\lambda_V(x, t)}}_{=\Psi_V S(t)}
\\
& S(0) \approx 1, I(0) \approx 0,
\\
&R(0)\approx 0, V(0) = 0
\\
& S(t) + \cancel{I(t)} + \cancel{R(t)} +\cancel{ V(t)}= 1
\end{aligned}
\begin{aligned}
S'(t) &= - \Psi_V S(t)
\\
V'(t) & = \Psi_V S(t)
\\
& S(0) \approx 1, V(0) = 0
\\
& S(t) + V(t) \approx 1
\end{aligned}
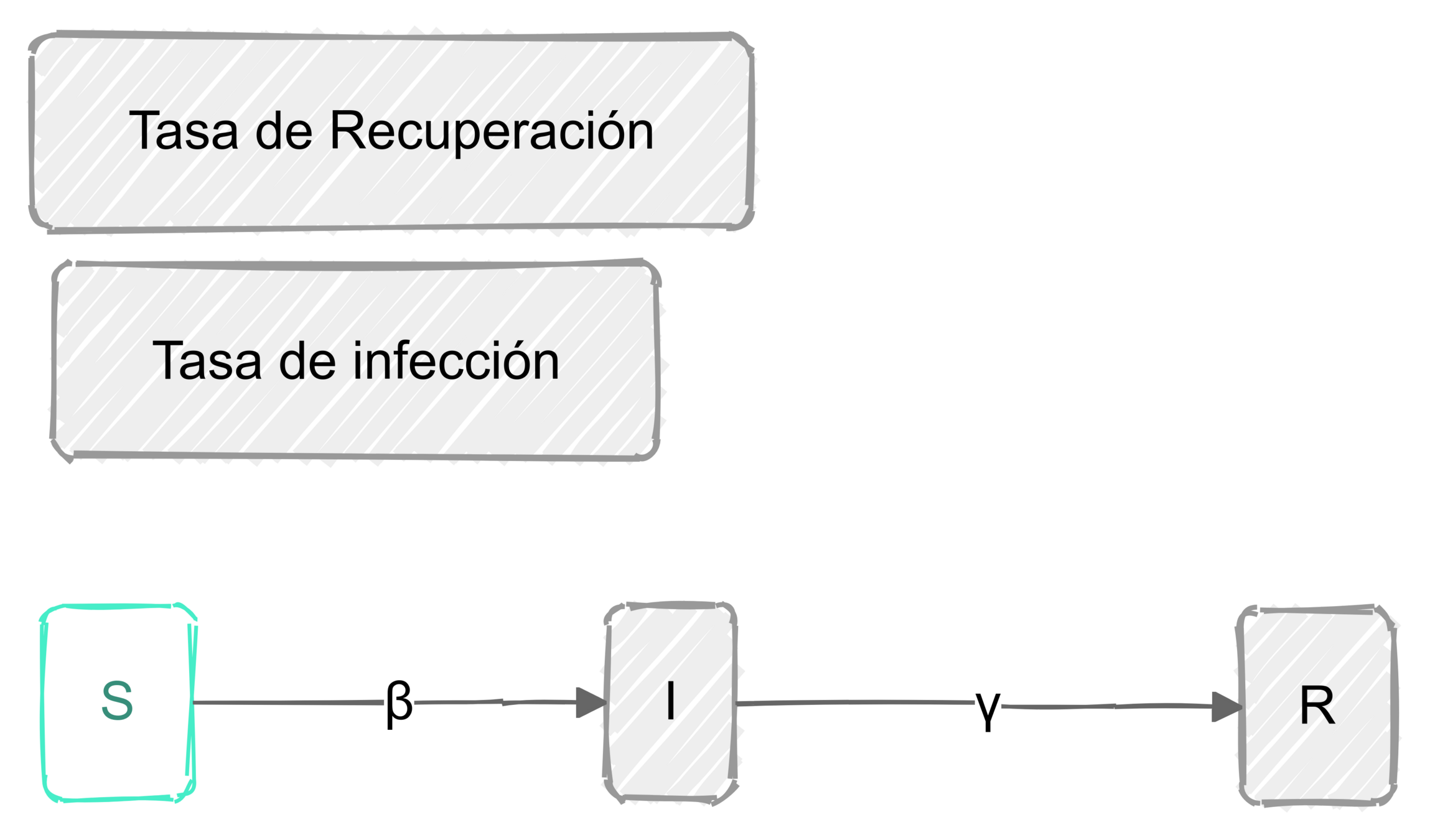
The effort invested in preventing or mitigating an epidemic through vaccination is proportional to the vaccination rate
\textcolor{orange}{\Psi_V}
Let us assume at the beginning of the outbreak:
\textcolor{orange}{S(0)\approx 1}
\begin{aligned}
S'(t) &= - \Psi_V S(t)
\\
V'(t) & = \Psi_V S(t)
\\
& S(0) \approx 1, V(0) = 0
\\
& S(t) + V(t) \approx 1
\end{aligned}
S(t) \approx N \exp(-\Psi_V t)
\begin{aligned}
V(t) \approx
\cancel{V(0)} +
\int_0^t
\Psi_V S(\tau) d\tau
\end{aligned}
\begin{aligned}
V(t)
&\approx
\cancel{V(0)} +
\int_0^t
\Psi_V S(\tau) d\tau
\\
&
\approx
\int_0^t
N \Psi_V
\exp(-\Psi_V \tau)
d\tau
\\
&
\approx
N \exp(-\Psi_V \tau) \mid_{\tau=t}^{\tau=0}
\\
&=
\cancel{N} \exp(1 - \exp(-\Psi_V t))
\end{aligned}
Then we estimate the number of vaccines with
X_{vac}(t) := \int_{0}^t
\Psi_v \Bigg(
\underbrace{S(\tau)}_{
\substack{
\text{target} \\
\text{pop.}
}
}\Bigg )
Then, for a vaccination campaign, let:
\begin{aligned}
\textcolor{orange}{T}:
&\text{ time horizon}
\\
\textcolor{green}{
X_{cov}:=
X_{vac}(}
\textcolor{orange}{T}
\textcolor{green}{)}:
&\text{ covering at time $T$}
\end{aligned}
\begin{aligned}
X_{cov} = &X_{vac}(T)
\\
\approx &
1 - \exp(-\textcolor{teal}{\lambda_V} T).
\\
\therefore &
\textcolor{teal}{\lambda_V} =
-\frac{1}{T}
\ln(1 - X_{cov})
\end{aligned}
Then we estimate the number of vaccines with
X_{vac}(t) := \int_{0}^t
\Psi_v \Bigg(
\underbrace{S(\tau)}_{
\substack{
\text{target} \\
\text{pop}
}
}\Bigg )
Then, for a vaccination campaign, let:
\begin{aligned}
\textcolor{orange}{T}:
&\text{ horizon time}
\\
\textcolor{green}{
X_{cov}:=
X_{vac}(}
\textcolor{orange}{T}
\textcolor{green}{)}:
&\text{ Coverage at time $T$}
\end{aligned}
\begin{aligned}
X_{cov} = &X_{vac}(T)
\\
\approx &
1 - \exp(-\textcolor{teal}{\lambda_V} T).
\\
\therefore &
\textcolor{teal}{\lambda_V} =
-\frac{1}{T}
\ln(1 - X_{cov})
\end{aligned}
The total population of Tuxtla Gutiérrez in 2020 was 604,147.
So to vaccinate 70% of this population in one year:
\begin{aligned}
604,147 &\times 0.00329
\\
\approx &
1987.64363 \ \text{dósis/día}
\end{aligned}
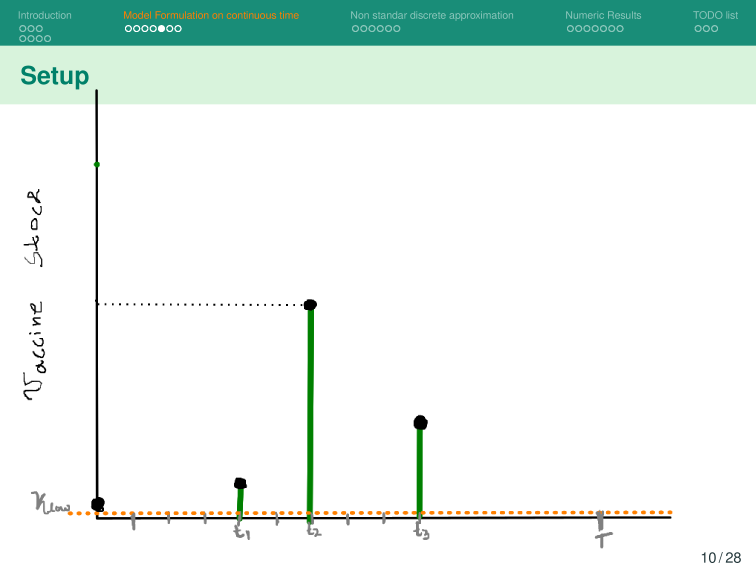
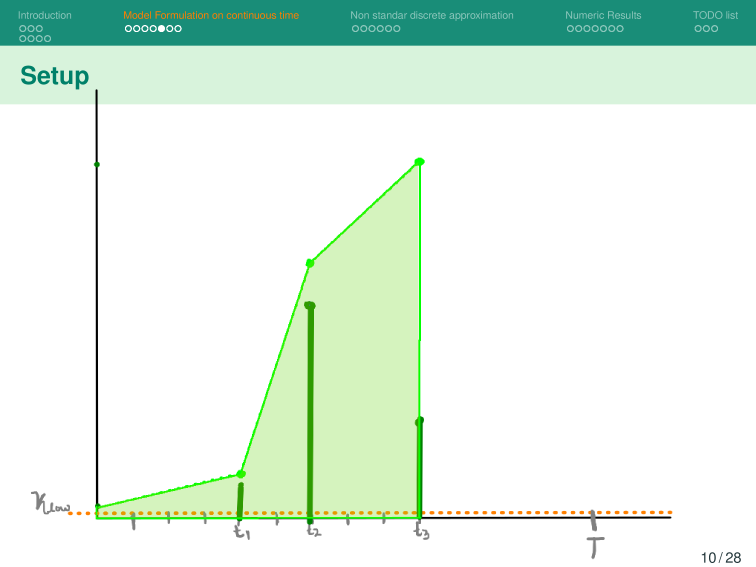
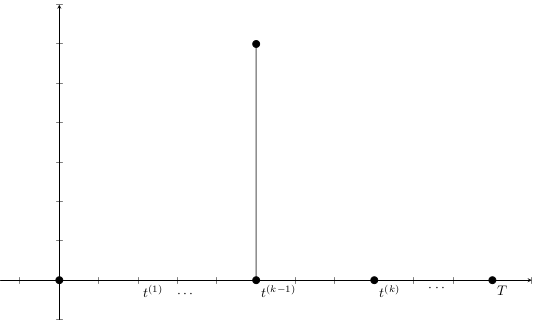
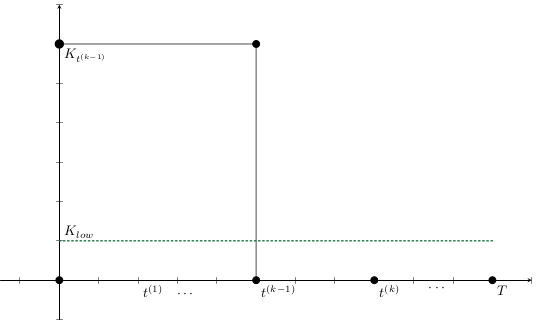
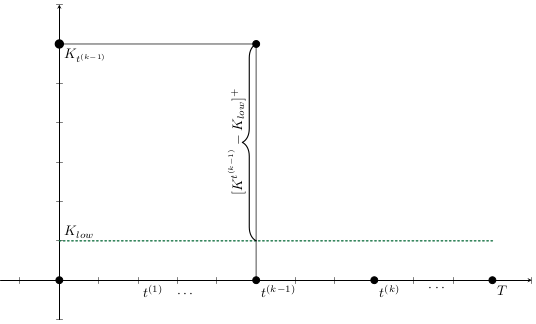
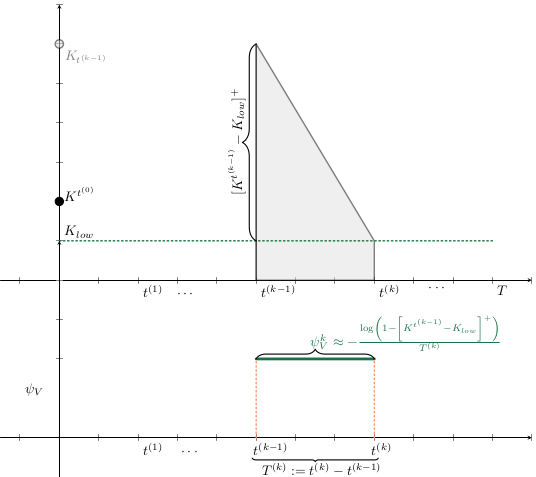
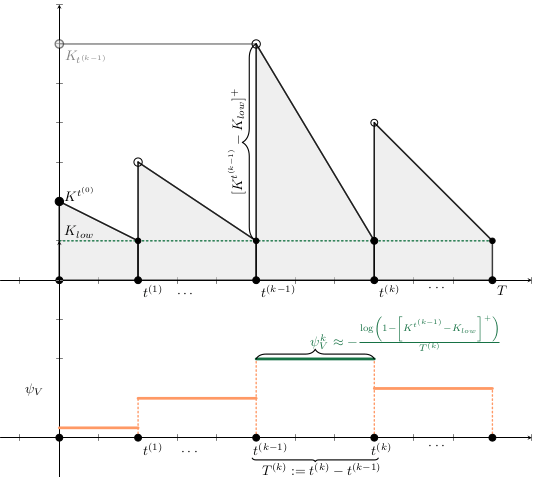
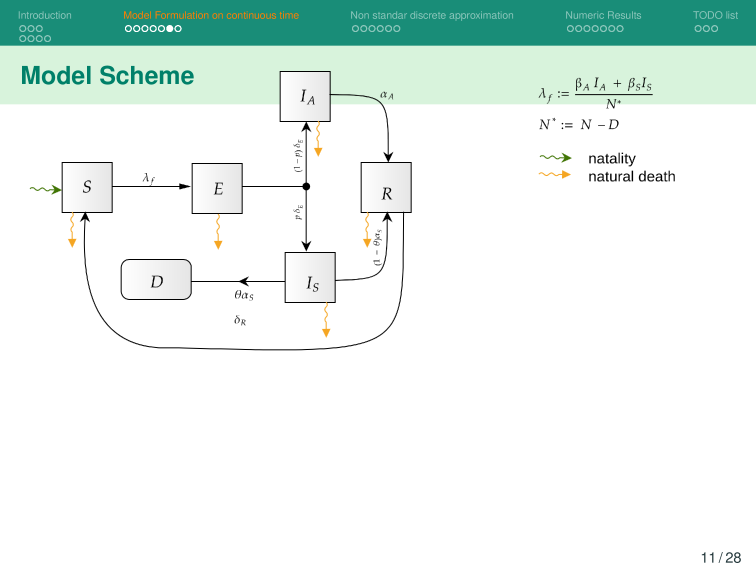
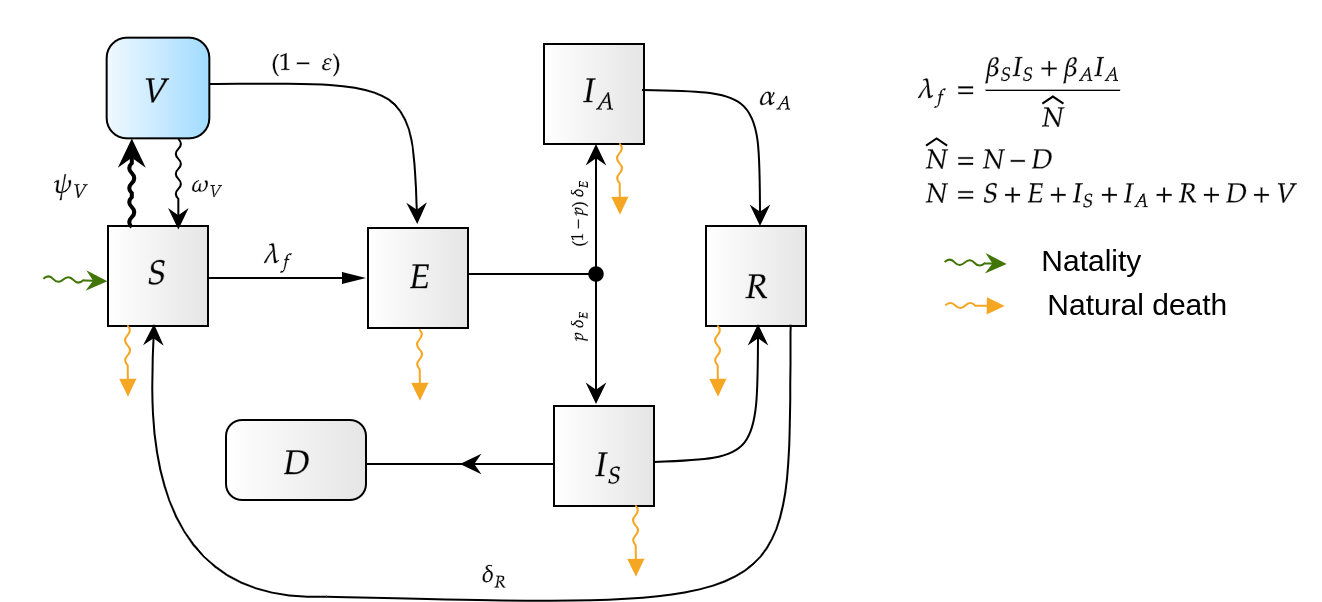
Base Model
Nonlinear control: HJB and DP
Given
\frac{dx}{dt} = f(x(t)),
\qquad t \in [0, \textcolor{red}{T}]
\frac{dx_{t}}{dt} =f(x_{t} ,a_{t})
Agent
a_t\in \mathcal{A}
x_t
J(x_t, a_t, 0, \textcolor{red}{T}) = Q(x_T, \textcolor{red}{T})
+ \int_0^{\textcolor{red}{\mathbf{T}}} \mathcal{L}(x_{\tau}, a_{\tau}) d_{\tau}
Objective:
Design
to follow
t. q. optimize cost
\text{accion } a_t\in \mathcal{A},
\text{estado } x_t
J(x_t, a_t, 0, T) .
\begin{aligned}
C(x_{t^{(k+1)}}, & a_{t^{(k+1)}})
=
\\
& C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\end{aligned}
\begin{aligned}
C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLL dt,
\\
C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLD(x_t, a_t) dt
\\
YLL(x_t, a_t) &:=
m_1 p \delta_E (E(t) - E^{t^{(k)}} ),
\\
YLD(x_t, a_t) &:=
m_2 \theta \alpha_S(E(t) - E^{t^{(k)}}),
\\
t &\in [t^{(k)},t^{(k + 1)}]
\end{aligned}
\begin{aligned}
C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
& = \int_{t^{(k)}}^{t^{(k+1)}} m_3(K_{Vac}(t) - K_{Vac}^{t^{(k)}}) dt
\\
C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=\int_{t^{(k)}}^{t^{(k+1)}} m_4(X_{vac}(t) - X_{vac}^{t^{(k)}}) dt
\end{aligned}
\begin{aligned}
&\min_{a_{0}^{(k)} \in \mathcal{A}_0}
c(x_{\cdot}, a_0):=
c_1(a_0^{(k)})\cdot T^{(k)} +
\sum_{n=0}^{N-1}
c_0(t_n, x_{t_n}) \cdot h
\\
\text{ s.t.} &
\\
&
x_{t_{n+1}}
= x_{t_n}
+ F(x_{t_n}, \theta, a_0) \cdot h,
\quad x_{t_0} = x(0),
%\\
%\text{where: }&
%\\
%t_n &:=
%n \cdot h, \quad
%n = 0, \cdots, N,
%\quad t_{N} = T.
\end{aligned}
\begin{aligned}
C(x_{t^{(k+1)}}, & a_{t^{(k+1)}})
=
\\
& C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\end{aligned}
\begin{aligned}
x_{t_{n+1}}^{(k)} &
= x_{t_n}^{(k)}
+ F(x_{t_n}^{(k)}, \theta^{(k)}, a_0^{(k)}) \cdot h^{(k)},
\quad x_{t_0^{(k)}} = x^{(k)}(0),
\\
\text{where: }&
\\
t_n^{(k)} &:=
n \cdot h^{(k)}, \quad
n = 0, \cdots, N^{(k)},
\quad t_{N}^{(k)} = T^{(k)}.
\end{aligned}
x_0,a_0,R_1,
x_0, a_0, R_1,
x_1, a_1, R_2,
\cdots,
x_t, a_t, R_{t+1}
\cdots,
x_{T-1}, a_{T-1}, R_T,
x_T
G_t := R_{t+1} + \cdots + R_{T-1} + R_{T}
\begin{aligned}
G_t &:= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3}+ \cdots
\\
&=
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+1+k}, \qquad \gamma \in [0,1)
\end{aligned}
\begin{aligned}
%C_{t+1}
&=
C(x_{t}, a_{t})
\\
%\Phi_{t+1}^{h}(x_t,a_t)
&=
x_t +\varphi(h,\theta, a^{\theta}_t)
\end{aligned}
Agent
R_{t+1}
x_{t+1}
a_t\in \mathcal{A}(x_t)
action
state
x_{t}
reward
R_{t}
G_t := R_{t+1} + \cdots + R_{T-1} + R_{T}
p(s^{\prime},r | s, a)
:= \mathbb{P}[x_t=s^{\prime}, R_{t}=r | x_{t-1}=s, a_t=a]
\begin{aligned}
r(s, a)
&:= \mathbb{E}[
R_t | x_{t-1}=s, a_{t-1}=a
]
\\
&=
\sum_{r\in \mathcal{R}}
r
\sum_{s^{\prime}\in S}
p(s^{\prime}, r | s, a)
\end{aligned}
\begin{aligned}
G_t &:= R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t-1} R_{T}
\\
&=\sum_{k=t+1}^{T}
\gamma^{k-t-1} R_k
\end{aligned}
Discounted return
Total return
\begin{aligned}
v_{\pi}(s) &:=
\mathbb{E}_{\pi}
[G_t | x_t = s]
\\
&=
\mathbb{E}_{\pi}
\left[
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+k+1}
\big| x_t =s
\right]
\end{aligned}
\pi(a|s):= \mathbb{P}[a_t = a|x_t=s]
\begin{aligned}
v_{\pi}(s) &:=
\mathbb{E}_{\pi}
[G_t | x_t = s]
\\
&=
\mathbb{E}_{\pi}
\left[
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+k+1}
\big| x_t =s
\right]
\\
& =
\mathbb{E}_{\pi}
\left[
R_{t+1} + \gamma G_{t+1} | x_t = s
\right]
\\
&=
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma
\mathbb{E}_{\pi}[G_{t+1} | x_{t+1}=s^{\prime}]
\right]
\\
&=
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma v_{\pi}(s^{\prime})
\right]
\end{aligned}
\begin{aligned}
v_{*}(s) &:=
\max_{\pi}
v_{\pi}(s)
\\
&=
\max_{a\in \mathcal{A}(s)}
\mathbb{E}_{\pi_{*}}
\left[
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+k+1}
\big| x_t =s
\right]
\\
& =
\max_{a\in \mathcal{A}(s)}
\mathbb{E}_{\pi}
\left[
R_{t+1} + \gamma G_{t+1} | x_t = s
\right]
\\
&=
\max_{a\in \mathcal{A}(s)}
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma
\mathbb{E}_{\pi}[G_{t+1} | x_{t+1}=s^{\prime}]
\right]
\\
&=
\max_{a\in \mathcal{A}(s)}
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma v_{\pi}(s^{\prime})
\right]
\end{aligned}
x_0, a_0, R_1,
x_1, a_1, R_2,
\cdots,
x_t, a_t, R_{t+1}
\cdots,
x_{T-1}, a_{T-1}, R_T,
x_T
\begin{aligned}
\gamma &= 0
\\
G_t &:= R_{t+1} + \cancel{\gamma R_{t+2}} + \cdots + \cancel{\gamma^{T-t-1} R_{T}}
\end{aligned}
Dopamine reward
J(x,\pi) = E\left[ \sum_{k=0}^M C(x_{t^{(k)}},a_{t^{(k)}}) | x_{t^{(0)}} = x , \pi \right]
\begin{aligned}
C(x_{t^{(k+1)}}, & a_{t^{(k+1)}})
=
\\
& C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\end{aligned}
\begin{aligned}
C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLL dt,
\\
C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLD(x_t, a_t) dt
\\
YLL(x_t, a_t) &:=
m_1 p \delta_E (E(t) - E^{t^{(k)}} ),
\\
YLD(x_t, a_t) &:=
m_2 \theta \alpha_S(E(t) - E^{t^{(k)}}),
\\
t &\in [t^{(k)},t^{(k + 1)}]
\end{aligned}
\begin{aligned}
C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
& = \int_{t^{(k)}}^{t^{(k+1)}} m_3(K_{Vac}(t) - K_{Vac}^{t^{(k)}}) dt
\\
C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=\int_{t^{(k)}}^{t^{(k+1)}} m_4(X_{vac}(t) - X_{vac}^{t^{(k)}}) dt
\end{aligned}
\frac{dx_{t}}{dt} =f(x_{t} ,a_{t})
Agent
a_t\in \mathcal{A}
C_t
x_t
\begin{aligned}
a_t^{(k)} &= p_i \cdot \Psi_V^{(k)}
\\
p_i &\in \mathcal{A}:=\{p_0, p_1, \dots, p_M\}
\\
p_i &\in [0, 1]
\end{aligned}
Deterministic control
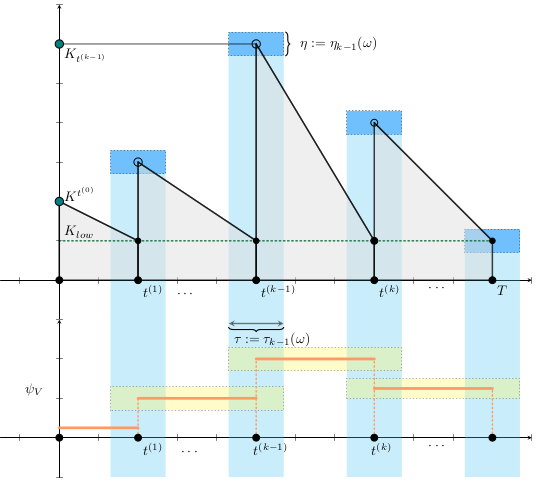
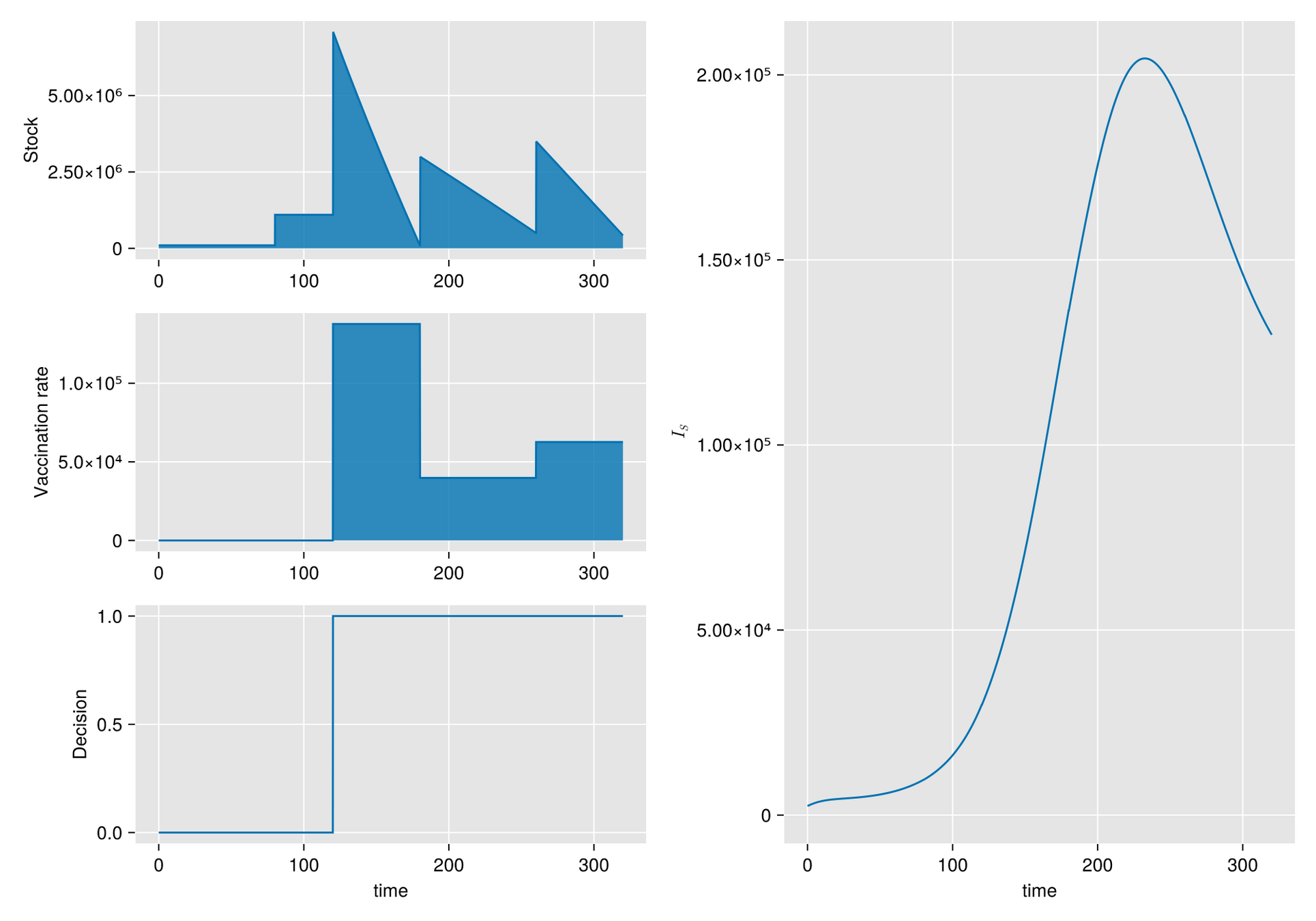
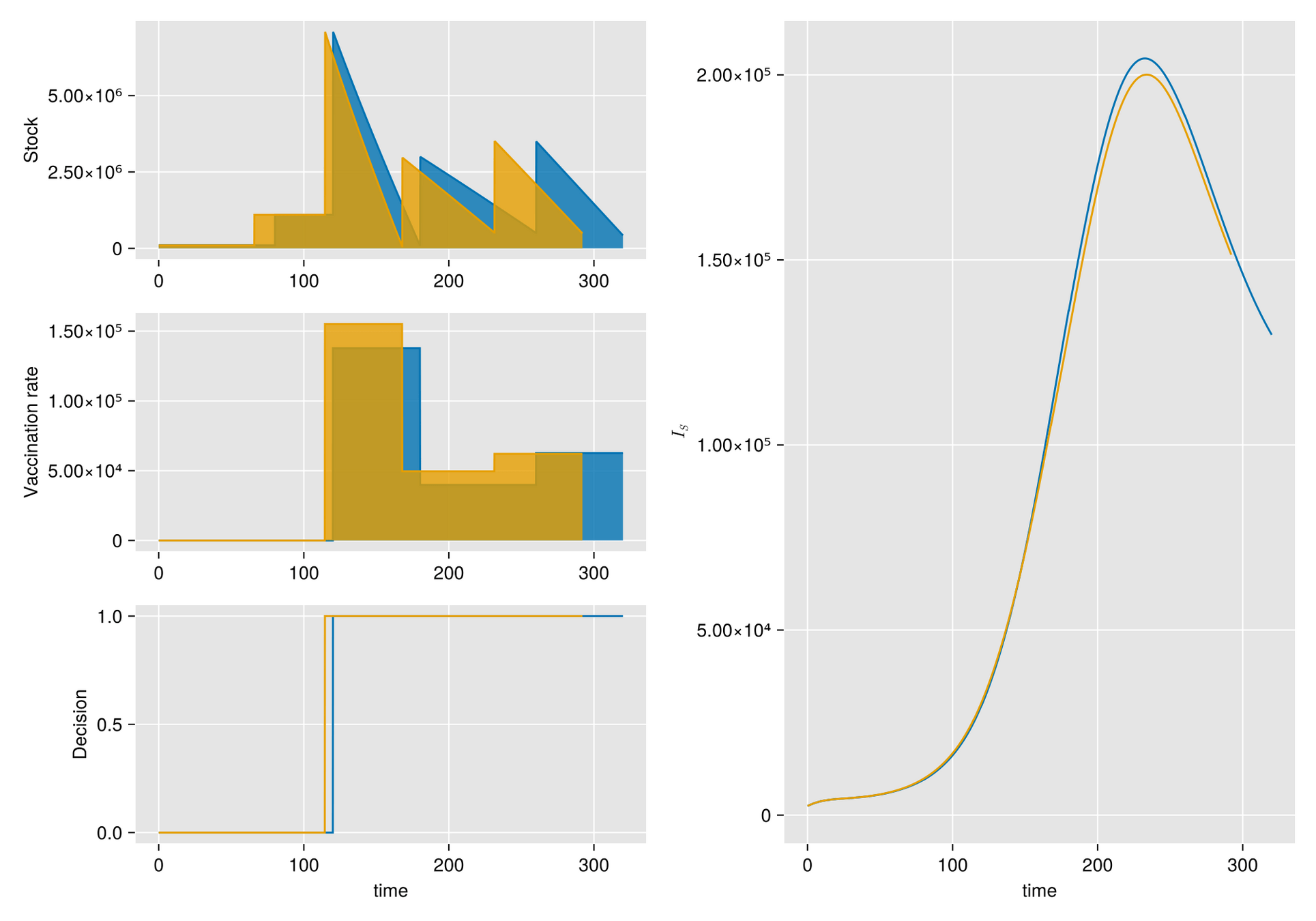
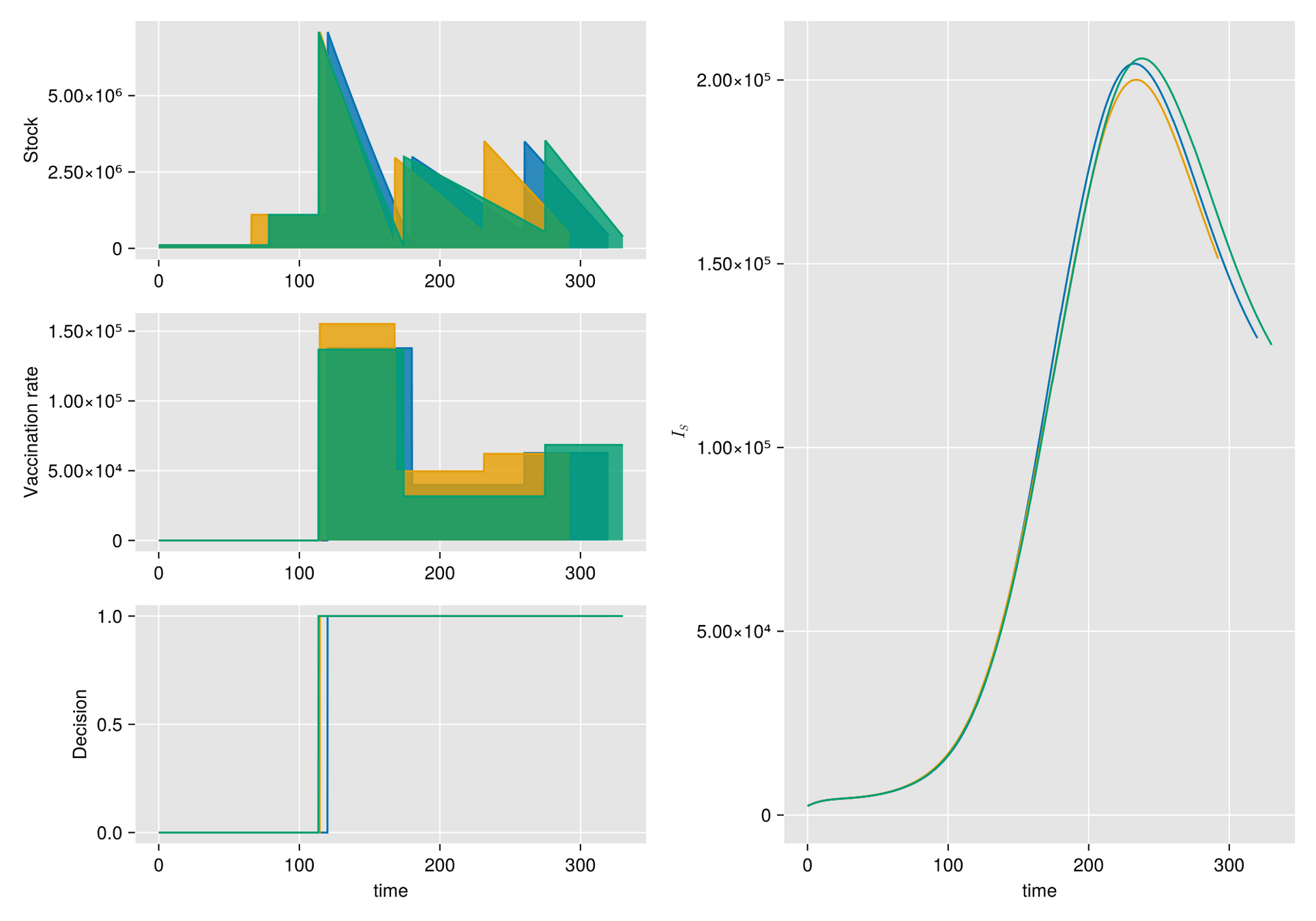
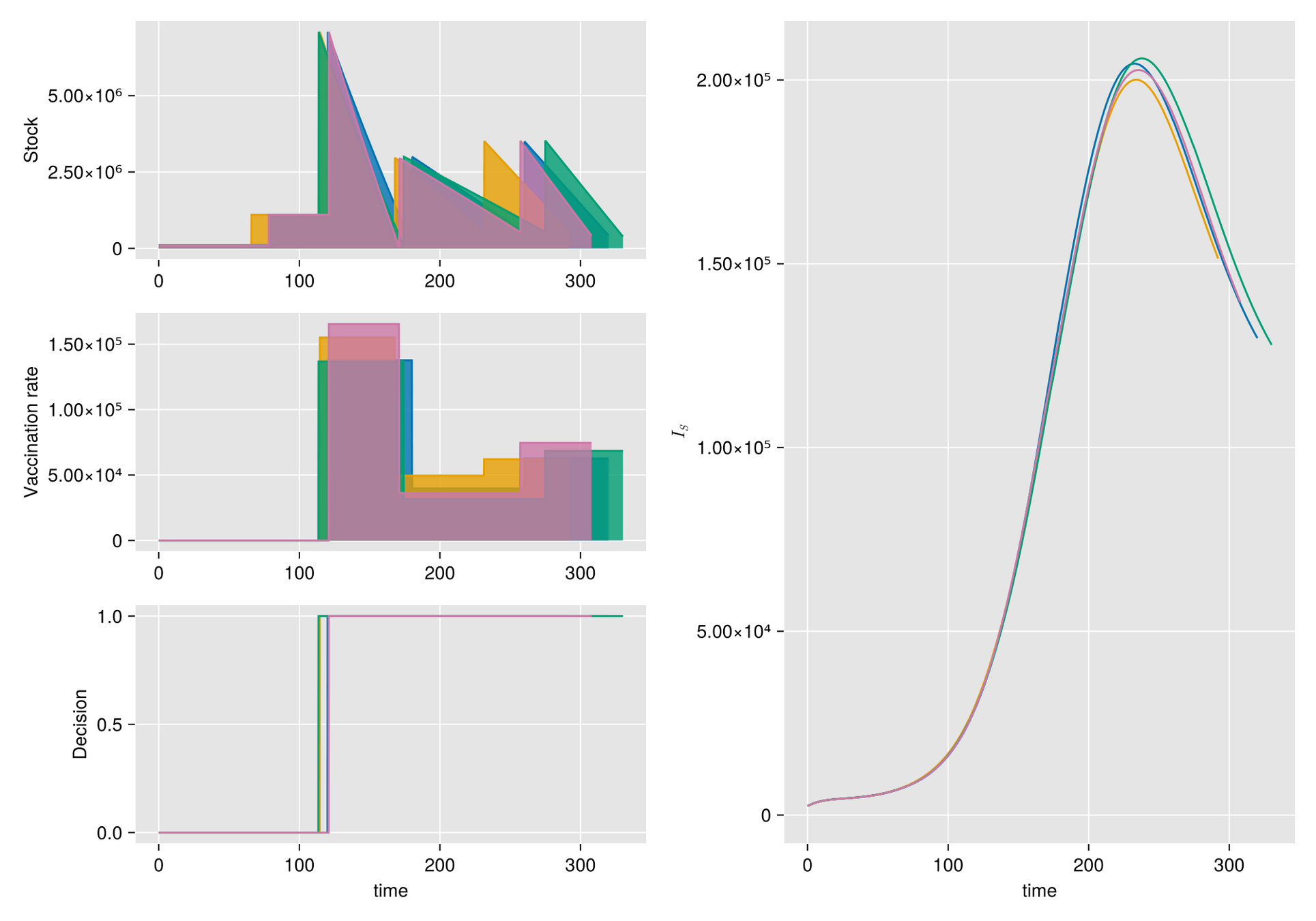
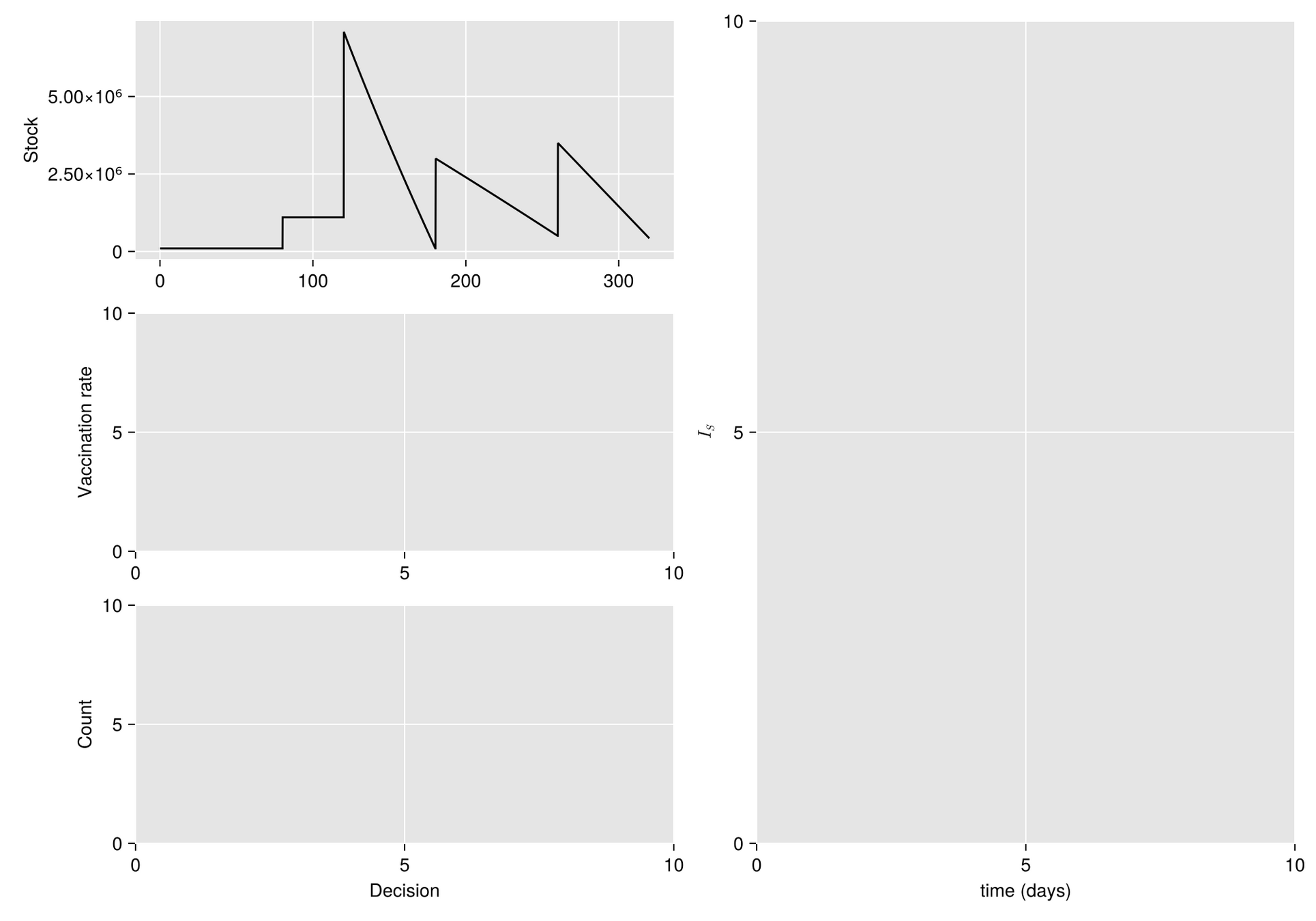
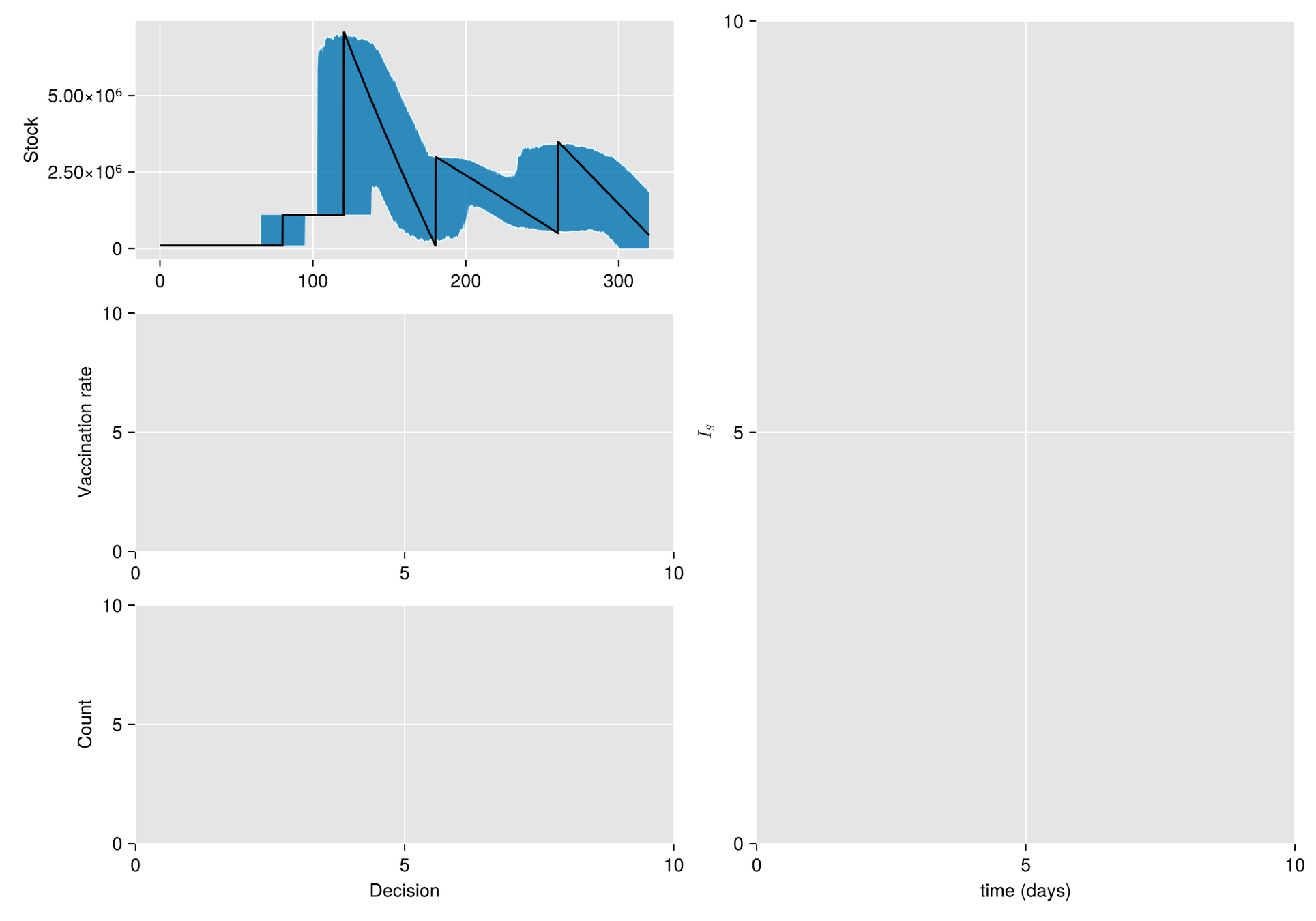
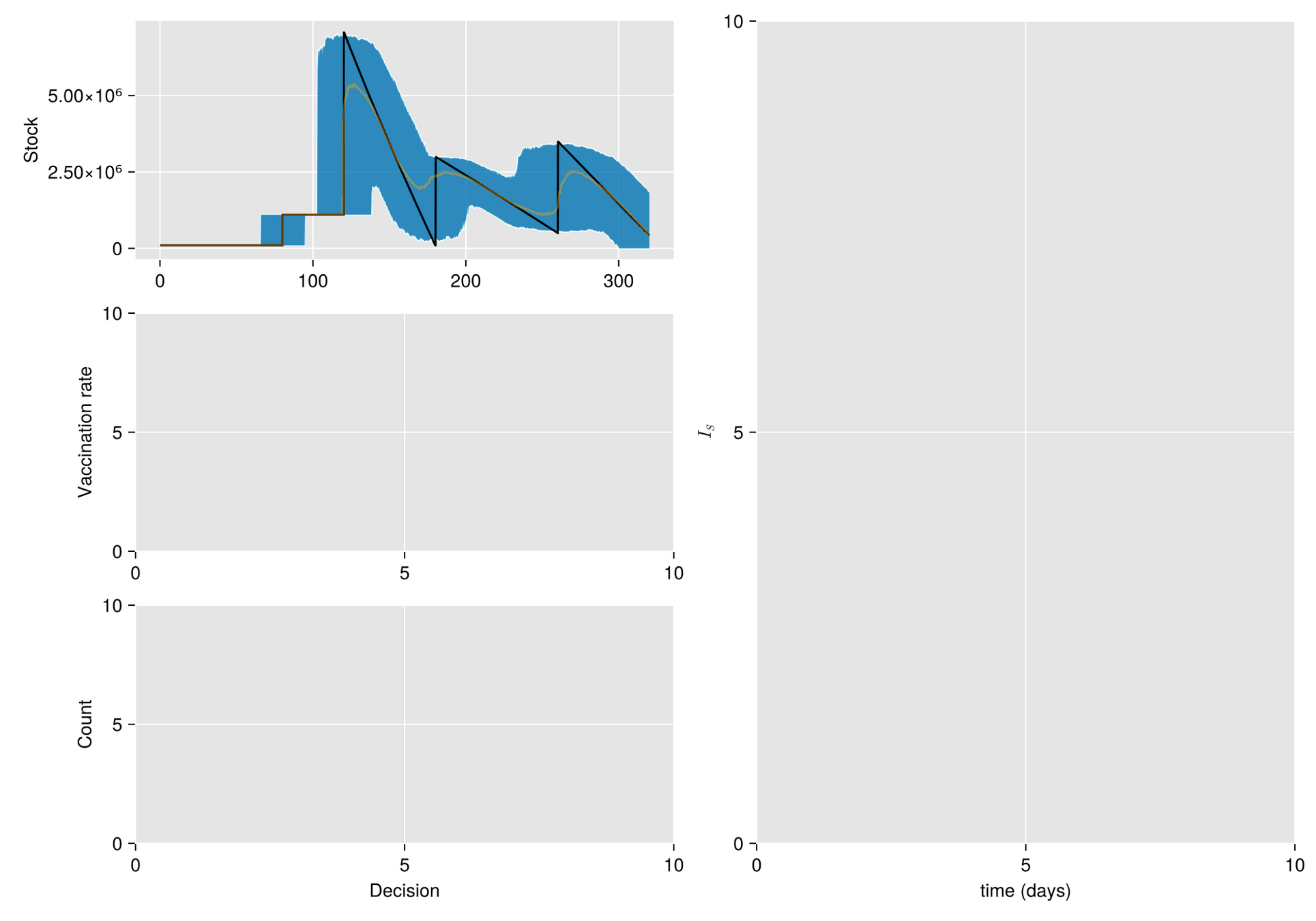
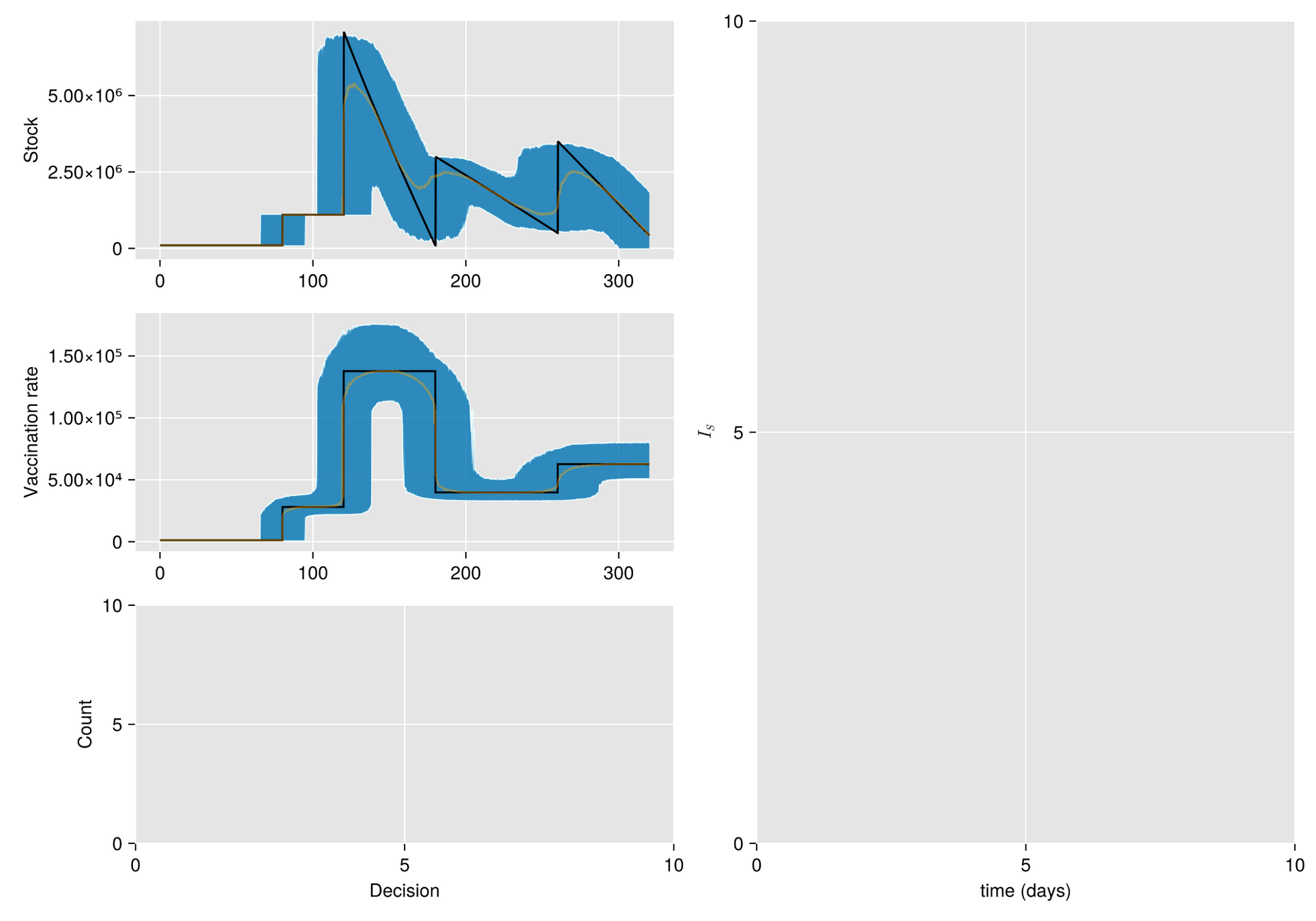
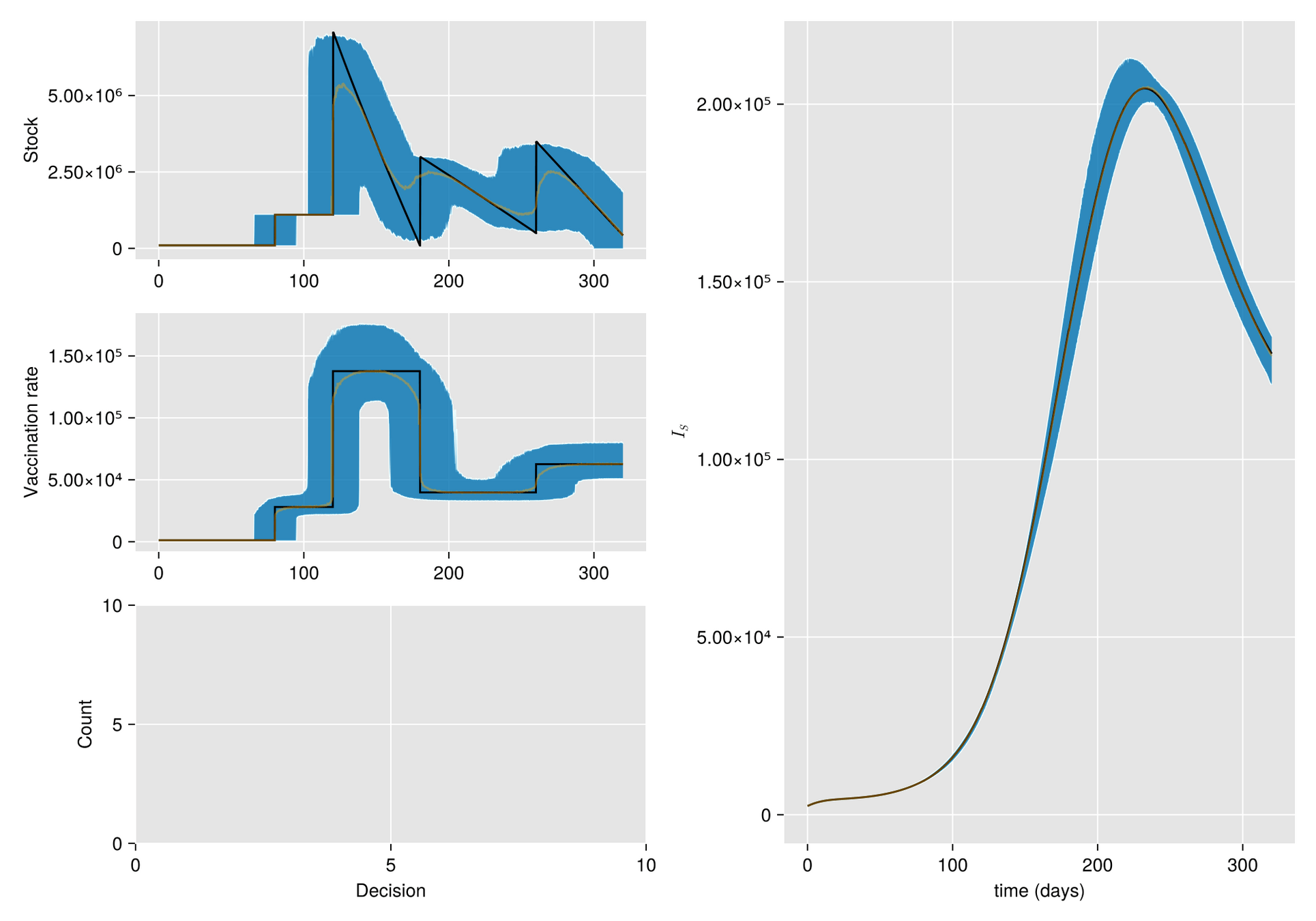
HJB (Dynamic Programming)- Curse of dimensionality
\approx \
\mathtt{HJB}
HJB(Neuro-Dynamic Programming)
Abstract dynamic programming.
Athena Scientific, Belmont, MA, 2013. viii+248 pp.
ISBN:978-1-886529-42-7
ISBN:1-886529-42-6
Rollout, policy iteration, and distributed reinforcement learning.
Revised and updated second printing
Athena Sci. Optim. Comput. Ser.
Athena Scientific, Belmont, MA, [2020], ©2020. xiii+483 pp.
ISBN:978-1-886529-07-6
Reinforcement learning and optimal control
Athena Sci. Optim. Comput. Ser.
Athena Scientific, Belmont, MA, 2019, xiv+373 pp.
ISBN: 978-1-886529-39-7
https://slides.com/sauldiazinfantevelasco/solabima-unison-2024-nov
¡Gracias!
SoLaBiMa-UNISON-2024-Nov
By Saul Diaz Infante Velasco
SoLaBiMa-UNISON-2024-Nov
Explore innovative strategies for managing scarce vaccines in inventory! See how uncertainty in delivery times and order sizes impacts epidemic control efforts.
