Aprendizaje reforzado y epidemiología: una invitación a las aplicaciones de los procesos Markovianos de decisión en Ciencia de Datos
“1er Congreso Multidisciplinario de la Facultad de Ciencias en Física y Matemáticas”
Yofre H. Garcia
Saúl Diaz-Infante Velasco
Jesús Adolfo Minjárez Sosa
sauldiazinfante@gmail.com
02 de octubre de 2024
Aprendizaje reforzado y epidemiología: una invitación a las aplicaciones de los procesos Markovianos de decisión en Ciencia de Datos
“1er Congreso Multidisciplinario de la Facultad de Ciencias en Física y Matemáticas”
Yofre H. Garcia
Saúl Diaz-Infante Velasco
Jesús Adolfo Minjárez Sosa
sauldiazinfante@gmail.com
02 de octubre de 2024
Aprendizaje reforzado y epidemiología: una invitación a las aplicaciones de los procesos Markovianos de decisión en Ciencia de Datos
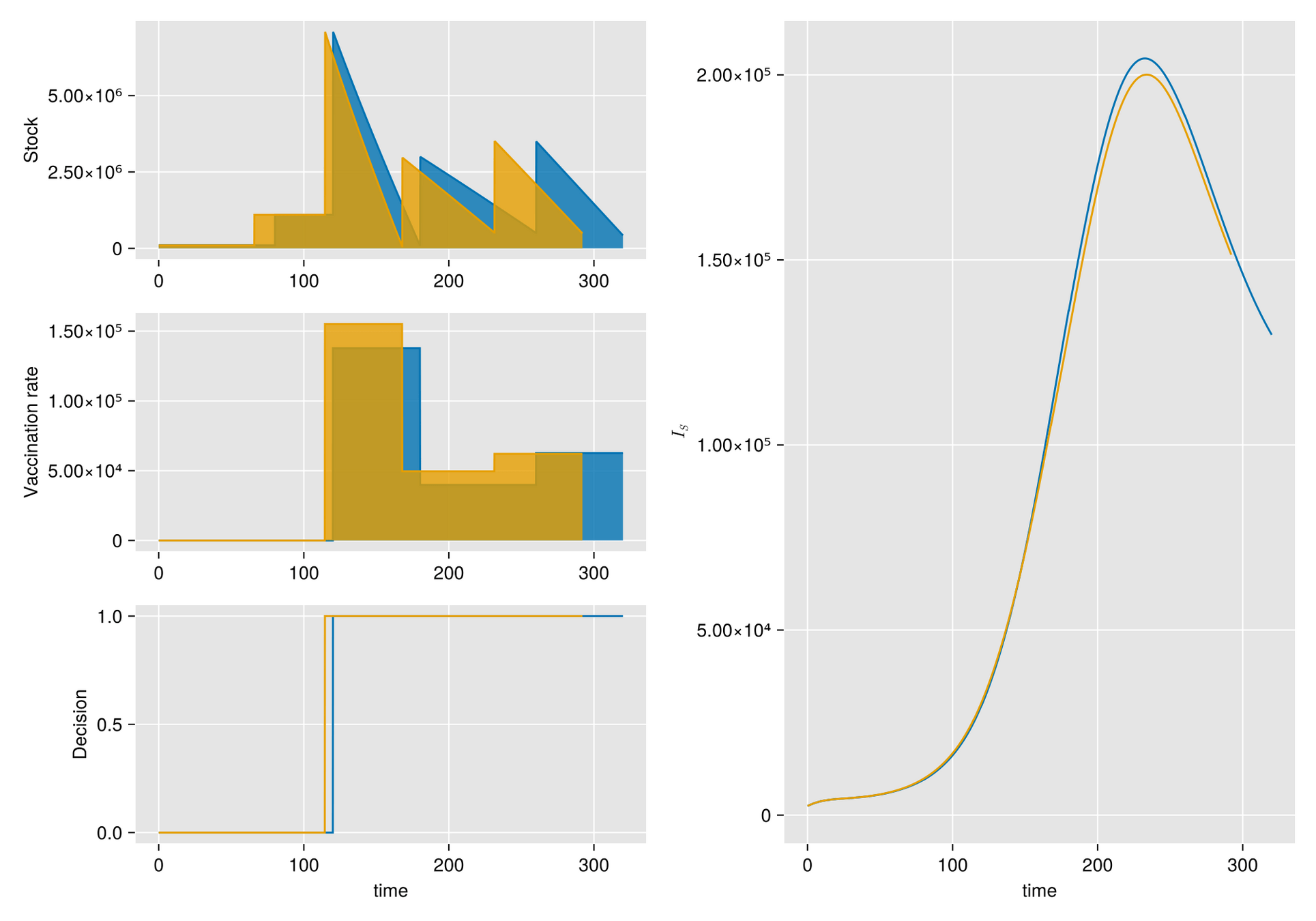
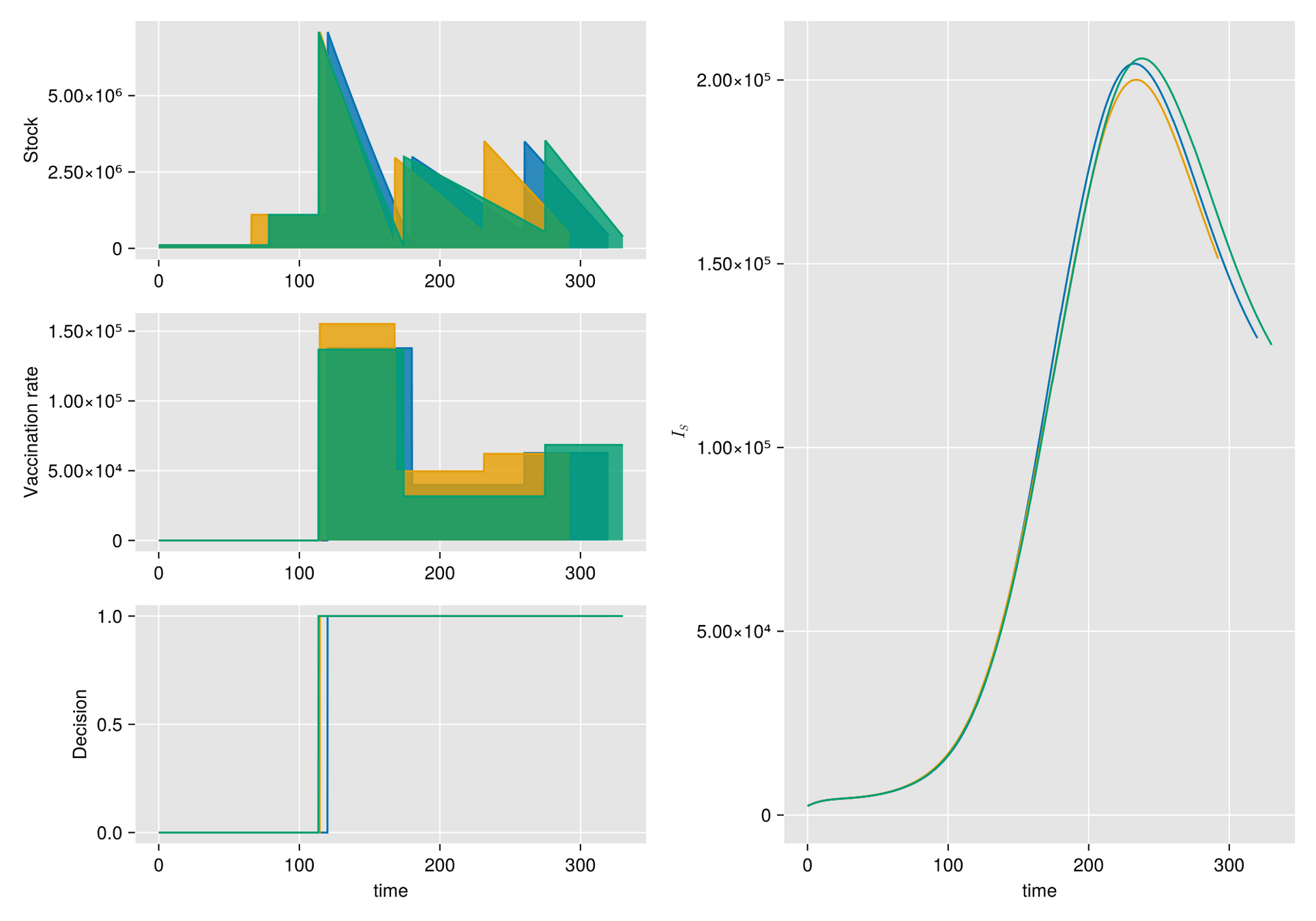
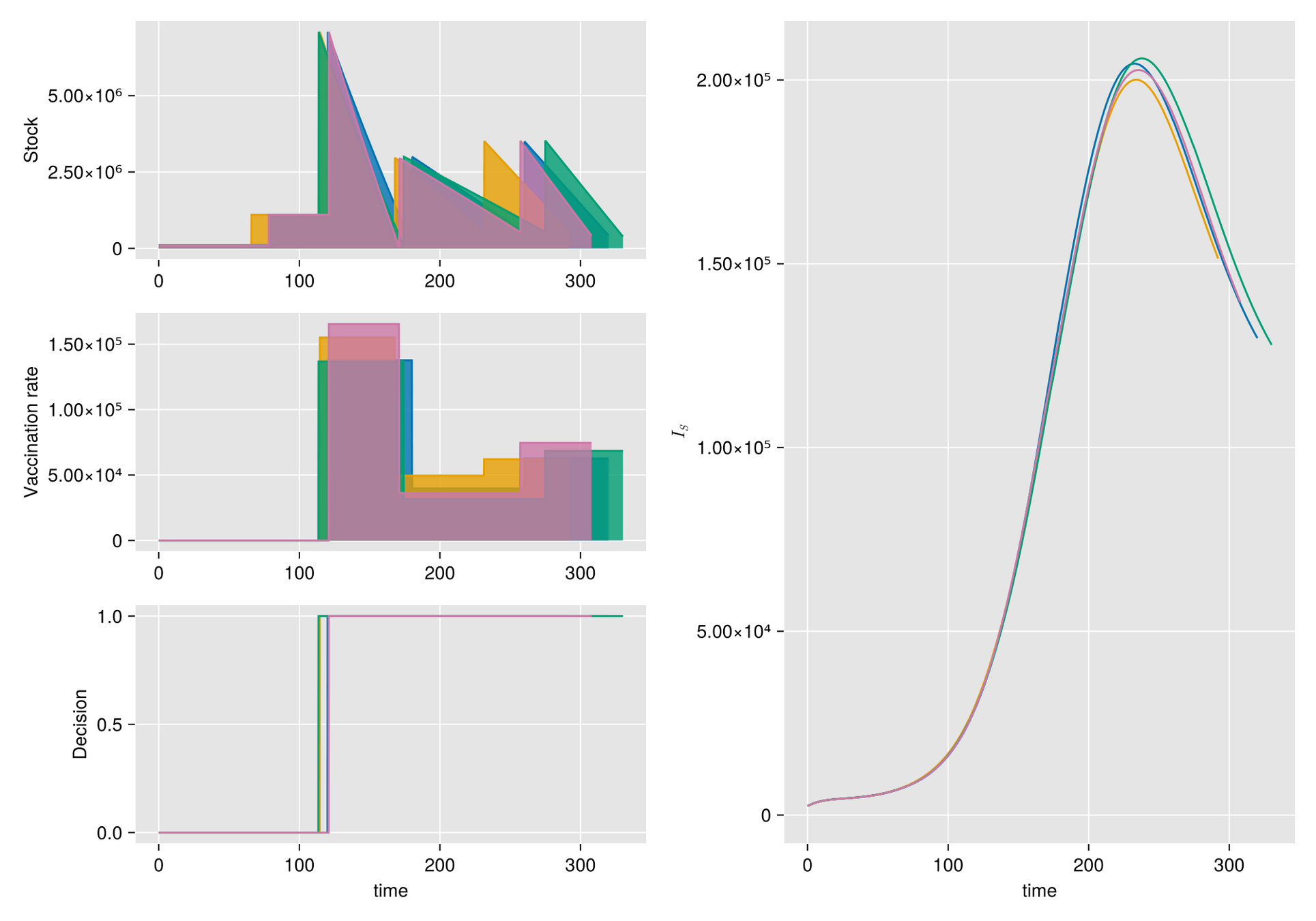
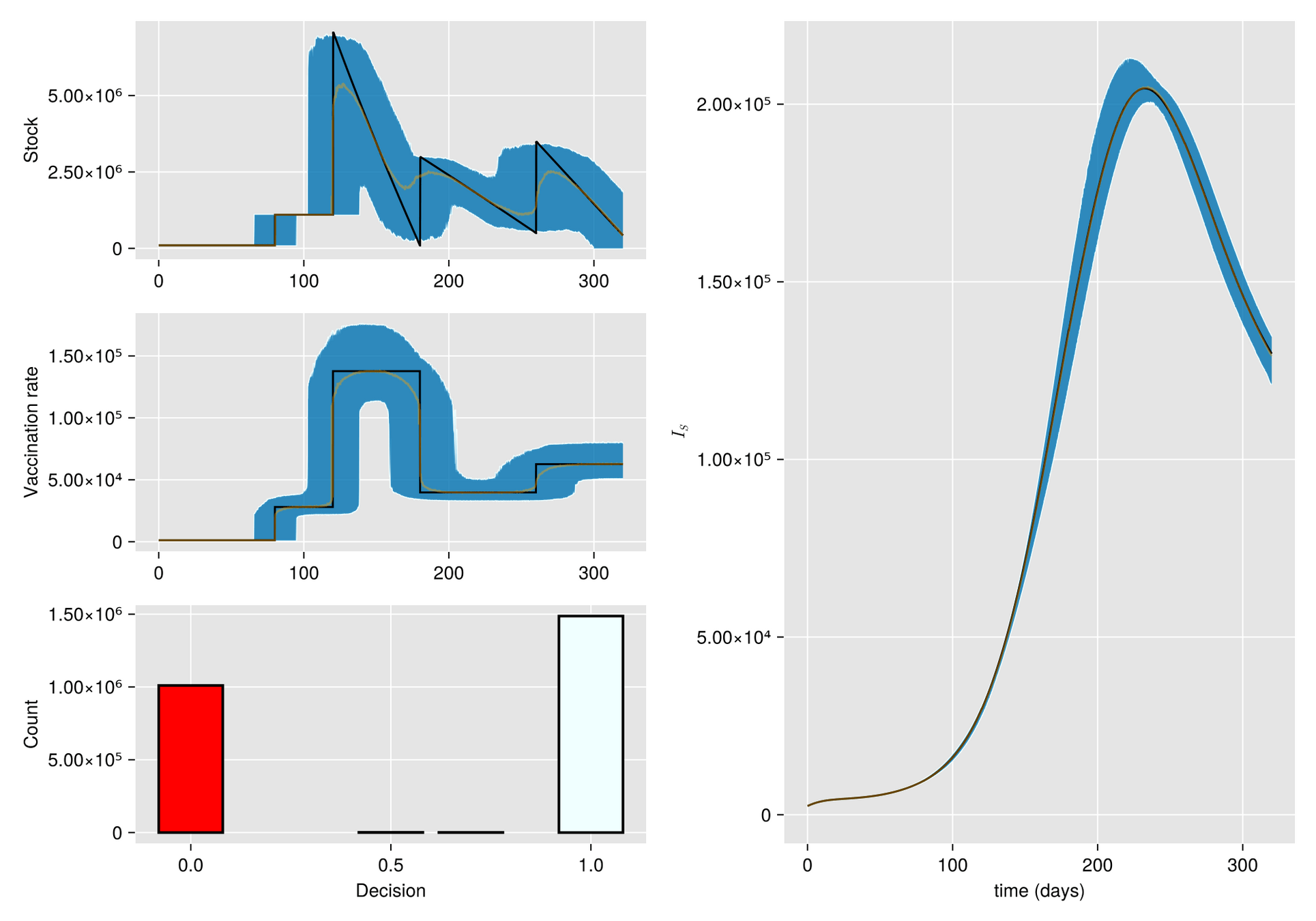
Argumento. Cuando hay escasez de vacunas, a veces la mejor respuesta es abstenerse de vacunarse, al menos por un tiempo.
Hipótesis. Bajo estas condiciones, el manejo de inventarios sufre importantes fluctuaciones aleatorias
Objetivo. Optimizar el manejo del inventario de vacunas y su efecto en una campaña de vacunación
El 13 de octubre de 2020, el gobierno Mexicano anunció un plan de entrega de vacunas por parte de Pfizer-BioNTech y otras empresas como parte de la campaña de vacunación contra el COVID-19.
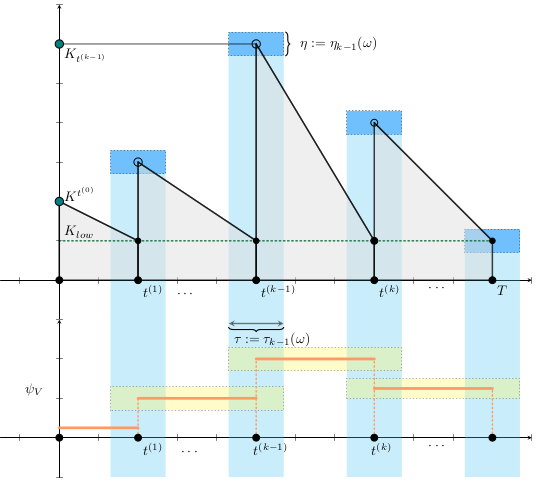
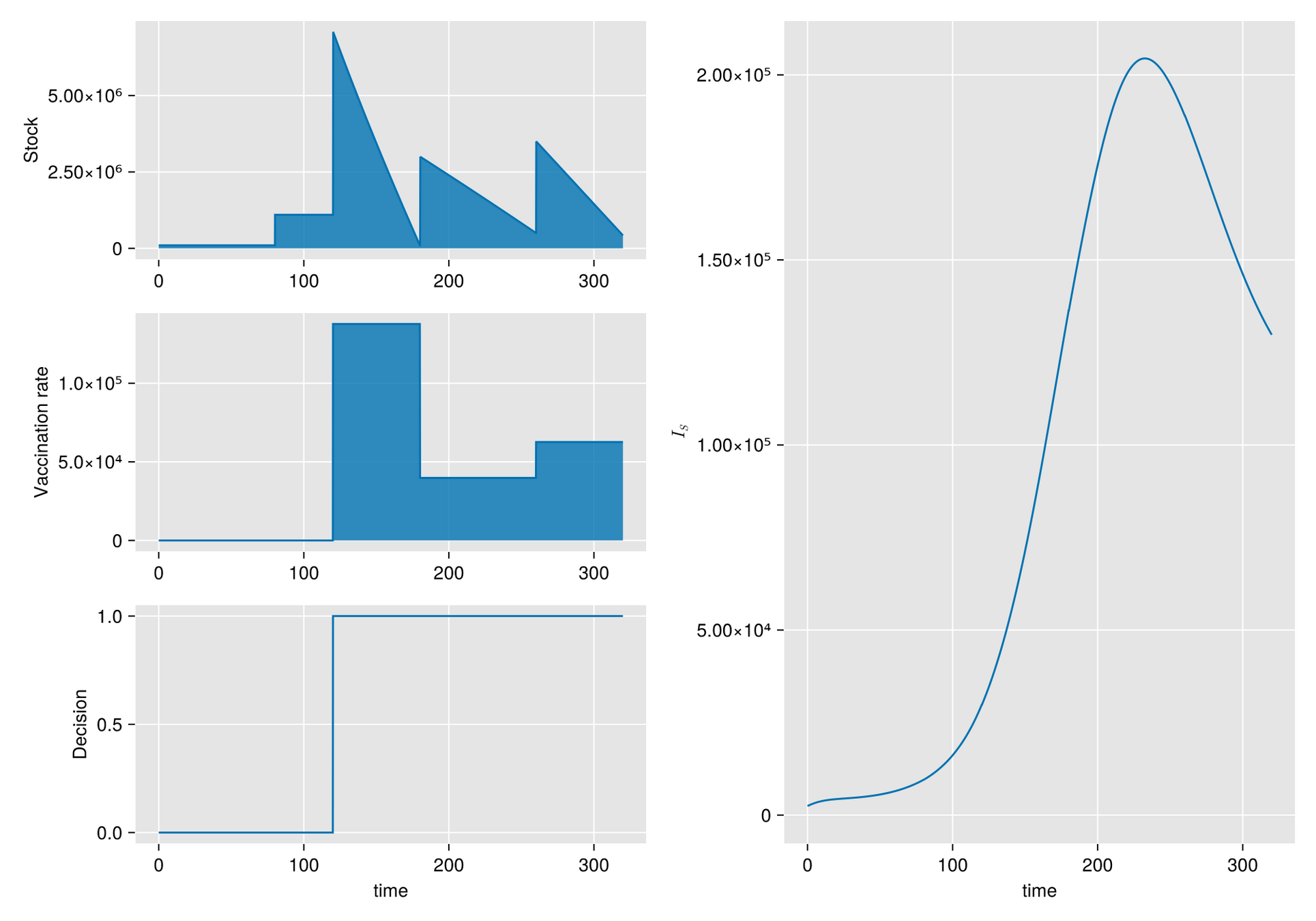
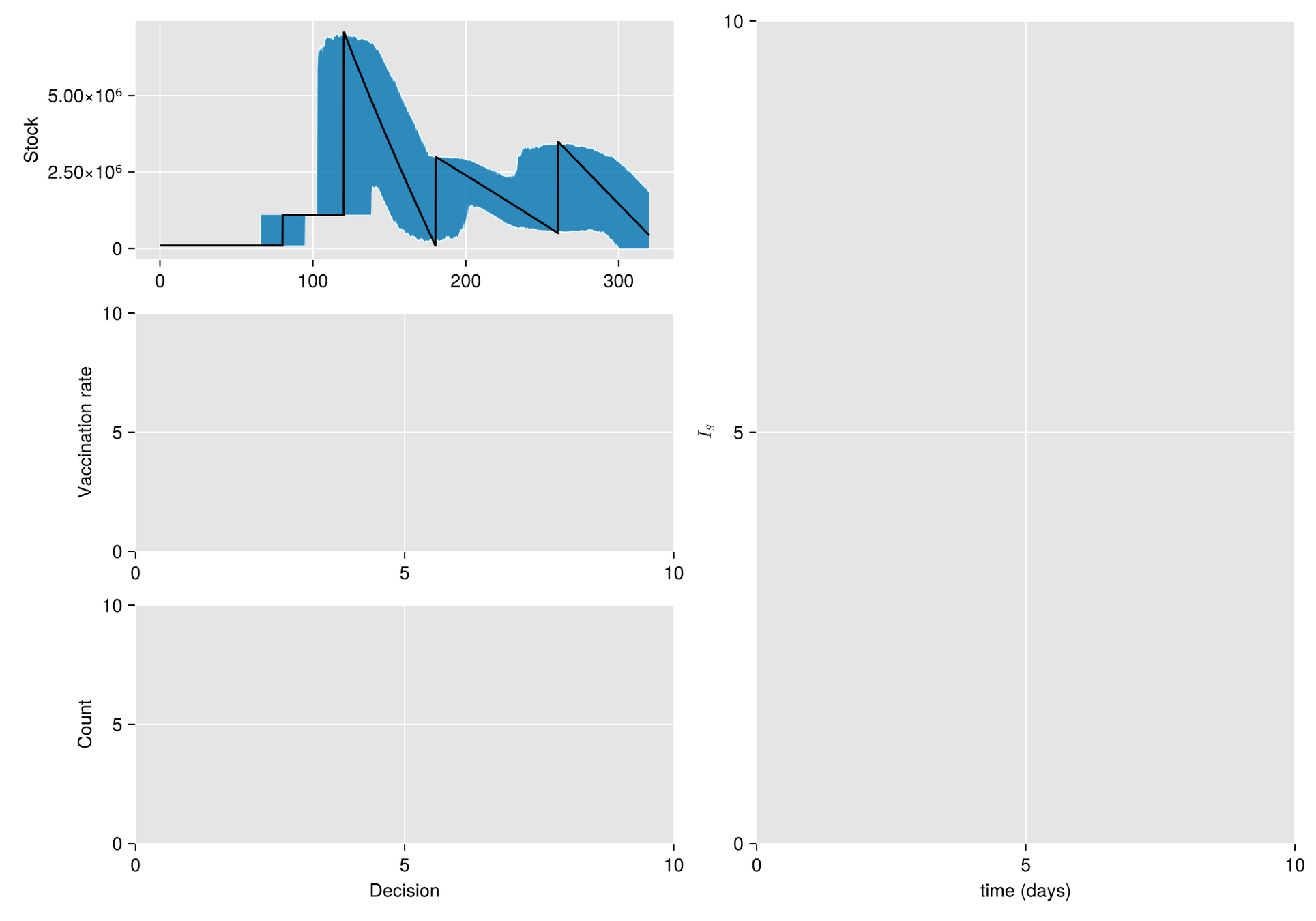
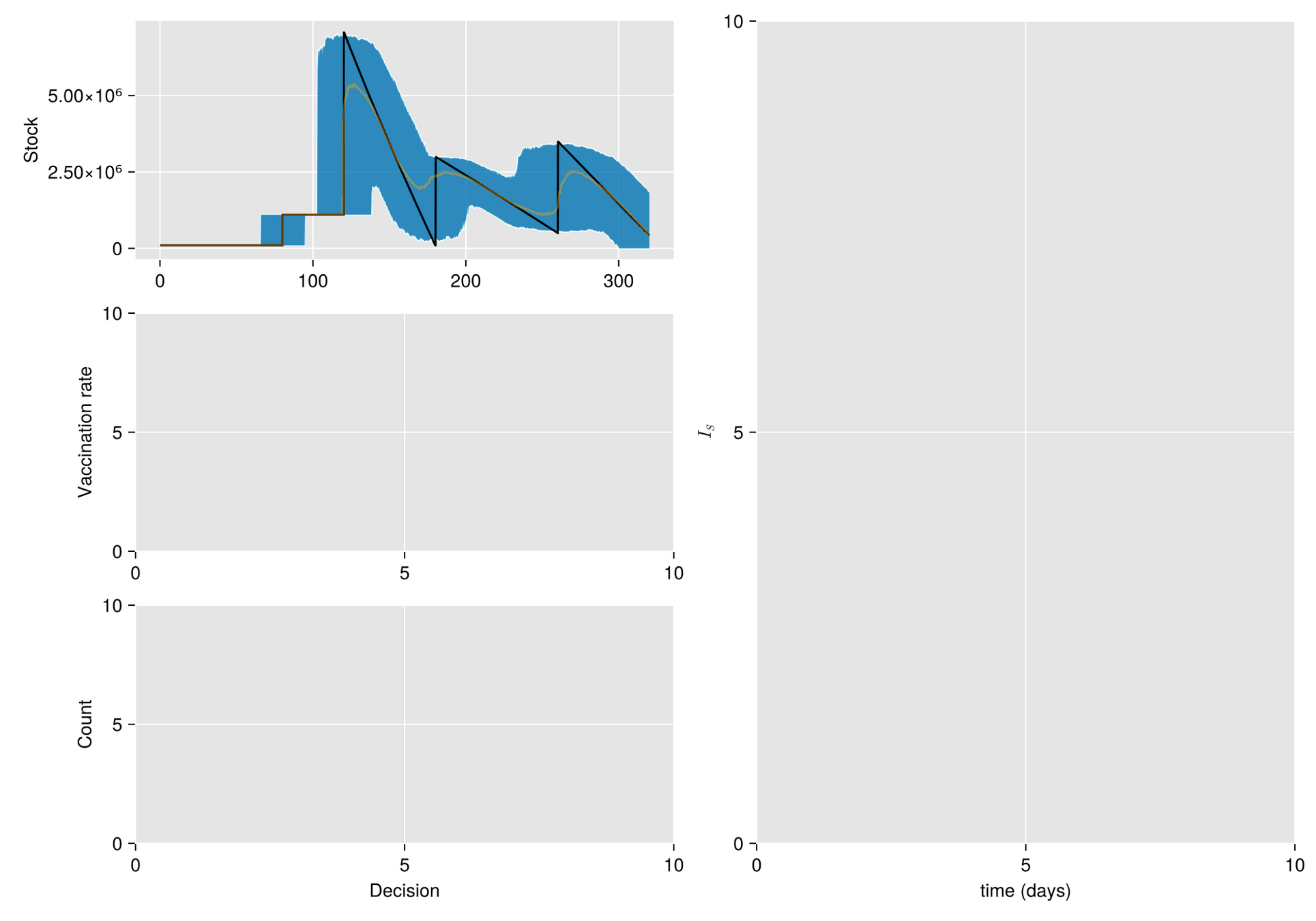
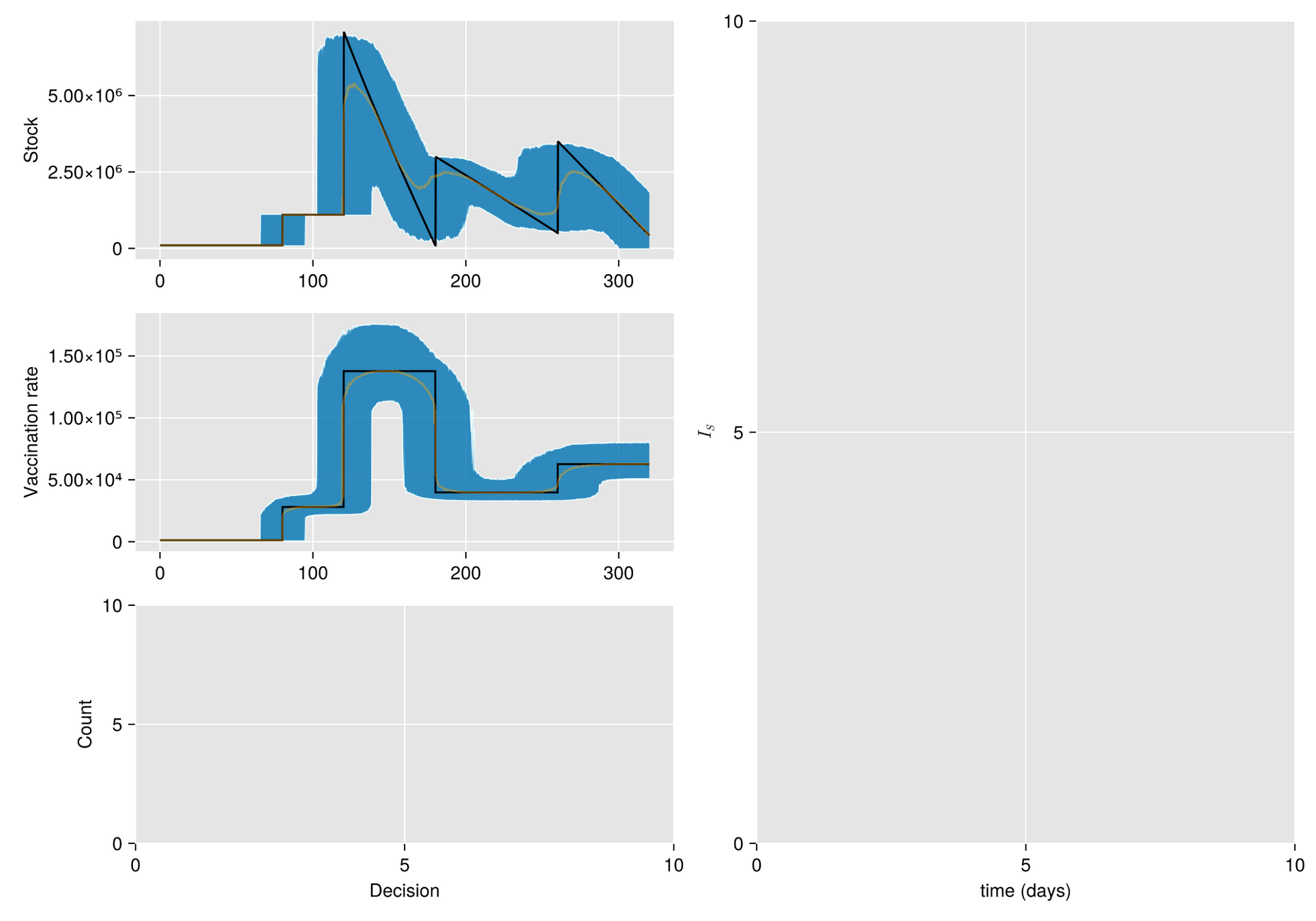
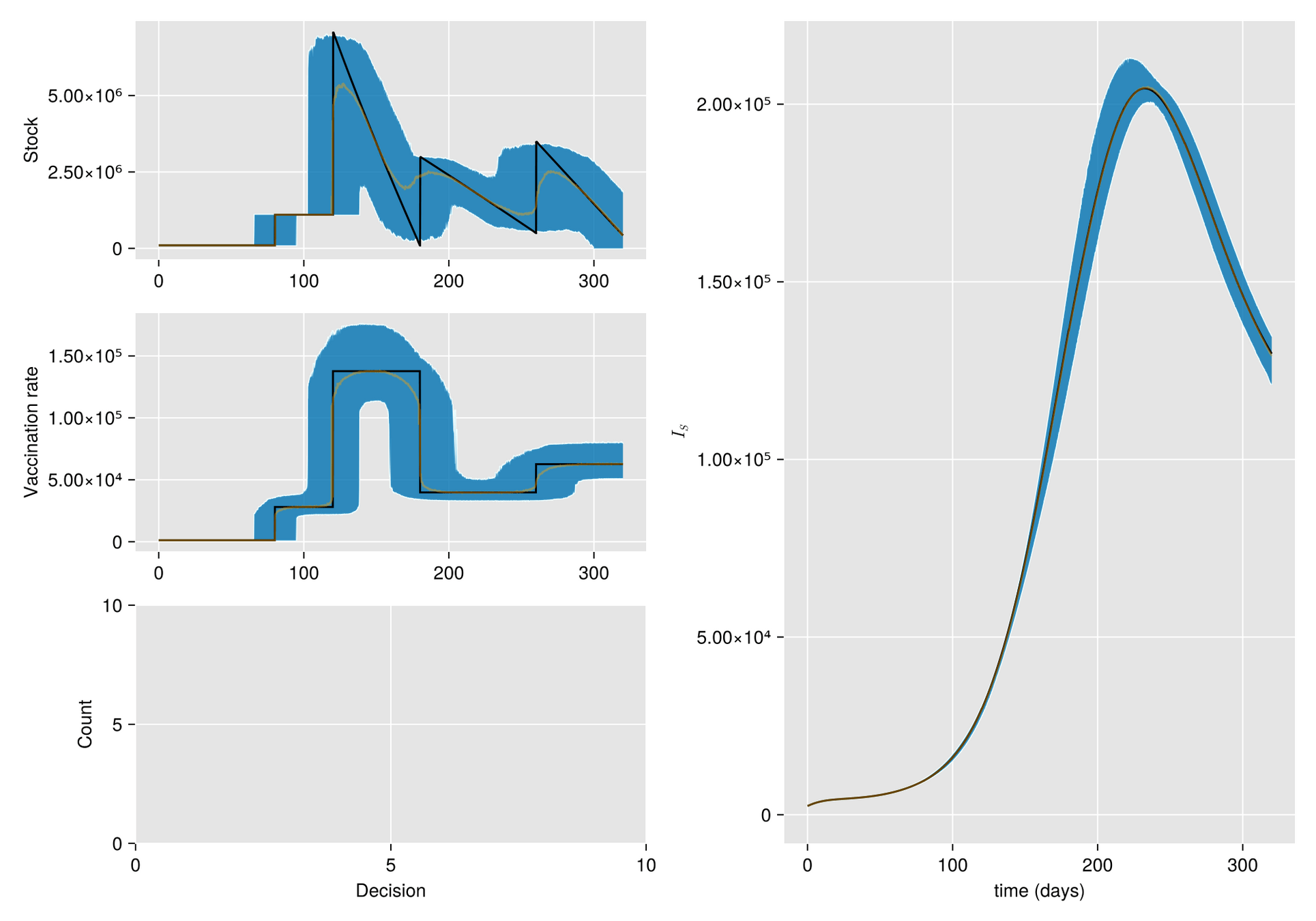
Métodos. Dado un calendario de envíos de vacunas, describimos la gestión de stock con protocolo de respaldo y cuantificamos las fluctuaciones aleatorias debido a un programa bajo alta incertidumbre.
Luego, incorporamos esta dinámica en un sistema de EDO que describe la enfermedad y evaluamos su respuesta.
1
Discovery of requirements for a project.
2
Research into the project space, competitors and the market.
3
Creating a Plan that sets the requirements for the design and build phases.
5
Review and Iterate on the designs with testing of ideas, client feedback and prototypes.
4
Design a number of iterations that capture the plans and requirements.
6
Build the project to an MVP to test and evaluate. Iterate using these learnings.
Text
Text
Control no lineal: HJB y DP
Dado
\frac{dx}{dt} = f(x(t))
\frac{dx_{t}}{dt} =f(x_{t} ,a_{t})
Agente
a_t\in \mathcal{A}
x_t
J(x_t, a_t, 0, T) = Q(x_T, T)
+ \int_0^T \mathcal{L}(x_{\tau}, a_{\tau}) d_{\tau}
Objetivo:
Diseño
para seguir
t. q. optimizar costo
\text{accion } a_t\in \mathcal{A},
\text{estado } x_t
J(x_t, a_t, 0, T) .
Para fijar ideas: Un modelo de población de crecimiento exponencial.
J(P_t, a_t, 0, T) =
Q(P_T, T)
+ \int_0^T \mathcal{L}(P_{\tau}, a_{\tau}) d_{\tau}
Objetivo:
Diseño
para dirigir
t. q. optimizar costo
\text{accion } a_t\in \mathcal{A},
\text{estado } P_t
J(P_t, a_t, 0, T) .
J(P_t, a_t, 0, T) =
Q(P_T, T)
+ \int_0^T
\underbrace{\mathcal{L}(P_{\tau}, a_{\tau})}_{\frac{1}{2} (w_1 P_{\tau} + a_{\tau}^ 2)} d_{\tau}
\begin{aligned}
\dfrac{dP_t}{dt}
& = (k + a_t P_t) , \qquad t \in [0,T]
\\
P_0 &= p_0
\end{aligned}
\begin{aligned}
\dfrac{dP_t}{dt}
& = kP_t, \qquad t \in [0,T]
\\
P_0 &= p_0
\end{aligned}
\begin{aligned}
\dfrac{dP_t}{P_t}
&= k \, dt
\\
\int \frac{1}{P_t} \, dP_t
&= \int k \, dt
\\
\ln |P_t|
&= kt + C
\\
|P_t|
&= e^{kt + C}
\\
|P_t|
&= C_1 e^{kt}
\\
P_t
&= P_0 e^{kt}
\end{aligned}
\begin{aligned}
\dfrac{dP_t}{dt}
& = kP_t, \qquad t \in [0,T]
\\
P_0 &= p_0
\end{aligned}
Control no lineal: HJB and DP
V(x_0, 0, T):=
\min_{a_t \in \mathcal{A}} J(x_t, a_t, 0, T)
V(x_0, 0, T) = V(x_0, 0, t) + V(x_0, t, T)
Principio de opt. de Bellman
Problema de Control
\frac{dx_t}{dt} = f(x_t, a_t)
\min_{a_t\in \mathcal{A}} J(x_t, a_t, 0, T) = Q(x_T, T)
+ \int_0^T \mathcal{L}(x_{\tau}, a_{\tau}) d_{\tau}
t.q-
x_T
x_t
x_0
\frac{\partial V}{\partial t} =
\min_{a_t\in \mathcal{A}}
\left[
\left(
\frac{\partial V}{\partial x}
\right)^{\top}
f(x,a) +
\mathcal{L}(x,a)
\right]
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
& S(0) = S_0, I(0)=I_0, R(0)=0
\\
& S(t) + I(t) + R(t )= 1
\end{aligned}
\end{equation*}
S+I+R = \underbrace{1}_{\leftrightarrow N }
\begin{aligned}
S'(t) &= -\beta IS
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
& S(0) = S_0, I(0)=I_0, R(0)=0
\\
& S(t) + I(t) + R(t )= 1
\end{aligned}
\dfrac{d(S+I+R)}{dt} = 0
\to {\text{población cte.}}
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
& S(0) = S_0, I(0)=I_0, R(0)=0
\\
& S(t) + I(t) + R(t )= 1
\end{aligned}
\end{equation*}
\lambda_V:=
\underbrace{ \textcolor{orange}{\xi}}_{cte.}
\cdot \ S(t)
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS - \textcolor{red}{\lambda_V(t)}
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
V'(t) & = \textcolor{red}{\lambda_V(t)}
\\
& S(0) = S_0, I(0)=I_0,
\\
&R(0)=0, V(0) = 0
\\
& S(t) + I(t) + R(t) + V(t)= 1
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS - \textcolor{red}{\lambda_V(x, t)}
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
V'(t) & = \textcolor{red}{\lambda_V(x,t)}
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
S'(t) &= -\beta IS - \textcolor{red}{\lambda_V(x, t)}
\\
I'(t) &= \beta IS - \gamma I
\\
R'(t) & = \gamma I
\\
V'(t) & = \textcolor{red}{\lambda_V(x,t)}
\end{aligned}
\end{equation*}
\lambda_V:=
\underbrace{ \textcolor{orange}{\Psi_V}}_{cte.}
\cdot \ S(t)
\begin{aligned}
S'(t) &= \cancel{-\beta IS} - \underbrace{\textcolor{red}{\lambda_V(x, t)}}_{=\Psi_V S(t)}
\\
I'(t) &= \cancel{\beta IS} - \cancel{\gamma I}
\\
{R'(t)} & = \cancel{\gamma I}
\\
V'(t) & = \underbrace{\textcolor{red}{\lambda_V(x, t)}}_{=\Psi_V S(t)}
\\
& S(0) \approx 1, I(0) \approx 0,
\\
&R(0)\approx 0, V(0) = 0
\\
& S(t) + \cancel{I(t)} + \cancel{R(t)} +\cancel{ V(t)}= 1
\end{aligned}
\begin{aligned}
S'(t) &= - \Psi_V S(t)
\\
V'(t) & = \Psi_V S(t)
\\
& S(0) \approx 1, V(0) = 0
\\
& S(t) + V(t) \approx 1
\end{aligned}
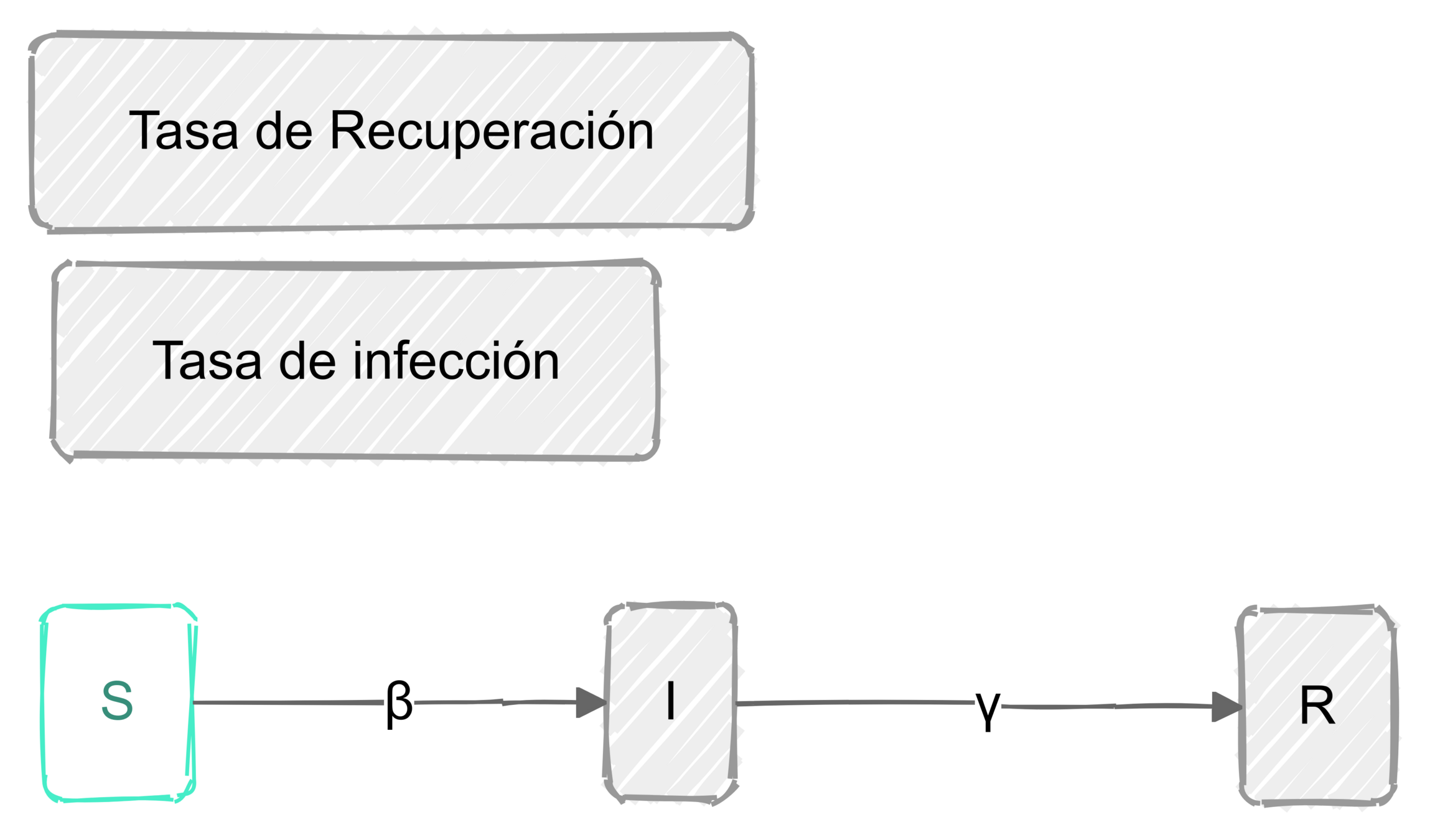
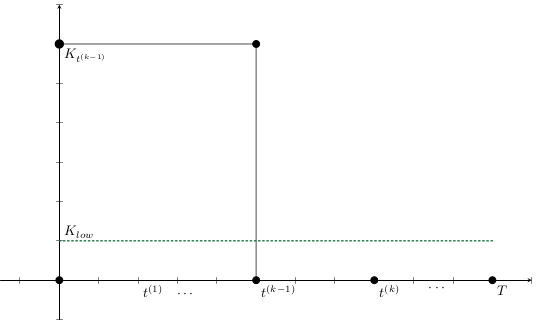
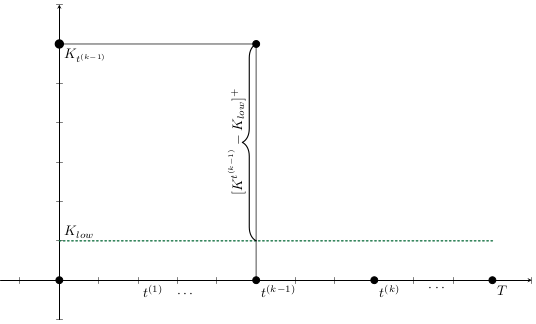
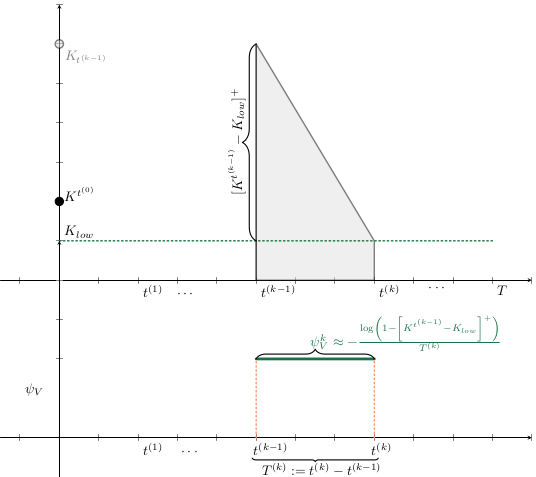
El esfuerzo invertido en prevenir o mitigar una epidemia mediante la vacunación es proporcional a la tasa de vacunación
\textcolor{orange}{\Psi_V}
Supongamos al inicio del brote:
\textcolor{orange}{S(0)\approx 1}
\begin{aligned}
S'(t) &= - \Psi_V S(t)
\\
V'(t) & = \Psi_V S(t)
\\
& S(0) \approx 1, V(0) = 0
\\
& S(t) + V(t) \approx 1
\end{aligned}
S(t) \approx N \exp(-\Psi_V t)
\begin{aligned}
V(t) \approx
\cancel{V(0)} +
\int_0^t
\Psi_V S(\tau) d\tau
\end{aligned}
\begin{aligned}
V(t)
&\approx
\cancel{V(0)} +
\int_0^t
\Psi_V S(\tau) d\tau
\\
&
\approx
\int_0^t
N \Psi_V
\exp(-\Psi_V \tau)
d\tau
\\
&
\approx
N \exp(-\Psi_V \tau) \mid_{\tau=t}^{\tau=0}
\\
&=
\cancel{N} \exp(1 - \exp(-\Psi_V t))
\end{aligned}
Entoces estimaos el número de vacunas con
X_{vac}(t) := \int_{0}^t
\Psi_v \Bigg(
\underbrace{S(\tau)}_{
\substack{
\text{población} \\
\text{objetivo}
}
}\Bigg )
Luego, para una campaña de vacunación, sean:
\begin{aligned}
\textcolor{orange}{T}:
&\text{ timepo de horizonte}
\\
\textcolor{green}{
X_{cov}:=
X_{vac}(}
\textcolor{orange}{T}
\textcolor{green}{)}:
&\text{ Cobertura objetivo a tiempo $T$}
\end{aligned}
\begin{aligned}
X_{cov} = &X_{vac}(T)
\\
\approx &
1 - \exp(-\textcolor{teal}{\lambda_V} T).
\\
\therefore &
\textcolor{teal}{\lambda_V} =
-\frac{1}{T}
\ln(1 - X_{cov})
\end{aligned}
Entoces estimaos el número de vacunas con
X_{vac}(t) := \int_{0}^t
\Psi_v \Bigg(
\underbrace{S(\tau)}_{
\substack{
\text{población} \\
\text{objetivo}
}
}\Bigg )
Luego, para una campaña de vacunación, sean:
\begin{aligned}
\textcolor{orange}{T}:
&\text{ timepo de horizonte}
\\
\textcolor{green}{
X_{cov}:=
X_{vac}(}
\textcolor{orange}{T}
\textcolor{green}{)}:
&\text{ Cobertura objetivo a tiempo $T$}
\end{aligned}
\begin{aligned}
X_{cov} = &X_{vac}(T)
\\
\approx &
1 - \exp(-\textcolor{teal}{\lambda_V} T).
\\
\therefore &
\textcolor{teal}{\lambda_V} =
-\frac{1}{T}
\ln(1 - X_{cov})
\end{aligned}
La población total de Tuxtla Gutiérrez en 2020 fue de 604,147.
Entonces para vacunar el 70% de esta población en un año:
\begin{aligned}
604,147 &\times 0.00329
\\
\approx &
1987.64363 \ \text{dósis/día}
\end{aligned}
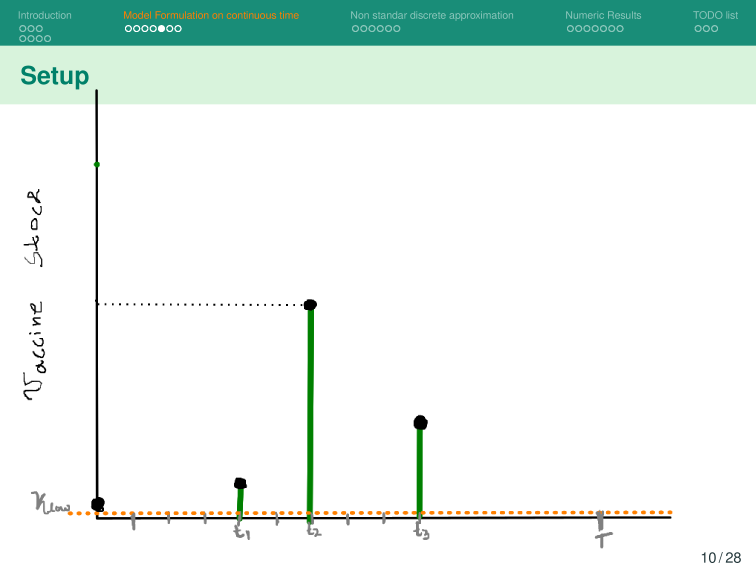
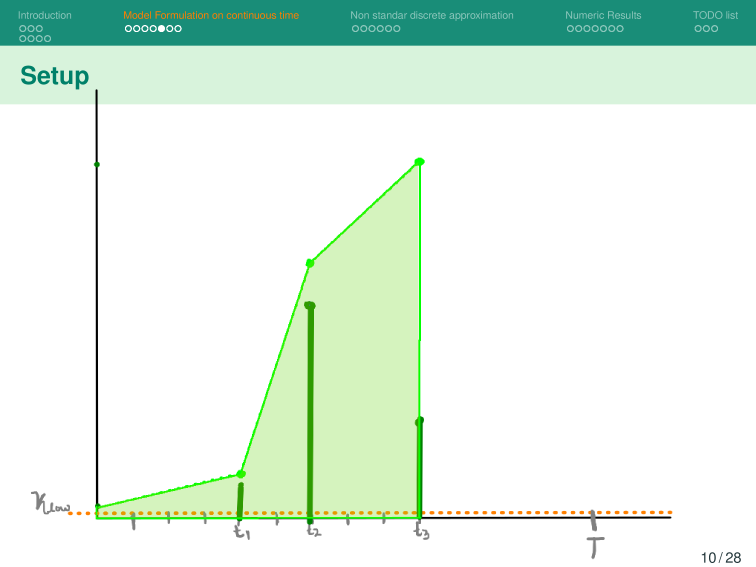
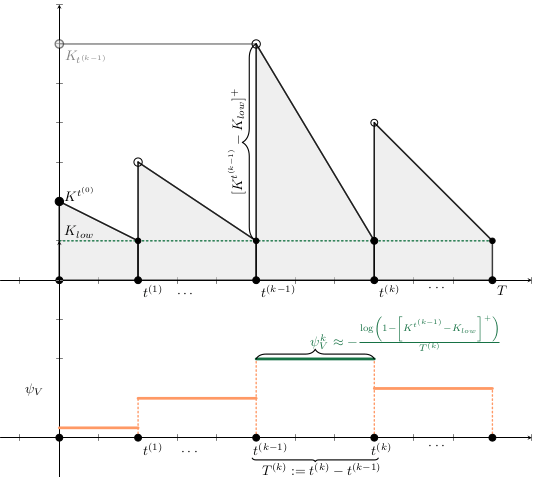
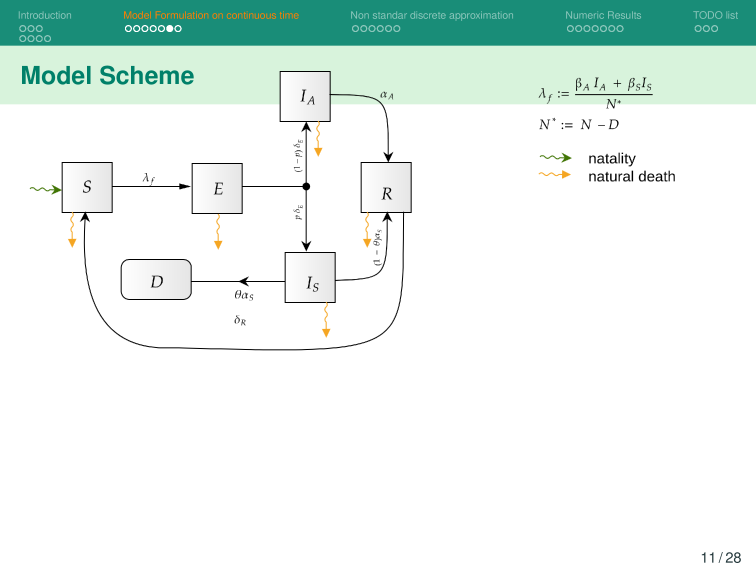
Modelo Base
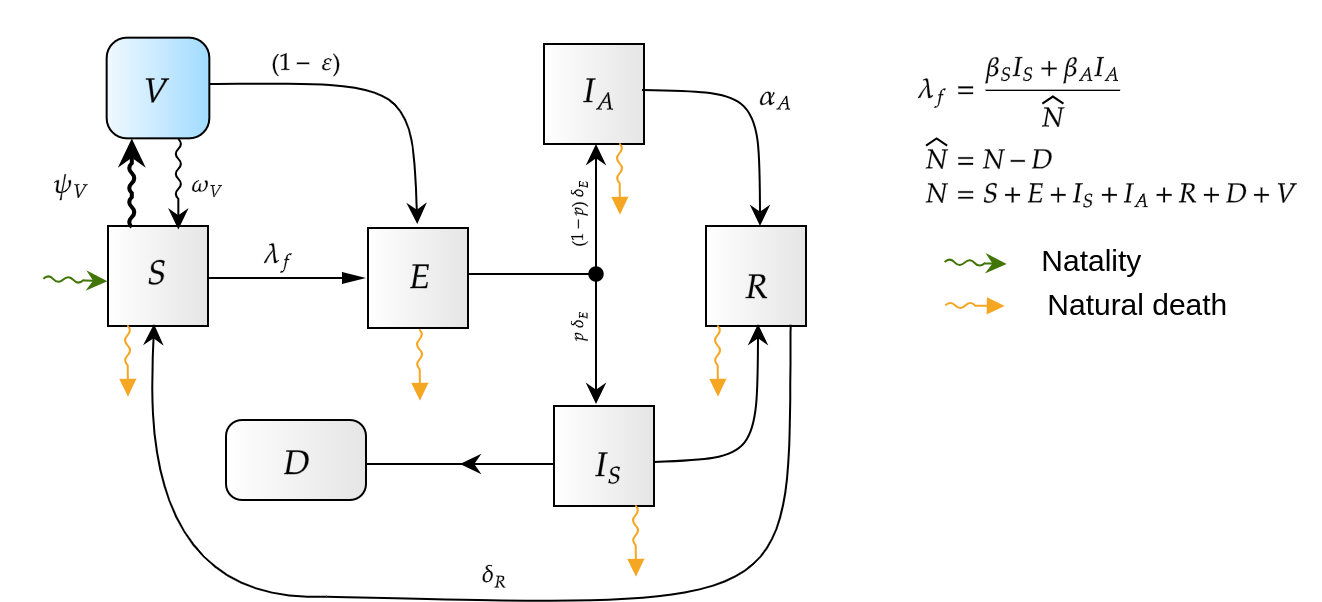
Control no lineal: HJB y DP
Dado
\frac{dx}{dt} = f(x(t)),
\qquad t \in [0, \textcolor{red}{T}]
\frac{dx_{t}}{dt} =f(x_{t} ,a_{t})
Agente
a_t\in \mathcal{A}
x_t
J(x_t, a_t, 0, \textcolor{red}{T}) = Q(x_T, \textcolor{red}{T})
+ \int_0^{\textcolor{red}{\mathbf{T}}} \mathcal{L}(x_{\tau}, a_{\tau}) d_{\tau}
Objetivo:
Diseño
para seguir
t. q. optimizar costo
\text{accion } a_t\in \mathcal{A},
\text{estado } x_t
J(x_t, a_t, 0, T) .
\begin{aligned}
C(x_{t^{(k+1)}}, & a_{t^{(k+1)}})
=
\\
& C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\end{aligned}
\begin{aligned}
C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLL dt,
\\
C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLD(x_t, a_t) dt
\\
YLL(x_t, a_t) &:=
m_1 p \delta_E (E(t) - E^{t^{(k)}} ),
\\
YLD(x_t, a_t) &:=
m_2 \theta \alpha_S(E(t) - E^{t^{(k)}}),
\\
t &\in [t^{(k)},t^{(k + 1)}]
\end{aligned}
\begin{aligned}
C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
& = \int_{t^{(k)}}^{t^{(k+1)}} m_3(K_{Vac}(t) - K_{Vac}^{t^{(k)}}) dt
\\
C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=\int_{t^{(k)}}^{t^{(k+1)}} m_4(X_{vac}(t) - X_{vac}^{t^{(k)}}) dt
\end{aligned}
\begin{aligned}
&\min_{a_{0}^{(k)} \in \mathcal{A}_0}
c(x_{\cdot}, a_0):=
c_1(a_0^{(k)})\cdot T^{(k)} +
\sum_{n=0}^{N-1}
c_0(t_n, x_{t_n}) \cdot h
\\
\text{ s.t.} &
\\
&
x_{t_{n+1}}
= x_{t_n}
+ F(x_{t_n}, \theta, a_0) \cdot h,
\quad x_{t_0} = x(0),
%\\
%\text{where: }&
%\\
%t_n &:=
%n \cdot h, \quad
%n = 0, \cdots, N,
%\quad t_{N} = T.
\end{aligned}
\begin{aligned}
C(x_{t^{(k+1)}}, & a_{t^{(k+1)}})
=
\\
& C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\end{aligned}
\begin{aligned}
x_{t_{n+1}}^{(k)} &
= x_{t_n}^{(k)}
+ F(x_{t_n}^{(k)}, \theta^{(k)}, a_0^{(k)}) \cdot h^{(k)},
\quad x_{t_0^{(k)}} = x^{(k)}(0),
\\
\text{where: }&
\\
t_n^{(k)} &:=
n \cdot h^{(k)}, \quad
n = 0, \cdots, N^{(k)},
\quad t_{N}^{(k)} = T^{(k)}.
\end{aligned}
x_0,a_0,R_1,
x_0, a_0, R_1,
x_1, a_1, R_2,
\cdots,
x_t, a_t, R_{t+1}
\cdots,
x_{T-1}, a_{T-1}, R_T,
x_T
G_t := R_{t+1} + \cdots + R_{T-1} + R_{T}
\begin{aligned}
G_t &:= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3}+ \cdots
\\
&=
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+1+k}, \qquad \gamma \in [0,1)
\end{aligned}
\begin{aligned}
%C_{t+1}
&=
C(x_{t}, a_{t})
\\
%\Phi_{t+1}^{h}(x_t,a_t)
&=
x_t +\varphi(h,\theta, a^{\theta}_t)
\end{aligned}
Agente
R_{t+1}
x_{t+1}
a_t\in \mathcal{A}(x_t)
acción
estado
x_{t}
recompensa
R_{t}
G_t := R_{t+1} + \cdots + R_{T-1} + R_{T}
p(s^{\prime},r | s, a)
:= \mathbb{P}[x_t=s^{\prime}, R_{t}=r | x_{t-1}=s, a_t=a]
\begin{aligned}
r(s, a)
&:= \mathbb{E}[
R_t | x_{t-1}=s, a_{t-1}=a
]
\\
&=
\sum_{r\in \mathcal{R}}
r
\sum_{s^{\prime}\in S}
p(s^{\prime}, r | s, a)
\end{aligned}
\begin{aligned}
G_t &:= R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t-1} R_{T}
\\
&=\sum_{k=t+1}^{T}
\gamma^{k-t-1} R_k
\end{aligned}
Retorno descontado
Retorno total
\begin{aligned}
v_{\pi}(s) &:=
\mathbb{E}_{\pi}
[G_t | x_t = s]
\\
&=
\mathbb{E}_{\pi}
\left[
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+k+1}
\big| x_t =s
\right]
\end{aligned}
\pi(a|s):= \mathbb{P}[a_t = a|x_t=s]
\begin{aligned}
v_{\pi}(s) &:=
\mathbb{E}_{\pi}
[G_t | x_t = s]
\\
&=
\mathbb{E}_{\pi}
\left[
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+k+1}
\big| x_t =s
\right]
\\
& =
\mathbb{E}_{\pi}
\left[
R_{t+1} + \gamma G_{t+1} | x_t = s
\right]
\\
&=
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma
\mathbb{E}_{\pi}[G_{t+1} | x_{t+1}=s^{\prime}]
\right]
\\
&=
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma v_{\pi}(s^{\prime})
\right]
\end{aligned}
\begin{aligned}
v_{*}(s) &:=
\max_{\pi}
v_{\pi}(s)
\\
&=
\max_{a\in \mathcal{A}(s)}
\mathbb{E}_{\pi_{*}}
\left[
\sum_{k=0}^{\infty}
\gamma^{k} R_{t+k+1}
\big| x_t =s
\right]
\\
& =
\max_{a\in \mathcal{A}(s)}
\mathbb{E}_{\pi}
\left[
R_{t+1} + \gamma G_{t+1} | x_t = s
\right]
\\
&=
\max_{a\in \mathcal{A}(s)}
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma
\mathbb{E}_{\pi}[G_{t+1} | x_{t+1}=s^{\prime}]
\right]
\\
&=
\max_{a\in \mathcal{A}(s)}
\sum_{a} \pi(a |s)
\sum_{s^{\prime}, r} p(s^{\prime},r | s, a)
\left[
r
+
\gamma v_{\pi}(s^{\prime})
\right]
\end{aligned}
x_0, a_0, R_1,
x_1, a_1, R_2,
\cdots,
x_t, a_t, R_{t+1}
\cdots,
x_{T-1}, a_{T-1}, R_T,
x_T
\begin{aligned}
\gamma &= 0
\\
G_t &:= R_{t+1} + \cancel{\gamma R_{t+2}} + \cdots + \cancel{\gamma^{T-t-1} R_{T}}
\end{aligned}
Recompensa de dopamina
J(x,\pi) = E\left[ \sum_{k=0}^M C(x_{t^{(k)}},a_{t^{(k)}}) | x_{t^{(0)}} = x , \pi \right]
\begin{aligned}
C(x_{t^{(k+1)}}, & a_{t^{(k+1)}})
=
\\
& C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\\
+& C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
\end{aligned}
\begin{aligned}
C_{YLL}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLL dt,
\\
C_{YLD}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=
\int_{t^{(k)}}^{t^{(k+1)}} YLD(x_t, a_t) dt
\\
YLL(x_t, a_t) &:=
m_1 p \delta_E (E(t) - E^{t^{(k)}} ),
\\
YLD(x_t, a_t) &:=
m_2 \theta \alpha_S(E(t) - E^{t^{(k)}}),
\\
t &\in [t^{(k)},t^{(k + 1)}]
\end{aligned}
\begin{aligned}
C_{stock}(x_{t^{(k+1)}},a_{t^{(k+1)}})
& = \int_{t^{(k)}}^{t^{(k+1)}} m_3(K_{Vac}(t) - K_{Vac}^{t^{(k)}}) dt
\\
C_{campaign}(x_{t^{(k+1)}},a_{t^{(k+1)}})
&=\int_{t^{(k)}}^{t^{(k+1)}} m_4(X_{vac}(t) - X_{vac}^{t^{(k)}}) dt
\end{aligned}
\frac{dx_{t}}{dt} =f(x_{t} ,a_{t})
Agente
a_t\in \mathcal{A}
C_t
x_t
\begin{aligned}
a_t^{(k)} &= p_i \cdot \Psi_V^{(k)}
\\
p_i &\in \mathcal{A}:=\{p_0, p_1, \dots, p_M\}
\\
p_i &\in [0, 1]
\end{aligned}
Control determinista
HJB (Dynamic Programming)- Maldición de la dimension
\approx \
\mathtt{HJB}
HJB(Neuro-Dynamic Programming)
Abstract dynamic programming.
Athena Scientific, Belmont, MA, 2013. viii+248 pp.
ISBN:978-1-886529-42-7
ISBN:1-886529-42-6
Rollout, policy iteration, and distributed reinforcement learning.
Revised and updated second printing
Athena Sci. Optim. Comput. Ser.
Athena Scientific, Belmont, MA, [2020], ©2020. xiii+483 pp.
ISBN:978-1-886529-07-6
Reinforcement learning and optimal control
Athena Sci. Optim. Comput. Ser.
Athena Scientific, Belmont, MA, 2019, xiv+373 pp.
ISBN: 978-1-886529-39-7
https://slides.com/sauldiazinfantevelasco/congreso_multisciplinario_fcfm-unach_2024
¡Gracias!
UNACH-2024-Nov
By Saul Diaz Infante Velasco
UNACH-2024-Nov
Explore innovative strategies for managing scarce vaccines in inventory! See how uncertainty in delivery times and order sizes impacts epidemic control efforts.
