Policy design for epidemiological traffic light based on control problems.
6to Taller de Teoria de Juegos y Toma de decisiones.
Saul Diaz Infante Velasco
Adrian Acuña Zegarra
Jorge Velasco Hernandez
sauldiazinfante@gmail.com
Guidelines for estimating the risk of the epidemiological traffic light
Vaccination camping
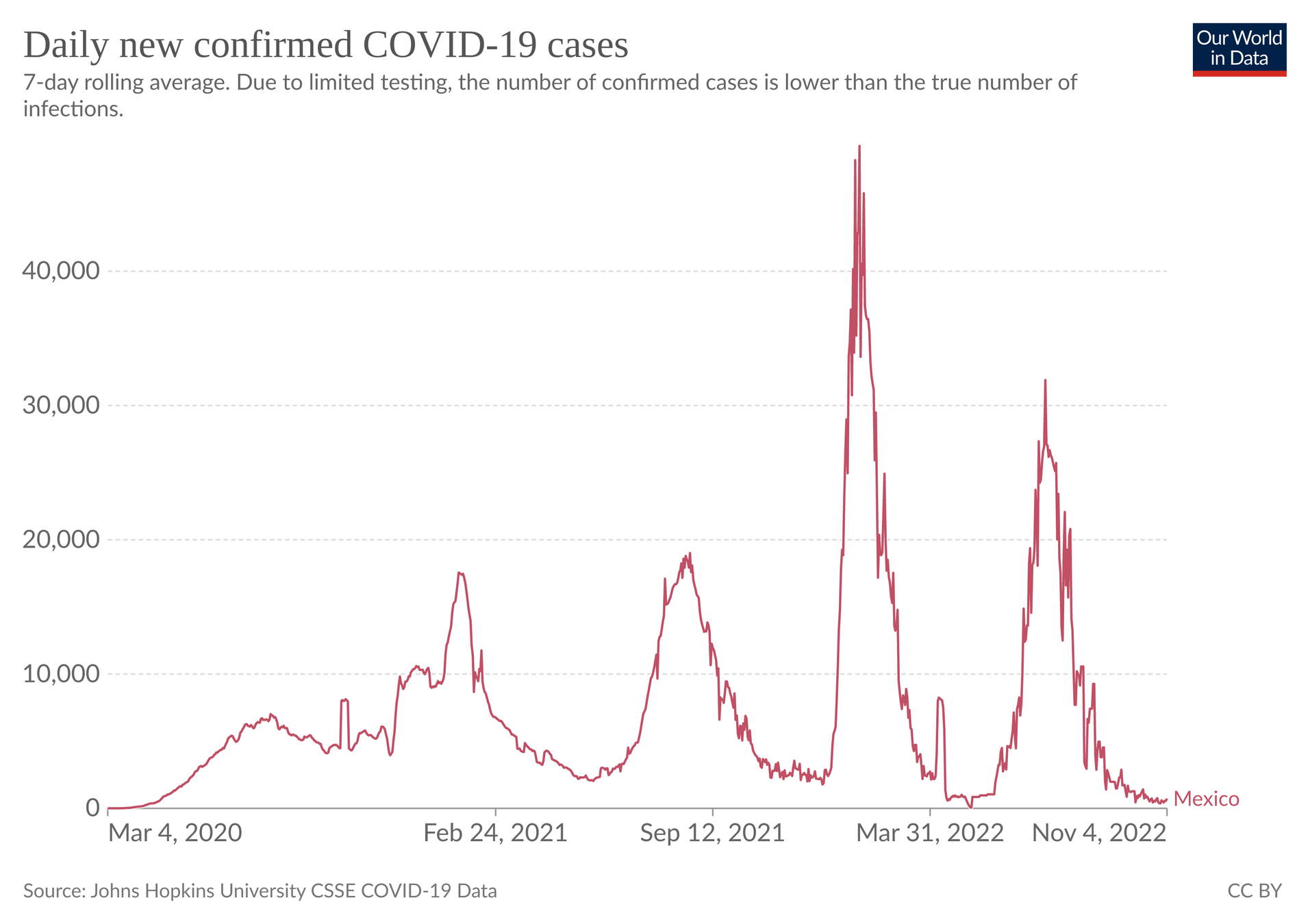
Omicron variant
Introduction
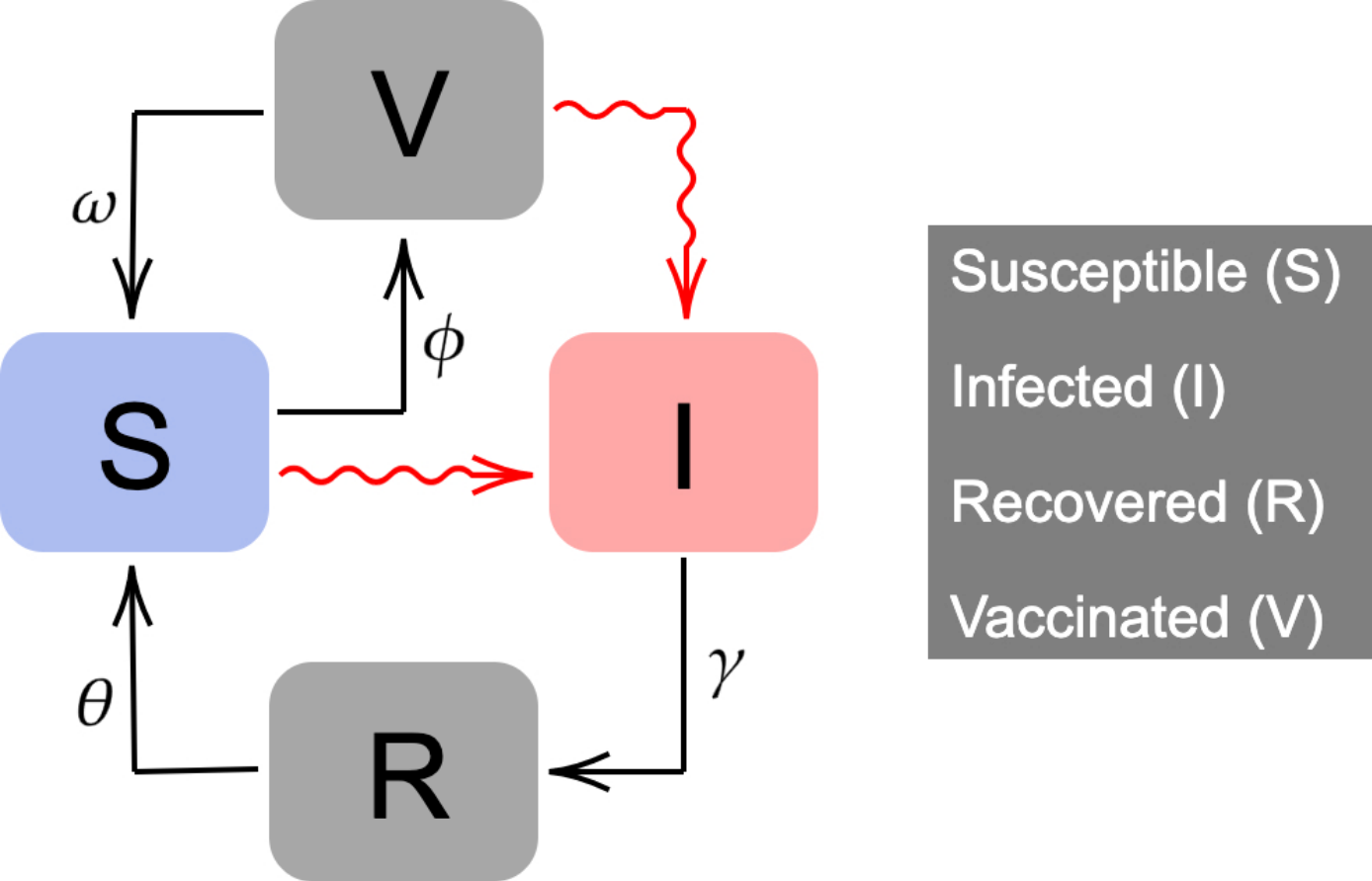
We propose an extension of the classic Kermack-McKendrick mathematical model. 𝑁(𝑡) is constant and is split into four compartments:
- susceptible (𝑆(𝑡)),
- infected (𝐼(𝑡)),
- recovered (𝑅(𝑡)),
- and vaccinated (𝑉 (𝑡)).
Susceptible individuals can become infected when interacting with an infectious individual. After a period of time (1∕𝛾), infected people recover. Recovered people lose their natural immunity after a period of time 1∕𝜃.
C_k(t^*) = 1 - \left(1 - \frac{I(t^*)}{N(t^*)}\right)^k
Risk index
Another closely related index that has been used to monitor and evaluate the development of this epidemic is the event gathering risk, developed by Chande (2020).
Chande, A., Lee, S., Harris, M. et al. Real-time, interactive website for US-county-level COVID-19 event risk assessment. at Hum Behav, 1313–1319 (2020). https://doi.org/10.1038/s41562-020-01000-9
Objective
Present a model for the design and evaluation of light-traffic epidemic polices based in control.
Outline
- Model Formulation: Risk Index and
- Functional Cost:Political economic implications
- Numerical experiments
- Perspectives
Objective and Outline
\mathcal{R}_t
\begin{aligned}
S' =& \mu N - \lambda(t)S
- (\phi + \mu) S + \omega V + \theta R
\\
I' =& \lambda(t) (S + (1 - \sigma)V)
- (\gamma + \mu) I
\\
V' =& \phi S - (1 - \sigma) \lambda(t)V - (\omega + \mu) V
\\
R' =& \gamma I - (\theta + \mu) R
\end{aligned}
\begin{aligned}
C^{\prime} =& k (1 - C)^{\left(1 - \frac{1}{k}\right)}
\left(1 - (1 - C)^{\frac{1}{k}}\right)
\\
& \times
\left(
\beta(t) (1 - C(t))
(S + (1 - \sigma)V) \frac{1}{N} - (\gamma + \mu)
\right).
\end{aligned}
\begin{aligned}
\beta(t) & =
\left(
1 +
a \cos
\left(
\frac{2\pi}{365} t
\right)
\right) \beta_0
\\
\lambda(t) & = \beta(t) (1 - C(t)) \frac{I(t)}{N}
\end{aligned}
# MODEL FORMULATION
C(t) = 1 - \left(1 - \frac{I(t)}{N}\right)^k
Risk index
gives the probability of finding at time t an infected person in a group of k individuals.
\begin{aligned}
C' =& k (1 - C)^{\left(1 - \frac{1}{k}\right)}
\left(1 - (1 - C)^{\frac{1}{k}}\right)
\\
&
\times
\left(
\beta(t) (1 - C(t))
(S + (1 - \sigma)V) \frac{1}{N} - (\gamma + \mu)
\right)
\end{aligned}
\begin{aligned}
x^{\prime} &= \mu - \hat{\lambda}(t)x - (\phi + \mu) x + \omega v + \theta z
\\
y^{\prime} &= \hat{\lambda}(t) (x + (1 - \sigma)v) - (\gamma + \mu) y
\\
v^{\prime} &= \phi x - (1 - \sigma) \hat{\lambda}(t)v - (\omega + \mu) v
\\
z^{\prime} &= \gamma y - (\theta + \mu) z
\\
C^{\prime} &= k (1 - C)^{\left(1 - \frac{1}{k}\right)}
\left(
1 - (1 - C)^{\frac{1}{k}}
\right)
\\
& \times
\left(
\beta(t) (1 - C(t)) (x + (1 - \sigma) v) - (\gamma + \mu)
\right)
\end{aligned}
# REPRODUCTIVE NUMBER
x = \frac{S}{N};
\quad y = \frac{I}{N};
\quad v = \frac{V}{N};
\quad z = \frac{R}{N}
Normalization
\begin{aligned}
\Omega =
\Big \{
&
(x, y, v, z, C)\in \mathbb{R}^5_+
:
\\
&
0\leq C\leq 1,
\\
&
0 \leq s,
\forall s \in \{x, v, y, z \},
\\
&
x + y + v + z = 1
\Big \}
\end{aligned}
Invariance
\mathcal{R}_0 = \frac{\beta_0(1 - C^*)(x^* + (1 - \sigma)v^*)}{(\gamma + \mu)}
Basic Reproductive number
\begin{aligned}
x^* &= \frac{\omega + \mu}{\phi + \omega + \mu}
\\
v^* &= \frac{\phi}{\phi + \omega + \mu}
\\
C^* &= 0
\end{aligned}
FDE
Effective reproduction number
\mathcal{R}_t = \frac{\beta(t)(1 - C(t))(x(t) + (1 - \sigma)v(t))}{(\gamma + \mu)}
# Light Traffic Policies and Optimal Control
\xi(t)^\top:= (s(t), y(t),v(t),z(t), C(t))
\xi(t) \xrightarrow{\varphi}
A(\xi):= \Big \{green, yellow, orange, red \Big\}
(u_{\beta}^{4}, u_k^{4})
(u_{\beta}^{1}, u_k^{1})
(u_{\beta}^{3}, u_k^{3})
(u_{\beta}^{2}, u_k^{2})
- A decision-maker can apply a strategy from a finite set of actions.
- The set of actions implies a particular effect accordingly to the light semaphore.
- We describe this effect by modulating the transmission rate and size of gathering :
\beta(t),\ k.
- A decision-maker can apply a strategy from a finite set of actions.
- The set of actions implies a particular effect accordingly to the light semaphore.
- We describe this effect by modulating the transmission rate and size of gathering.
\begin{aligned}
\widehat{\lambda}(u_{\beta}, T_j):=
&
\beta(t)(1 - u_{\beta}) (1 - C(t)) y(t)
\\
k(u_k, T_j):=
& (1 - u_k) k
\end{aligned}
\begin{aligned}
x^{\prime} =&
\mu - \widehat{\lambda}(u_{\beta}, t) x - (\phi + \mu) x + \omega v + \theta z
\\
y^{\prime} =&
\widehat{\lambda}(u_{\beta}, t) (x + (1 - \sigma)v) - (\gamma + \mu) y
\\
v^{\prime} =&
\phi x - (1 - \sigma)
\widehat{\lambda}(u_{\beta}, t) v - (\omega + \mu) v
\\
z^{\prime} =&
\gamma y - (\theta + \mu) z
\\
C^{\prime} =&
k(u_k, T_j)
(1 - C) ^ {
\left(
1 - \frac{1}{k(u_k, T_j)}
\right)
}
\left(
1 - (1 - C) ^ \frac{1}{k(u_k, T_j)}
\right)
\\
& \times
\left[
\beta(t) (1 - u_{\beta}) (1 - C(t)) (x + (1 - \sigma) v)
- (\gamma + \mu)
\right]
\end{aligned}
T_i
T_{i+1}
T_{i-1}
\overbrace{\text{decision period}}^{p_j := t_j - t_{j-1}}
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
%}
{
J
\left(
\xi^{[p_i]}, u_{\beta} ^{[j]}, u_k^{[j]}
\right)
}
:=
\underbrace{
\int_{0}^T
a_I y(s) + a_C C(s)
}_{YLD+Risk}
ds
+
\underbrace{
\int_{0}^T
a_{\beta} u_{\beta}^2(s)
+
a_k u_k^2(s)
}_{\text{political and economic implications}}
ds.
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
%}
{
J
\left(
\xi^{[p_i]}, u_{\beta} ^{[j]}, u_k^{[j]}
\right)
}
:=
\underbrace{
\int_{0}^T
a_I y(s) + a_C C(s)
}_{YLD+Risk}
ds
+
\underbrace{
\int_{0}^T
a_{\beta} u_{\beta}^2(s)
+
a_k u_k^2(s)
}_{\text{political and economic implications}}
ds.
- The decision maker only chooses a strategy of the mentioned above and accordingly to the light traffic protocol. That is, the controller decides which color from the plausible light-traffic action--being {green, yellow, orange, red} of the available actions.
- The corresponding authorities meet every certain number of weeks on a regular basis and takes a decision.
- The taken decision minimize the functional J subject to the mentioned dynamics.
Hypothesis
(OCP) Decide in each stage (a week), the light color that minimize functional cost J
\begin{aligned}
\beta(t) := &
\left(
1 +
a \cos
\left(
\frac{2\pi}{365} t
\right)
\right) \beta_0
\\
\widehat{\lambda}(u_{\beta}, t_j):=
&
\beta(t)(1 - u_{\beta}) (1 - C(t)) y(t)
\\
k(u_k, t_j):=
& (1 - u_k) k
\end{aligned}
\begin{aligned}
x^{\prime} =&
\mu - \widehat{\lambda}(u_{\beta}, t) x - (\phi + \mu) x + \omega v + \theta z
\\
y^{\prime} =&
\widehat{\lambda}(u_{\beta}, t) (x + (1 - \sigma)v) - (\gamma + \mu) y
\\
v^{\prime} =&
\phi x - (1 - \sigma)
\widehat{\lambda}(u_{\beta}, t) v - (\omega + \mu) v
\\
z^{\prime} =&
\gamma y - (\theta + \mu) z
\\
C^{\prime} =&
k(u_k, t_j)
(1 - C) ^ {
\left(
1 - \frac{1}{k(u_k, t_j)}
\right)
}
\left(
1 - (1 - C) ^ \frac{1}{k(u_k, t_j)}
\right)
\\
& \times
\left[
\beta(t) (1 - u_{\beta}) (1 - C(t)) (x + (1 - \sigma) v)
- (\gamma + \mu)
\right]
\end{aligned}
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
{
\min
}
J
\left(
\xi^{[p_i]},
u_{\beta} ^ {[j]},
u_k ^ {[j]}
\right)
:=
\underbrace{
\int_{T_{i-1}} ^ {T_{i}}
a_I y(s) + a_C C(s)
}_{YLD+Risk}
ds
+
\underbrace{
\int_{T_{i-1}} ^{T_{i}}
a_{\beta} u_{\beta}^2(s)
+
a_k u_k ^ 2(s)
}_{
\substack{
\text{political and economic}
\\
\text{implications}
}
} ds.
subject to:
Counterfactual vs controlled dynamics
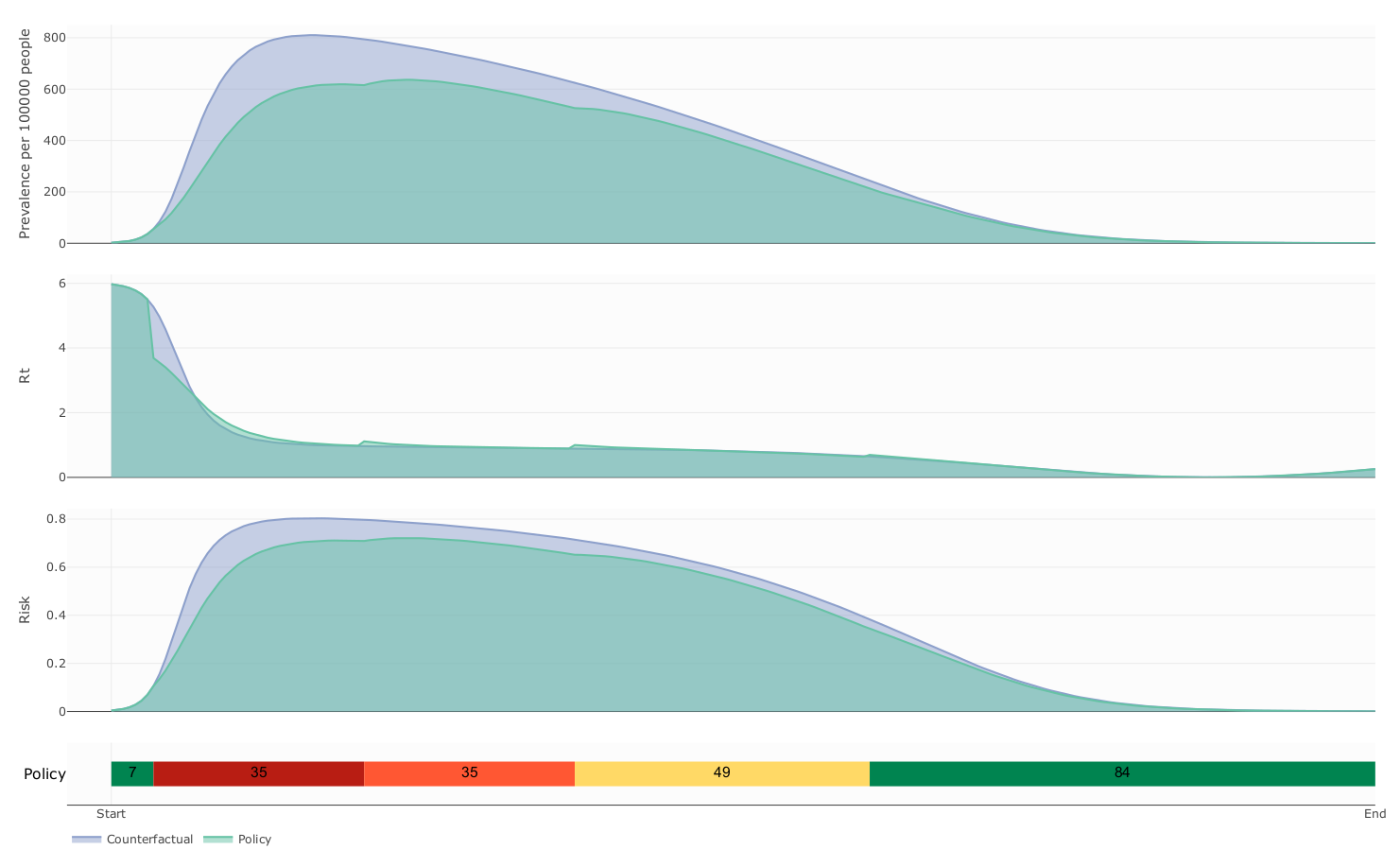
Counterfactual vs controlled dynamics
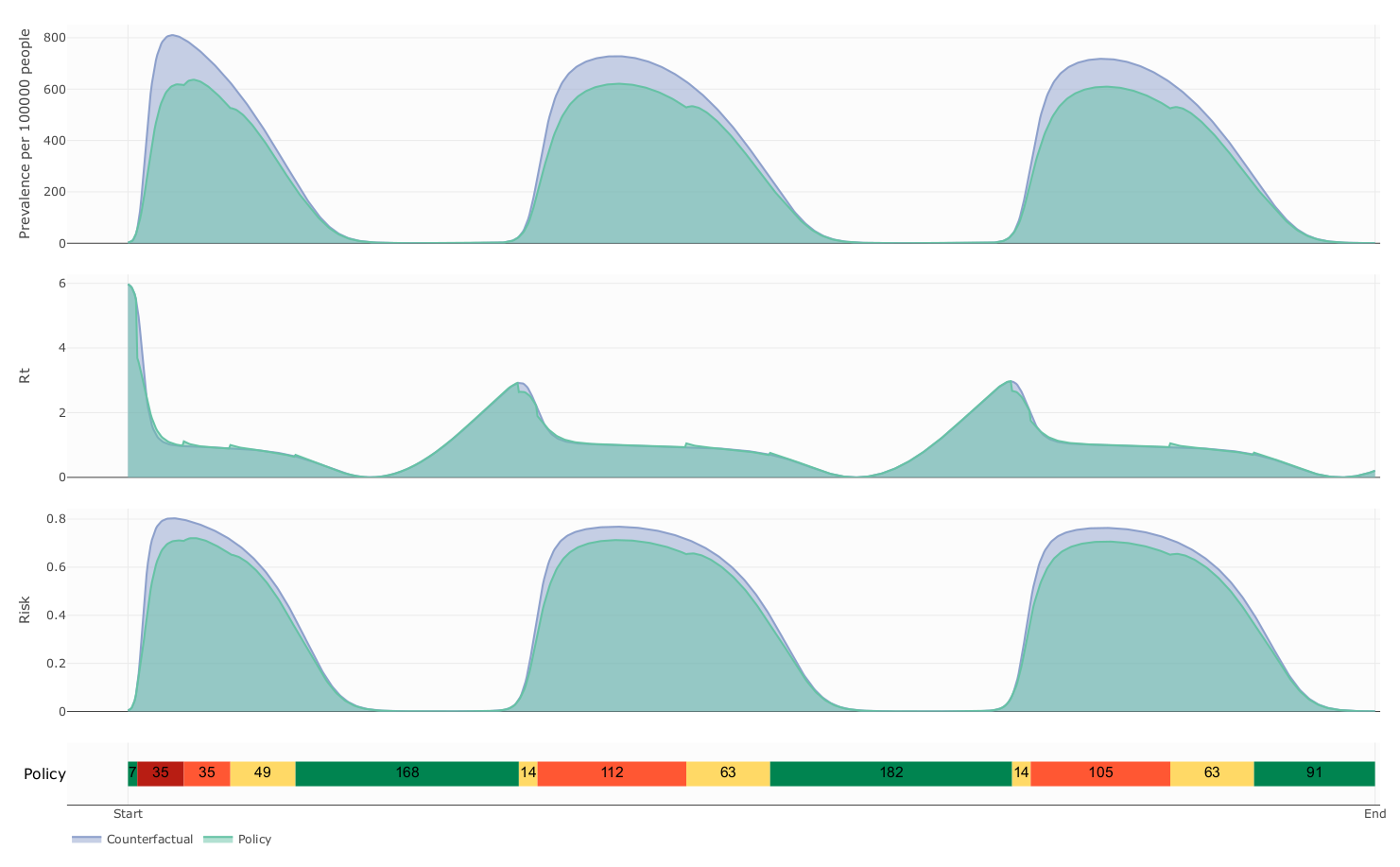
Counterfactual vs controlled dynamics
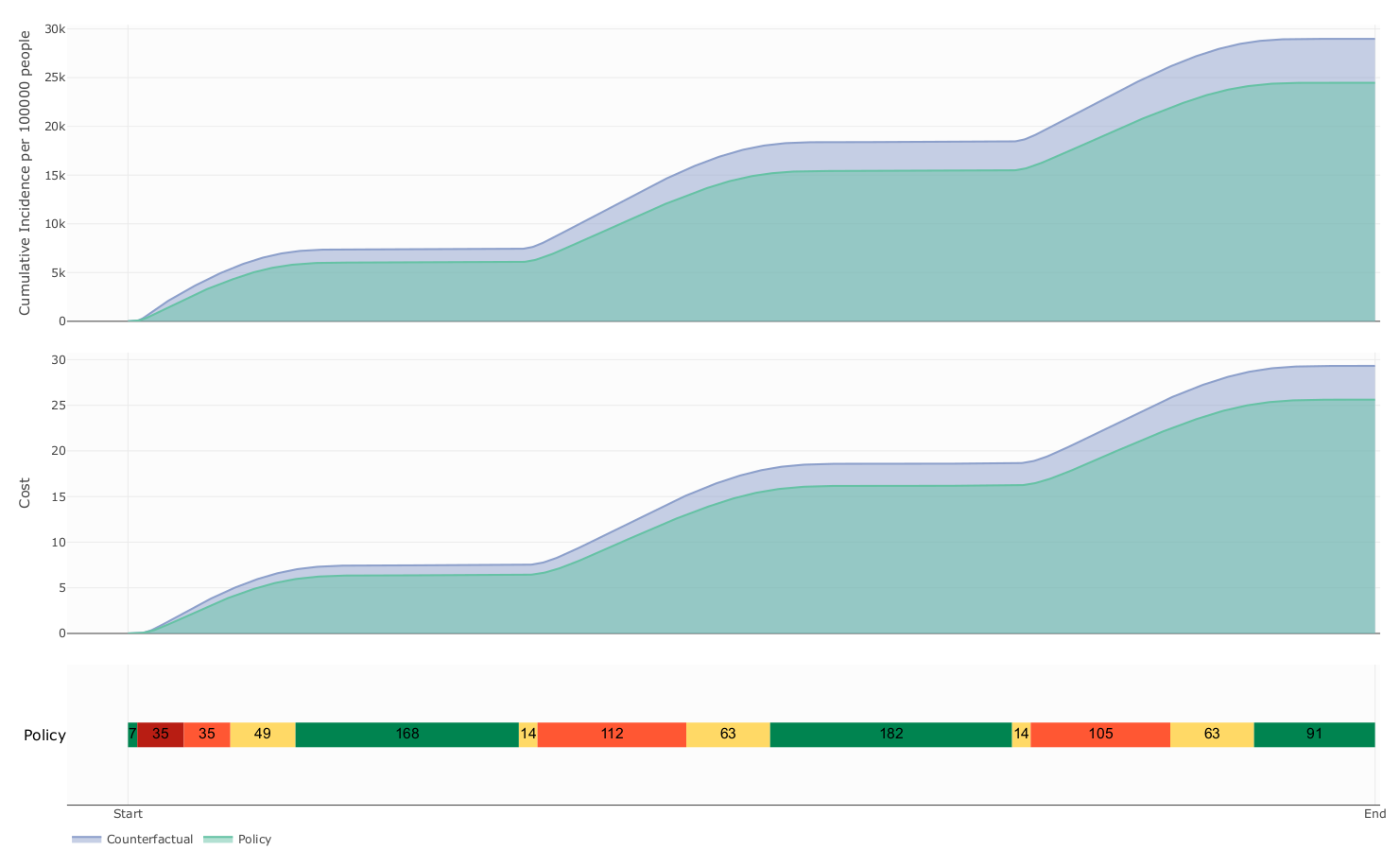
The influence of mobility restriction expenses over prevalence and cost
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
{
J
\left(
\xi^{[p_i]},
u_{\beta} ^ {[j]},
u_k ^ {[j]}
\right)
}
:=
%
\int_{T_{i-1}} ^ {T_{i}}
a_I y(s) + a_C C(s)
ds
+
\int_{T_{i-1}} ^{T_{i}}
a_{\beta}
u_{\beta}^2(s)
+
a_k u_k ^ 2(s)
ds.
Expenses
due to mobility restrictions
a_{\beta} \searrow
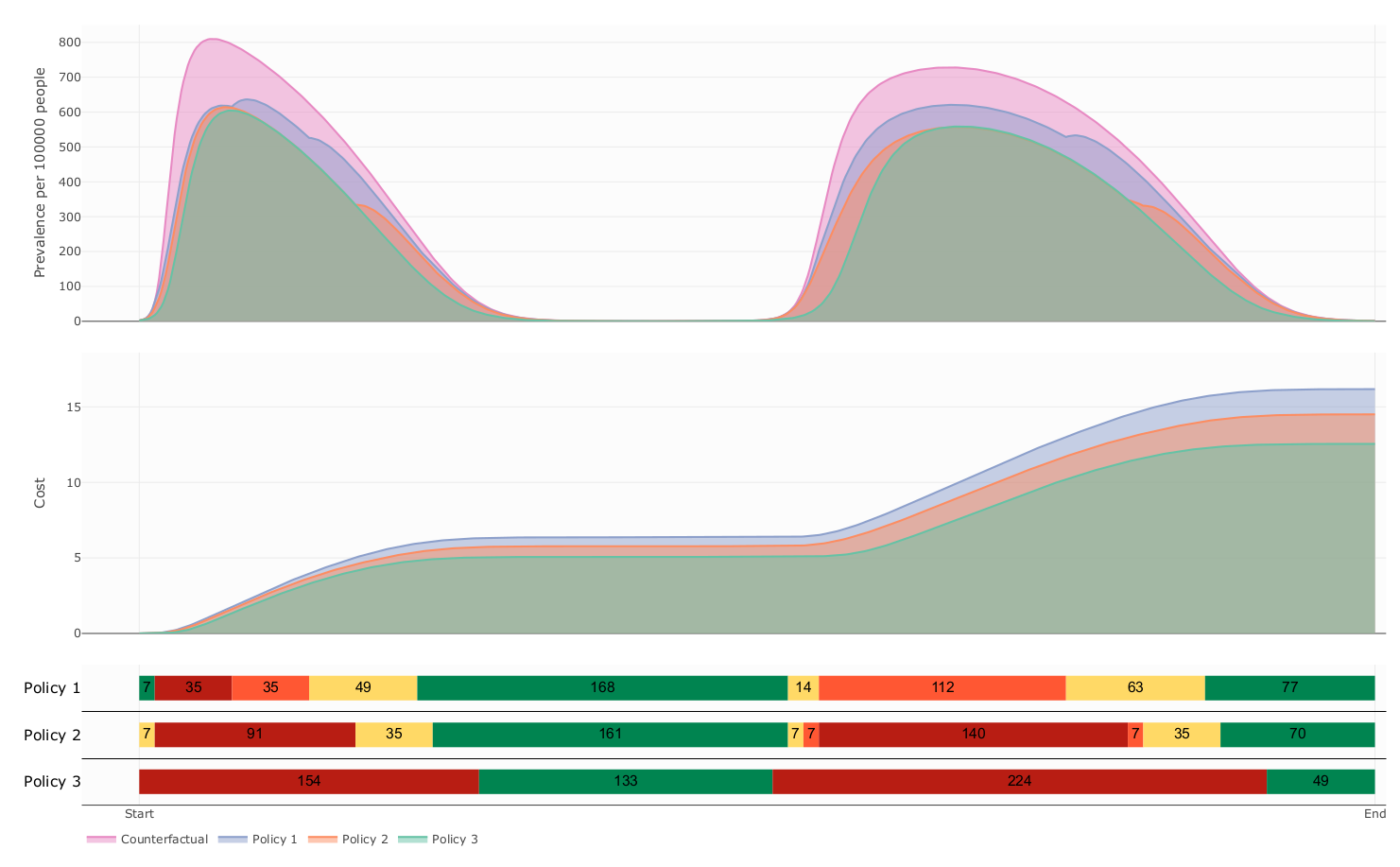
The influence of decision period span over prevalence and cost
\underset{
\substack{
j \in A \\
A:=\{\text{green, yellow, orange, red} \}
}
}
{
J
\left(
\xi^{[p_i]},
u_{\beta} ^ {[j]},
u_k ^ {[j]}
\right)
}
:=
%
\int_{T_{i-1}} ^ {T_{i}}
a_I y(s) + a_C C(s)
ds
+
\int_{T_{i-1}} ^{T_{i}}
a_{\beta}
u_{\beta}^2(s)
+
a_k u_k ^ 2(s)
ds.
\underbrace{p_i:=T_{i+1} - T_i}_{\substack{decision \\ period}}
p_i \nearrow
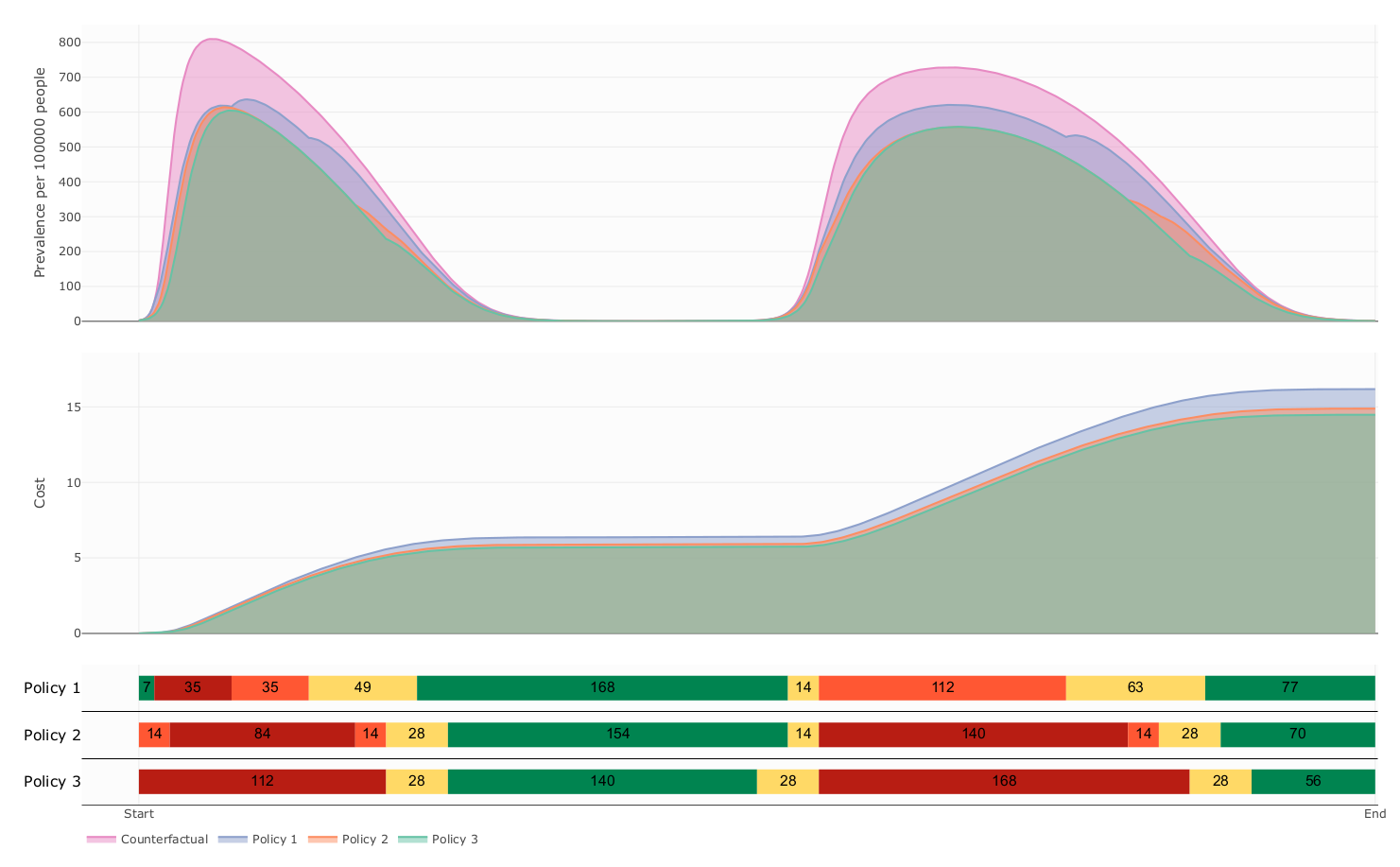
- Our model suggest that this kind of Policies follows a delicate balanced between health benefit and economic cost
Perspectives
- Uncertainty quantification
- Partial information
- Games
References
- Chande, A., Lee, S., Harris, M. et al. Real-time, interactive website for US-county-level COVID-19 event risk assessment. Nat Hum Behav 4, 1313–1319 (2020). https://doi.org/10.1038/s41562-020-01000-9
- Chan, H.F., Skali, A., Savage, D.A. et al. Risk attitudes and human mobility during the COVID-19 pandemic. Sci Rep 10, 19931 (2020). https://doi.org/10.1038/s41598-020-76763-2
- P. van den Driessche, James Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, Volume 180, Issues 1–2, 2002,Pages 29-48,ISSN 0025-5564, https://doi.org/10.1016/S0025-5564(02)00108-6.
https://slides.com/sauldiazinfantevelasco/code
Copy of VI Workshop on Game Theory and Decision Theory
By Saul Diaz Infante Velasco
