Media competition and social disagreement
Jacopo Perego, Sevgi Yuksel
Outline
- Introduction
- Model and main results
- Spatial interpretation
- Conclusion
Introduction
- The paper studies competition in the market for news (political information)
- Main results:
- Competition leads to informational specialization
- Competition makes every agent worse off
- Why should we care? It is important to understand
- how competition affects the strategic needs of information providers
- The possible consequences of competition on the political process
Example
- A new health-care bill is under discussion (details not fully known to the public)
- promote overall healthcare quality
- expand the budget deficit
- induce more redistribution
- Voters acquire information from the media before they approve/disapprove the policy
- News outlets compete for profits by allocating their limited resources (journalists, airtime, etc.)
- greater consensus \(\to\) more likely to get implemented
Model
- Uncertain policy \(\omega = (\omega_0, \omega_1, \omega_2), \; \omega_k \stackrel{i.i.d.}{\sim} \mathcal{N}(0, 1)\) for \(k \in \{0, 1, 2\}\)
- One vertical component - valence \(\omega_0\)
- Two horizontal components - ideological \(\omega_1, \omega_2\)
- Policy implemented with probability = approval rate
- Finite number of identical, non-partisan firms \(n \in N\)
- Firm \(n\) chooses editorial strategy \( b_n = (b_{n, 0}, b_{n, 1}, b_{n, 2})\)
- Firm \(n\) charges \(p_n(\theta_i)\)
- Finite number of heterogenous, Bayesian agents \(i \in I\)
- Agent \(i\) has payoff type \(\theta_i = (\theta_{i, 0}, \theta_{i, 1}, \theta_{i, 2}) \) independently drawn from uniform distribution \(\mathcal{F}\)
Assumptions explained
-
Agent \(i\)'s payoff type: \(\theta_i = (\theta_{i, 0}, \theta_{i, 1}, \theta_{i, 2}) \)
- Agents have identical preferences over \(\omega_0 \implies \\ \theta_{i, 0} = 1 \; \forall i\)
- Agents have heterogenous preferences over horizontal components \( \omega_1, \omega_2 \implies \) \( \theta_{i, 1}^2 + \theta_{i, 2}^2 = 1 \)
- Firm \(n\)'s editorial strategy \(b_n\) faces constraint \(\lVert b_n \rVert = \sqrt{b_{n, 0}^2 + b_{n, 1}^2 + b_{n, 2}^2} \leq 1\)
Model Timeline
Firms and agents interact over 3 consecutive stages:
Firms choose editorial strategies \((b_n)_{n=1}^N\)
Agents' types \(\theta_i\) revealed
Agents acquire information, pay price \(p_n(\theta_i)\), privately observe signal \( s_i (\omega, b_n) = \omega \cdot b_n + \epsilon_i \), \( \epsilon_i \sim \mathcal{N}(0, 1)\)
Approve/disapprove policy;
payoff: \(u(\omega, \theta_i) = \omega \cdot \theta_i\) or 0
\(\theta_i = (\theta_{i, 0}, \theta_{i, 1}, \theta_{i, 2}) \)
\( \theta_{i, 0} = 1, \; \theta_{i, 1}^2 + \theta_{i, 2}^2 = 1 \)
\( b_n = (b_{n, 0}, b_{n, 1}, b_{n, 2})\)
\(\lVert b_n \rVert \leq 1 \) for \(k \in \{0, 1, 2\}\)
Firms observe each other's strategies and agents' types
Firms set prices \(p_n(\theta_i)\)
Equilibrium
- Solution concept: Perfect Bayesian Equilibrium
-
Theorem 1. A pure-strategy equilibrium exists
- solved via backward induction
- Theorem 2. The equilibrium is unique.
Stage 3
Recall that an agent faces two choices:
- where to acquire information, and
- conditioning on obtained information, whether to approve the policy or not
When would the agent approve the policy, given the signal she obtained?
- Lemma 1. Equilibrium approval strategy: approves if and only if \( \mathbb{E}_\omega (u(\omega, \theta_i) | s_i(\omega, b_n)) \geq 0 \)
Stage 3 - value of information
Recall that an agent faces two choices:
- where to acquire information, and
conditioning on obtained information, whether to approve the policy or not
Information has instrumental value!
Lemma 2. Value of Information is defined as
\[ v(b_n | \theta_i) = \frac{\lvert \theta_i \cdot b_n \rvert }{I\sqrt{2\pi (1 + \lVert b_n \rVert^2 )}} \]
- difference between agent's expected equilibrium payoff associated with observing a signal from a firm \(n\) and the one associated with observing no signal at all
Stage 3 conclusion
At equilibrium, agent \(i\) has
-
information acquisition strategy: choose the firm with the highest \(v(b_n | \theta_i)\) net price \(p_n(\theta_i)\).
- Formally,
For type \(\theta_i\), given \( (b_n, p_n(\theta_i))_{n=1}^N \), agent will choose firm \(n\) such that
\[ v(b_n|\theta_i) - p_n(\theta_i) \geq v(b_m|\theta_i) - p_m(\theta_i) \;\; \forall m \in [N] \]
- Formally,
- approval strategy: approve policy if and only if \( \mathbb{E}_\omega (u(\omega, \theta_i) | s_i(\omega, b_n)) \geq 0 \)
Stage 2 & 1
Recall that a firm faces two choices:
- Stage 1: Editorial strategy \(b_n\)
- Stage 2: What price to charge for the information it provides, observing other firms' editorial strategies and agents' types
Stage 2
Recall that a firm faces two choices:
- Stage 1: Editorial strategy \(b_n\)
- Stage 2: What price to charge for the information it provides, observing other firms' editorial strategies and agents' types
What we know so far: agents will choose the firms with the highest value of information net price
\(\to\) What kind of prices will prevail in equilibrium?
Stage 2 - Example
- Suppose two firms compete for type \(\theta_i\).
- Suppose that for editorial strategies \(b_1, b_2 \), \(v(b_1|\theta_i) > v(b_2|\theta_i) \)
- Firm 1's information has more value for \(\theta_i\)
- The lowest price that firm 2 can charge to be competitive: \( p_2(\theta_i) = 0 \)
- When firm 2 charges 0, agent \(i\) will still choose firm 1 at equilibrium as long as \[v(b_1|\theta_i) - p_1(\theta_i) > v(b_2|\theta_i) - \underbrace{p_2(\theta_i)}_{=0} \]
\[\implies p_1(\theta_i) < v(b_1|\theta_i) - v(b_2 | \theta_i) \]
Stage 2 - Generalization
- For \(N=2\), firm 1 "wins" by setting price \(p_1(\theta_i) < v(b_1|\theta_i) - v(b_2 | \theta_i) \)
- Generalizing to \(N > 2\), firm \(n\) wins type \(\theta_i\) if and only if \[ v(b_n|\theta_i) \geq \max_{m \neq n} v(b_m|\theta_i) \]
- The equilibrium profit for firm \(n\) from type \(\theta_i\) is \[ \max_m v(b_m|\theta_i) - \max_{m \neq n} v(b_m | \theta_i) \geq 0 \]
- Firm \(n\)'s total profit: \[ \sum_{i=1}^I \max_m v(b_m|\theta_i) - \max_{m\neq n} v(b_m | \theta_i) \]
Stage 1
- Recall: firms choose their editorial strategies before observing agents' types
- Stage 2: Firm \(n\)'s total profit: \[ \sum_{i=1}^I \max_m v(b_m|\theta_i) - \max_{m\neq n} v(b_m | \theta_i) \]
- Agent's types are i.i.d according to uniform distribution
- Firm \(n\)'s expected profit is \[ \Pi_n (b_n) = I \mathbb{E}_{\theta_i} \left( \max_m v(b_m | \theta_i) - \max_{m \neq n} v(b_m | \theta_i) \right)\]
Choosing an editorial strategy
- Transform the problem of choosing an editorial strategy \(b_n\) into an equivalent location problem on a disk
Recall:
Firms choose \( b_n = (b_{n, 0}, b_{n, 1}, b_{n, 2})\) given constraint \(\lVert b_n \rVert \leq 1 \) for \(k \in \{0, 1, 2\}\)
Agent \(i\)'s type \(\theta_i = (\theta_{i, 0}, \theta_{i, 1}, \theta_{i, 2}) \) with \( \theta_{i, 0} = 1, \; \theta_{i, 1}^2 + \theta_{i, 2}^2 = 1 \)
We can transform any type \(\theta_i\) uniquely to \(\theta_i = (1, \cos(t_i), \sin(t_i) )\), where \( t_i \in T = [-\pi, \pi]\)
We can transform all \(b_n\) such that \(\lVert b_n \rVert = 1\) to \( b_n = (\sqrt{x_n}, \sqrt{1 - x_n} \cos(t_n), \sqrt{1-x_n} \sin(t_n) ) \) with unique pair \( (x_n, t_n) \in [0, 1] \times T \)
Choosing an editorial strategy
- Agent \(i\)'s "new" type: \(t_i \in [-\pi, \pi]\)
- \( \theta_i = (1, \cos(t_i), \sin(t_i) )\)
- Firm \(n\)'s "new" editorial strategy: \( (x_n, t_n) \in [0, 1]\times [-\pi, \pi] \)
- \(b_n = (\sqrt{x_n}, \sqrt{1-x_n}\cos(t_n), \sqrt{1-x_n}\sin(t_n))\)
- Interpretation
- \(t_i\) is a location on a circle; drawn uniformly from \(T\)
- \(x_n\) captures how generalist the firm is
- \(t_n \in T\) is the firm's target type
- note this is not the same as \(t_i\)
- \( (x_n, t_n)\) corresponds to a location on the disk
Choosing an editorial strategy
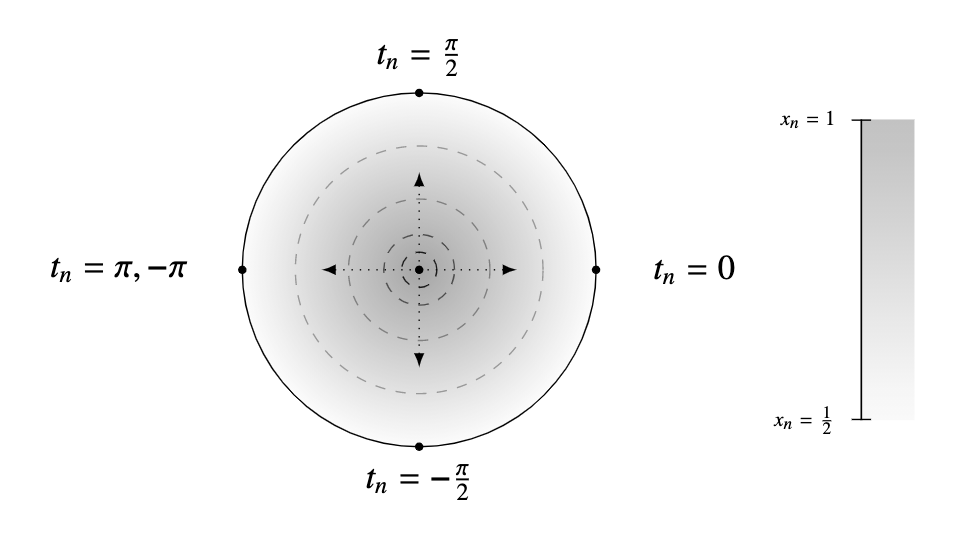
Where would a maximally generalist firm locate at?
\(b_n = (1, 0, 0)\)
"new" value of information
Lemma 2. Value of Information is defined as
\[ v(b_n | \theta_i) = \frac{\lvert \theta_i \cdot b_n \rvert }{I\sqrt{2\pi (1 + \lVert b_n \rVert^2 )}} \]
This can be rewritten as
Recall: \( \theta_i = (1, \cos(t_i), \sin(t_i))\)
\( b_n = (\sqrt{x_n}, \sqrt{1-x_n}\cos(t_n), \\\sqrt{1-x_n}\sin(t_n)) \)
Interpretation: value of information is the sum of two terms
- \(\sqrt{x_n}\) is the valence component, which all agents care about
- \( \sqrt{1-x_n}(\cos(t_i - t_n))\) is the ideological component
"new" value of information
Eq.2 Value of Information is defined as
\[ v(b_n | \theta_i) = \frac{1}{2I\sqrt{\pi}}\cdot \left| \sqrt{x_n} + \sqrt{1-x_n} \cos(t_i-t_n) \right| \]
This clarifies the tradeoff when choosing editorial strategies:
- more generalist \(\to\) high value even when agent's type is far away from target type
- more specialist \(\to\) high value when agent's type is ideologically close to target type
Example
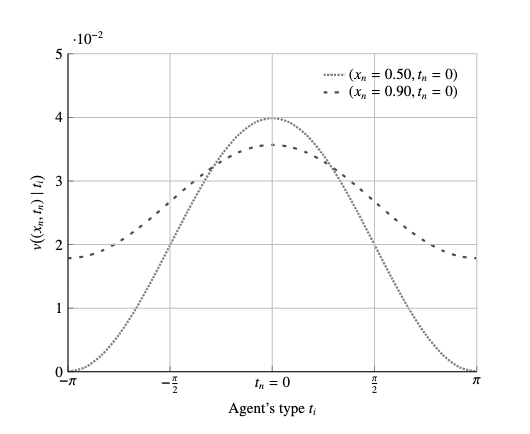
target type \(t_n = 0\)
Going back to choosing a strategy
Recall:
\[ v(b_n | \theta_i) = \frac{1}{2I\sqrt{\pi}}\cdot \left| \sqrt{x_n} + \sqrt{1-x_n} \cos(t_i-t_n) \right| \]
Firm \(n\)'s first-best editorial strategy for an agent of type \(t_i\):
- choose \(t_n = t_i \to \) this maximizes \( \cos(t_i - t_n) = 1\)
- \( \sqrt{x_n} + \sqrt{1-x_n}\) is maximized when \(x_n = 1/2\), i.e. assign equal weight to valence and ideology
First-best value: \( \bar{\mathcal{V}} = v((\frac{1}{2}, t_i )| t_i) \)
Equilibrium is unique
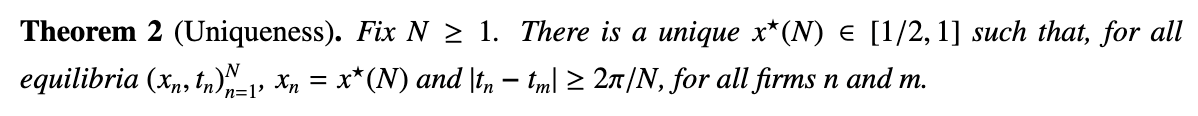
In equilibrium,
- all firms are equally specialized
- graphically: firms locate equidistantly from the center of the disk
- degree of specialization, \( 1 - x^*(N) \) is uniquely pinned down by \(N\)
- firms editorial strategies satisfy \( |t_n - t_m| \geq \frac{2\pi}{N} \) for all \(n\) and \(m\)
- graphically: evenly spread out
What happens in equilibrium when the market for news become more competitive?
i.e. has more firms
Competition leads to informational specialization
Firms specialize by providing relatively less information on the valence component and relatively more information on the ideological components
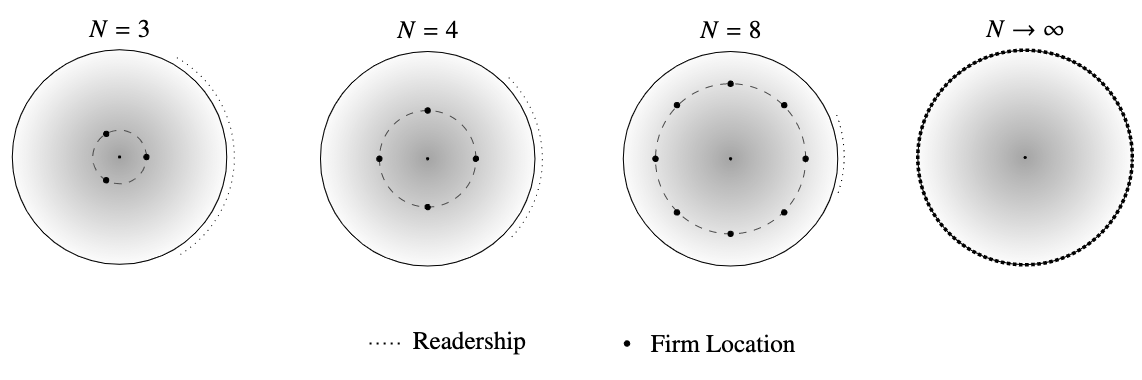
Competition leads to informational specialization
Theorem 2: In equilibrium, firm's expected readership is an arc of length \(2\pi/N\) centered around firm's target type \(t_n\)
As the number of firms \(N\) increases, expected readership \(2\pi/N\) decreases.

Decreased readership is more ideologically homogeneous.
\(\to\) Firms specialize (\(x_n\) decreases)
Competition leads to informational specialization
- How do firms differentiate when they sell information?
- Increase the relative informativeness of private-interest components at the expense of the common-interest components
- Equilibrium interactions between vertical and horizontal competition:
- As competition increases, firms disinvest from vertical features (beneficial to all consumers) and instead focus on horizontal features (beneficial only to a segment)
Competition amplifies social disagreement
- Type \(t_i\)'s equilibrium opinion of policy: \(z_i (t_i) = \mathbb{E}_\omega [u(\omega, t_i) | s_i^*(\omega)] \)
- By Lemma 1, agent will only approve policy when her opinion is non-negative
- Social agreement: expected correlation in the opinions of two agents, \(i\) and \(j\)
\[\mathcal{S}(N) = \mathbb{E}_{t_i, t_j} [\text{Corr}(z_i(t_i), z_j(t_j))]\] - \(\mathcal{S}\) is strictly decreasing in \(N\).
Example
- Consider agents \(i, j\) with \(t_i = 0, t_j = \pi/2\)
- \( \theta_1 = (1, 1, 0), \theta_2 = (1, 0, 1)\)
- \(i\) cares about \(\omega_1\), \(j\) cares about \(\omega_2\)
- Low competition \(\to\) less specialization, \(x^*(N) \) takes higher value
- signals are highly informative about \(\omega_0\) even if obtained from different firms
- higher correlation between opinions \(z_i(t_i)\) and \(z_j(t_j)\)
- Takeaway: competition pushes profit-maximizing firms to provide information about dimensions that agents disagree more
Welfare implications of increased disagreement
- Agent's expected welfare decreases as competition increases
- Agent \(i\)'s expected welfare:
\[ \mathcal{U}(N) = \mathbb{E}_{\omega, t} [ A^*(\omega, t) u(\omega, t_i) -p^*(t_i) ] \] - Expected welfare can be decomposed to
\[ \mathcal{U}(N) = \mathcal{V}(N) + \mathcal{G}(N) - \mathcal{P}(N)\]
where \(\mathcal{V}(N)\) is expected value of information
\(\mathcal{G}(N)\) is the impact of other's approval decisions on \(i\)'s utility
\(\mathcal{P}(N)\) is expected price for acquired information
Welfare implications of increased disagreement
\[ \mathcal{U}(N) = \mathcal{V}(N) + \mathcal{G}(N) - \mathcal{P}(N)\]
- \(\mathcal{V}(N)\): information's direct effect on agent's welfare
- measures how an agent values the information that she personally acquires
- \(\mathcal{G}(N)\): information's indirect effect on agent's welfare
- measures how an agent values the information that other agents acquire
Welfare implications of increased disagreement
\[ \mathcal{U}(N) = \mathcal{V}(N) + \mathcal{G}(N) - \mathcal{P}(N)\]
- \(\mathcal{V}(N)\): information's direct effect on agent's welfare
- \(\mathcal{G}(N)\): information's indirect effect on agent's welfare
As competition increases, \(\mathcal{V}(N)\) increases as it's more specific to agent's taste.
Social disagreement \(\to\) \(\mathcal{G}(N)\) decreases
When the society is large enough, \(\mathcal{V}(N)+\mathcal{G}(N)\) decreases.
- increase in \(\mathcal{V}\) cannot compensate for decrease in \(\mathcal{G}\)
Welfare implications of increased disagreement
- Political information has value because it allows agents to influence outcomes in a way that aligns with their preferences.
- However, outcomes have consequences for all members of the society.
- Individual information acquisition strategies (acquire information with highest value net price) have social externalities on others.
Conclusion
- Information has social externalities
- Increased competition between profit-maximizing firms lead to informational specialization
- Increased specialization of firms lead to greater social disagreement
Thank you for listening!
Unused slides from here on
Motivating example
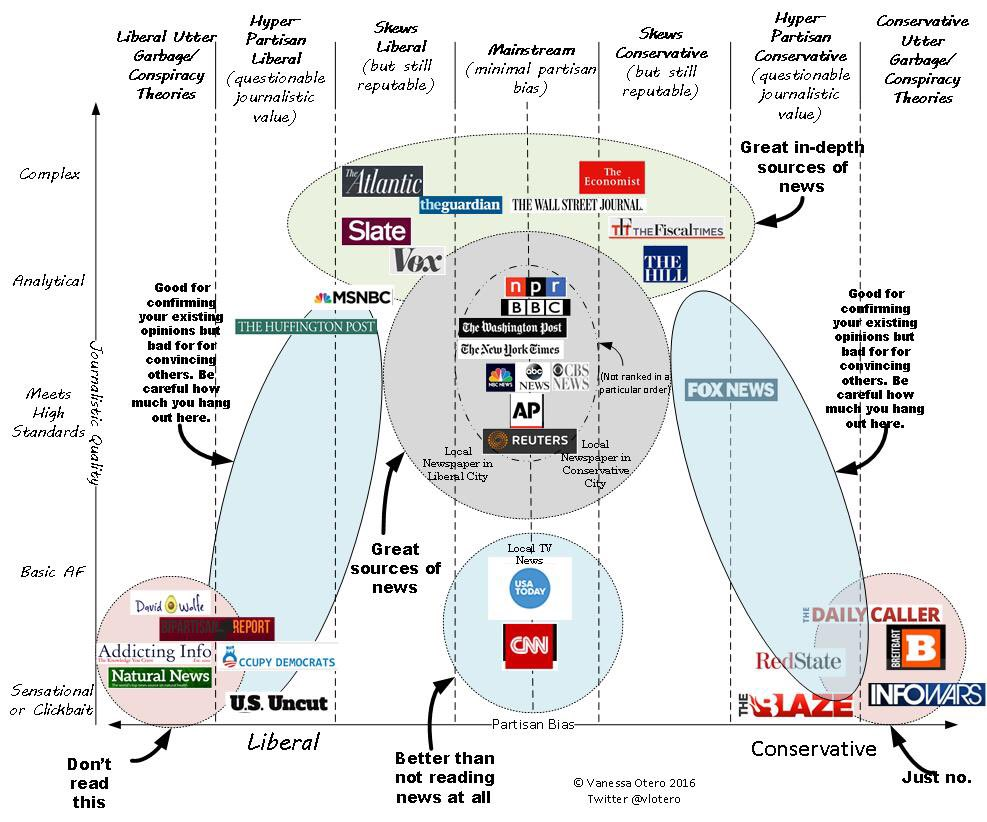
Where do you obtain your news?
Stage 3
Recall that an agent faces two choices:
- where to acquire information, and
- conditioning on obtained information, whether to approve the policy or not
Equilibrium behavior:
- Suppose agent \(i\) chooses to acquire information from firm \(n\)
- Recall agent \(i\)'s payoff is \(u(\omega, \theta_i) \) if policy approved; 0 otherwise
Proof of Lemma 2
Define \(A_{-i}(\omega, \theta_{-i}) \) to be the approval rate excluding type \(\theta_i\).
Expected utility if \(\theta_i\) does not receive any information:
Since \( \omega_k \sim \mathcal{N}(0, 1)\), \(\mathbb{E}_\omega [u(\omega, \theta_i)] = 0\); original equation becomes
Proof of Lemma 2
Expected utility when \(\theta_i\) observes signal induced by \(b_n\):
by the law of iterated expectations,
Recall: \( u(\omega, \theta_i) =\omega\cdot\theta_i \sim \mathcal{N}(0, \lVert \theta_i \rVert ^2 )\)
\( s_i(\omega,b_n) = b_n \cdot \omega + \epsilon_i \sim \mathcal{N}(0, 1 + \lVert b_n \rVert ^2) \)
\(\to\) this part cancels out with the first part
Media competition and social disagreement
By Sheng Long
Media competition and social disagreement
- 67



