Intro to Machine Learning

https://introml.mit.edu/

Lecture 2: Linear regression and regularization

Shen Shen

Sept 6, 2024

(many slides adapted from Tamara Broderick)

6.390-personal@mit.edu

Logistical issues? Personal concerns?
We’d love to help out!

plus ~40 awesome LAs

Optimization + first-principle physics 

Outline

  • Recap: ML set up, terminology
  • Ordinary least-square regression
    • Closed-form solutions (when exists)
    • Cases when closed-form solutions don't exist
      • mathematically, practically, visually
  • Regularization
  • Hyperparameter and cross-validation

Outline

  • Recap: ML set up, terminology
  • Ordinary least-square regression
    • Closed-form solutions (when exists)
    • Cases when closed-form solutions don't exist
      • mathematically, practically, visually
  • Regularization
  • Hyperparameter and cross-validation

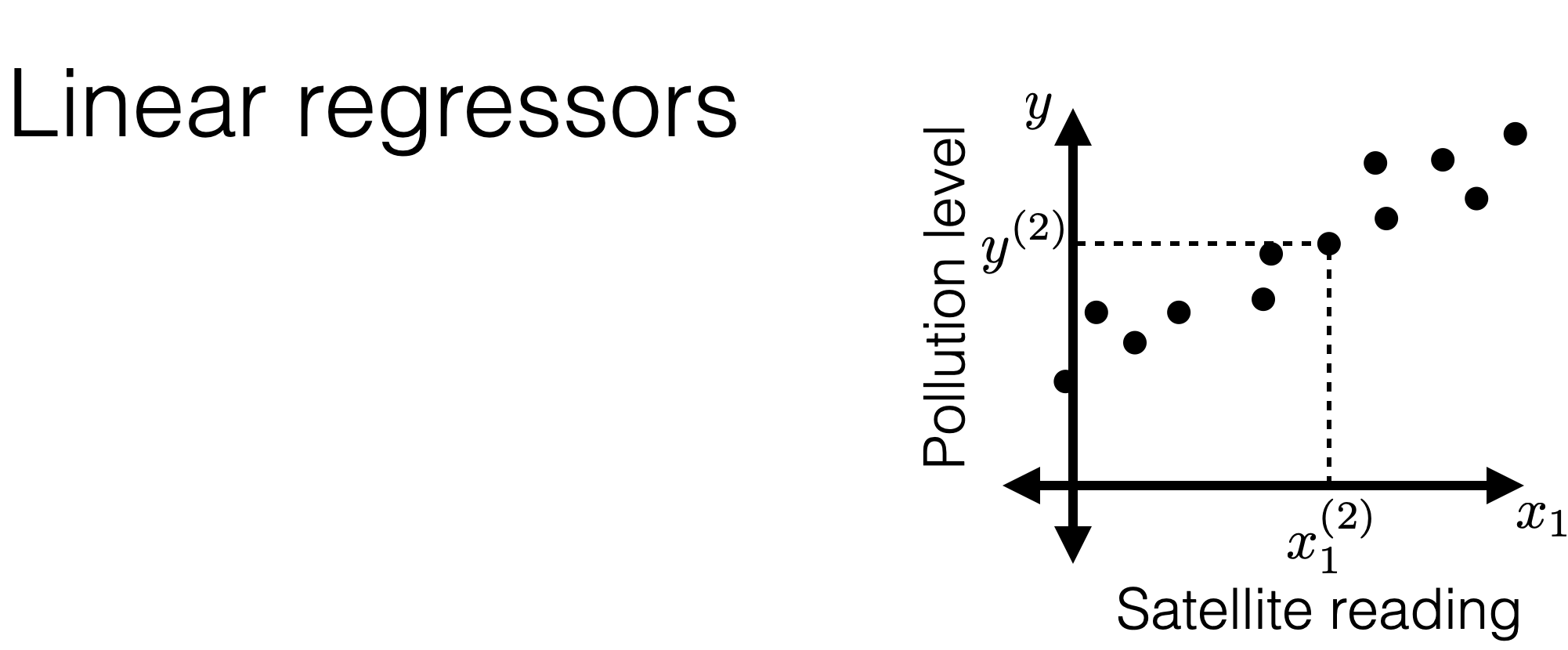
Recall lab1 intro

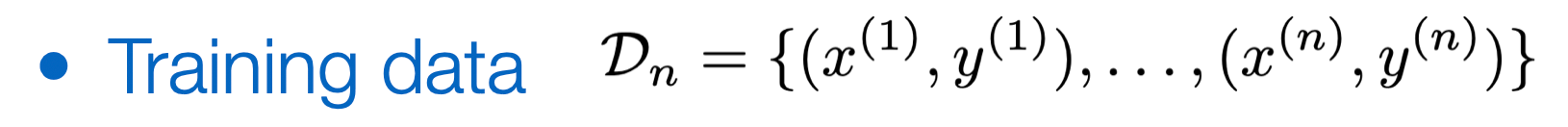
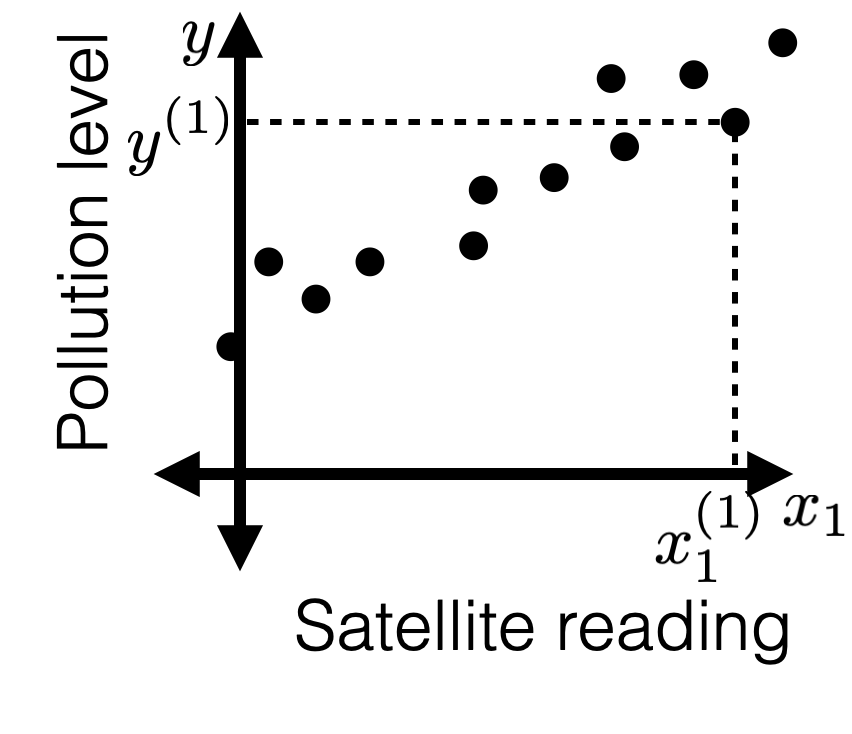
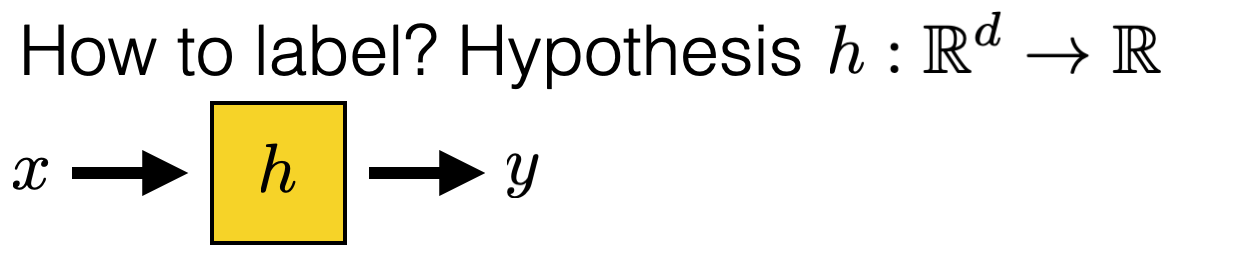
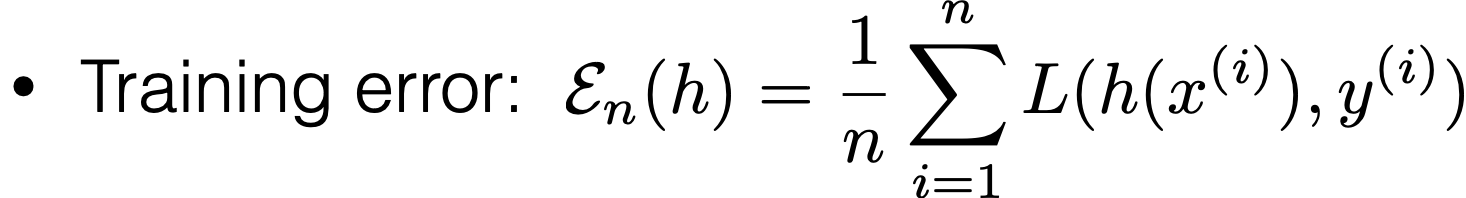
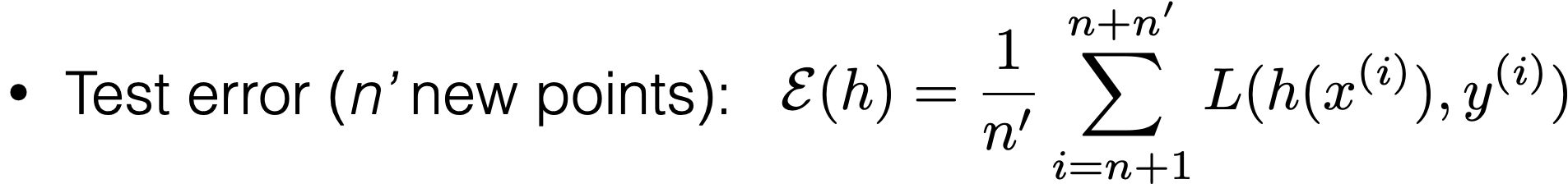
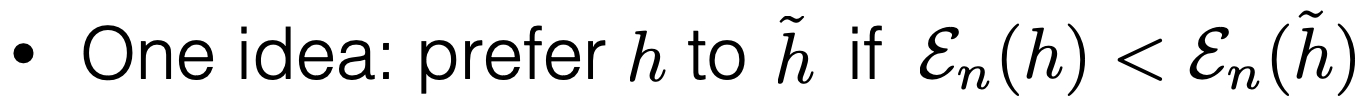
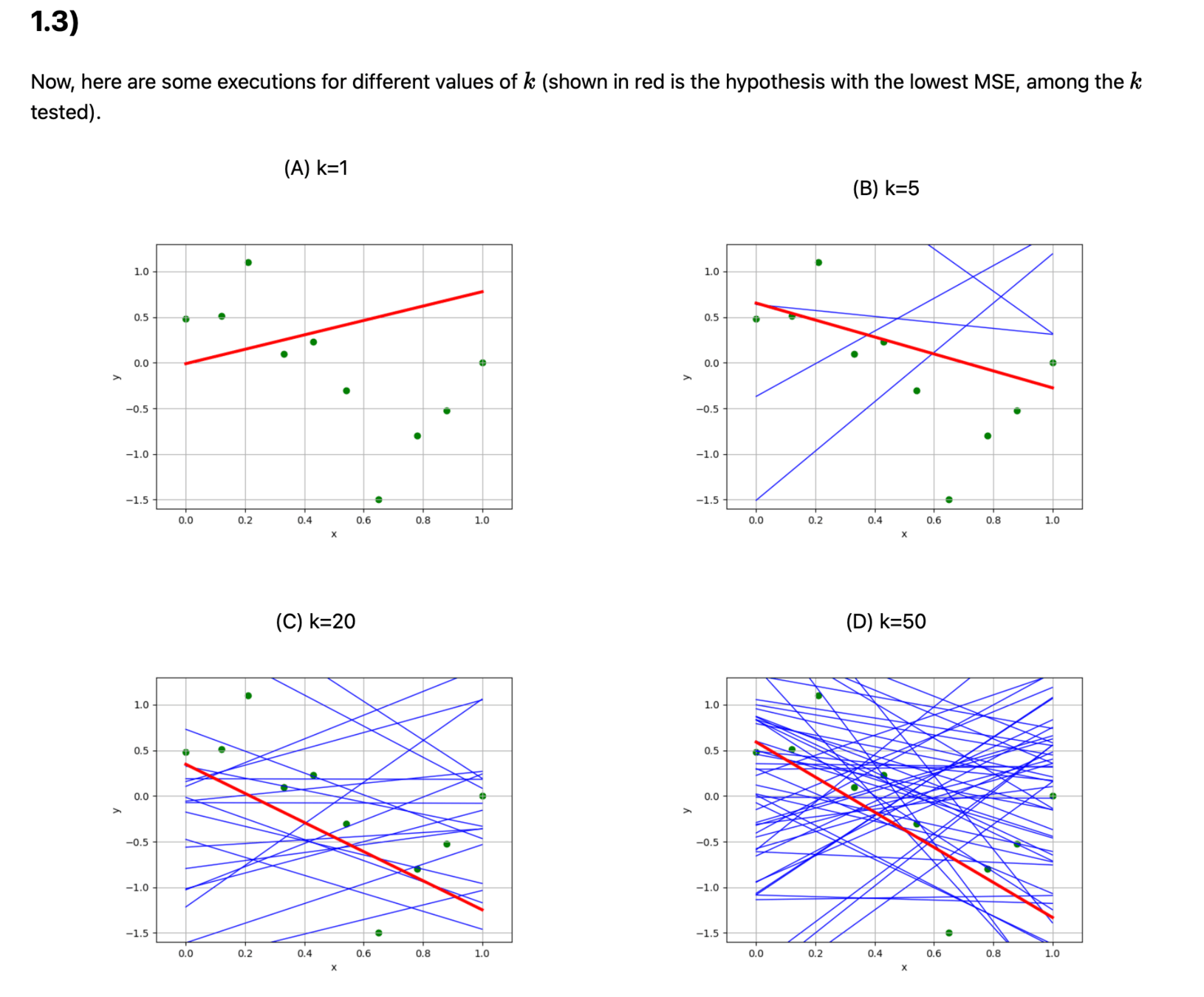
Recall lab1 Q1

def random_regress(X, Y, k):
    d, n = X.shape

    # generate k random hypotheses
    ths = np.random.randn(d, k)
    th0s = np.random.randn(1, k)

    # compute the mean squared error of each hypothesis on the data set
    errors = lin_reg_err(X, Y, ths, th0s.T)

    # Find the index of the hypotheses with the lowest error
    i = np.argmin(errors)

    # return the theta and theta0 parameters that define that hypothesis
    theta, theta0 = ths[:,i:i+1], th0s[:,i:i+1]
    return (theta, theta0), errors[i]

Outline

  • Recap: ML set up, terminology
  • Ordinary least-square regression
    • Closed-form solutions (when exists)
    • Cases when closed-form solutions don't exist
      • mathematically, practically, visually
  • Regularization
  • Hyperparameter and cross-validation

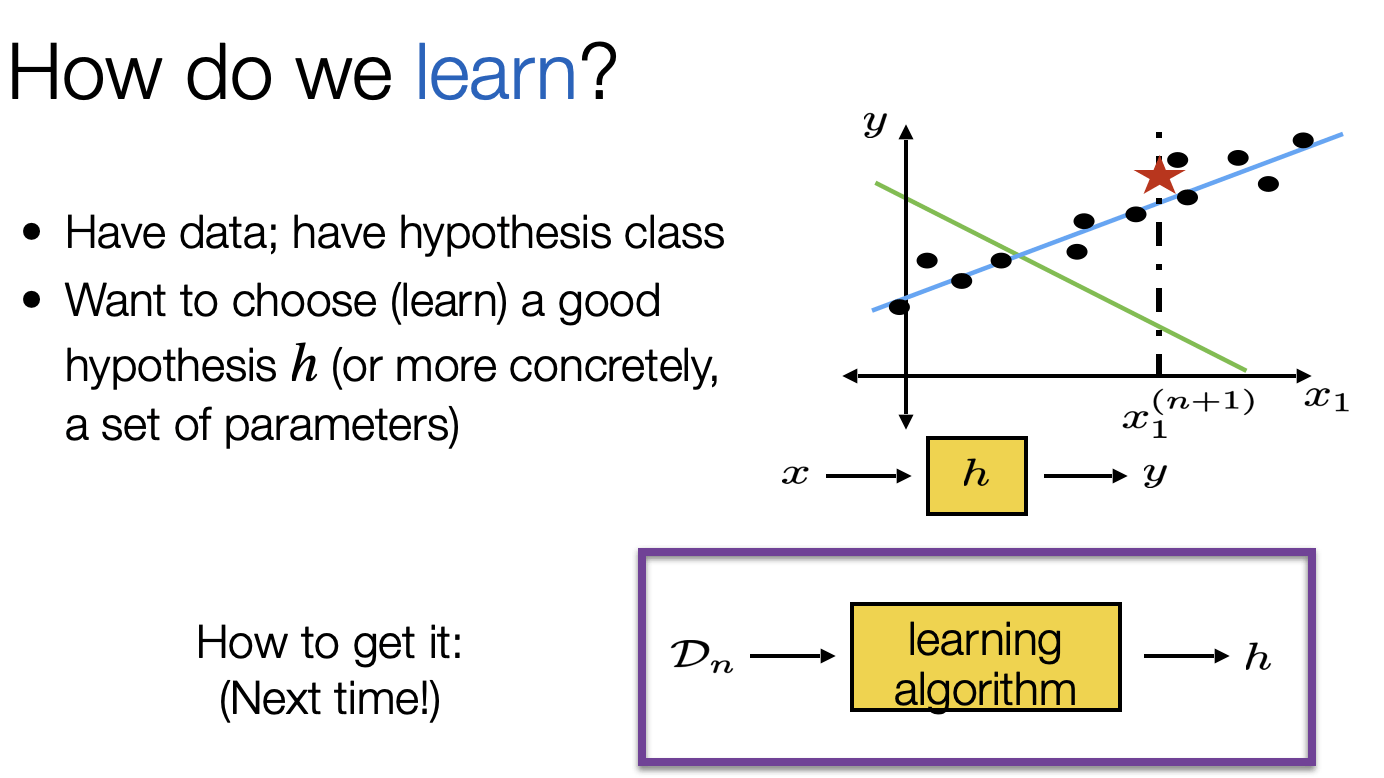
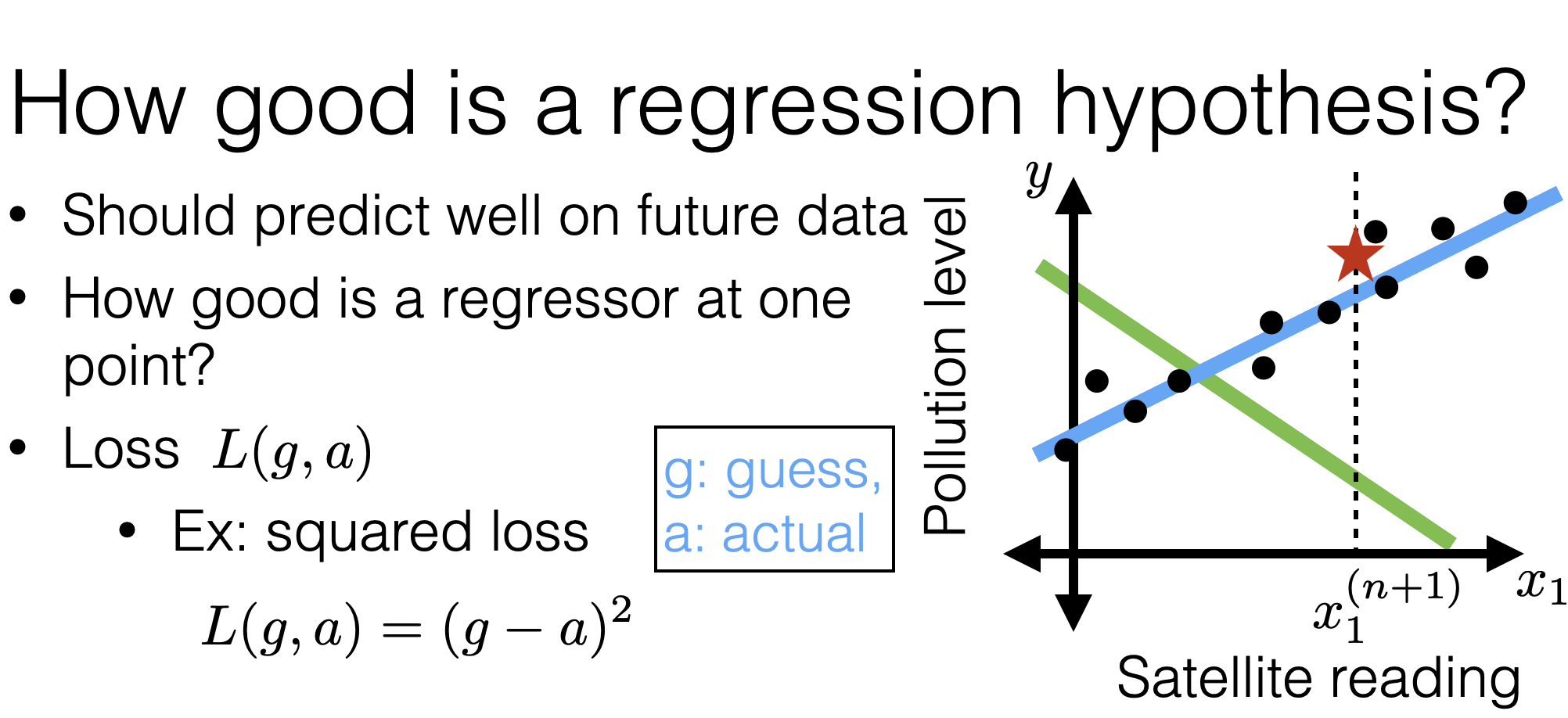
Linear regression: the analytical way

  • How about we just consider all hypotheses in our class and choose the one with lowest training error?
  • We’ll see: not typically straightforward
  • But for linear regression with square loss: can do it!
  • In fact, sometimes, just by plugging in an equation!
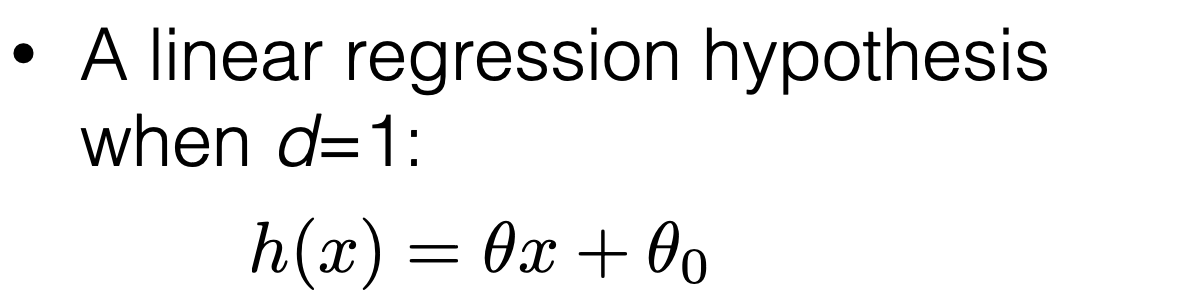
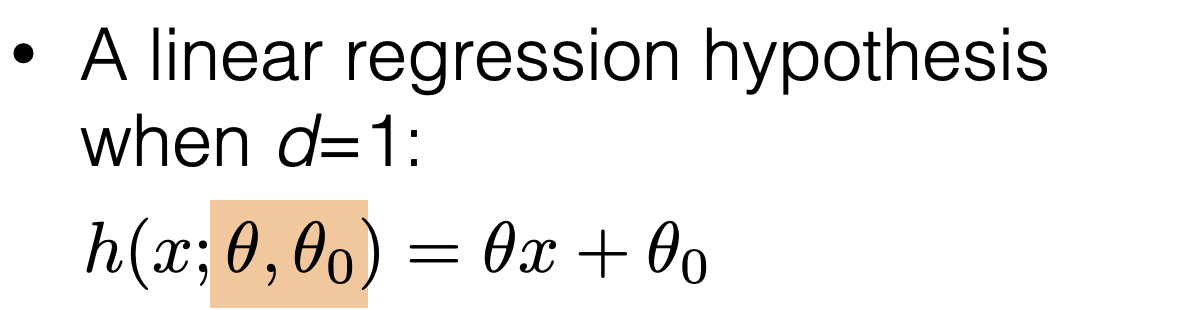
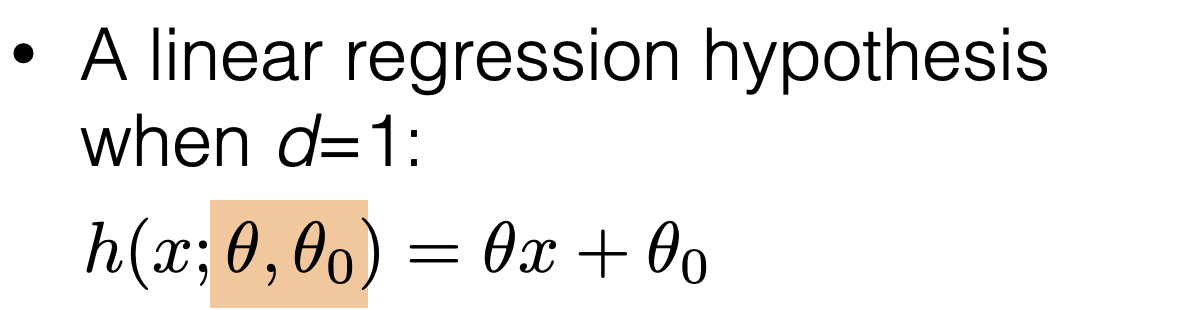
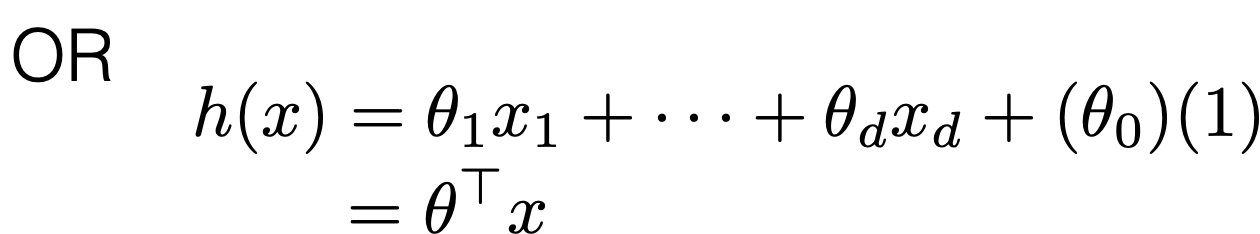
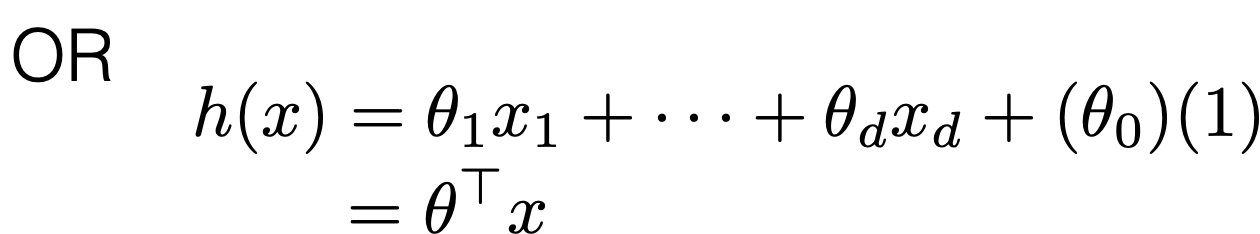
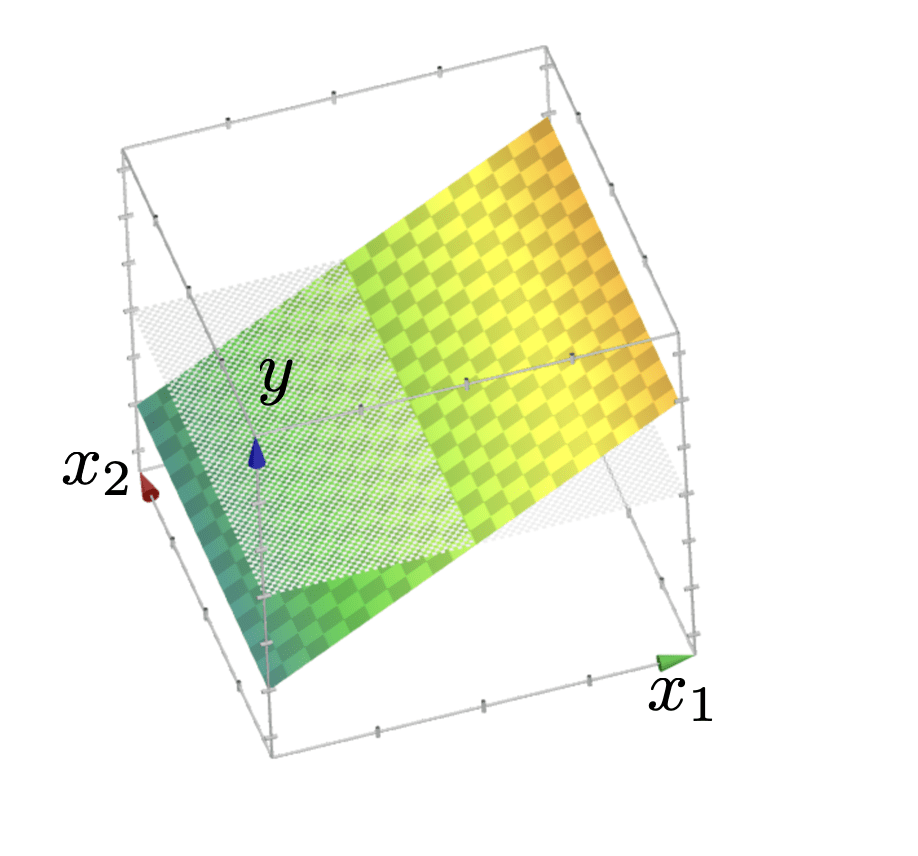
  • Recall: training error: \[\frac{1}{n} \sum_{i=1}^n L\left(h\left(x^{(i)}\right), y^{(i)}\right)\]
  • With squared loss:                          \[\frac{1}{n} \sum_{i=1}^n\left(h\left(x^{(i)}\right)-y^{(i)}\right)^2\]
  • Using linear hypothesis (with extra "1" feature):                       \[\frac{1}{n} \sum_{i=1}^n\left(\theta^{\top} x^{(i)}-y^{(i)}\right)^2\]
  • With given data, the error only depends on \(\theta\), so let's call the error \(J(\theta)\)

Now training error:   \[ J(\theta) = \frac{1}{n} \sum_{i=1}^n\left(\theta^{\top} x^{(i)}-y^{(i)}\right)^2\]

 

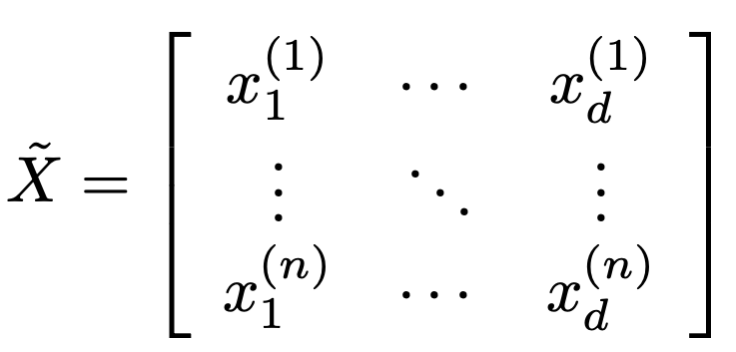
Define

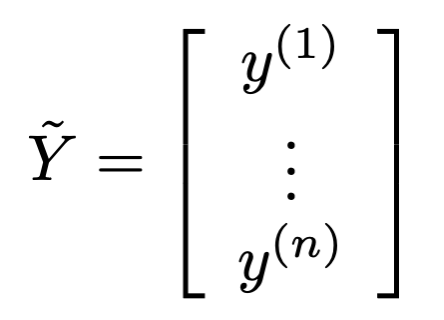
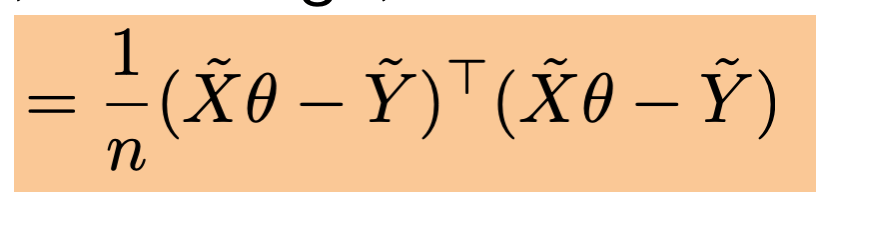
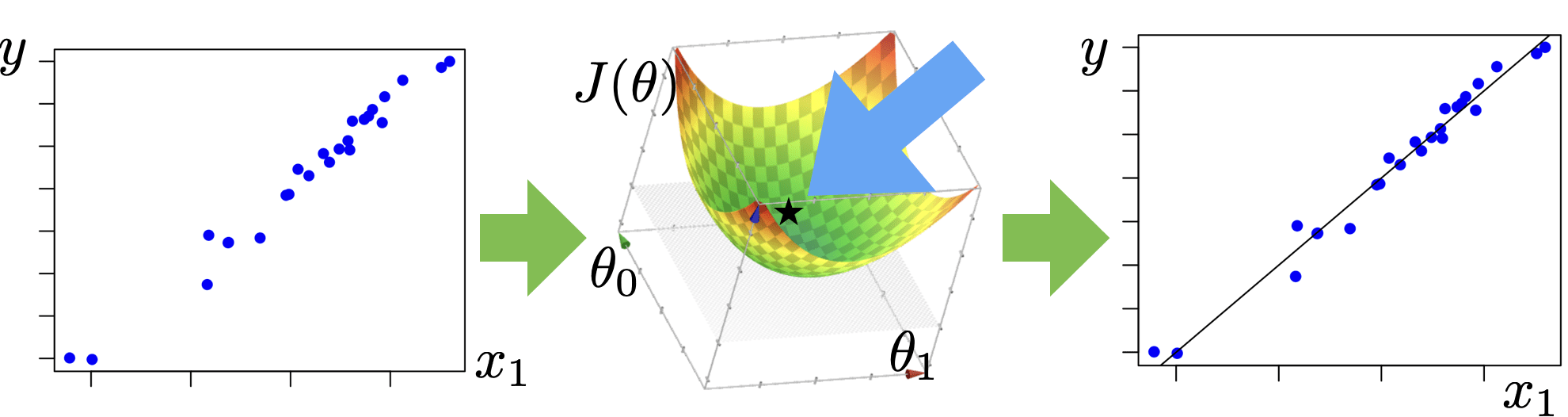
  • Goal: find \(\theta\) to minimize                     \[J(\theta)=\frac{1}{n}(\tilde{X} \theta-\tilde{Y})^{\top}(\tilde{X} \theta-\tilde{Y})\]
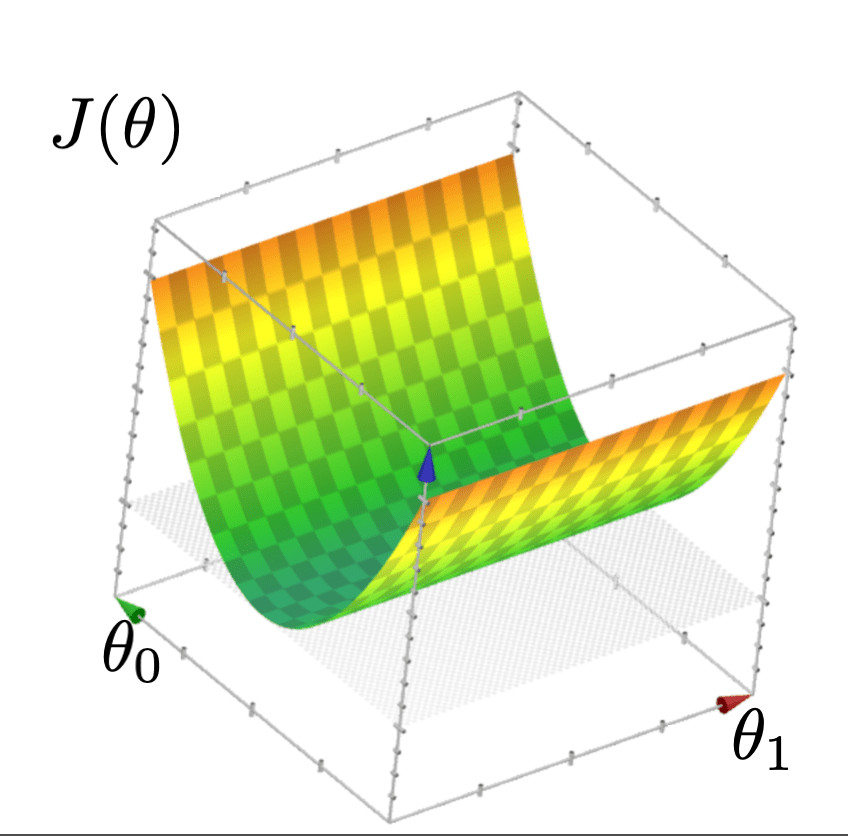
  • Q: what kind of function is \(J(\theta)\) and what does it look like?
  • A: Quadratic function that looks like either a "bowl" or "half-pipe"

🥰

🥺

  • When                     \[J(\theta)=\frac{1}{n}(\tilde{X} \theta-\tilde{Y})^{\top}(\tilde{X} \theta-\tilde{Y})\] looks like a "bowl" (typically does)
  • Uniquely minimized at a point if gradient at that point is zero and function "curves up" [see linear algebra]
\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}

Set Gradient \(\nabla_\theta J(\theta) \stackrel{\text { set }}{=} 0\)

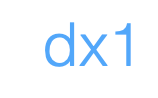
The beauty of \( \theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}\): simple, general, unique minimizer

  • \(\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}\) is not well-defined if \(\left(\tilde{X}^{\top} \tilde{X}\right)\) is not invertible
  • Indeed, \(\left(\tilde{X}^{\top} \tilde{X}\right)\) is not invertible if and only if \(\tilde{X}\) is not full column rank
  • Now, the catch (we'll see, all lead to half-pipe case) 
  • Indeed, \(\left(\tilde{X}^{\top} \tilde{X}\right)\) is not invertible if and only if \(\tilde{X}\) is not full column rank
  1. if \(n\)<\(d\) 
  2. if columns (features) in \( \tilde{X} \) have linear dependency
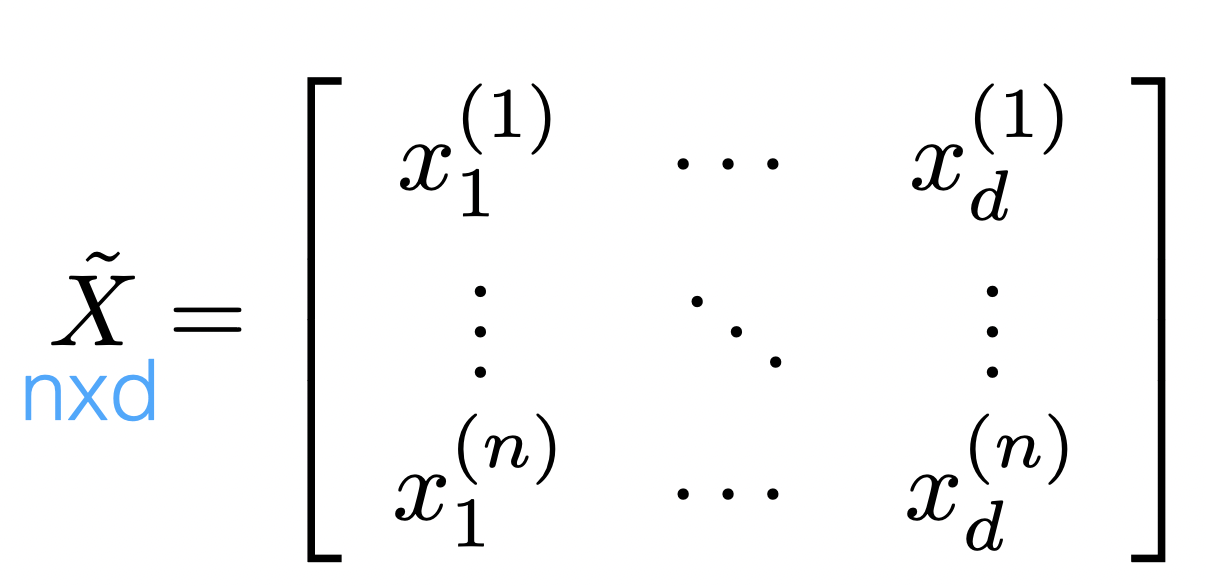
  • Recall

\(\tilde{X}\) is not full column rank

\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}
Quick Summary:
  1. if \(n\)<\(d\) (i.e. not enough data)
  2. if columns (features) in \( \tilde{X} \) have linear dependency (aka co-linearity)

 

  • This 👈  formula is not well-defined
  • Infinitely many optimal hyperplanes

Typically 

🥺

🥰

Outline

  • Recap: ML set up, terminology
  • Ordinary least-square regression
    • Closed-form solutions (when exists)
    • Cases when closed-form solutions don't exist
      • mathematically, practically, visually
  • Regularization
  • Hyperparameter and cross-validation

🥰

🥺

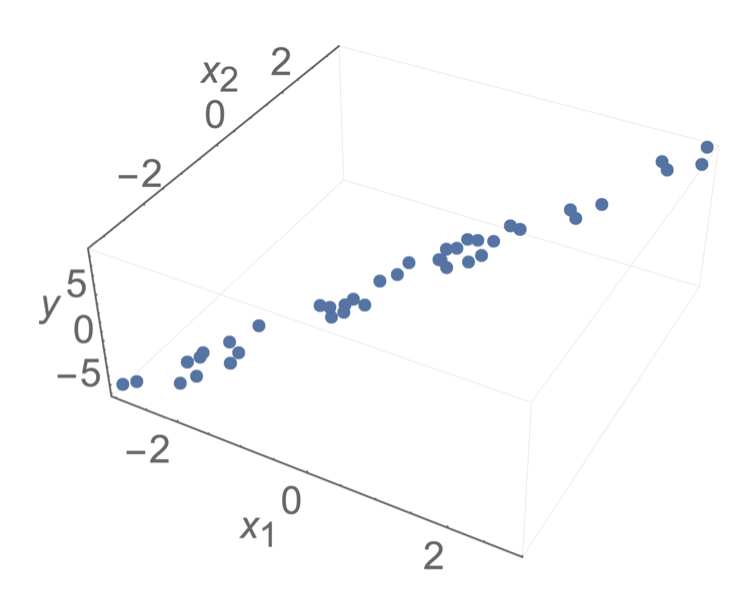
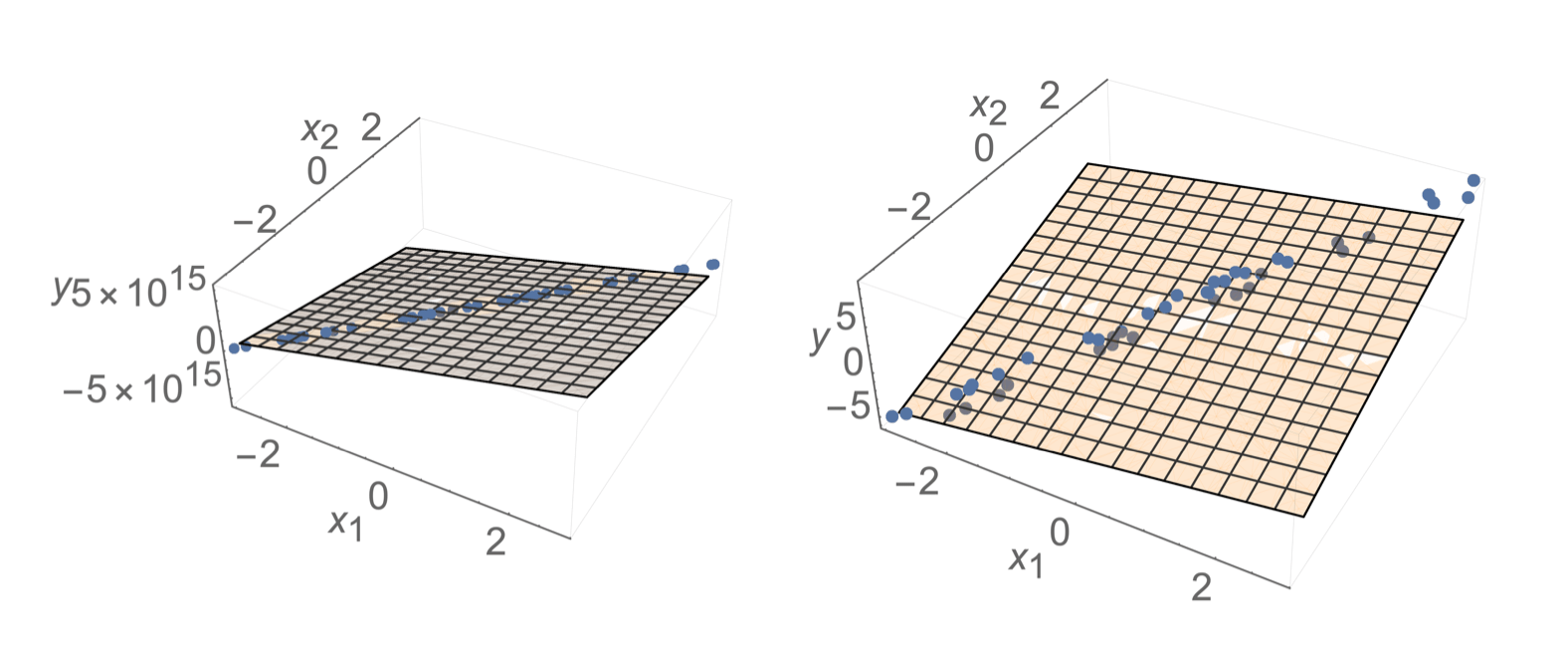
  • Sometimes, noise can resolve the invertibility issue
  • but still lead to undesirable results
  • How to choose among hyperplanes?
  • Prefer \(\theta\) with small magnitude

Ridge Regression

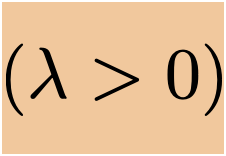
  • Add a square penalty on the magnitude
  • \(J_{\text {ridge }}(\theta)=\frac{1}{n}(\tilde{X} \theta-\tilde{Y})^{\top}(\tilde{X} \theta-\tilde{Y})+\lambda\|\theta\|^2\)
  • \(\lambda \) is a so-called "hyperparameter"
  • Setting \(\nabla_\theta J_{\text {ridge }}(\theta)=0\) we get
  • \(\theta^*=\left(\tilde{X}^{\top} \tilde{X}+n \lambda I\right)^{-1} \tilde{X}^{\top} \tilde{Y}\)
  • \(\theta^*\) (here) always exists, and is always the unique optimal parameters
  • (If there's an offset, see recitation/hw for discussion.)

Outline

  • Recap: ML set up, terminology
  • Ordinary least-square regression
    • Closed-form solutions (when exists)
    • Cases when closed-form solutions don't exist
      • mathematically, practically, visually
  • Regularization
  • Hyperparameter and cross-validation

Cross-validation

Cross-validation

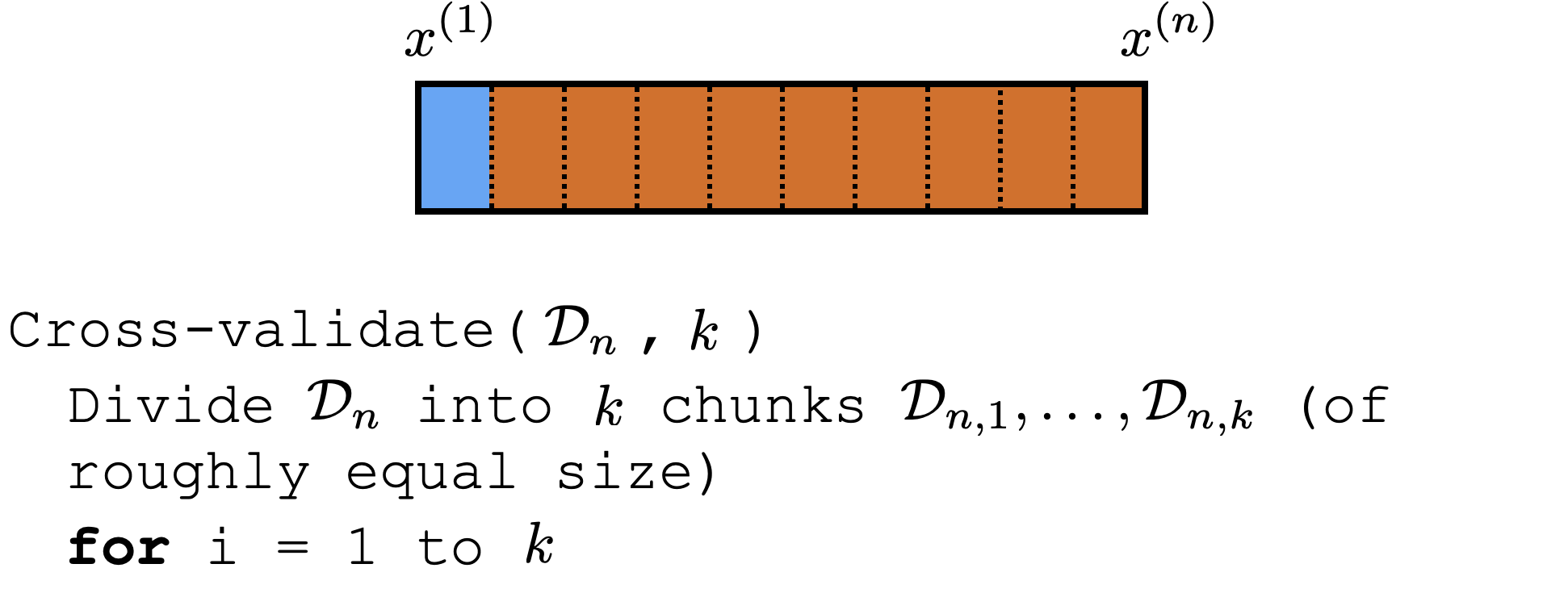
Cross-validation

\dots

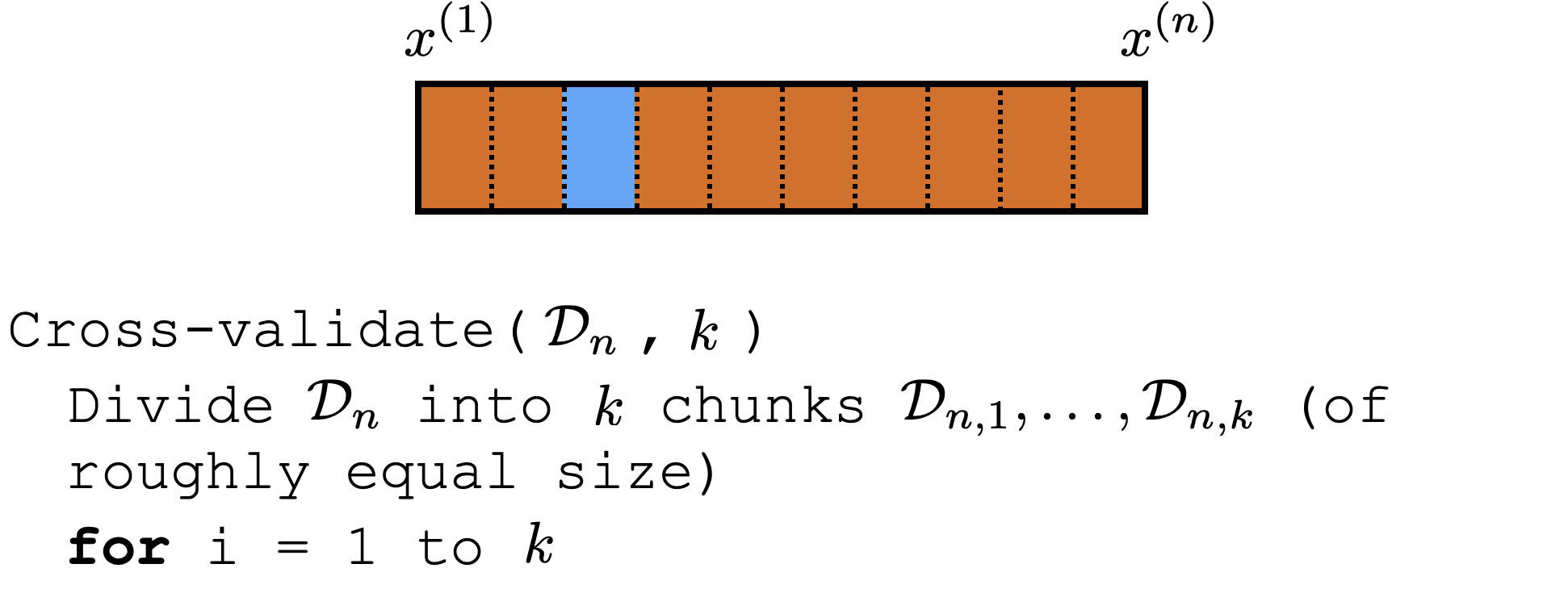
Cross-validation

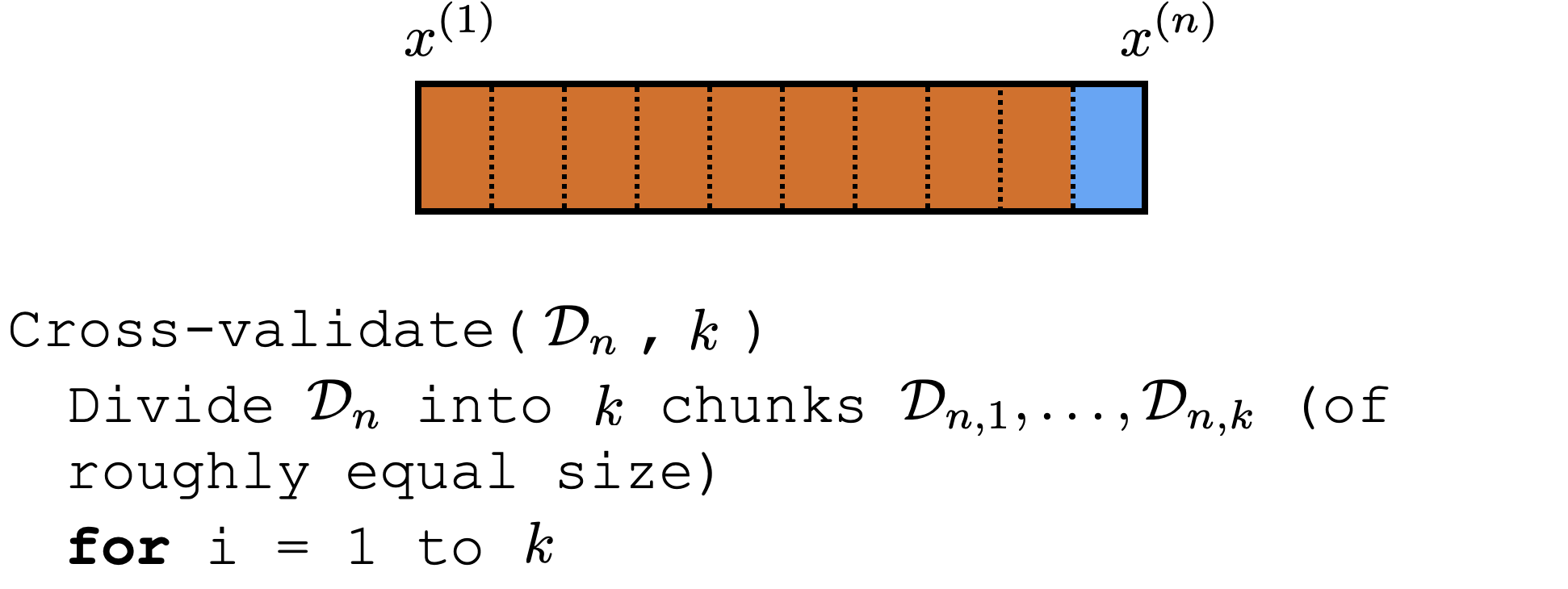
Cross-validation

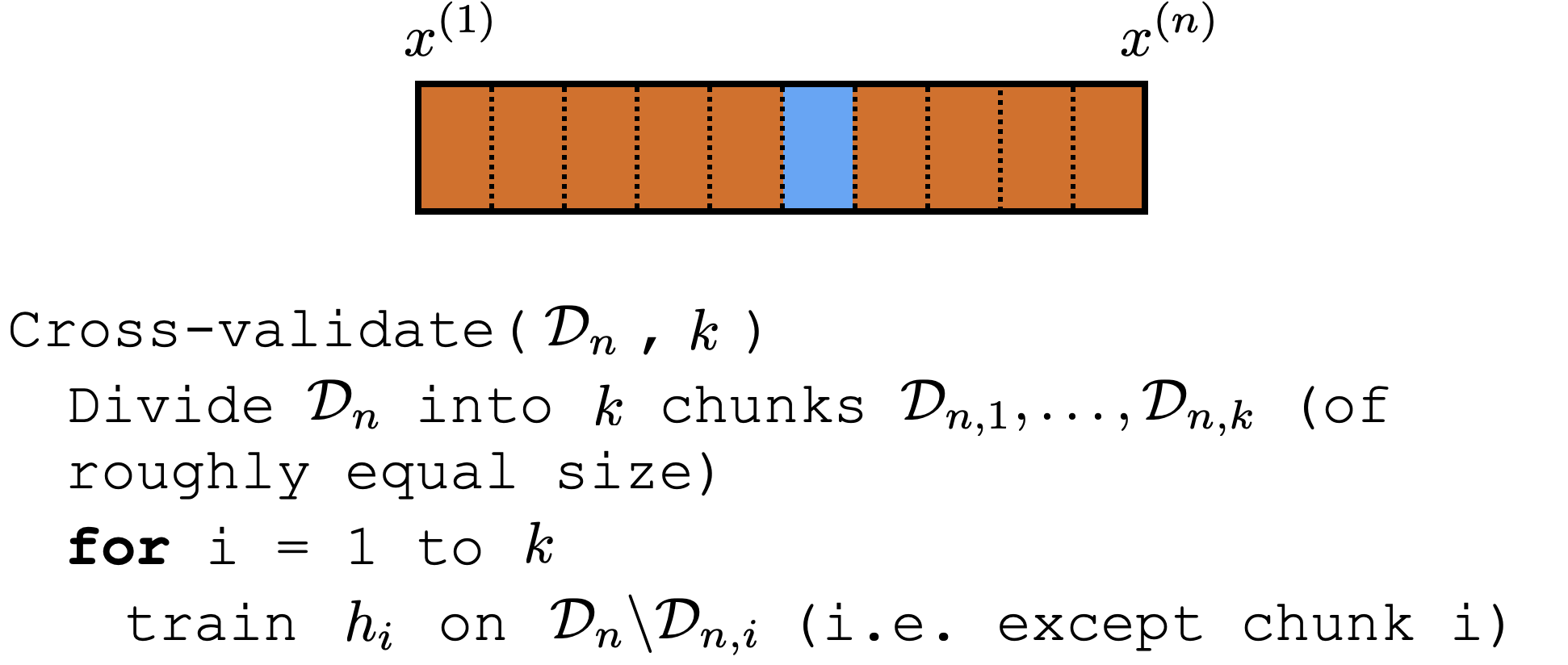
Cross-validation

Cross-validation

Comments on (cross)-validation

  • good idea to shuffle data first

  • a way to "reuse" data

  • it's not to evaluate a hypothesis

  • rather, it's to evaluate learning algorithm (e.g. hypothesis class choice, hyperparameters)

  • Could e.g. have an outer loop for picking good hyperparameter or hypothesis class

Summary

  • For the ordinary least squares (OLS), we can find the optimizer analytically, using basic calculus!  Take the gradient and set it to zero. (Generally need more than gradient info; suffices in OLS)
  • Two scenarios when analytical formula does not exist. We need to be careful about understanding the consequences.
  • Regularization can help battle overfitting (sensitive model).
  • Validation/cross-validation are a way to choose regularization hyper parameters. 

Summary

  • What does it mean for linear regression to be well posed.  
  • When there are many possible solutions, we need to indicate our preference somehow.
  • Regularization is a way to construct a new optimization problem.
  • Least-squares regularization leads to the ridge-regression formulation.  Good news: we can still solve it analytically!
  • Hyperparameters and how to pick them; cross-validation.

Thanks!

We'd love to hear your thoughts.

6.390 IntroML (Fall24) - Lecture 2 Linear Regression and Regularization

By Shen Shen

6.390 IntroML (Fall24) - Lecture 2 Linear Regression and Regularization

  • 46

More from Shen Shen

  • 6.390 IntroML (Fall24) - Lecture 10 Clustering
    Shen Shen
    9
  • 6.390 IntroML (Fall24) - Lecture 9 Transformers
    Shen Shen
    35
  • 6.390 IntroML (Fall24) - Lecture 8 Convolutional Neural Networks
    Shen Shen
    22