https://introml.mit.edu/

Lecture 5: Features

 

Shen Shen

Sept 27, 2024

Intro to Machine Learning

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer

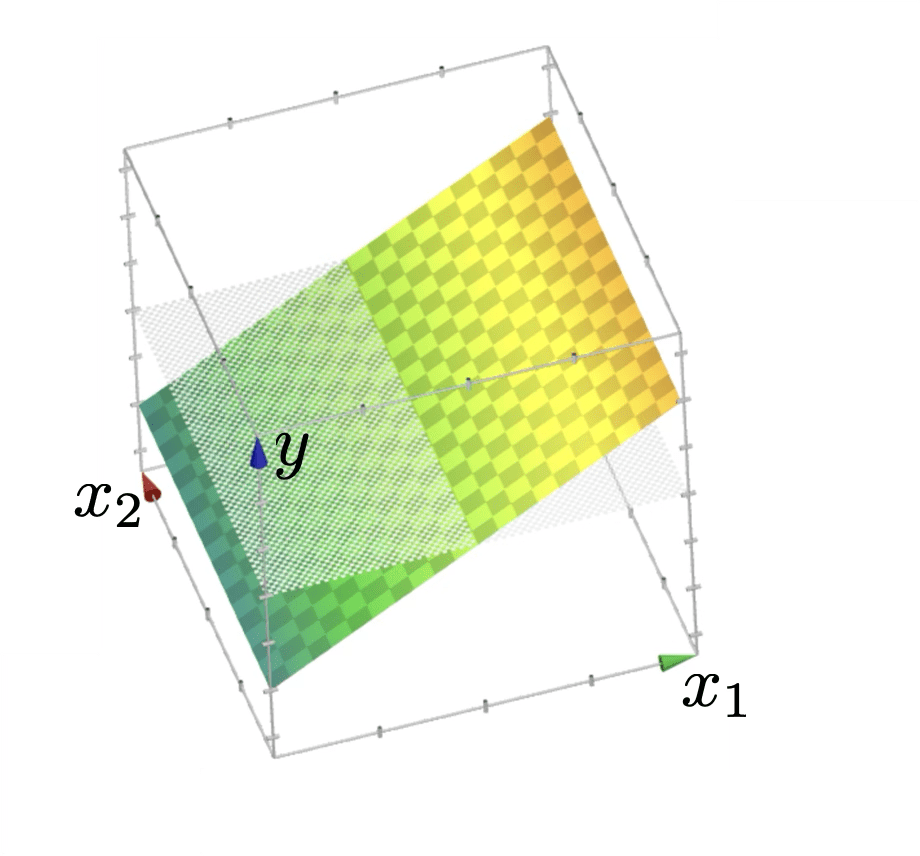
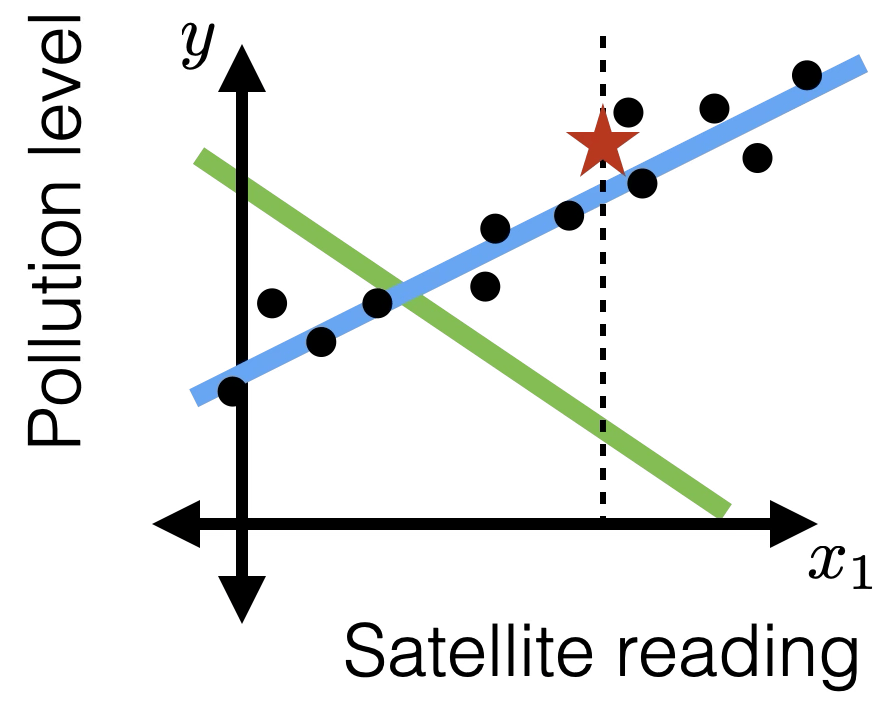
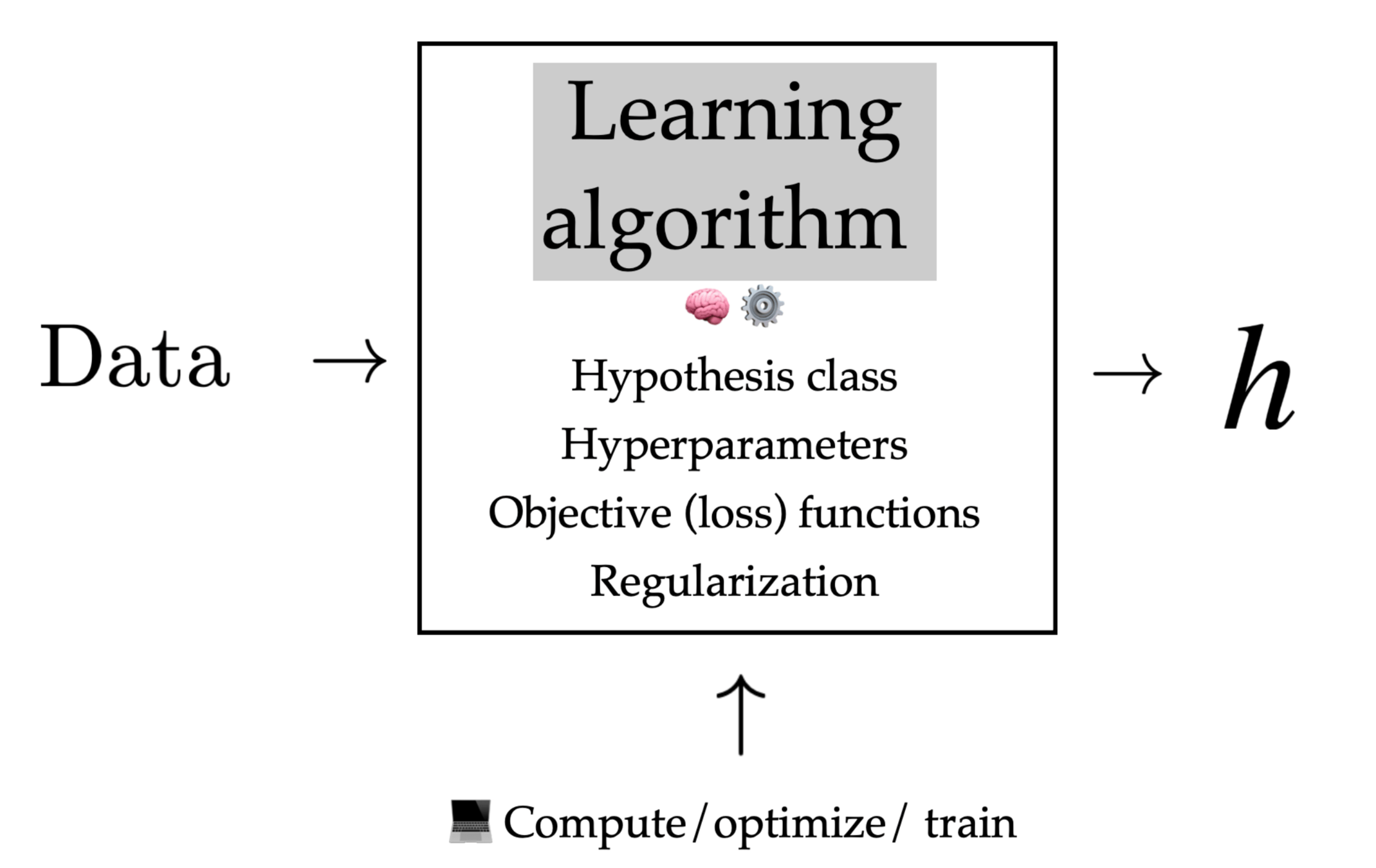
linear regressor \(y = \theta^{\top} x+\theta_0\)

Recap:

the regressor is linear in the feature \(x\)

z = \theta^{\top} x+\theta_0
\{x: \theta^{\top} x+\theta_0>0\}
\{x: \theta^{\top} x+\theta_0<0\}

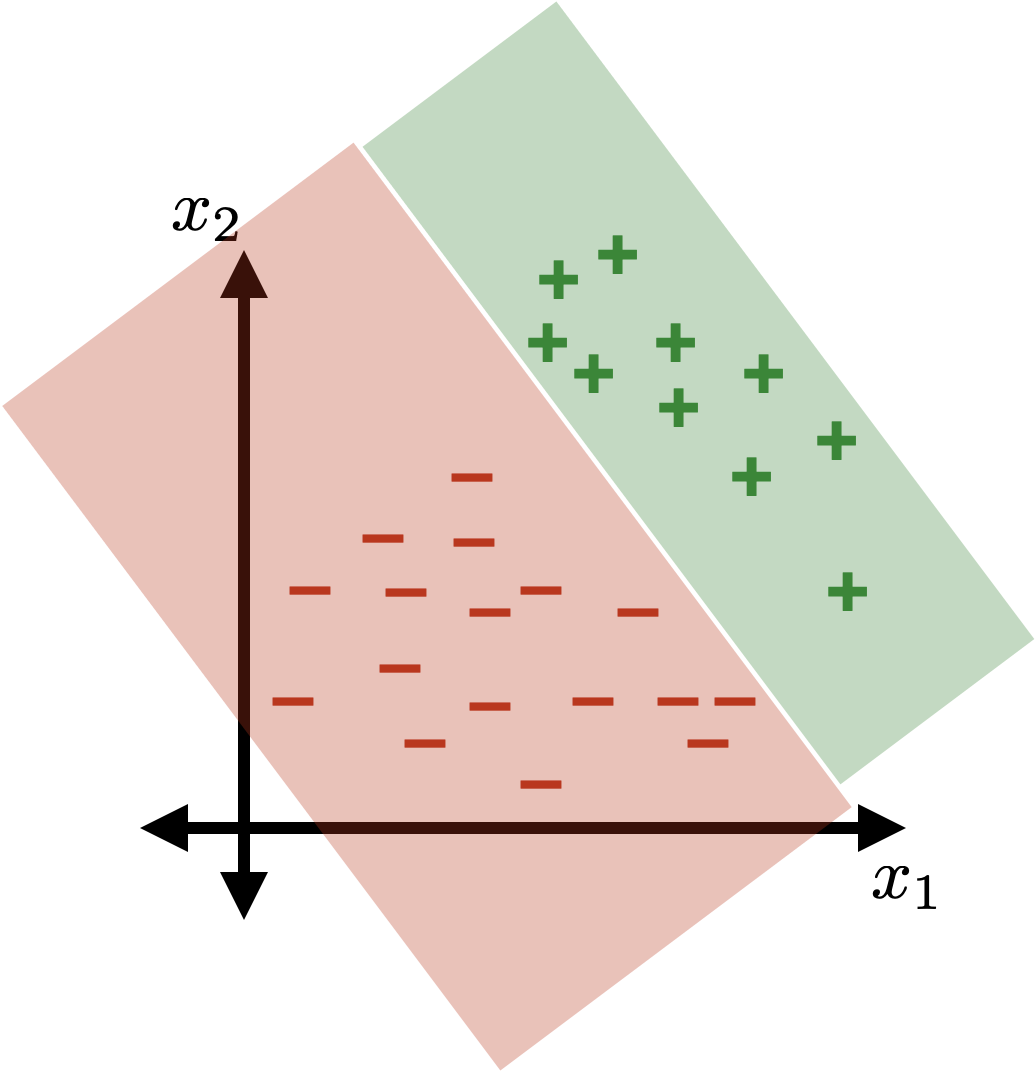
linear (sign-based) classifier

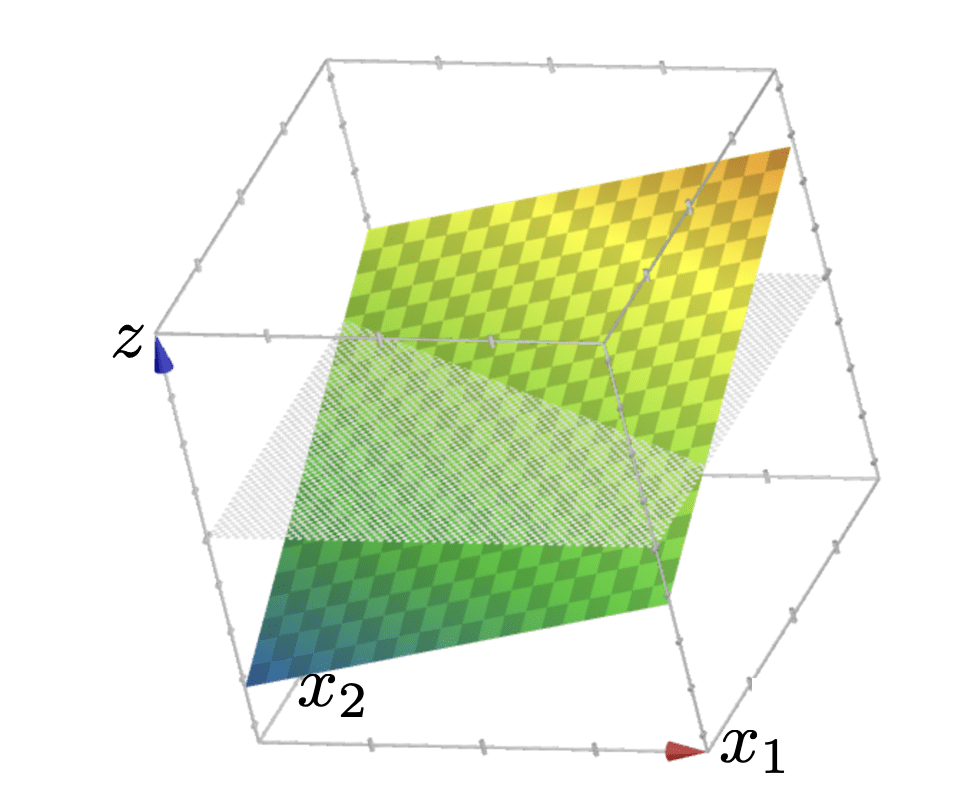
Recap:

separator

\{x: \theta^{\top} x+\theta_0 = 0\}

the separator is linear in the feature \(x\)

\{x: \sigma(\theta^{\top} x+\theta_0)>0.5\}
\{x: \sigma(\theta^{\top} x+\theta_0)<0.5\}

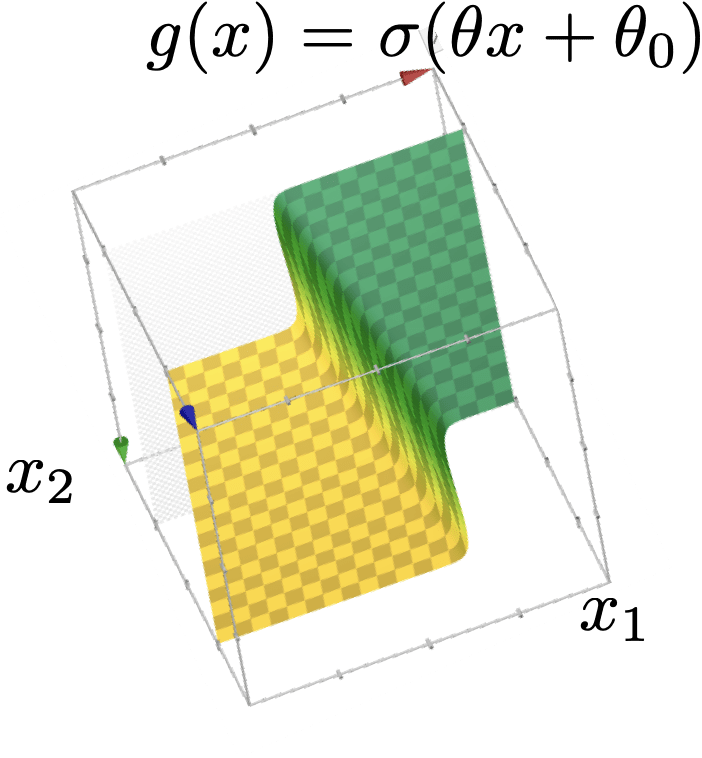
linear logistic classifier

\(g(x)=\sigma\left(\theta^{\top} x+\theta_0\right)\)

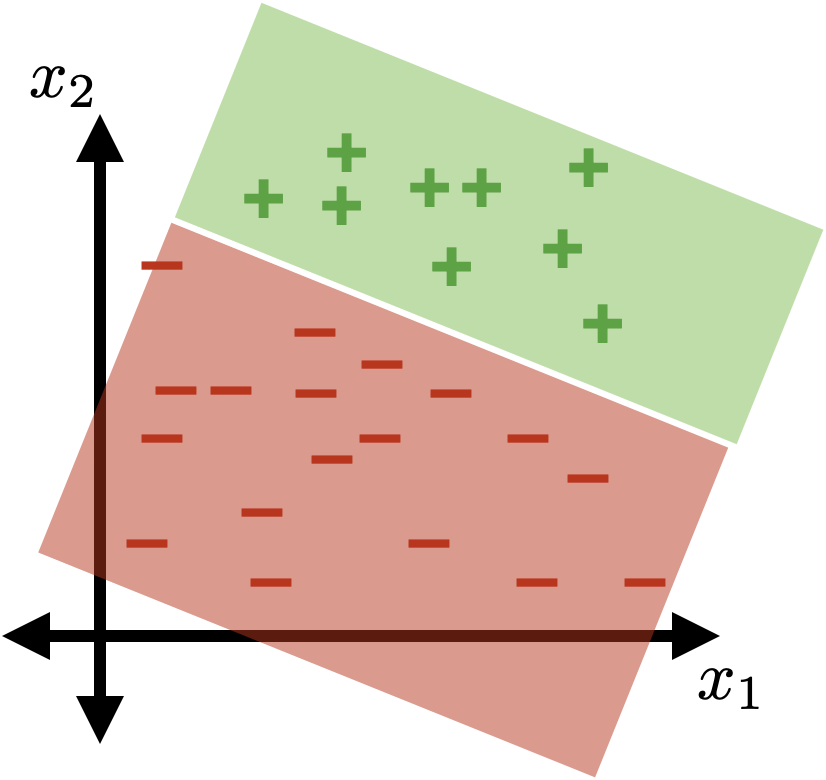
Recap:

separator

the separator is linear in the feature \(x\)

\{x: \theta^{\top} x+\theta_0 = 0\}

Image classification played a pivotal role in kicking off the current wave of AI enthusiasm.

Linear classification played a pivotal role in kicking off the first wave of AI enthusiasm.

👆

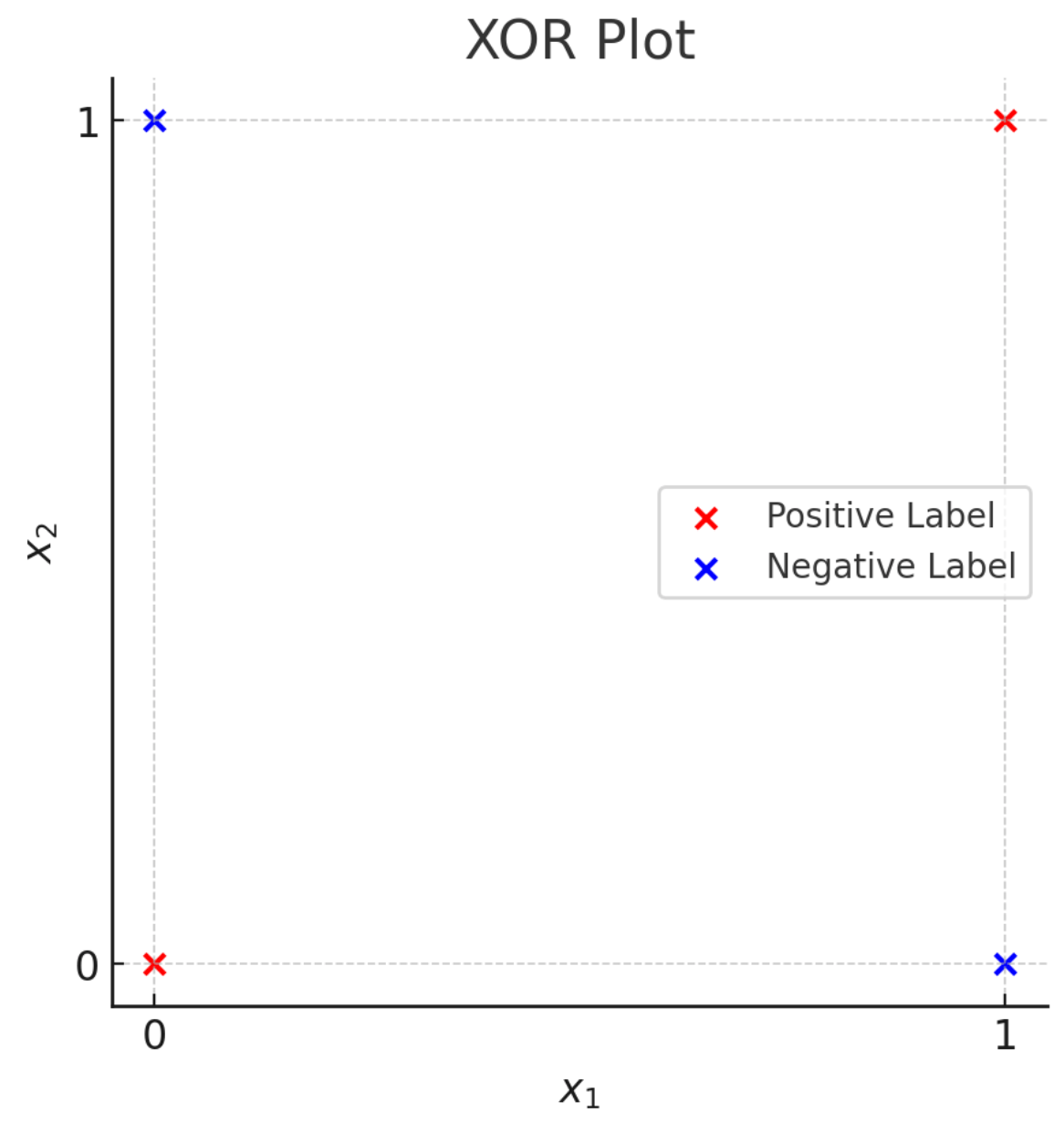
Not linearly separable.

👇

Linear tools cannot solve interesting tasks.

Linear tools cannot, by themselves, solve interesting tasks.

Many cool ideas can "help out" linear tools. We'll focus on one today.

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer

old features \(x \in \mathbb{R^d}\)

\longrightarrow

new features \(\phi(x) \in \mathbb{R^{d^{\prime}}}\)

non-linear in \(x\)

linear in \(\phi\)

\longrightarrow

non-linear transformation

\theta_1\phi_1(x) + \theta_2\phi_2(x) + \dots \theta_{d'}\phi_{d'}(x)

Linearly separable in \(\phi(x) = x^2\) space

Not linearly separable in \(x\) space

-3
-2
-1
0
1
2
3
4
5
6
7
8
9
x
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
\phi(x)

transform via \(\phi(x) = x^2\)

\Downarrow

Linearly separated in \(\phi(x) = x^2\) space, e.g. predict positive if \(\phi \geq 3\)

Non-linearly separated in \(x\) space,  e.g. predict positive if  \(x^2 \geq 3\)

-3
-2
-1
0
1
2
3
4
5
6
7
8
9
x
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
\phi(x)
\Downarrow

transform via \(\phi(x) = x^2\)

\{ x: x_1^2+x_2^2>0\}
\{ x: x_1^2+x_2^2<0\}
= x_1^2
\phi_2
z = \phi_1 + \phi_2
=x_2^2
\phi_1
x_1
x_2
z = x_1^2 + x_2^2

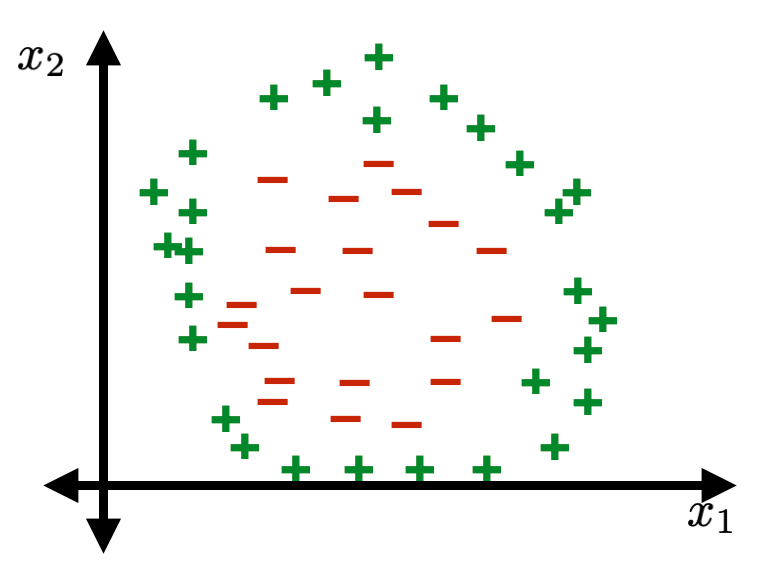
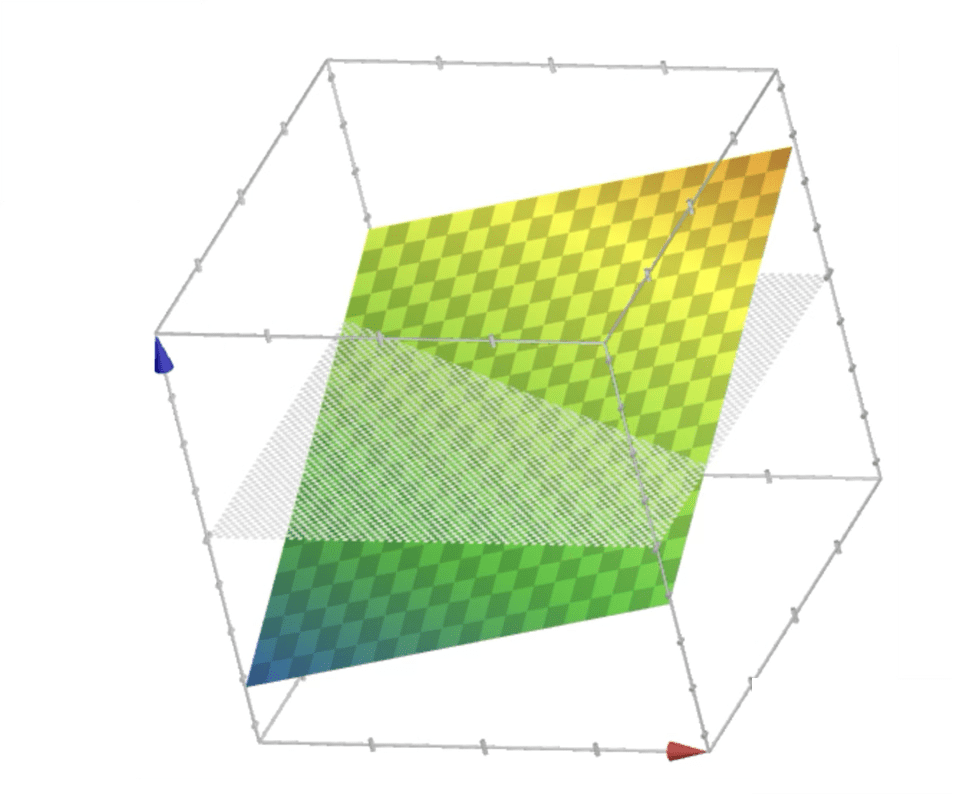
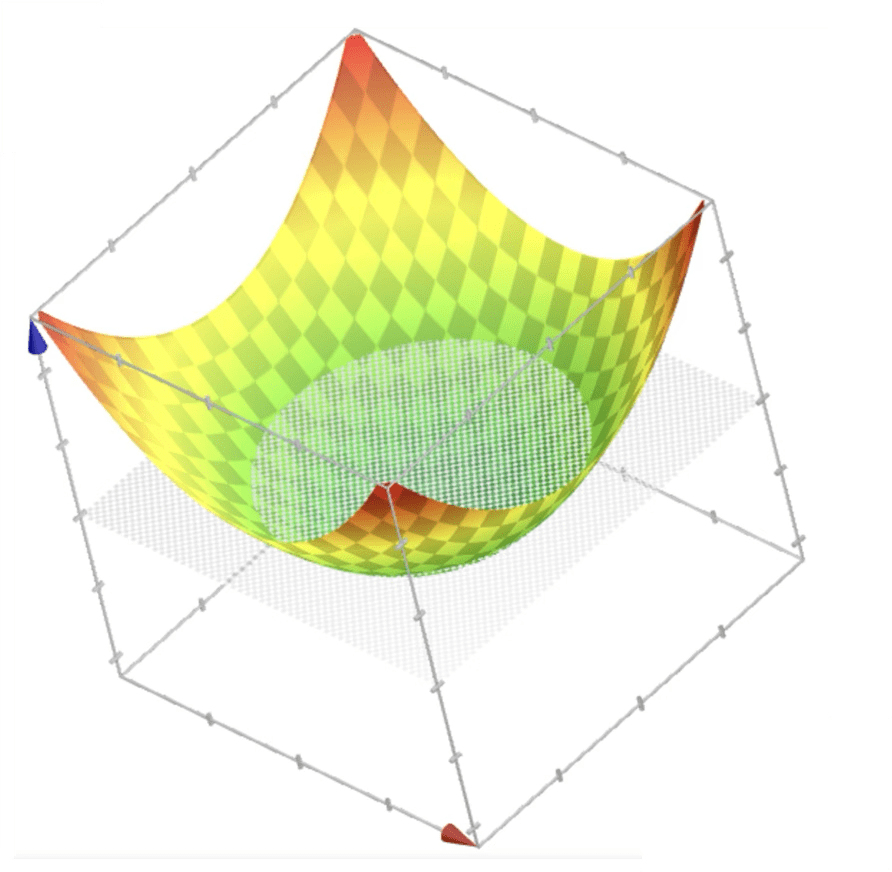
systematic polynomial features construction

d = 1
d = 2
\dots
\dots
  • Elements in the basis are the monomials of original features raised up to power \(k\)
  • With a given \(d\) and a fixed \(k\), the basis is fixed. 
1, x_{1}
k = 1
1, x_{1}, x_{1}^{2}
k = 2
1, x_{1}, x_{1}^{2}, x_{1}^{3}
k = 3
1
1, x_{1}, x_{2}
1, x_{1}, x_{2}, x_{1}^{2}, x_{1}x_{2}, x_{2}^{2}
1, x_{1}, x_{2}, x_{1}^{2}, x_{1}x_{2}, x_{2}^{2}, x_{1}^{3}, x_{1}^{2}x_{2}, x_{1}x_{2}^{2}, x_{2}^{3}
k = 0
1

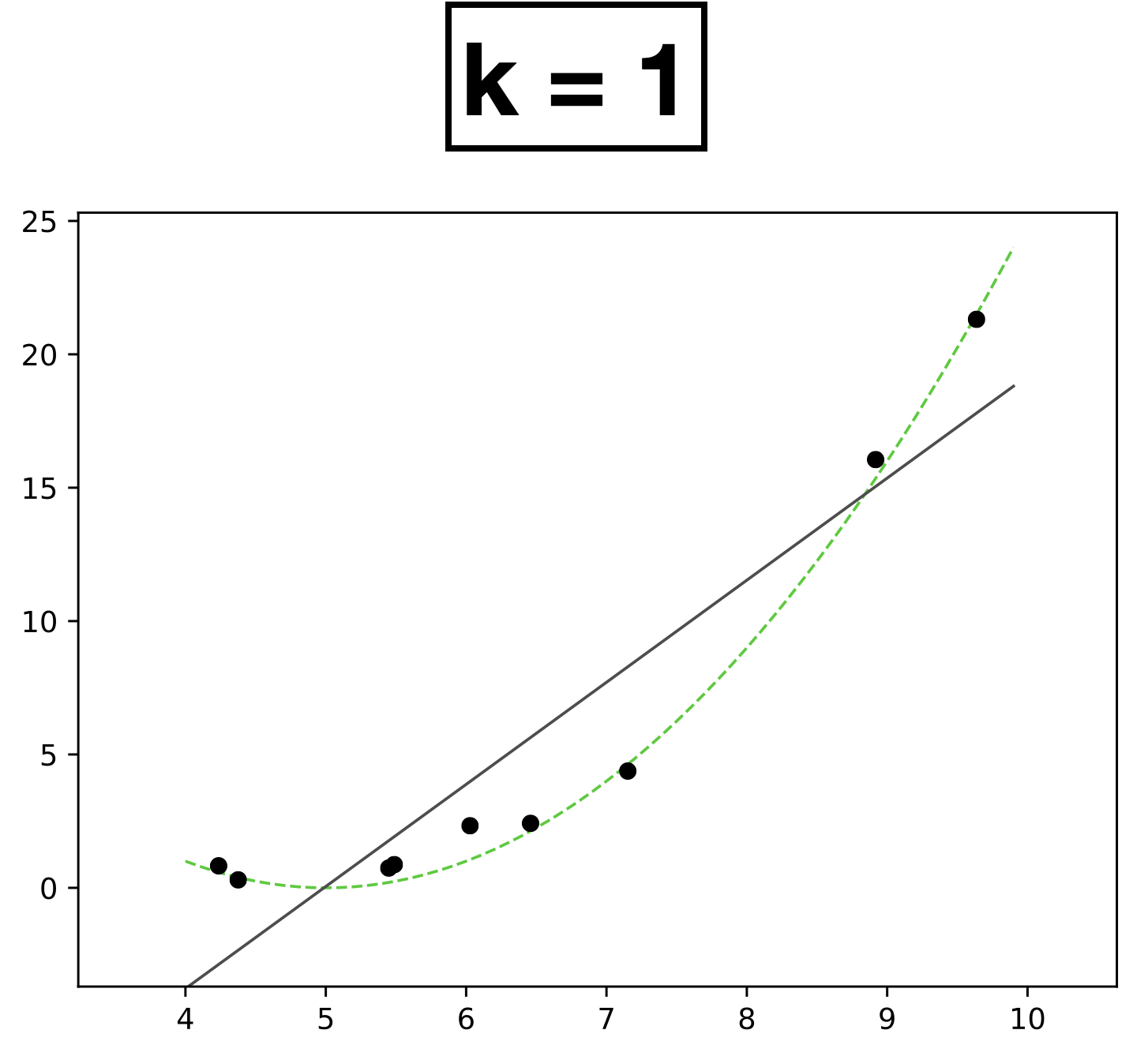
9 data points; each has feature \(x \in \mathbb{R},\)  label \(y \in \mathbb{R}\)

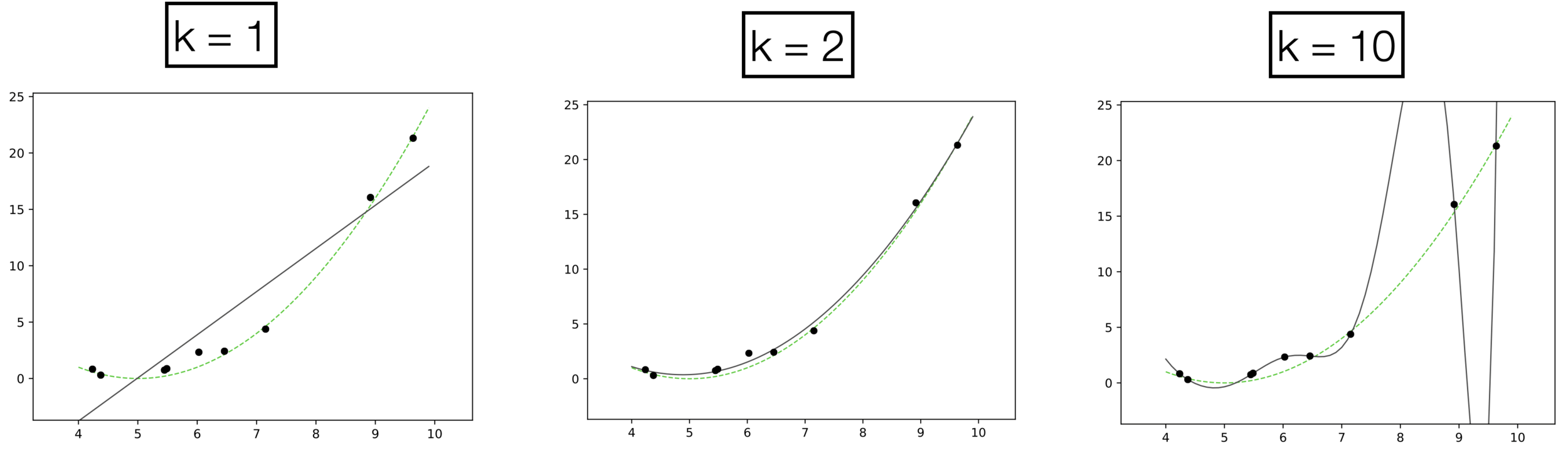
  • Choose \(k = 1\)
  • New features \(\phi=[1; x]\)
  • \( h(x; \textcolor{blue}{\theta}) = \textcolor{blue}{\theta_0} + \textcolor{blue}{\theta_1} \textcolor{gray}{x} \)
  • Learn 2 parameters for linear function
x
y
x
y
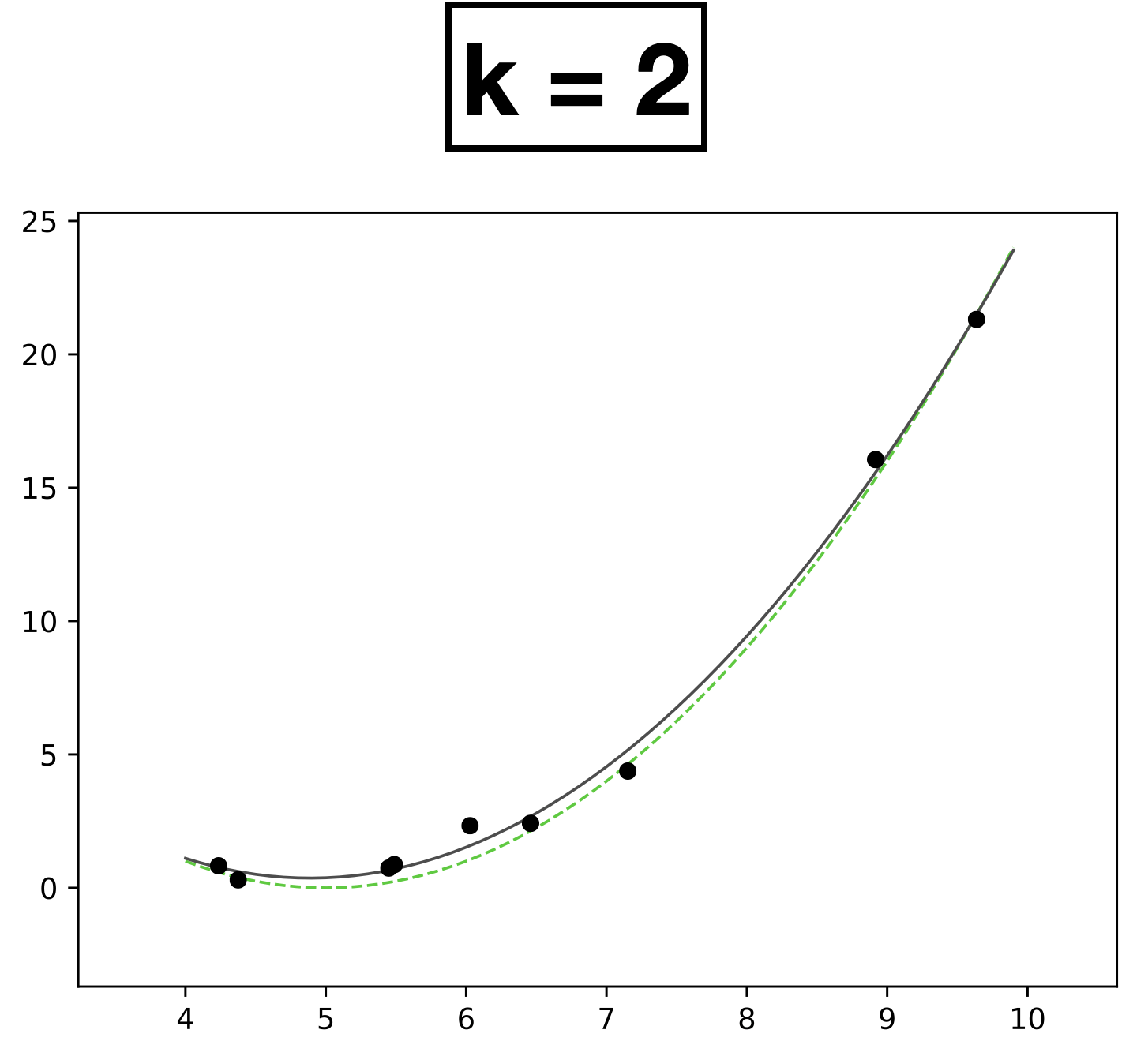
  • Choose \(k = 2\)
  • New features \(\phi=[1; x; x^2]\)
  • \( h(x; \textcolor{blue}{\theta}) = \textcolor{blue}{\theta_0} + \textcolor{blue}{\theta_1} \textcolor{gray}{x} +\textcolor{blue}{\theta_2} \textcolor{gray}{x^2} \)
  • Learn 3 parameters for quadratic function
x
y
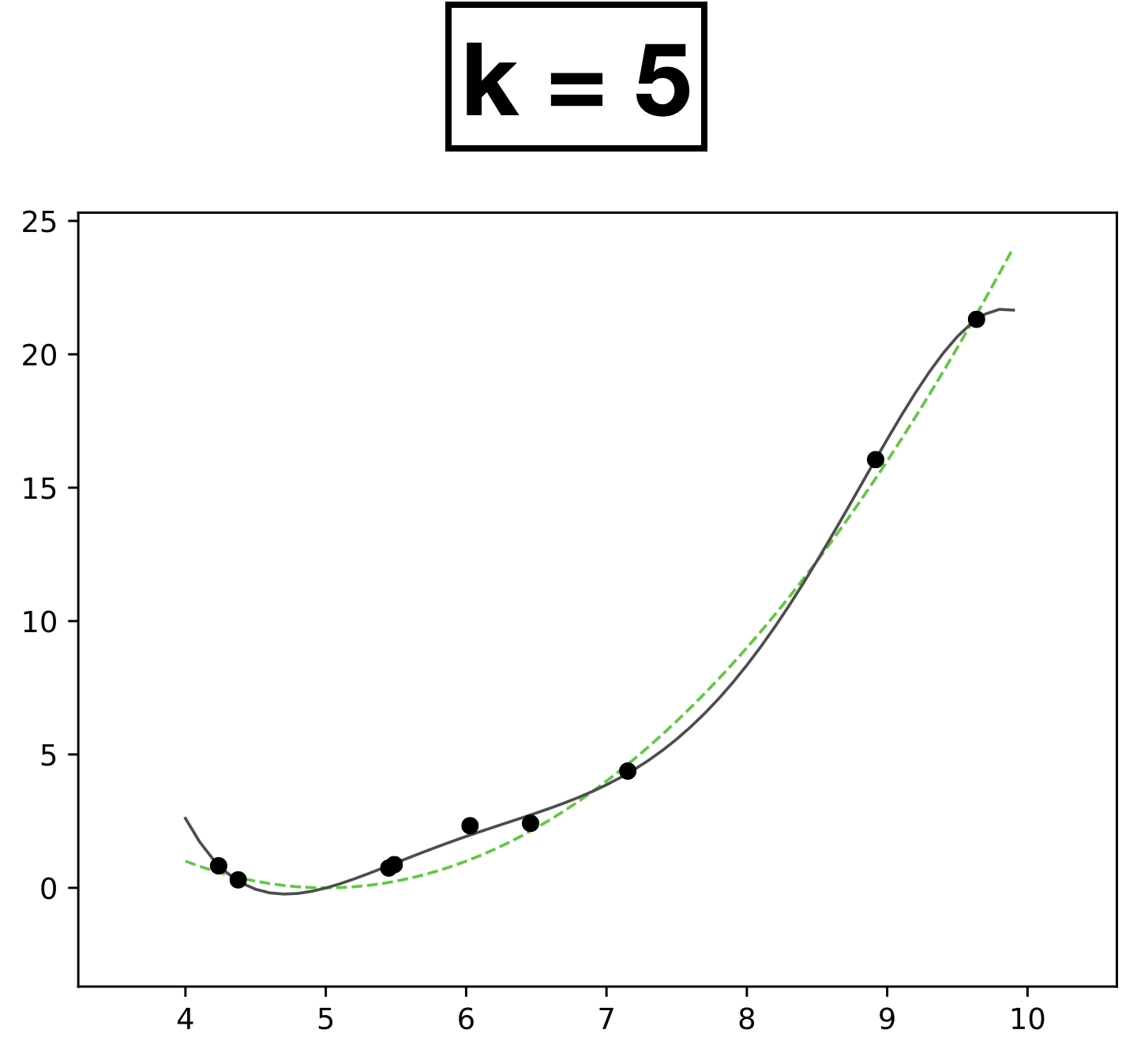
  • Choose \(k = 5\)
  • New features \(\phi=[1; x; x^2;x^3;x^4;x^5]\)
  • \( h(x; \textcolor{blue}{\theta}) = \textcolor{blue}{\theta}_0 + \textcolor{blue}{\theta_1} \textcolor{gray}{x} + \textcolor{blue}{\theta_2} \textcolor{gray}{x^2} + \textcolor{blue}{\theta_3} \textcolor{gray}{x^3} + \textcolor{blue}{\theta_4} \textcolor{gray}{x^4} + \textcolor{blue}{\theta_5} \textcolor{gray}{x^5} \)
  • Learn 6 parameters for degree-5 polynomial function
k=7
k=8
k=10

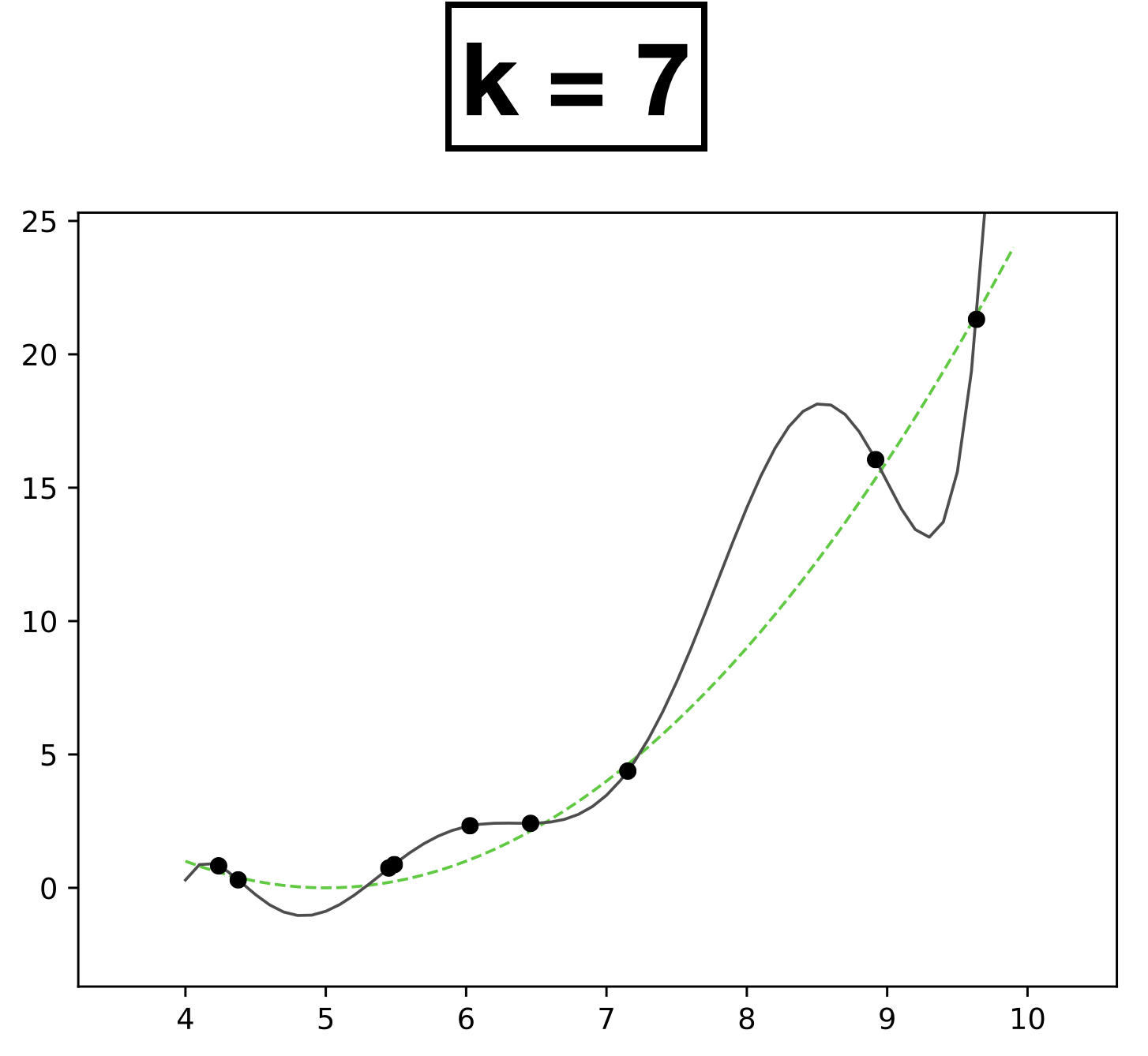
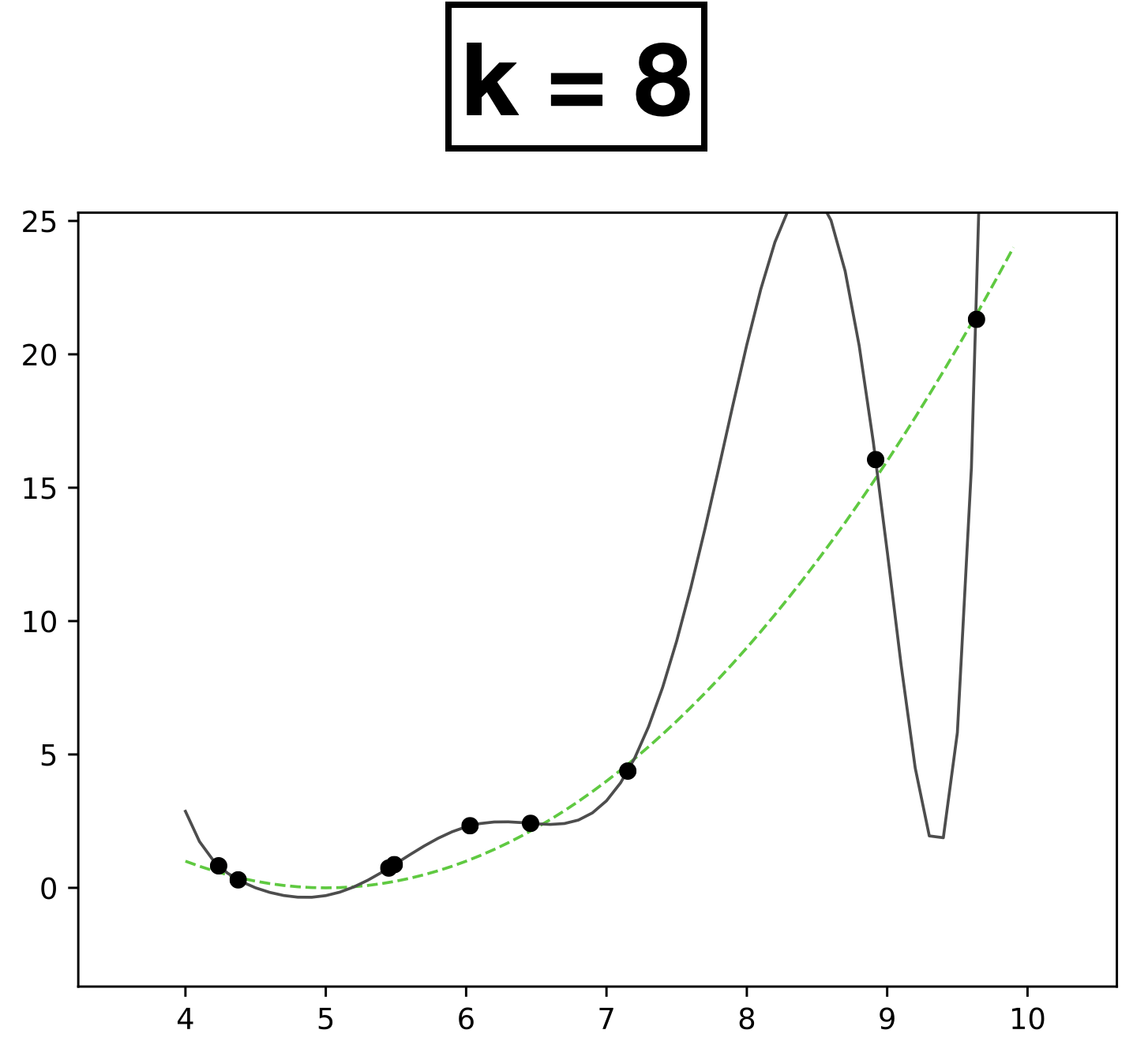
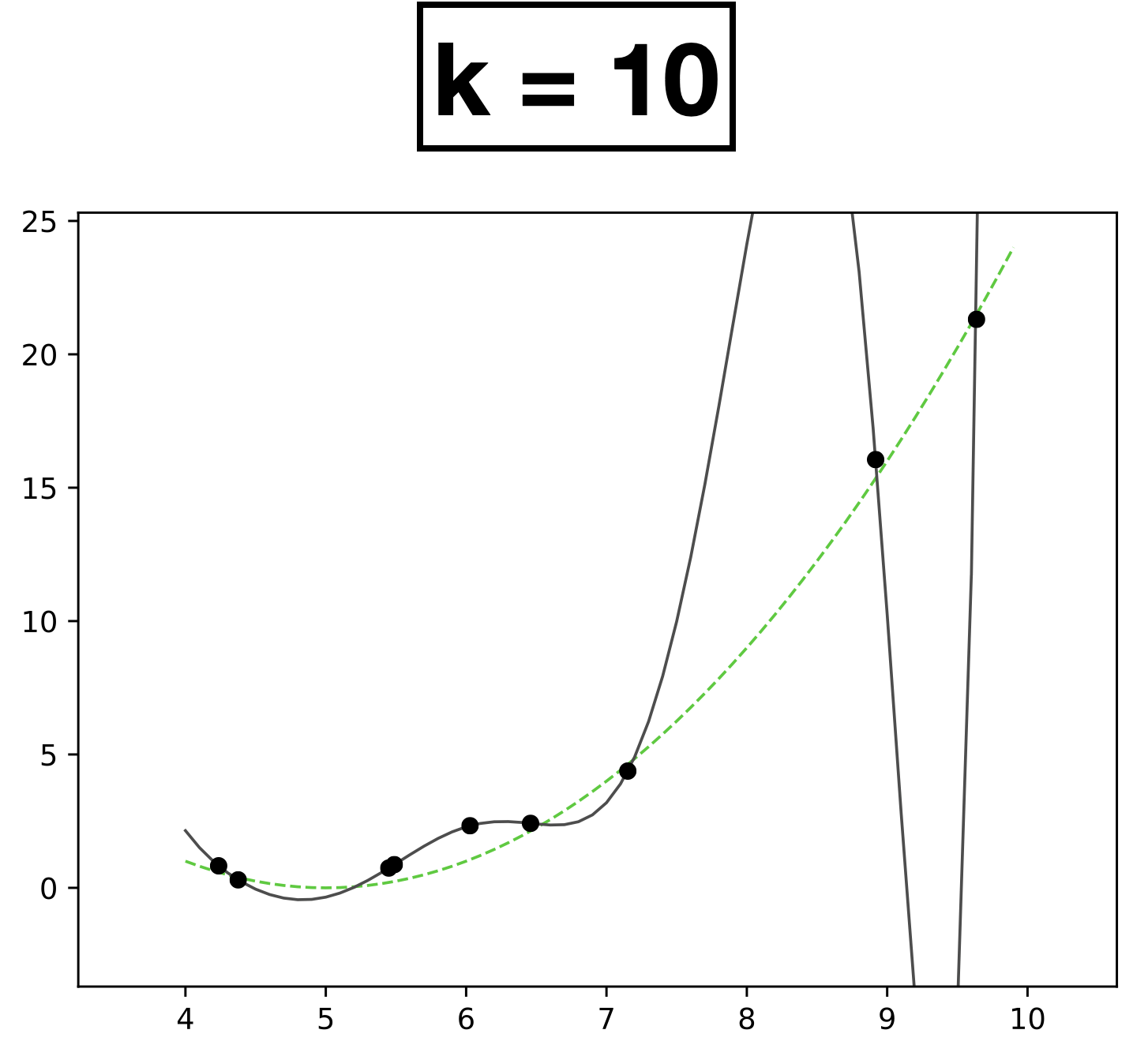
Underfitting

Appropriate model

Overfitting

high error on train set

high error on test set

low error on train set

low error on test set

very low error on train set 

very high error on test set

k=1
k=2
k=10

Underfitting

Appropriate model

Overfitting

  • \(k\) is a hyperparameter that controls the capacity (expressiveness) of the hypothesis class.
  • Complex models with many rich features and free parameters have high capacity.
  • How to choose \(k?\) Validation/cross-validation.
k=1
k=2
k=10

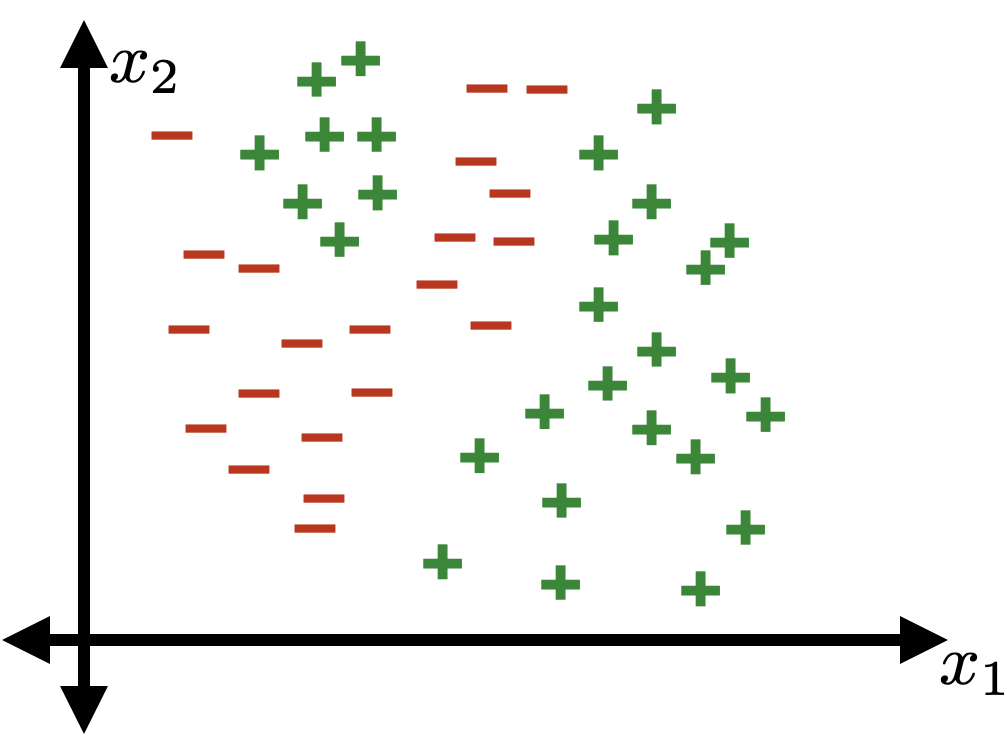
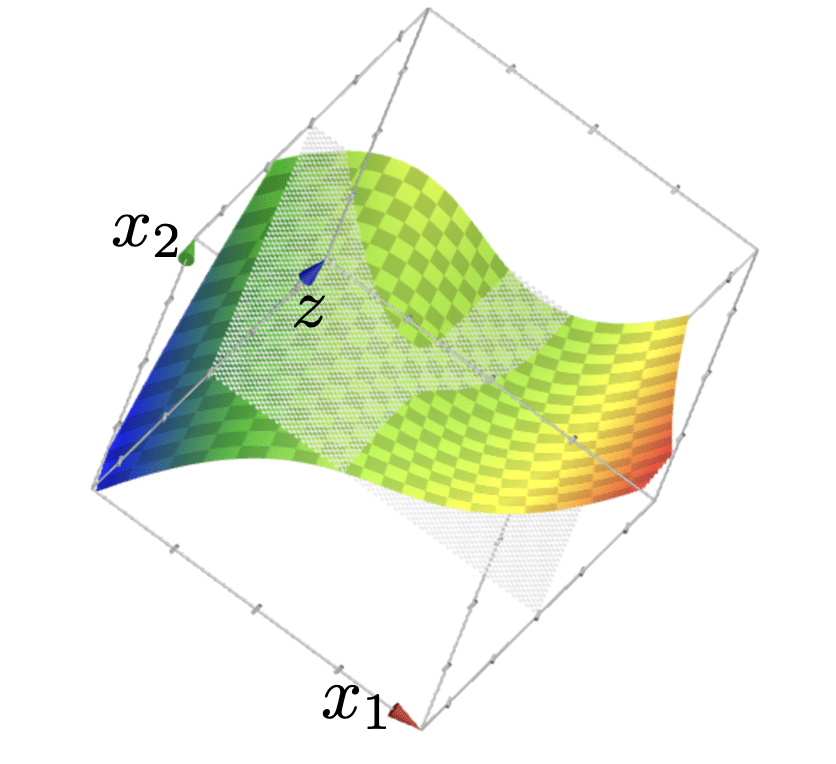
Similar overfitting can happen in classification

Using polynomial features of order 3

Quick summary

  • Linear models are mathematically and algorithmically convenient but not expressive enough -- by themselves -- for most jobs.
  • We can express really rich hypothesis classes by performing a fixed non-linear feature transformation first, then applying our linear regression or classification methods.
  • Can think of fixed transformation as "adapters", enabling us to use old tools in broader situations. 
  • Standard feature transformations: polynomials; radial basis functions, absolute-value function.
  • Historically, for a period of time, the gist of ML boils down to "feature engineering".
  • Nowadays, neural networks can automatically extract out features. 

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer

A more realistic ML analysis

1. Establish a high-level goal, and find good data.

2. Encode data in useful form for the ML algorithm. 

3. Choose a loss, and a regularizer. Write an objective function to optimize.

4. Optimize the objective function & return a hypothesis.

5. Evaluate, validate, interpret, revisit or revise previous steps as needed. 

so far we've focused on 3-4 only.

Encode data in useful form for the ML algorithm.

Identify relevant info and encode as real numbers

Encode in such a way that's reasonable for the task. 

\dots

Example: diagnose whether people have heart disease based on their available info.

x^{(1)}
y^{(1)}
\underbrace{\hspace{.7cm}}

label

\underbrace{\hspace{6cm}}

features

has heart disease? pain? job medicines resting heart rate (bpm) family income (USD)
p1 no no nurse aspirin 55 133000
p2 no no admin beta blockers, aspirin 71 34000
p3 yes yes nurse beta blockers 89 40000
p4 no no doctor none 67 120000
  • go collect training data.
  • ​Turn binary labels to {0,1}, save mapping to recover predictions of new points 
encoding = {"yes": 1, "no": 0}
z
=
has heart disease? pain? job medicines resting heart rate (bpm) family income (USD)
p1 0 no nurse aspirin 55 133000
p2 0 no admin beta blockers, aspirin 71 34000
p3 1 yes nurse beta blockers 89 40000
p4 0 no doctor none 67 120000
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
\sigma(
)
has heart disease? pain? job medicines resting heart rate (bpm) family income (USD)
p1 no no nurse aspirin 55 133000
p2 no no admin beta blockers, aspirin 71 34000
p3 yes yes nurse beta blockers 89 40000
p4 no no doctor none 67 120000
\sigma(
)

risk factor

prob(heart disease)

  • ​Encode binary feature answers to {0,1}, has nice interpretation
pain? job medicines resting heart rate (bpm) family income (USD)
p1 0 nurse aspirin 55 133000
p2 0 admin beta blockers, aspirin 71 34000
p3 1 nurse beta blockers 89 40000
p4 0 doctor none 67 120000 
encoding = {"yes": 1, "no": 0}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}
\theta_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

person feeling pain has 

person not feeling pain has 

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
z =

😍

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer

problem with this idea:

  • Ordering matters
  • Incremental in job category affects \(z\) by a fixed \(\theta_{\text {job }}\)amount

For "jobs", if use natural number encoding:

encoding = {"nurse": 1, "admin": 2, "pharmacist": 3, "doctor": 4, "social worker": 5}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job} \\ \text {} }}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

nurse has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
2\theta_{\substack{\text {job} \\ \text {} }}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

admin has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
3\theta_{\substack{\text {job} \\ \text {} }}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

pharmacist has

🥺

one_hot_encoding = {
  "nurse":         [1, 0, 0, 0, 0], # Φ{job1}
  "admin":         [0, 1, 0, 0, 0], # Φ{job2}
  "pharmacist":    [0, 0, 1, 0, 0], # Φ{job3}
  "doctor":        [0, 0, 0, 1, 0], # Φ{job4}
  "social_worker": [0, 0, 0, 0, 1]} # Φ{job5}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job1} \\ \text {} }}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

nurse has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job2} \\ \text {} }}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

admin has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {job3} \\ \text {} }}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

pharmacist has

😍

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
\theta^T _{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\text {job1}} \phi_{\text {job1}} + \theta_{\text {job2}} \phi_{\text {job2}} + \theta_{\text {job3}} \phi_{\text {job3}} + \theta_{\text {job4}} \phi_{\text {job4}} +\theta_{\text {job5}} \phi_{\text {job5}}
one_hot_encoding = {
  "nurse":         [1, 0, 0, 0, 0], # Φ{job1}
  "admin":         [0, 1, 0, 0, 0], # Φ{job2}
  "pharmacist":    [0, 0, 1, 0, 0], # Φ{job3}
  "doctor":        [0, 0, 0, 1, 0], # Φ{job4}
  "social_worker": [0, 0, 0, 0, 1]} # Φ{job5}

😍

pain? job medicines resting heart rate (bpm) family income (USD)
p1 0 [1,0,0,0,0] aspirin 55 133000
p2 0 [0,1,0,0,0] beta blockers, aspirin 71 34000
p3 1 [1,0,0,0,0] beta blockers 89 40000
p4 0 [0,0,0,1,0] none 67 120000

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer
one_hot_encoding = {
  "aspirin":      [1, 0, 0, 0], #Φ{combo1}
  "aspirin & bb": [0, 1, 0, 0], #Φ{combo2}
  "bb":           [0, 0, 1, 0], #Φ{combo3}
  "none":         [0, 0, 0, 1]} #Φ{combo4}

What about one-hot encoding?

For medicines, hopefully obvious why natural number encoding isn't a good idea. 

the natural "association" in combo1, combo2, and combo3 are lost

also, if a combo is very rare (which happens), say only 1 out of 1k surveyed person took combo2, then very hard to learn a meaningful \(\theta_{\text{combo2}}\)

\theta_{\text {combo1}} \phi_{\text {combo1}} + \theta_{\text {combo2}} \phi_{\text {combo2}} + \theta_{\text {combo3}} \phi_{\text {combo3}} + \theta_{\text {combo4}} \phi_{\text {combo4}}

🥺

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
\theta^T _{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}

😍

factored_encoding = {
  # encode as answer to
  # [taking aspirin?, taking bb?]
  # [Φ{aspirin}, Φ{bb}]
    "aspirin":      [1, 0],
    "aspirin & bb": [1, 1], 
    "bb":           [0, 1], 
    "none":         [0, 0]}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
\theta^T _{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta_{\text {aspirin}} \phi_{\text {aspirin}} + \theta_{\text {beta-blockers}} \phi_{\text {beta-blockers}}
factored_encoding = {
  # encode as answer to
  # [taking aspirin?, taking bb?]
  # [Φ{aspirin}, Φ{bb}]
    "aspirin":      [1, 0],
    "aspirin & bb": [1, 1], 
    "bb":           [0, 1], 
    "none":         [0, 0]}

😍

pain? job medicines resting heart rate (bpm) family income (USD)
p1 0 [1,0,0,0,0] [1,0] 55 133000
p2 0 [0,1,0,0,0] [1,1] 71 34000
p3 1 [1,0,0,0,0] [0,1] 89 40000
p4 0 [0,0,0,1,0] [0,0] 67 120000

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer

🥺

resting heart rate (bpm) family income (USD)
p1 55 133000
p2 71 34000
p3 89 40000
p4 67 120000
30k
31k
32k
33k
34k
2k
1k
0
-1k
-2k
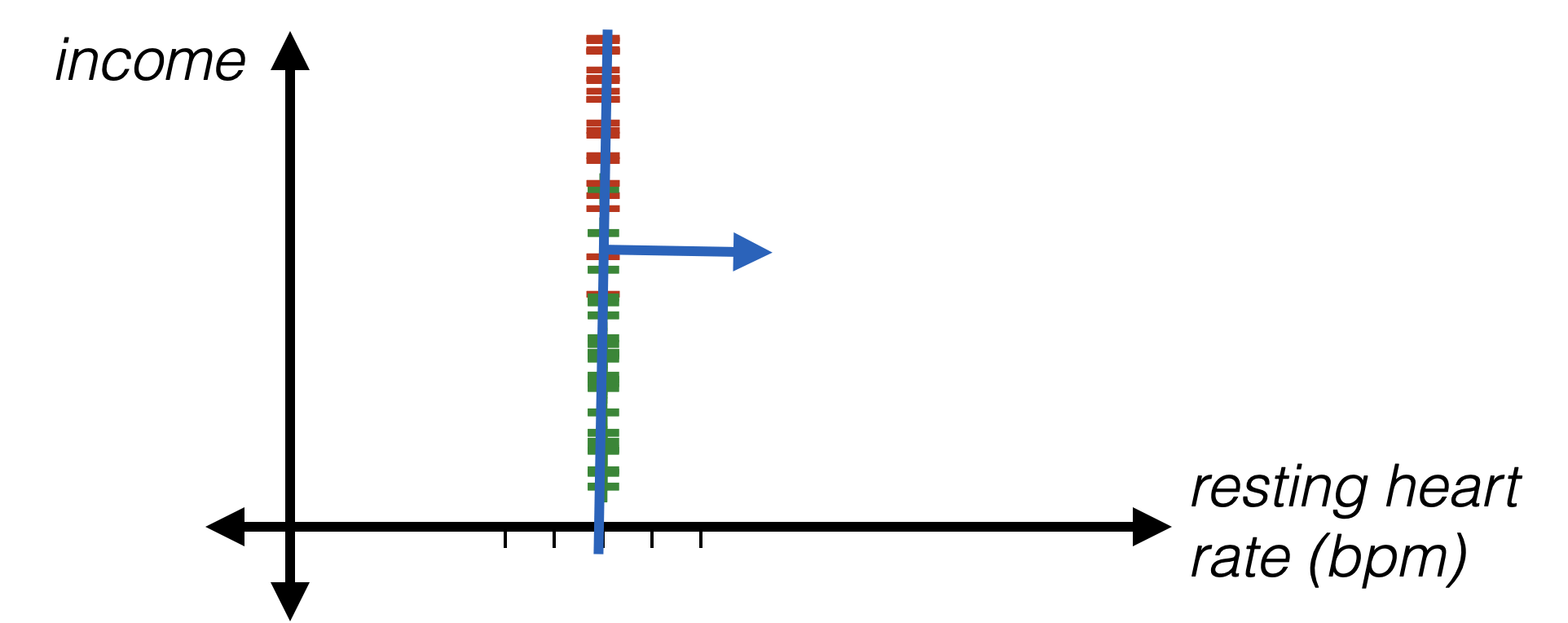
  • Idea: standardize numerical data. For \(i\)th feature and data point \(j\):
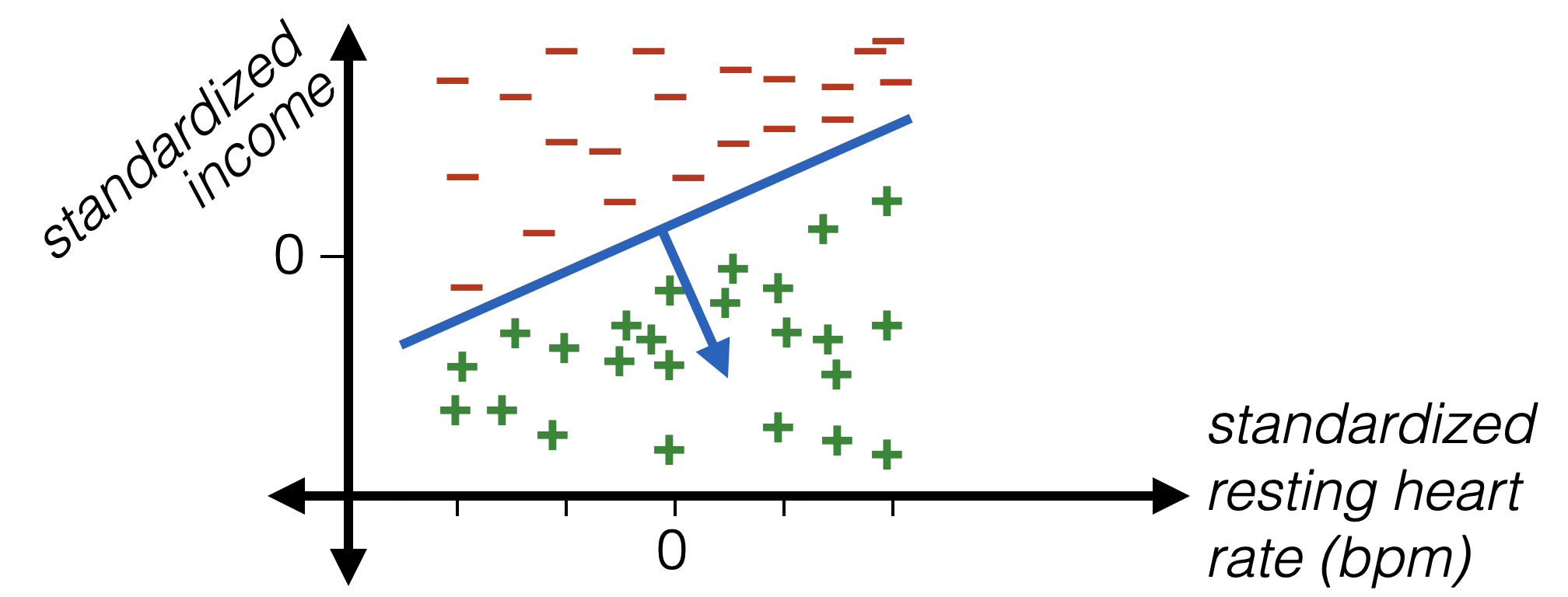
\phi_i^{(j)}=\frac{x_i^{(j)}-\operatorname{mean}_i}{\operatorname{std dev}_i}

may also be easier to visualize and interpret learned parameters if we standardize data.

😍

pain? job medicines resting heart rate (bpm) family income (USD)
p1 0 [1,0,0,0,0] [1,0] -1.5 2.075
p2 0 [0,1,0,0,0] [1,1] 0.1 -0.4
p3 1 [1,0,0,0,0] [0,1] 1.9 -0.25
p4 0 [0,0,0,1,0] [0,0] -0.3 1.75

Outline

  • Recap, linear models and beyond
  • Systematic feature transformations
    • Polynomial features
    • Expressive power
  • Hand-crafting features​​
    • One-hot
    • Factored
    • Standardization/normalization
    • Thermometer
pain? job medicines resting heart rate (bpm) family income (USD) agree exercising helps?
p1 0 [1,0,0,0,0] [1,0] -1.5 2.075 strongly disagree
p2 0 [0,1,0,0,0] [1,1] 0.1 -0.4 disagree
p3 1 [1,0,0,0,0] [0,1] 1.9 -0.25 neutral
p4 0 [0,0,0,1,0] [0,0] -0.3 1.75 agree 

Imagine we added another question in survey: "how much do you agree that exercising could help preventing heart disease?"

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ \theta_{\substack{\text{deg of} \\ \text{agreement}}}x_{\substack{\text{deg of} \\ \text{agreement}}}

problem with this idea (again):

  • Ordering matters
  • Incremental in job category affects \(z\) by a fixed \(\theta_{\substack{\text{deg of} \\ \text{agreement}}}\)amount

For "degree of agreemenet", if use natural number encoding:

encoding = {"strongly agree": 1, "agree": 2, "neutral": 3, "disagree": 4, "strongly disagree": 5}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

🥺

+ \theta_{\substack{\text{deg of} \\ \text{agreement}}}x_{\substack{\text{deg of} \\ \text{agreement}}}

disagreed has

+ 4 \theta_{\substack{\text{deg of} \\ \text{agreement}}}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

neutral has

+ 3 \theta_{\substack{\text{deg of} \\ \text{agreement}}}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

agreed has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ \theta_{\substack{\text{deg of} \\ \text{agreement}}}
\theta_{\text {level1}} \phi_{\text {level1}} + \theta_{\text {level2}} \phi_{\text {level2}} + \theta_{\text {level3}} \phi_{\text {level3}} + \theta_{\text {level4}} \phi_{\text {level4}} +\theta_{\text {level5}} \phi_{\text {level5}}
one_hot_encoding = {
  "strongly disagree":[1, 0, 0, 0, 0], # Φ{level1}
  "disagree":         [0, 1, 0, 0, 0], # Φ{level2}
  "neutral":          [0, 0, 1, 0, 0], # Φ{level3}
  "agree":            [0, 0, 0, 1, 0], # Φ{level4}
  "strongly agree":   [0, 0, 0, 0, 1]} # Φ{level5}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ \theta_{\substack{\text{deg of} \\ \text{agreement}}}x_{\substack{\text{deg of} \\ \text{agreement}}}

disagreed has

+ \theta_{\substack{\text{level2} \\ \text{}}}
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

neutral has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ \theta_{\substack{\text{level3} \\ \text{}}}

agreed has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ \theta_{\substack{\text{level4} \\ \text{}}}

🥺

thermometer_encoding = {
  "strongly disagree":[1, 0, 0, 0, 0], # Φ{level1}
  "disagree":         [1, 1, 0, 0, 0], # Φ{level2}
  "neutral":          [1, 1, 1, 0, 0], # Φ{level3}
  "agree":            [1, 1, 1, 1, 0], # Φ{level4}
  "strongly agree":   [1, 1, 1, 1, 1]} # Φ{level5}

😍

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ \theta_{\substack{\text{deg of} \\ \text{agreement}}}x_{\substack{\text{deg of} \\ \text{agreement}}}
\theta_{\text {level1}} \phi_{\text {level1}} + \theta_{\text {level2}} \phi_{\text {level2}} + \theta_{\text {level3}} \phi_{\text {level3}} + \theta_{\text {level4}} \phi_{\text {level4}} +\theta_{\text {level5}} \phi_{\text {level5}}

disagreed has

+(\theta_{\substack{\text{level1} \\ \text{}}} + \theta_{\substack{\text{level2} \\ \text{}}})
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

neutral has

+ (\theta_{\substack{\text{level1} \\ \text{}}} + \theta_{\substack{\text{level2} \\ \text{}}} + \theta_{\substack{\text{level3} \\ \text{}}})
\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =

agreed has

\theta_{\substack{\text { heart } \\ \text { rate } }}x_{\substack{\text { heart } \\ \text { rate }}}
\theta_{\substack{\text {pain} \\ \text {} }}x_{\substack{\text {pain } \\ \text {}}}
\theta^T_{\substack{\text {job} \\ \text {} }}x_{\substack{\text {job} \\ \text {}}}
\theta^T_{\substack{\text {pill} \\ \text {} }}x_{\substack{\text {pill} \\ \text {}}}
\theta_{\substack{\text {income} \\ \text {} }}x_{\substack{\text {income} \\ \text {}}}
+
+
+
+
z =
+ (\theta_{\substack{\text{level1} \\ \text{}}} +\theta_{\substack{\text{level2} \\ \text{}}} + \theta_{\substack{\text{level3} \\ \text{}}} + \theta_{\substack{\text{level4} \\ \text{}}})

Summary

  • Linear models are mathematically and algorithmically convenient but not expressive enough -- by themselves -- for most jobs.
  • We can express really rich hypothesis classes by performing a fixed non-linear feature transformation first, then applying our linear (regression or classification) methods.
  • When we “set up” a problem to apply ML methods to it, it’s important to encode the inputs in a way that makes it easier for the ML method to exploit the structure.
  • Foreshadowing of neural networks, in which we will learn complicated continuous feature transformations.

Thanks!

We'd love to hear your thoughts.

6.390 IntroML (Fall24) - Lecture 5 Features

By Shen Shen

6.390 IntroML (Fall24) - Lecture 5 Features

  • 37

More from Shen Shen

  • 6.390 IntroML (Fall24) - Lecture 11 Markov Decision Processes
    Shen Shen
    15
  • 6.390 IntroML (Fall24) - Lecture 10 Clustering
    Shen Shen
    26
  • 6.390 IntroML (Fall24) - Lecture 9 Transformers
    Shen Shen
    38
  • 6.390 IntroML (Fall24) - Lecture 8 Convolutional Neural Networks
    Shen Shen
    26