Lecture 9: Transformers
Shen Shen
November 1, 2024
Intro to Machine Learning
Outline
- Recap, convolutional neural networks
- Transformers example use case: large language models
- Transformers key ideas:
- Input, and (query, key, value) embedding
- Attention mechanism
- (Applications and case studies)
[video credit Lena Voita]
- Looking locally
- Parameter sharing
- Template matching
- Translational equivariance
Recap: convolution
Enduring principles:
- Chop up signal into patches (divide and conquer)
- Process each patch independently and identically (and in parallel)
[image credit: Fredo Durand]
Transformers follow similar principles:
1. Chop up signal into patches (divide and conquer)
2. Process each patch identically, and in parallel
Enduring principles:
- Chop up signal into patches (divide and conquer)
- Process each patch independently, identically, and in parallel
but not independently; each patch's processing depends on all other patches, allowing us to take into account the full context.
Outline
- Recap, convolutional neural networks
- Transformers example use case: large language models
- Transformers key ideas:
- Input, and (query, key, value) embedding
- Attention mechanism
- (Applications and case studies)
Large Language Models (LLMs) are trained in a self-supervised way
- Scrape the internet for unlabeled plain texts.
- Cook up “labels” (prediction targets) from the unlabeled texts.
- Convert “unsupervised” problem into “supervised” setup.
"To date, the cleverest thinker of all time was Issac. "
feature
label
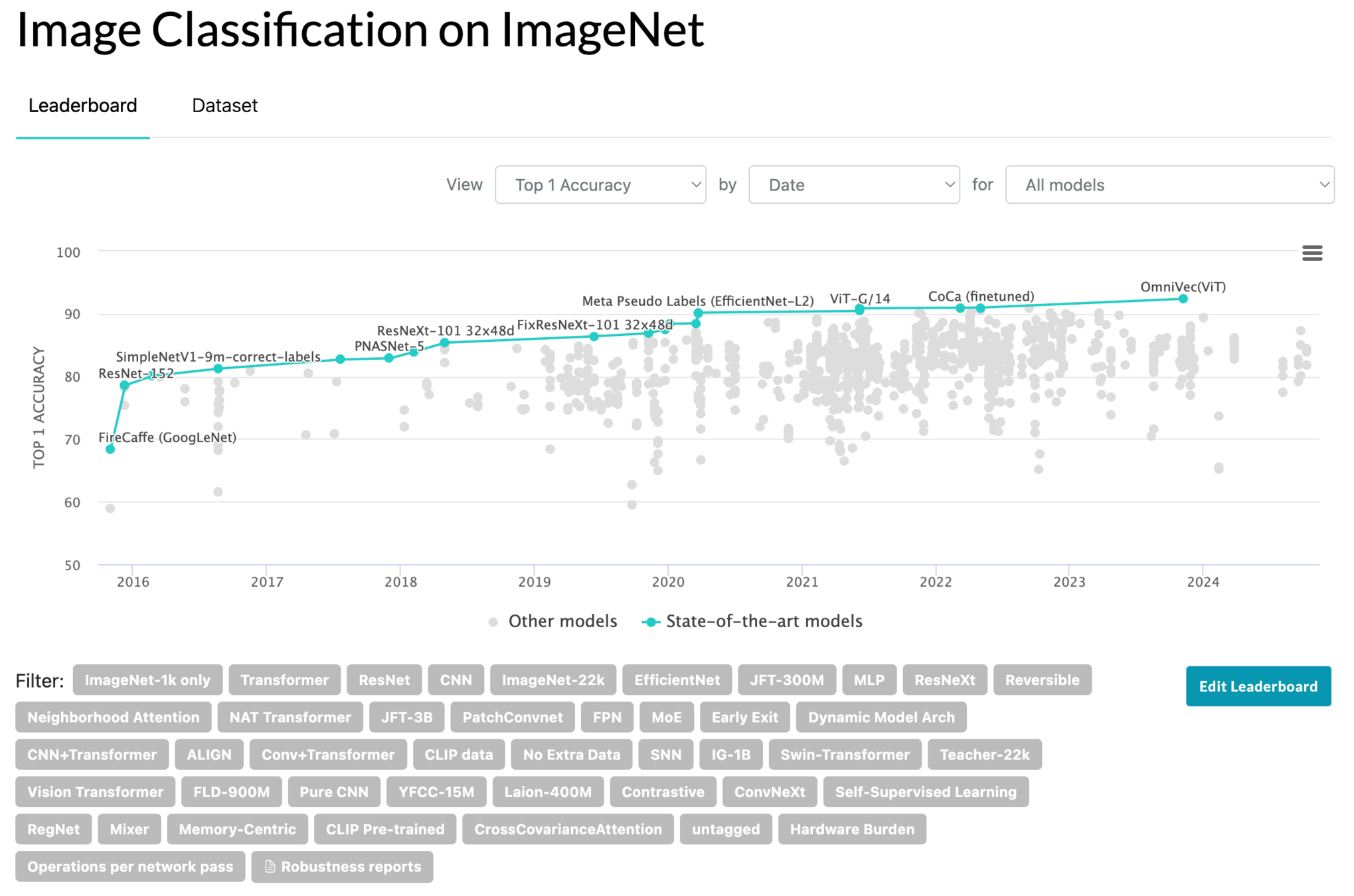
To date, the
cleverest
\dots
To date, the cleverest
thinker
To date, the cleverest thinker
was
\dots
\dots
\dots
To date, the cleverest thinker of all time was
Issac
e.g., train to predict the next-word
Auto-regressive
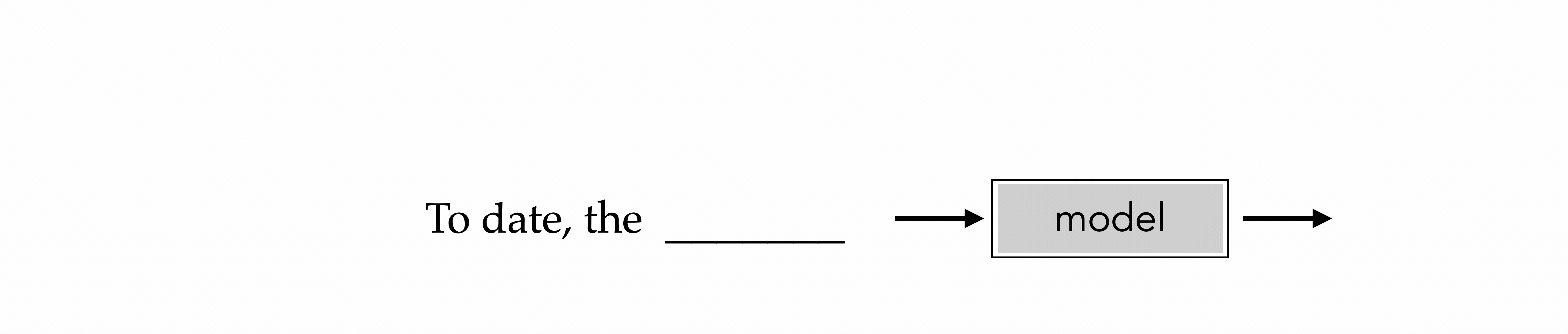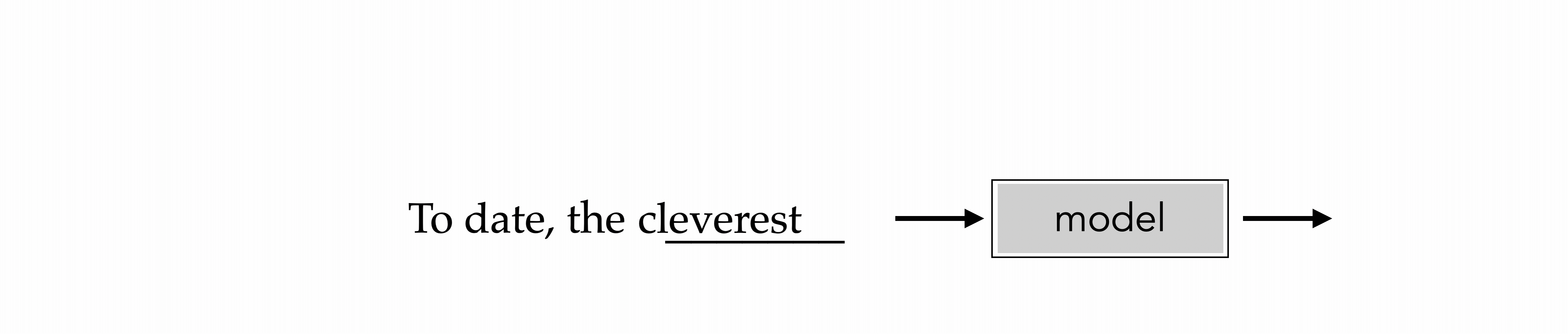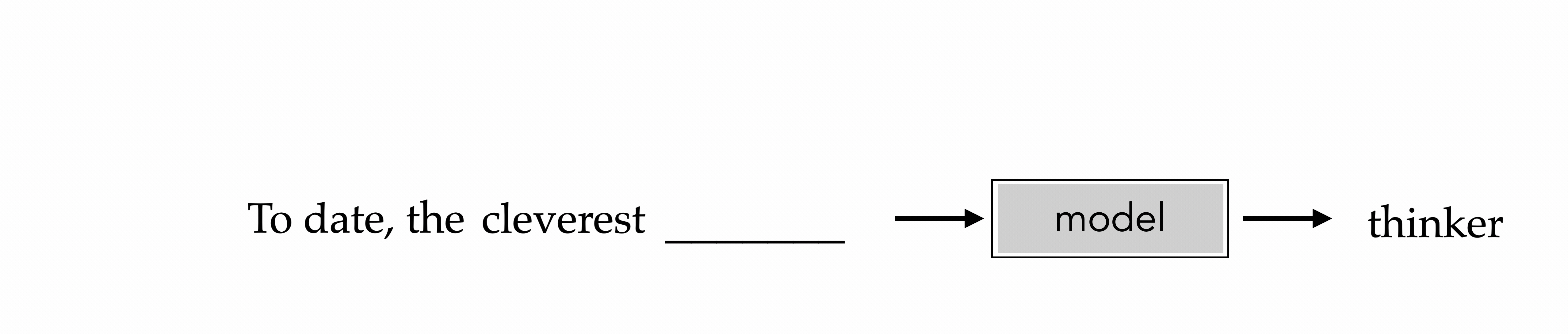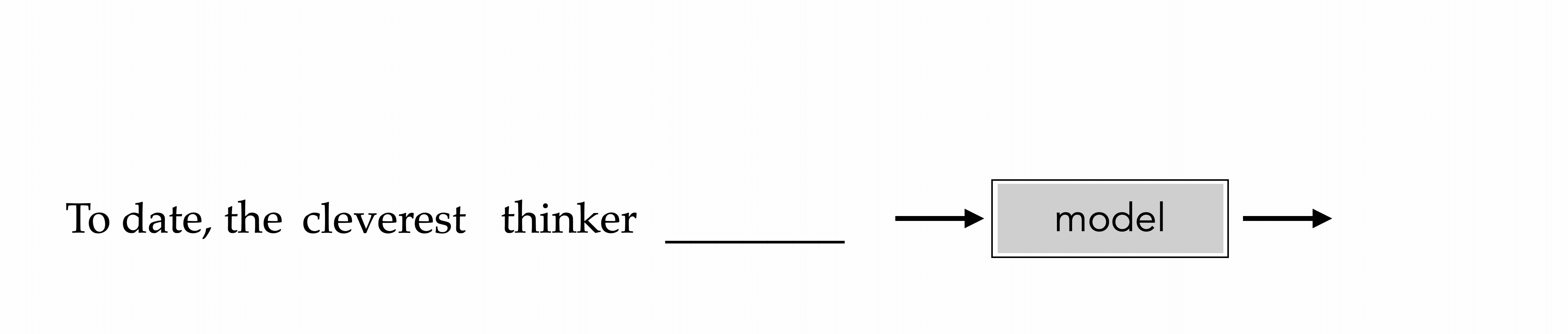
For LLMs (and many other applications), the model used are transformers
[video edited from 3b1b]
[image edited from 3b1b]
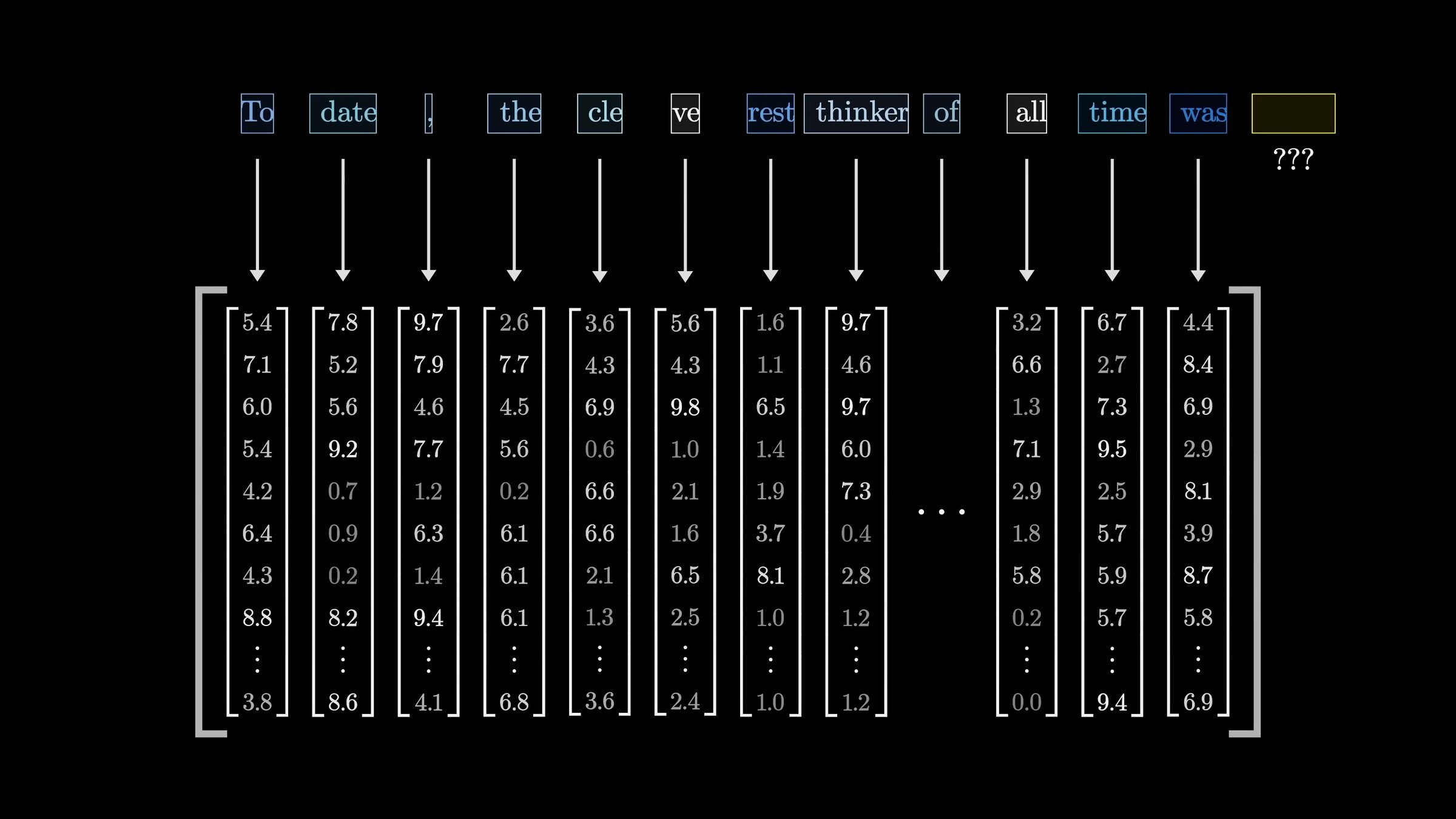
\(n\)
\underbrace{\hspace{5.98cm}}
\left\{
\begin{array}{l}
\\
\\
\\
\\
\\
\\
\\
\end{array}
\right.
\(d\)
input embedding (e.g. via a fixed encoder)
[video edited from 3b1b]
[video edited from 3b1b]
[image edited from 3b1b]
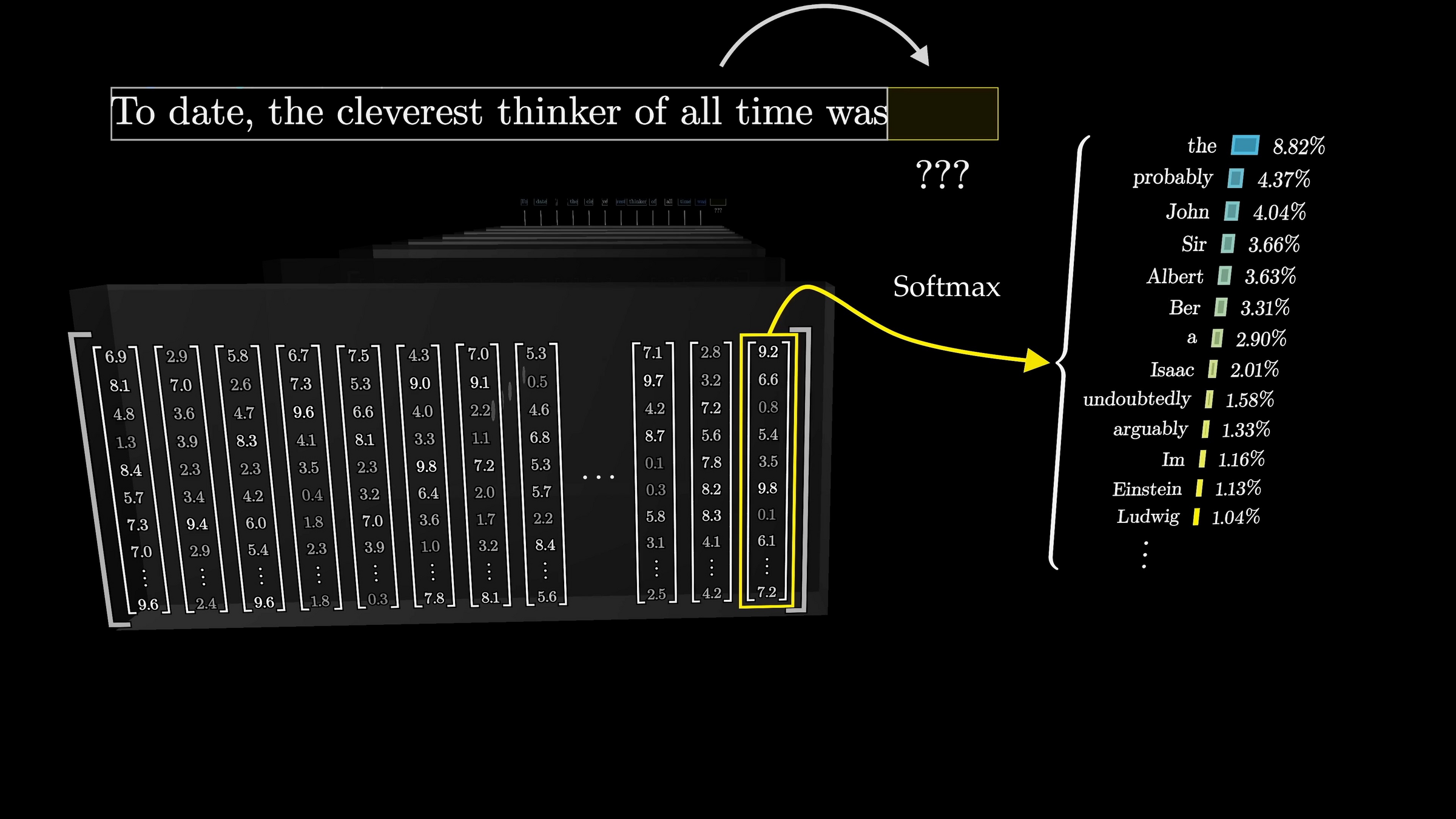
Cross-entropy loss encourages the internal weights update so as to make this probability higher
Outline
- Recap, convolutional neural networks
- Transformers example use case: large language models
-
Transformers key ideas:
- Input, and (query, key, value) embedding
- Attention mechanism
- (Applications and case studies)
a
robot
must
obey
\left\{
\begin{array}{l}
\\
\\
\\
\end{array}
\right.
distribution over the vocabulary
Transformer
"A robot must obey the orders given it by human beings ..."
push for Prob("robot") to be high
push for Prob("must") to be high
push for Prob("obey") to be high
push for Prob("the") to be high
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
a
robot
must
obey
input embedding
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
transformer block
\left\{
\begin{array}{l}
\\
\\
\\
\\
\end{array}
\right.
\(L\) blocks
[video edited from 3b1b]
embedding
a
robot
must
obey
input embedding
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
transformer block
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
A sequence of \(n\) tokens, each token in \(\mathbb{R}^{d}\)
a
robot
must
obey
input embedding
\(\dots\)
transformer block
transformer block
transformer block
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
a
robot
must
obey
input embedding
output embedding
transformer block
\(\dots\)
\(\dots\)
\(\dots\)
attention layer
fully-connected network
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
\(\dots\)
[video edited from 3b1b]
[video edited from 3b1b]
a
robot
must
obey
input embedding
output embedding
transformer block
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
attention layer
fully-connected network
x^{(1)}
x^{(2)}
x^{(3)}
W_k
W_v
W_q
the usual weights
x^{(4)}
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention layer
attention mechanism
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
- sequence of \(d\)-dimensional input tokens \(x\)
- learnable weights, \(W_q, W_v, W_k\), all in \(\mathbb{R}^{d \times d_k}\)
- map the input sequence into \(d_k\)-dimensional (\(qkv\)) sequence, e.g., \(q_1 = W_q^Tx^{(1)}\)
- the weights are shared, across the sequence of tokens -- parallel processing
\((q,k,v)\)
embedding
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_4
q_4
k_4
v_4
v_4
v_4
input
embedding
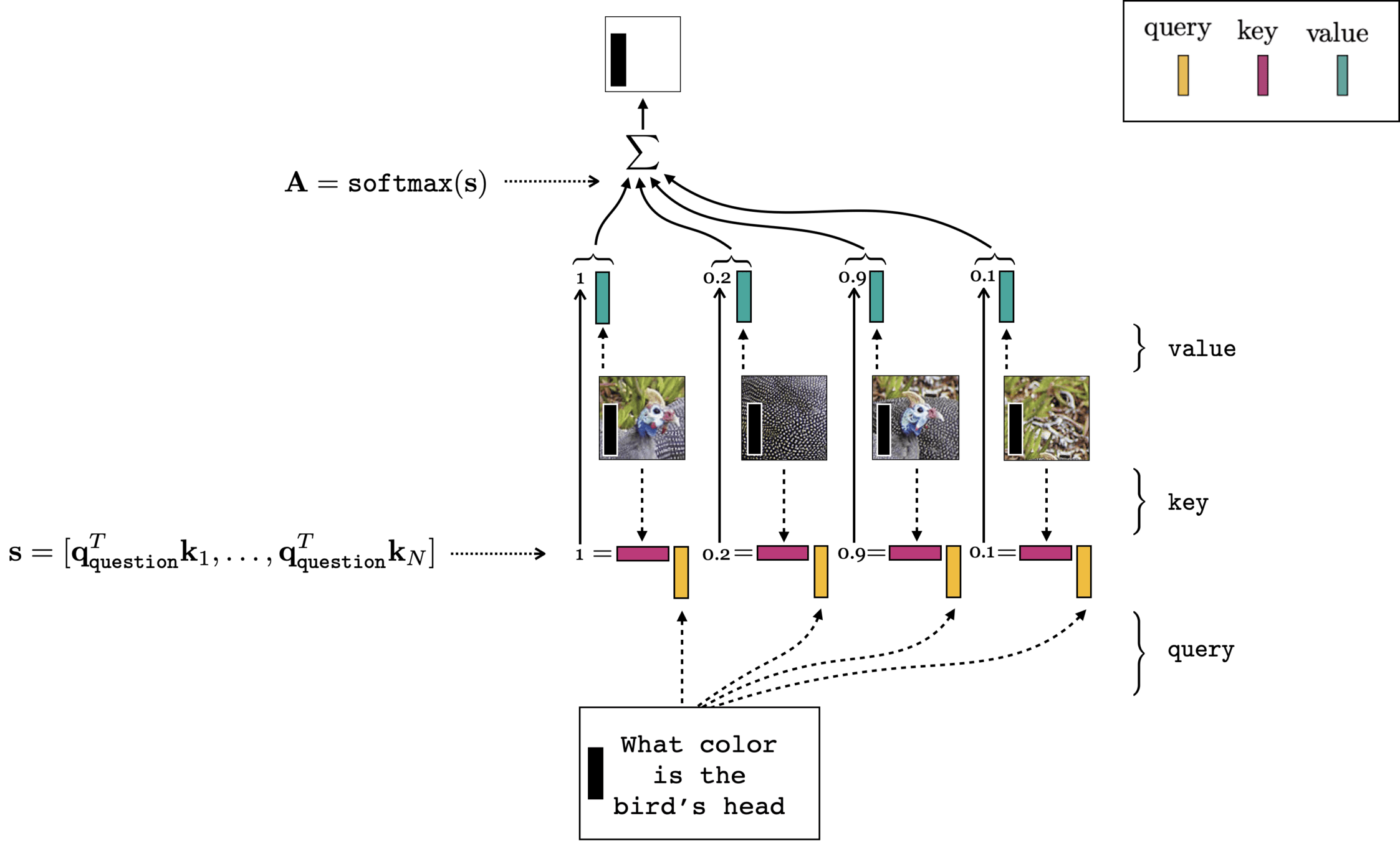
Let's think about dictionary look-up:
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}Having good (query, key, value) embedding enables effective attention.
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "lemon"
output = dict_en2fr[query]apple
pomme
banane
citron
banana
lemon
Key
Value
lemon
\(:\)
\(:\)
\(:\)
Query
Output
citron
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]What if we run
Python would complain. 🤯
orange
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
Query
Output
???
What if we run
But we can probably see the rationale behind this:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
We implicitly assumed the (query, key, value) are represented in 'good' embeddings.
If we are to generalize this idea, we need to:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
get this sort of percentage
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.1
pomme
0.1
banane
0.8
citron
+
+
apple
banana
lemon
orange
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
apple
banana
lemon
orange
,
,
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
dot-product similarity
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
dot-product similarity
[video edited from 3b1b]
dot-product similarity
apple
banana
lemon
orange
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
pomme
banane
citron
+
+
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
0.1
0.1
0.8
=[\quad \quad \quad ]
apple
banana
lemon
orange
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.8
pomme
0.1
banane
0.1
citron
+
+
=[\quad \quad \quad ]
0.1
0.1
0.8
pomme
banane
citron
+
+
and output
weighted average over values
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
???
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
q_1
q_1
q_1
q_1
k_1
k_2
k_3
k_4
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
???
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
q_1
q_1
q_1
q_1
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
a_{11}
a_{14}
a_{12}
a_{13}
v_4
v_2
v_3
v_1
a_{11}
a_{14}
a_{12}
a_{13}
=
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
must
obey
a
robot
???
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
q_1
q_1
q_1
q_1
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
=
v_4
v_2
v_3
v_1
+
+
+
=
a_{11}
a_{14}
a_{12}
a_{13}
a_{11}
a_{14}
a_{12}
a_{13}
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
???
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
q_2
q_2
q_2
q_2
k_1
k_2
k_3
k_4
...
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
=
a_{21}
a_{24}
a_{22}
a_{23}
q_2
q_2
q_2
q_2
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
v_4
v_2
v_3
v_1
a_{21}
a_{24}
a_{22}
a_{23}
???
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
=
=
a_{21}
a_{24}
a_{22}
a_{23}
q_2
q_2
q_2
q_2
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
v_4
v_2
v_3
v_1
+
+
+
a_{21}
a_{24}
a_{22}
a_{23}
???
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
q_3
q_3
q_3
q_3
k_1
k_2
k_3
k_4
...
???
...
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
=
a_{31}
a_{34}
a_{32}
a_{3 3}
q_3
q_3
q_3
q_3
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
v_4
v_2
v_3
v_1
a_{31}
a_{34}
a_{32}
a_{33}
???
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
=
=
a_{31}
a_{34}
a_{32}
a_{3 3}
q_3
q_3
q_3
q_3
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
v_4
v_2
v_3
v_1
+
+
+
a_{31}
a_{34}
a_{32}
a_{33}
???
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
q_4
q_4
q_4
q_4
k_1
k_2
k_3
k_4
...
???
...
...
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
=
a_{41}
a_{44}
a_{42}
a_{43}
q_4
q_4
q_4
q_4
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
???
v_1
v_2
v_3
v_4
a_{41}
a_{42}
a_{43}
a_{44}
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
d_k
=
a_{41}
a_{44}
a_{42}
a_{43}
q_4
q_4
q_4
q_4
k_1
k_2
k_3
k_4
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
,
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
/\sqrt{d_k}
???
=
v_2
v_3
v_1
v_4
+
+
+
a_{41}
a_{44}
a_{42}
a_{43}
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
q_4
q_1
q_2
q_3
Q =
k_2
k_1
= K
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
q_4
q_1
q_2
q_3
Q =
k_2
k_1
= K
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
(q_1)^Tk_1
q_1
Q =
k_2
k_1
= K
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
(q_1)^Tk_3
q_4
q_2
q_3
q_1
q_2
Q =
k_2
k_1
= K
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
(q_2)^Tk_1
q_4
q_3
q_4
q_2
q_3
Q =
k_2
k_1
= K
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
(q_3)^Tk_4
q_4
q_2
q_1
q_4
q_1
Q =
k_2
k_1
= K
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
(q_4)^Tk_2
q_1
q_2
q_3
q_4
q_1
q_2
q_3
Q =
k_2
k_1
= K
A =
\Bigg[
\begin{array}{l}
\end{array}
\Bigg.
\Bigg]
\begin{array}{l}
\end{array}
\Bigg.
a_{41}
a_{42}
a_{43}
a_{44}
=
a_{31}
a_{34}
a_{32}
a_{3 3}
a_{21}
a_{24}
a_{22}
a_{23}
a_{11}
a_{14}
a_{12}
a_{13}
k_3
k_4
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times d_k}
\mathbb{R}^{n \times n}
each row sums up to 1
(
)
softmax
/\sqrt{d_k}
(
)
softmax
/\sqrt{d_k}
(
)
softmax
/\sqrt{d_k}
(
)
softmax
/\sqrt{d_k}
attention matrix
v_4
v_4
q_1
a_{41}
a_{42}
a_{43}
a_{44}
a_{31}
a_{34}
a_{32}
a_{3 3}
a_{21}
a_{24}
a_{22}
a_{23}
a_{11}
a_{14}
a_{12}
a_{13}
q_1
q_2
q_3
v_4
q_4
k_4
v_4
v_1
k_1
v_2
k_2
v_3
k_3
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
+
+
+
a_{11}
a_{14}
a_{12}
a_{13}
a_{41}
a_{42}
a_{43}
a_{44}
a_{31}
a_{34}
a_{32}
a_{3 3}
a_{21}
a_{24}
a_{22}
a_{23}
a_{11}
a_{14}
a_{12}
a_{13}
=
v_4
v_2
v_3
v_1
v_4
v_4
q_1
q_1
q_2
q_3
v_4
q_4
k_4
v_4
v_1
k_1
v_2
k_2
v_3
k_3
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
\in \mathbb{R}^{d_k}
v_4
v_4
q_1
=
a_{41}
a_{42}
a_{43}
a_{44}
a_{31}
a_{34}
a_{32}
a_{3 3}
a_{21}
a_{24}
a_{22}
a_{23}
a_{11}
a_{14}
a_{12}
a_{13}
+
+
+
a_{21}
a_{24}
a_{22}
a_{23}
v_1
q_1
k_1
v_2
q_2
k_2
v_3
q_3
k_3
v_4
q_4
k_4
v_4
v_4
v_2
v_3
v_1
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
\in \mathbb{R}^{d_k}
v_4
v_4
q_1
=
a_{41}
a_{42}
a_{43}
a_{44}
a_{31}
a_{34}
a_{32}
a_{3 3}
a_{21}
a_{24}
a_{22}
a_{23}
a_{11}
a_{14}
a_{12}
a_{13}
+
+
+
a_{31}
a_{34}
a_{32}
a_{33}
v_1
q_1
k_1
v_2
q_2
k_2
v_3
q_3
k_3
v_4
q_4
k_4
v_4
v_4
v_2
v_3
v_1
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
\in \mathbb{R}^{d_k}
v_4
v_4
q_1
=
a_{41}
a_{42}
a_{43}
a_{44}
a_{31}
a_{34}
a_{32}
a_{3 3}
a_{21}
a_{24}
a_{22}
a_{23}
a_{11}
a_{14}
a_{12}
a_{13}
+
+
+
a_{41}
a_{44}
a_{42}
a_{43}
v_1
q_1
k_1
v_2
q_2
k_2
v_3
q_3
k_3
v_4
q_4
k_4
v_4
v_4
v_2
v_3
v_1
attention mechanism
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
\in \mathbb{R}^{d_k}
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
one attention head
attention mechanism
attention layer
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
\dots
multi-headed attention layer
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
each head
- can be processed in parallel to all other heads
- learns its own independent \(W_q, W_k, W_v\)
- creates its own \((q,k,v)\) sequence
- inside each head, the sequence of \(n\) \((q,k,v)\) tokens can be processed in parallel
- computes its own attention output sequence
- inside each head, the sequence of \(n\) output tokens can be processed in parallel
we then learn yet another weight \(W_h\) to sum up the outputs from individual head, to be the multi-headed attention layer output.
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
\dots
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
multi-headed attention layer
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
a
robot
must
obey
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
\dots
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
v_1
k_1
q_1
W_k
W_v
W_q
W_k
W_v
W_q
v_2
k_2
q_2
W_k
W_v
W_q
W_k
W_v
W_q
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
attention mechanism
multi-headed attention layer
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
W_h
all in \(\mathbb{R}^{d}\)
Some other ideas commonly used in practice:
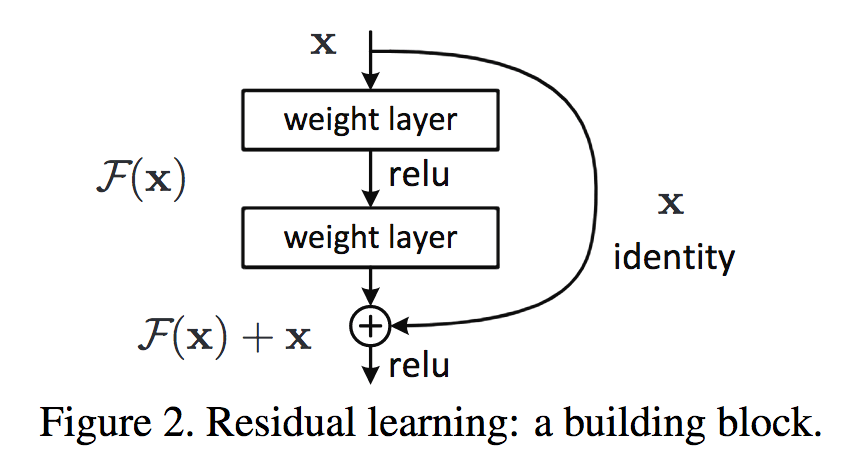
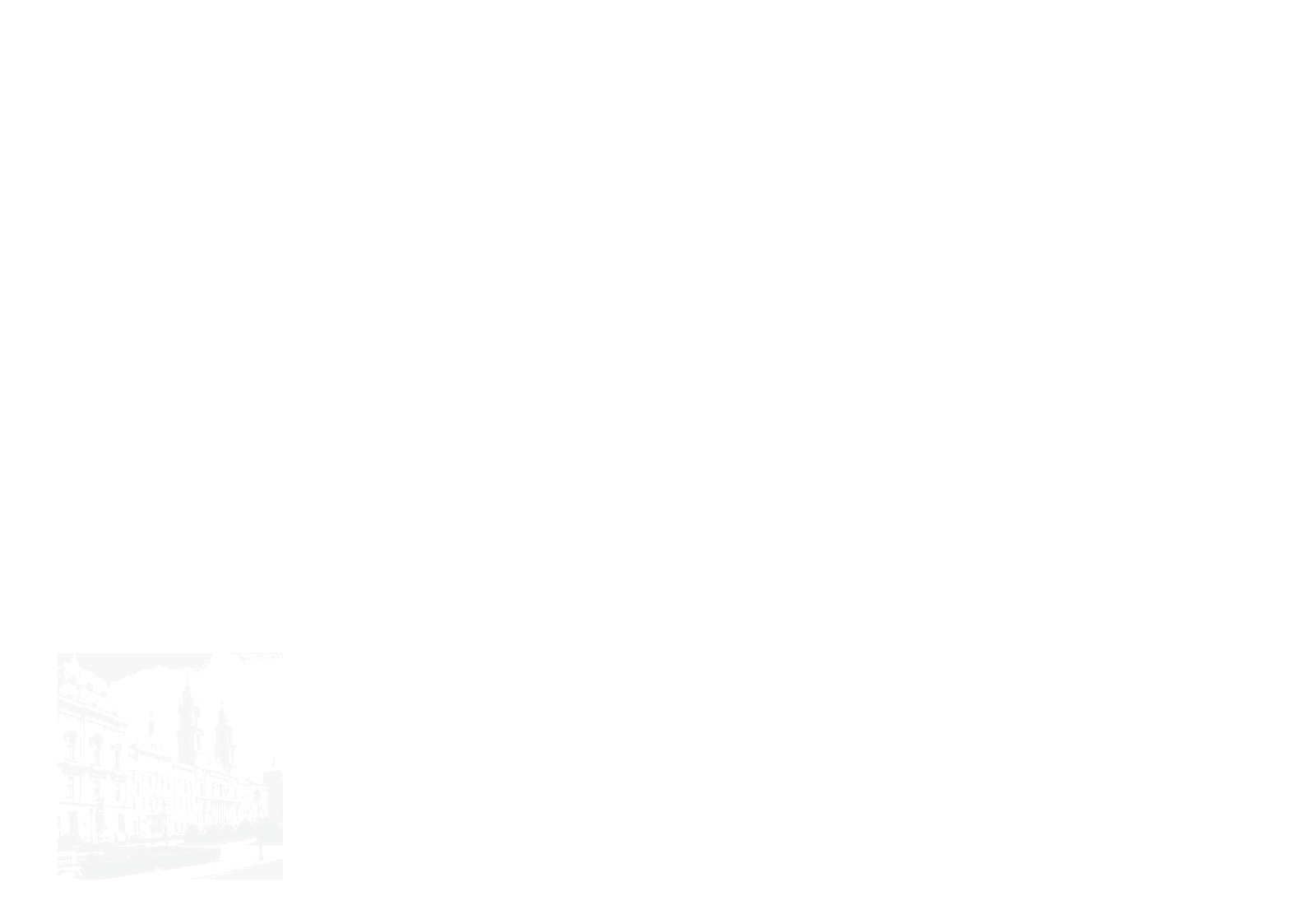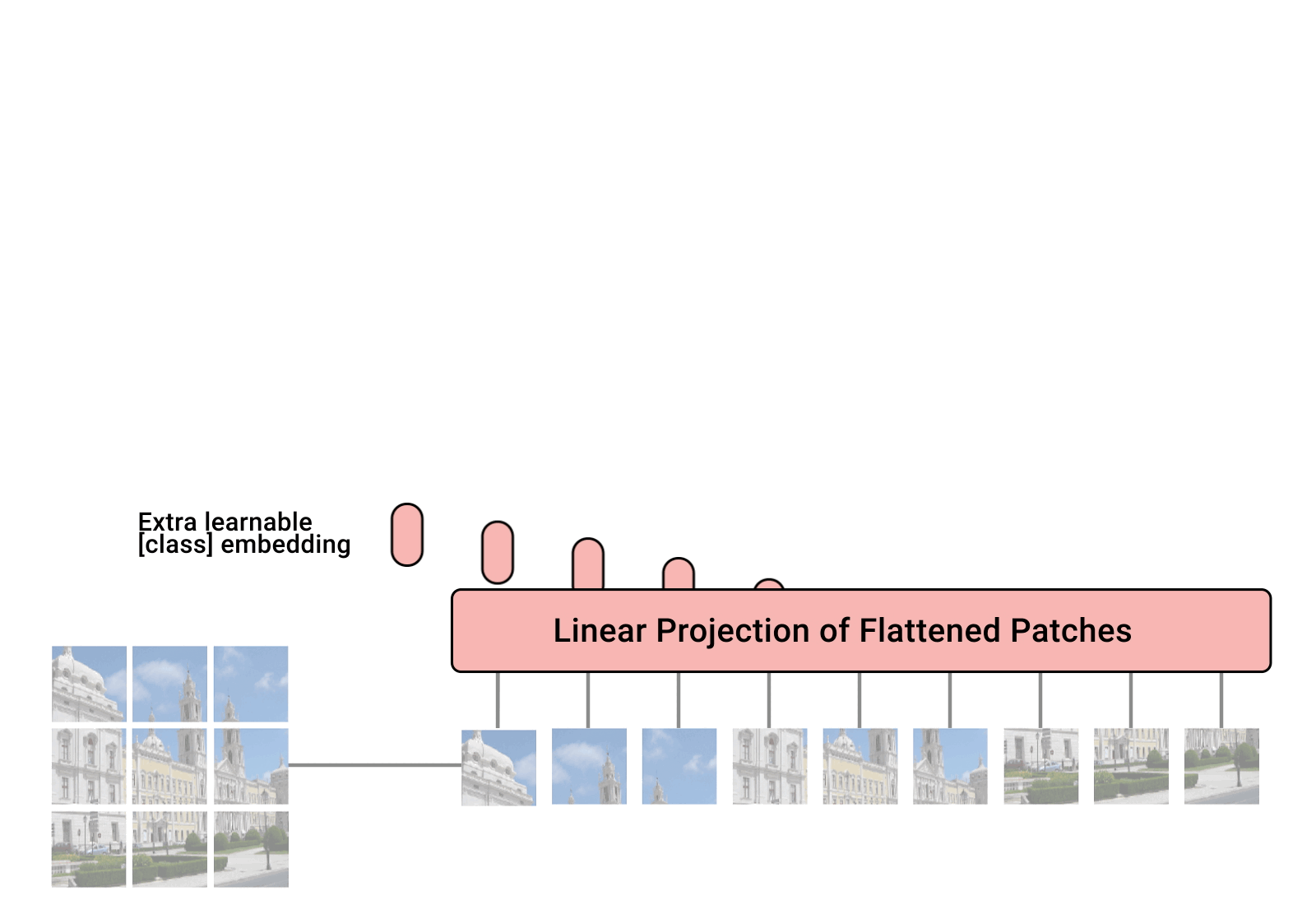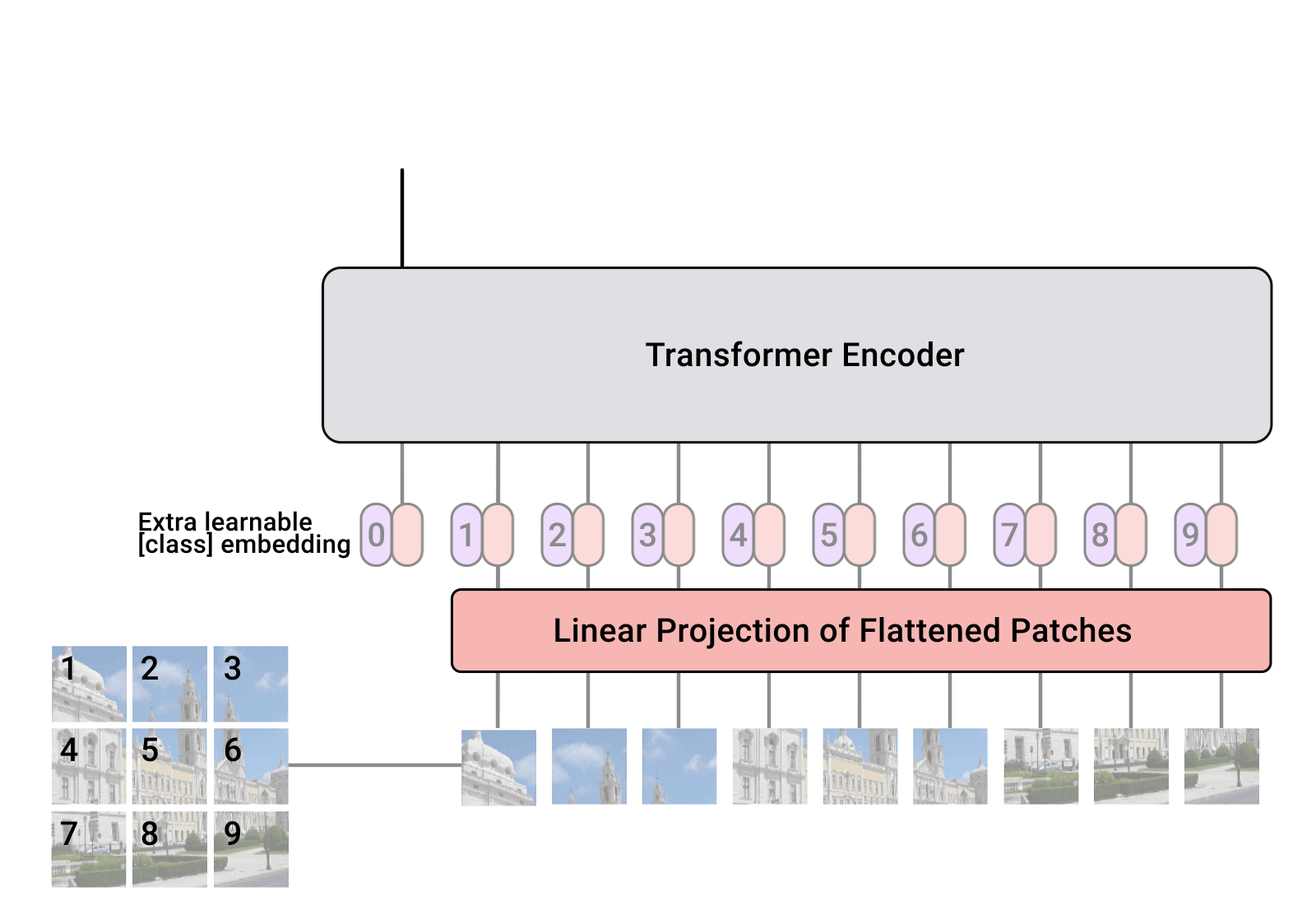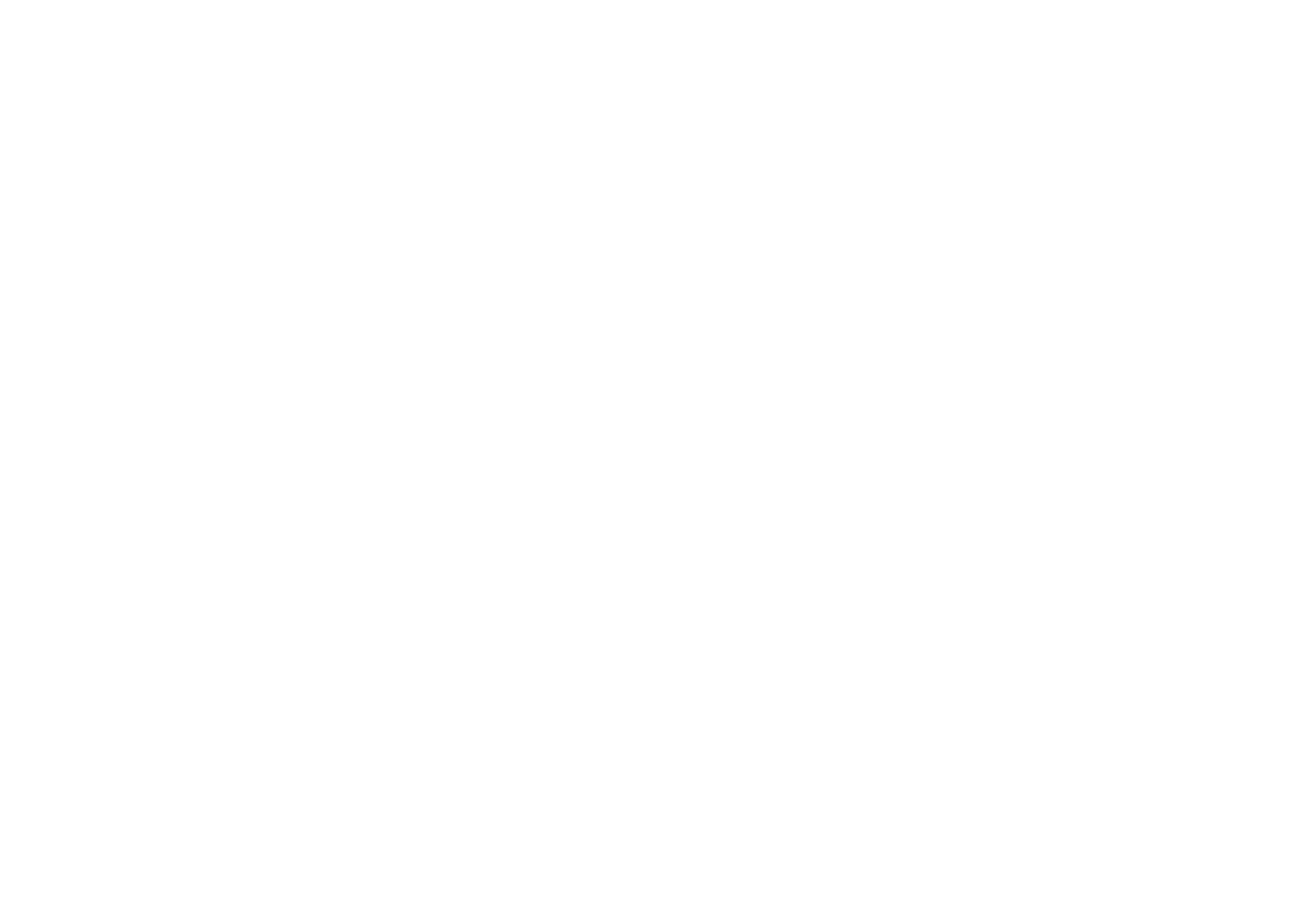
masking
Layer normlization
Residual connection
Positional encoding
We will see the details in hw/lab
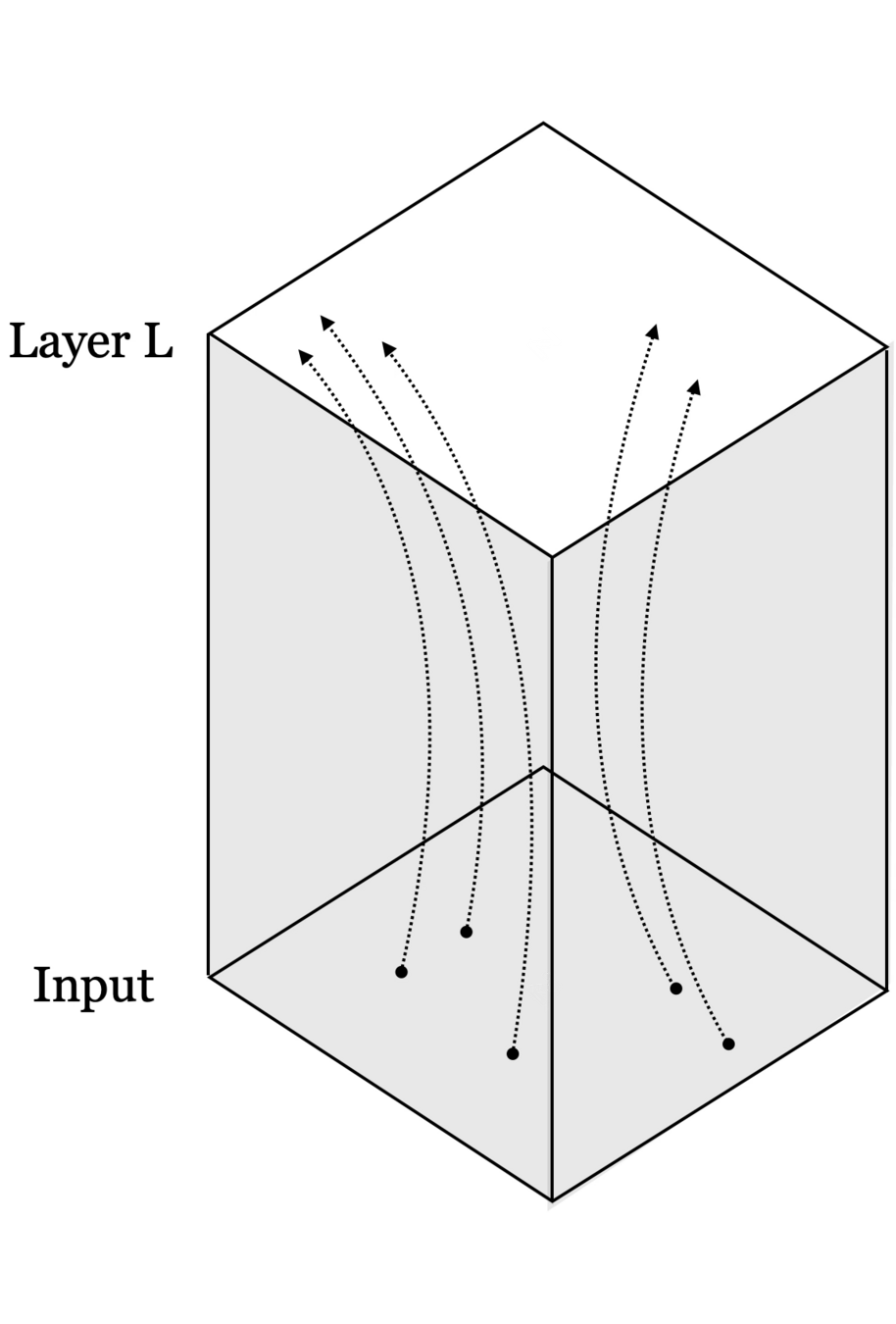
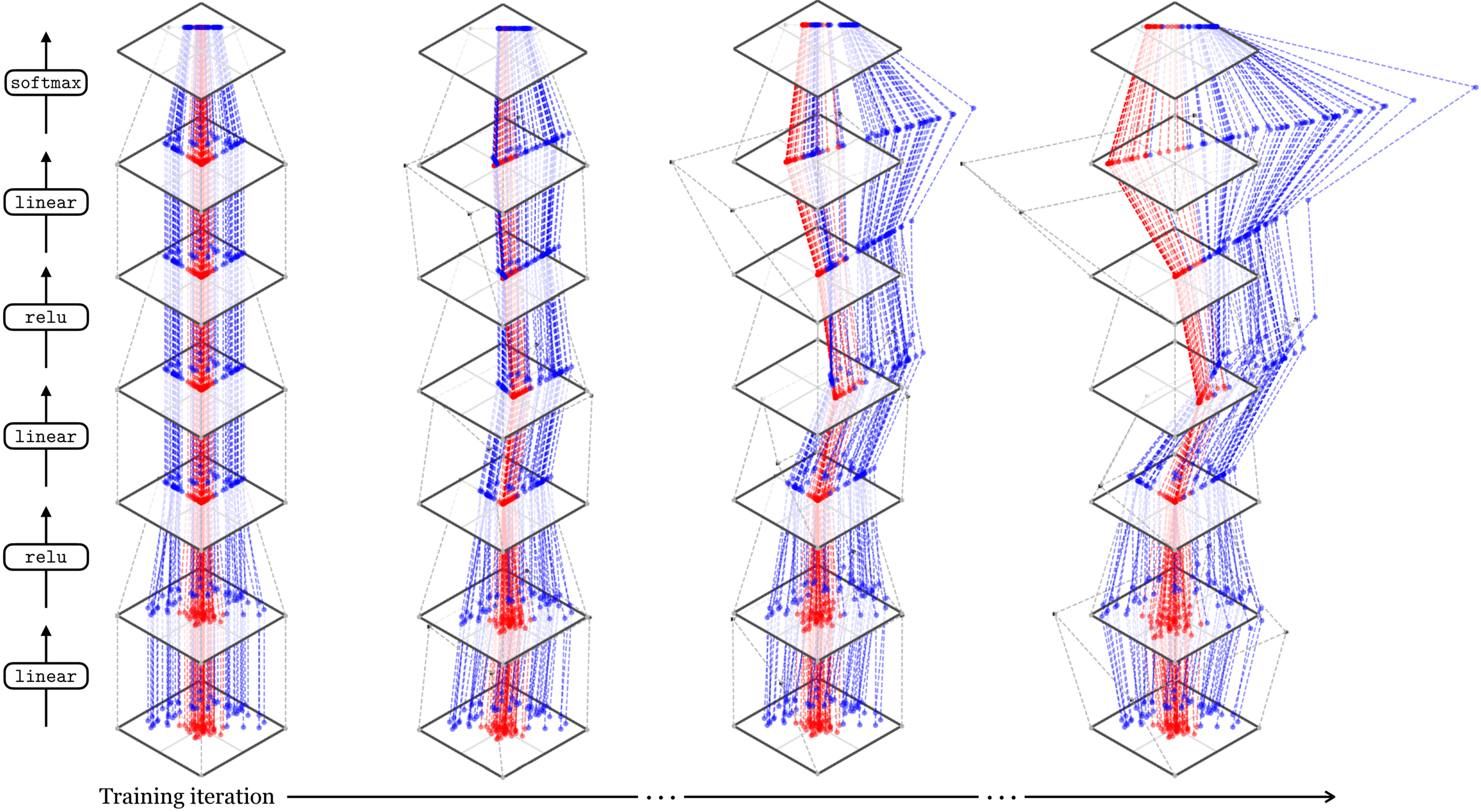
Neural networks are representation learners
Deep nets transform datapoints, layer by layer
Each layer gives a different representation (aka embedding) of the data
Recall
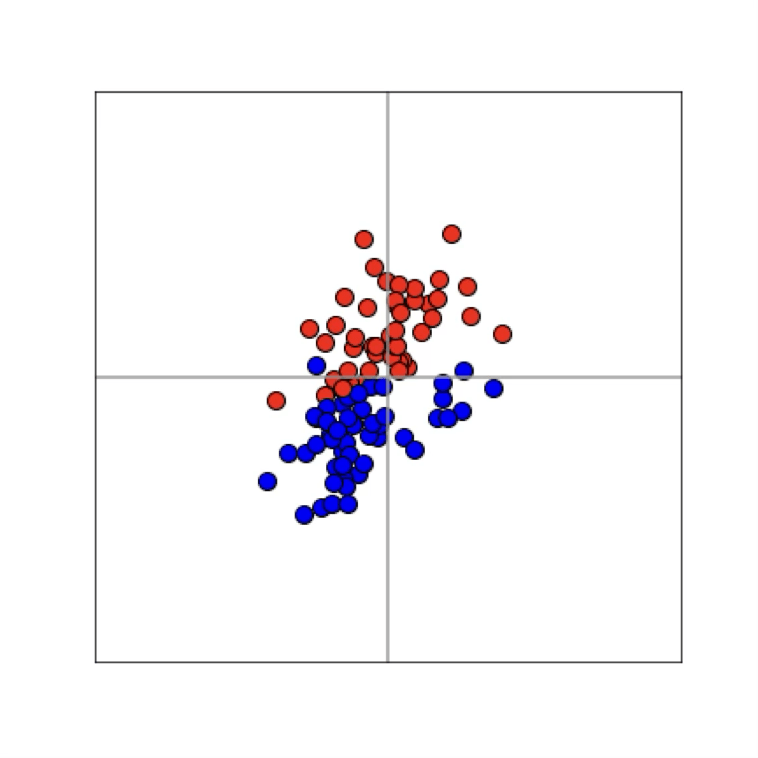
Training data
x
z_1
a_1
z_2
g
{z}_1=\text { linear }(x)
{a}_1=\text { ReLU}(z_1)
g=\text {softmax}(z_2)
{z}_2=\text { linear }(a_1)
x\in \mathbb{R^2}
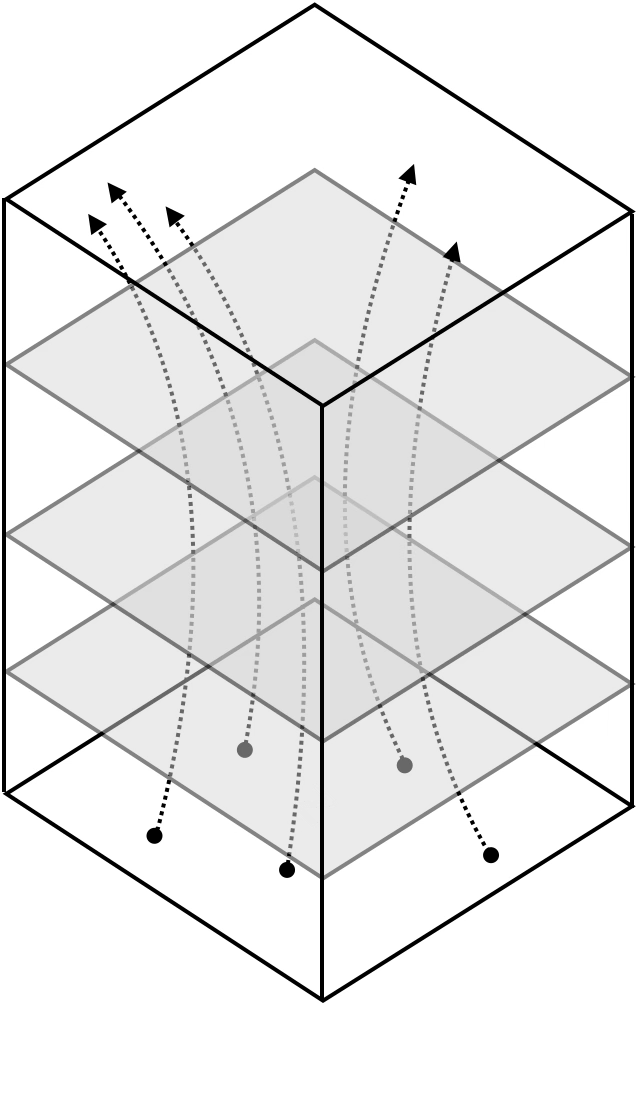
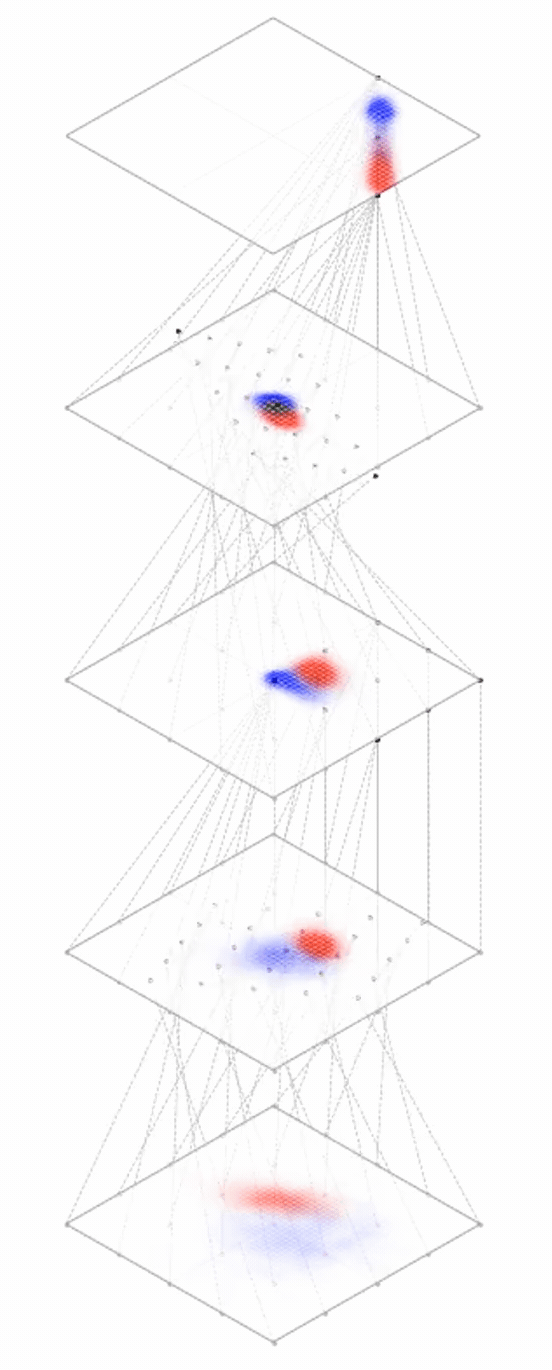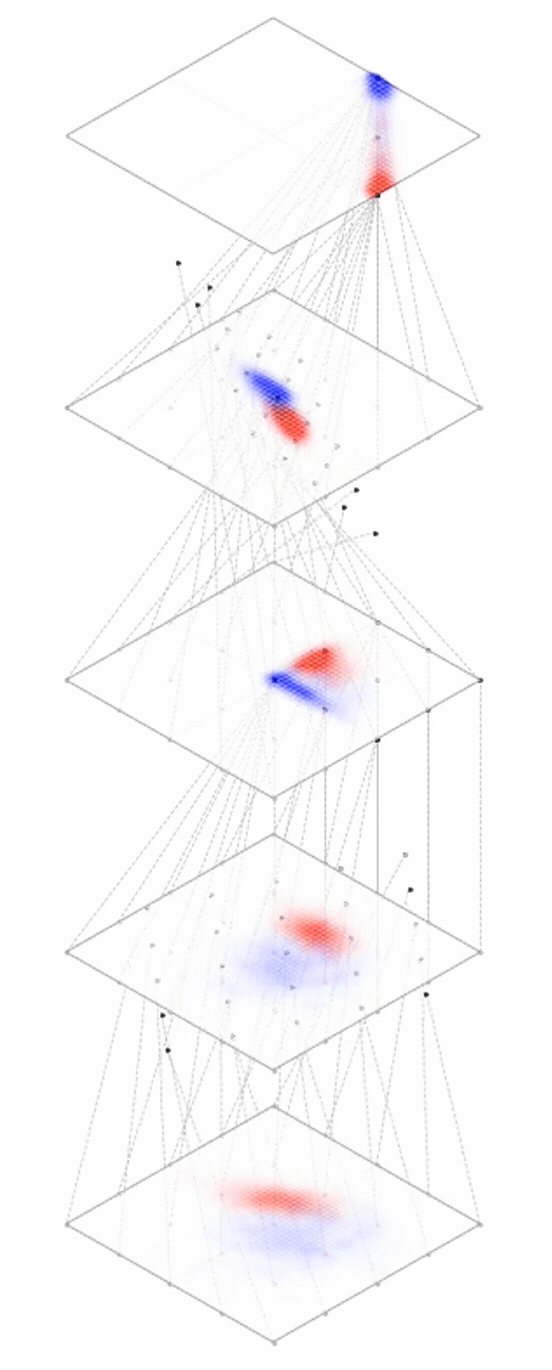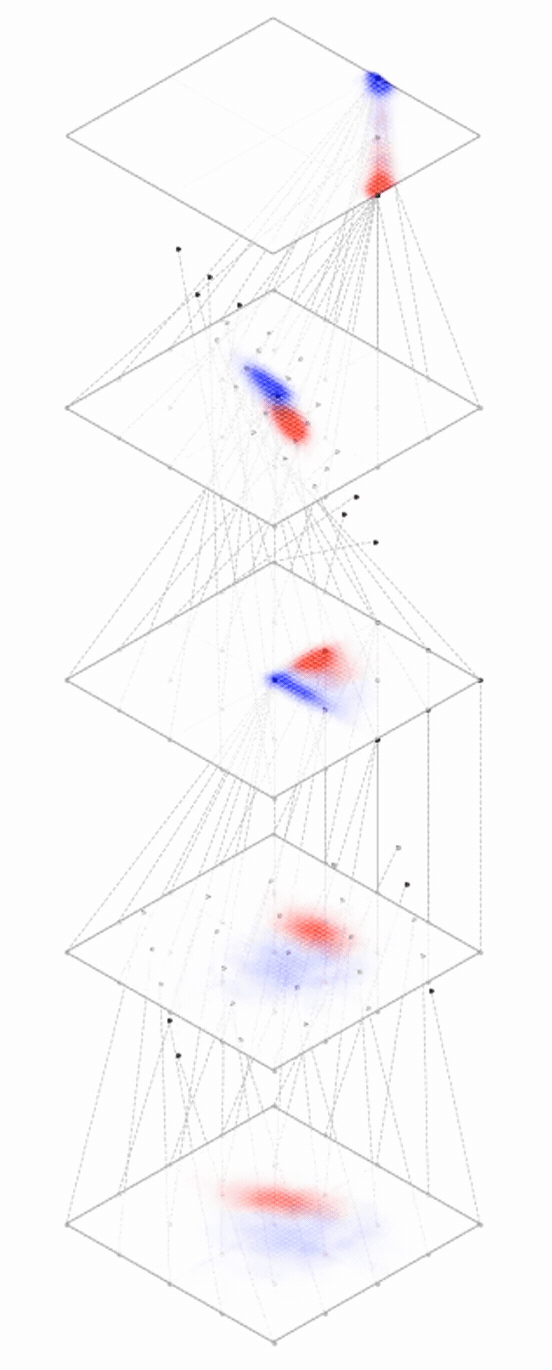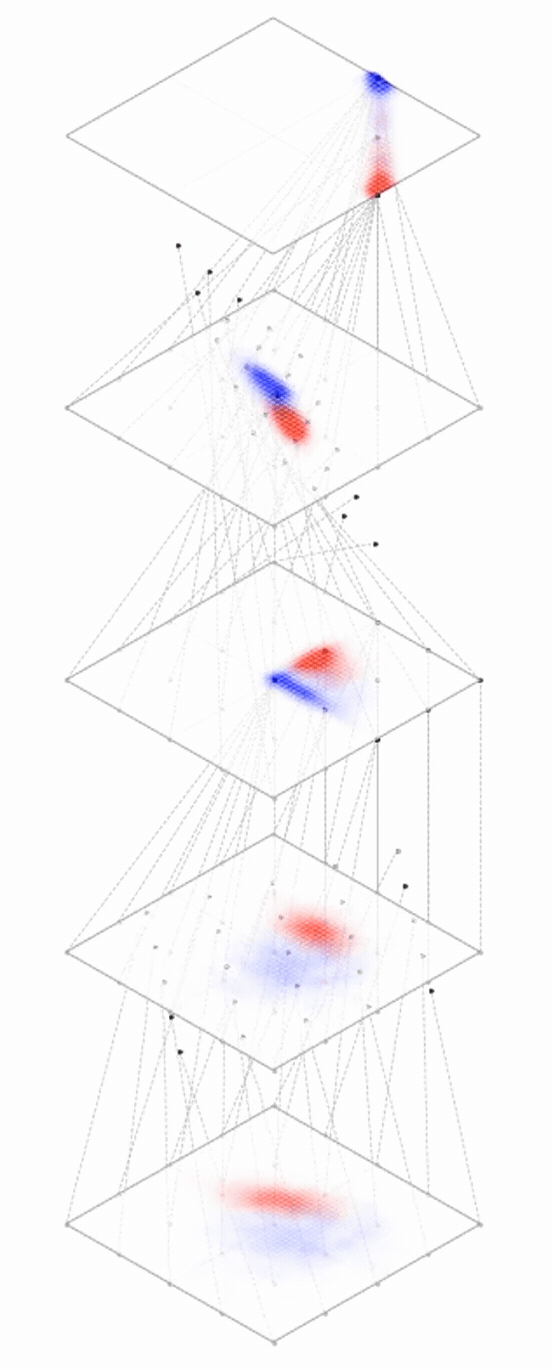
maps from complex data space to simple embedding space
Recall
\left(
\begin{array}{l}
\\
\\
\\
\\
\\
\\
\end{array}
\right.
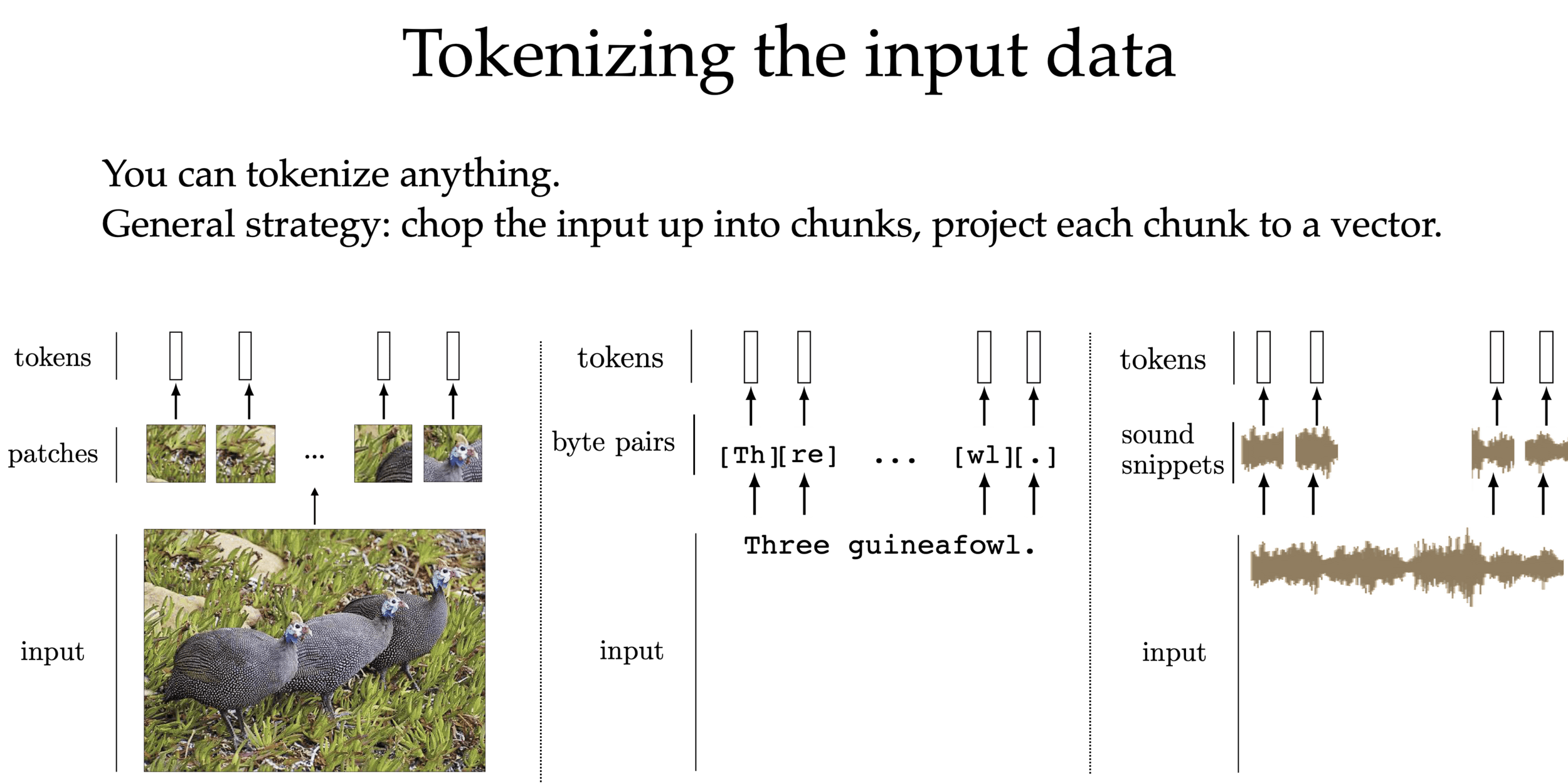
We can tokenize anything.
General strategy: chop the input up into chunks, project each chunk to an embedding
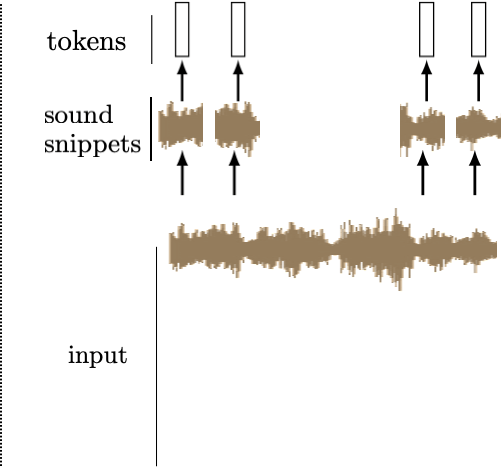
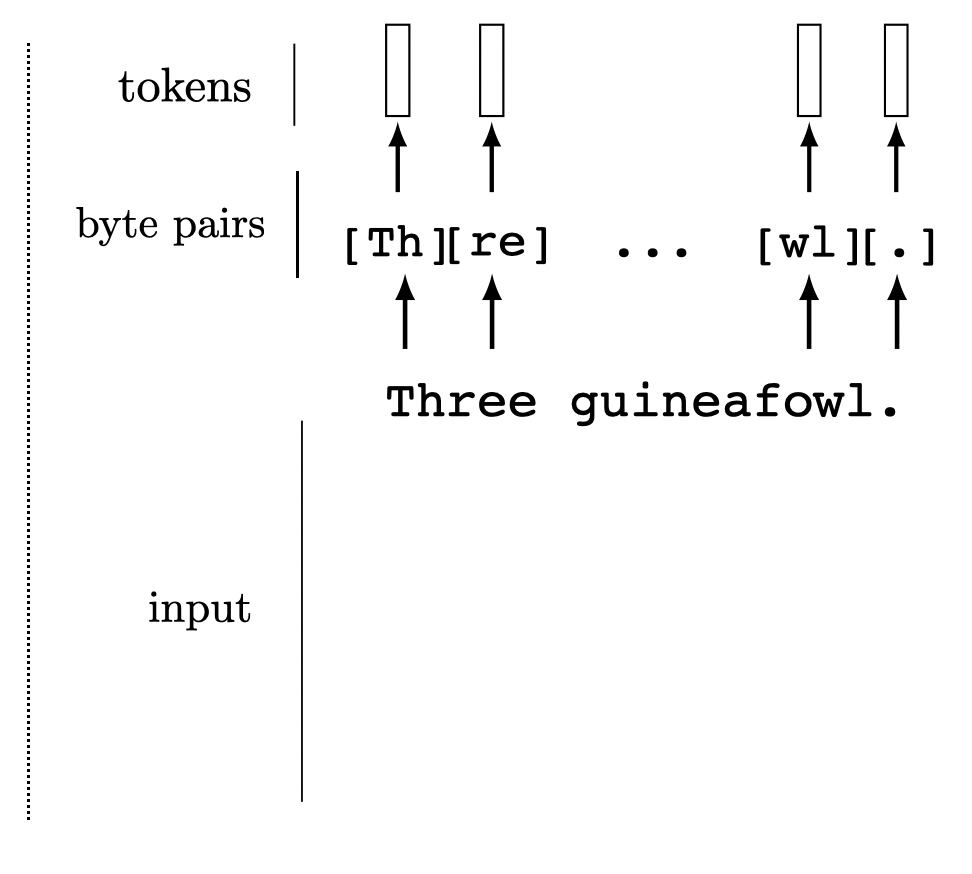
this projection can be fixed from a pre-trained model, or trained jointly with downstream task
\underbrace{\hspace{2.78cm}}
a sequence of \(n\) tokens
a projection, e.g. via a fixed, or learned linear transformation
\left\{
\begin{array}{l}
\\
\end{array}
\right.
\left\{
\begin{array}{l}
\\
\end{array}
\right.
each token \(\in \mathbb{R}^{d}\) embedding
100-by-100
\underbrace{\hspace{2.6cm}}
each token \(\in \mathbb{R}^{400}\)
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
20-by-20
\left\{
\begin{array}{l}
\\
\end{array}
\right.
\underbrace{\hspace{2.78cm}}
a sequence of \(n=25\) tokens
suppose just flatten
Multi-modality (text + image)
- (query, key, value) come from different input modality
- cross-attention
[Bahdanau et al. 2015]
Input sentence: “The agreement on the European Economic Area was signed in August 1992”
Output sentence: “L’accord sur la
zone économique européenne a été signé en août 1992”
[“DINO”, Caron et all. 2021]
Success mode:
Success mode:
[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]
Failure mode:
[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]
Failure mode:
[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]
Failure mode:
\left)
\begin{array}{l}
\\
\\
\\
\\
\\
\\
\end{array}
\right.
Summary
- Transformers combine many of the best ideas from earlier architectures—convolutional patch-wise processing, relu nonlinearities, residual connections —with several new innovations, in particular, embedding and attention layers.
- Transformers start with some generic hard-coded embeddings, and layer-by-layer, creates better and better embeddings.
- Parallel processing everything in attention: each head is processed in parallel, and within each head, the \(q,k,v\) token sequence is created in parallel, the attention scores is computed in parallel, and the attention output is computed in parallel.
Thanks!
for your attention!
We'd love to hear your thoughts.
- A token is just transformer lingo for a vector of neurons
- But the connotation is that a token is an encapsulated bundle of information
- with transformers we will operate over tokens rather than over neurons
array of neurons
array of tokens
set of tokens
set of neurons
seq. of
tokens in \(\mathbb{R}^d\)
learned embeddings
a
robot
must
obey
v_1
k_1
q_1
v_2
k_2
q_2
v_3
k_3
q_3
v_4
q_4
k_4
v_4
v_4
v_4
q_1
attention head
GPT
a
robot
must
obey
\dots
\dots
\dots
\dots
\left\{
\begin{array}{l}
\\
\\
\\
\\
\\
\end{array}
\right.
distribution over the entire vocabulary
x^{(i)} \in \mathbb{R}^{d}
q^{(i)} \in \mathbb{R}^{d_k}
k^{(i)} \in \mathbb{R}^{d_k}
v^{(i)} \in \mathbb{R}^{d_k}
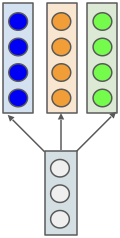
- Which color is query/key/value respectively?
- How do we go from \(x\) to \(q, k, v\)?
via learned projection weights
命
W_k
W_v
W_q
x^{(i)} \in \mathbb{R}^{d}
q^{(i)} \in \mathbb{R}^{d_k}
k^{(i)} \in \mathbb{R}^{d_k}
v^{(i)} \in \mathbb{R}^{d_k}
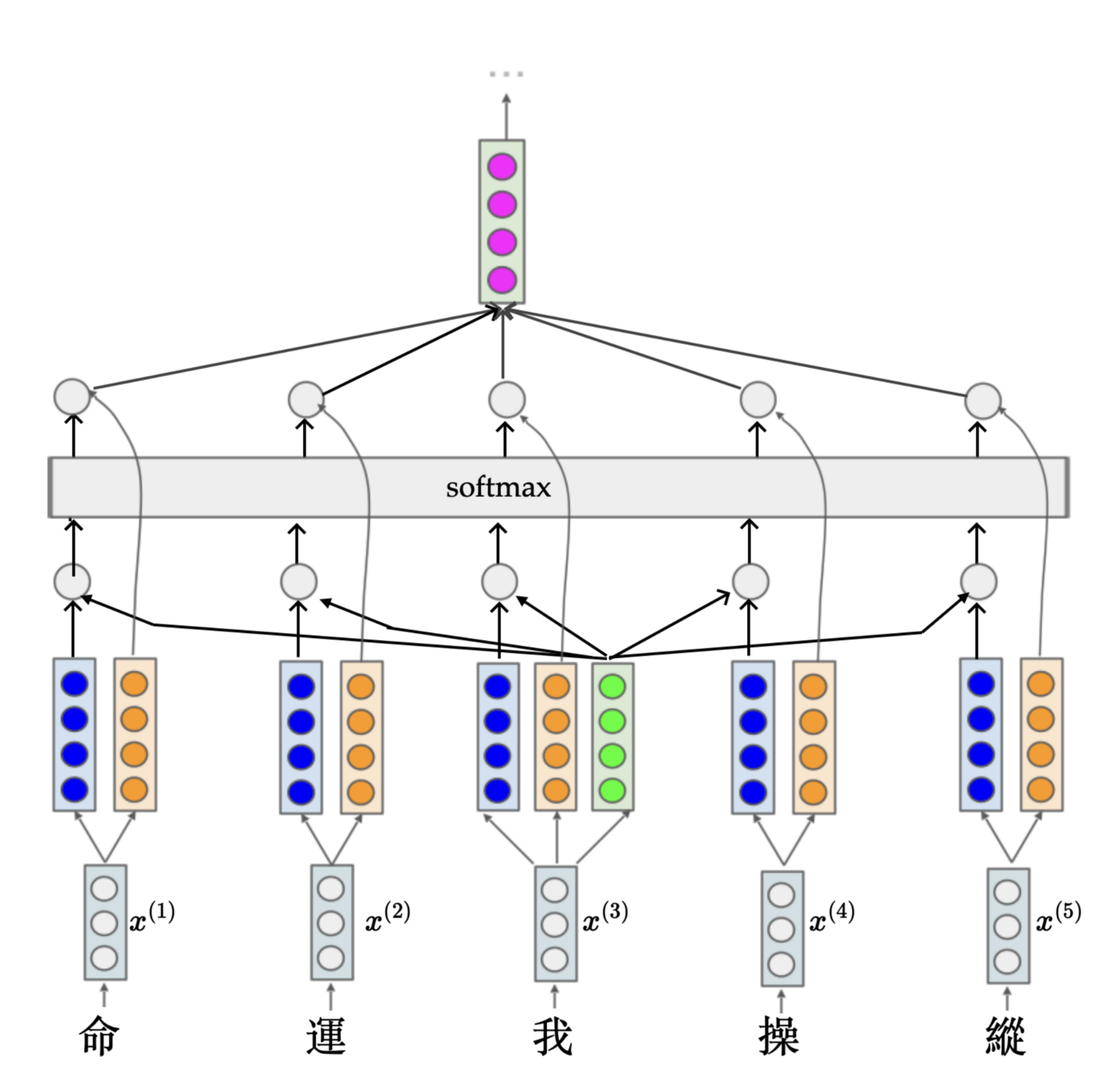
- Importantly, all these learned projection weights \(W\) are shared along the token sequence:
- These three weights \(W\) -- once learned -- do not change based on input token \(x.\)
- If the input sequence had been longer, we can still use the same weights in the same fashion --- just maps to a longer output sequence.
- This is yet another parallel processing (similar to convolution)
- But each \((q,k,v)\) do depend on the corresponding input \(x\) (can be interpreted as dynamically changing convolution filter weights)
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
x^{(5)}
命
運
我
操
縱
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
a
robot
must
obey
input embedding
output embedding
transformer block
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
attention layer
fully-connected network
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
6.390 IntroML (Fall24) - Lecture 9 Transformers
By Shen Shen
