Lecture 11: Markov Decision Processes
Intro to Machine Learning
Toddler demo, Russ Tedrake thesis, 2004
uses vanilla policy gradient (actor-critic)
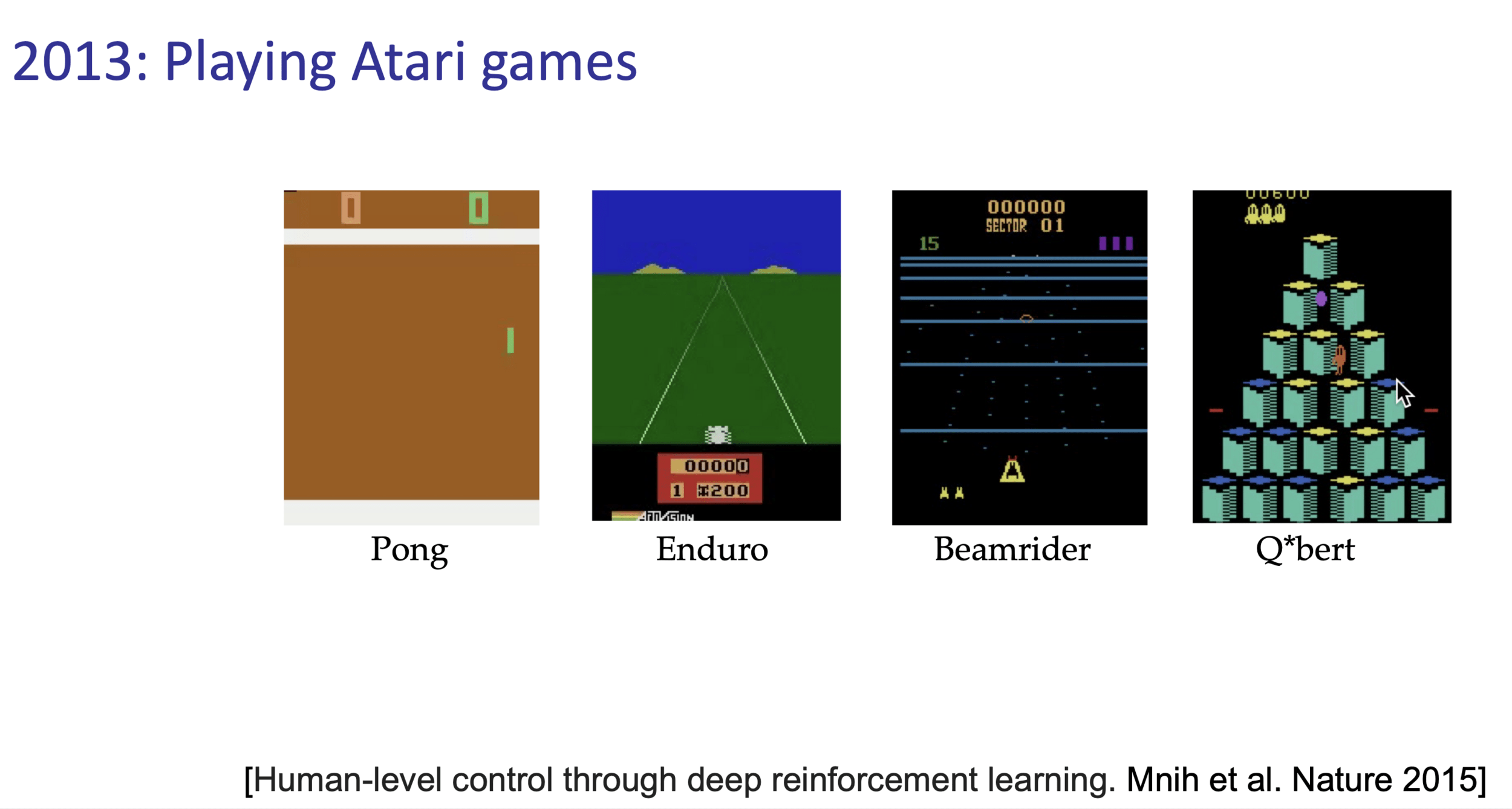
Reinforcement Learning with Human Feedback
Outline
- Markov Decision Processes Definition
-
Policy Evaluation
-
State value functions: \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
- Markov Decision Processes Definition
-
Policy Evaluation
-
State value functions: \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Markov Decision Processes
-
Research area initiated in the 50s by Bellman, known under various names:
-
Stochastic optimal control (Control theory)
-
Stochastic shortest path (Operations research)
-
Sequential decision making under uncertainty (Economics)
-
Reinforcement learning (Artificial intelligence, Machine learning)
-
-
A rich variety of elegant theory, mathematics, algorithms, and applications—but also considerable variation in notation.
-
We will use the most RL-flavored notations.
- (state, action) results in a transition \(\mathrm{T}\) into a next state:
-
Normally, we get to the “intended” state;
-
E.g., in state (7), action “↑” gets to state (4)
-
-
If an action would take Mario out of the grid world, stay put;
-
E.g., in state (9), “→” gets back to state (9)
-
-
In state (6), action “↑” leads to two possibilities:
-
20% chance to (2)
-
80% chance to (3).
-
-
80\%
20\%
Running example: Mario in a grid-world
- 9 possible states \(s\)
- 4 possible actions \(a\): {Up ↑, Down ↓, Left ←, Right →}
1
1
1
1
-10
-10
-10
-10
reward of (3, \(\downarrow\))
reward of \((3,\uparrow\))
reward of \((6, \downarrow\))
reward of \((6,\rightarrow\))
- (state, action) pairs give rewards:
- in state 3, any action gives reward 1
- in state 6, any action gives reward -10
- any other (state, action) pair gives reward 0
-
discount factor: a scalar of 0.9 that reduces the 'worth' of future rewards depending on when Mario receives them.
- So, e.g., for (3, \(\leftarrow\)) pair, Mario gets
- at the start of the game, a reward of 1
- at the 2nd time step, a discounted reward of 0.9
- at the 3rd time step, a further discounted reward of \((0.9)^2\) ... and so on
- So, e.g., for (3, \(\leftarrow\)) pair, Mario gets
Mario in a grid-world, cont'd
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
Markov Decision Processes - Definition and terminologies
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
Markov Decision Processes - Definition and terminologies
80\%
20\%
\(\mathrm{T}\left(7, \uparrow, 4\right) = 1\)
\(\mathrm{T}\left(9, \rightarrow, 9\right) = 1\)
\(\mathrm{T}\left(6, \uparrow, 3\right) = 0.8\)
\(\mathrm{T}\left(6, \uparrow, 2\right) = 0.2\)
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep state and action.
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
- \(\mathrm{R}(s, a)\) : reward, takes in a (state, action) pair and returns a reward.
Markov Decision Processes - Definition and terminologies
reward of \((3,\uparrow\))
reward of \((6,\rightarrow\))
\(\mathrm{R}\left(3, \uparrow \right) = 1\)
\(\mathrm{R}\left(6, \rightarrow \right) = -10\)
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep state and action.
- \(\mathrm{R}(s, a)\) is deterministic and bounded.
- \(\mathcal{S}\) : state space, contains all possible states \(s\).
- \(\mathcal{A}\) : action space, contains all possible actions \(a\).
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\) : the probability of transition from state \(s\) to \(s^{\prime}\) when action \(a\) is taken.
- \(\mathrm{R}(s, a)\) : reward, takes in a (state, action) pair and returns a reward.
- \(\gamma \in [0,1]\): discount factor, a scalar.
- \(\pi{(s)}\) : policy, takes in a state and returns an action.
The goal of an MDP is to find a good policy.
Markov Decision Processes - Definition and terminologies
In 6.390,
- \(\mathcal{S}\) and \(\mathcal{A}\) are small discrete sets, unless otherwise specified.
- \(s^{\prime}\) and \(a^{\prime}\) are short-hand for the next-timestep state and action.
- \(\mathrm{R}(s, a)\) is deterministic and bounded.
- \(\pi(s)\) is deterministic.
- \(a_t = \pi(s_t)\)
- \(r_t = \mathrm{R}(s_t,a_t)\)
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Reward \(\mathrm{R}(s, a)\)
time
a trajectory (also called an experience or rollout) of horizon \(h\)
\(\quad \tau=\left(s_0, a_0, r_0, s_1, a_1, r_1, \ldots s_{h-1}, a_{h-1}, r_{h-1}\right)\)
\underbrace{\hspace{4.2cm}}
initial state
all depends on \(\pi\)
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
r_2
r_3
r_4
s_0
s_1
a_0
a_1
r_0
r_1
s_{h-2}
a_{h-2}
r_{h-2}
s_{h-1}
a_{h-1}
r_{h-1}
- \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Outline
- Markov Decision Processes Definition
-
Policy Evaluation
-
State value functions: \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
Reward \(\mathrm{R}(s, a)\)
r_2
r_3
r_4
r_0
r_1
r_{h-2}
r_{h-1}
Starting in a given \(s_0\), how good is it to follow a given policy \(\pi\) for \(h\) time steps?
One idea:
But if we start at \(s_0=6\) and follow the "always-up" policy:
??
-10
\uparrow
6
👈
80\%
20\%
states and one special transition:
rewards:
trajectory:
\mathrm{R}(s_0, \pi(s_0))
\gamma \mathrm{R}(s_1, \pi(s_1))
\gamma^3\mathrm{R}(s_3, \pi(s_3))
\gamma^2 \mathrm{R}(s_2, \pi(s_2))
\dots
+
+
+
+
\gamma^{h-1}\mathrm{R}(s_{h-1}, \pi(s_{h-1}))
+
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
s_0
s_1
a_0
a_1
s_{h-2}
a_{h-2}
s_{h-1}
a_{h-1}
time
Starting in a given \(s_0\), how good is it to follow a given policy \(\pi\) for \(h\) time steps?
\mathbb{E}\Big[
\Big]
Value functions:
- \(\mathrm{V}_h^\pi(s):\) expected sum of discounted rewards starting in state \(s\) and follow \(\pi\) for \(h\) steps
- Value is long-term; reward is immediate (one-time)
- Horizon-0 values \(\mathrm{V}_0^\pi(s)\) defined as 0 for all states
\mathrm{R}(s_0, \pi(s_0))
\gamma \mathrm{R}(s_1, \pi(s_1))
\gamma^3\mathrm{R}(s_3, \pi(s_3))
\gamma^2 \mathrm{R}(s_2, \pi(s_2))
\dots
+
+
+
+
\gamma^{h-1}\mathrm{R}(s_{h-1}, \pi(s_{h-1}))
+
=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right]
\mathrm{V}_h^\pi(s):=
in 6.390, this expectation is only w.r.t. the transition probabilities \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
(eq. 1️⃣)
\( h\) terms
evaluate \(\mathrm{V}_h^\pi(s)\) under the "always-up" policy
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\underbrace{\hspace{4.6cm}}
\mathrm{V}_h^\uparrow(s)=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \uparrow \right) \mid s_0=s\right]
= \mathbb{E}\Big[\mathrm{R}(s_0, \uparrow)+\gamma \mathrm{R}(s_1, \uparrow) + \dots + \gamma^{h-1}\mathrm{R}(s_{h-1}, \uparrow)\Big]
\mathrm{V}^{\uparrow}_0(s) = 0
0
0
0
0
0
0
0
horizon \(h\) = 0: no step left
0
0
0
0
0
0
1
-10
horizon \(h\) = 1: receive the rewards
\mathrm{V}^{\uparrow}_1(s) = \mathrm{R}(s, \uparrow)
0
0
0
0
0
\mathrm{R}(1, \uparrow) + \gamma \mathrm{R}(1, \uparrow)
0
\mathrm{R}(2, \uparrow) + \gamma \mathrm{R}(2, \uparrow)
1.9
\mathrm{R}(3, \uparrow) + \gamma \mathrm{R}(3, \uparrow)
0
\mathrm{R}(4, \uparrow) + \gamma \mathrm{R}(1, \uparrow)
= 1 + 0.9 *(1) \Rightarrow 1.9
\mathrm{R}(5, \uparrow) + \gamma \mathrm{R}(2, \uparrow)
horizon \(h = 2\)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{V}^{\uparrow}_2(s): \mathbb{E}\Big[\mathrm{R}(s_0, \uparrow)+\gamma \mathrm{R}(s_1, \uparrow)\Big]
\( 2\) terms
\underbrace{\hspace{2cm}}
-9
0
0
-9.28
\mathrm{R}(6, \uparrow) + \gamma [.2 \mathrm{R}(2, \uparrow) + .8 \mathrm{R}(3, \uparrow)]
\mathrm{R}(8, \uparrow) + \gamma \mathrm{R}(5, \uparrow)
\mathrm{R}(7, \uparrow) + \gamma \mathrm{R}(4, \uparrow)
\mathrm{R}(9, \uparrow) + \gamma \mathrm{R}(6, \uparrow)
= -10 + 0.9*(0.2*0+0.8*1)
\Rightarrow -9.28
= 0 + 0.9*(-10)\Rightarrow -9
action \(\uparrow\)
\mathrm{R}(6, \uparrow)
20\%
80\%
action \(\uparrow\)
\mathrm{R}(2, \uparrow)
\gamma
action \(\uparrow\)
\mathrm{R}(3, \uparrow)
\gamma
horizon \(h = 2\)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
0
0
0
1.9
0
\( 2\) terms
\underbrace{\hspace{2cm}}
\mathrm{V}^{\uparrow}_2(s): \mathbb{E}\Big[\mathrm{R}(s_0, \uparrow)+\gamma \mathrm{R}(s_1, \uparrow)\Big]
V^{\uparrow}_3(6)
action \(\uparrow\)
action \(\uparrow\)
action \(\uparrow\)
action \(\uparrow\)
action \(\uparrow\)
20\%
80\%
80\%
\mathrm{R}(6, \uparrow)
\gamma \mathrm{R}(2, \uparrow)
20\%
+
+
\gamma \mathrm{R}(2, \uparrow)
\gamma^2 \mathrm{R}(2, \uparrow)
\gamma \mathrm{R}(3, \uparrow)
\mathrm{R}(6, \uparrow)
\gamma^2\mathrm{R}(3, \uparrow)
\gamma^2 \mathrm{R}(2, \uparrow)
\gamma \mathrm{R}(3, \uparrow)
20\%
+
80\%
\gamma^2\mathrm{R}(3, \uparrow)
+
=
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{R}(6, \uparrow)
\gamma \mathrm{R}(2, \uparrow)
20\%
+
+
\gamma^2 \mathrm{R}(2, \uparrow)
\gamma \mathrm{R}(3, \uparrow)
80\%
+
\gamma^2\mathrm{R}(3, \uparrow)
=
+
[
]
]
[
=
+
\left[\mathrm{R}(3, \uparrow) + \gamma \mathrm{R}(3, \uparrow)\right]
\gamma
+
80\%
\mathrm{R}(6, \uparrow)
\left[\mathrm{R}(2, \uparrow) + \gamma \mathrm{R}(2, \uparrow)\right]
\gamma
20\%
=
80\%
\gamma
20\%
+
V^{\uparrow}_2(2)
\gamma
+
\mathrm{R}(6, \uparrow)
\mathrm{V}^{\uparrow}_2(3)
horizon \(h = 3\)
\( 3\) terms
\underbrace{\hspace{3.5cm}}
\mathrm{V}^{\uparrow}_3(s): \mathbb{E}\Big[\mathrm{R}(s_0, \uparrow)+\gamma \mathrm{R}(s_1, \uparrow)+\gamma^2 \mathrm{R}(s_2, \uparrow)\Big]
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
the immediate reward for taking the policy-prescribed action \(\pi(s)\) in state \(s\).
horizon-\(h\) value in state \(s\): the expected sum of discounted rewards, starting in state \(s\) and following policy \(\pi\) for \(h\) steps.
\mathrm{V}^{\uparrow}_3(6)
=
80\%
\gamma
20\%
+
\mathrm{V}^{\uparrow}_2(2)
\gamma
+
\mathrm{R}(6, \uparrow)
\mathrm{V}^{\uparrow}_2(3)
\((h-1)\) horizon future value at a next state \(s^{\prime}\)
sum of future values weighted by the probability of reaching that next state \(s^{\prime}\)
discounted by \(\gamma\)
(eq. 2️⃣)
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
Bellman Recursion (finite horizon \(h\))
= 0 + 0.9\times[-10]
\mathrm{V}^{\uparrow}_{2}(9) = \mathrm{R}(9, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{1}(6)]
= -9
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{V}^{\uparrow}_1(s) = \mathrm{R}(s,\uparrow)
\mathrm{V}^{\uparrow}_2(s)
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
Bellman Recursion (finite horizon \(h\))
= -10 +.9[.2\times0+0.8\times1.9]
\mathrm{V}^{\uparrow}_{3}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \times \mathrm{V}^{\uparrow}_{2}(2) + .8\times \mathrm{V}^{\uparrow}_{2}(3)]
= -8.632
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{V}^{\uparrow}_1(s) = \mathrm{R}(s,\uparrow)
\mathrm{V}^{\uparrow}_2(s)
\mathrm{V}^{\uparrow}_3(s)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{V}^{\uparrow}_4(s)
\mathrm{V}^{\uparrow}_5(s)
\mathrm{V}^{\uparrow}_6(s)
= -10 +.9[.2\times0+0.8\times4.10]
\mathrm{V}^{\uparrow}_{6}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \times \mathrm{V}^{\uparrow}_{5}(2) + .8\times \mathrm{V}^{\uparrow}_{5}(3)]
= -7.048
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
Bellman Recursion (finite horizon \(h\))
\dots
\mathrm{V}^{\uparrow}_{60}(s)
\mathrm{V}^{\uparrow}_{61}(s)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
Bellman Recursion (finite horizon \(h\))
\mathrm{V}^{\uparrow}_{59}(s)
= -10 +.9[.2\times0+0.8\times9.98]
\mathrm{V}^{\uparrow}_{61}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \times \mathrm{V}^{\uparrow}_{60}(2) + .8\times \mathrm{V}^{\uparrow}_{60}(3)]
= -2.8144
\dots
\mathrm{V}^{\uparrow}_{60}(s)
\mathrm{V}^{\uparrow}_{61}(s)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
\dots
\mathrm{V}^{\uparrow}_{\infty}(s)
- As we extend the horizon, value differences shrink
- because longer-term rewards are heavily discounted
- so, as \(h \to \infty,\) the value functions stop changing
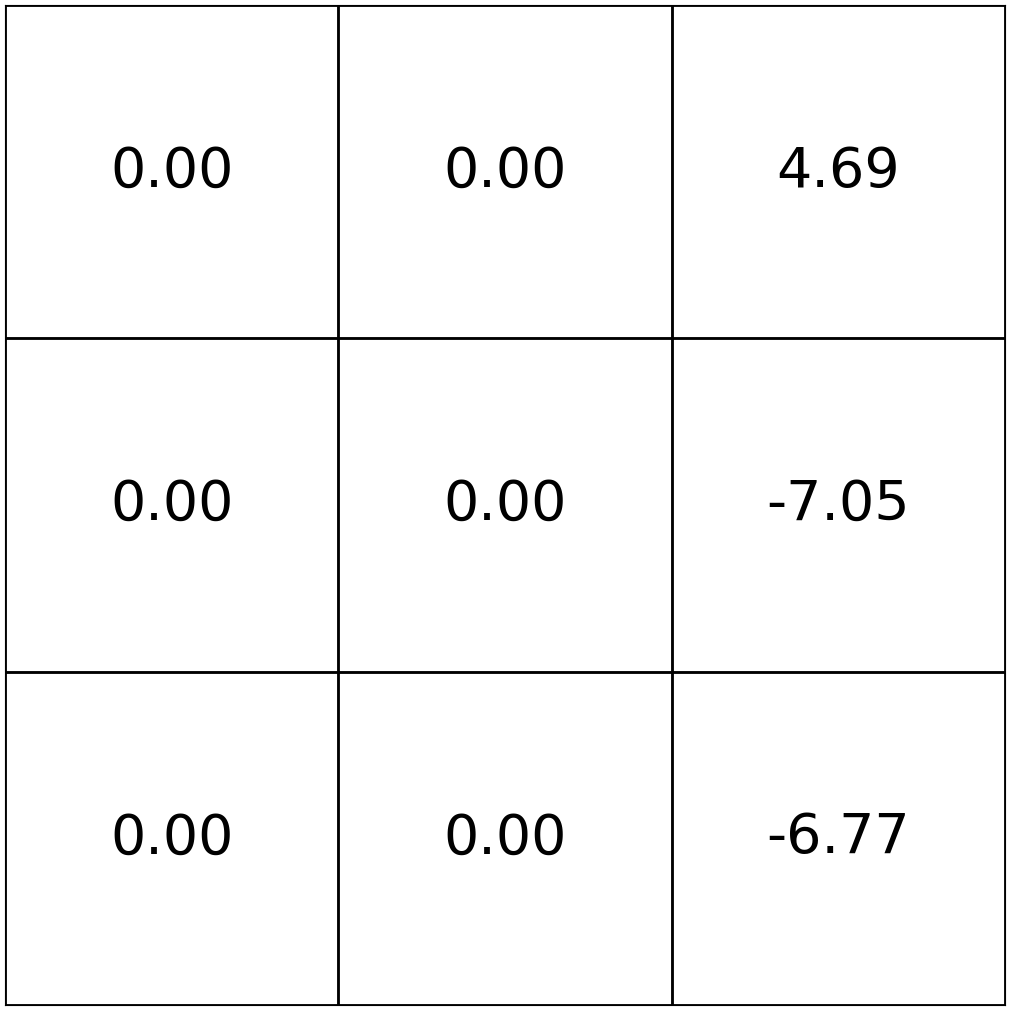
- convergence can be seen, e.g., via \(\mathrm{V}^{\uparrow}_{\infty}(3)=1+.9+.9^2+.9^3 + \dots =10\)
Value functions converge as \(h \to \infty\)
Typically, \(\gamma < 1\) to ensure \(\mathrm{V}_{\infty}\) is finite.
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
Recursion (finite \(h\)) 2️⃣
As horizon \(h \to \infty,\) the Bellman recursion becomes the Bellman equation
Equation \((h\to \infty)\) 3️⃣
\mathrm{V}^\pi_{\infty}(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}^\pi_{\infty}\left(s^{\prime}\right)
\mathrm{V}_h^\pi(s)=\mathrm{R}\left(s, \pi(s)\right)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
\mathrm{V}^{\uparrow}_{\infty}(s)
\mathrm{V}^{\uparrow}_{\infty}(3) = \mathrm{R}(3, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{\infty}(3)]
= 1 + .9 \times 10 \Rightarrow 10
= -10 +.9[.2\times0+0.8\times10]\Rightarrow -2.8
\mathrm{V}^{\uparrow}_{\infty}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \times \mathrm{V}^{\uparrow}_{\infty}(2) + .8\times \mathrm{V}^{\uparrow}_{\infty}(3)]
A system of \(|\mathcal{S}|\) self-consistent linear equations, one for each state
finite-horizon Bellman recursions
infinite-horizon Bellman equations
\mathrm{V}^\pi_{\infty}(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}^\pi_{\infty}\left(s^{\prime}\right)
\mathrm{V}_{h}^\pi(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}_{h-1}^\pi\left(s^{\prime}\right)
\pi(s)
\mathrm{V}^{\pi}_{h}(s)
Policy Evaluation
Quick summary
Use the definition and sum up expected rewards:
Or, leverage the recursive structure:
\mathrm{V}_h^\pi(s):=\mathbb{E}\left[\sum_{t=0}^{h-1} \gamma^t \mathrm{R}\left(s_t, \pi\left(s_t\right)\right) \mid s_0=s, \pi\right]
1️⃣
2️⃣
3️⃣
Outline
- Markov Decision Processes Definition
-
Policy Evaluation
-
State value functions: \(\mathrm{V}^{\pi}\)
-
Bellman recursions and Bellman equations
-
-
Policy Optimization
-
Optimal policies \(\pi^*\)
-
Optimal action value functions: \(\mathrm{Q}^*\)
-
Value iteration
-
- Intuitively, an optimal policy \(\pi^*\) is a policy that yields the highest possible value \(\mathrm{V}_h^{*}({s})\) from every state
- An MDP has a unique optimal value \(\mathrm{V}_h^{*}({s})\)
- Optimal policy \(\pi^*\) might not be unique
Optimal policy \(\pi^*\)
e.g. in the "Luigi game", all rewards are 1,
then any policy is an optimal policy
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
- Formally: an optimal policy \(\pi^*\) is such that: \(\mathrm{V}_h^{\pi^*}(s) = \max_{\pi} \mathrm{V}_h^{\pi}(s) = \mathrm{V}_h^*(s), \forall s \in \mathcal{S}\)
- How to search for an optimal policy \(\pi^*\)?
- Even if we tediously enumerate over all \(\pi\), do policy evaluation, compare values to get \(\mathrm{V}^{*}_h(s)\)...it's not yet clear how to choose actions.
\(\mathrm{V}^*(s)\) is defined over states, not actions.
It tells us where we'd like to be — not what we should do to get there.
Optimal policy \(\pi^*\)
Bellman recursion under an optimal policy
\(\mathrm{V}_h^*(s) = \max_{a} \big[\mathrm{R}(s, a) + \gamma \sum_{s'} \mathrm{T}(s, a, s') \mathrm{V}_{h-1}^*(s') \big]\)
Policy \(\pi(s)\)
Transition \(\mathrm{T}\left(s, a, s^{\prime}\right)\)
Reward \(\mathrm{R}(s, a)\)
time
\dots
s_2
s_3
s_4
s_5
a_2
a_3
a_4
r_2
r_3
r_4
s_0
s_1
a_0
a_1
r_0
r_1
s_{h-2}
a_{h-2}
r_{h-2}
s_{h-1}
a_{h-1}
r_{h-1}
\underbrace{\hspace{6.2cm}}
\underbrace{\hspace{7.2cm}}
Optimality recursion
if we've acted optimally for \(h\) steps: \(\mathrm{V}_h^*(s)\)
we must have acted optimally from the first step onward \(\mathrm{V}_{h-1}^*(s')\)
4️⃣
Define the optimal state-action value functions \(\mathrm{Q}^*_h(s, a):\)
the expected sum of discounted rewards, obtained by
- starting in state \(s\)
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{V}_h^*(s) = \max_{a} \big[\mathrm{R}(s, a) + \gamma \sum_{s'} \mathrm{T}(s, a, s') \mathrm{V}_{h-1}^*(s') \big]\)
\(=\max_{a}\left[\mathrm{Q}^*_{h}(s, a)\right]\)
\(\mathrm{Q}^*\) satisfies the Bellman recursion:
\(\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right)\)
4️⃣
5️⃣
\underbrace{\hspace{4.2cm}}
\(\mathrm{Q}^*_{h}(s, a)\)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
\mathrm{Q}^*_0(s, a)
\mathrm{Q}^*_1(s, a)
=\mathrm{R}(s, a)
Consider \(\mathrm{Q}^*_2(3, \downarrow)\)
- receive \(\mathrm{R}(3,\downarrow)\)
\( = 1 + .9\times10\)
- next state \(s'\) = 6, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(6, a^{\prime}\right)\)
\( = -8\)
-8
\(\mathrm{Q}_2^*(3, \downarrow) = \mathrm{R}(3,\downarrow) + \gamma \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(6, a^{\prime}\right)\)
\mathrm{Q}^*_2(s, a)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
\mathrm{Q}^*_1(s, a)
Let's consider \(\mathrm{Q}_2^*(3, \leftarrow)\)
- receive \(\mathrm{R}(3,\leftarrow)\)
\( = 1 + .9\times0 \)
- next state \(s'\) = 2, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
\( = 1\)
1
\(\mathrm{Q}_2^*(3, \leftarrow) = \mathrm{R}(3,\leftarrow) + \gamma \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
\mathrm{Q}^*_2(s, a)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
-8
\mathrm{Q}^*_1(s, a)
Let's consider \(\mathrm{Q}^*_2(3, \uparrow)\)
- receive \(\mathrm{R}(3,\uparrow)\)
\( = 1 + .9 \times 1\)
- next state \(s'\) = 3, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
\( = 1.9\)
1.9
\(\mathrm{Q}^*_2(3, \uparrow) = \mathrm{R}(3,\uparrow) + \gamma \max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
\mathrm{Q}^*_2(s, a)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
1
-8
\mathrm{Q}^*_1(s, a)
\mathrm{Q}^*_2(s, a)
Let's consider \(\mathrm{Q}^*_2(3, \rightarrow)\)
- receive \(\mathrm{R}(3,\rightarrow)\)
\( = 1 + .9\times1\)
- next state \(s'\) = 3, act optimally for the remaining one timestep
- receive \(\max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
\( = 1.9\)
1.9
\(\mathrm{Q}^*_2(3, \rightarrow) = \mathrm{R}(3,\rightarrow) + \gamma \max _{a^{\prime}} \mathrm{Q}^*_{1}\left(3, a^{\prime}\right)\)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
1.9
1
-8
\mathrm{Q}^*_1(s, a)
- act optimally at the next state \(s^{\prime}=6\)
receive \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(6, a^{\prime}\right)\)
- receive \(\mathrm{R}(6,\rightarrow)\)
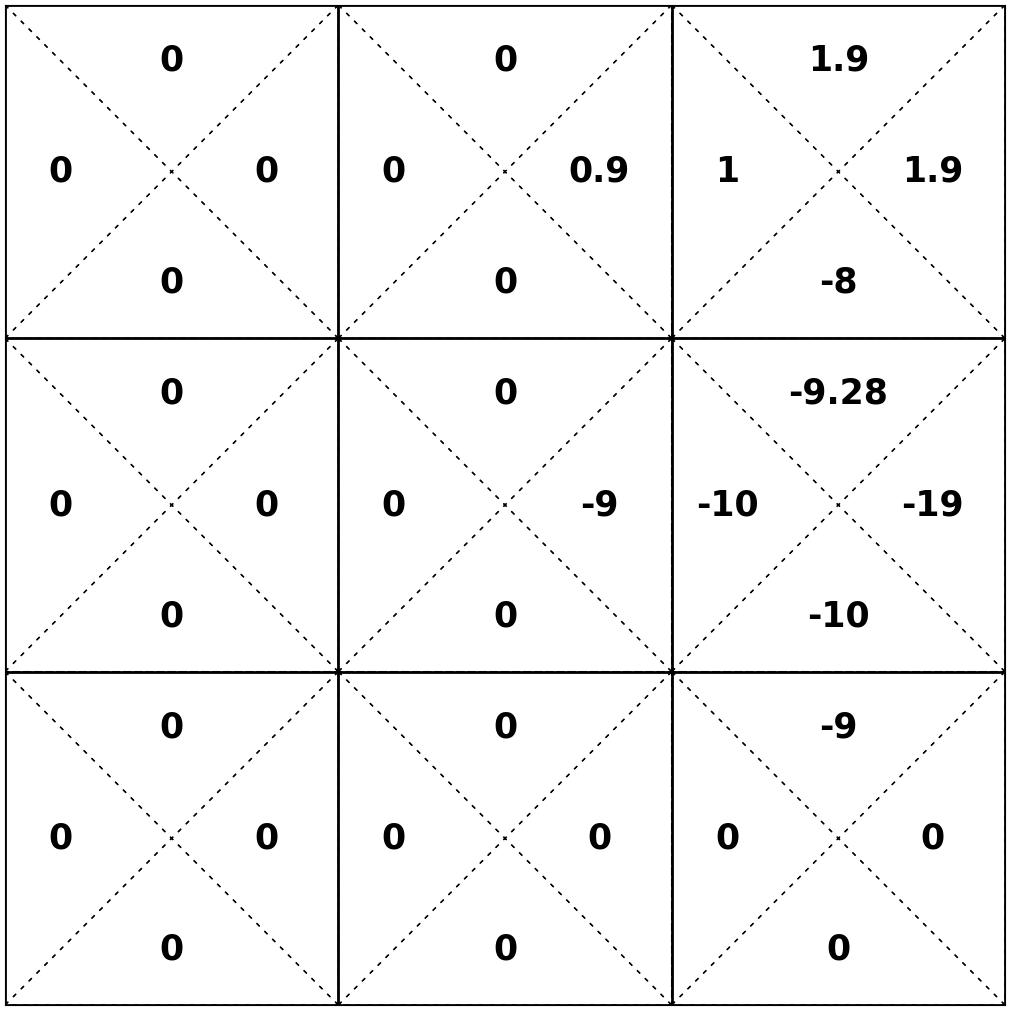
Let's consider \(\mathrm{Q}_2^*(6, \rightarrow) \)
\(\mathrm{Q}_2^*(6, \rightarrow)=\mathrm{R}(6,\rightarrow) + \gamma[\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(6, a^{\prime}\right)] \)
\mathrm{Q}^*_2(s, a)
\( = -10 + .9 \times -10 \Rightarrow -19\)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
\mathrm{Q}^*_1(s, a)
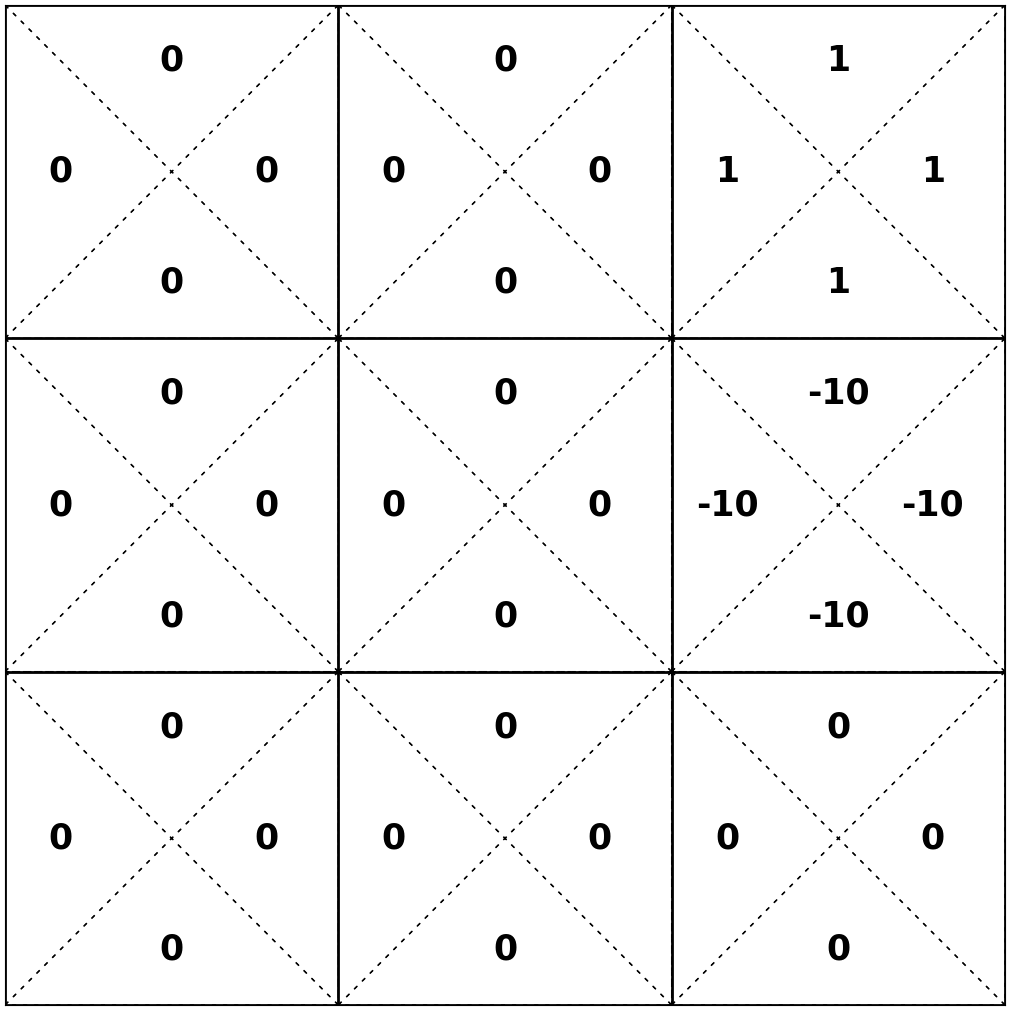
- act optimally at the next state \(s^{\prime}\)
- 20% chance, \(s'\) = 2, act optimally, get \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)\)
- 80% chance, \(s'\) = 3, act optimally, get \(\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)\)
\(= -10 + .9 [.2 \times 0+ .8 \times 1] \Rightarrow -9.28\)
- receive \(\mathrm{R}(6,\uparrow)\)
Let's consider \(\mathrm{Q}_2^*(6, \uparrow) \)
\(\mathrm{Q}_2^*(6, \uparrow)=\mathrm{R}(6,\uparrow) + \gamma[.2 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)] \)
\mathrm{Q}^*_1(s, a)
\mathrm{Q}^*_2(s, a)
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Rewards:
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
\mathrm{Q}^*_3(s, a)
- act optimally at the next state \(s^{\prime}\)
- 20% chance, \(s'\) = 2, act optimally, get \(\max _{a^{\prime}} \mathrm{Q}_{2}^*\left(2, a^{\prime}\right)\)
- 80% chance, \(s'\) = 3, act optimally, get \(\max _{a^{\prime}} \mathrm{Q}_{2}^*\left(3, a^{\prime}\right)\)
- receive \(\mathrm{R}(6,\uparrow)\)
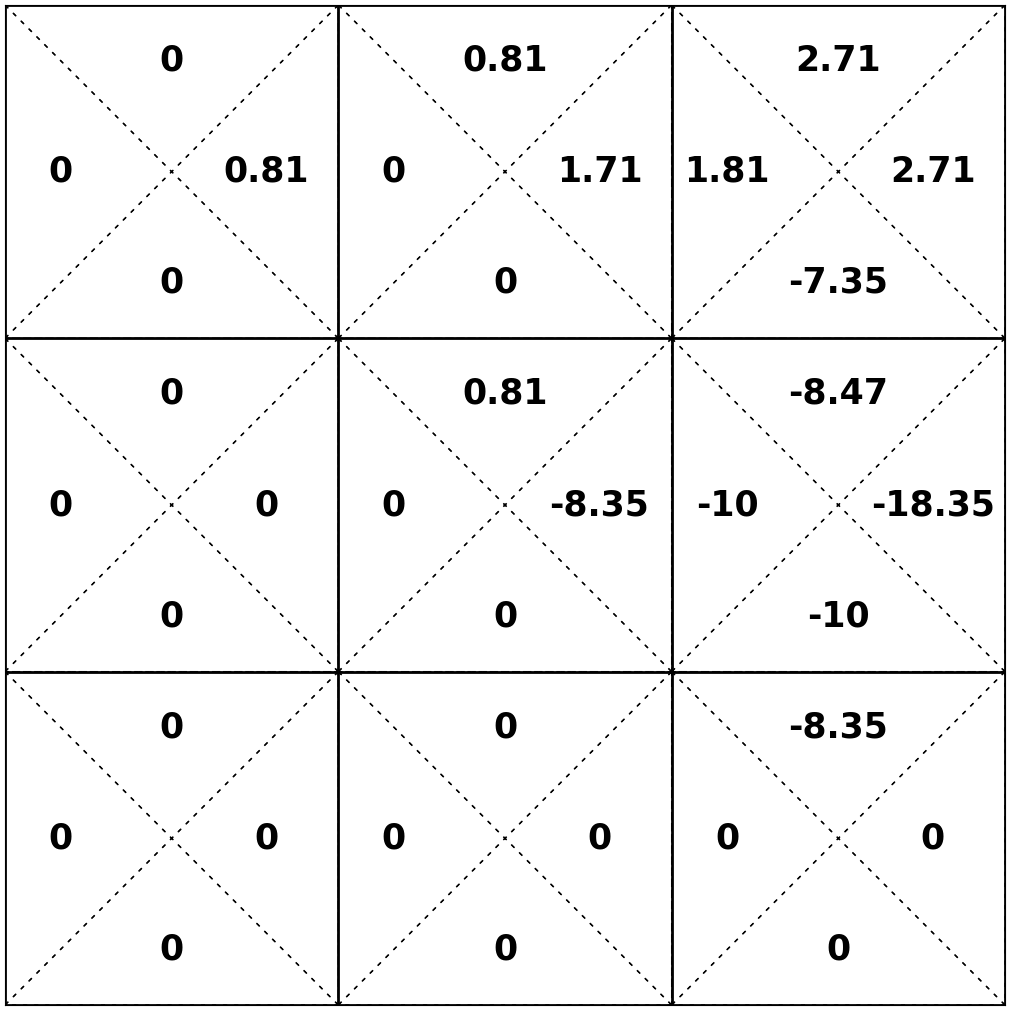
Let's consider \(\mathrm{Q}_3^*(6, \uparrow) \)
\(= -10 + .9 [.2 \times 0.9 + .8 \times 1.9] \Rightarrow -8.47\)
\(\mathrm{Q}_3^*(6, \uparrow)=\mathrm{R}(6,\uparrow) + \gamma[.2 \max _{a^{\prime}} \mathrm{Q}_{2}^*\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} \mathrm{Q}_{2}^*\left(3, a^{\prime}\right)] \)
Rewards:
\mathrm{Q}^*_2(s, a)
- for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
- \(\mathrm{Q}_{\text {old }}(\mathrm{s}, \mathrm{a})=0\)
- while True:
- for \(s \in \mathcal{S}, a \in \mathcal{A}\) :
- \(\mathrm{Q}_{\text {new }}(s, a) \leftarrow \mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime}\right) \max _{a^{\prime}} \mathrm{Q}_{\text {old }}\left(s^{\prime}, a^{\prime}\right)\)
- if \(\max _{s, a}\left|Q_{\text {old }}(s, a)-Q_{\text {new }}(s, a)\right|<\epsilon:\)
- return \(\mathrm{Q}_{\text {new }}\)
- \(\mathrm{Q}_{\text {old }} \leftarrow \mathrm{Q}_{\text {new }}\)
\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right)
Value Iteration
if run this block \(h\) times and break, then the returns are exactly \(\mathrm{Q}^*_h\)
\{
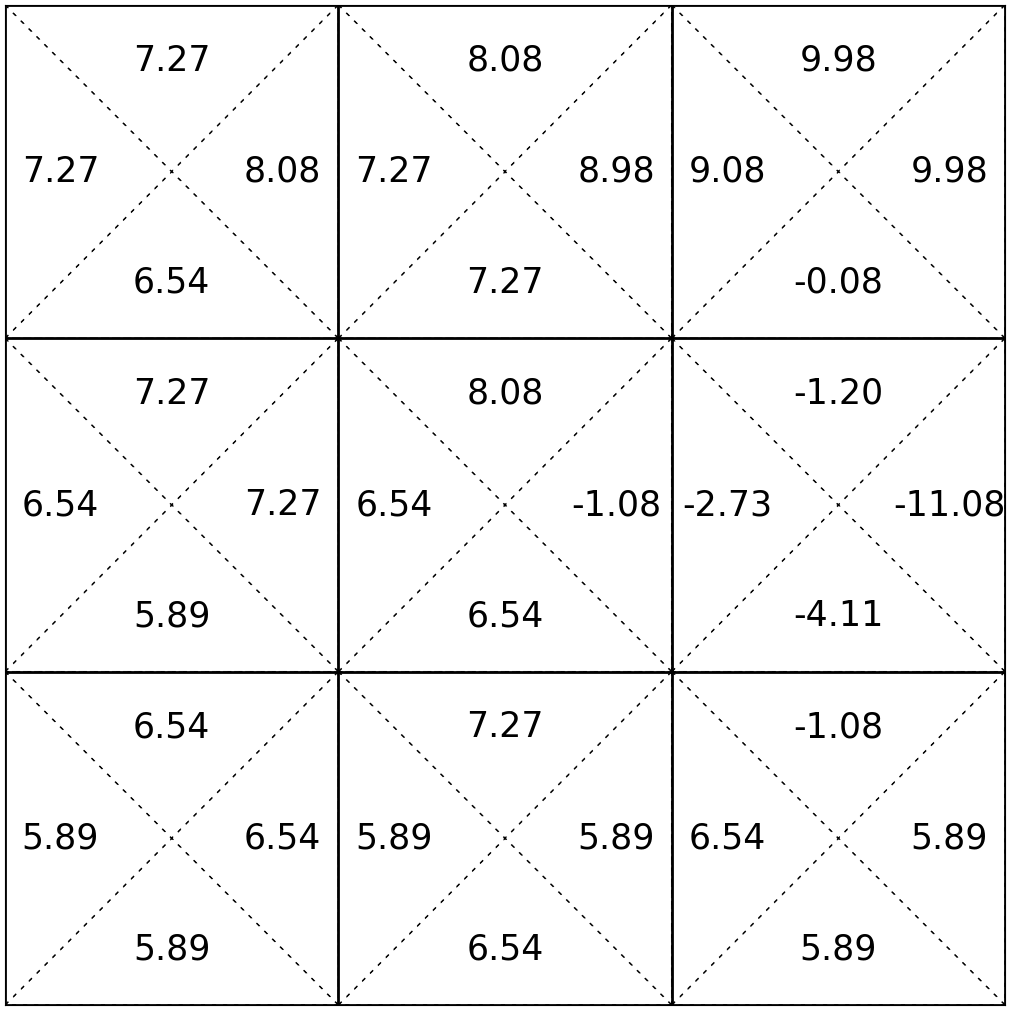
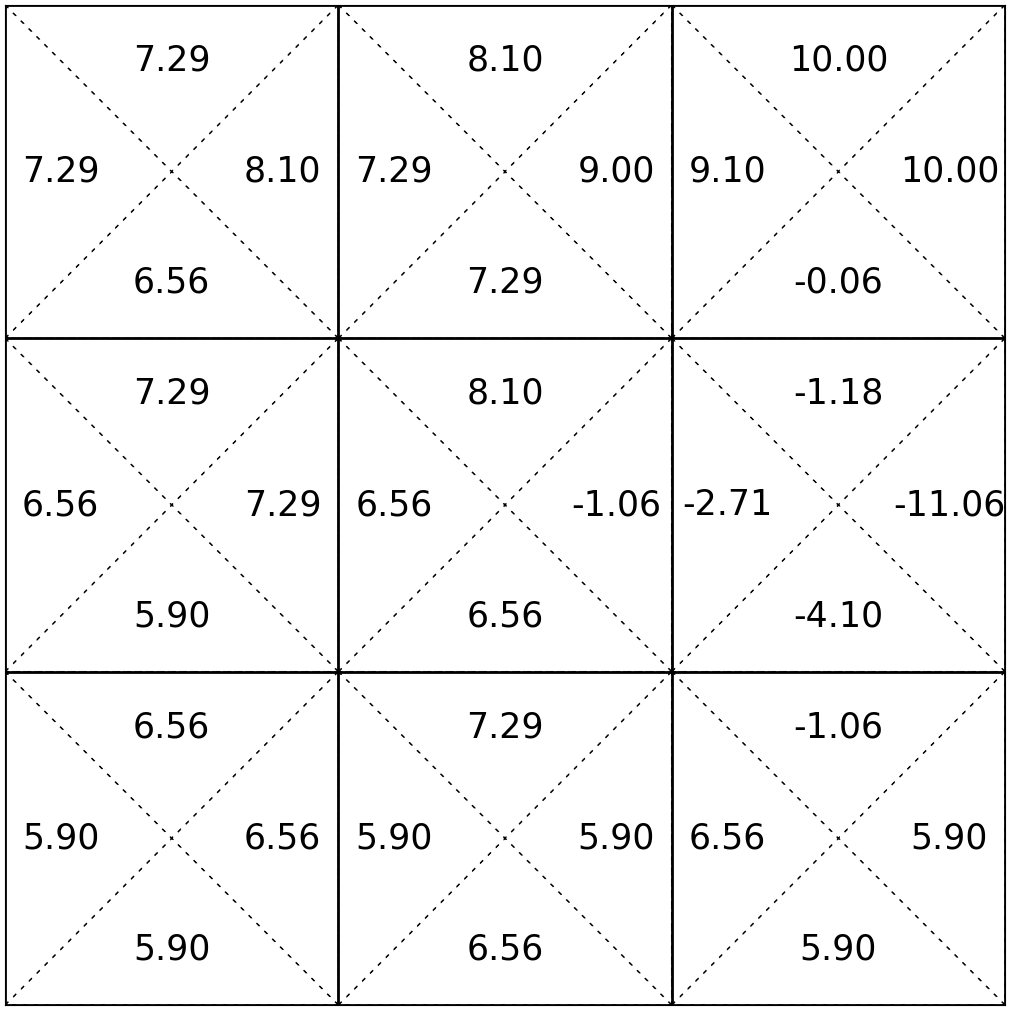
\(\mathrm{Q}^*_{\infty}(s, a)\)
Value iteration: what we just did, iteratively invoke 5️⃣
\{
\mathrm{Q}_1^*(s, a)
\mathrm{Q}_2^*(s, a)
\pi_h^*(s)=\arg \max _a \mathrm{Q}^*_h(s, a)
Optimal policy easily extracted: 6️⃣
\mathrm{Q}_3^*(s, a)
\mathrm{Q}_{\infty}^*(s, a)
\dots
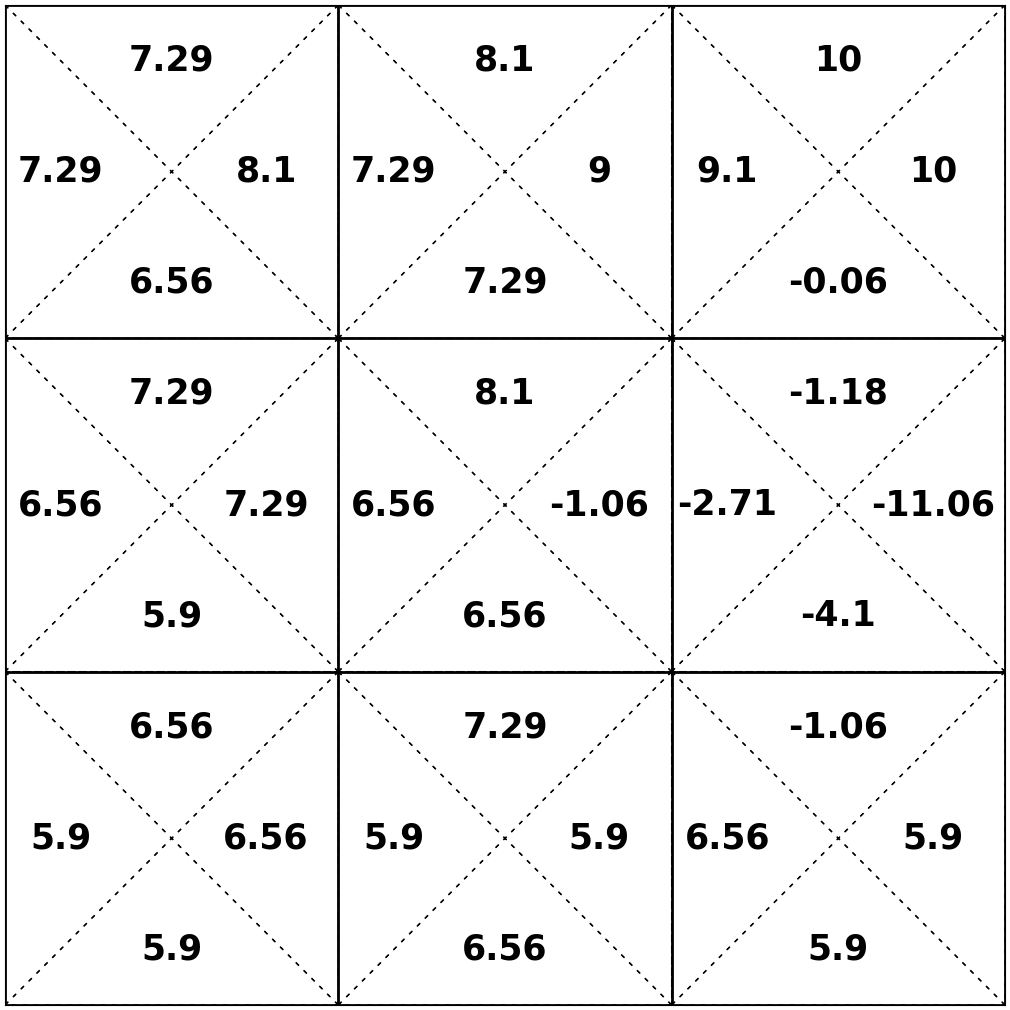
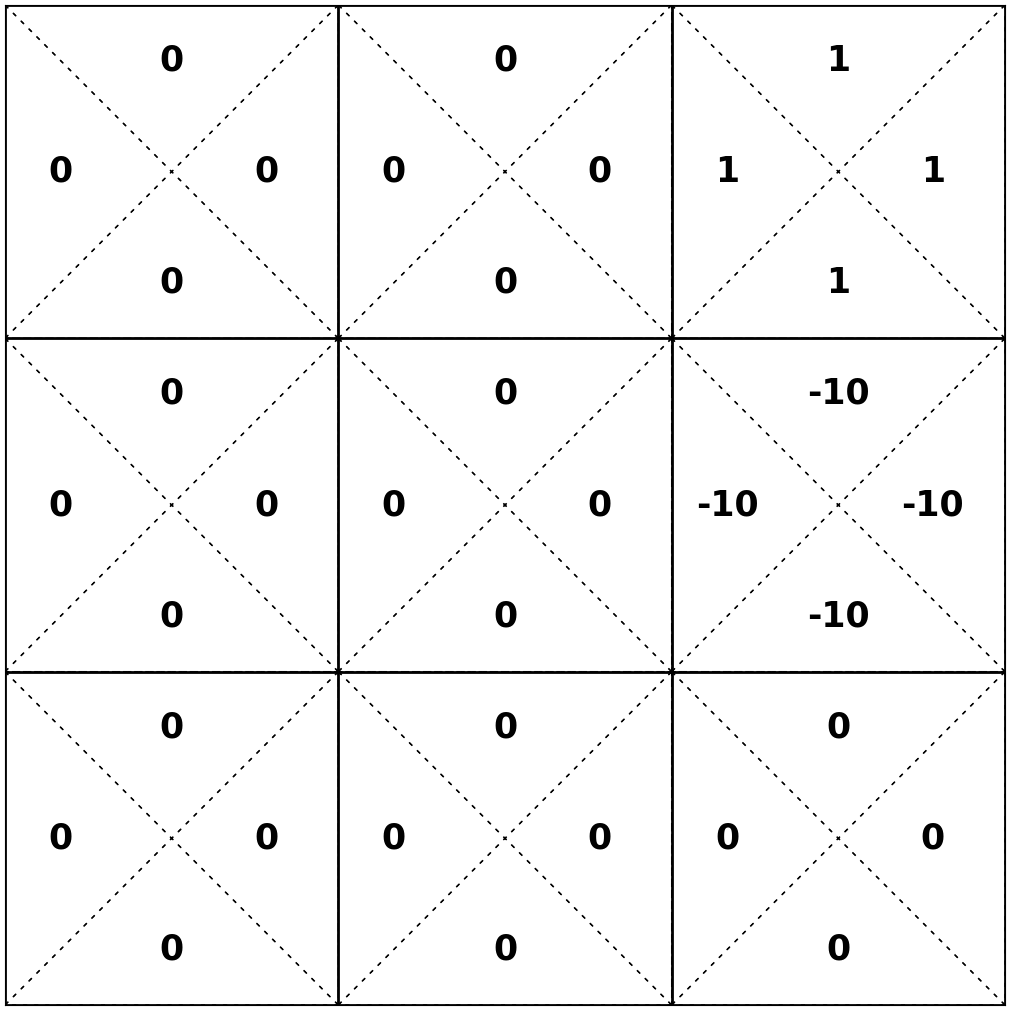
e.g. the best actions to take in state 5
- For finite \(h\), optimal policy \(\pi^*_h\) depends on how many time steps are left
- When \(h \rightarrow \infty\), time no longer matters, i.e., there exists a stationary \(\pi^*\)
\(\mathrm{V}\) values vs. \(\mathrm{Q}\) values
- \(\mathrm{V}\) is defined over states; \(\mathrm{Q}\) is defined over (state, action) pairs.
- \(\mathrm{V}_h^*({s})\) can be derived from \(\mathrm{Q}^*_h(s,a)\), and vise versa.
- \(\mathrm{Q}^*\) is easier to read "optimal actions" from.
- We care more about \(\mathrm{V}^{\pi}\) and \(\mathrm{Q}^*.\)
\(\mathrm{V}_{h}^*(s)=\max_{a}\left[\mathrm{Q}^*_{h}(s, a)\right]\)
\mathrm{V}^{\uparrow}_{61}(s)
\mathrm{V}^{\uparrow}_{62}(s)
\mathrm{V}^{\uparrow}_{\infty}(s)
\mathrm{V}^{*}_{61}(s)
\mathrm{V}^{*}_{62}(s)
\mathrm{V}^{*}_{\infty}(s)
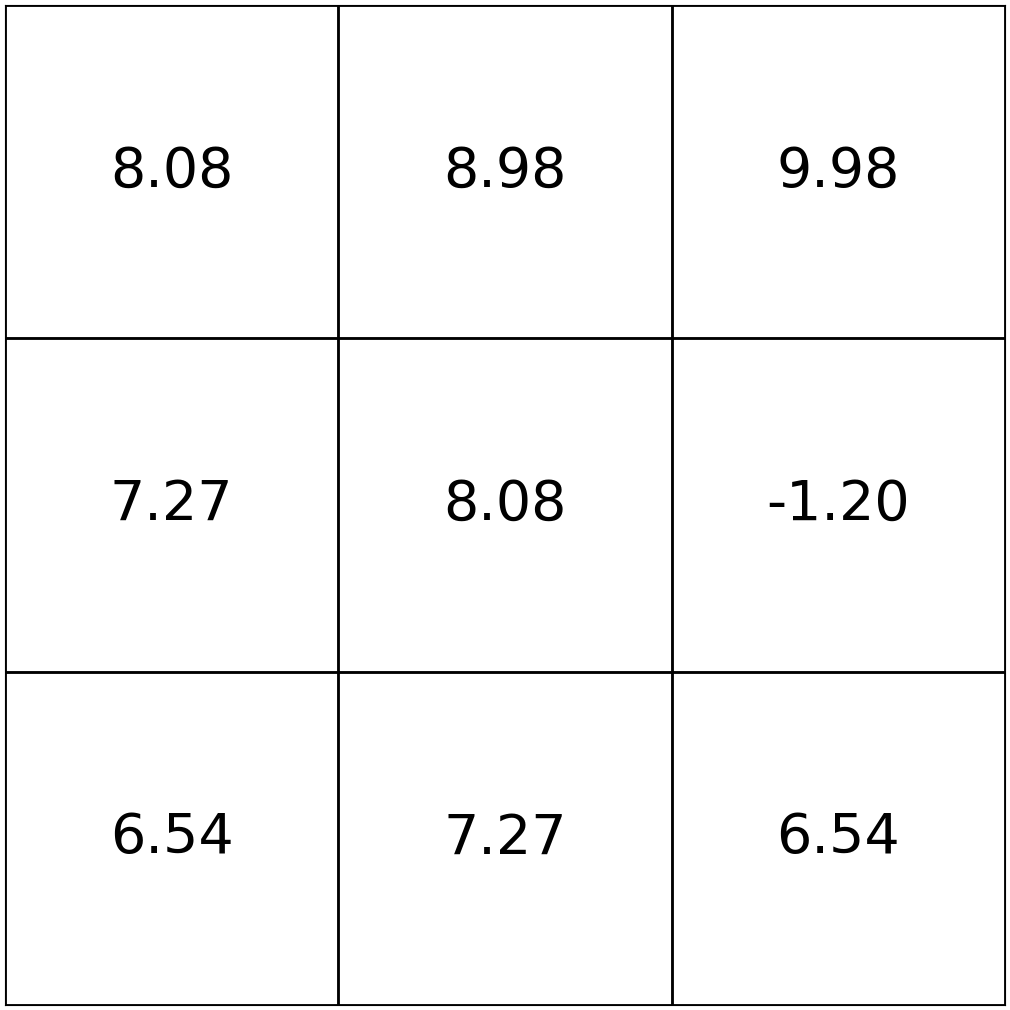
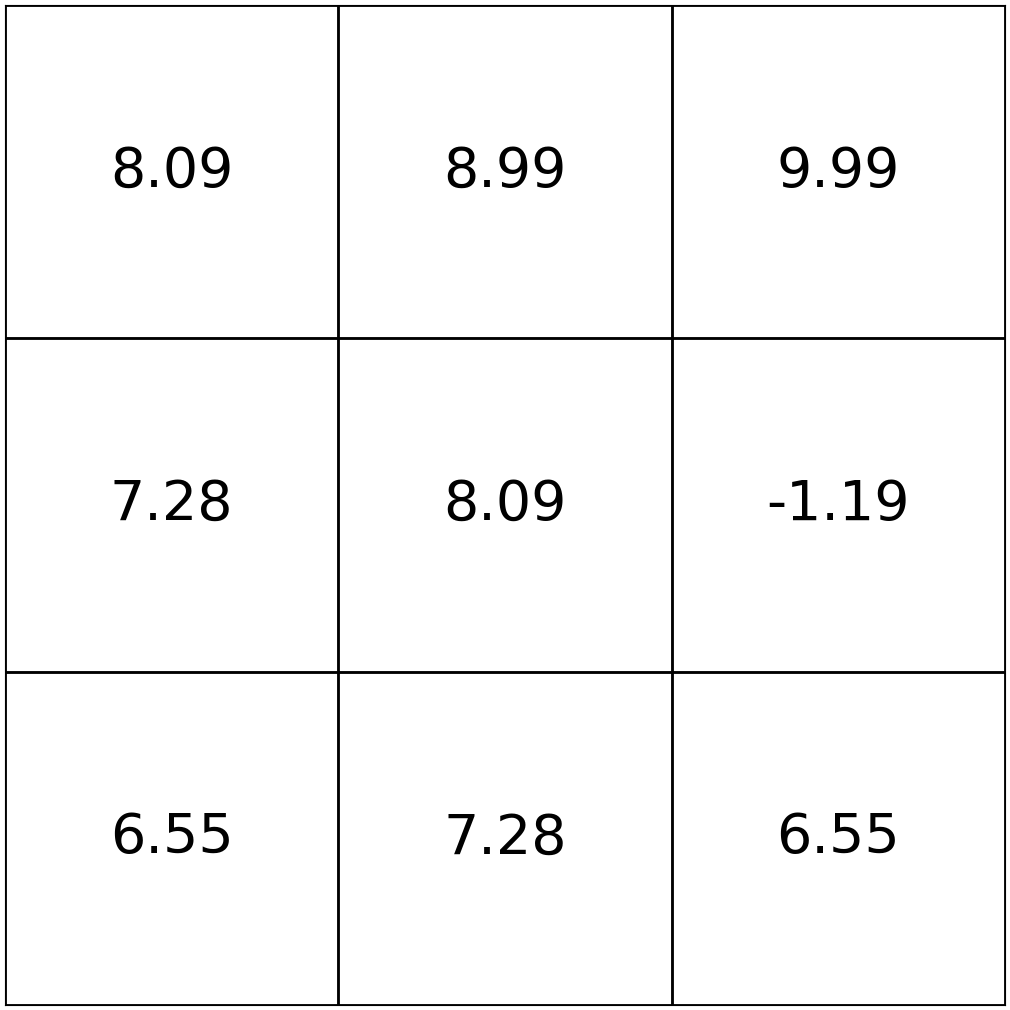
\(\mathrm{\pi}_{h}^*(s)=\arg\max_{a}\left[\mathrm{Q}^*_{h}(s, a)\right]\)
\mathrm{Q}^{*}_{61}(s,a)
\mathrm{Q}^{*}_{62}(s,a)
\mathrm{Q}^{*}_{\infty}(s,a)
Summary
- Markov decision processes (MDP) are a nice mathematical framework for making sequential decisions. It's the foundation to reinforcement learning.
- An MDP is defined by a five-tuple, and the goal is to find an optimal policy that leads to high expected cumulative discounted rewards.
- To evaluate how good a given policy \(\pi \) is, we can calculate \(\mathrm{V}^{\pi}(s)\) via
- the summation-over-rewards definition
- Bellman recursion for finite horizon and Bellman equation for infinite horizon
- To find an optimal policy, we can recursively find \(\mathrm{Q}^*(s,a)\) via the value iteration algorithm, and then act greedily w.r.t. the \(\mathrm{Q}^*\) values.
Thanks!
We'd love to hear your thoughts.
- An MDP has a unique optimal value \(\mathrm{V}_h^{*}({s})\)
- Optimal policy \(\pi^*\) might not be unique (e.g. symmetric world)
1.9
1.9
1
-8
-9.28
\(\mathrm{Q}_2^*(6, \uparrow) =\mathrm{R}(6,\uparrow) + \gamma[.2 \max _{a^{\prime}} \mathrm{Q}_{1}^*\left(2, a^{\prime}\right)+ .8\max _{a^{\prime}} \mathrm{Q}_{1}^*\left(3, a^{\prime}\right)] \)
\mathrm{Q}^*_h (s, a)=\mathrm{R}(s, a)+\gamma \sum_{s^{\prime}} \mathrm{T}\left(s, a, s^{\prime} \right) \max _{a^{\prime}} \mathrm{Q}^*_{h-1}\left(s^{\prime}, a^{\prime}\right), \forall s,a,h
in general
- starting in state \(s\),
- take action \(a\), for one step
- act optimally thereafter for the remaining \((h-1)\) steps
\mathrm{Q}_1^*(s, a)
=\mathrm{R}(s, a)
\mathrm{Q}_2^*(s, a)
\(\mathrm{Q}^*_h(s, a)\): the value for
\(\gamma = 0.9\)
States and one special transition:
80\%
20\%
Recall:
\mathrm{V}^{\uparrow}_{\infty}(s)
states and
one special transition:
rewards
- \(\pi(s) = ``\uparrow",\ \forall s\)
- \(\gamma = 0.9\)
80\%
20\%
= -10 +.9[.2*0+0.8*10]\Rightarrow -2.8
\mathrm{V}^{\uparrow}_{\infty}(6) = \mathrm{R}(6, \uparrow) + \gamma [.2 \times \mathrm{V}^{\uparrow}_{\infty}(2) + .8\times \mathrm{V}^{\uparrow}_{\infty}(3)]
\mathrm{V}^{\uparrow}_{\infty}(3) = \mathrm{R}(3, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{\infty}(3)]
= 1 + .9 \times 10 \Rightarrow 10
\mathrm{V}^{\uparrow}_{\infty}(9) = \mathrm{R}(9, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{\infty}(6)]
= 0 + 0.9 * [-2.8] \Rightarrow -2.52
self-consistent set of equations apply to the other five states as well
\mathrm{V}^{\uparrow}_{\infty}(2) = \mathrm{R}(2, \uparrow) + \gamma [\mathrm{V}^{\uparrow}_{\infty}(2)]
= 0 + .9 \times 0 \Rightarrow 0
Bellman Equation (horizon \(h \to \infty\))
\mathrm{V}^\pi_{\infty}(s)= \mathrm{R}(s, \pi(s))+ \gamma \sum_{s^{\prime}} \mathrm{T}\left(s, \pi(s), s^{\prime}\right) \mathrm{V}^\pi_{\infty}\left(s^{\prime}\right)
6.390 IntroML (Fall25) - Lecture 11 Markov Decision Processes
By Shen Shen
