Intro to Machine Learning
Lecture 12: Unsupervised Learning
Shen Shen
May 3, 2024
(many slides adapted from Phillip Isola and Tamara Broderick)
Logistics
- This is the last regular lecture; next week is the last regular week.
- Friday, May 10
- Lecture time, discuss future topics (generativeAI).
- By the end of the day, all assignments will be due.
- Tuesday, May 14
- 20-day extensions applicable through this day.
- Last regular OHs (for checkoffs/hw etc); afterwards only Instructor OHs.
- 6-8pm, 10-250, final exam review.
- The end-of-term subject evaluations are open. We'd love to hear your thoughts on 6.390: this provides valuable feedback for us and other students, for future semesters!
- Check out final exam logistics on introML homepage.
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
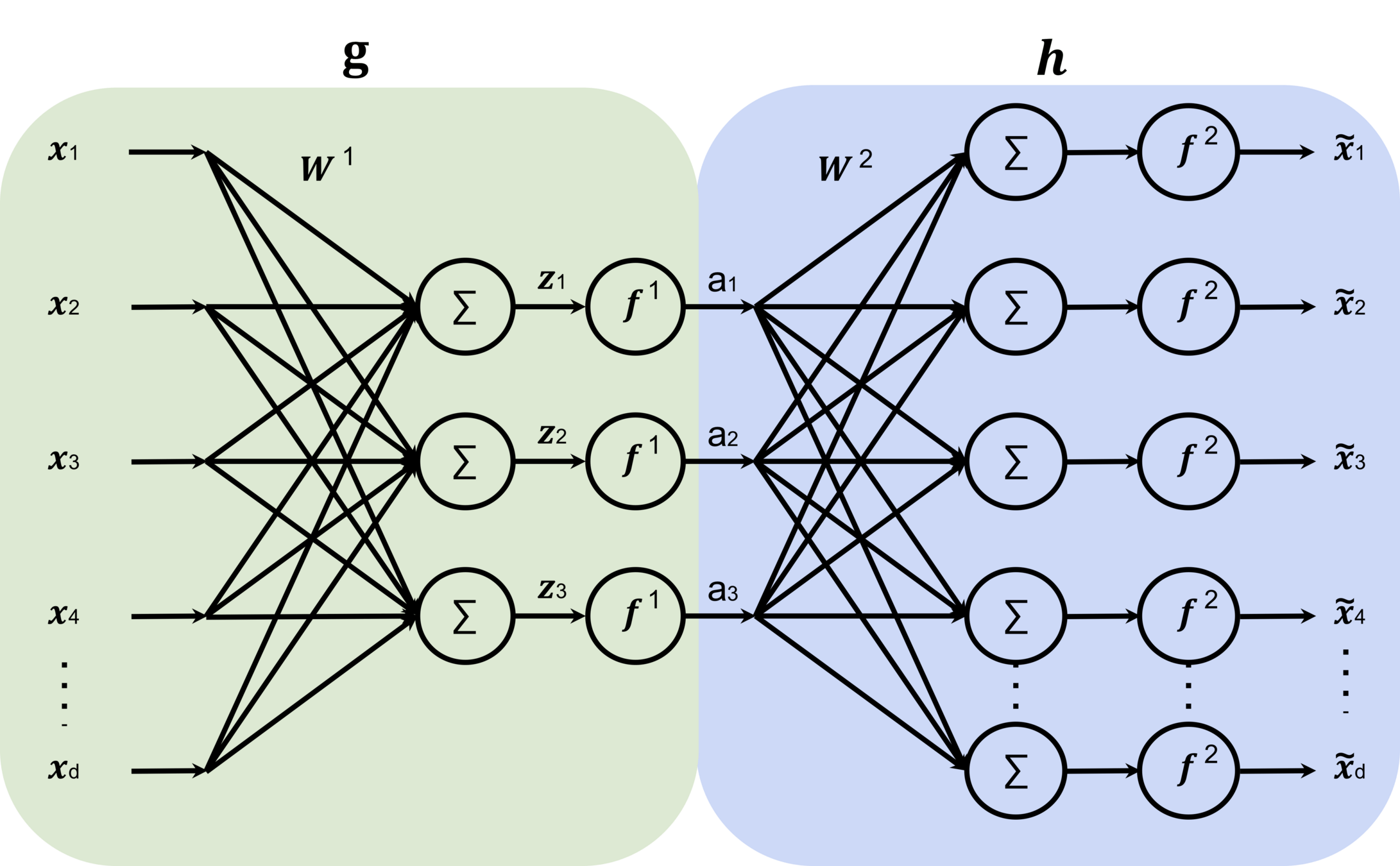
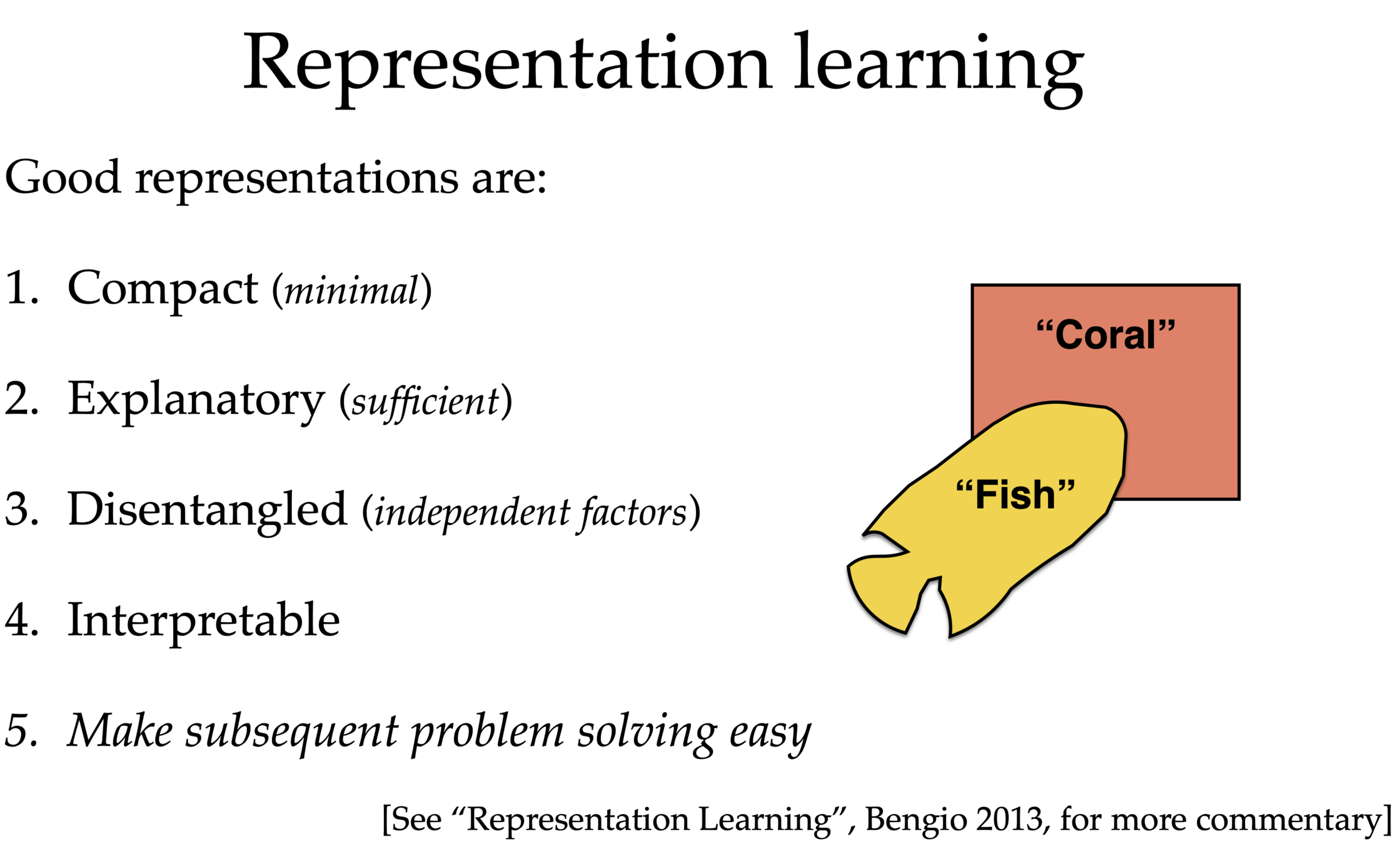
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
f: x \rightarrow y
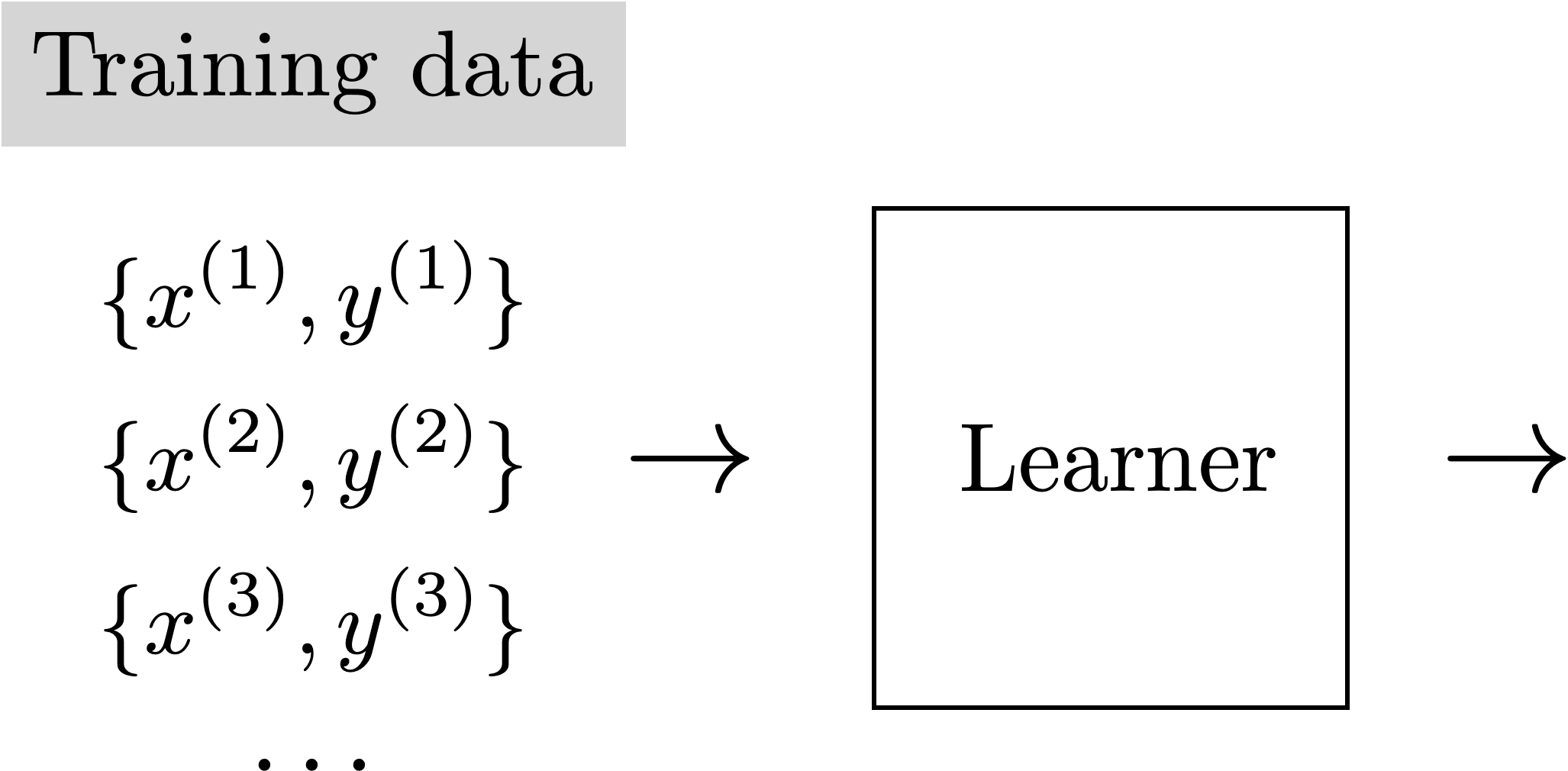
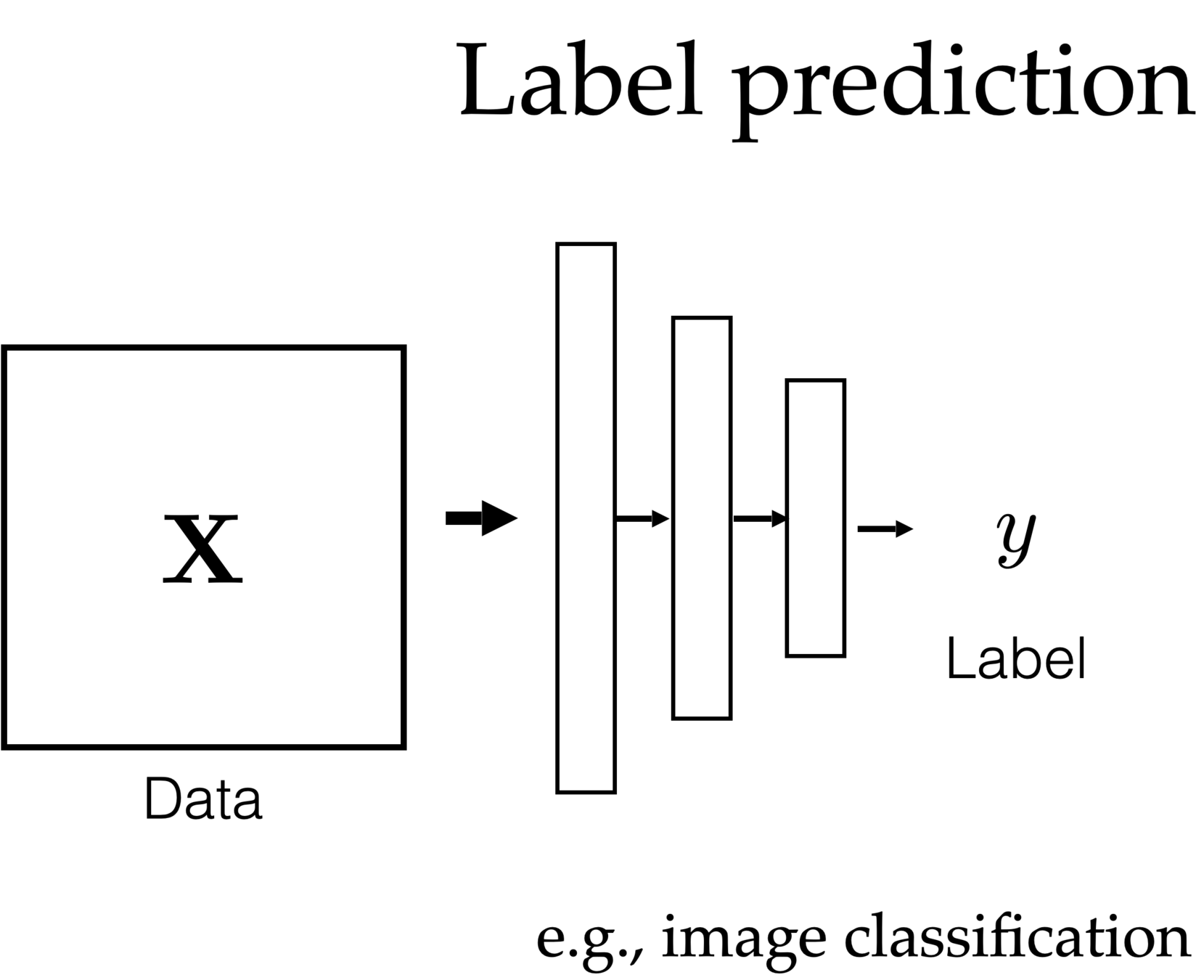
Supervised learning
- explicit supervision via labels \(y\).
- both regression or classification are trying to predict accurate, exact labels.
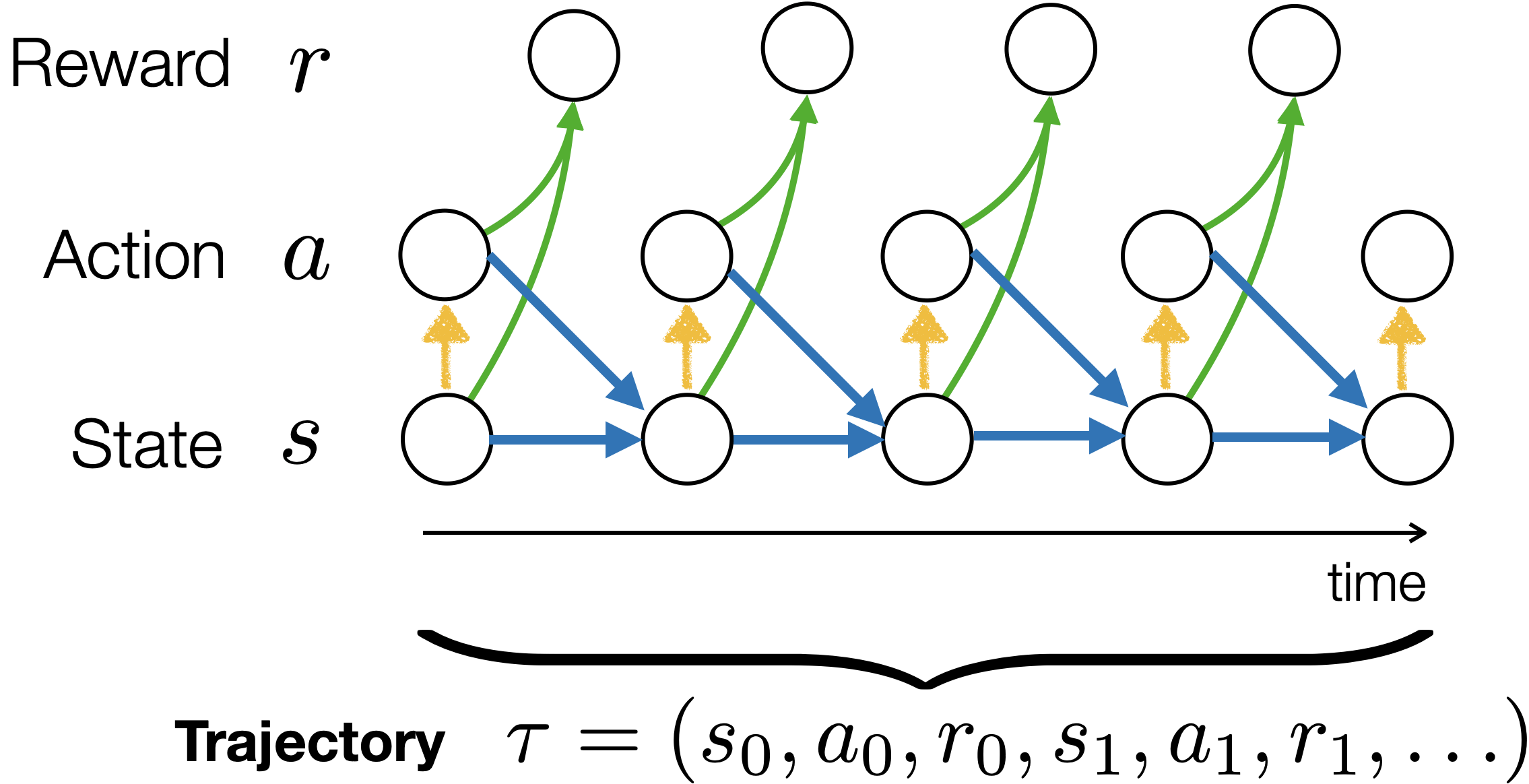
Reinforcement learning
- implicit(evaluative), sequential, iterative supervision via rewards.
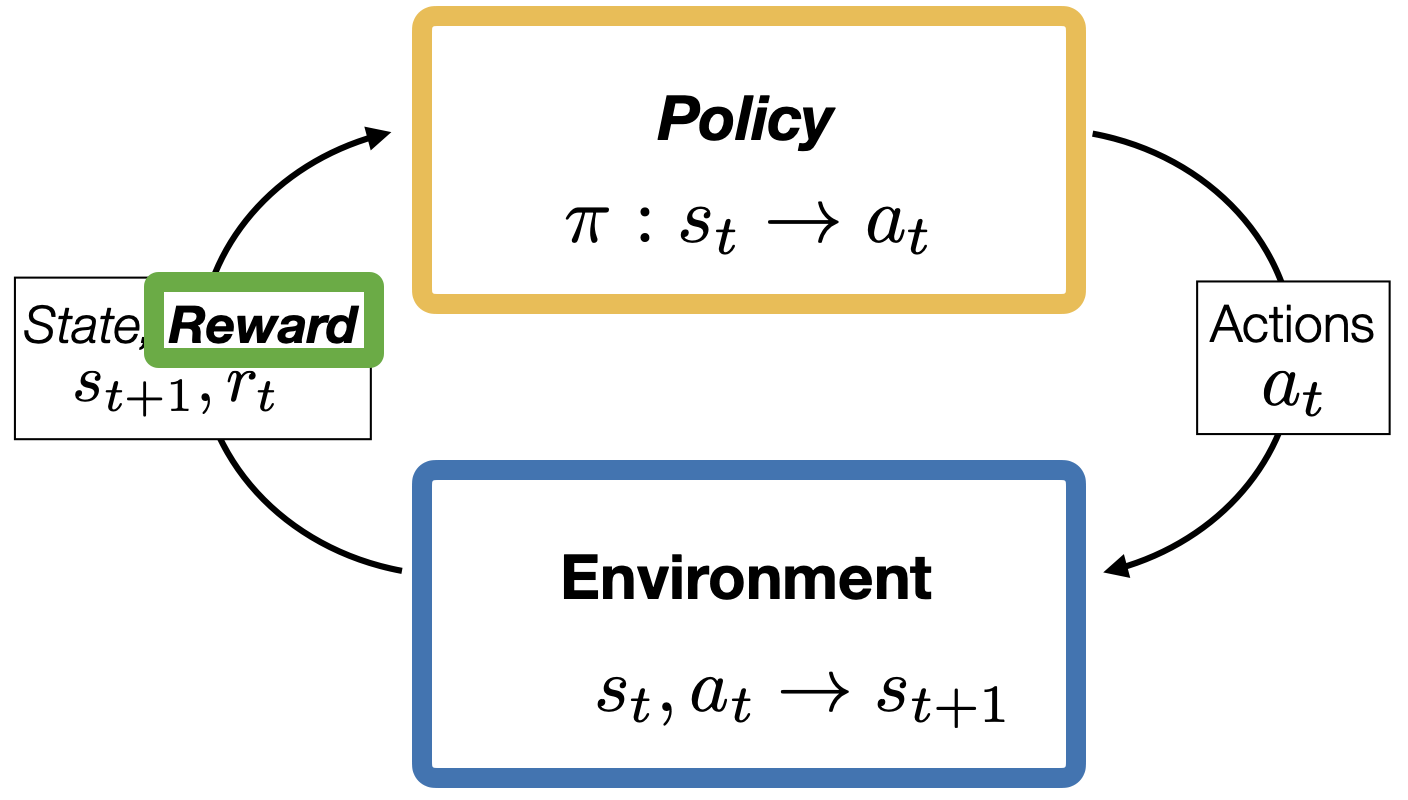
Learner
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
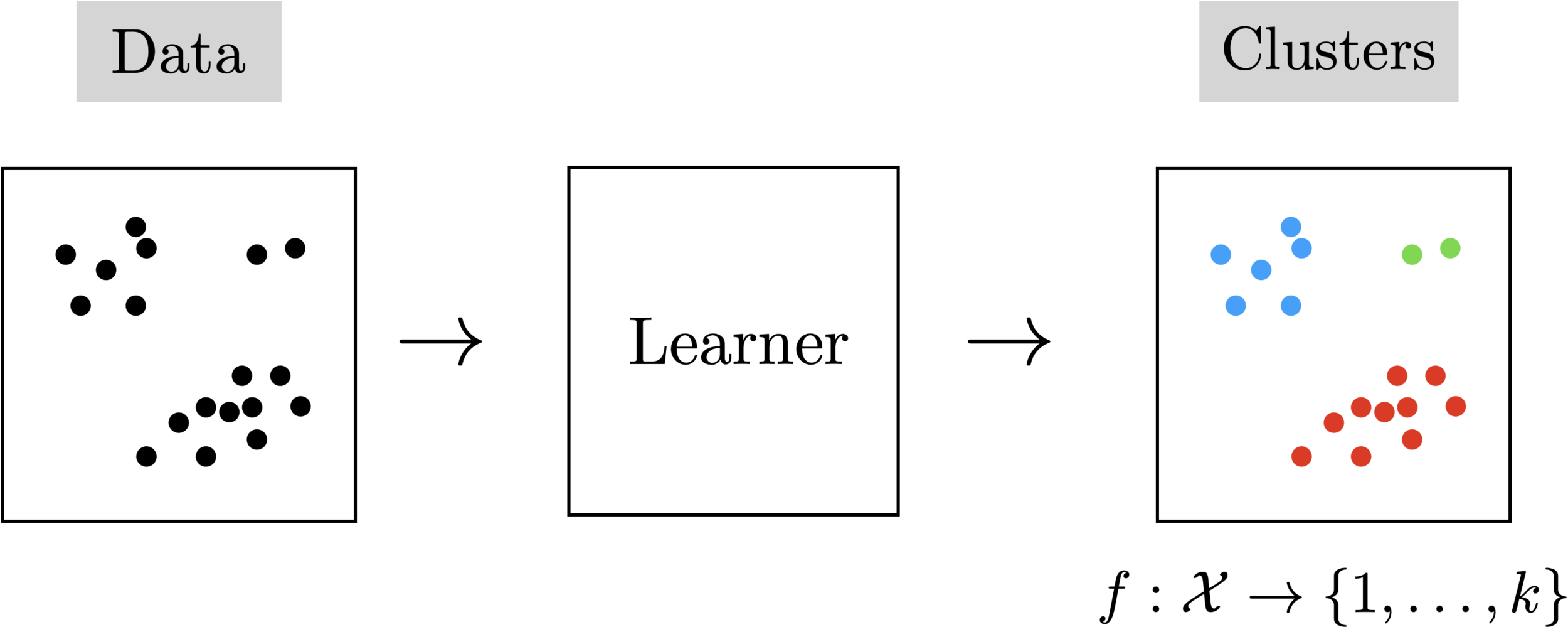
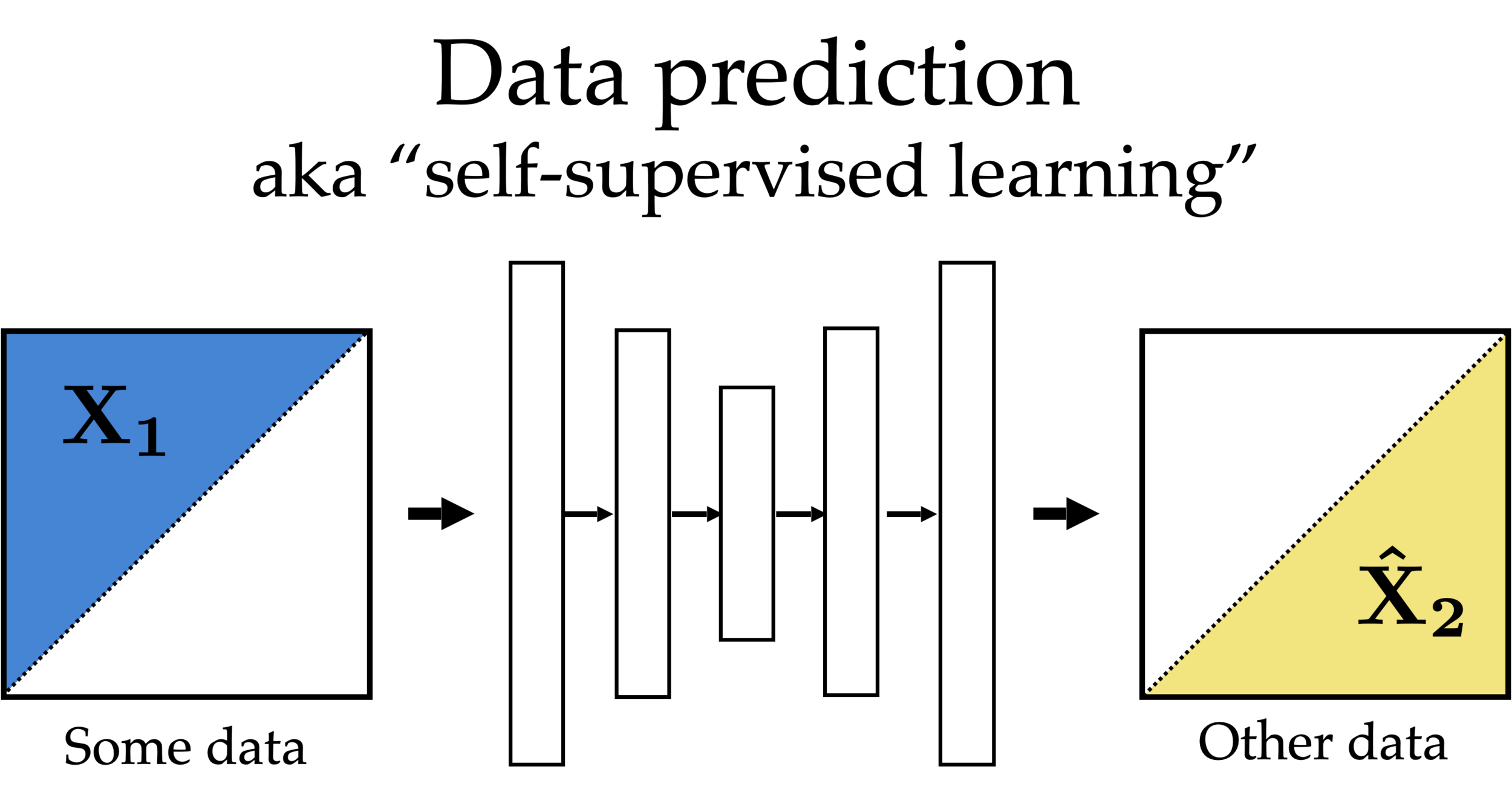
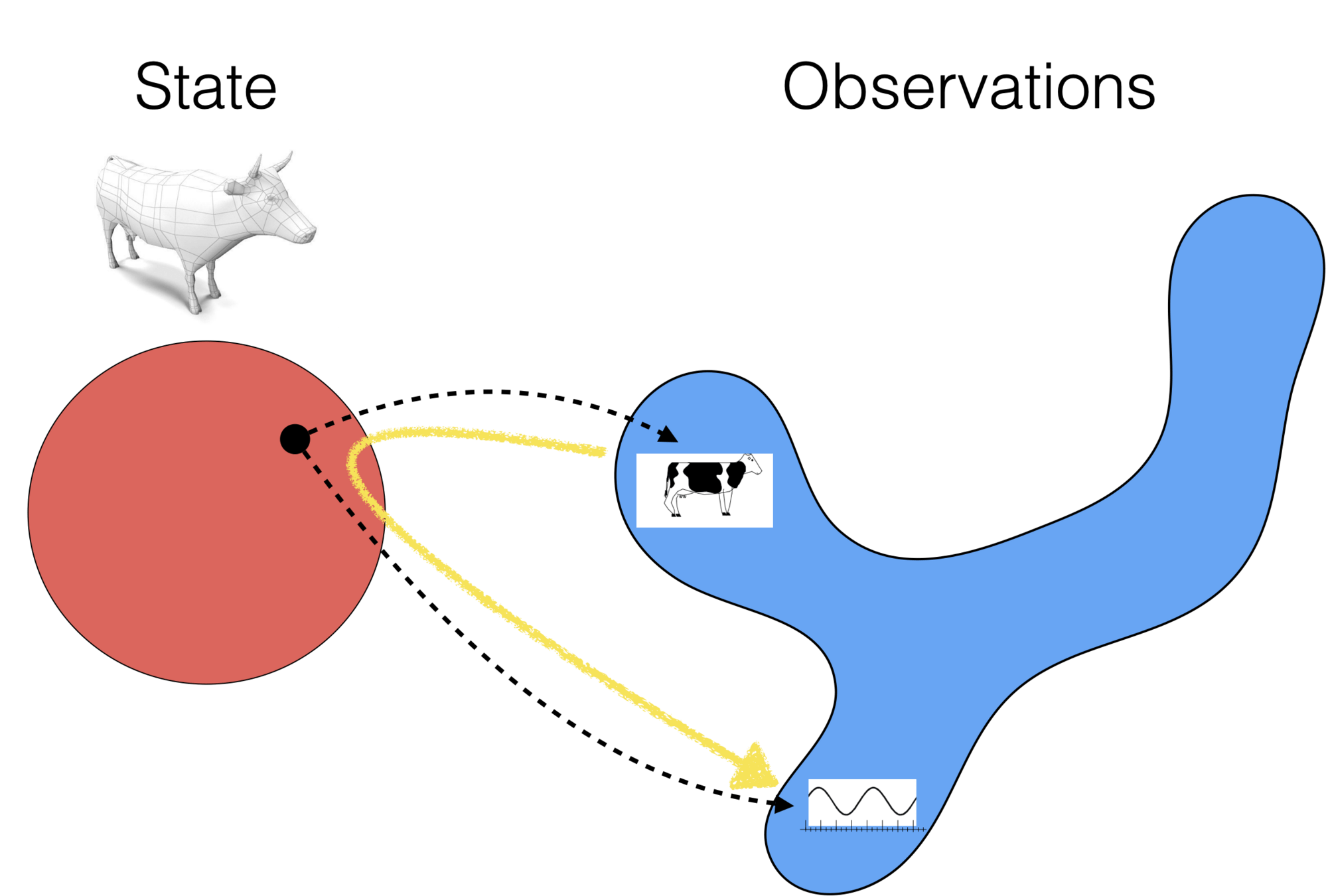
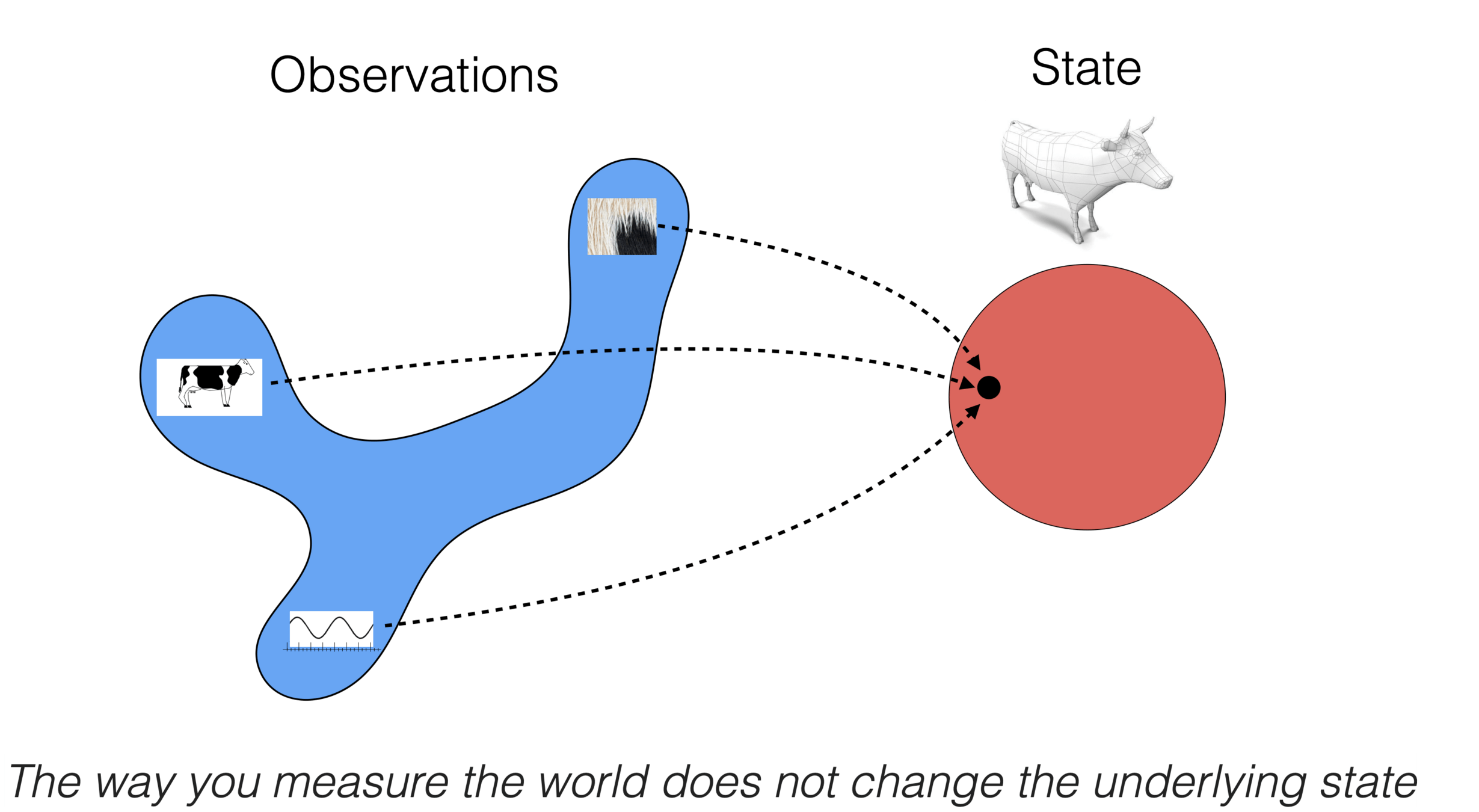
Unsupervised learning
- No supervision, i.e., no labels nor rewards.
- try to learn something "interesting" using only the features
- Clustering: learn "similarity" of the
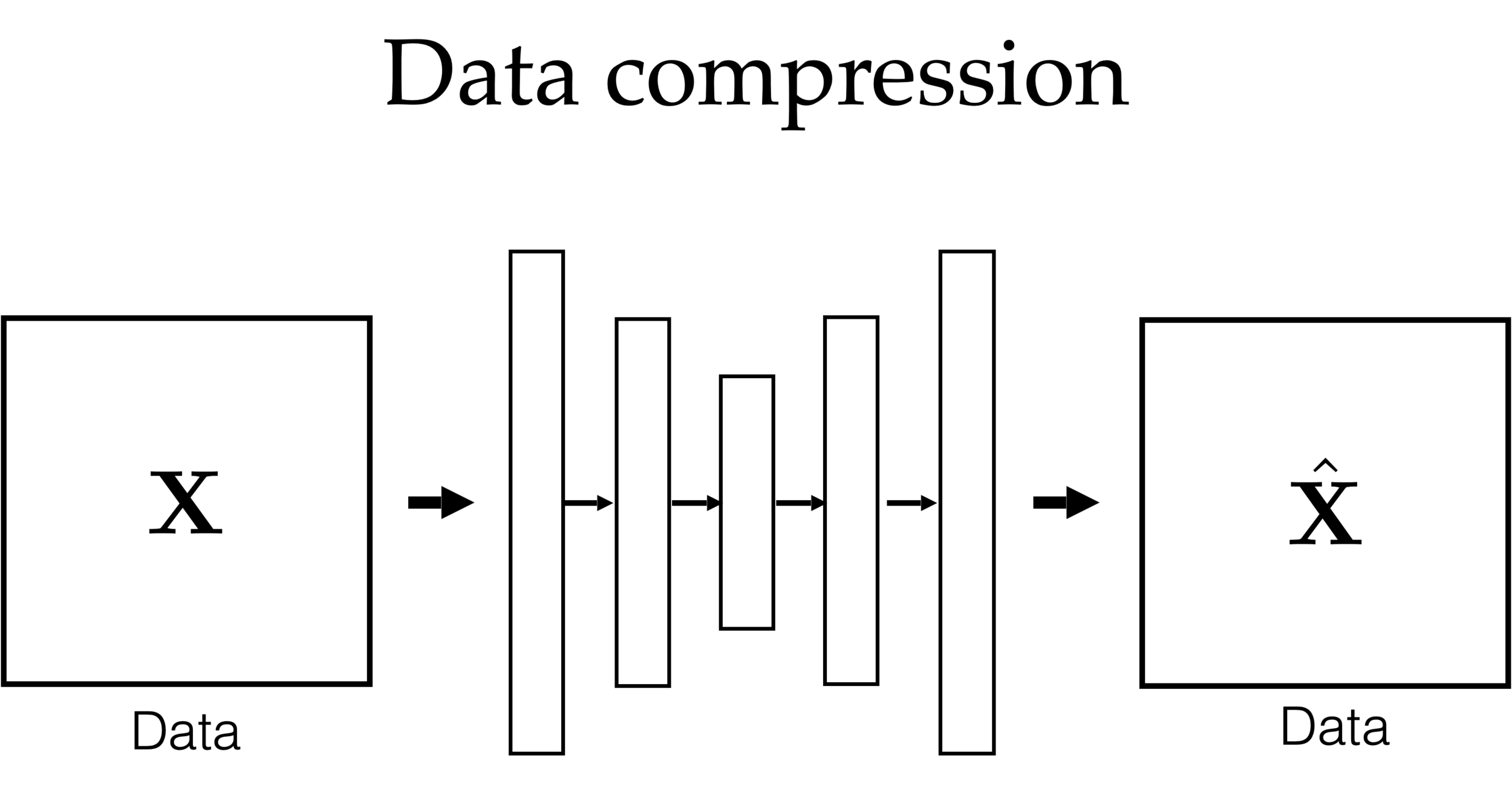
- Autoencoder: learn compression/reconstruction/representation
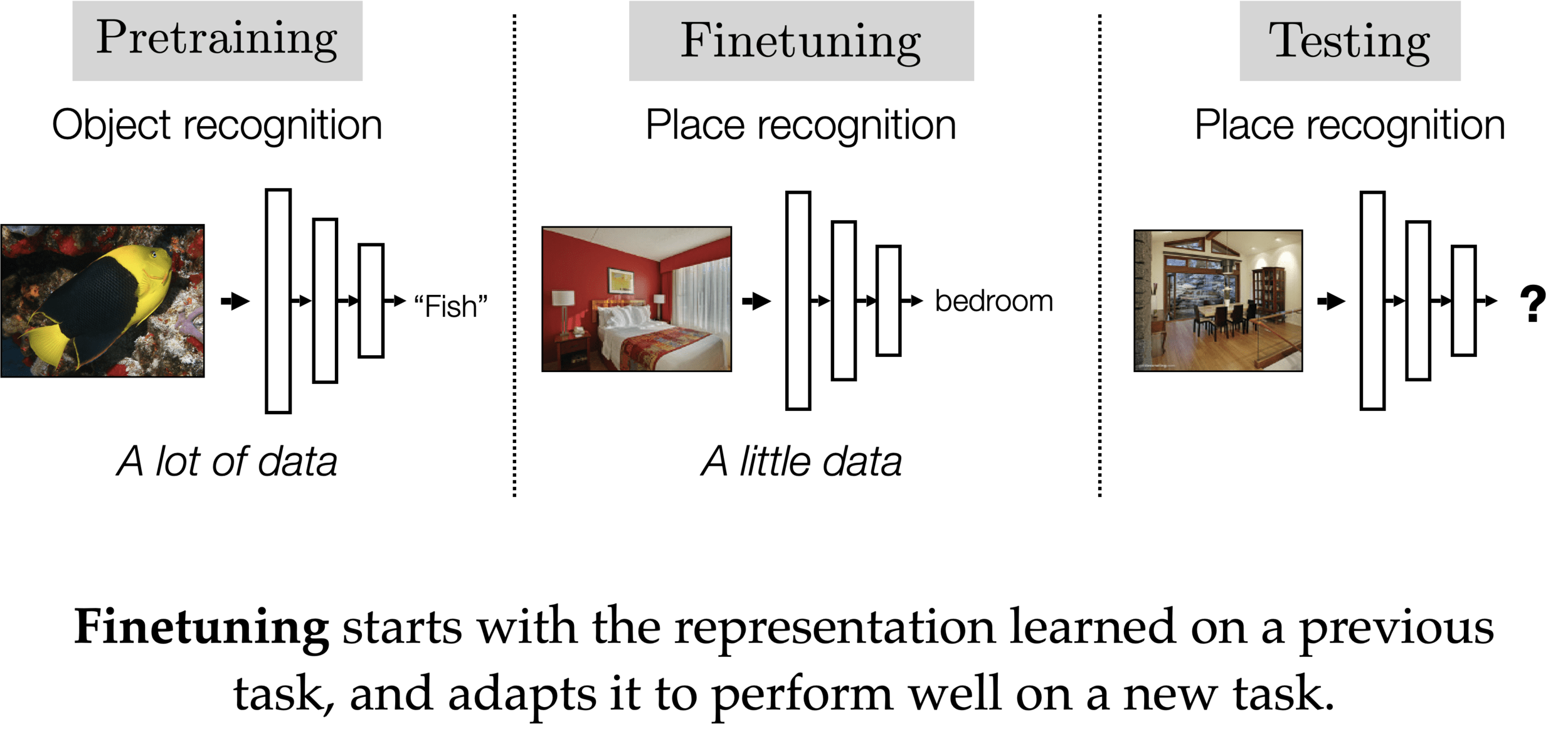
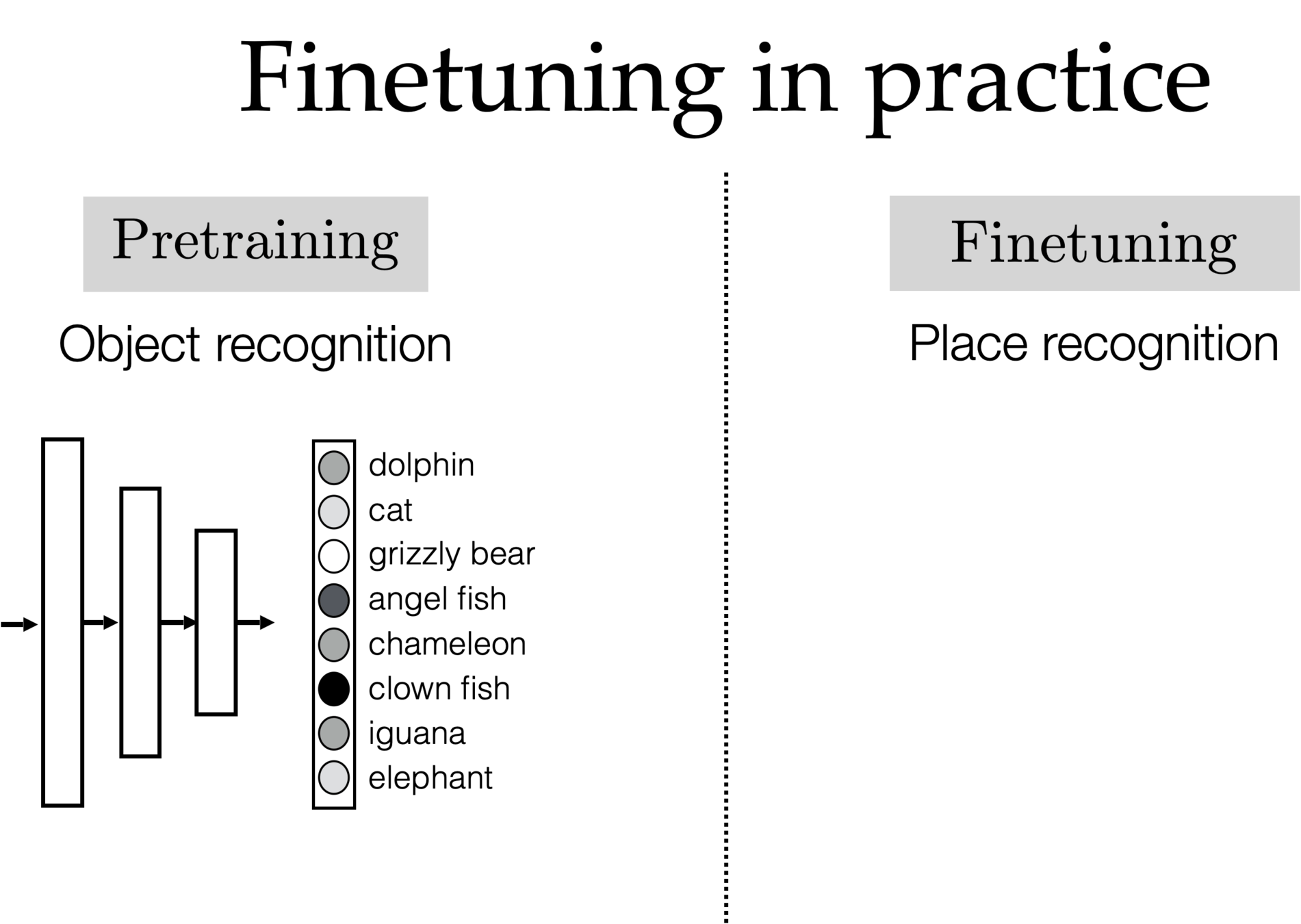
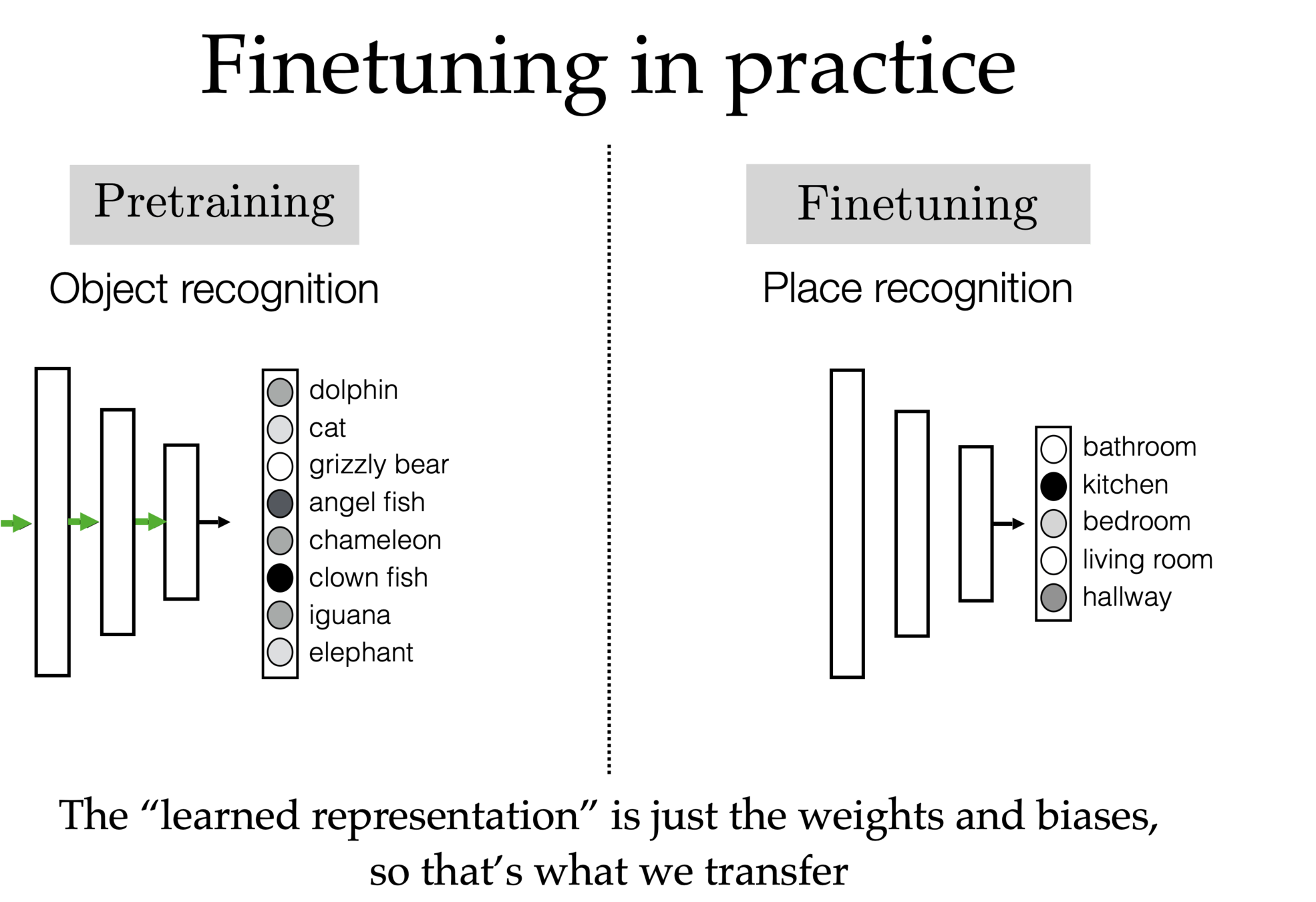
- useful paradigm on its own; often empowers downstream tasks.
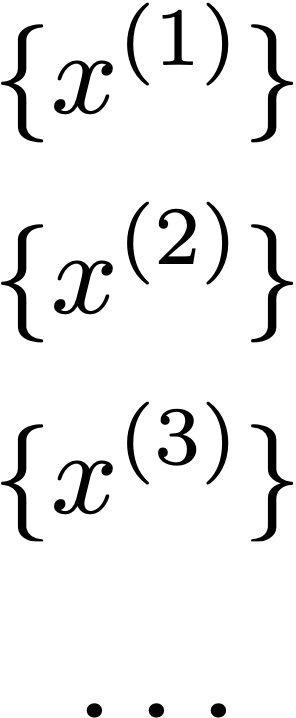
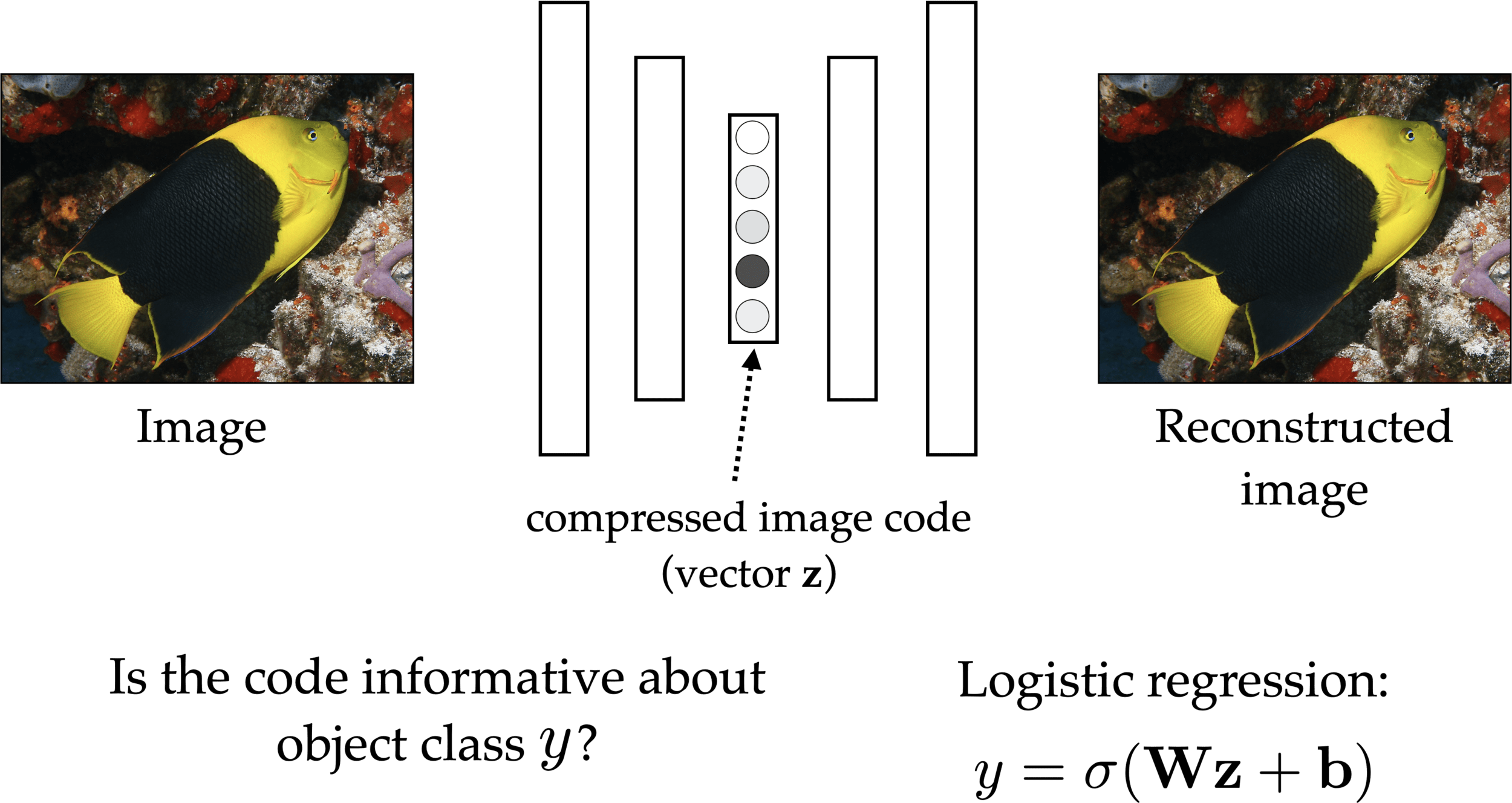
Autoencoder
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
x_1
x_2
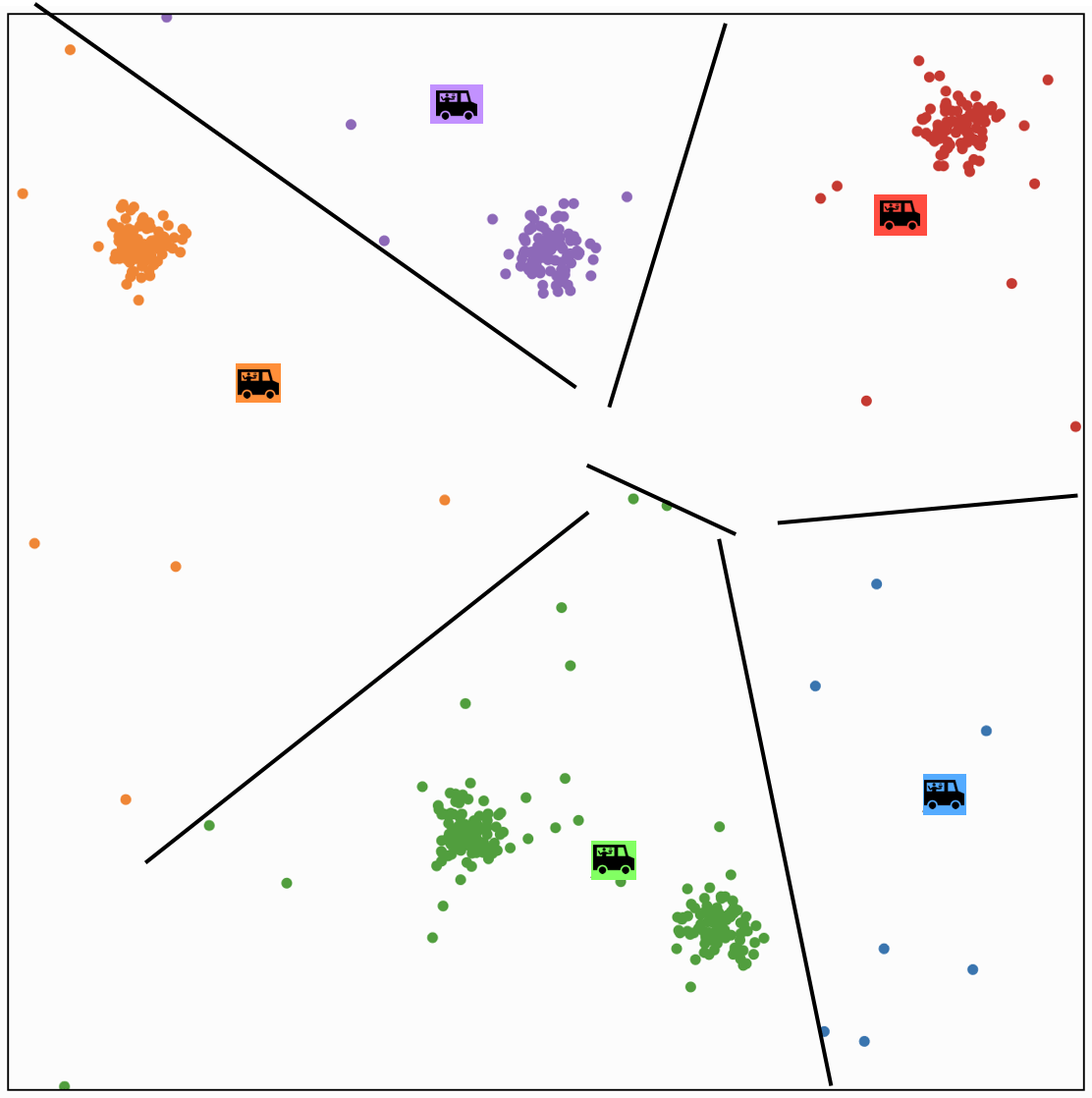
Food distribution placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Food truck \(j\) location \(\mu^{(j)}\)
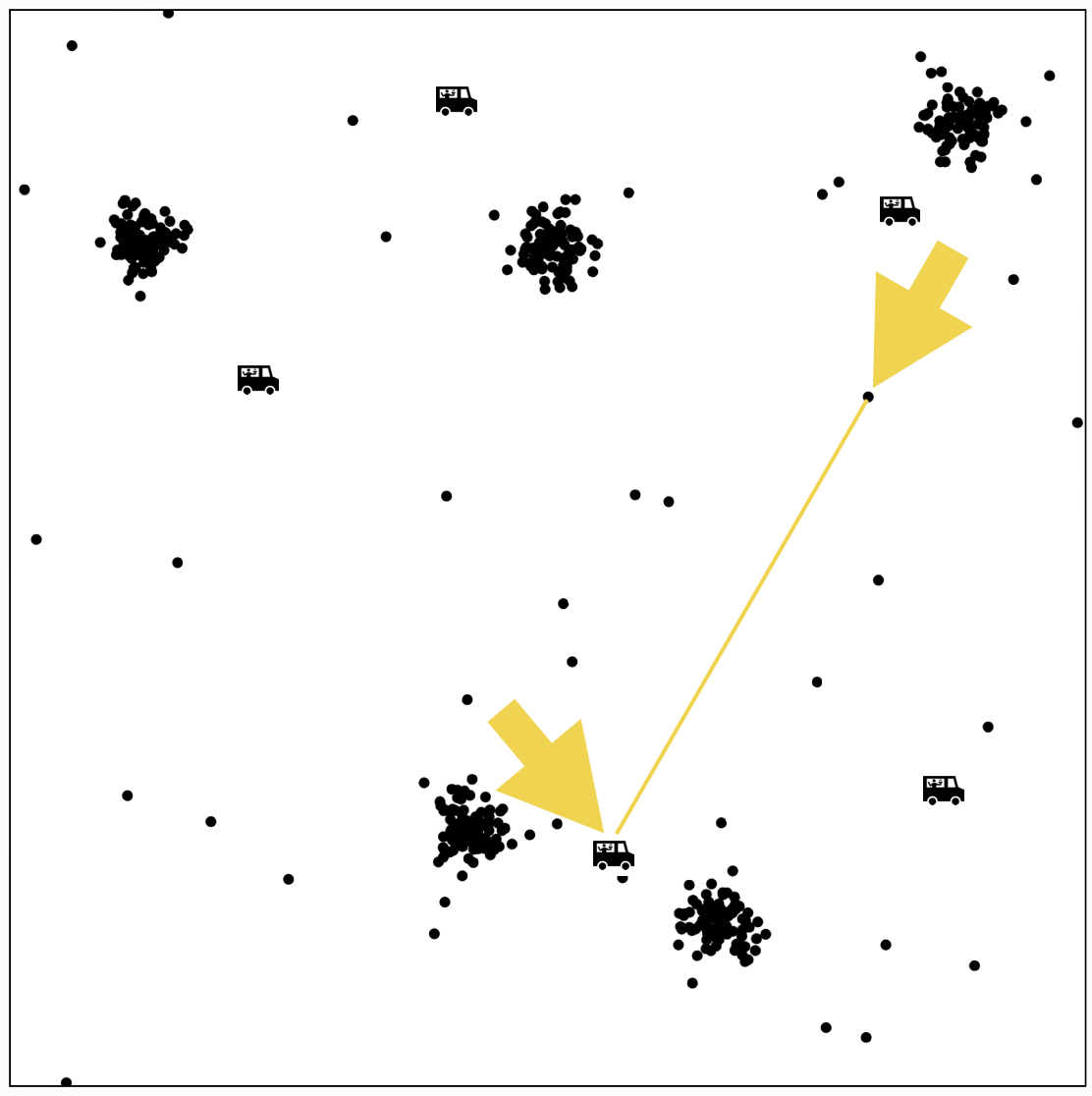
- Q: where should I have my \(k\) food trucks park?
- want to minimize the "loss" of people we serve
- Loss if \(i\) walks to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
- Index of the truck where person \(i\) is chosen to walk to: \(y^{(i)}\)
x_1
x_2
Food distribution placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
x_1
x_2
Food distribution placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have my \(k\) food trucks park?
x_1
x_2
Food distribution placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have my \(k\) food trucks park?
- Food truck \(j\) location \(\mu^{(j)}\)
- Want to minimize the "loss" of people we serve
x_1
x_2
Food distribution placement
- \(x_1\): longitude, \(x_2\): latitude
- Person \(i\) location \(x^{(i)}\)
- Q: where should I have my \(k\) food trucks park?
- Food truck \(j\) location \(\mu^{(j)}\)
Want to minimize the "loss" of people we serve - Loss if \(i\) walks to truck \(j\) : \(\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
- Index of the truck where person \(i\) is chosen to walk to: \(y^{(i)}\)
Loss over all people \(\sum_{i=1}^n \sum_{j=1}^k \mathbf{1}\left\{y^{(i)}=j\right\}\left\|x^{(i)}-\mu^{(j)}\right\|_2^2\)
\(k\)-means objective
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu\) random initialization
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu\) random initialization
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
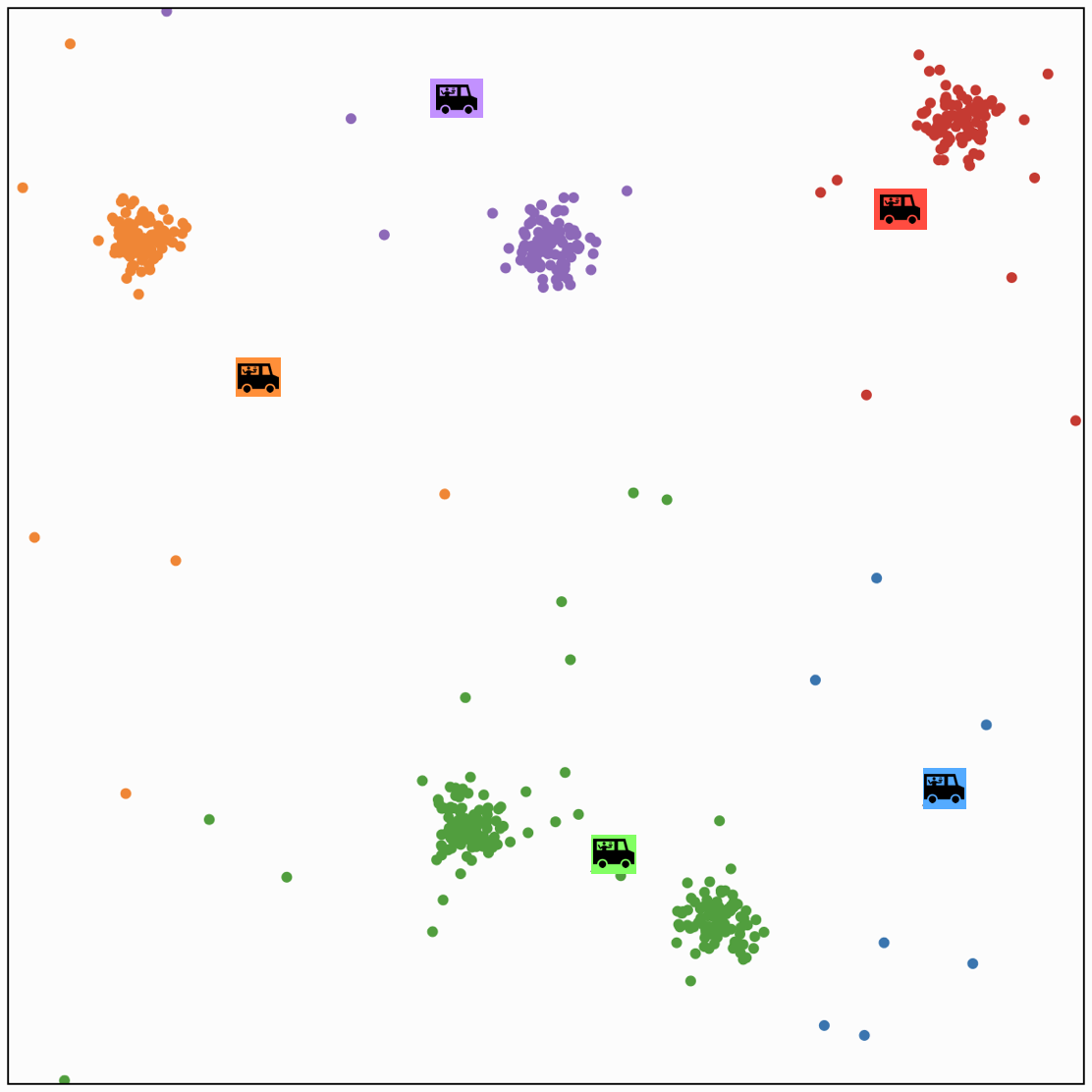
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
each person \(i\) gets assigned to a food truck \(j\), color-coded.
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu\) random initialization
each person \(i\) gets assigned to a food truck \(j\), color-coded.
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
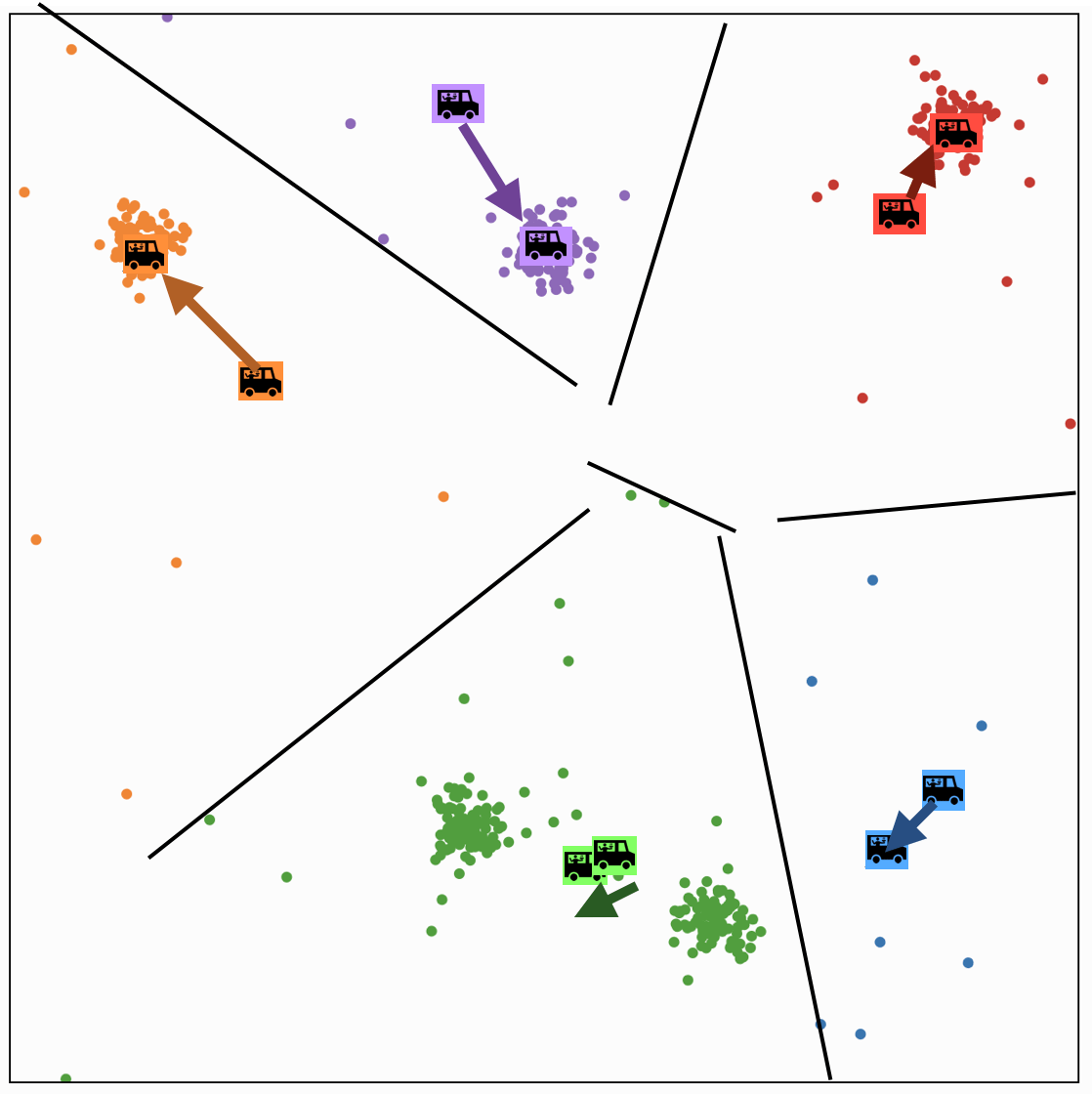
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
food truck \(j\) gets moved to the "central" location of all ppl assigned to it
\(N_j = \sum_{i=1}^n \mathbf{1}\left\{y^{(i)}=j\right\}\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
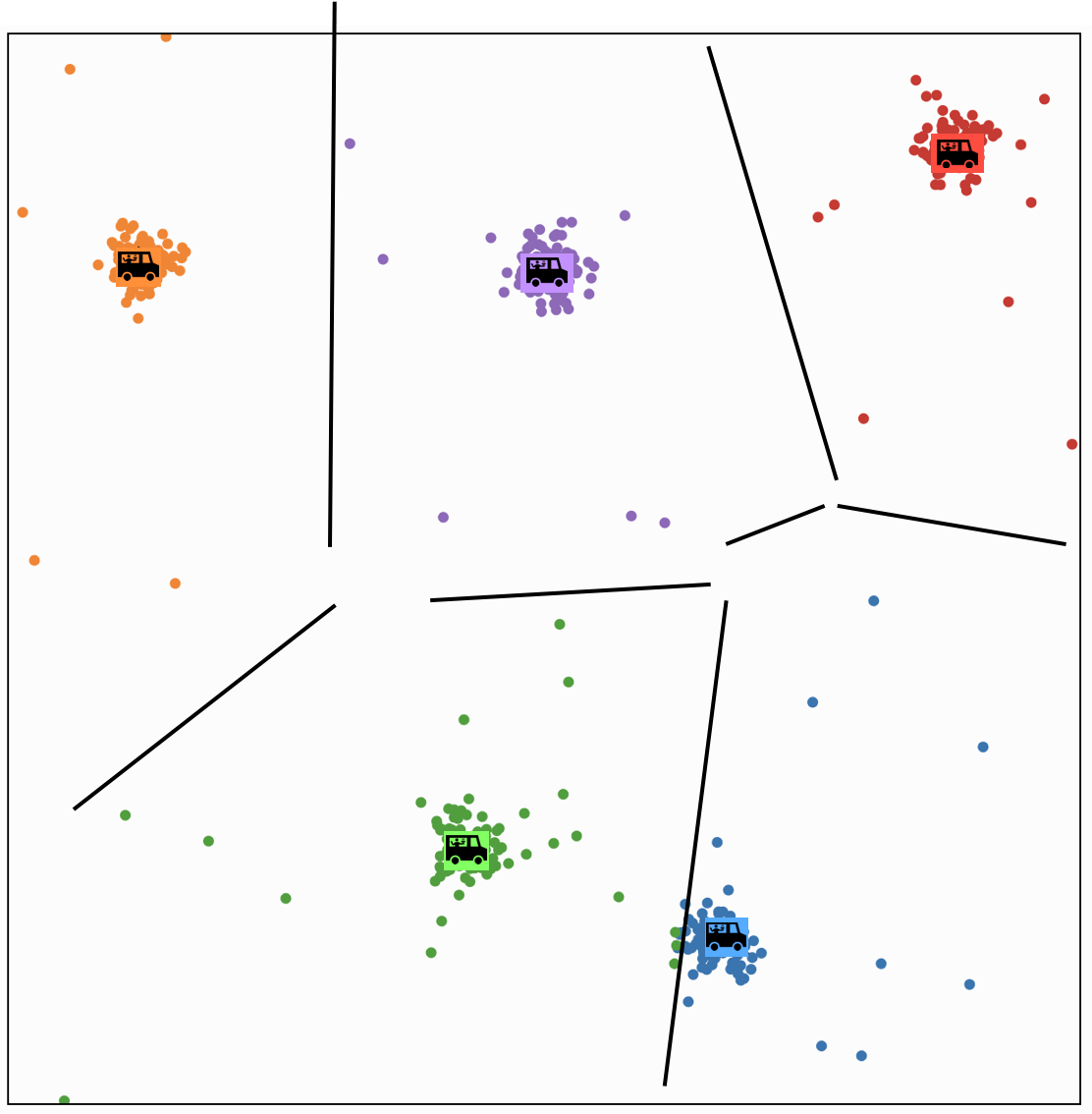
continue (ppl assignment then truck movement) update
at some point.
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu=\) random initialization
2 for \(t=1\) to \(\tau\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
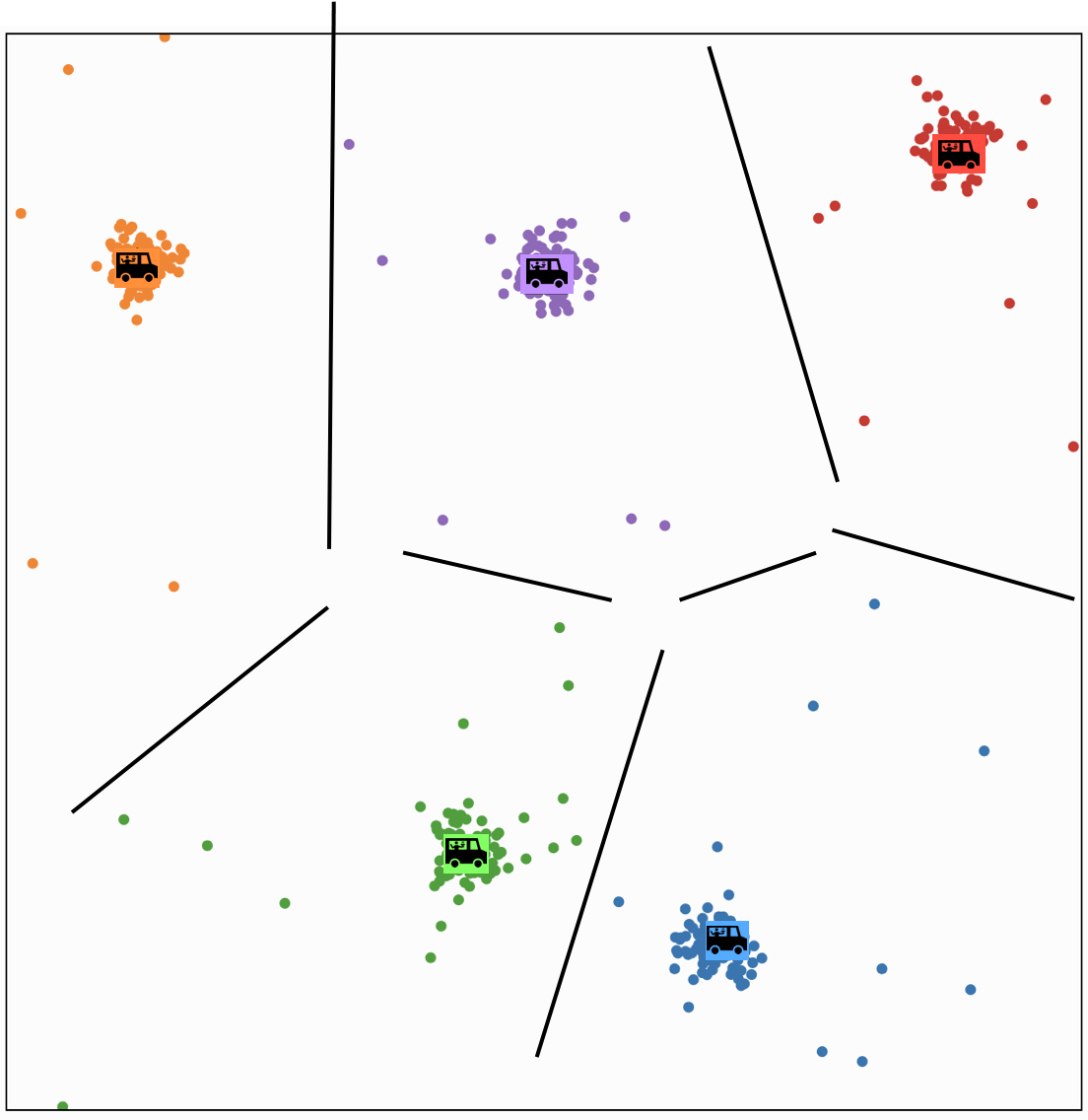
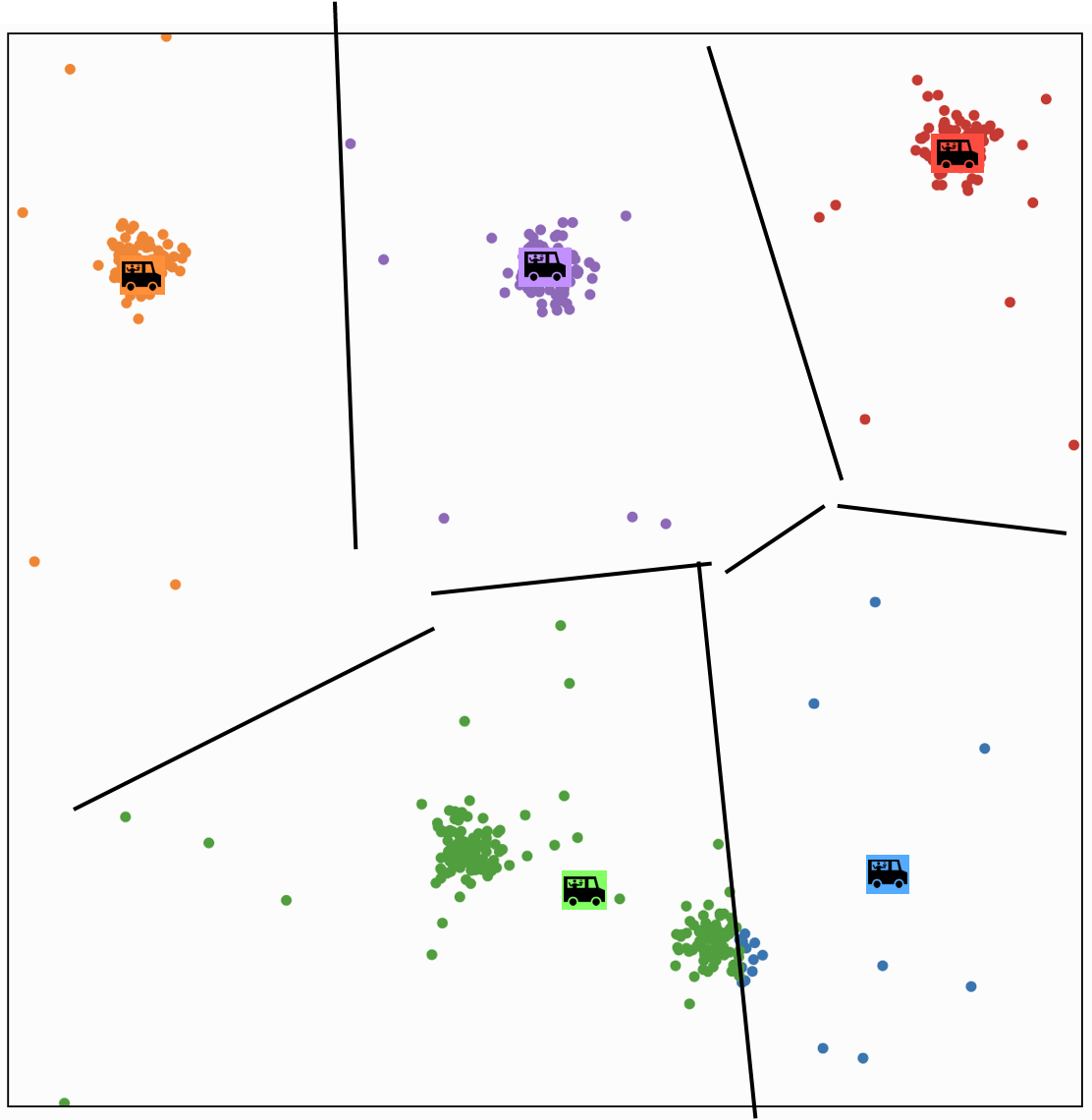
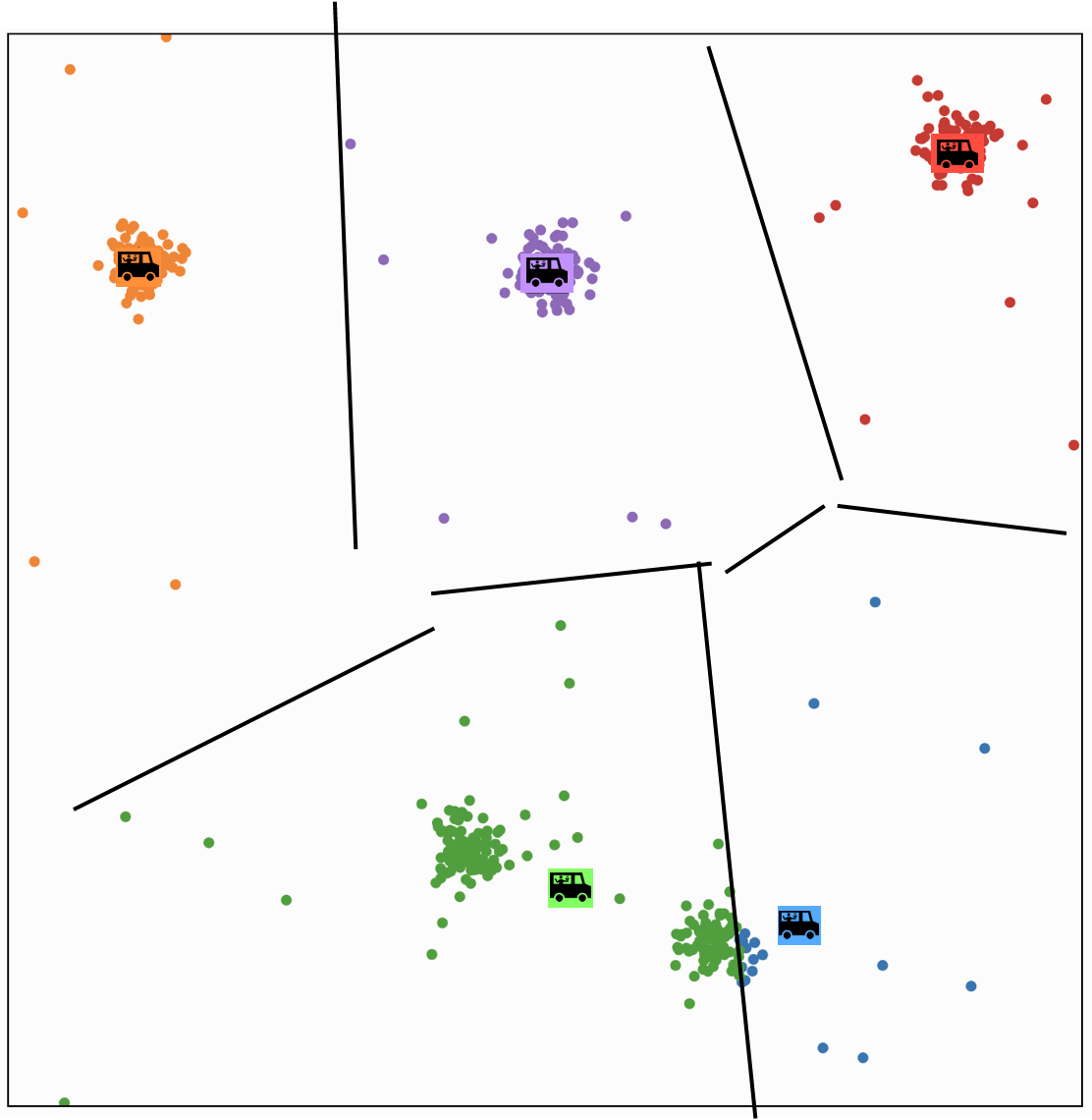
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
(ppl assignment and truck location) will stop changing
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
3 \(y_{o l d}=y\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
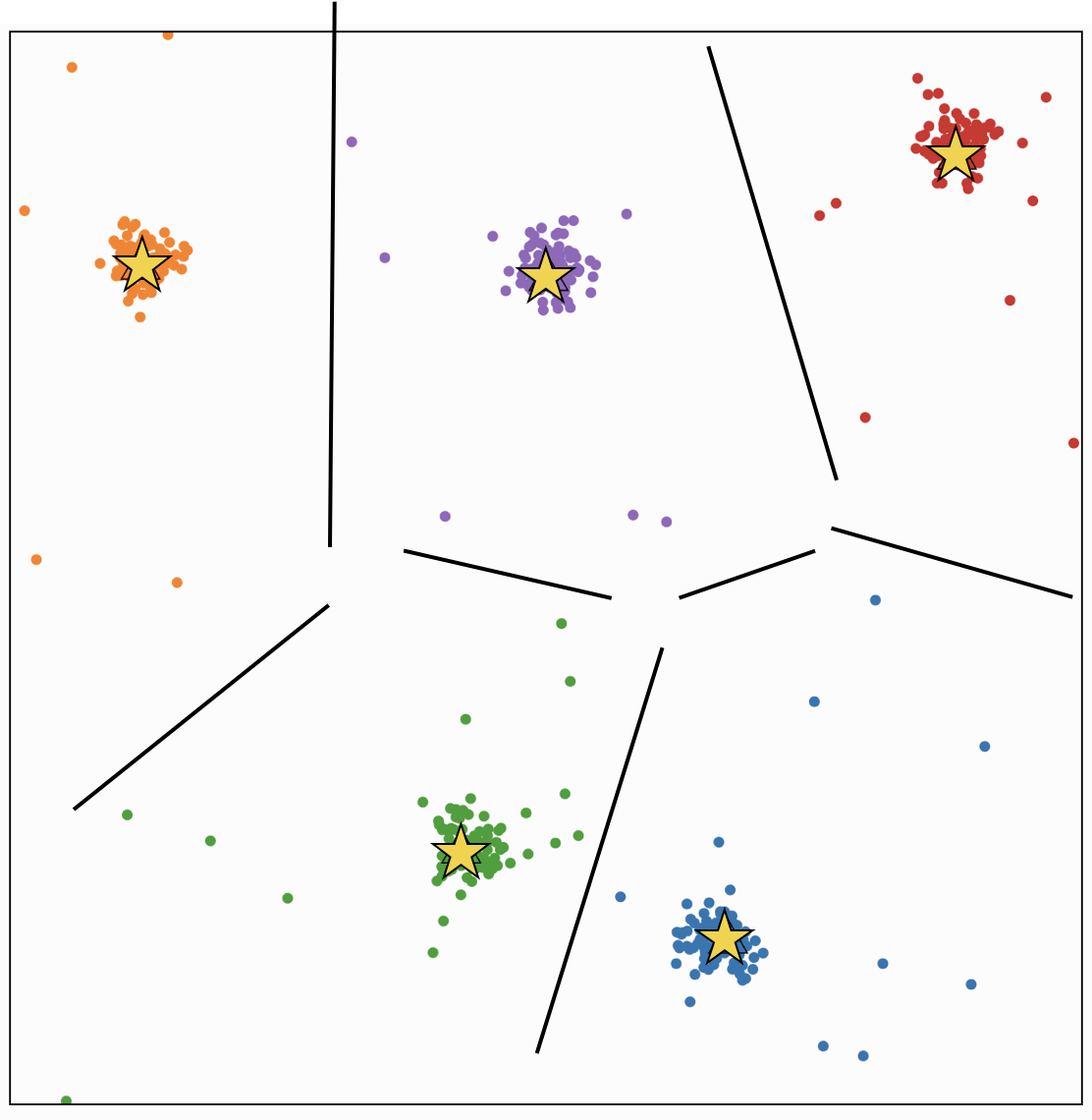
\(k\)-means
Compare to classification
- Did we just do \(k\)-class classification?
- Looks like we assigned label \(y^{(i)}\), which takes \(k\) different values, to each feature vector \(x^{(i)}\)
- But we didn't use any labeled data
- The "labels" here don't have meaning; I could permute them and have the same result
- Output is really a partition of the data
Compare to classification
- So what did we do?
- We clustered the data: we grouped the data by similarity
- Why not just plot the data? We should! Whenever we can!
- But also: Precision, big data, high dimensions, high volume
- An example of unsupervised learning: no labeled data, and we're finding patterns
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
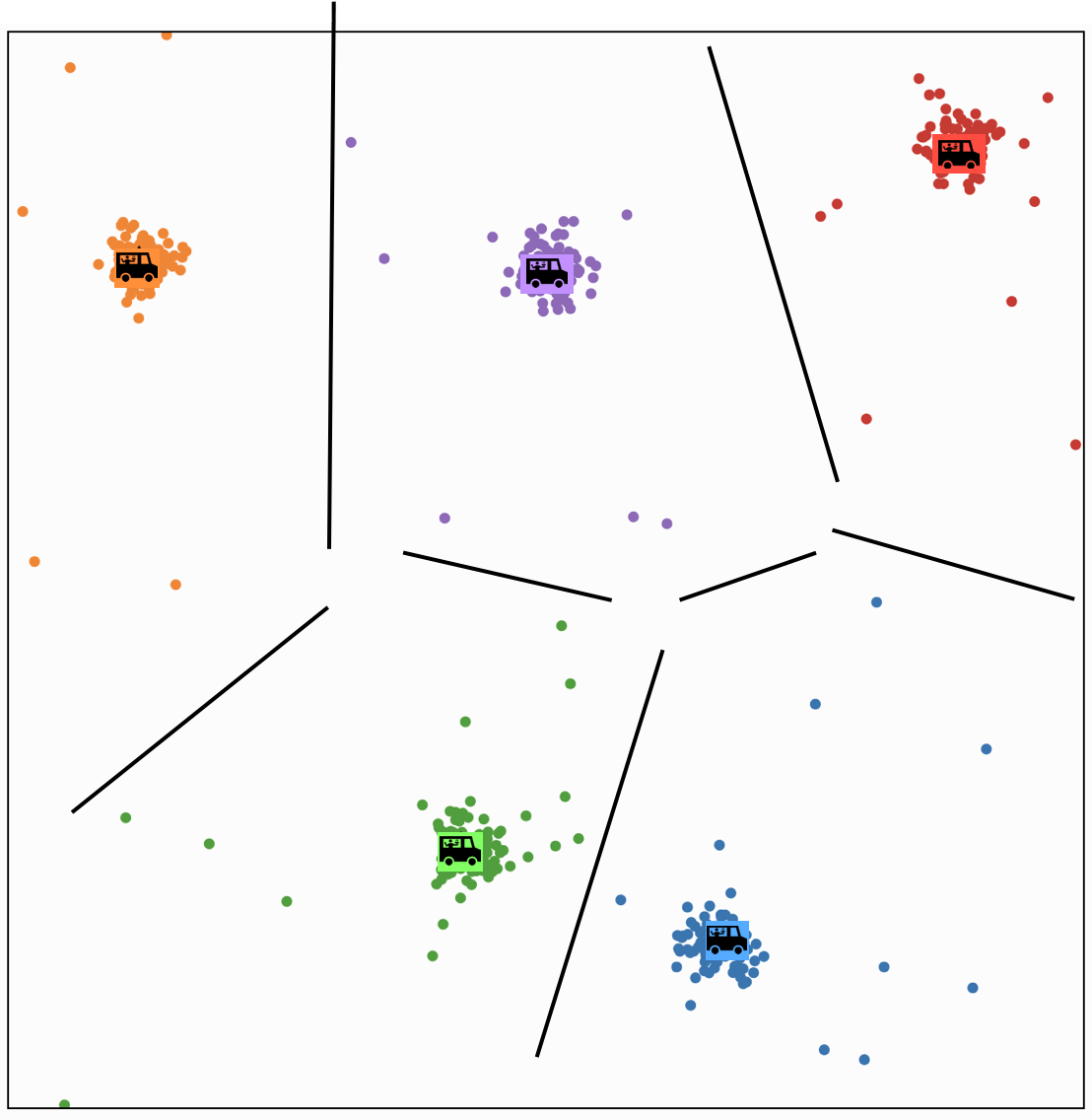
Effect of initialization
- A theorem say if run for enough outer iterations (line 2), the k-means algorithm will converge to a local minimum of the k-means objective
- That local minimum could be bad!
- The initialization can make a big difference.
- Some options: random restarts.
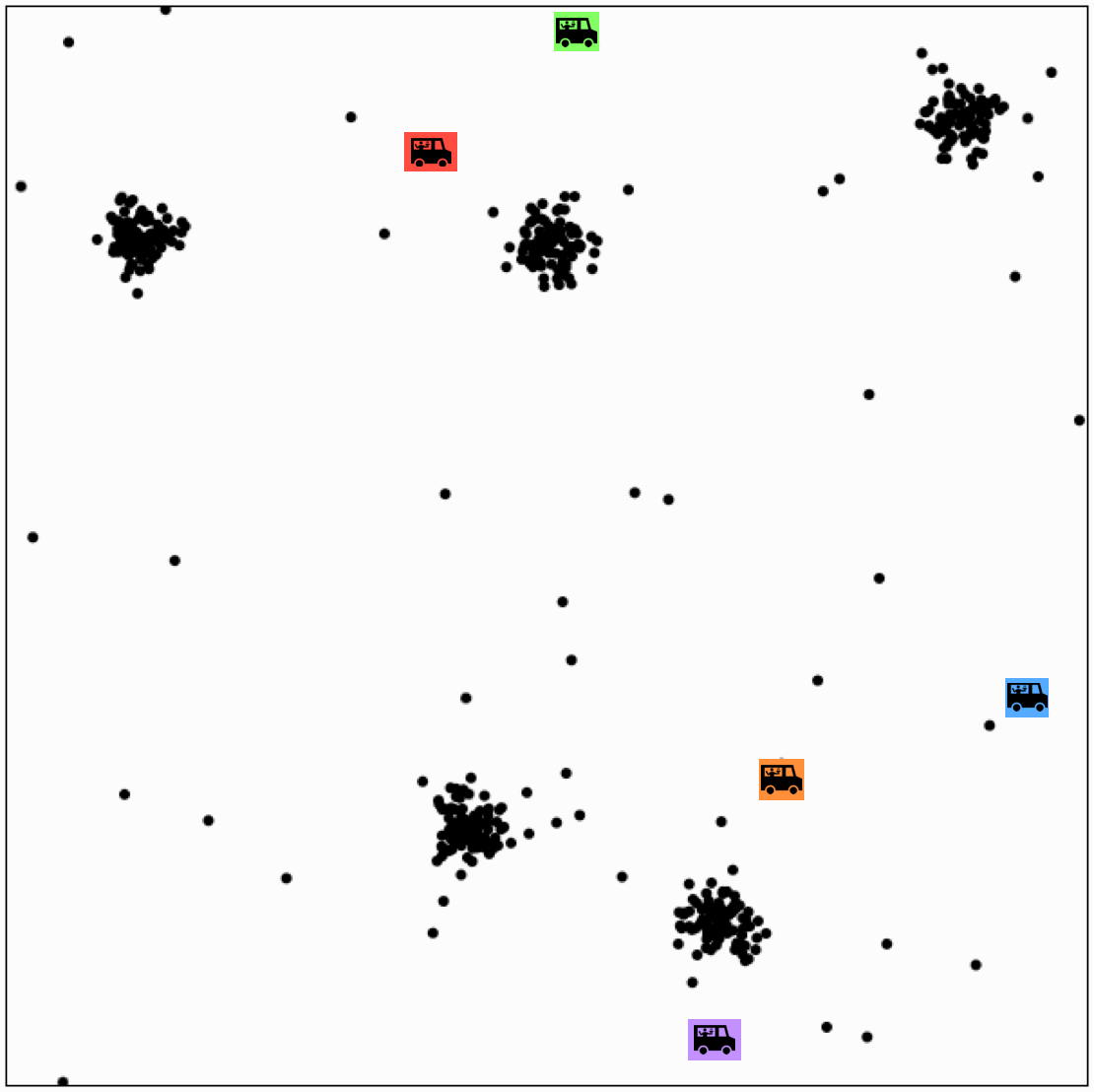
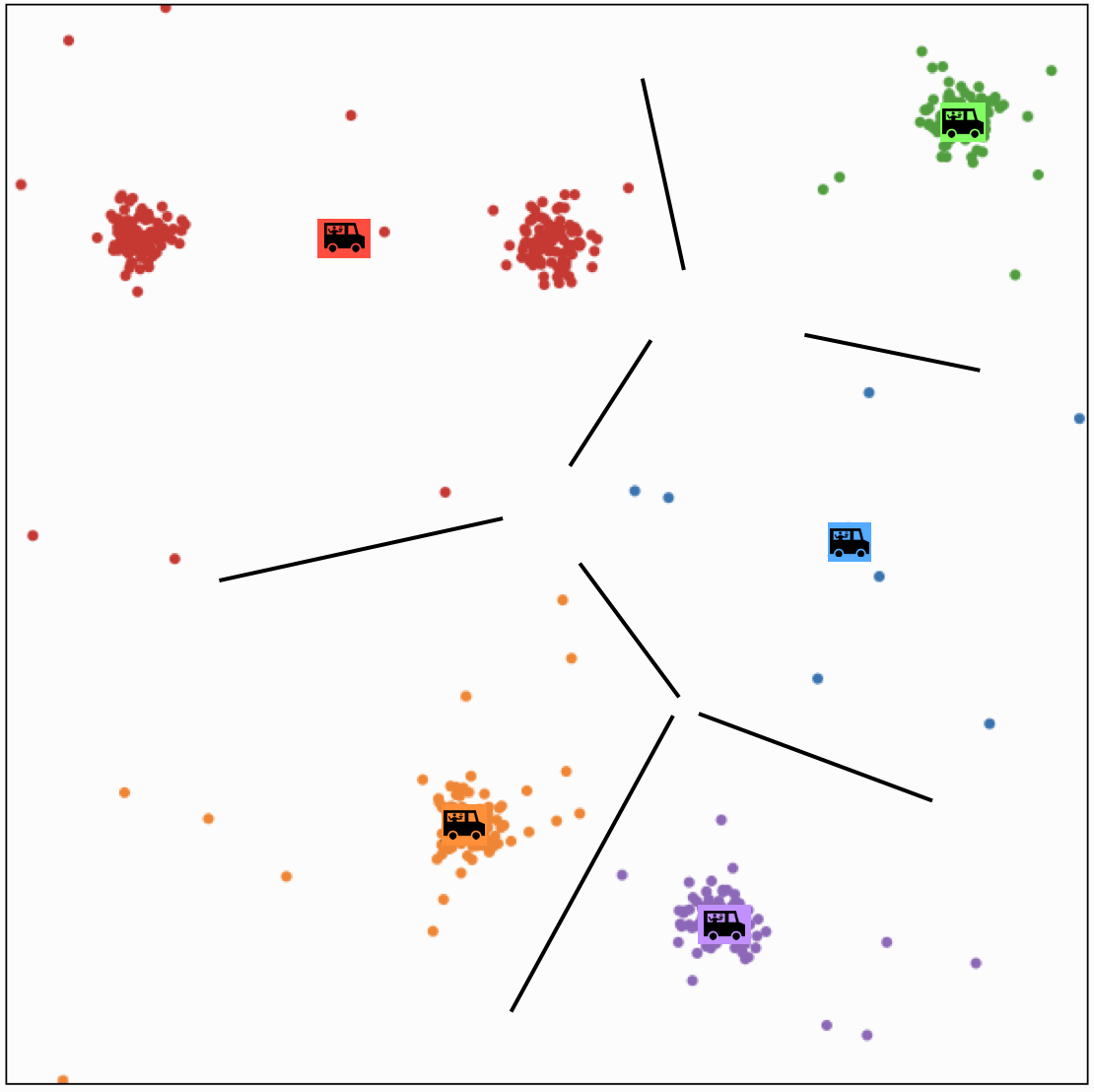
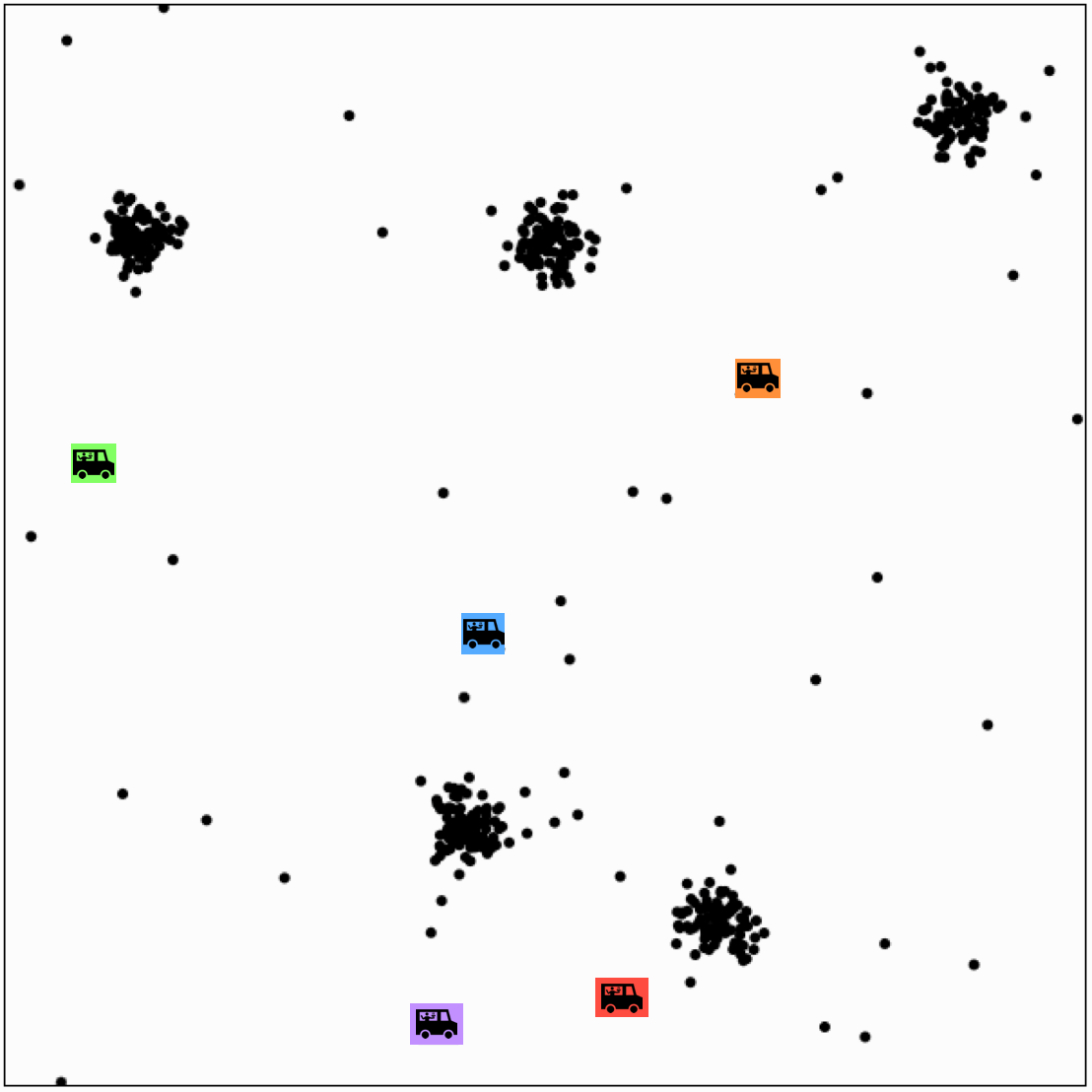
Effect of initialization
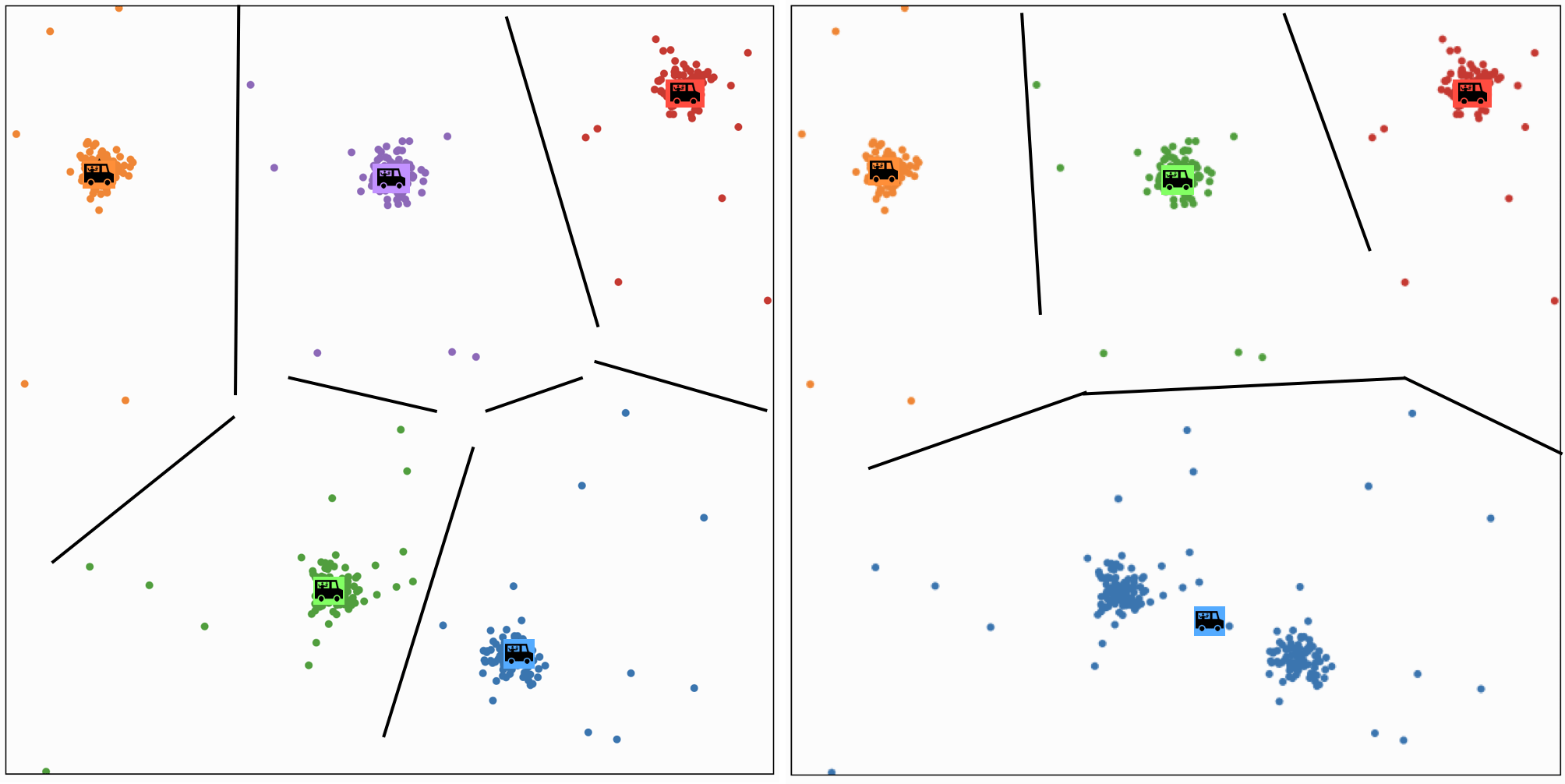
Effect of \(k\)
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
x
\mathcal{F}
\tilde{x}=\mathcal{F}(x;\theta)
\min_{\theta} ||x - \tilde{x}||^2
x
\mathcal{F}
\tilde{x}=\mathcal{F}(x)
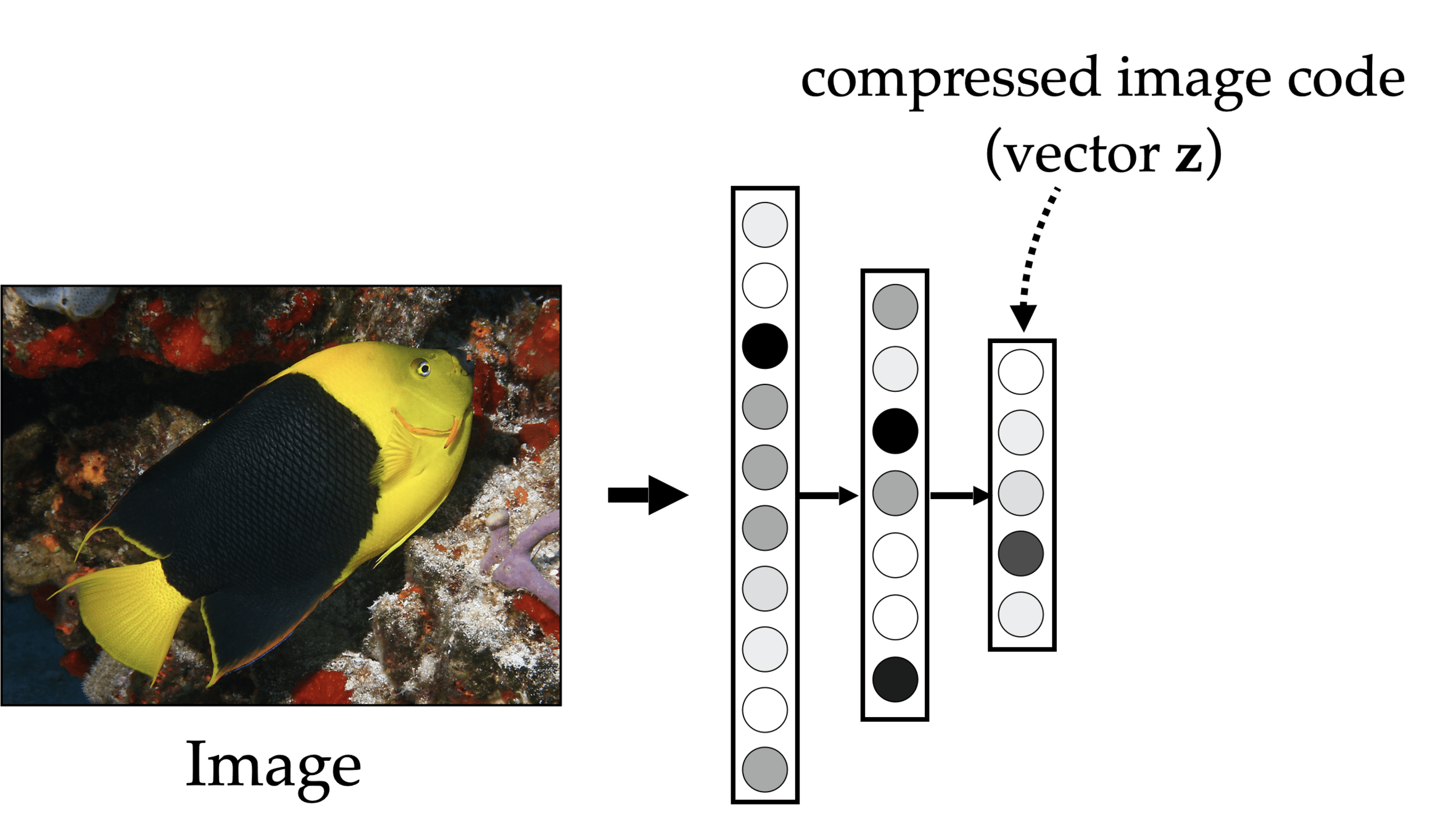
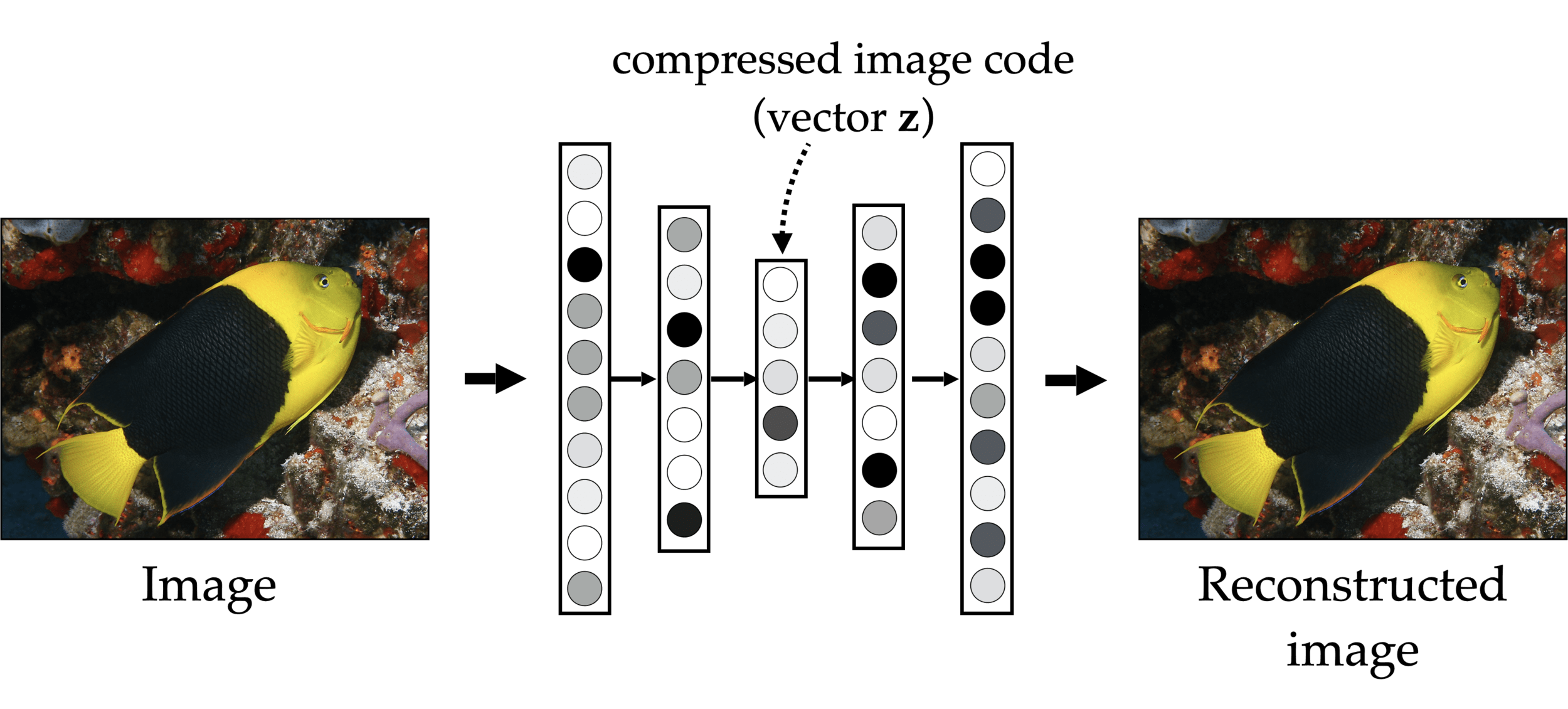
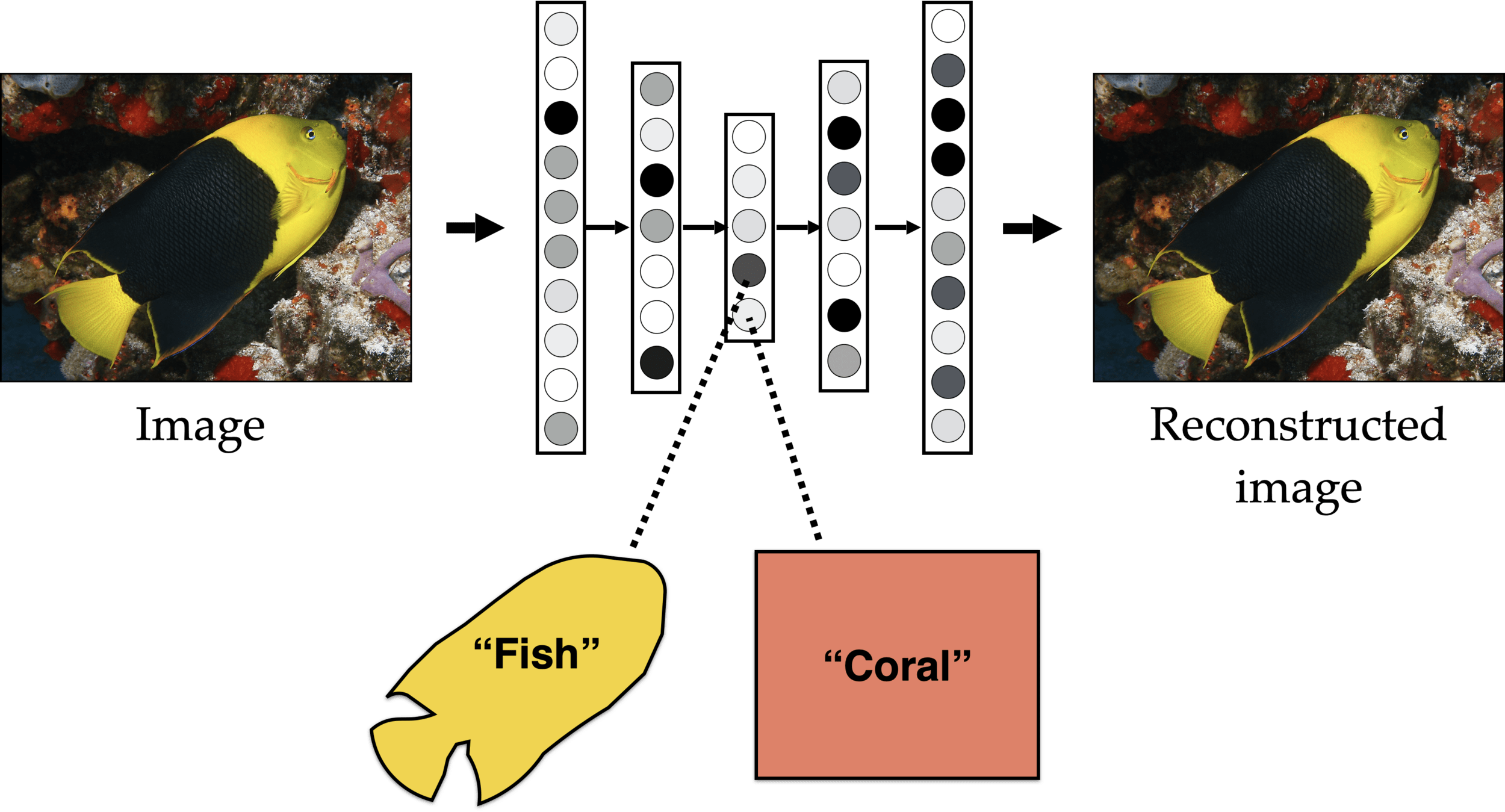
Outline
- Recap: Supervised learning and reinforcement learning
- Unsupervised learning
- Clustering: \(k\)-means algorithm
- Clustering vs. classification
- Initialization matters
- \(k\) matters
- Auto-encoder
- Compact representation
- Unsupervised learning again -- representation learning and beyond
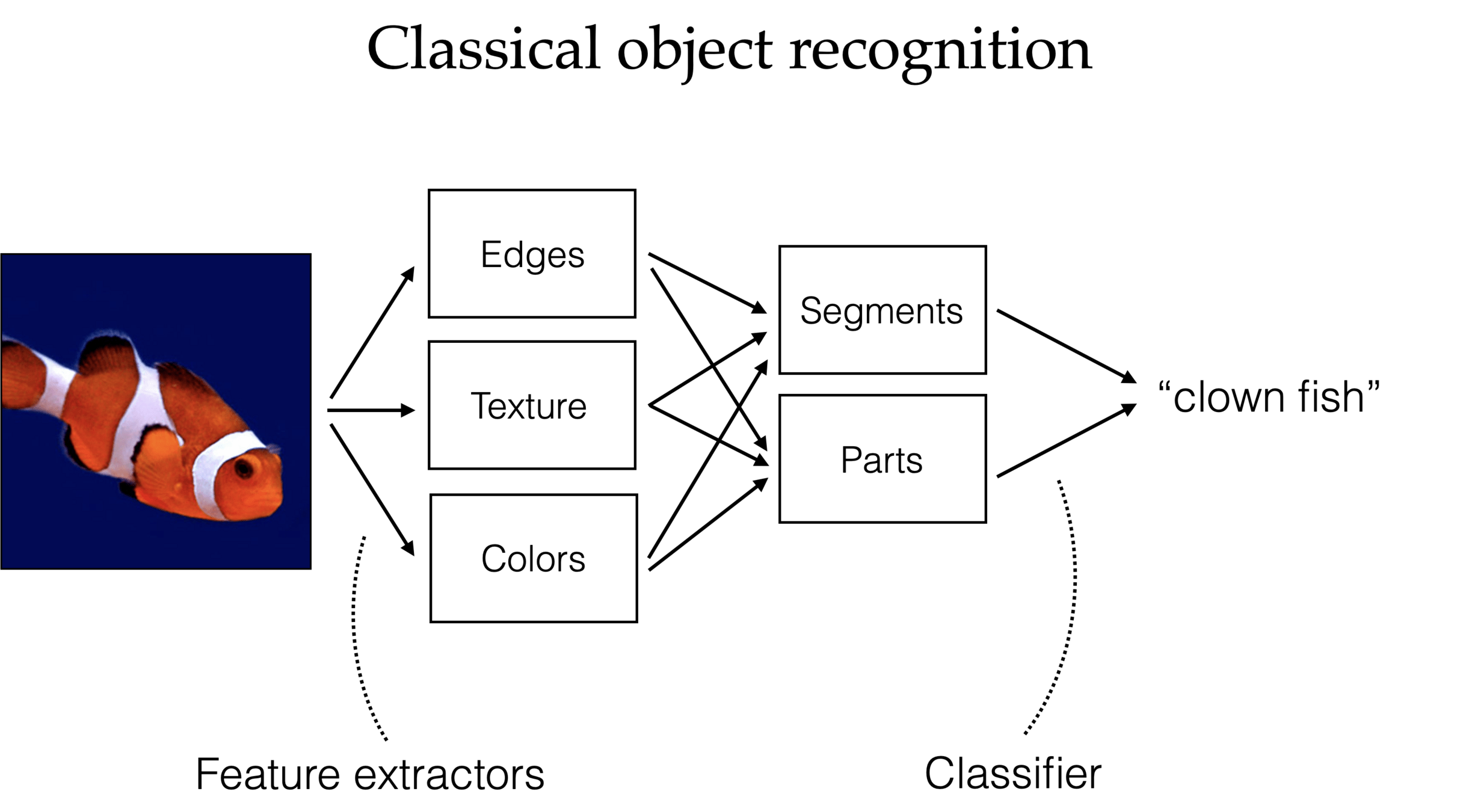
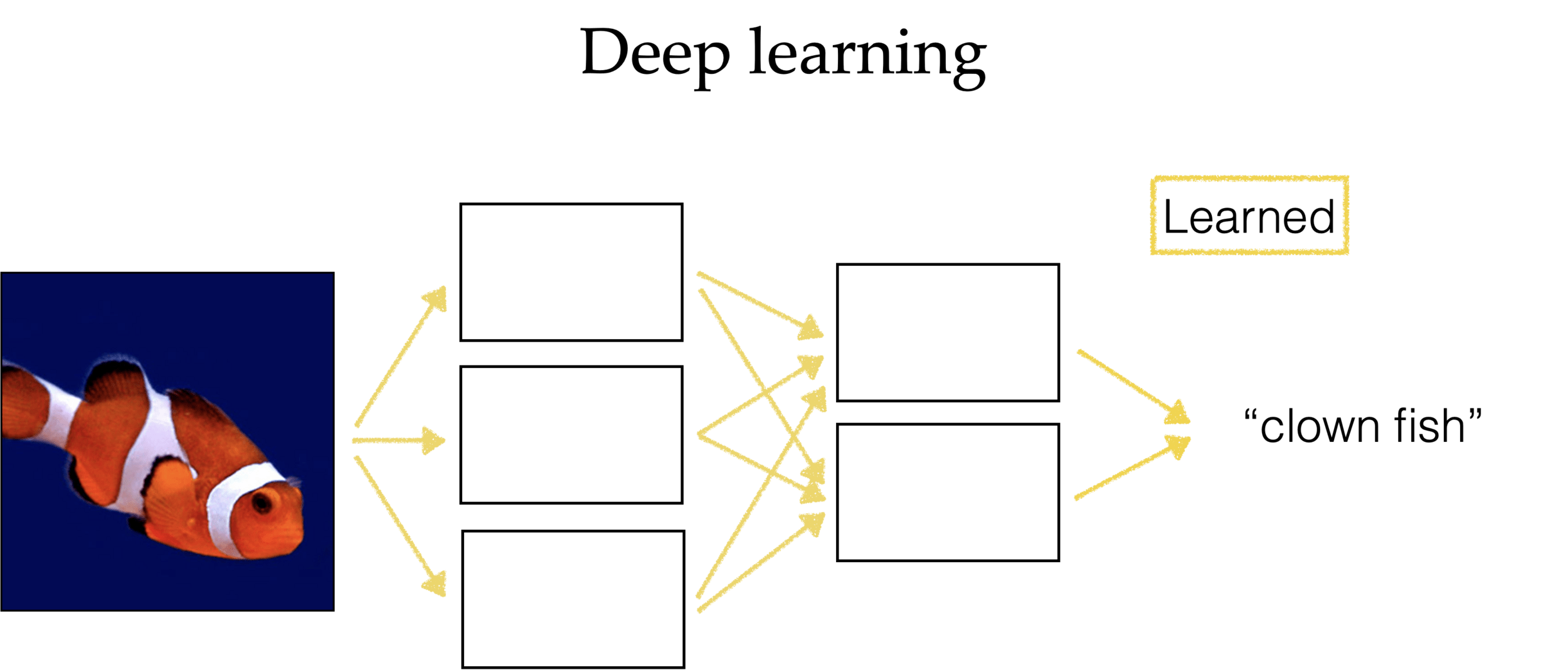
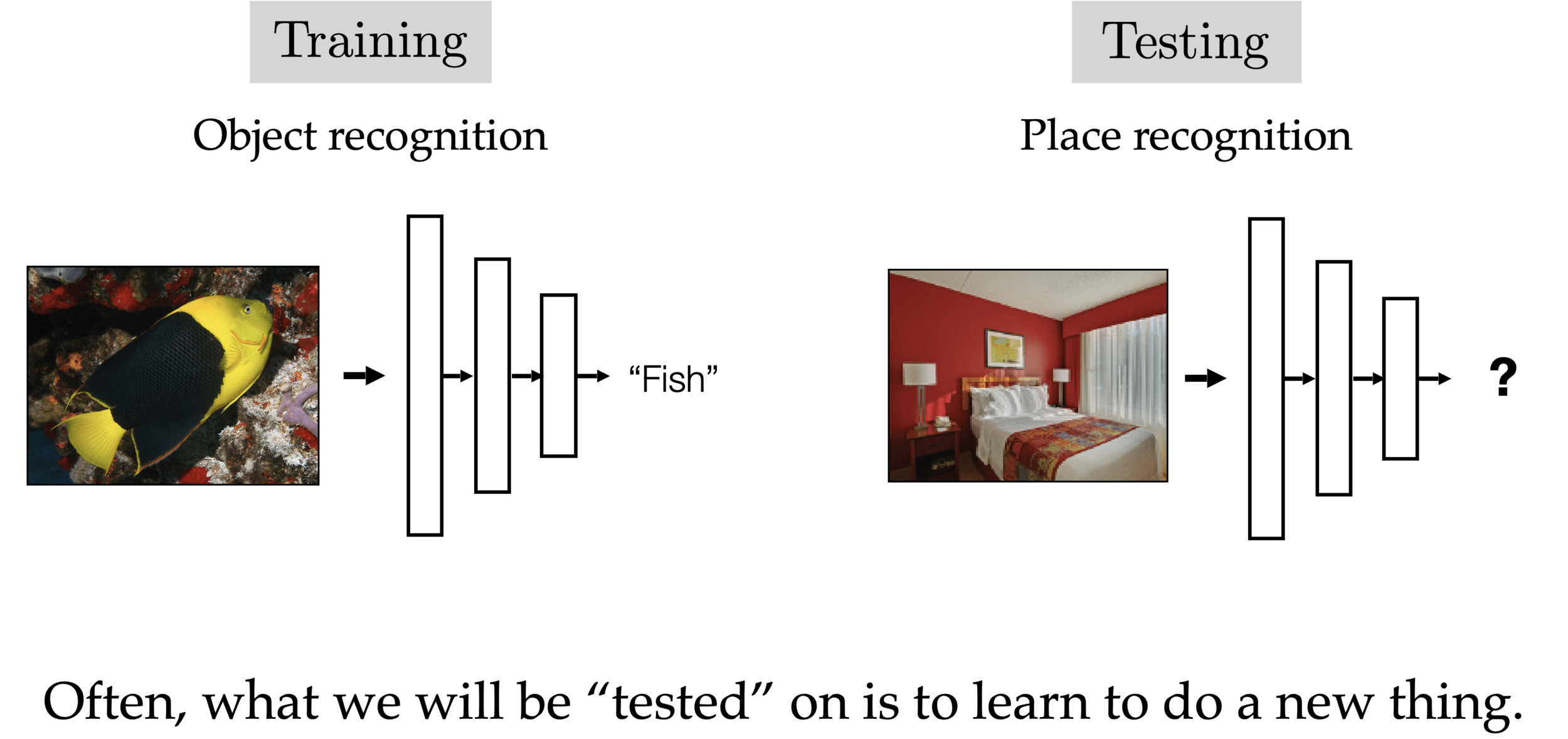
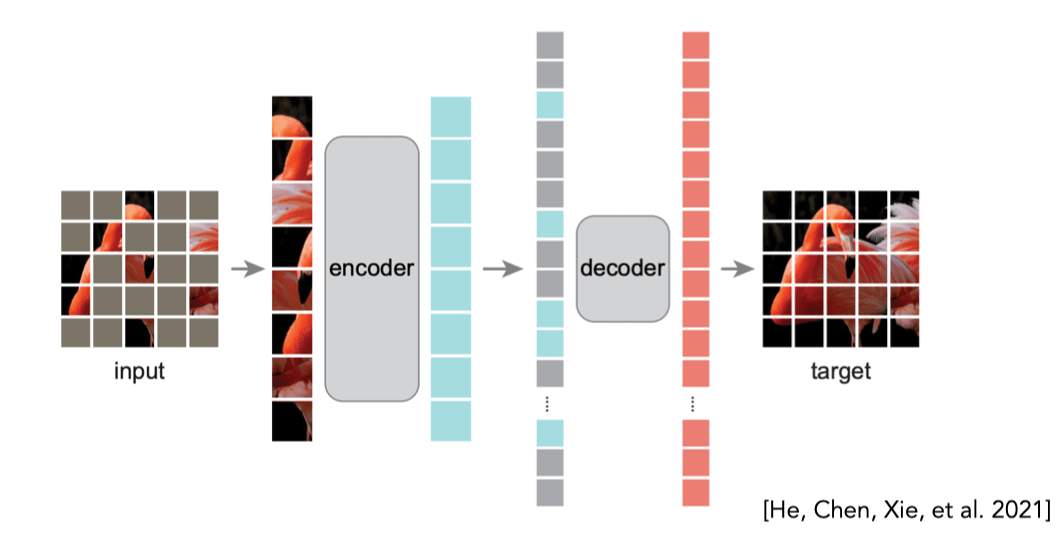
Self-supervision (masking)
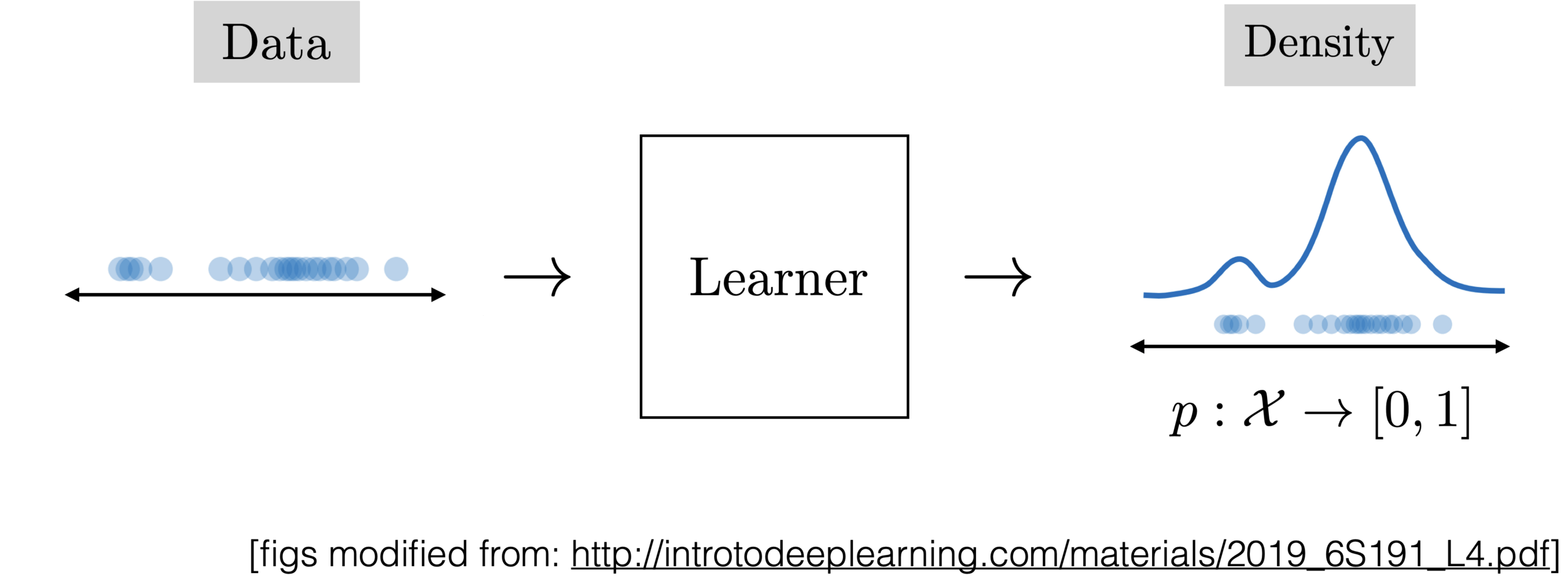
(Density estimation)
Dall-E 2 (UnCLIP):
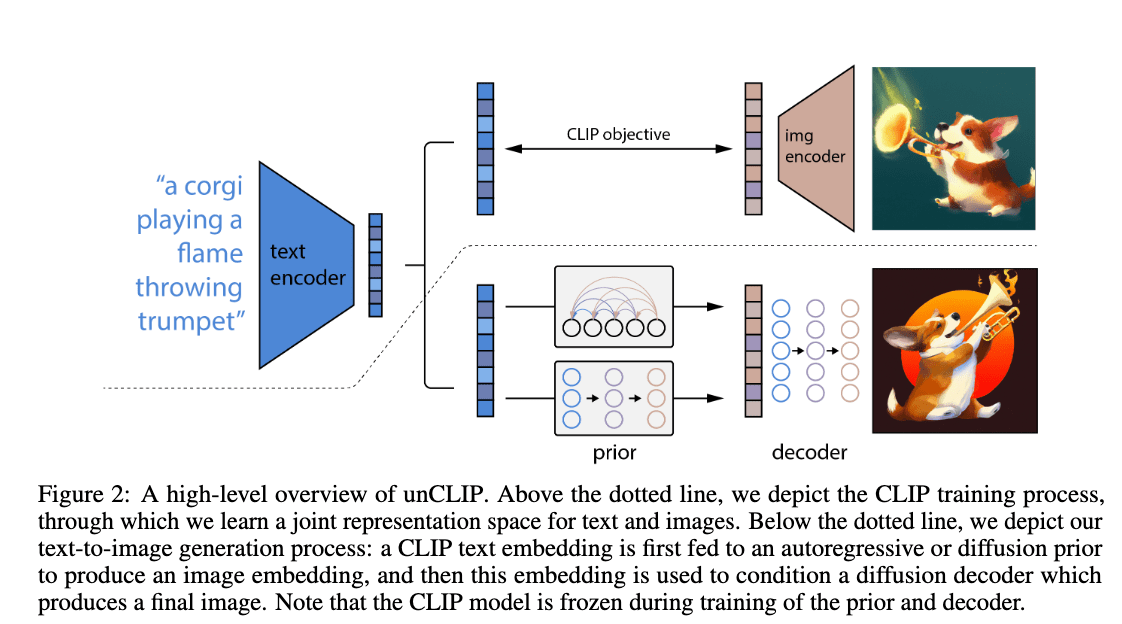
[https://arxiv.org/pdf/2204.06125.pdf]
Thanks!
We'd appreciate your feedback on the lecture.
Outline
- Unsupervised learning takes in a data set of X’s and tries to find some interesting or useful underlying structure
Clustering is an important kind of unsupervised learning in which we try to divide the x’s into a finite set of groups that are in some sense similar.
One of the most tricky things about clustering is picking the objective function. A widely used one is the k-means objective (eq 12.1 in notes). It also requires a distance metric on x’s.
We could try to optimize using generic optimization methods (e.g. gradient descent) but there’s a convenient special-purpose method for finding a local optimum: the k-means algorithm.The solution obtained by k-means algorithm is sensitive to initialization.
Choosing the number of clusters is an important problem. It’s a kind of judgment call: we can optimize the k-means objective by having each x in its own cluster, so this has more to do with the initial abstract objective of finding interesting or useful underlying structure in the data.
K-MEANS\((k, \tau, \left\{x^{(i)}\right\}_{i=1}^n)\)
1 \(\mu, y=\) random initialization
2 for \(t=1\) to \(\tau\)
3 \(y_{o l d}=y\)
4 for \(i=1\) to \(n\)
\(5 \quad \quad\quad\quad \quad y^{(i)}=\arg \min _j\left\|x^{(i)}-\mu^{(j)}\right\|^2\)
6 for \(j=1\) to \(k\)
\(7 \quad \quad\quad\quad \quad \mu^{(j)}=\frac{1}{N_j} \sum_{i=1}^n \mathbb{1}\left(y^{(i)}=\mathfrak{j}\right) x^{(i)}\)
8 if \(y==y_{\text {old }}\)
9\(\quad \quad \quad\quad \quad\)break
10 return \(\mu, y\)
introml-sp24-lec12
By Shen Shen
