Intro to Machine Learning
Lecture 3: Gradient Descent Methods
Shen Shen
Feb 16, 2024
(many slides adapted from Tamara Broderick)
Outline
- Recall (Ridge regression) => Why care about GD
-
Optimization primer
-
Gradient, optimality, convexity
-
-
GD as an optimization algorithm for generic function
-
GD as an optimization algorithm for ML applications
-
Loss function typically a finite sum
-
-
Stochastic gradient descent (SGD) for ML applications
-
Pick one out of the finite sum
-
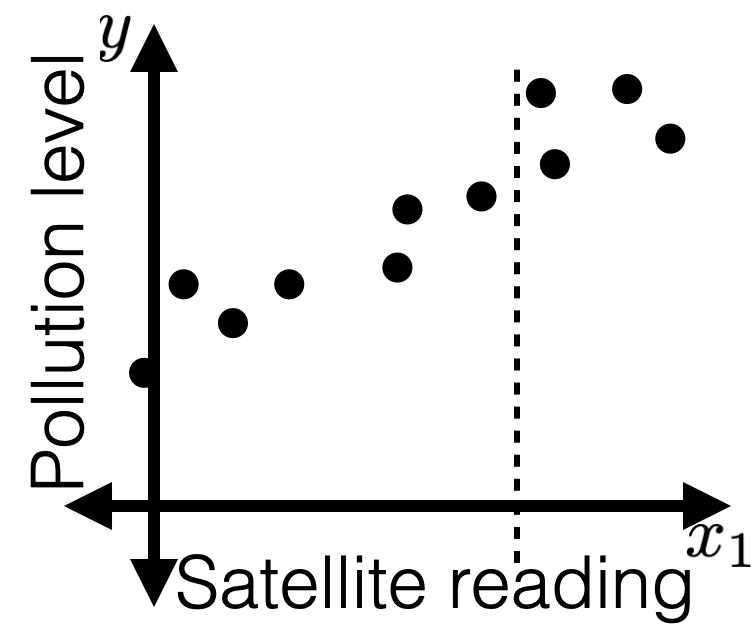
Recall
- A general ML approach
- Collect data
- Choose hypothesis class, hyperparameter, loss function
- Train (optimize for) "good" hypothesis by minimizing loss. e.g. ridge regression
- Great when have analytical solutions
- But don't always have them (recall, half-pipe)
- Even when do have analytical solutions, can be expensive to compute (recall, lab2, Q2.8,)
- Want a more general, efficient way! => GD methods
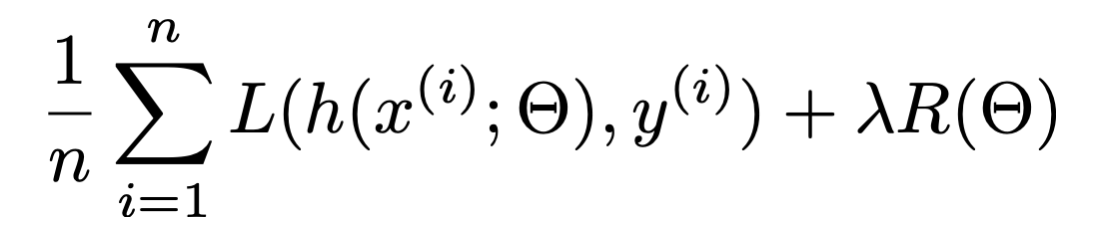
Outline
- Recall (Ridge regression) => Why care about GD
-
Optimization primer
-
Gradient, optimality, convexity
-
-
GD as an optimization algorithm for generic function
-
GD as an optimization algorithm for ML applications
-
Loss function typically a finite sum
-
-
Stochastic gradient descent (SGD) for ML applications
-
Pick one out of the finite sum
-
Gradient
- Def: For \(f: \mathbb{R}^m \rightarrow \mathbb{R}\), its gradient \(\nabla f: \mathbb{R}^m \rightarrow \mathbb{R}^m\) is defined at the point \(p=\left(x_1, \ldots, x_m\right)\) in \(m\)-dimensional space as the vector
\nabla f(p)=\left[\begin{array}{c}
\frac{\partial f}{\partial x_1}(p) \\
\vdots \\
\frac{\partial f}{\partial x_m}(p)
\end{array}\right]
f(x, y, z) = x^2 + y^3 + z
e.g.
another example
\nabla f(x, y, z) = \begin{bmatrix}
2x \\
3y^2 \\
1
\end{bmatrix}
When gradient is zero:
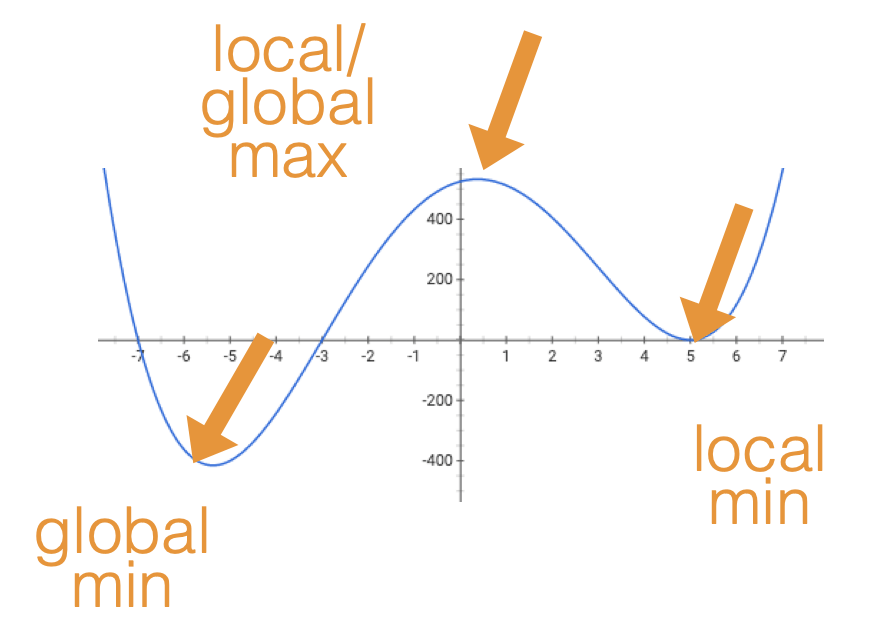
5 cases:
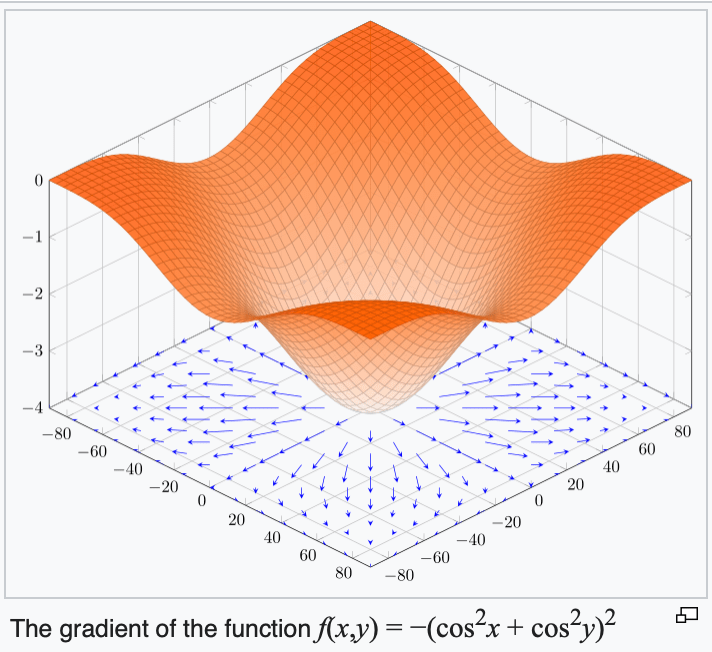
When minimizing a function, we'd hope to get a global min
Convex Functions
- A function \(f\) on \(\mathbb{R}^m\) is convex if any line segment connecting two points of the graph of \(f\) lies above or on the graph.
- (\(f\) is concave if \(-f\) is convex.)
- For convex functions, local minima are all global minima.
Simple examples
Convex functions
Non-convex functions
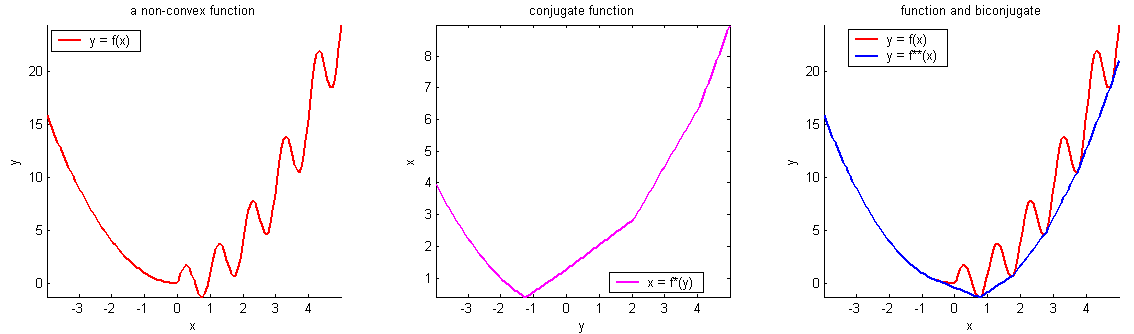
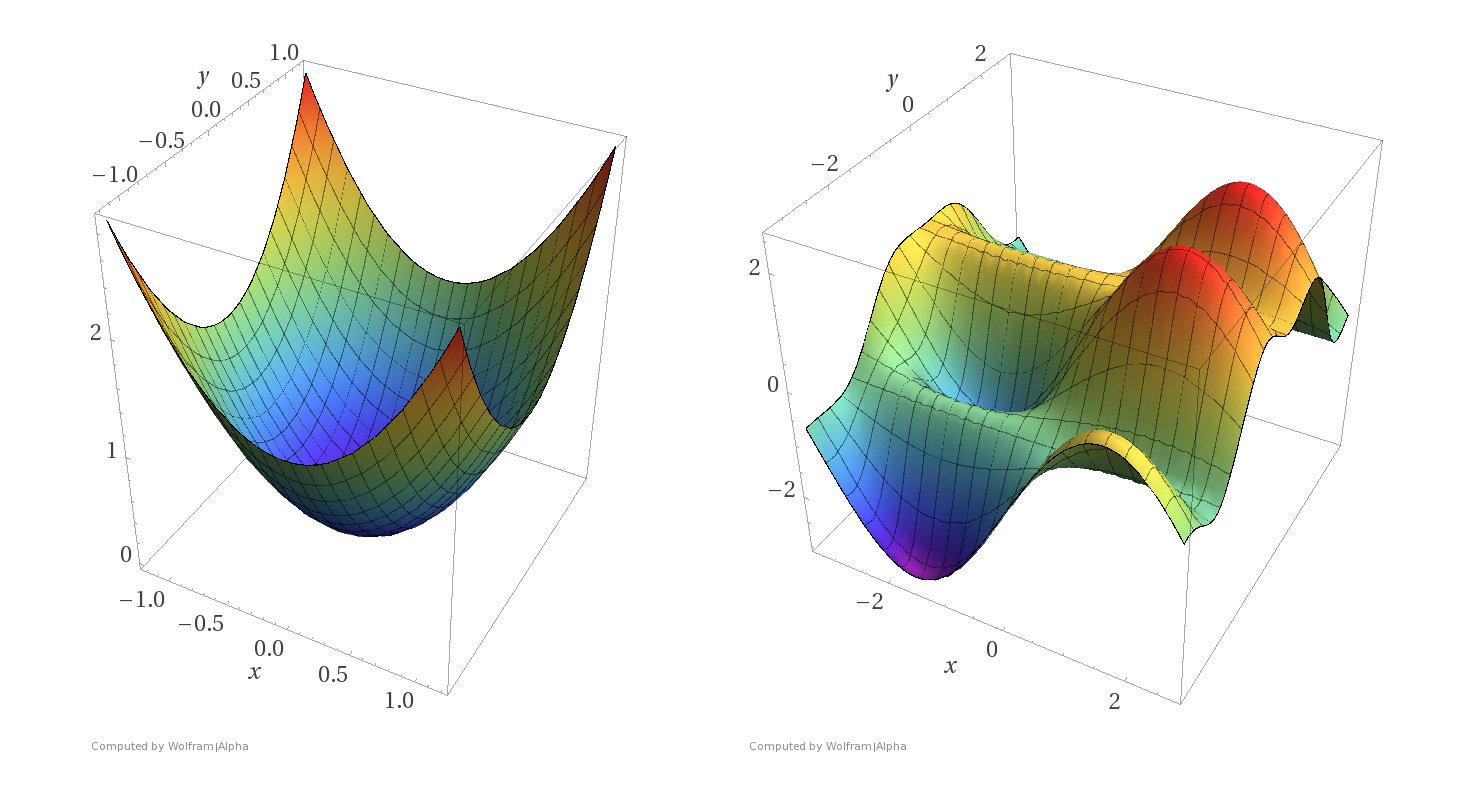
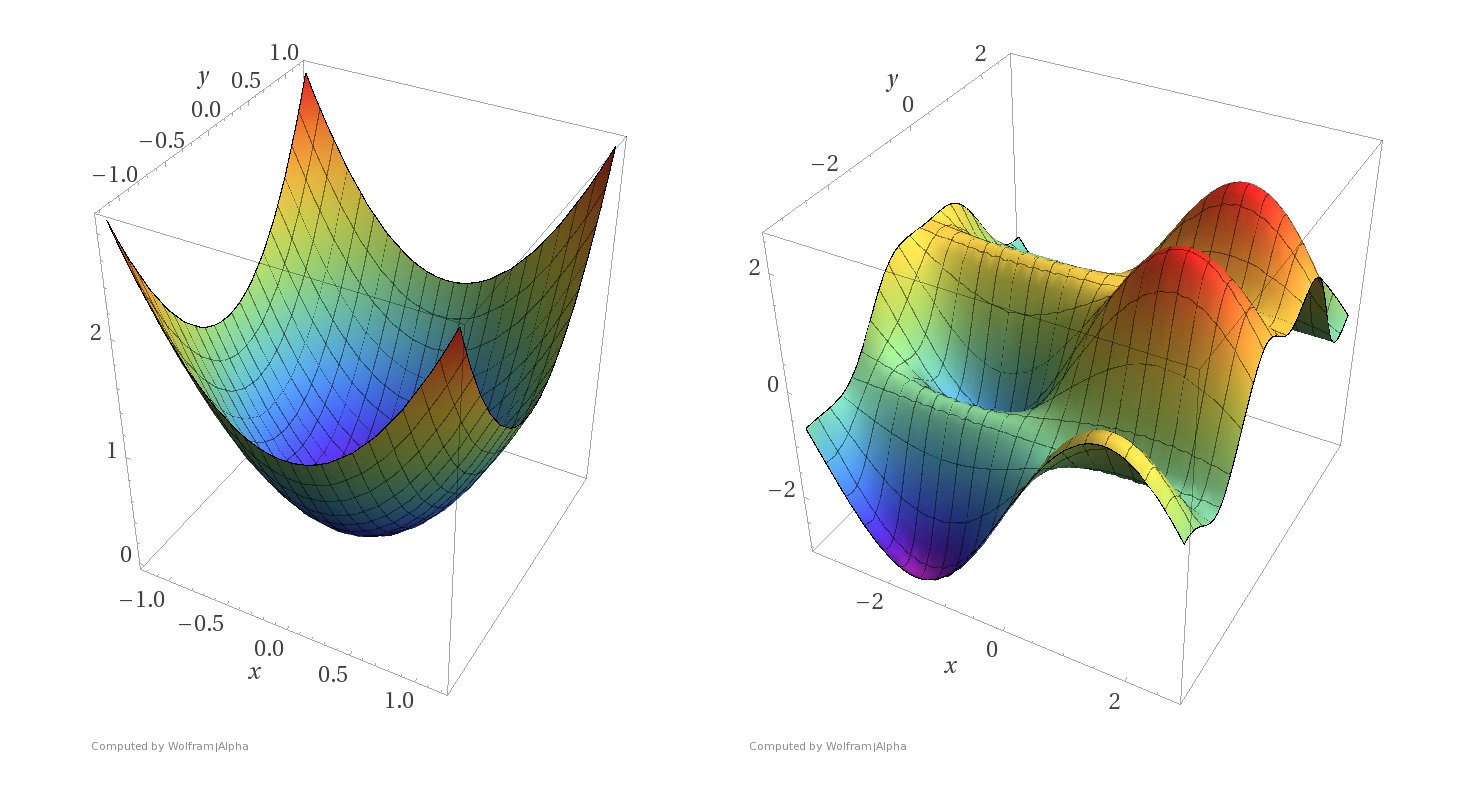
Convex Functions (cont'd)
What do we need to know:
- Intuitive understanding of the definition
- If given a function, can determine if it's convex or not. (We'll only ever give at most 2D, so visually is enough)
- Understand how (stochastic) gradient descent algorithms would behave differently depending on if convexity is satisfied.
- For this class, OLS loss function is convex, ridge regression loss is (strictly) convex, and later cross-entropy loss function is convex too.
Outline
- Recall (Ridge regression) => Why care about GD
-
Optimization primer
-
Gradient, optimality, convexity
-
-
GD as an optimization algorithm for generic function
-
GD as an optimization algorithm for ML applications
-
Loss function typically a finite sum (over data)
-
-
Stochastic gradient descent (SGD) for ML applications
-
Pick one data out of the finite sum
-
hyperparameters
Gradient descent properties
if violated:
can't run gradient descent
Gradient descent properties
if violated:
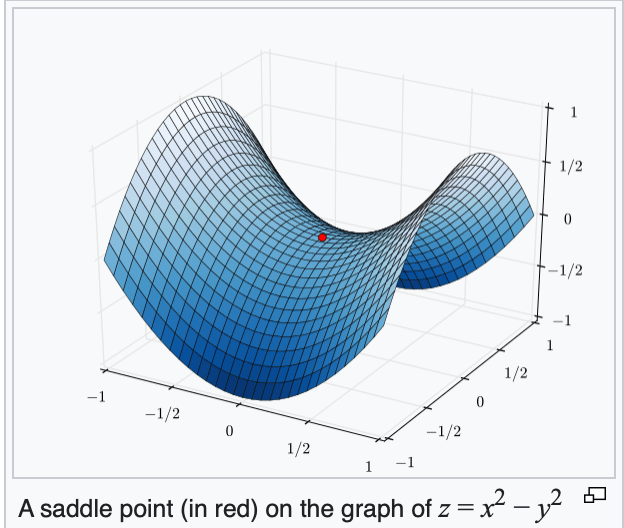
e.g. get stuck at a saddle point
Gradient descent properties
if violated:
e.g. may not terminate
Gradient descent properties
if violated:
see demo, and lab
Recall: need step-size sufficiently small
run long enough
Outline
- Recall (Ridge regression) => Why care about GD
-
Optimization primer
-
Gradient, optimality, convexity
-
-
GD as an optimization algorithm for generic function
-
GD as an optimization algorithm for ML applications
-
Loss function typically a finite sum
-
-
Stochastic gradient descent (SGD) for ML applications
-
Pick one out of the finite sum
-
Outline
- Recall (Ridge regression) => Why care about GD
-
Optimization primer
-
Gradient, optimality, convexity
-
-
GD as an optimization algorithm for generic function
-
GD as an optimization algorithm for ML applications
-
Loss function typically a finite sum
-
-
Stochastic gradient descent (SGD) for ML applications
-
Pick one out of the finite sum
-
Gradient descent on ML objective
- ML objective functions has typical form: finite sum
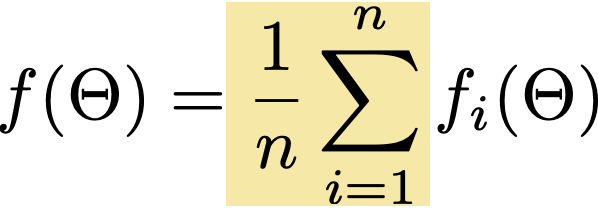
- For instance, MSE we've seen so far:
- Because (gradient of sum) = (sum of gradient), gradient of an ML objective :
\nabla f(\Theta)= \frac{1}{n} \sum_{i=1}^n \nabla f_i(\Theta)
- gradient of that MSE w.r.t. \(\theta\):
\frac{2}{n} \sum_{i=1}^n\left(\theta^{\top} x^{(i)}+\theta_0-y^{(i)}\right) x^{(i)}
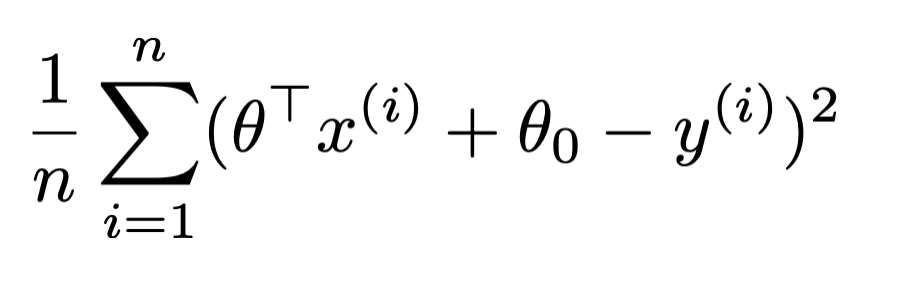
Outline
- Recall (Ridge regression) => Why care about GD
-
Optimization primer
-
Gradient, optimality, convexity
-
-
GD as an optimization algorithm for generic function
-
GD as an optimization algorithm for ML applications
-
Loss function typically a finite sum
-
-
Stochastic gradient descent (SGD) for ML applications
-
Pick one out of the finite sum
-
Stochastic gradient descent
\nabla f(\Theta)= \frac{1}{n} \sum_{i=1}^n \nabla f_i(\Theta)
\approx \nabla f_i(\Theta)
for a randomly picked \(i\)
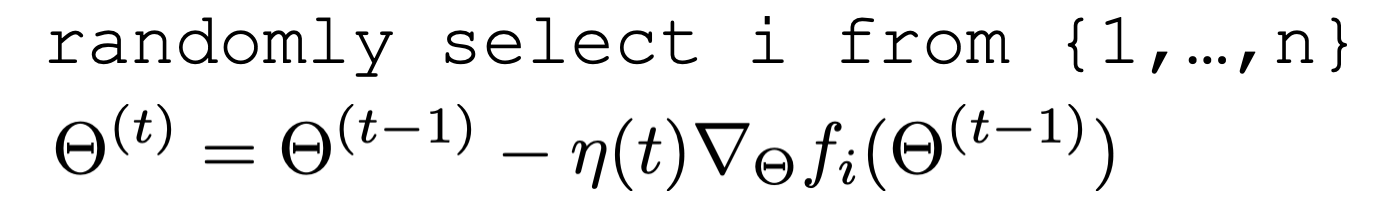
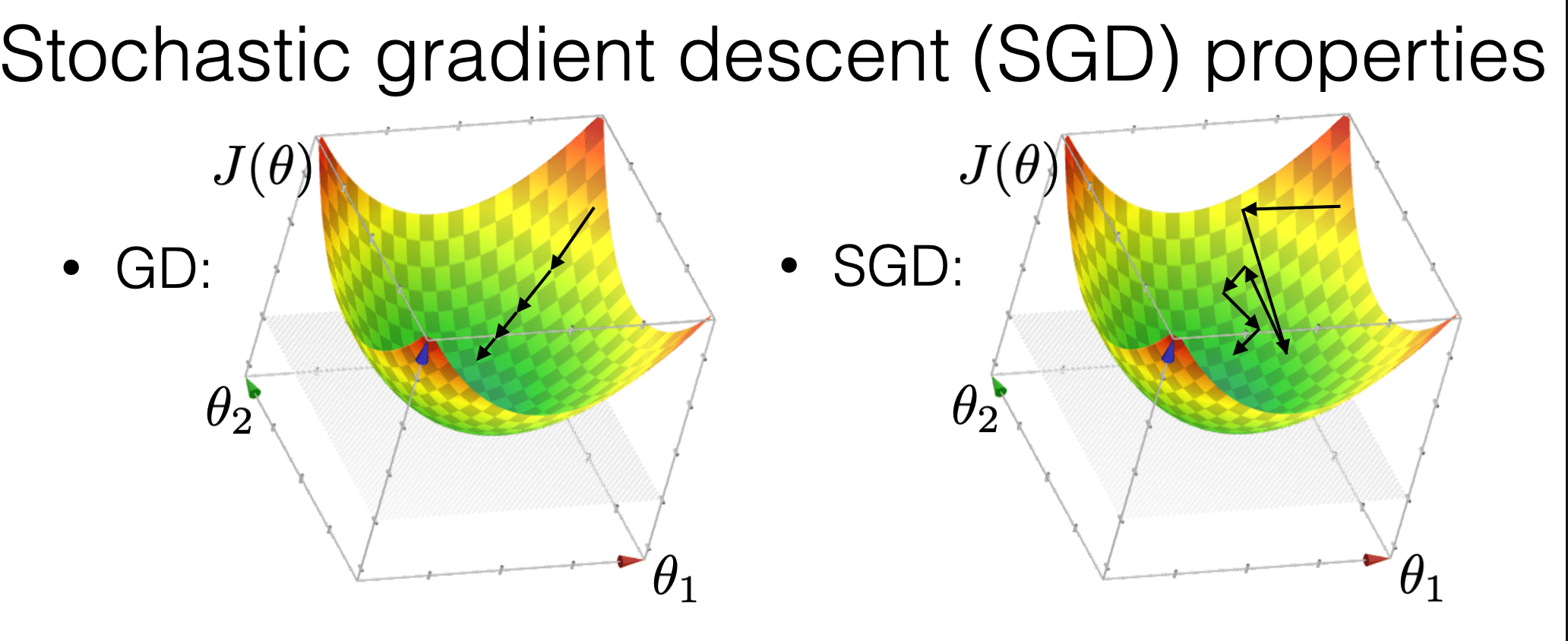
More "random"
More "demanding"
Thanks!
We'd love it for you to share some lecture feedback.
introml-sp24-lec3
By Shen Shen
