Intro to Machine Learning
Lecture 7: Convolutional Neural Networks
Shen Shen
March 22, 2024
(videos edited from 3b1b; some slides adapted from Phillip Isola and Kaiming He)
Outline
- Recap (fully-connected net)
- Motivation and big picture ideas of CNN
- Convolution operation
- 1d and 2d convolution mechanics
- interpretation:
- local connectivity
- weight sharing
- 3d tensors
- Max pooling
- Larger window
- Typical architecture and summary
f_1(\cdot)
\Sigma
\dots
x_1
x_2
x_m
f_1(\cdot)
\Sigma
f_1(\cdot)
\Sigma
f_1(\cdot)
\Sigma
\dots
f_2(\cdot)
\Sigma
f_2(\cdot)
\Sigma
\dots
f_2(\cdot)
\Sigma
\dots
W_1
W_2
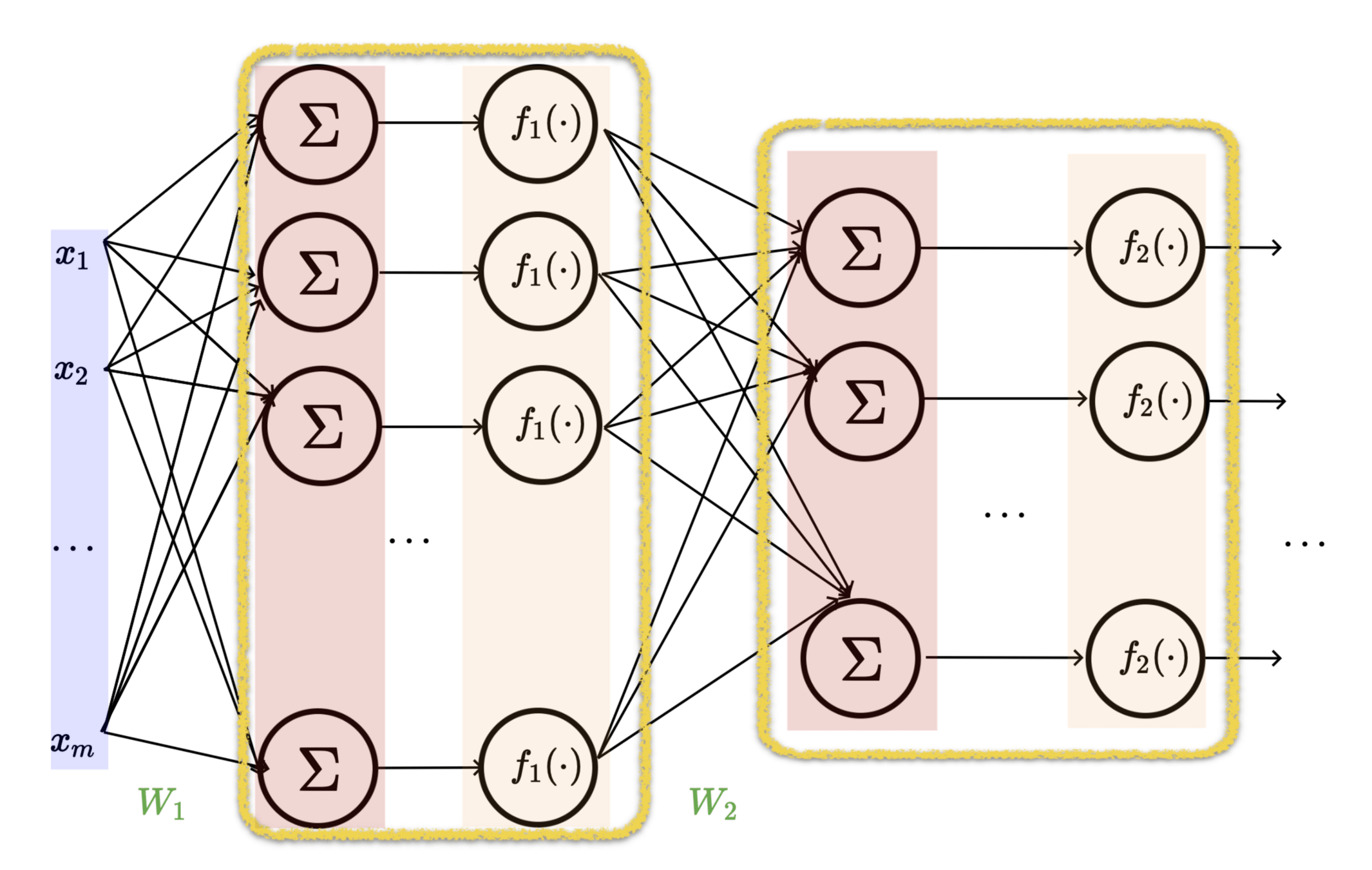
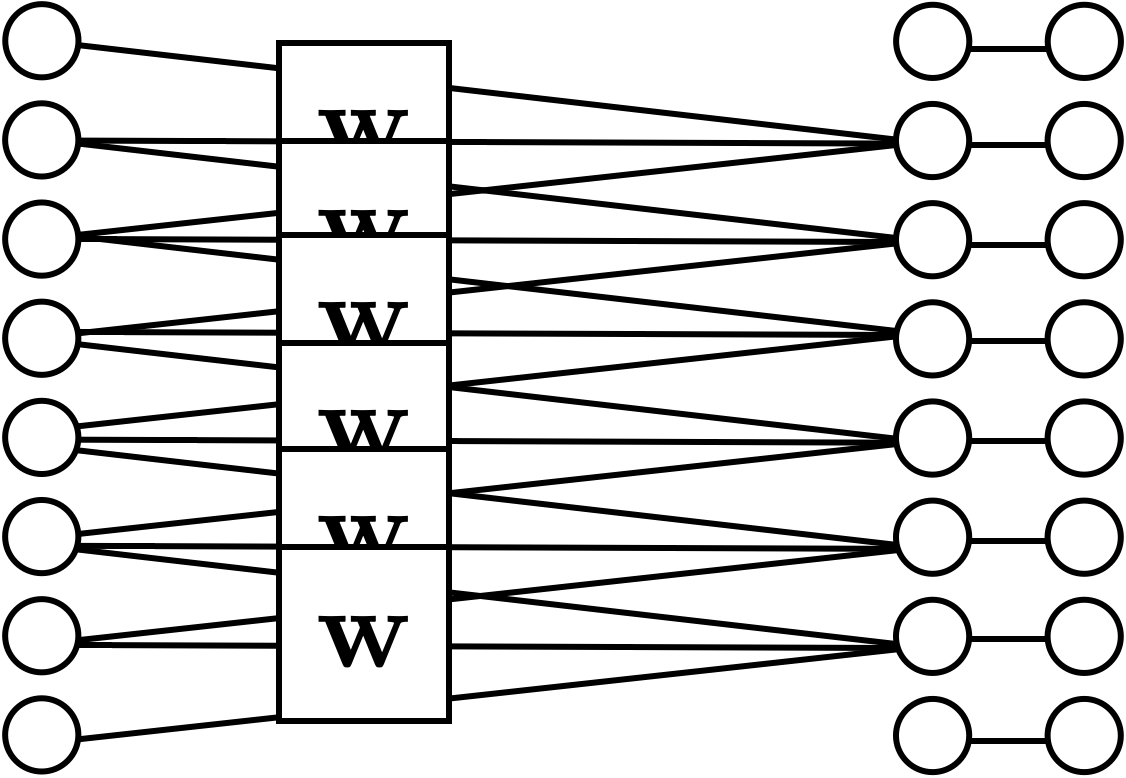
learnable weights
layer
linear combo
activations
input
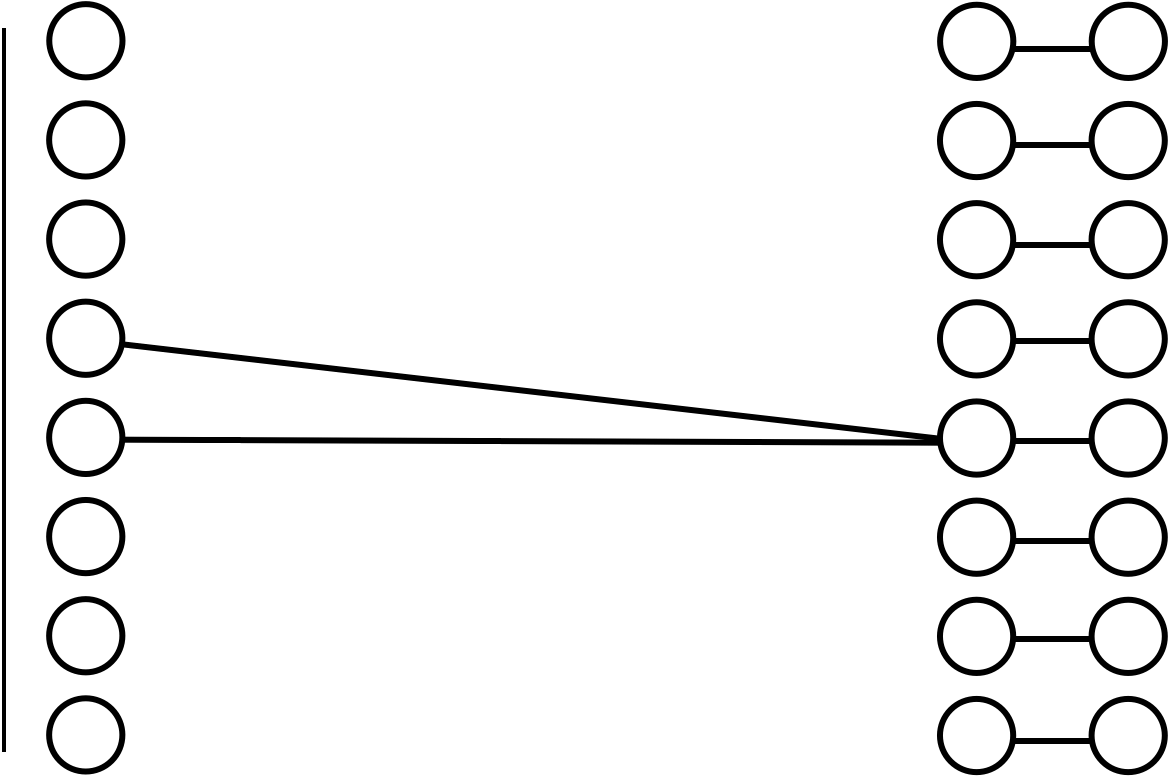
A (feed-forward) neural network is
Recap: Backpropogation
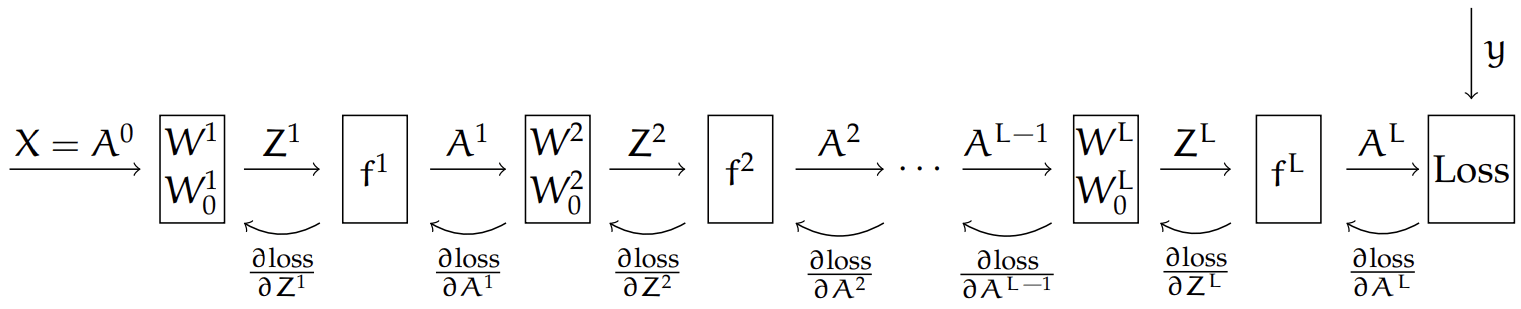
Outline
- Recap (fully-connected net)
- Motivation and big picture ideas of CNN
- Convolution operation
- 1d and 2d convolution mechanics
- interpretation:
- local connectivity
- weight sharing
- 3d tensors
- Max pooling
- Larger window
- Typical architecture and summary
convolutional neural networks
-
Why do we need a special network for images?
-
Why is CNN (the) special network for images?
9
Why do we
need a special net for images?
Q: Why do we need a specialized network?
👈 426-by-426 grayscale image
Use the same small 2-layer network?
need to learn ~3M parameters
Imagine even higher-resolution images, or more complex tasks...
A: fully-connected nets don't scale well to (interesting) images
Why do we think
9?
is
Why do we think any of
9?
is a
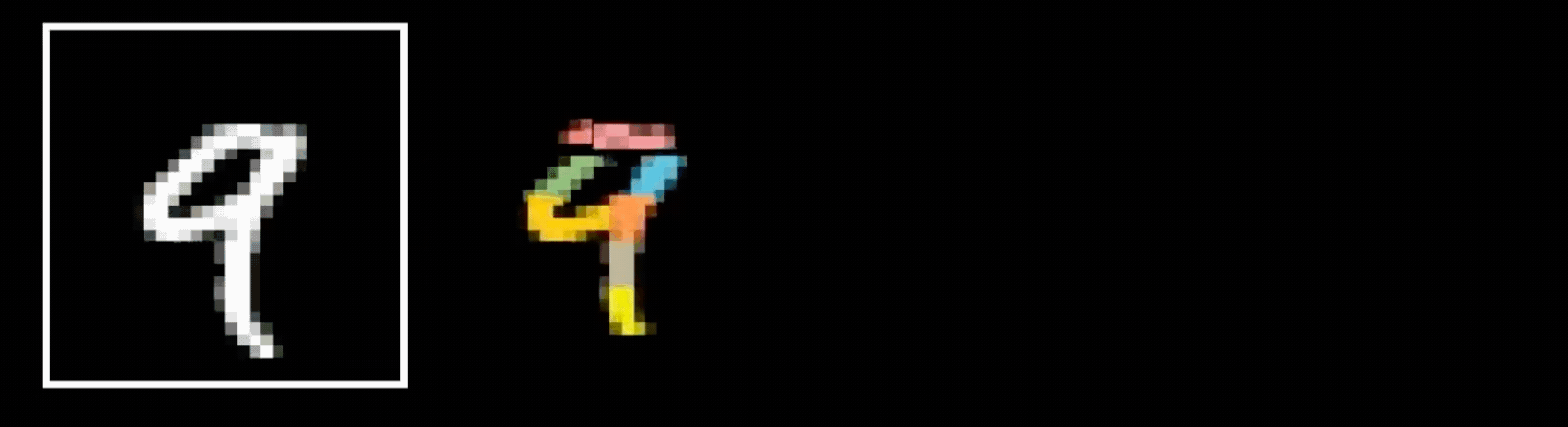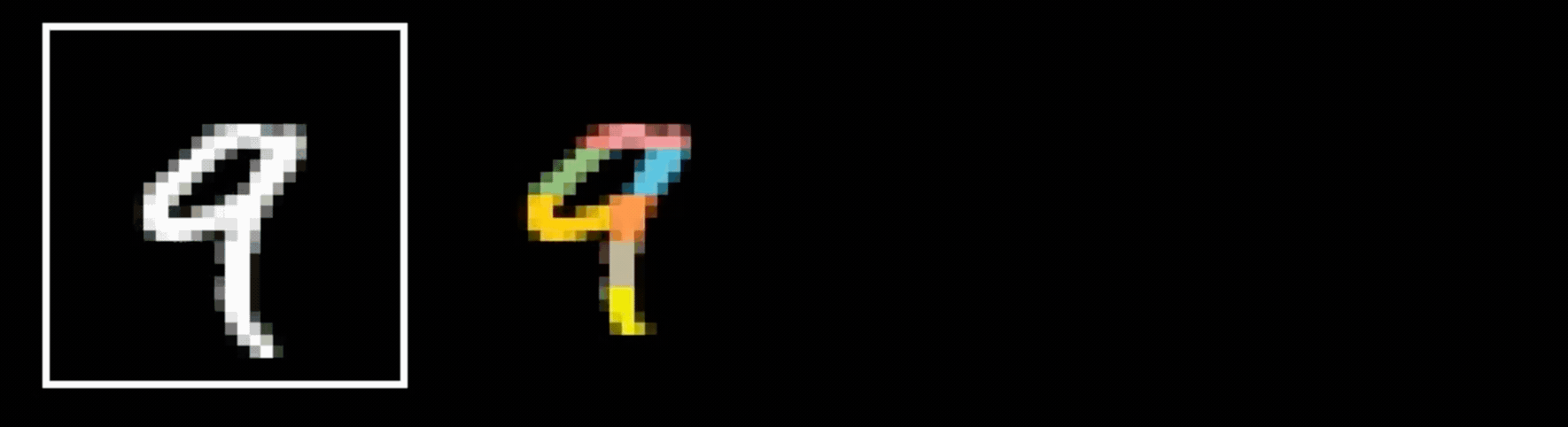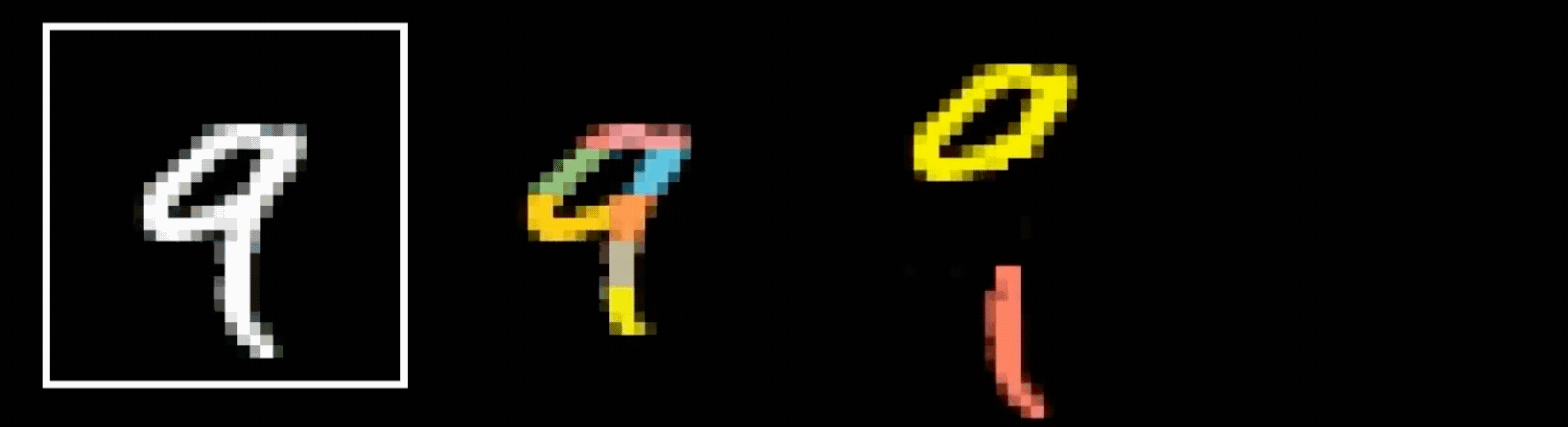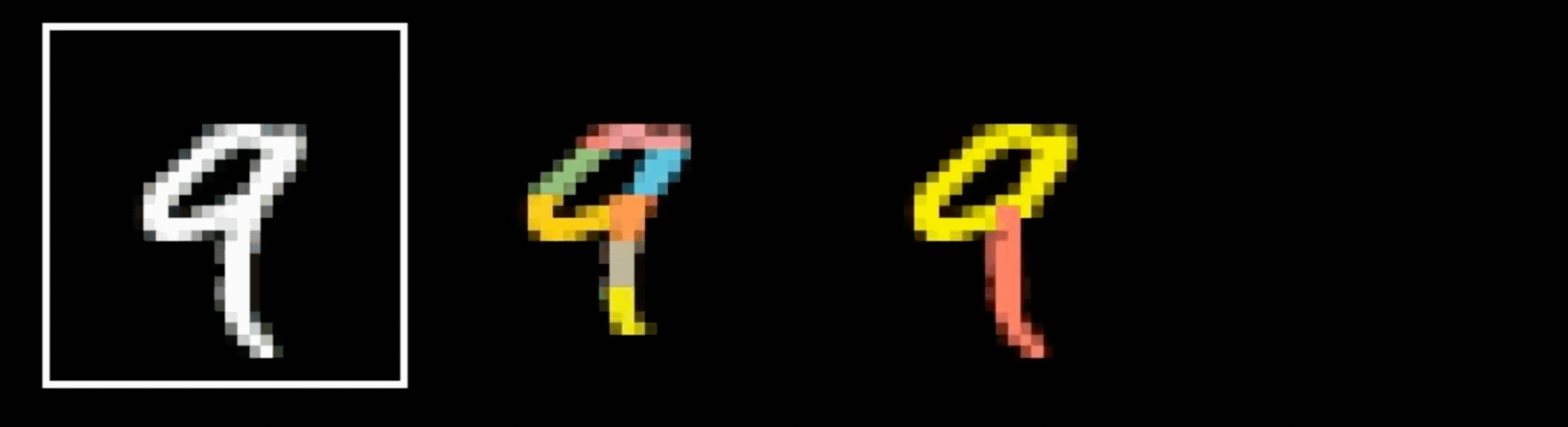
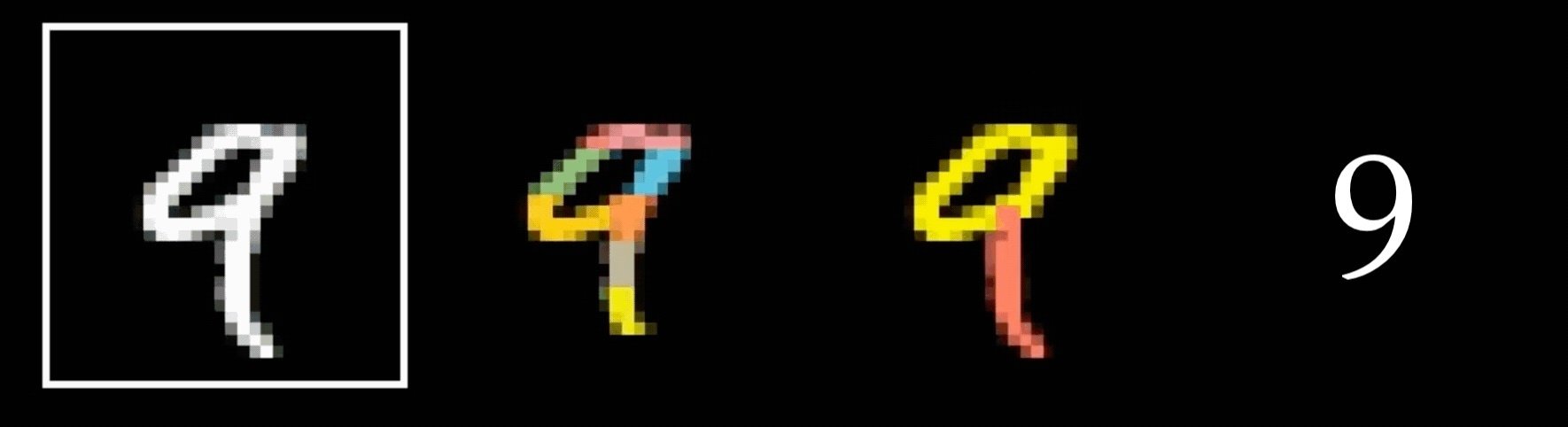
- Visual hierarchy
layering would help take care of that
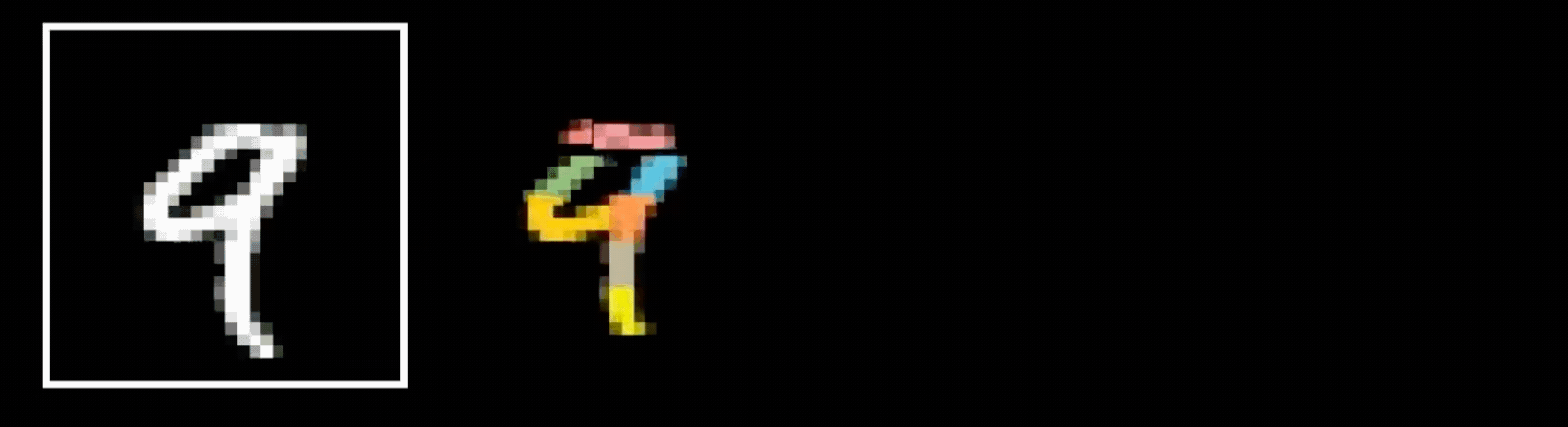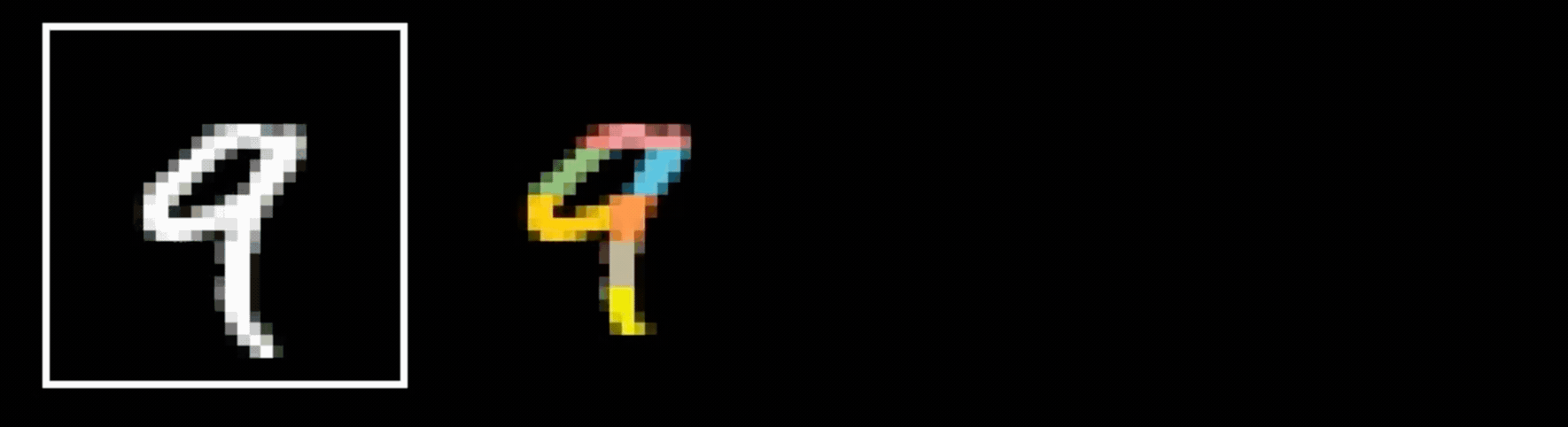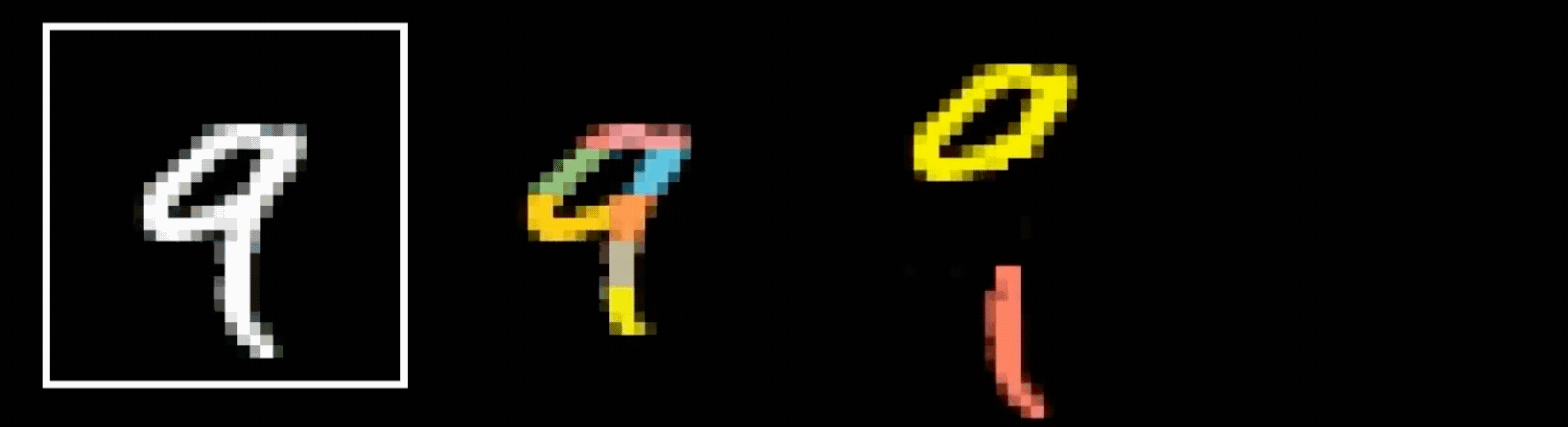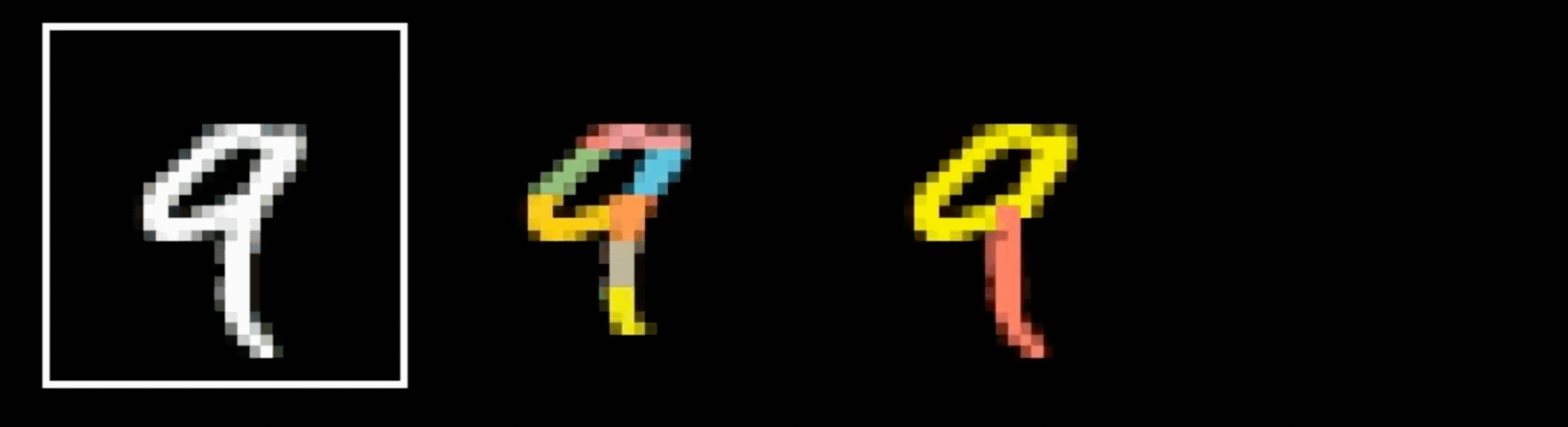
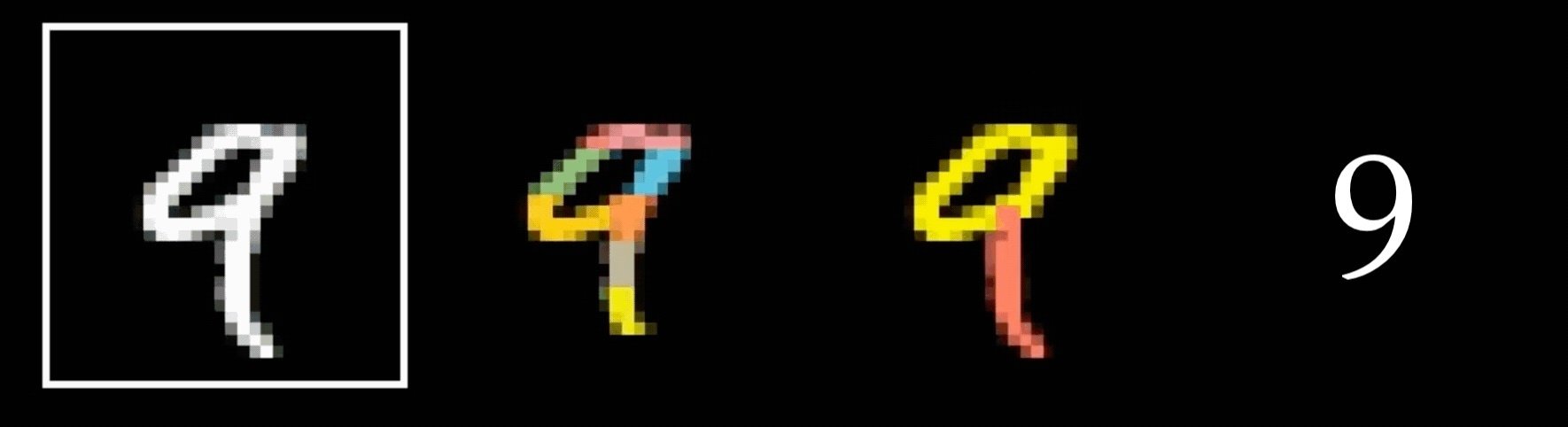
- Visual hierarchy
- Spatial locality
- Translational invariance
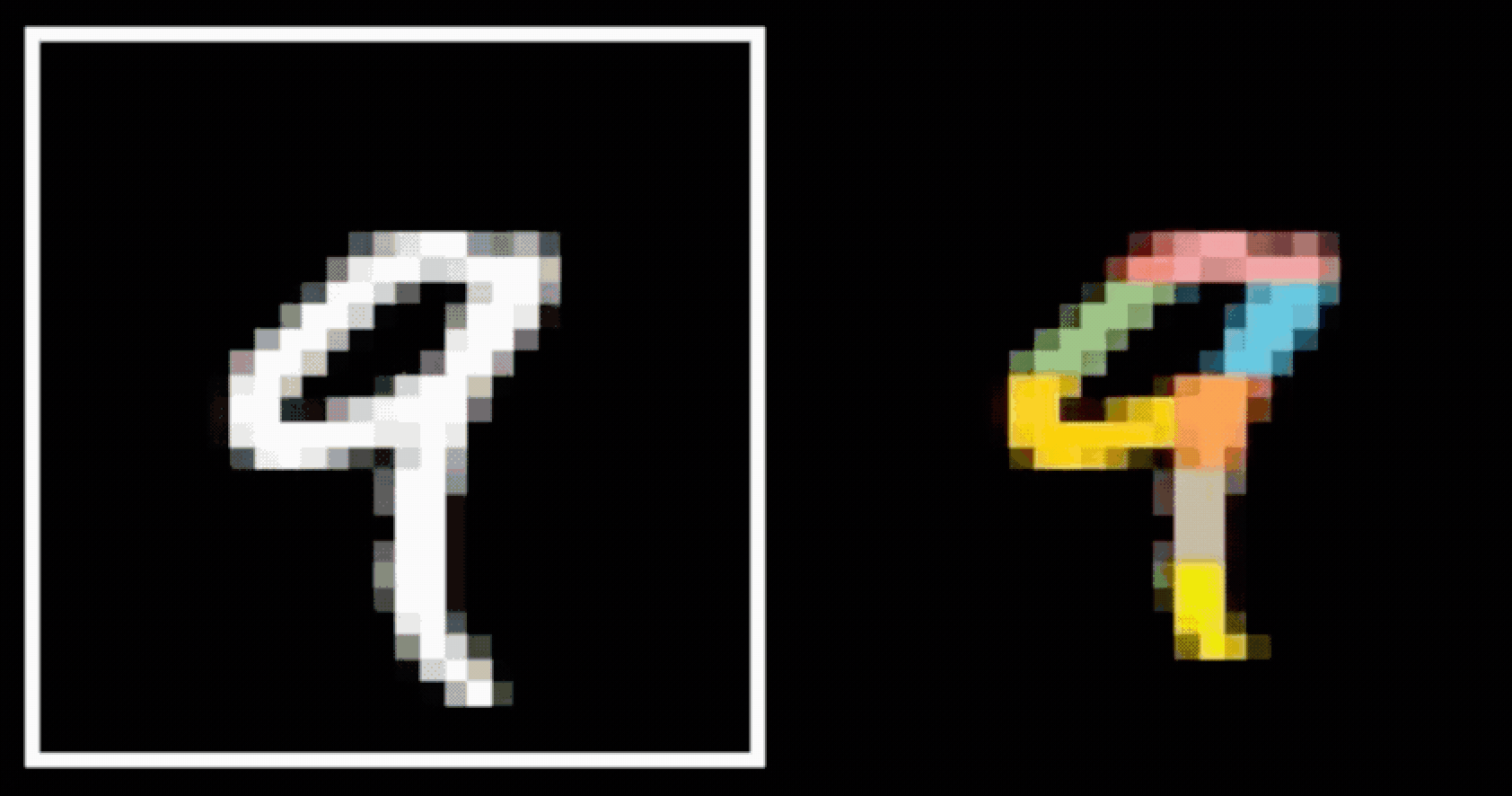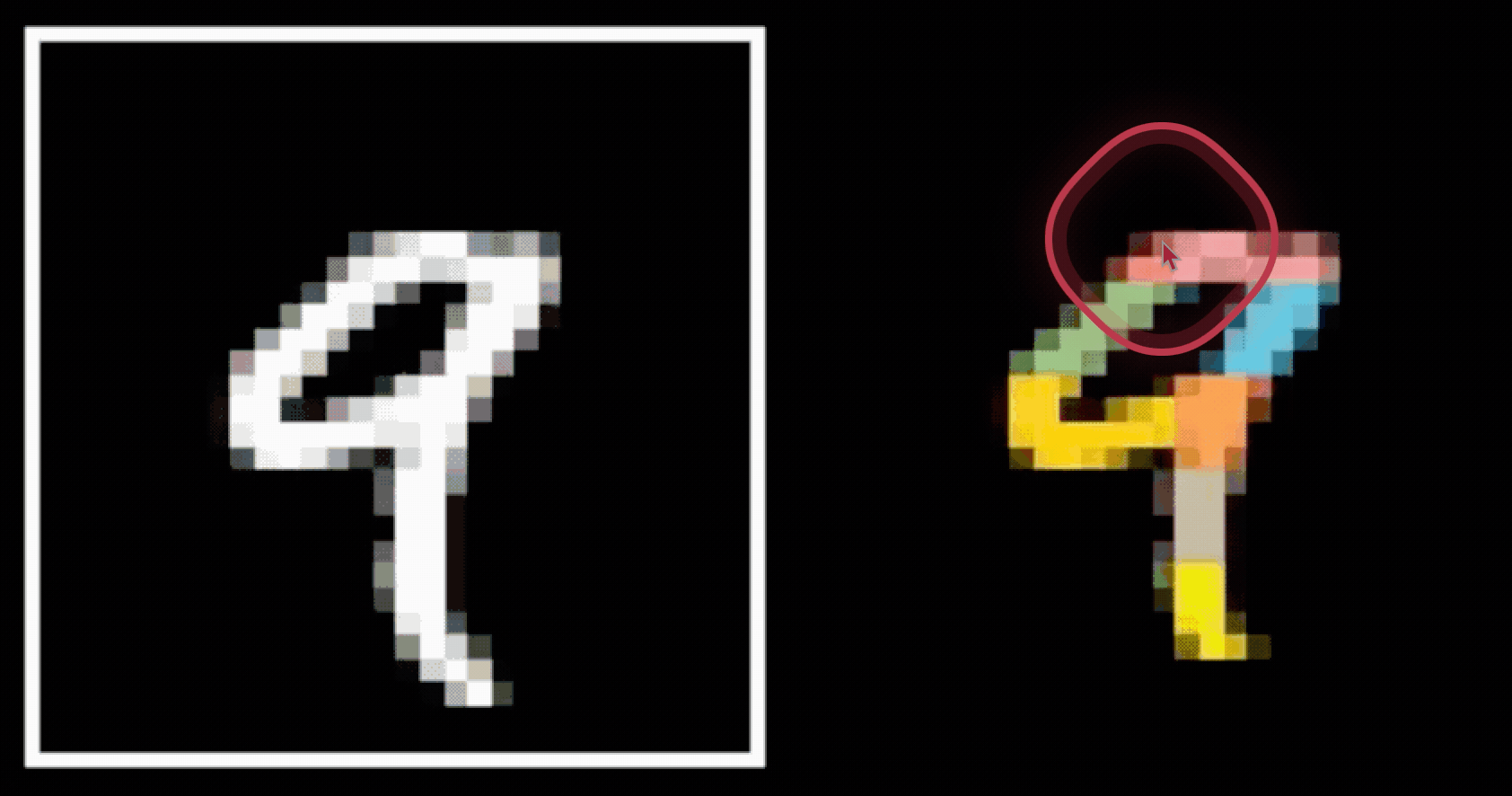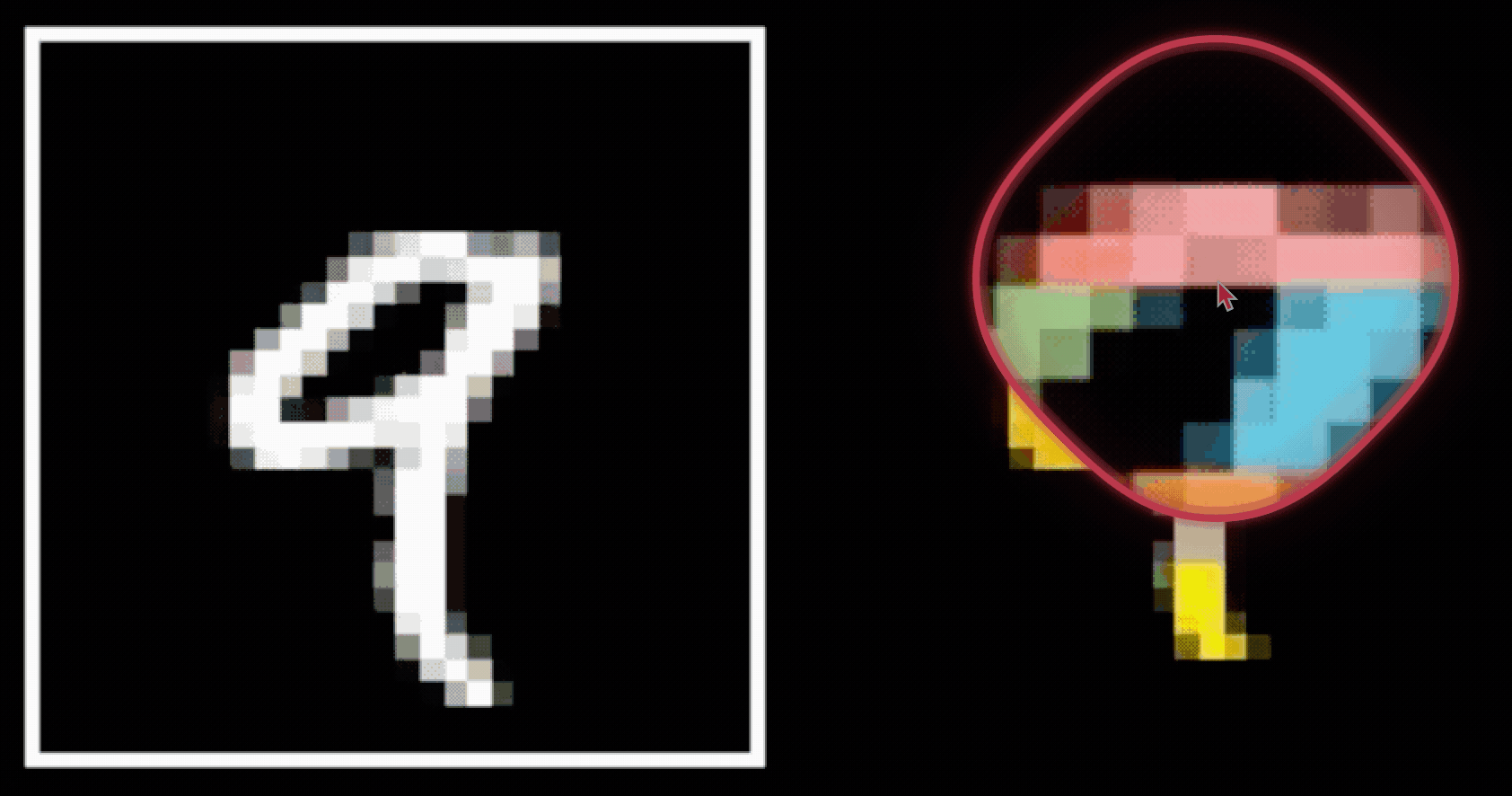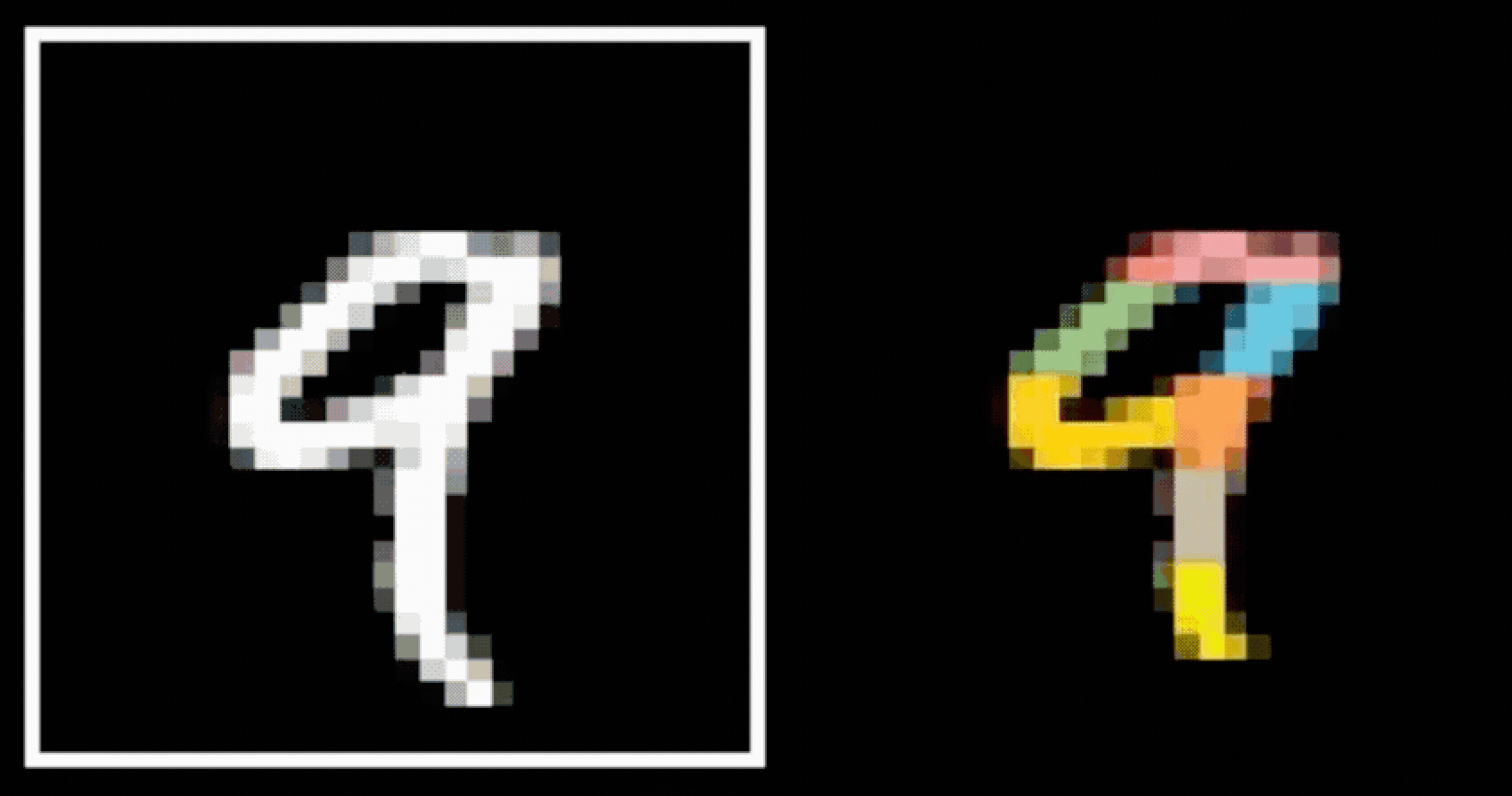
CNN cleverly exploits
to handle images efficiently
via
- layering (with nonlinear activations)
- convolution
- pooling
- Visual hierarchy
- Spatial locality
- Translational invariance
cleverly exploits
to handle efficiently
via
Outline
- Recap (fully-connected net)
- Motivation and big picture ideas of CNN
- Convolution operation
- 1d and 2d convolution mechanics
- interpretation:
- local connectivity
- weight sharing
- 3d tensors
- Max pooling
- Larger window
- Typical architecture and summary
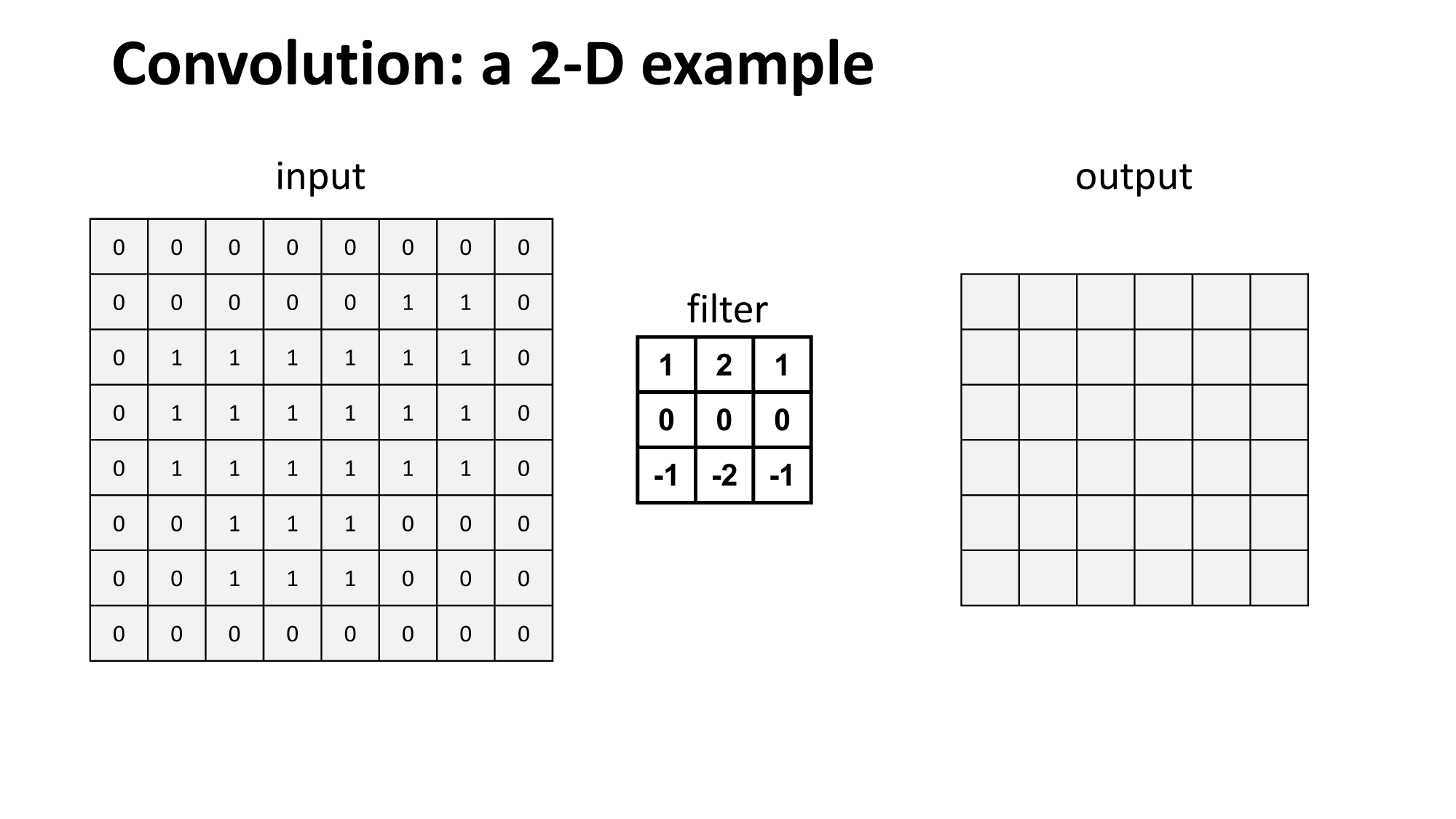
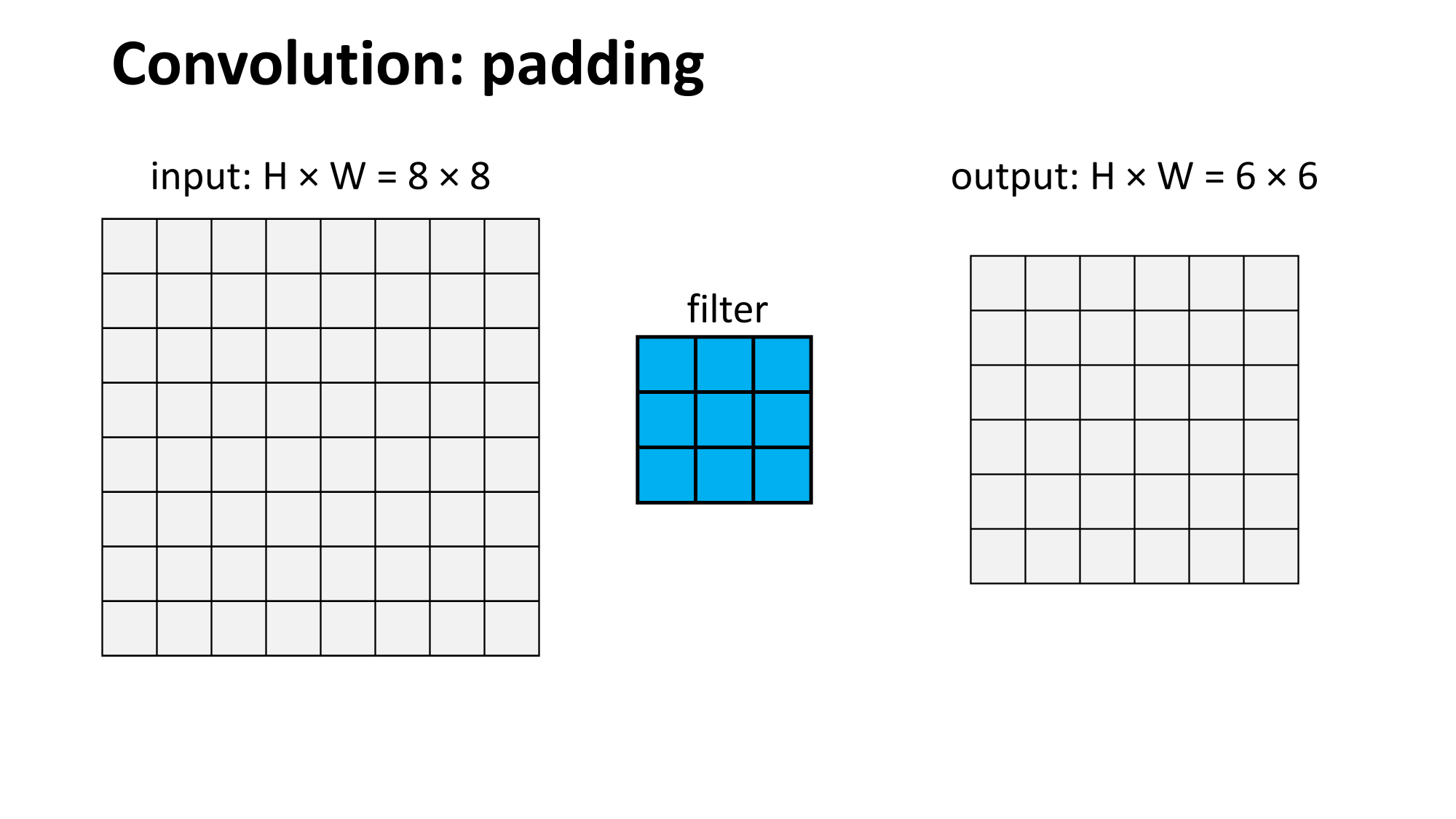
Convolutional layer might sound foreign, but...
0
1
0
1
1
-1
1
input image
filter
output image
1
(0*-1)+(1*1)=1
0
1
0
1
1
-1
1
input image
filter
output image
1
-1
(1*-1)+(0*1)=-1
0
1
0
1
1
-1
1
input image
filter
output image
1
-1
1
(0*-1)+(1*1)=1
0
1
0
1
1
-1
1
input image
filter
output image
1
-1
1
0
(1*-1)+(1*1)=0
0
1
-1
1
1
-1
1
input image
filter
output image
1
-1
2
0
(0*-1)+(1*1)=1
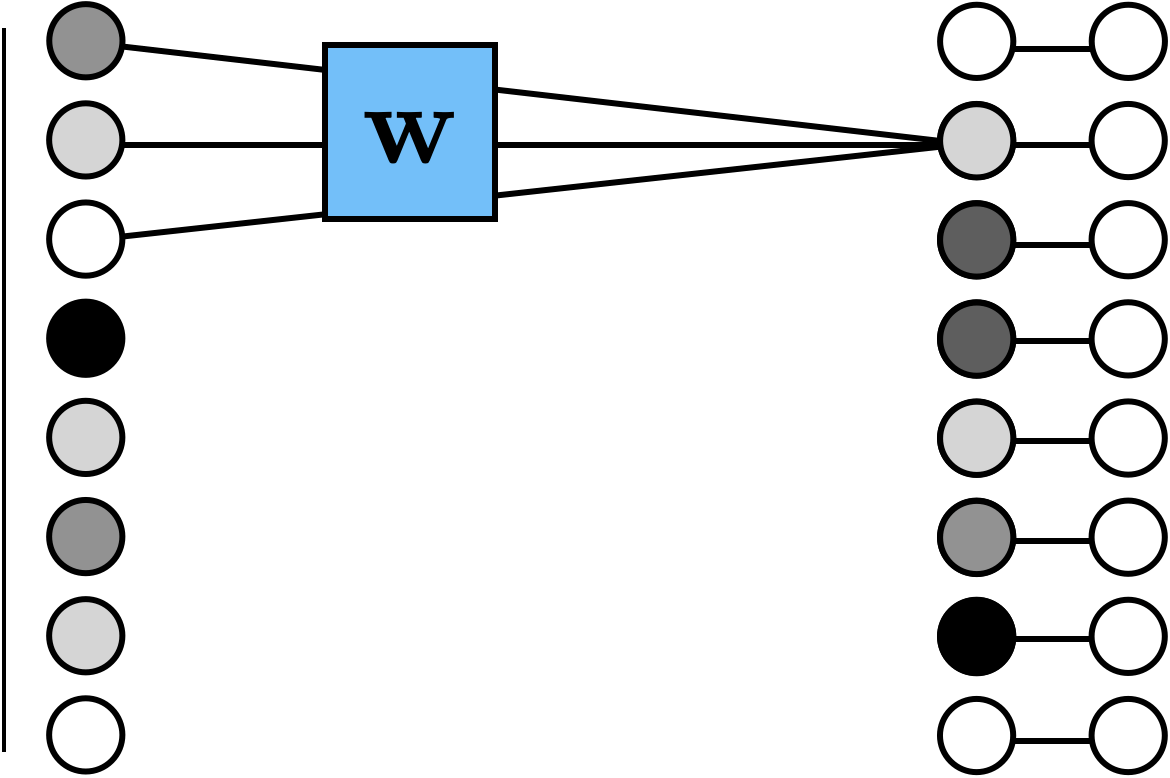
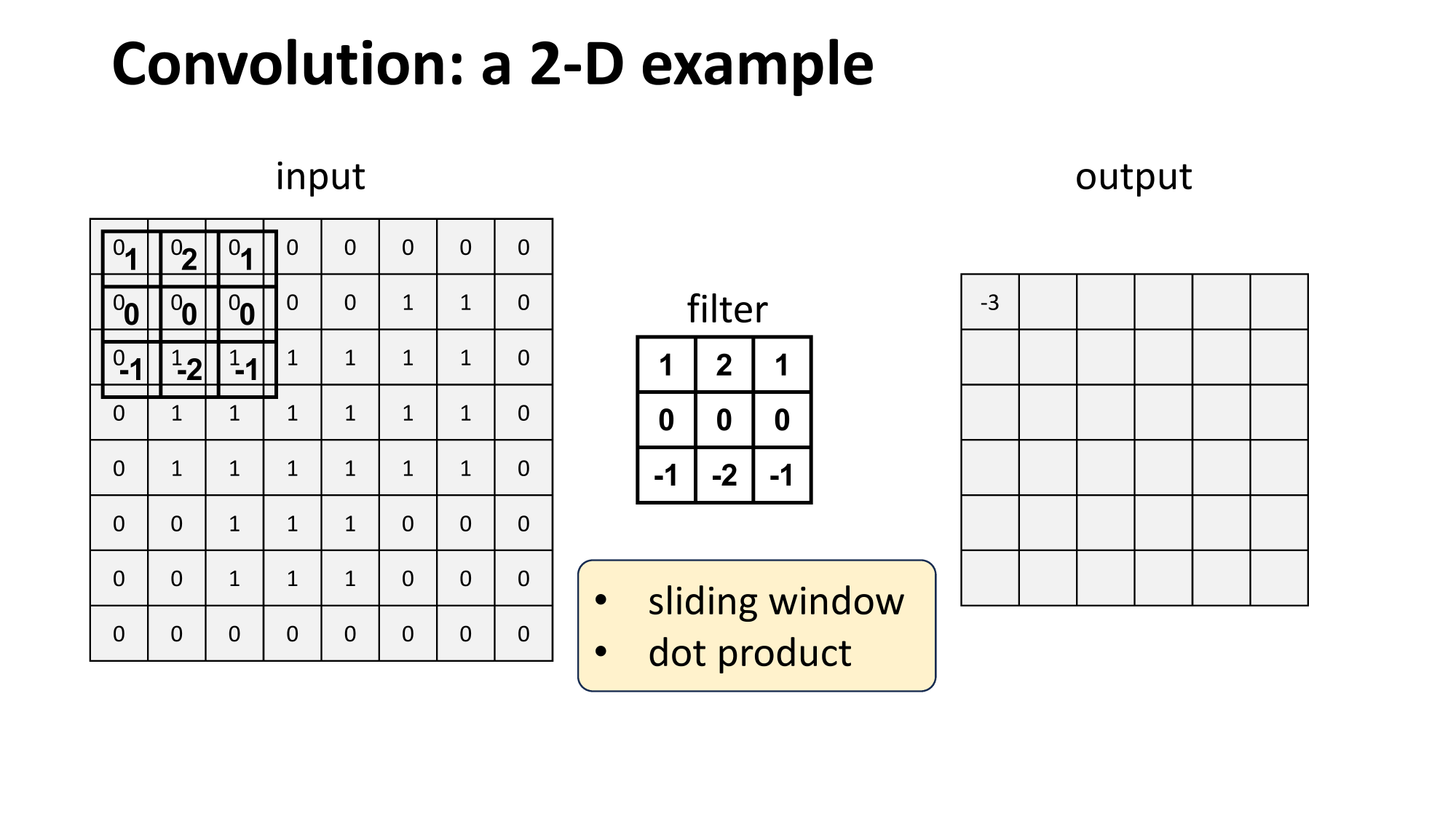
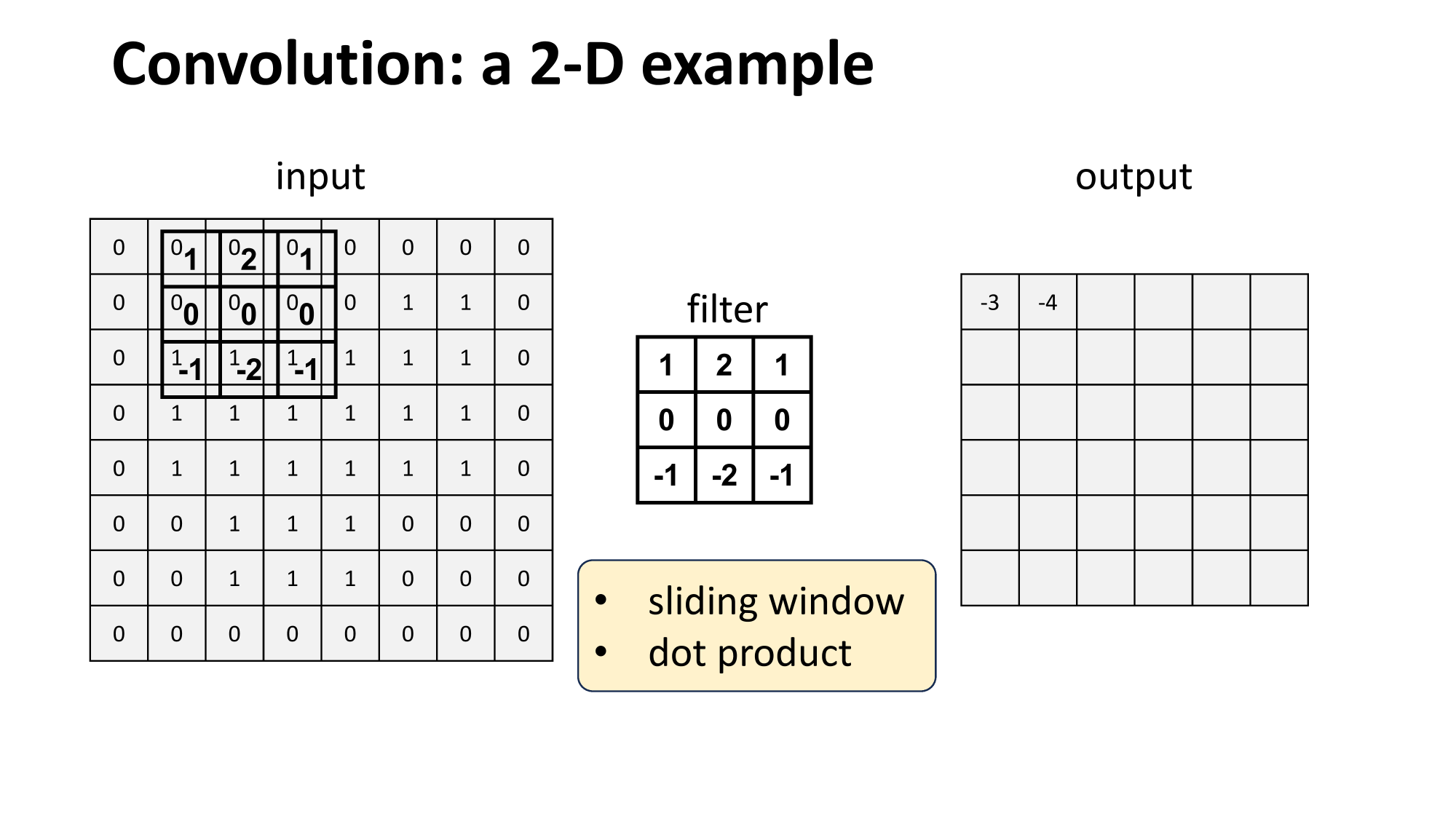
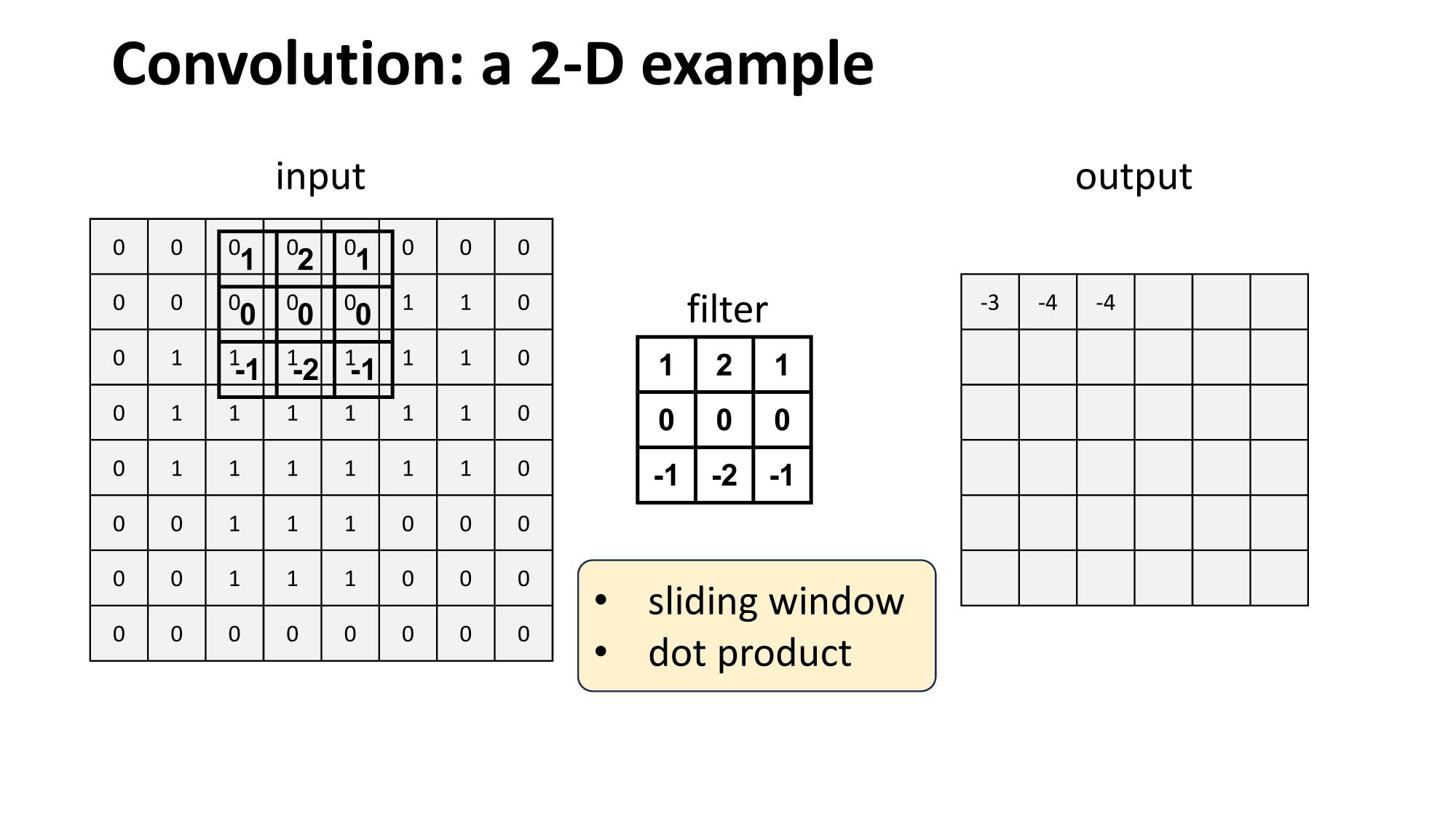
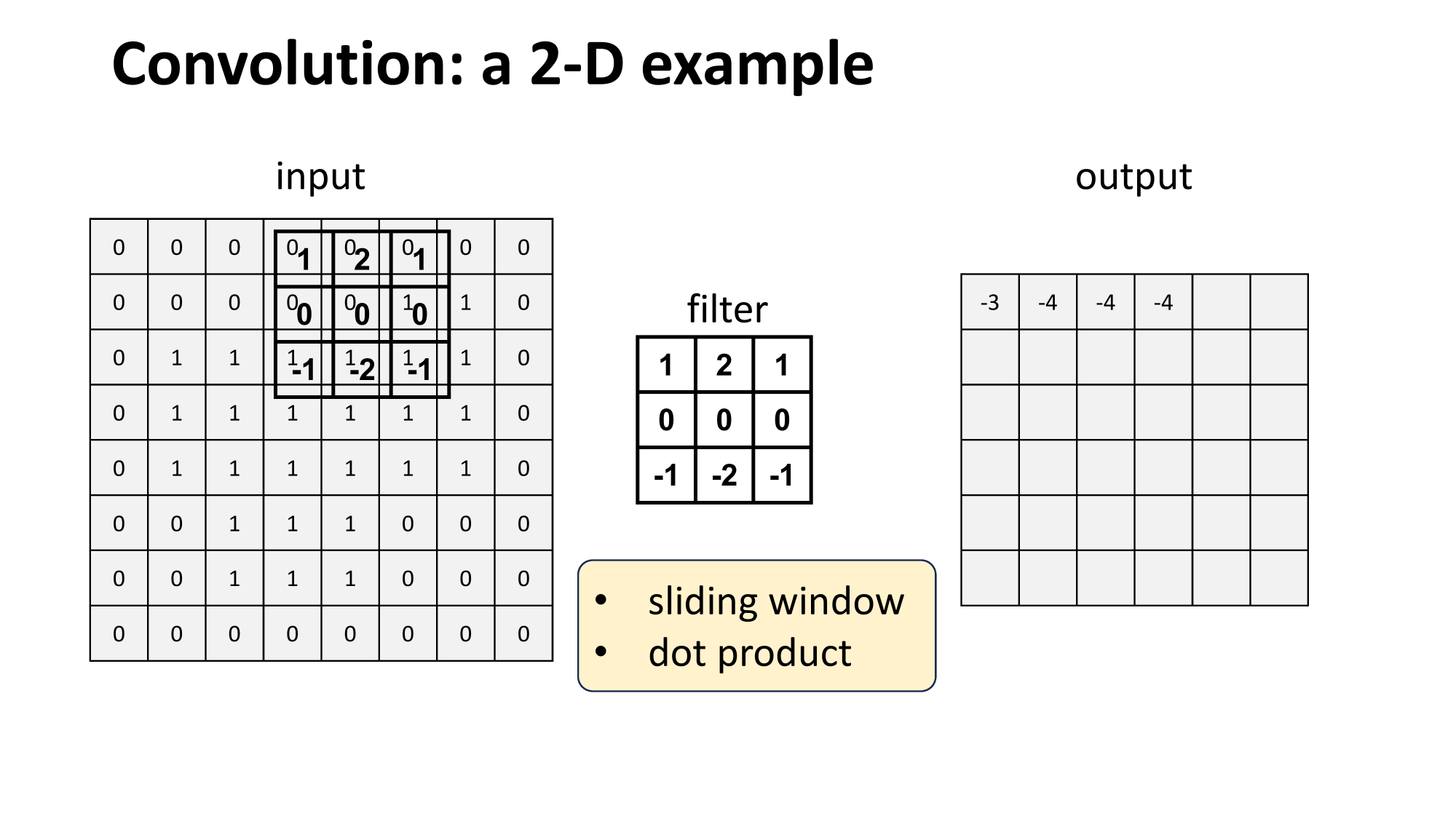
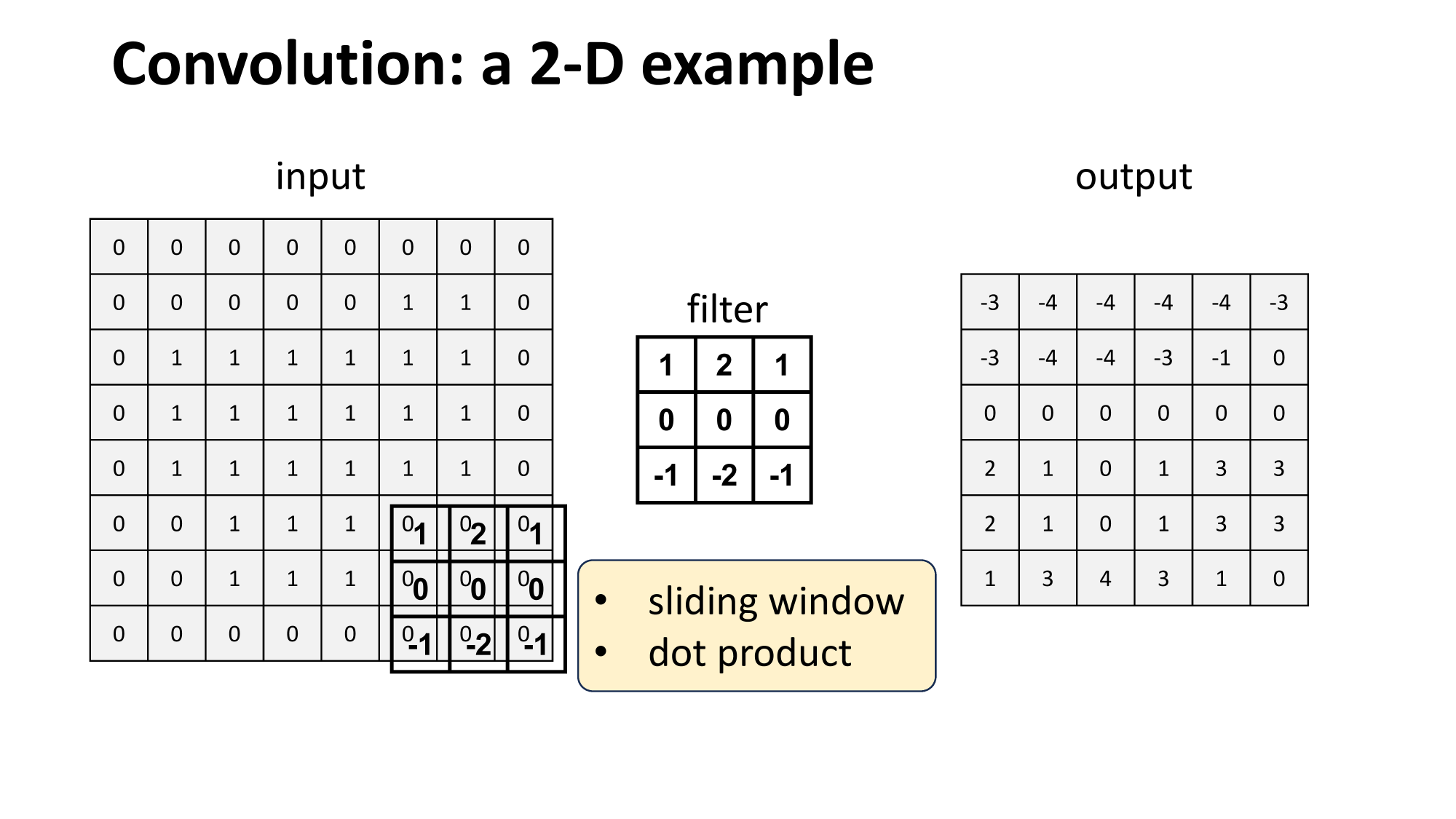
- 'look' locally
- parameter sharing
- "template" matching
(-1*-1)+(1*1)=2
- 'look' locally
w
z
a
x
0
1
-1
1
1
-1
1
input image
filter
output image
1
-1
2
0
fully-connected layer
- parameter sharing
0
1
0
1
1
-1
1
convolve
with
=
1
-1
1
0
0
0
1
-1
-1
0
0
0
0
0
1
0
0
0
-1
1
0
1
-1
0
0
or dot
with
- parameter sharing
0
1
0
1
1
0
1
0
1
1
convolve with ?
=
dot-product with ?
=
0
1
0
1
1
0
1
0
1
1
convolve with
dot-product with
1
I_{5\times5}
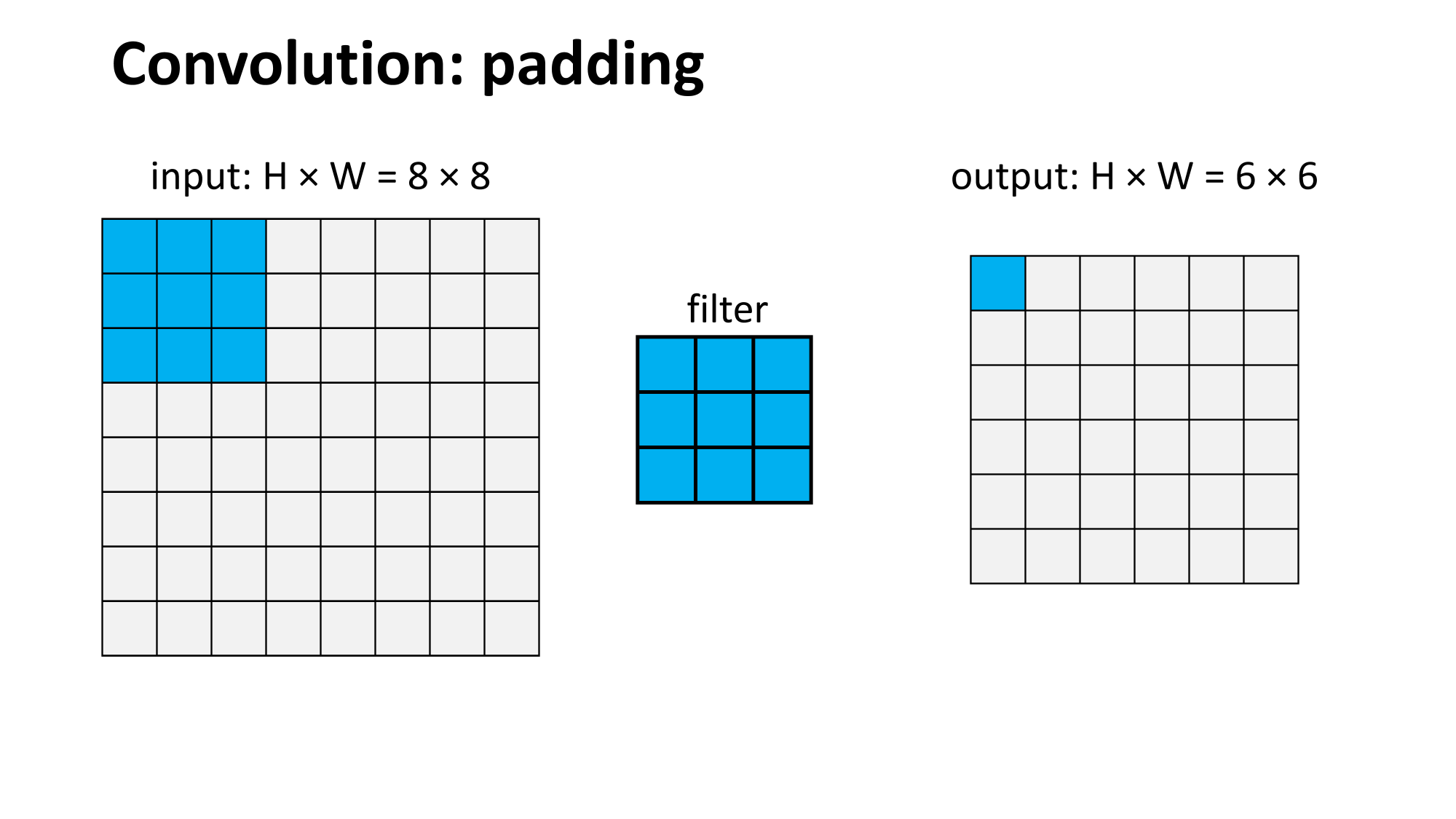
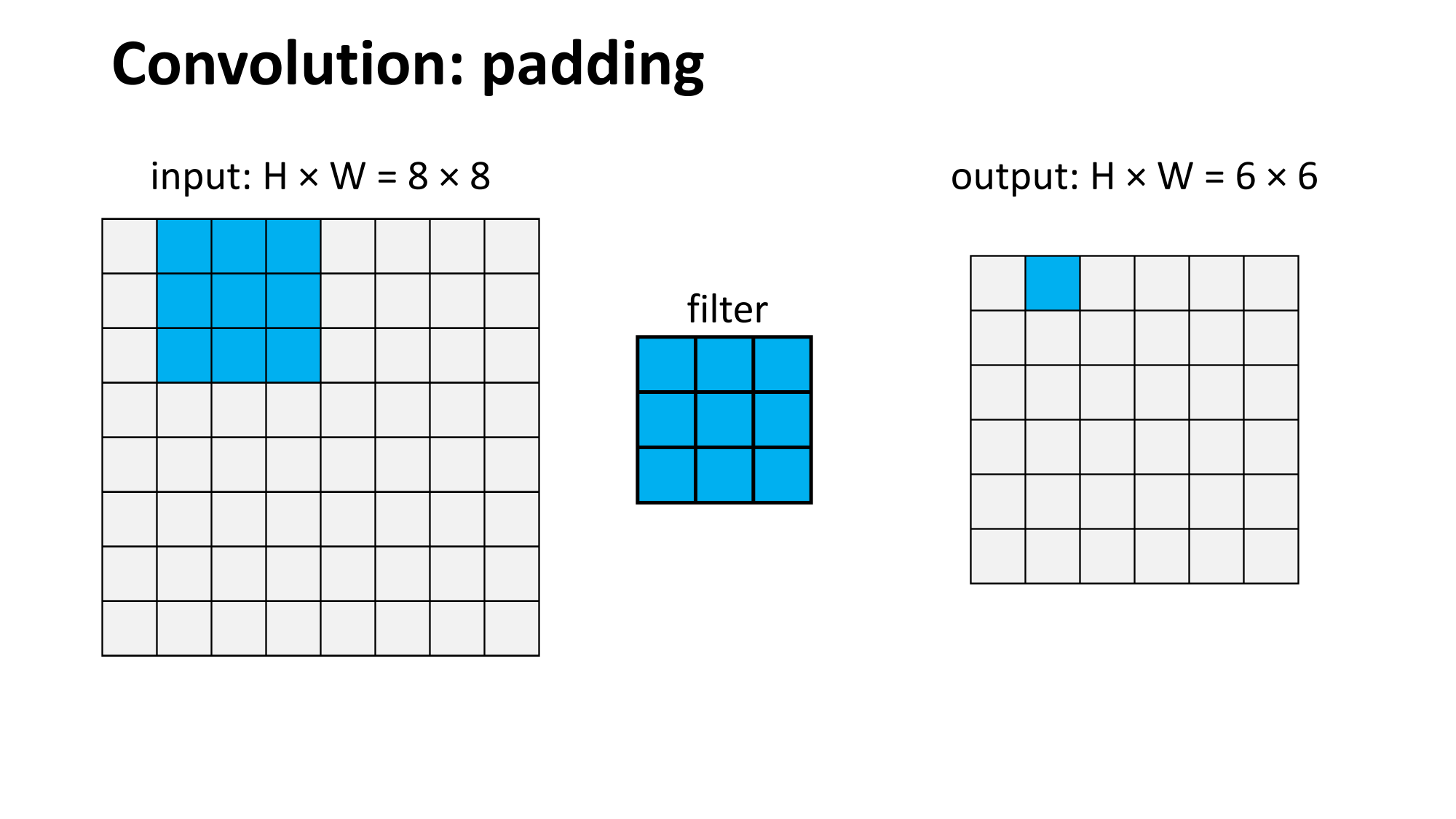
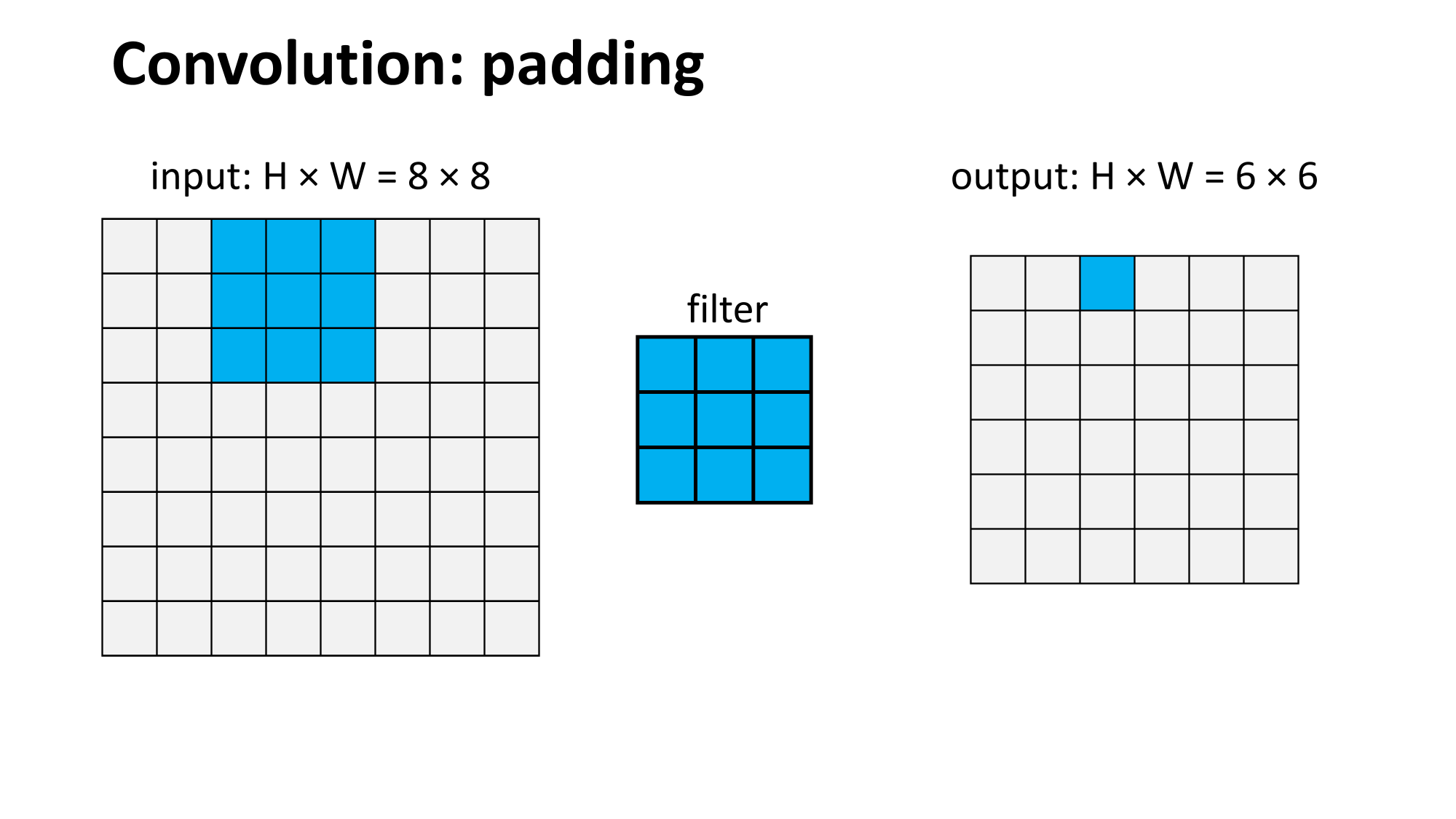
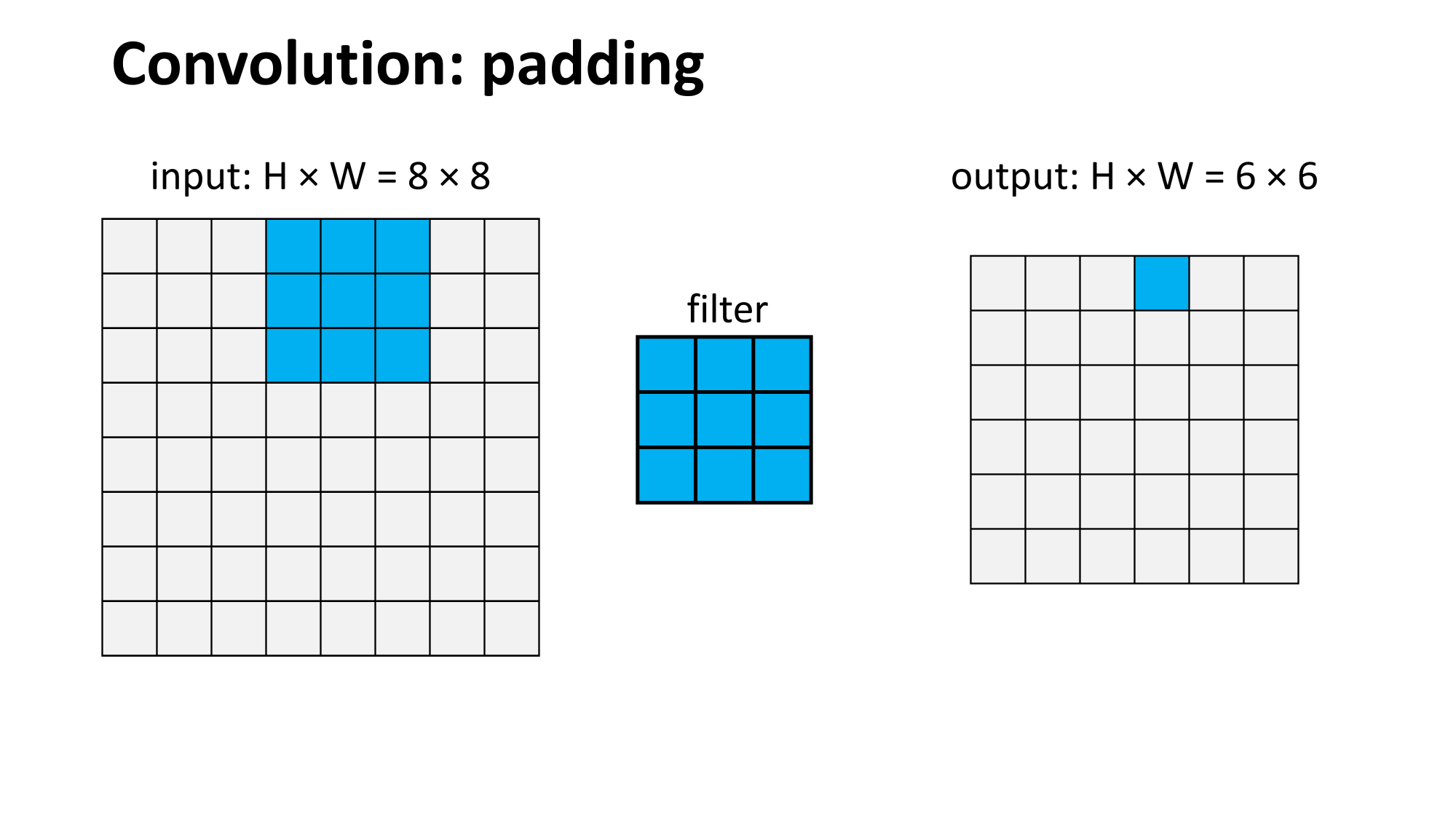
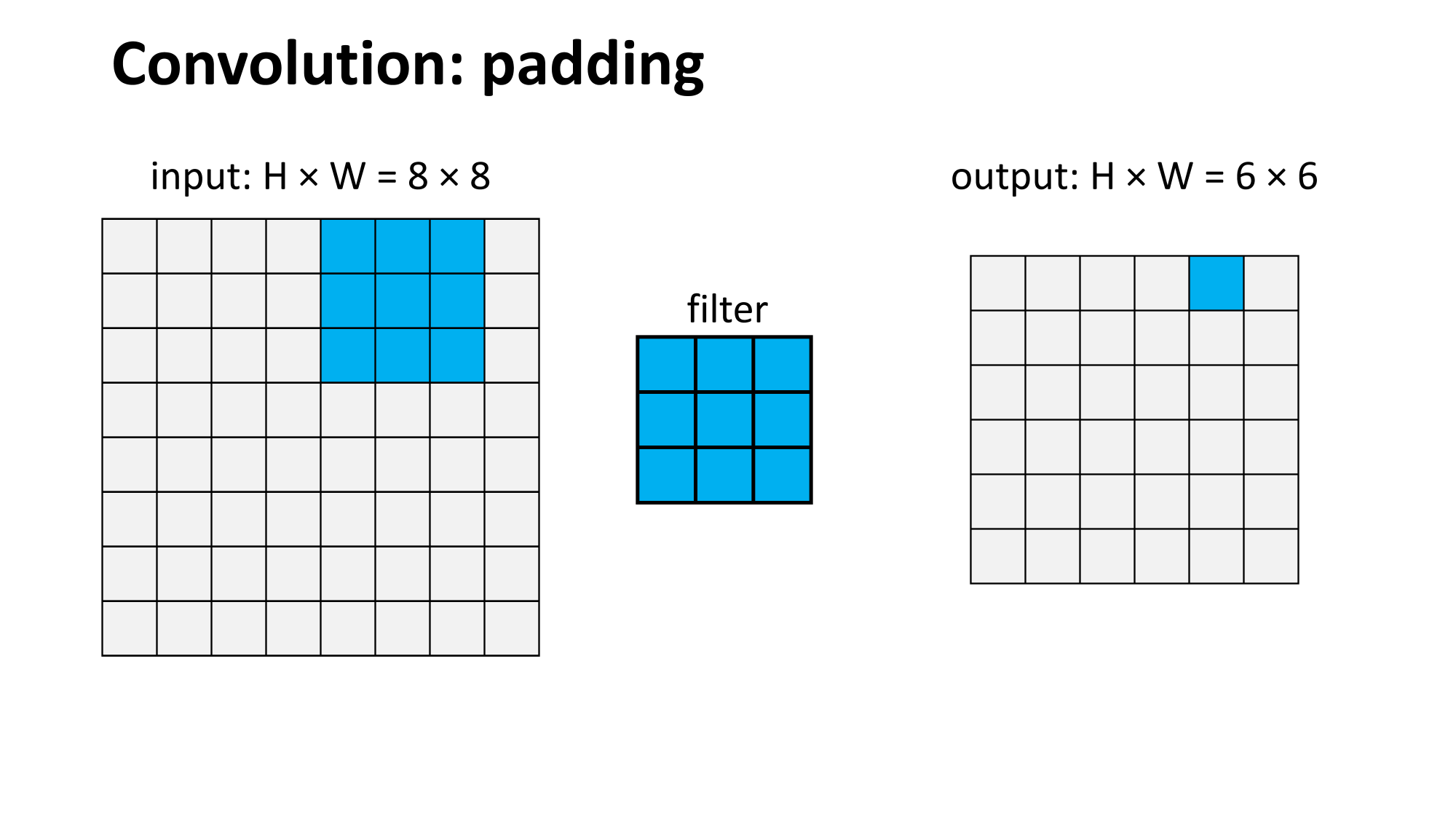
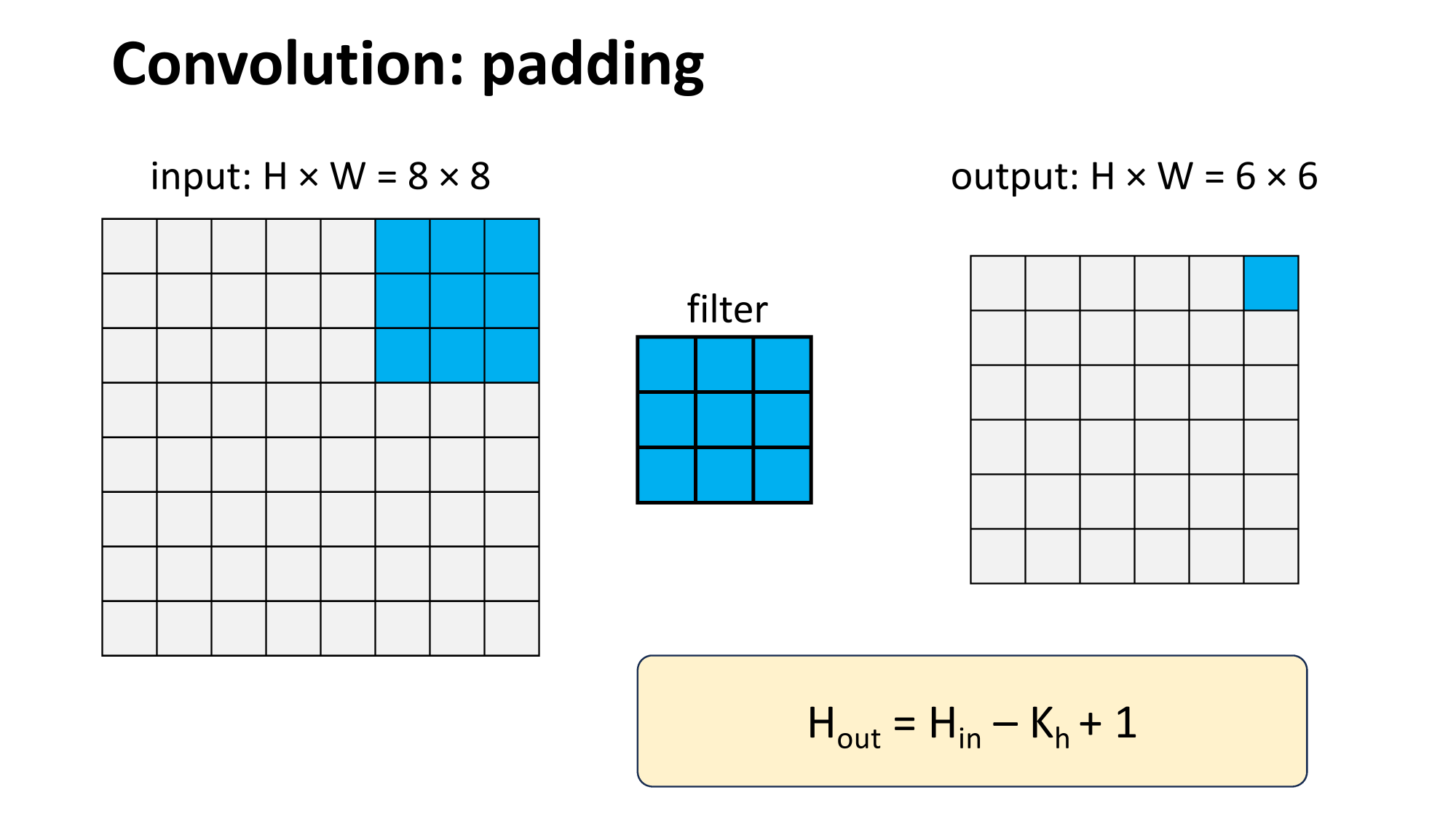
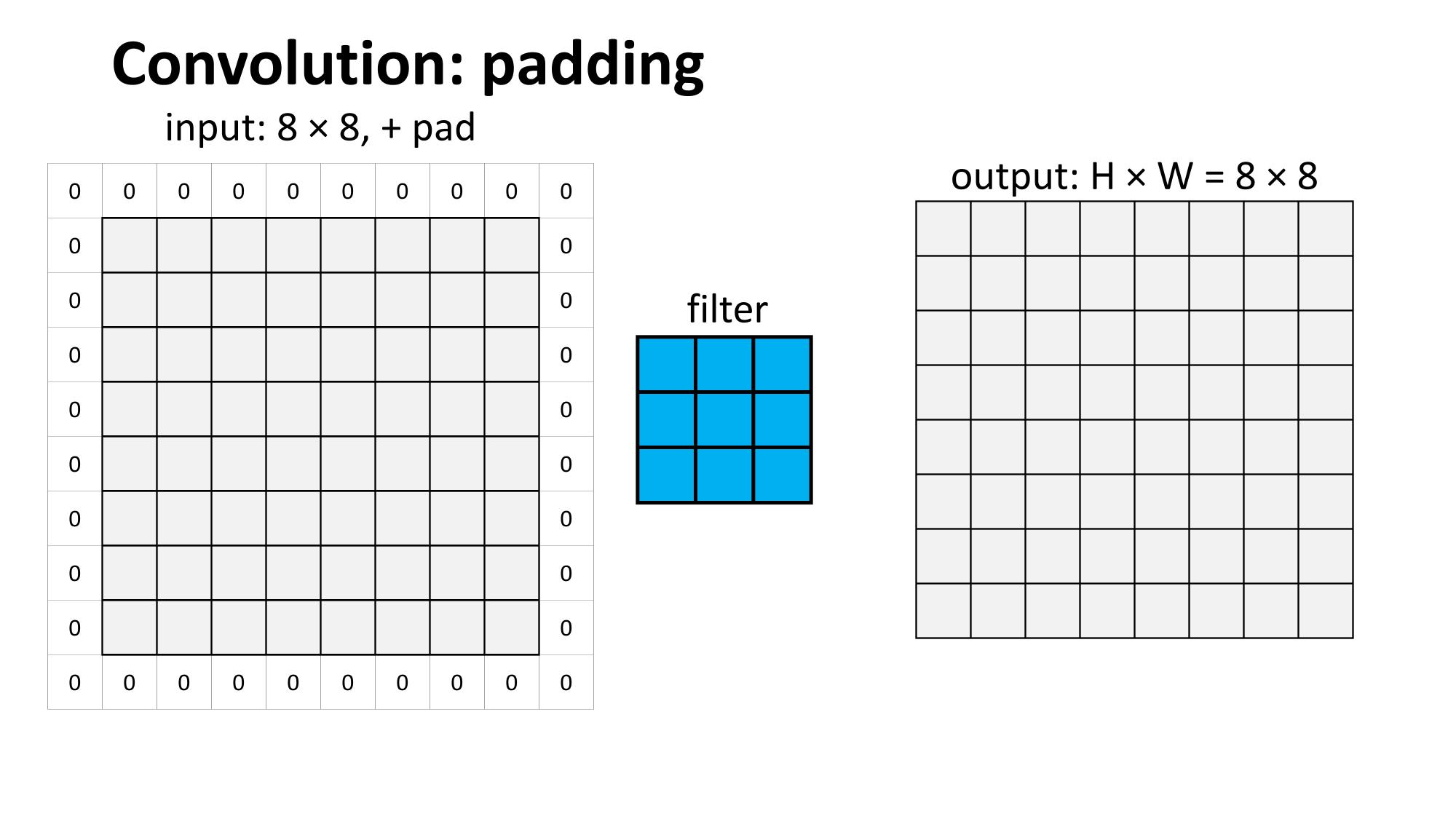
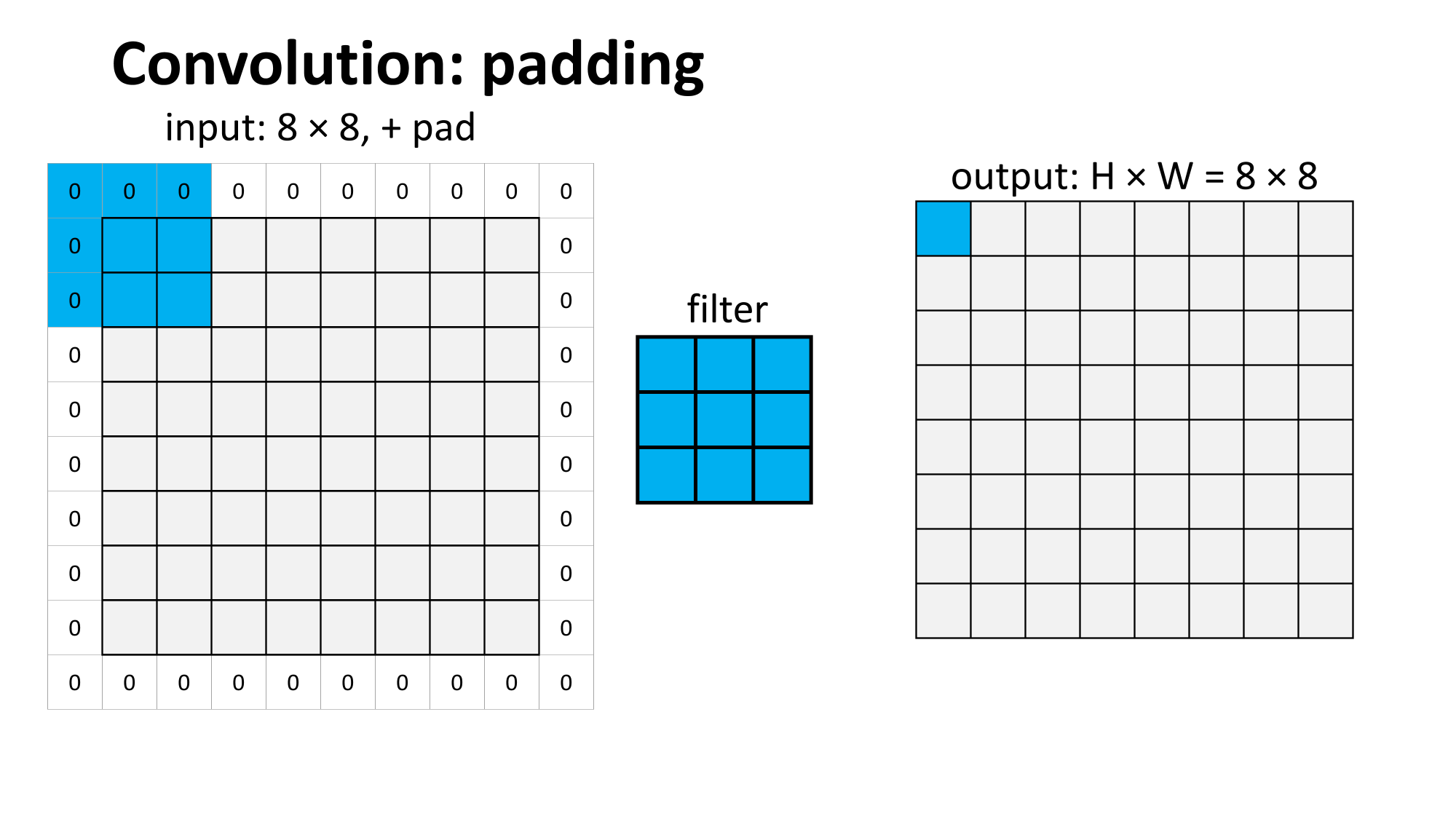
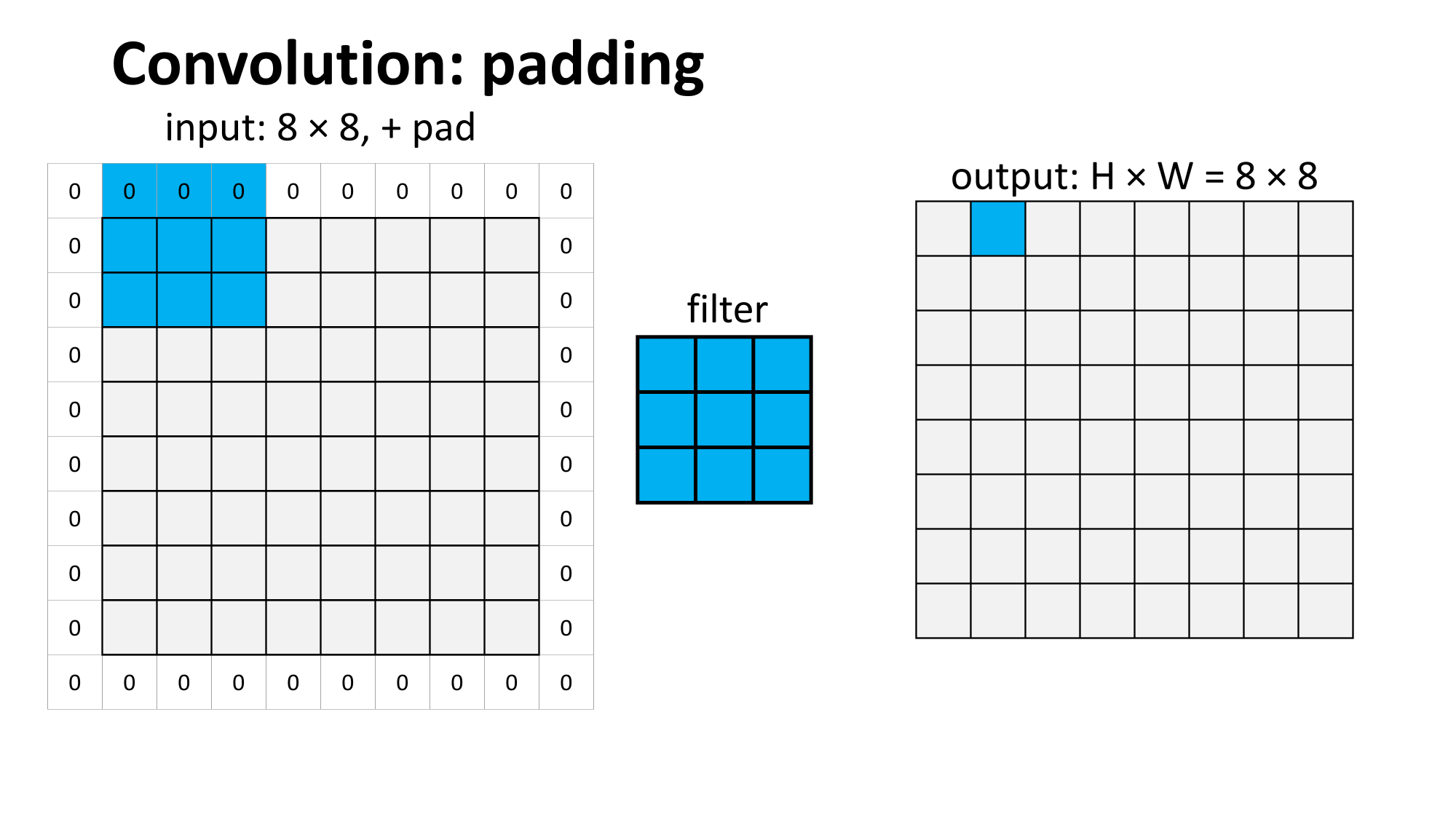
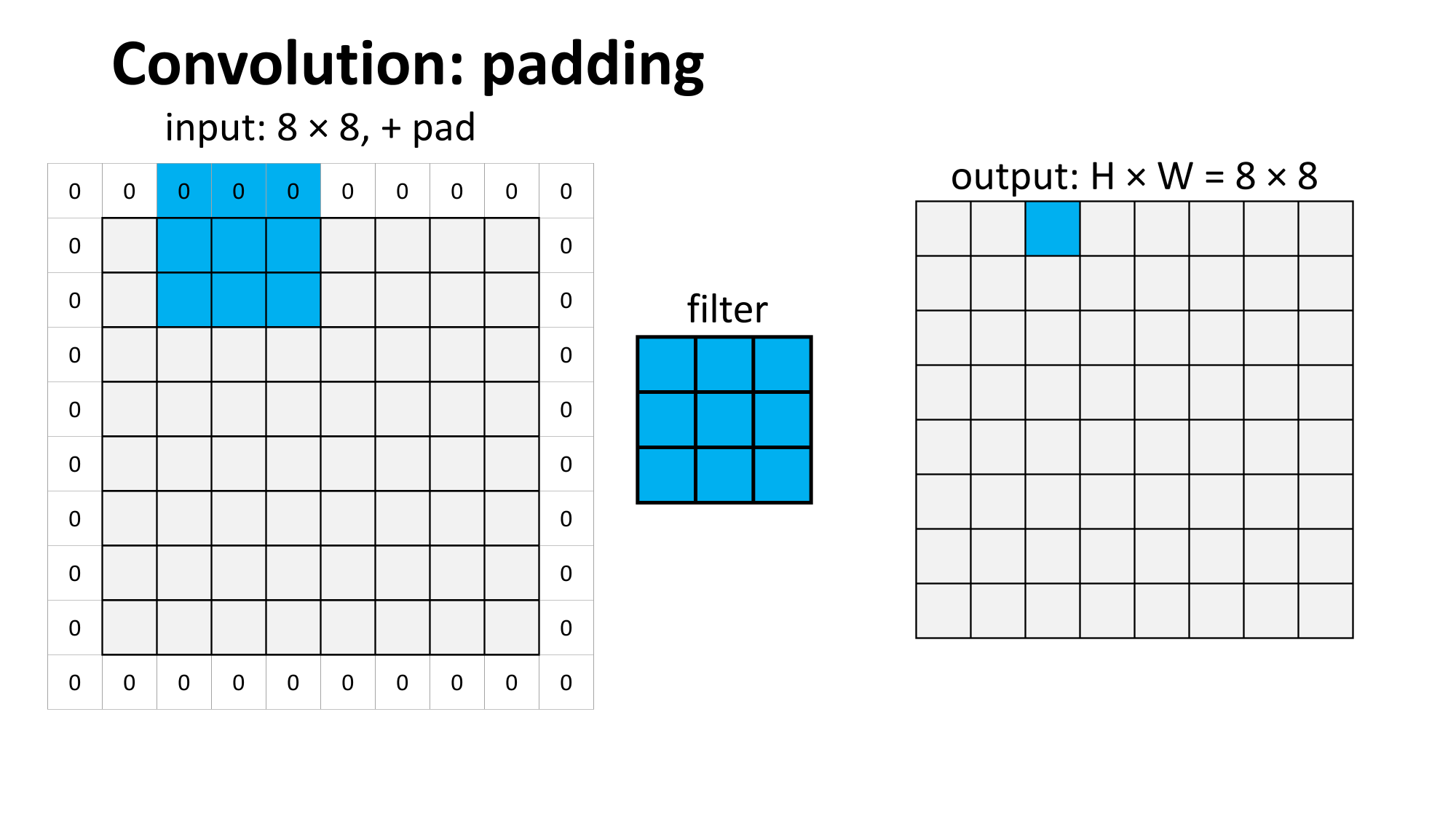
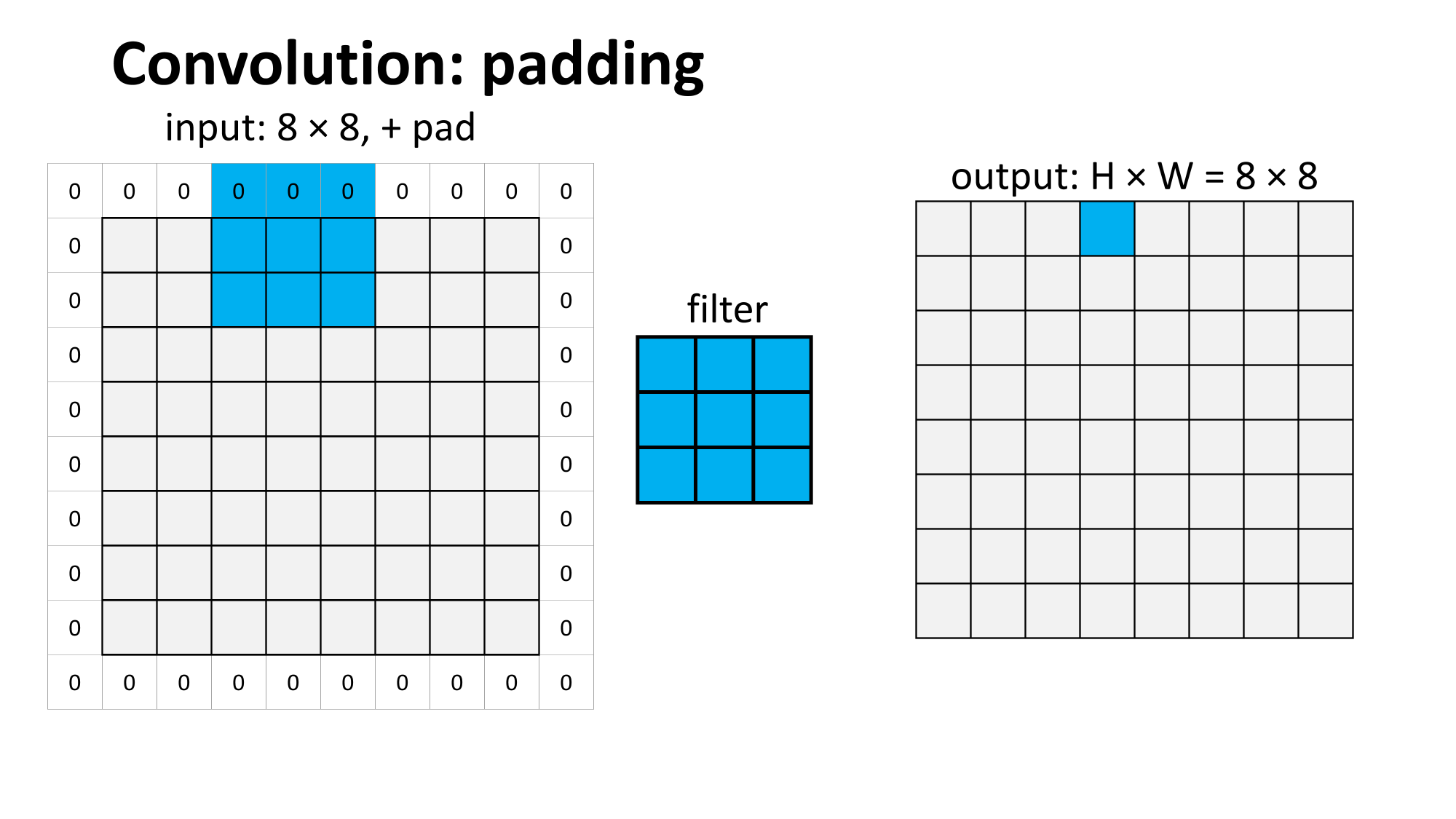
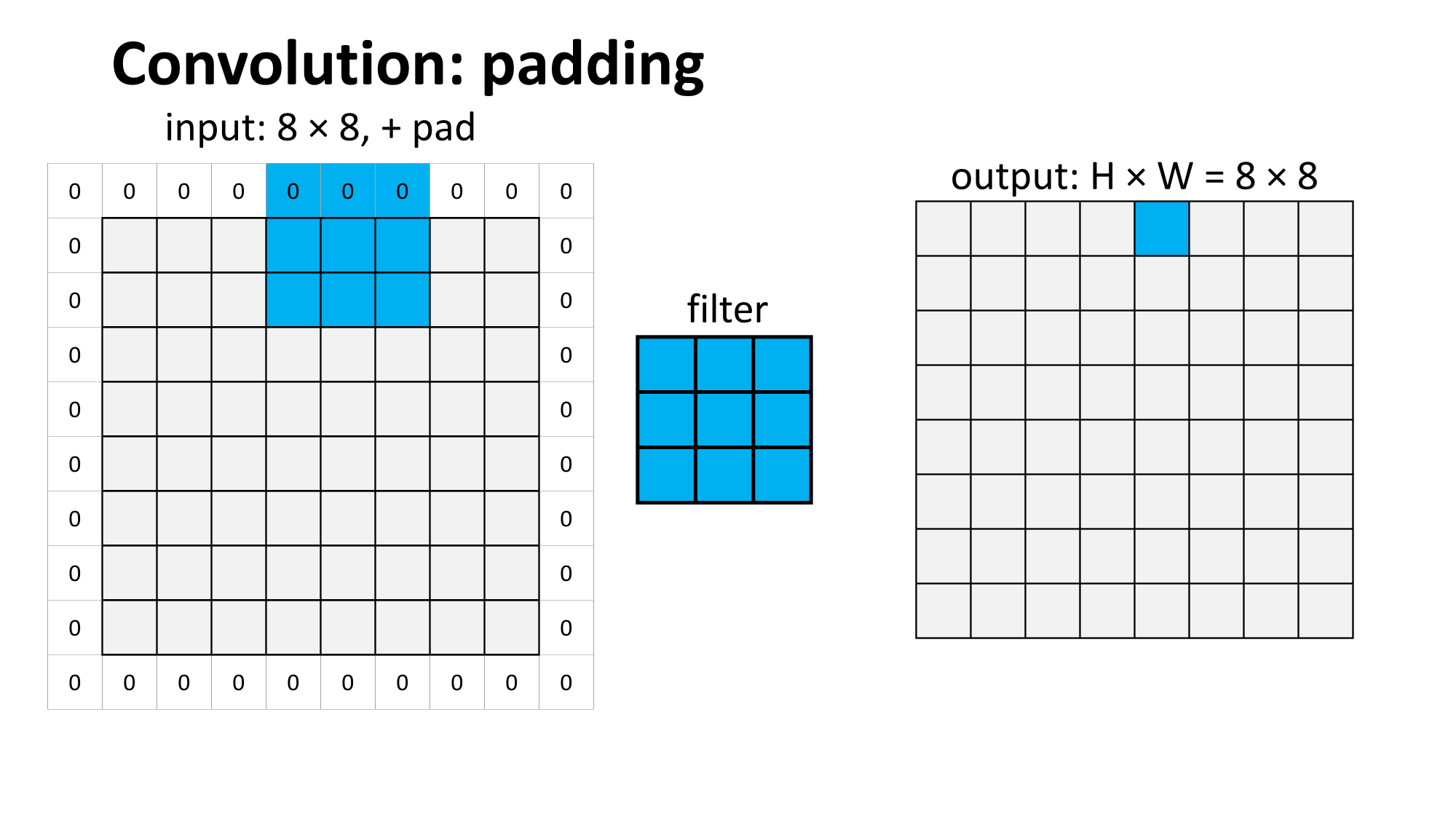
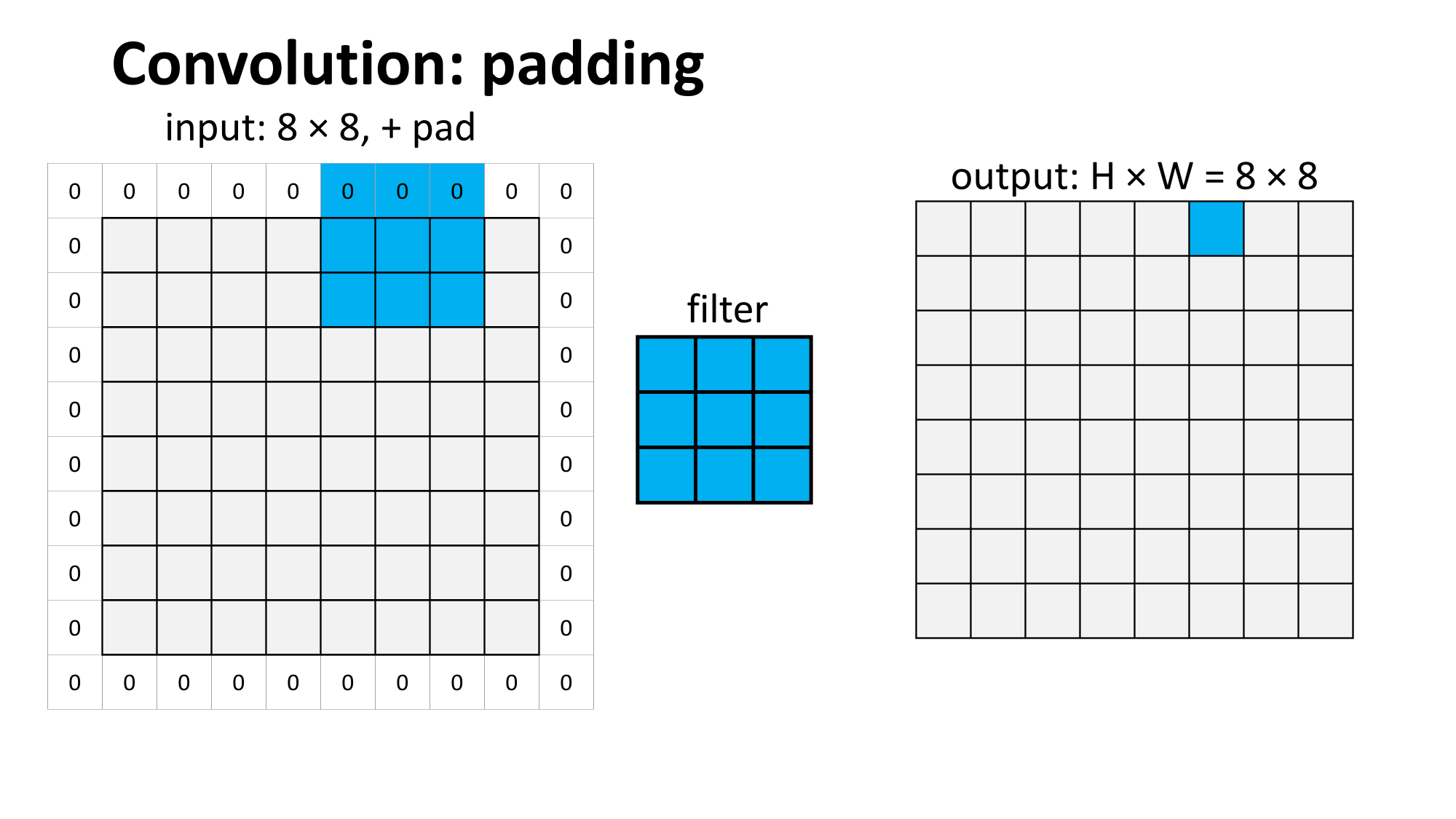
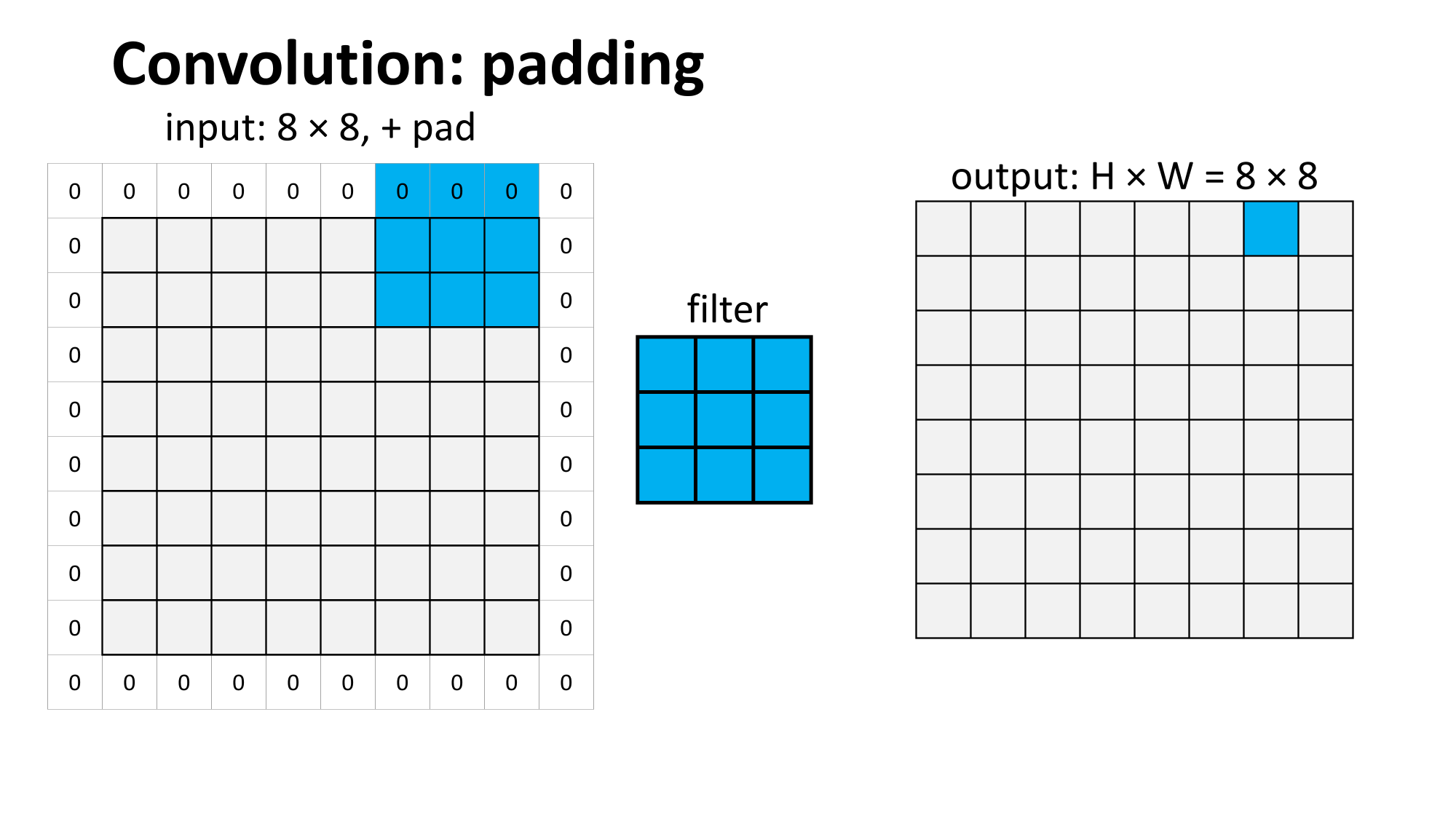
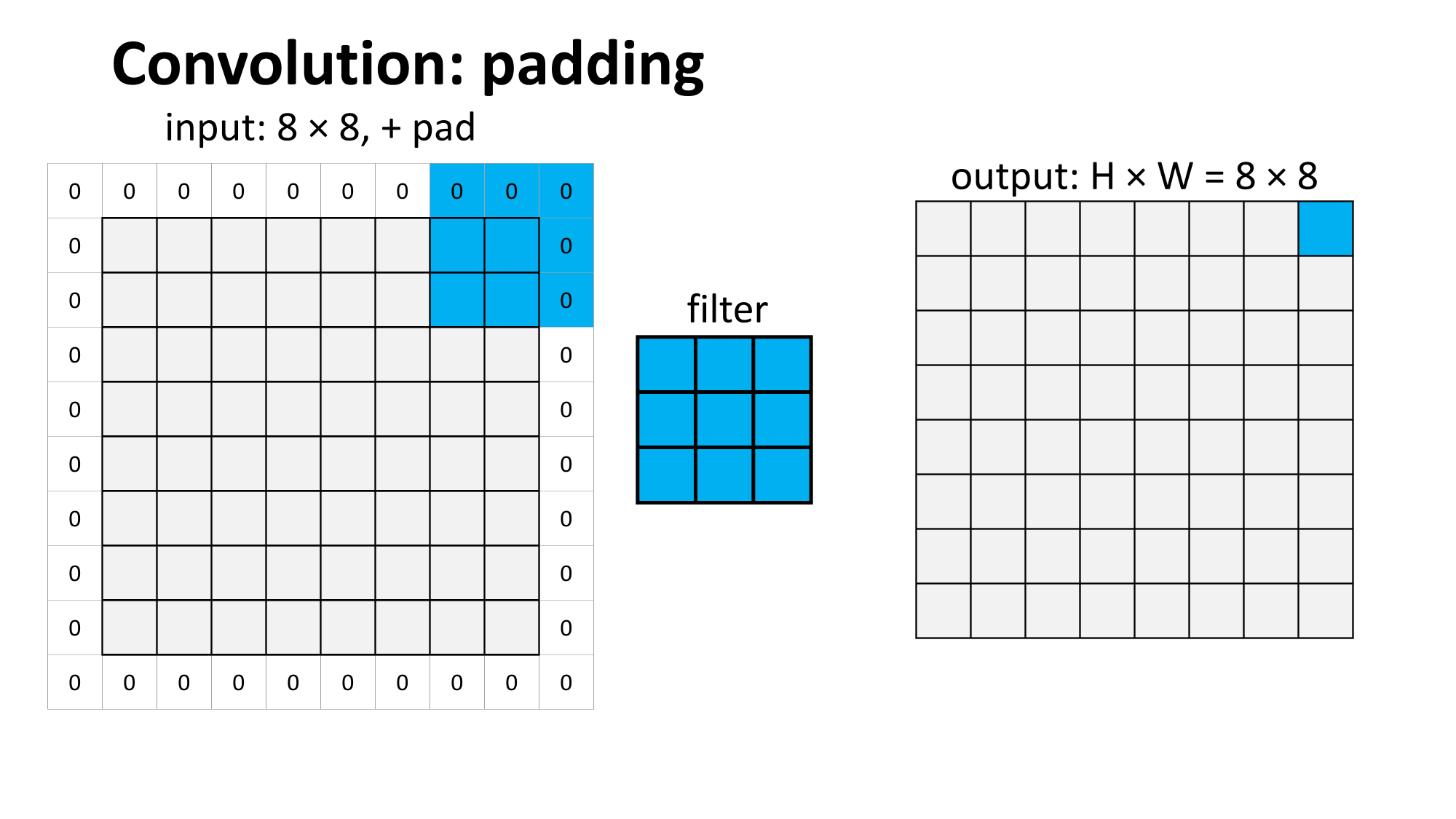
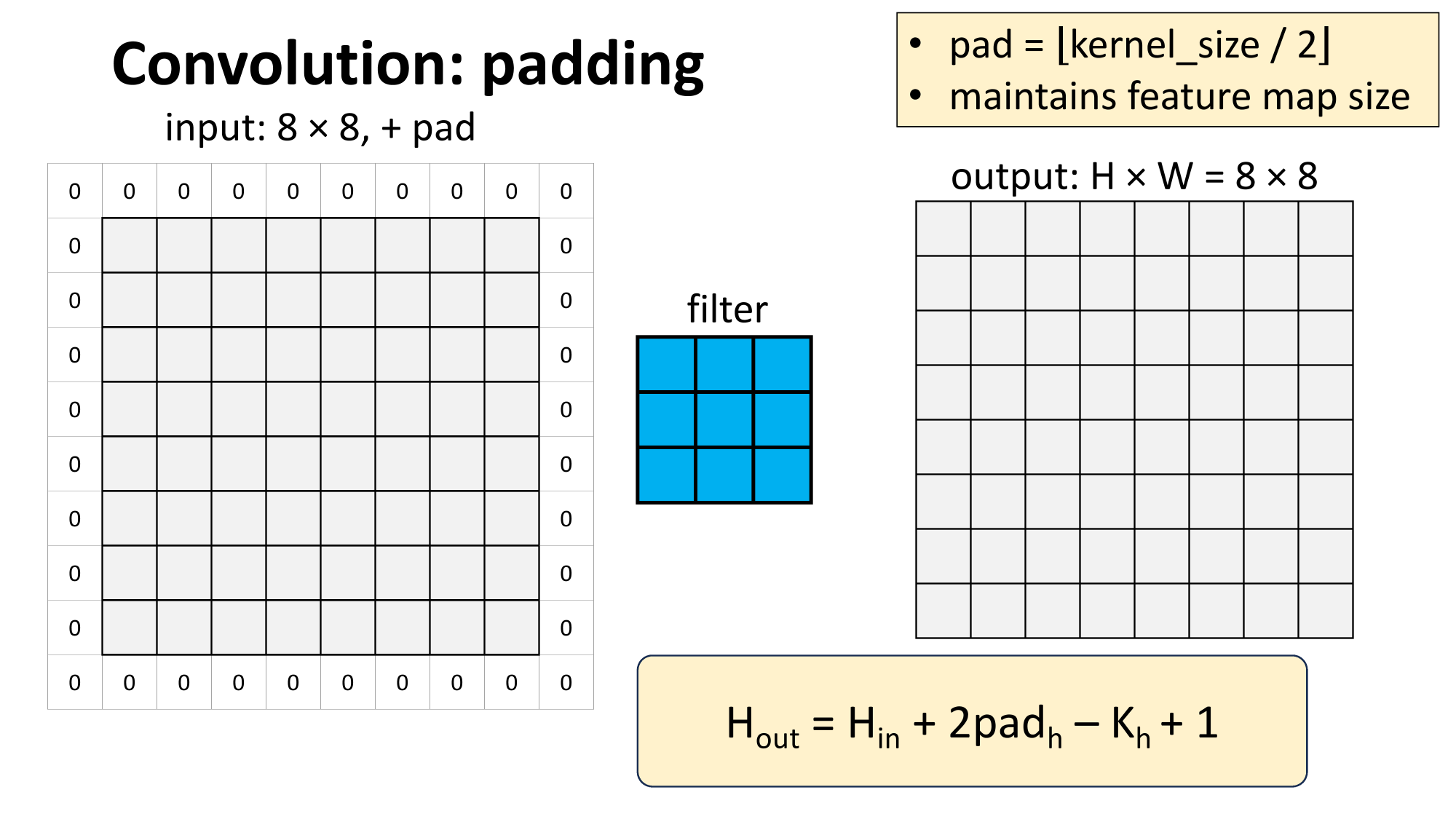
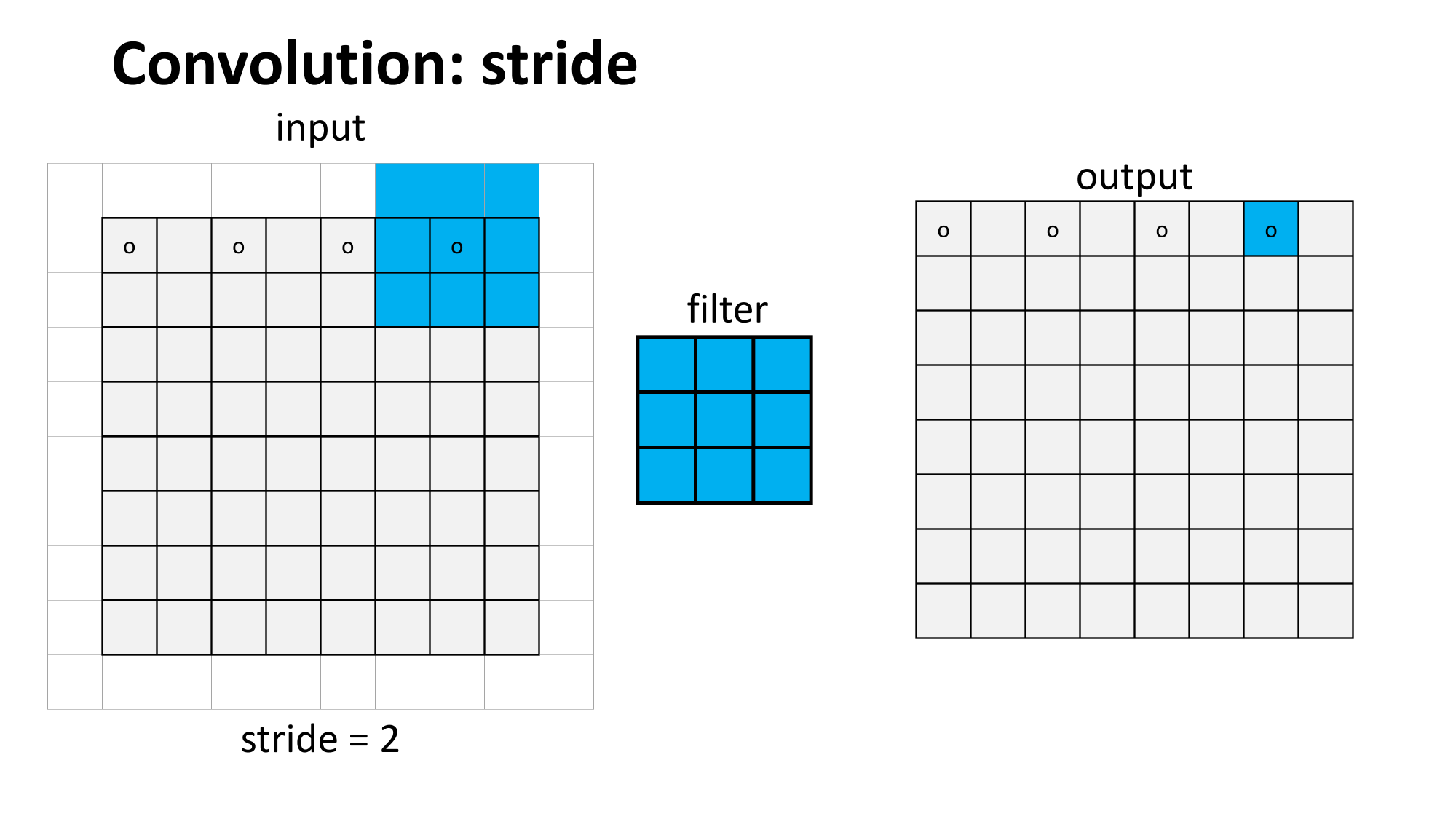
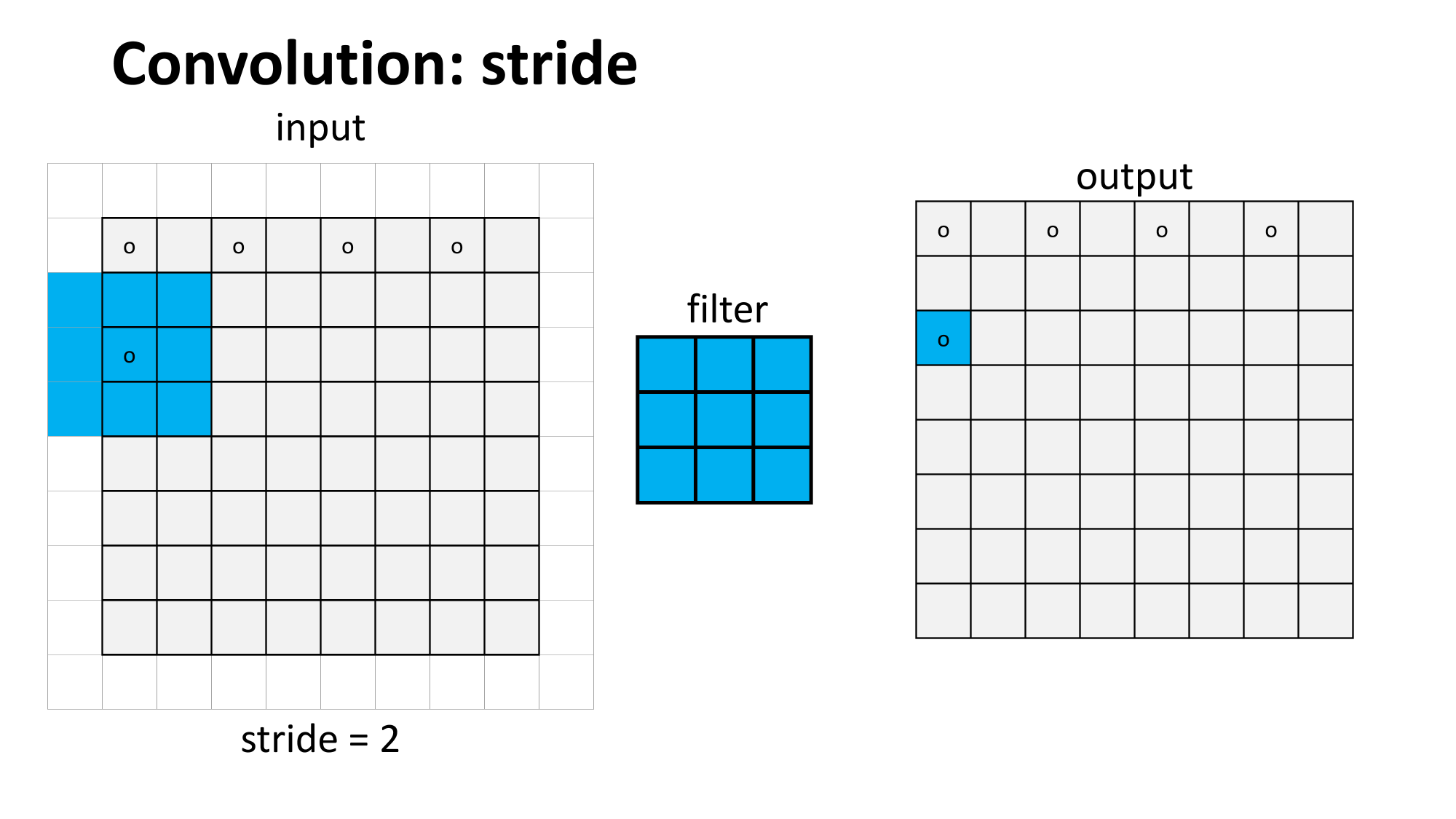
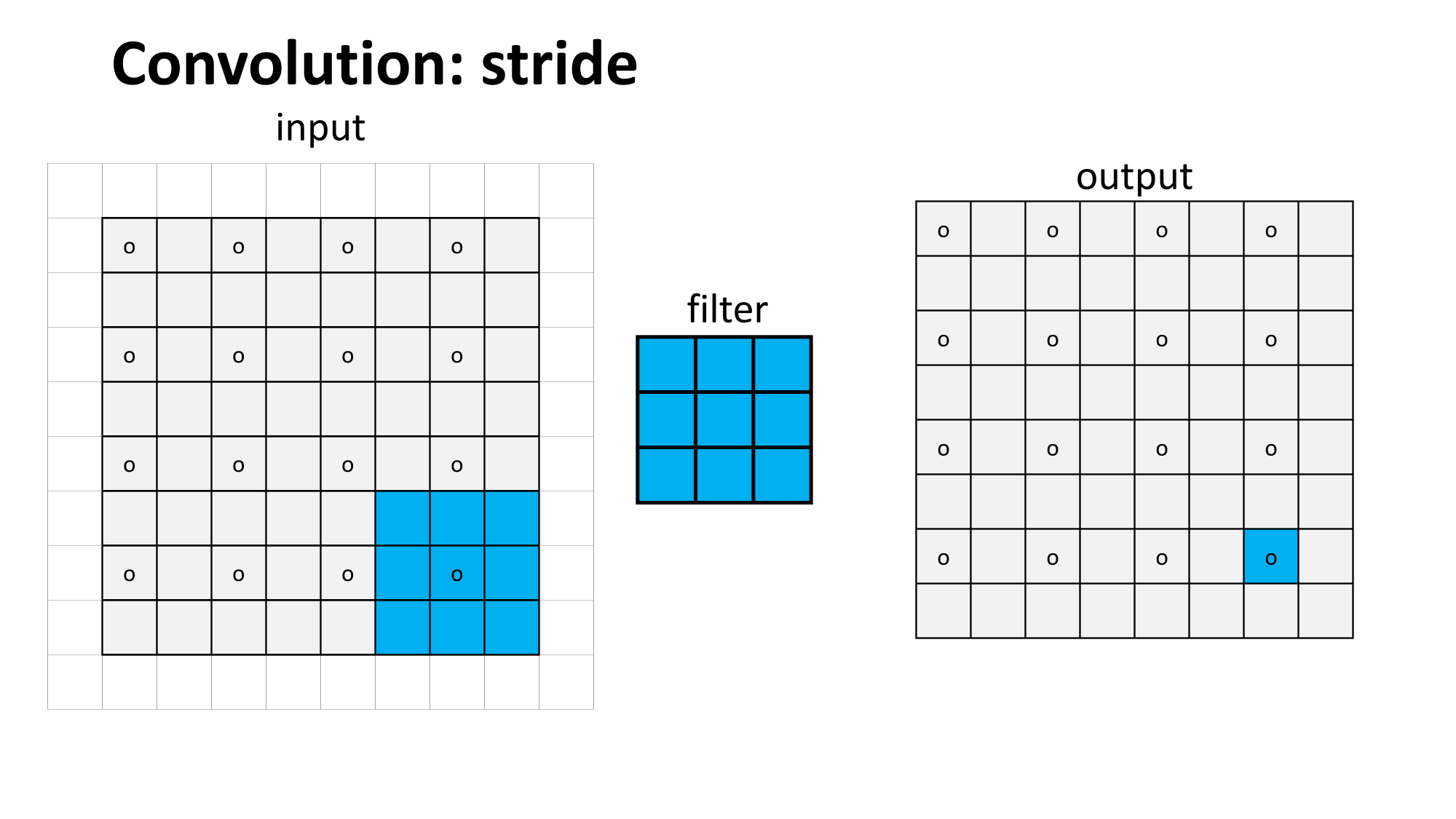
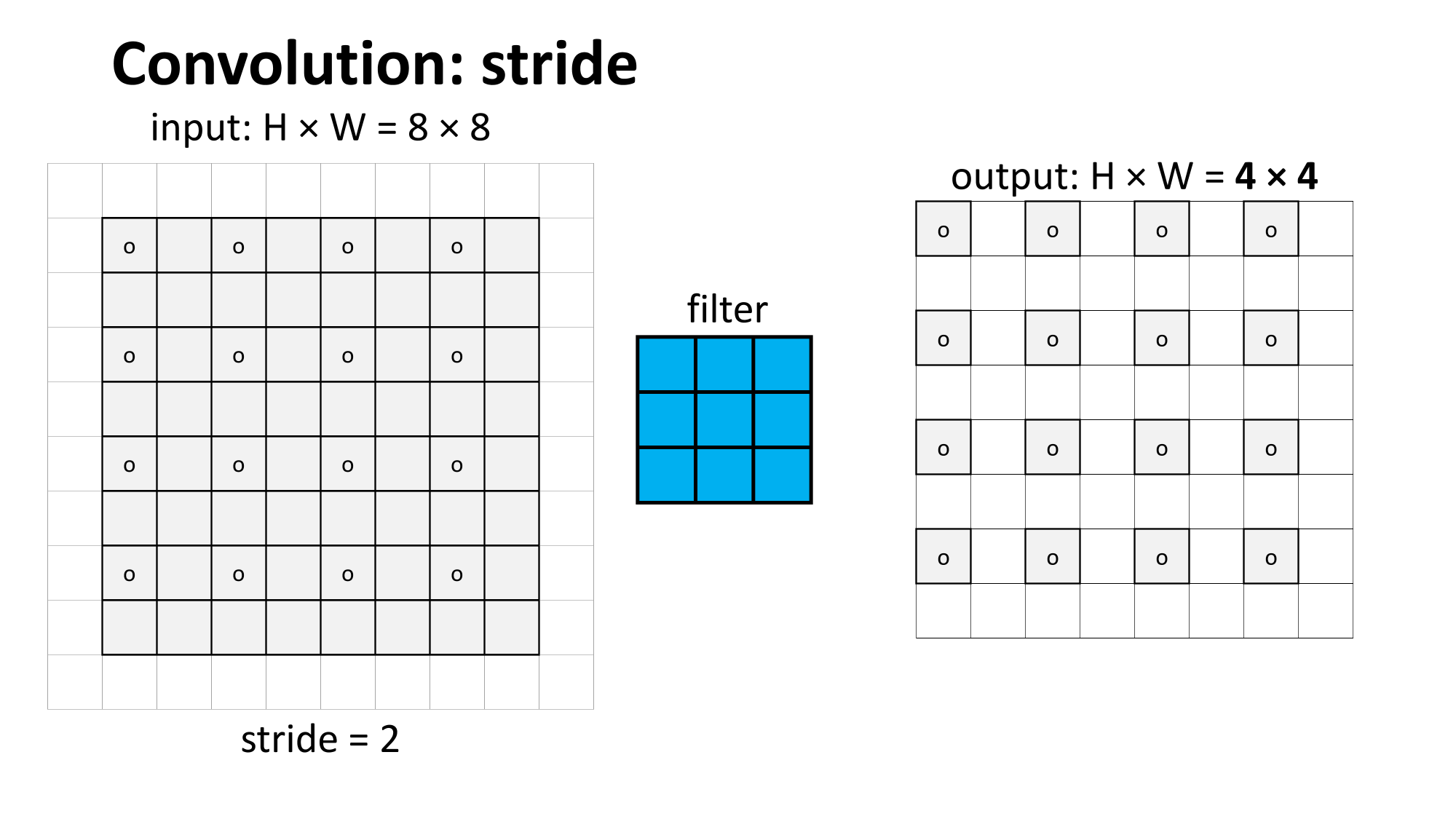
Outline
- Recap (fully-connected net)
- Motivation and big picture ideas of CNN
- Convolution operation
- 1d and 2d convolution mechanics
- interpretation:
- local connectivity
- weight sharing
- 3d tensors
- Max pooling
- Larger window
- Typical architecture and summary
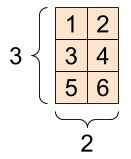
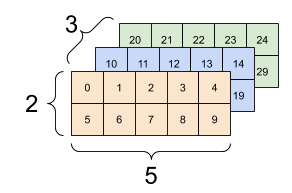
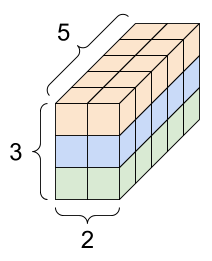
A tender intro to tensor:
[image credit: tensorflow]
red
green
blue
image channels
image width
image
height
image channels
image width
image
height
input tensor
filter
output
- 3d tensor input, depth \(d\)
- 3d tensor filter, depth \(d\)
- 2d tensor (matrix) output
input tensor
filters
outputs
\dots
\dots
input tensor
filters
output tensor
\dots
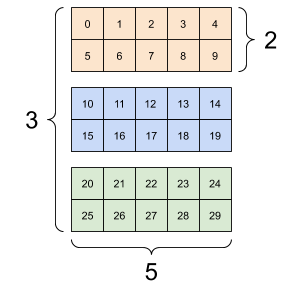
- 3d tensor input, depth \(d\)
- \(k\) 3d filters:
- each filter of depth \(d\)
- each filter makes a 2d tensor (matrix) output
- total output 3d tensor, depth \(k\)
\dots
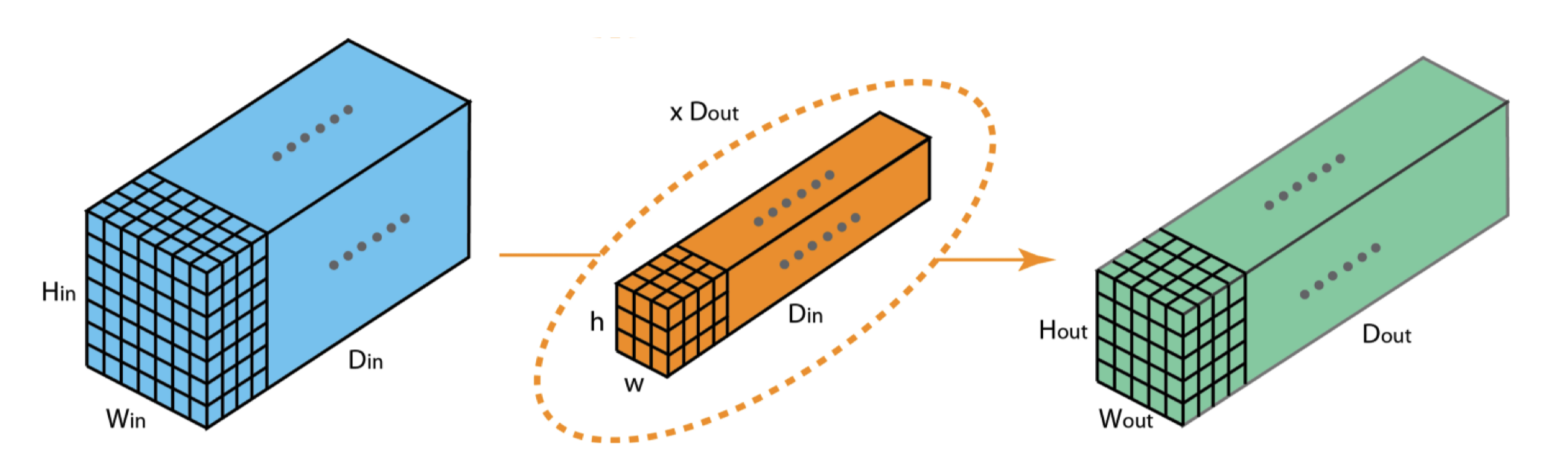
[image credit: medium]
Outline
- Recap (fully-connected net)
- Motivation and big picture ideas of CNN
- Convolution operation
- 1d and 2d convolution mechanics
- interpretation:
- local connectivity
- weight sharing
- 3d tensors
- Max pooling
- Larger window
- Typical architecture and summary
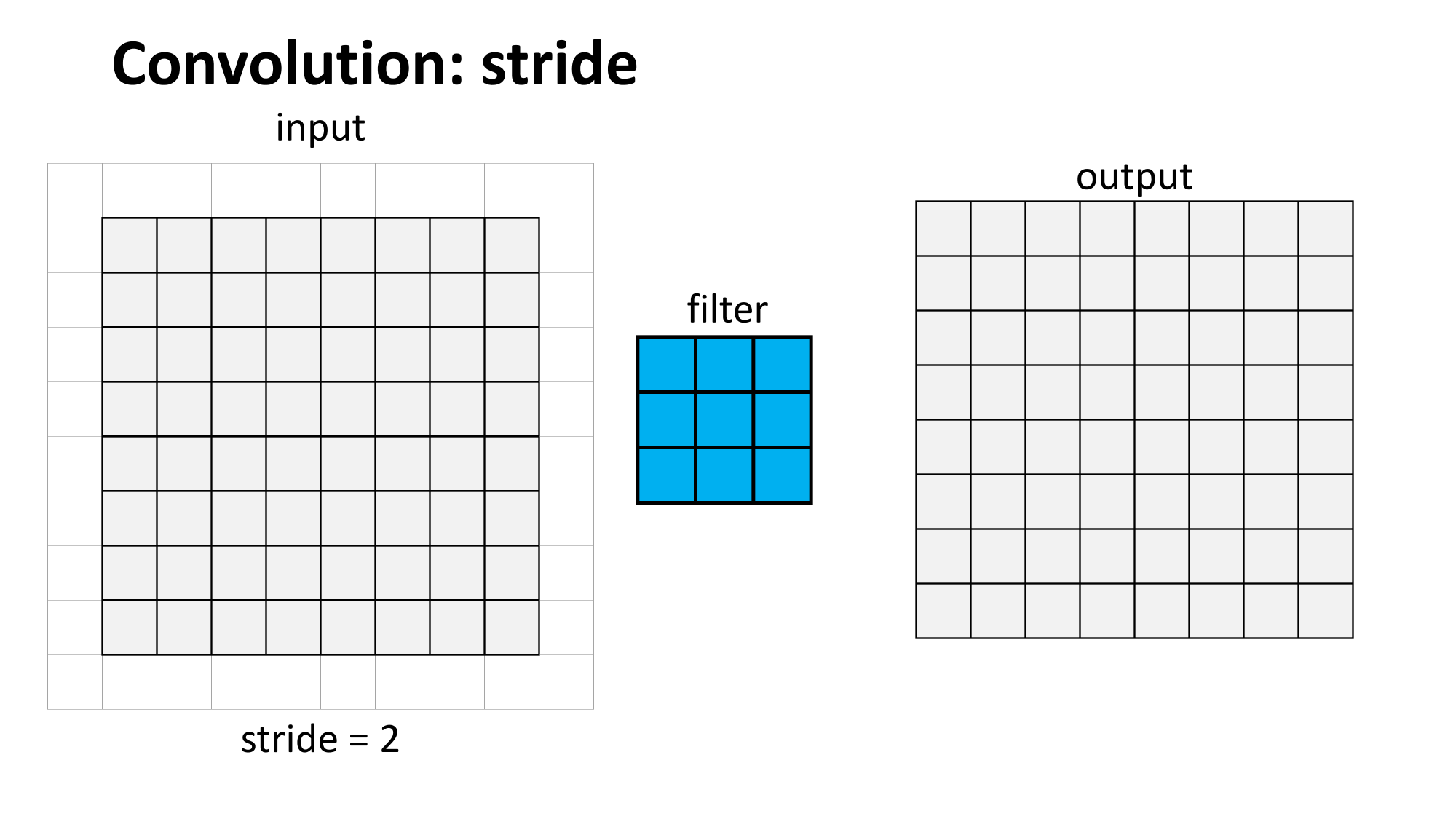
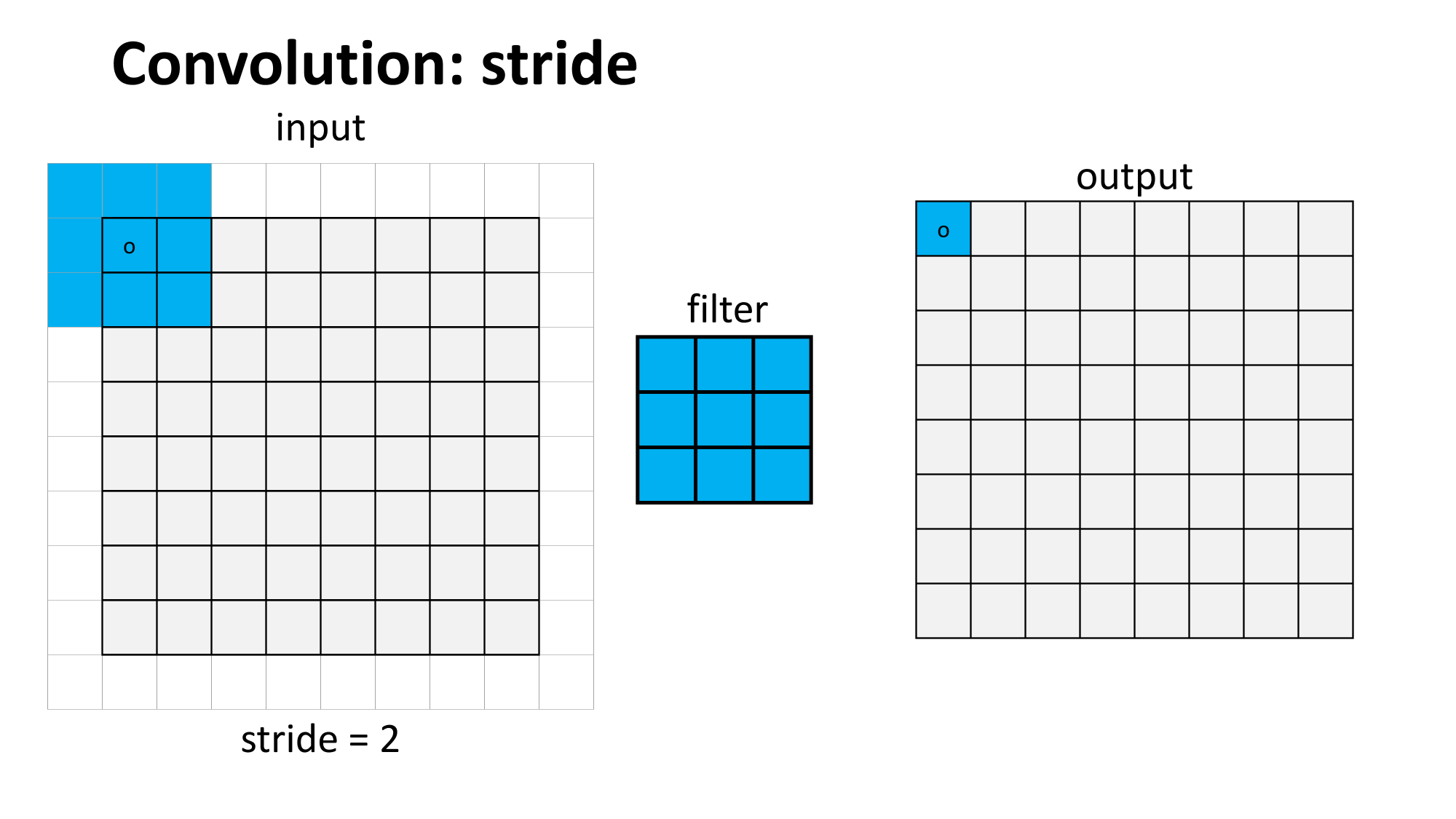
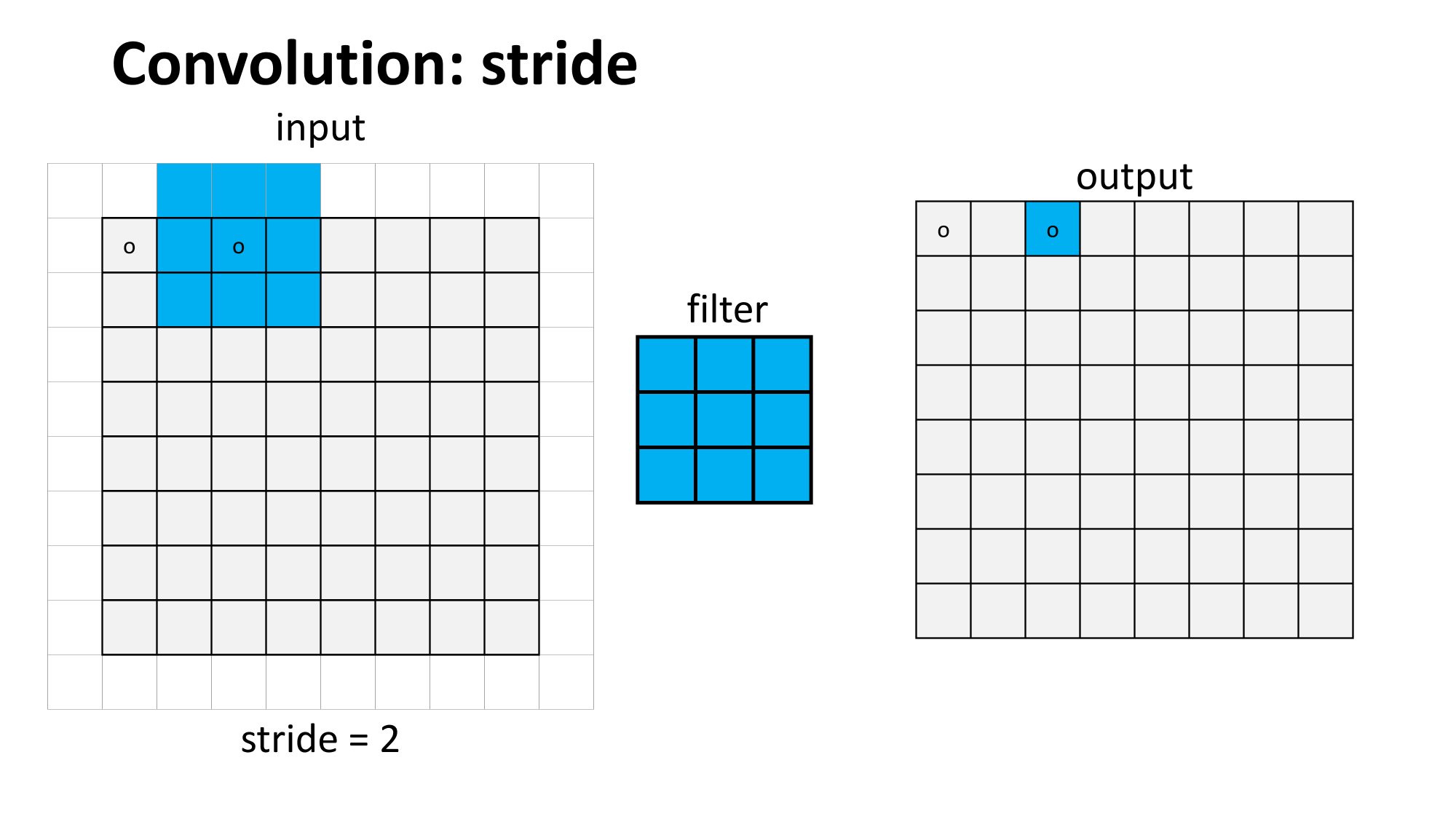
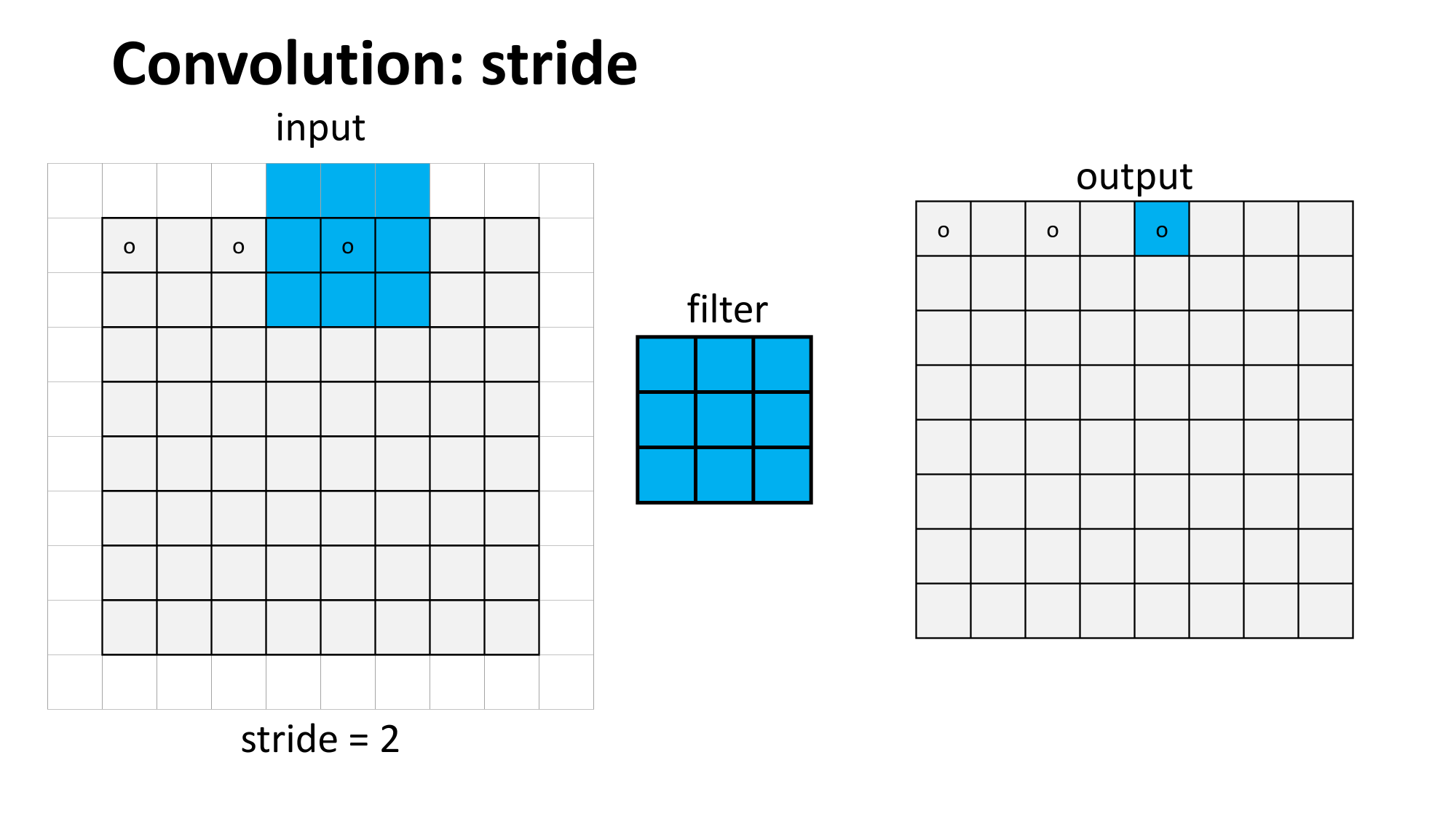
sliding window
(w. stride)
sliding window
(w. stride)
convolution
max pooling
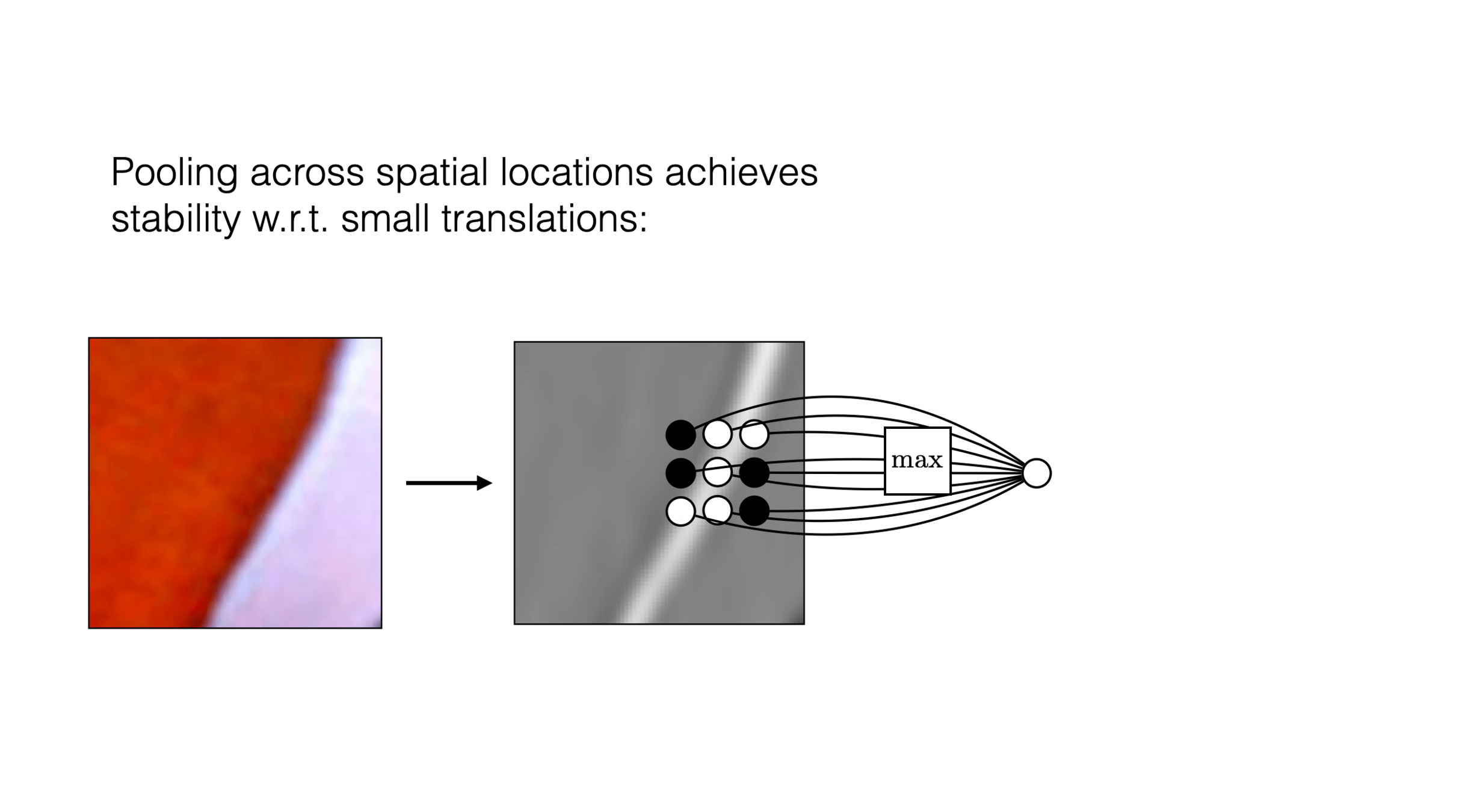
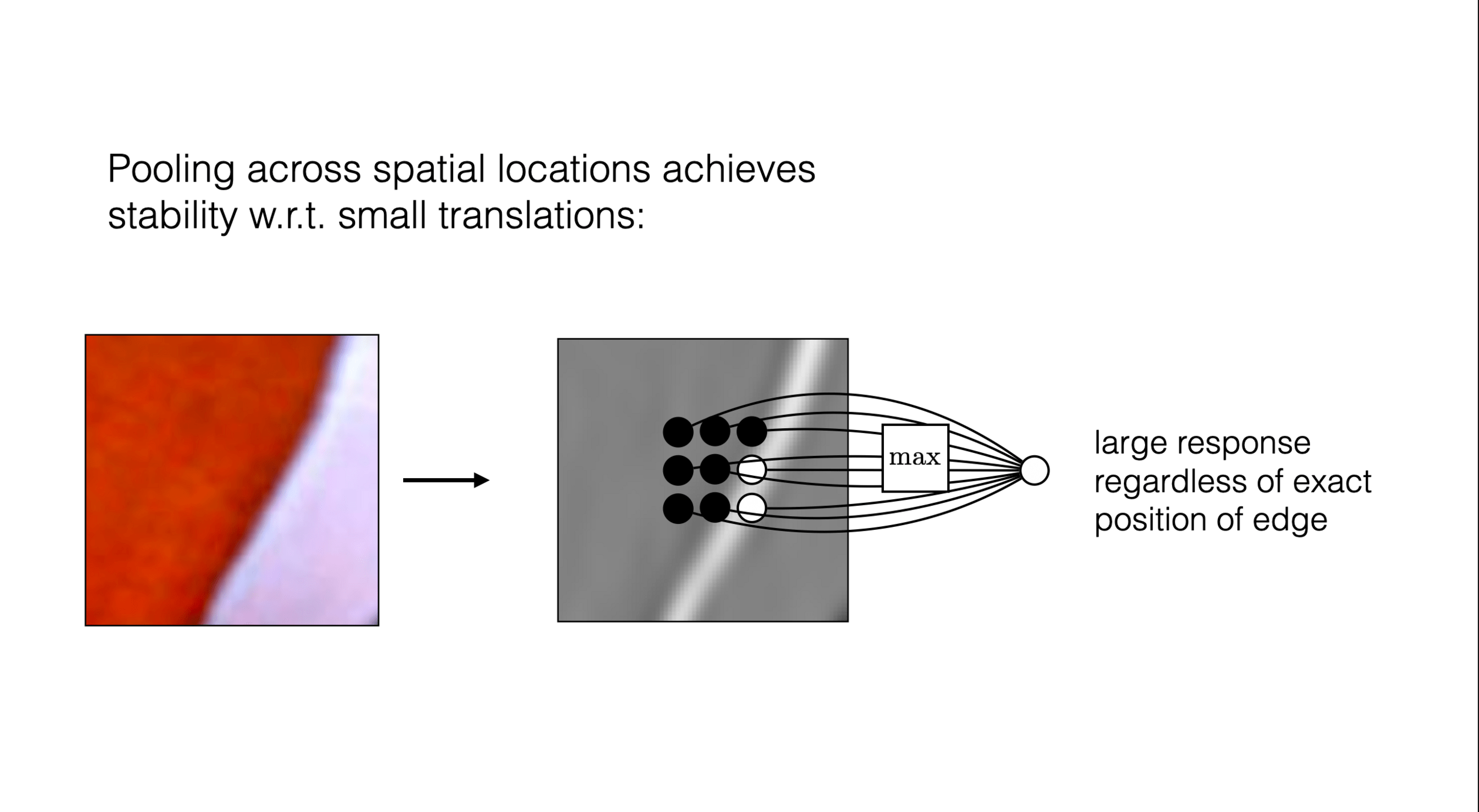
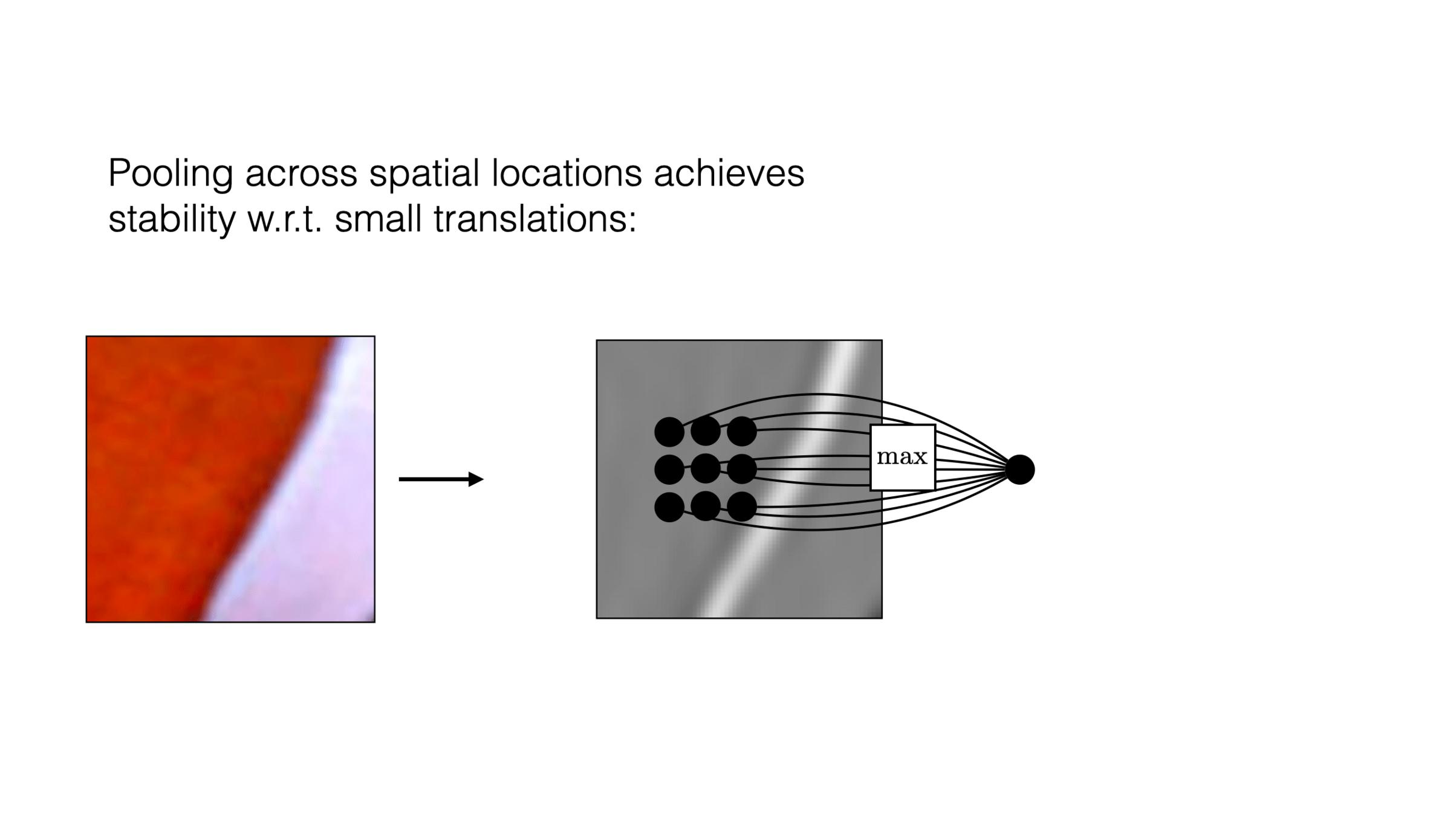
Outline
- Recap (fully-connected net)
- Motivation and big picture ideas of CNN
- Convolution operation
- 1d and 2d convolution mechanics
- interpretation:
- local connectivity
- weight sharing
- 3d tensors
- Max pooling
- Larger window
- Typical architecture and summary
Thanks!
We'd love it for you to share some lecture feedback.
introml-sp24-lec7
By Shen Shen
