Intro to Machine Learning
Lecture 8: Transformers
Shen Shen
April 5, 2024
(many slides adapted from Phillip Isola and Kaiming He)
Outline
- Recap: CNN
- Transformers
- Tokens
- Attention
- Self-attention
- Learned Embedding
- Full-stack
- (Applications and interpretation)
red
green
blue
image channels
image width
image
height
image channels
image width
image
height
input tensor
filter
output
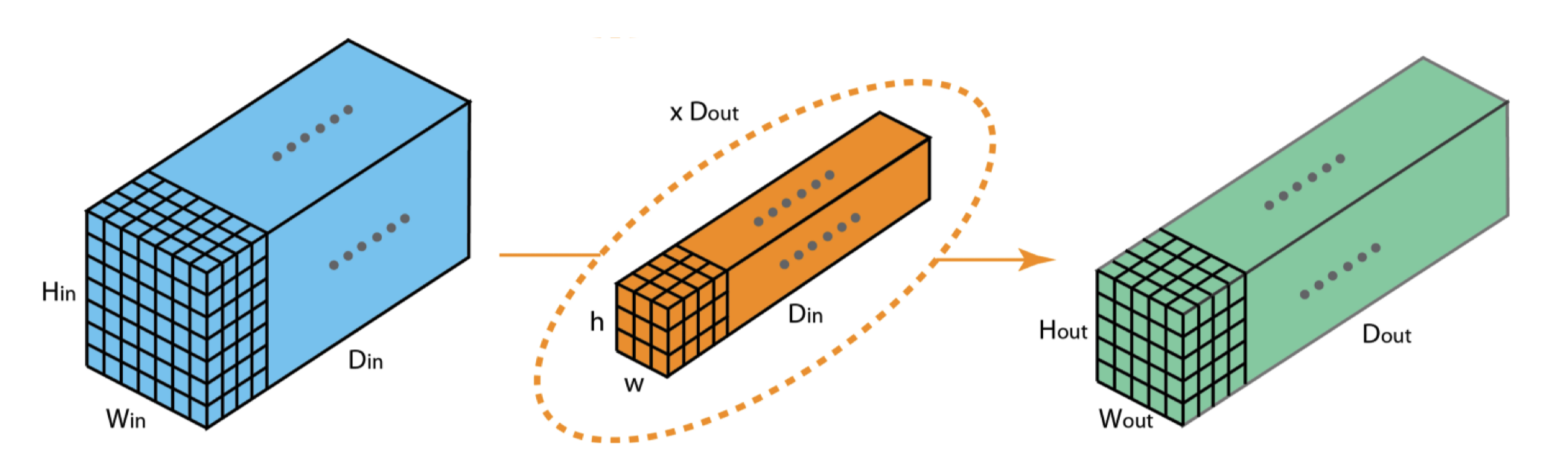
- 3d tensor input, depth \(d\)
- 3d tensor filter, depth \(d\)
- 2d tensor (matrix) output
input tensor
filters
outputs
\dots
\dots
input tensor
filters
output tensor
\dots
- 3d tensor input, depth \(d\)
- \(k\) 3d filters:
- each filter of depth \(d\)
- each filter makes a 2d tensor (matrix) output
- total output 3d tensor, depth \(k\)
\dots
[image credit: medium]
cont'd
Enduring principles:
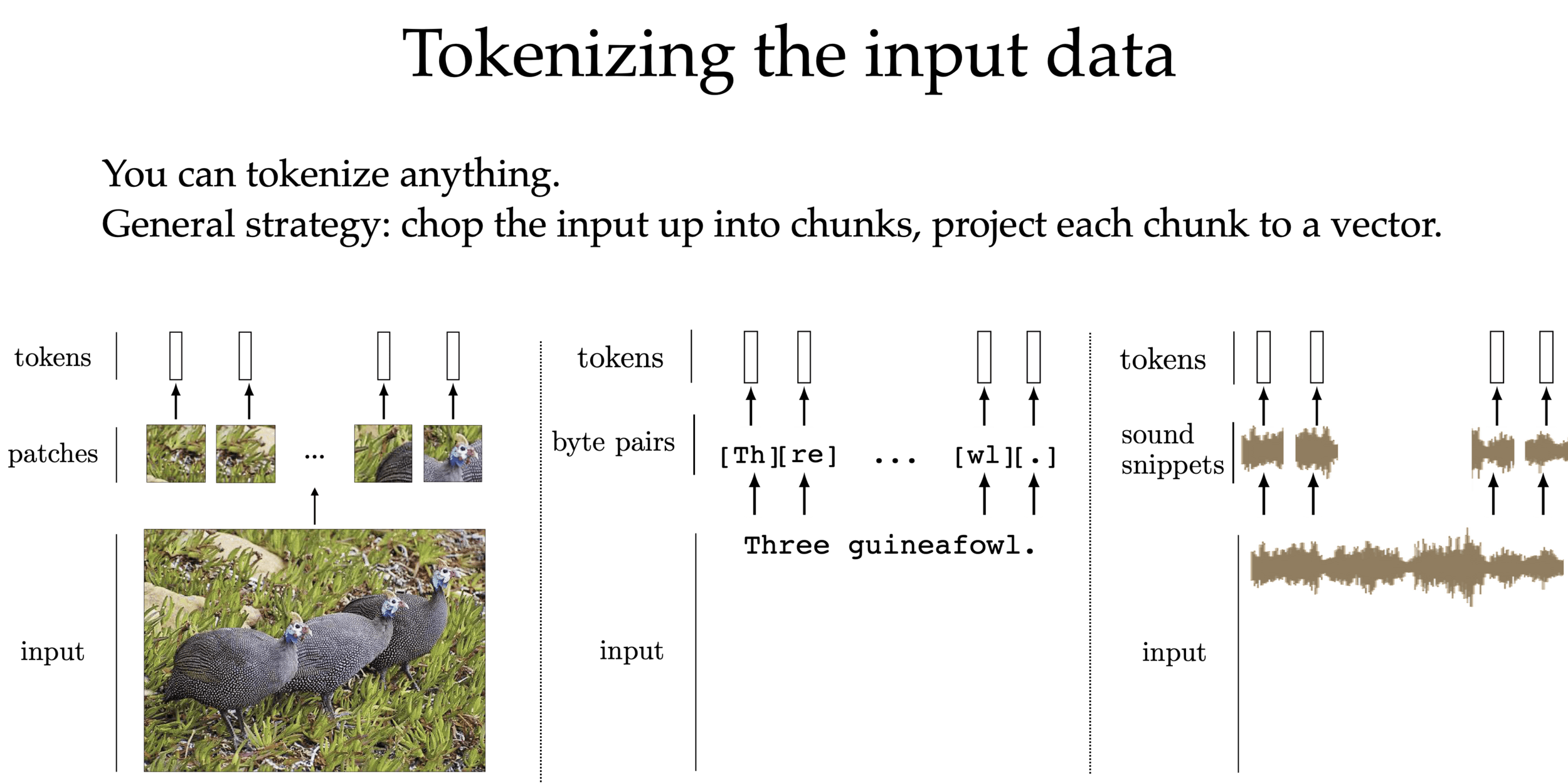
- Chop up signal into patches (divide and conquer)
- Process each patch identically (and in parallel)
Lessons from CNNs
Enduring principles:
- Chop up signal into patches (divide and conquer)
- Process each patch identically (and in parallel)
Follow the same principles:
1. via tokenization
2. via attention mechanism
Transformers
(conceptually: transformers are CNNs where the filter weights -- or here the attention -- dynamically change depending on the patch)
Outline
- Recap: CNN
- Transformers
- Tokens
- Attention
- Self-attention
- Learned Embedding
- Full-stack
- (Applications and interpretation)
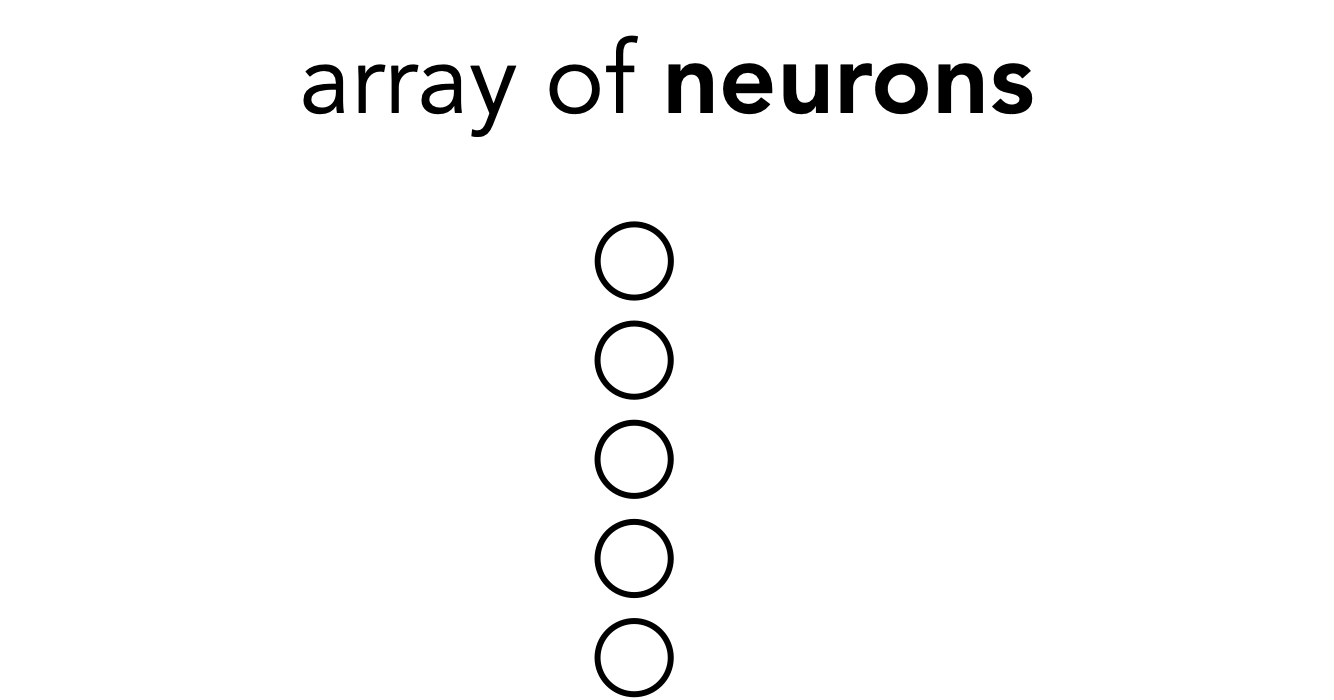
- A token is just transformer lingo for a vector of neurons
- But the connotation is that a token is an encapsulated bundle of information; with transformers we will operate over tokens rather than over neurons
Tokens
x^{(i)} \in \mathbb{R}^d
Token notations
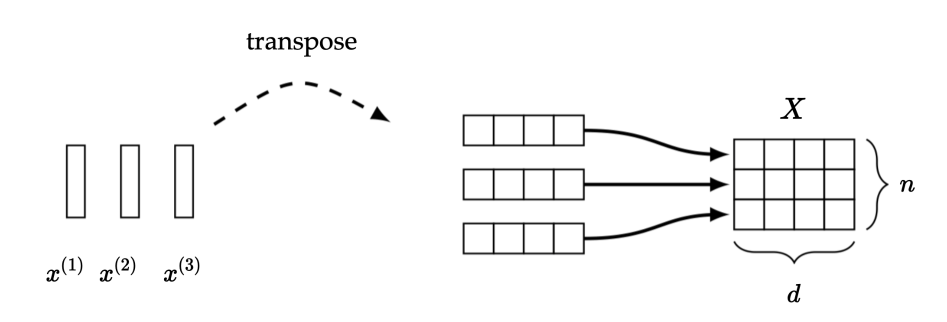
- \(d\) is the size of each token ( \(x^{(i)} \in \mathbb{R}^{d}\))
- \(n\) is the number of tokens
Outline
- Recap: CNN
- Transformers
- Tokens
- Attention
- Self-attention
- Learned Embedding
- Full-stack
- (Applications and interpretation)
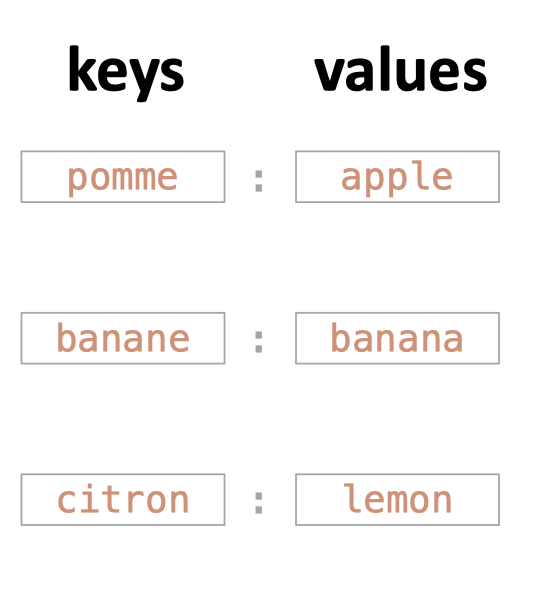
dict_fr2en = {
"pomme": "apple",
"banane": "banana",
"citron": "lemon"
}
Attention mechanism
Let's start by thinking about dictionary look up
dict_fr2en = {
"pomme": "apple",
"banane": "banana",
"citron": "lemon"
}
query = "citron"
output = dict_fr2en[query]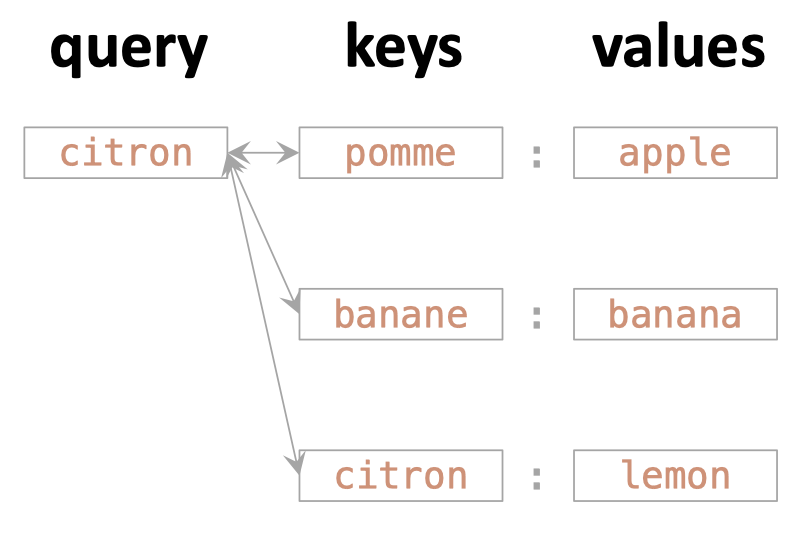
dict_fr2en = {
"pomme": "apple",
"banane": "banana",
"citron": "lemon"
}
query = "citron"
output = dict_fr2en[query]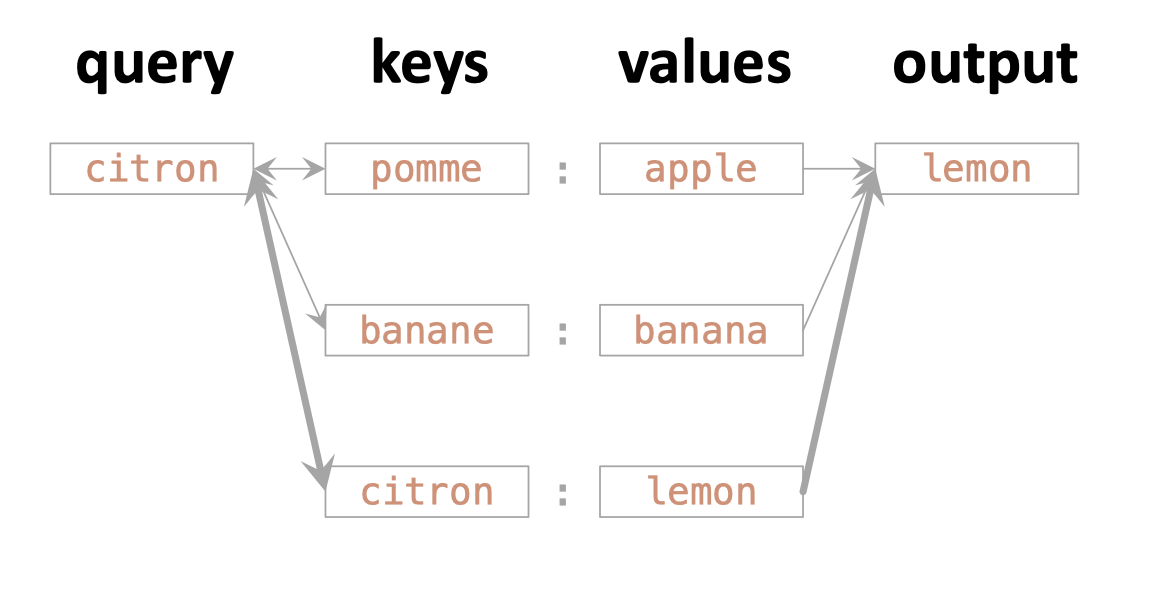
dict_fr2en = {
"pomme": "apple",
"banane": "banana",
"citron": "lemon"
}
What if we'd like to run
query = "orange"
output = dict_fr2en[query]Python would complain.
output = 0.8 * "lemon" + 0.1 * "apple" + 0.1 * "banana"But you might see the rationale of:
- Why did the weights \([0.8, 0.1, 0.1]\) make sense?
"soft" look up.
Actually one way of understanding "attention"
- Can we generalize the thought process somewhat?
Sensible "abstraction/embedding"
(though python would still complain)
Attention
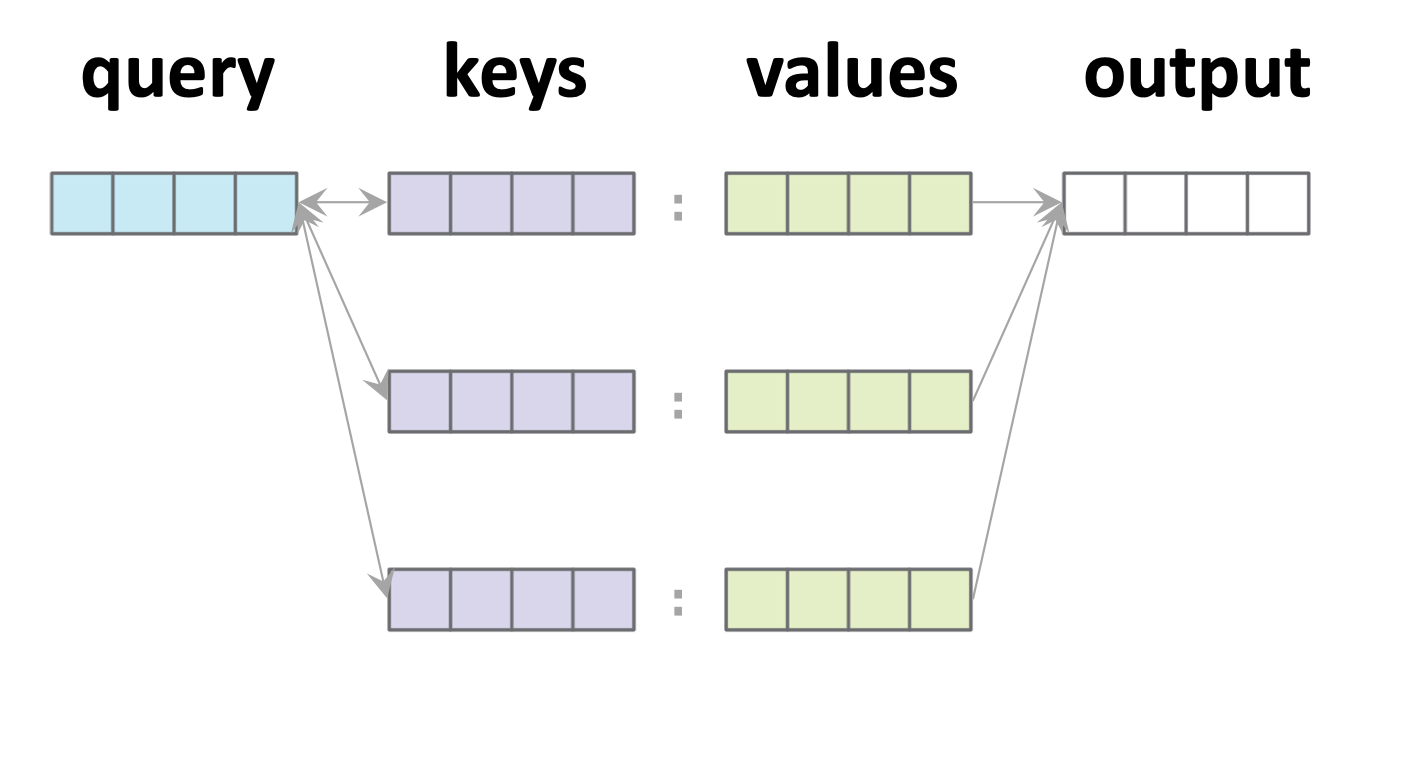
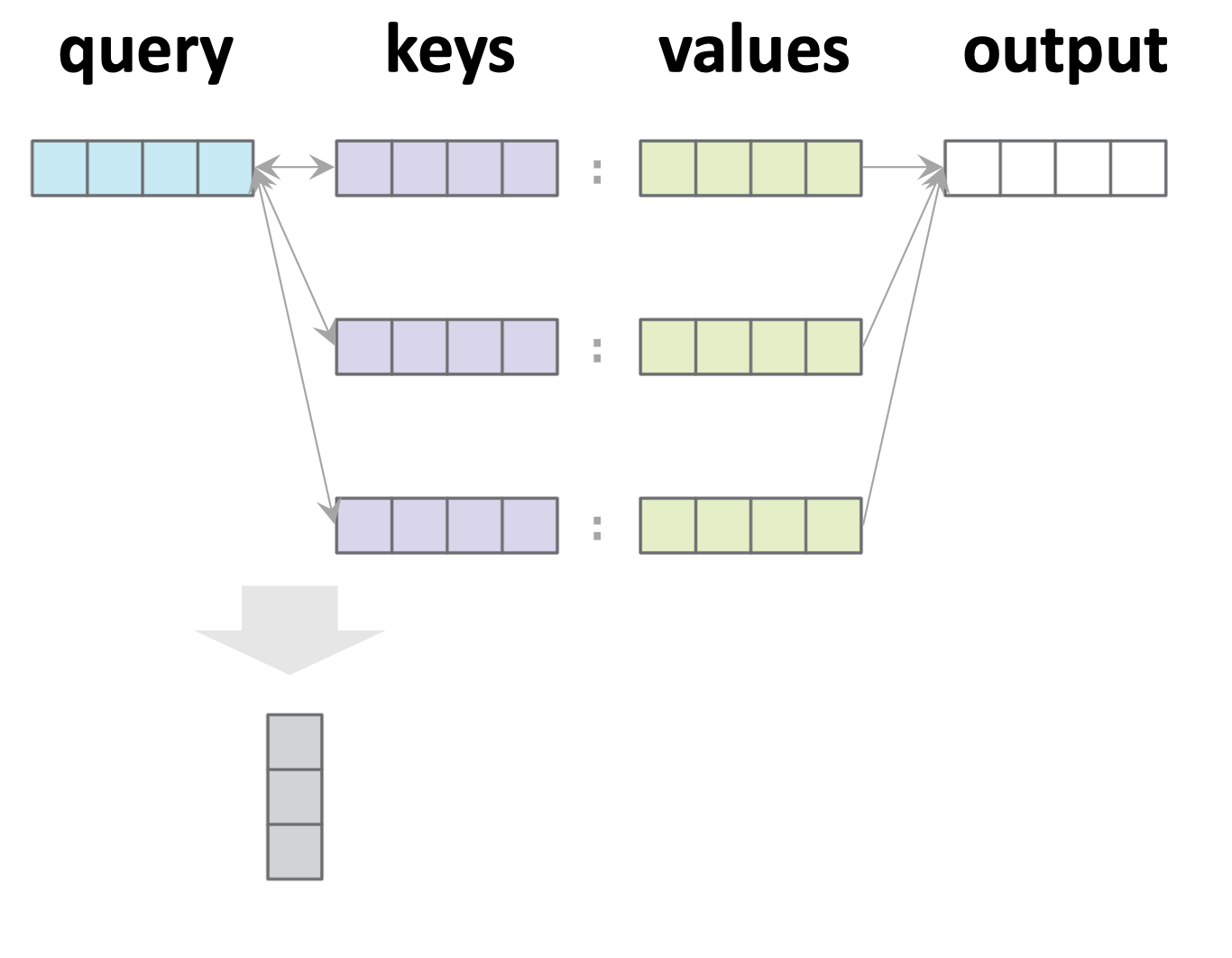
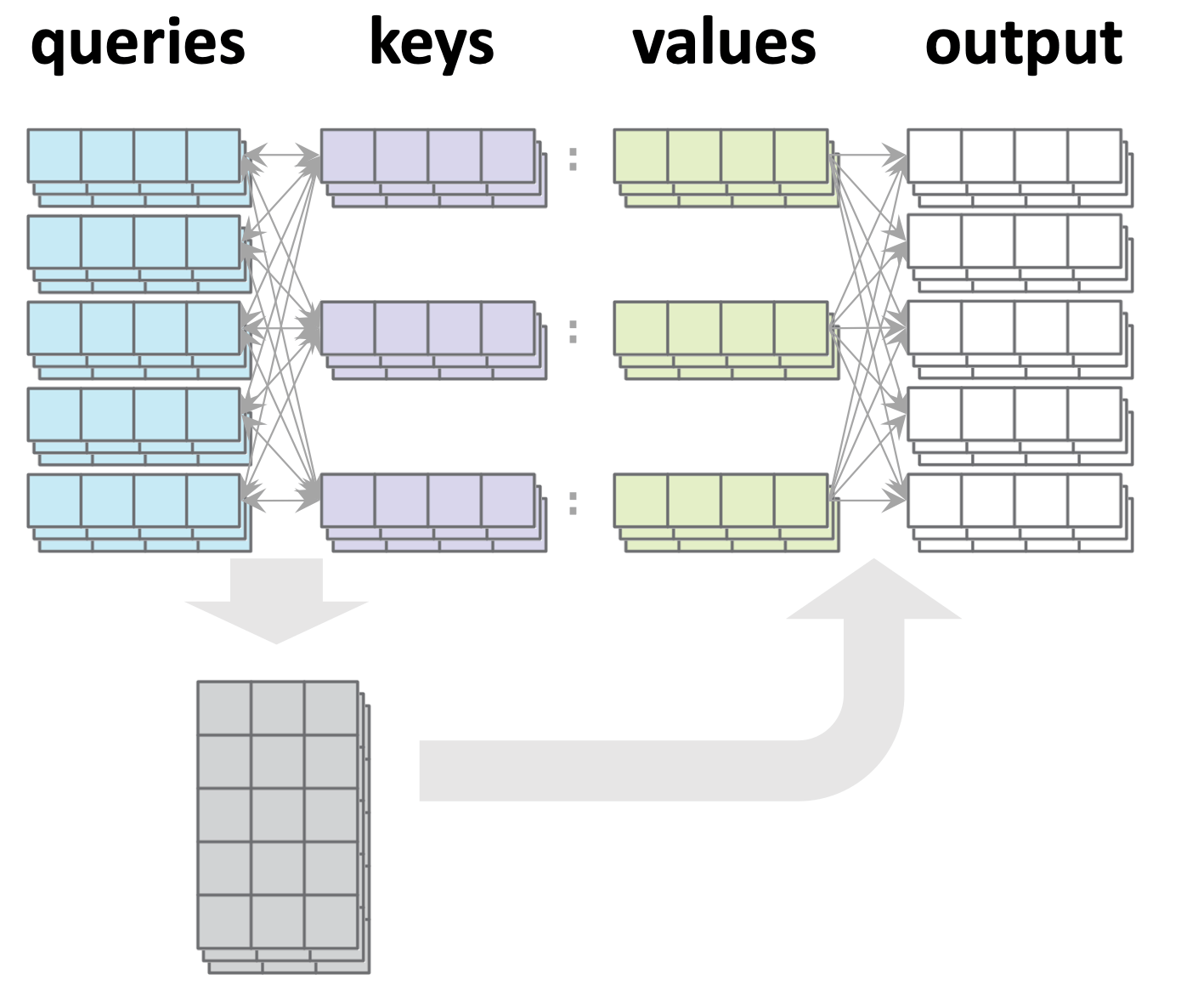
Single-query example:
1. Similarity score w/ key \(j\):
s_j = ({q}^T k_j)
2. Attention weights (softmax'd scores):
3. Output: attention-weighted sum:
=[e^{s_1}, e^{s_2}, \ldots, e^{s_n}]/\Sigma_j e^{s_j}
- \(n\): number of keys
- \(d_q\): dim(query embedding)
- \(d_k\): dim(key embedding)
- \(d_v\): dim(value embedding)
/\sqrt{d_k}
\text{softmax}([q^{\top} k_1, q^{\top} k_2, q^{\top} k_3, \ldots, q^{\top} k_n]/\sqrt{d_k})
a =
= \text{softmax}([s_1, s_2, s_3, \ldots, s_n])
y =\sum\nolimits_j a_j v_j
1. Similarity score of (query \(i\) and key \(j\)):
2. Attention weights (softmax'd scores):
3. Output: attention-weighted sum:
- \(n_{q}\): number of queries
- \(n_k\): number of keys
- \(d_q\): dim(query embedding)
- \(d_k\): dim(key embedding)
- \(d_v\): dim(value embedding)
/\sqrt{d_k}
s_{ij} = ({q_i}^T k_j)
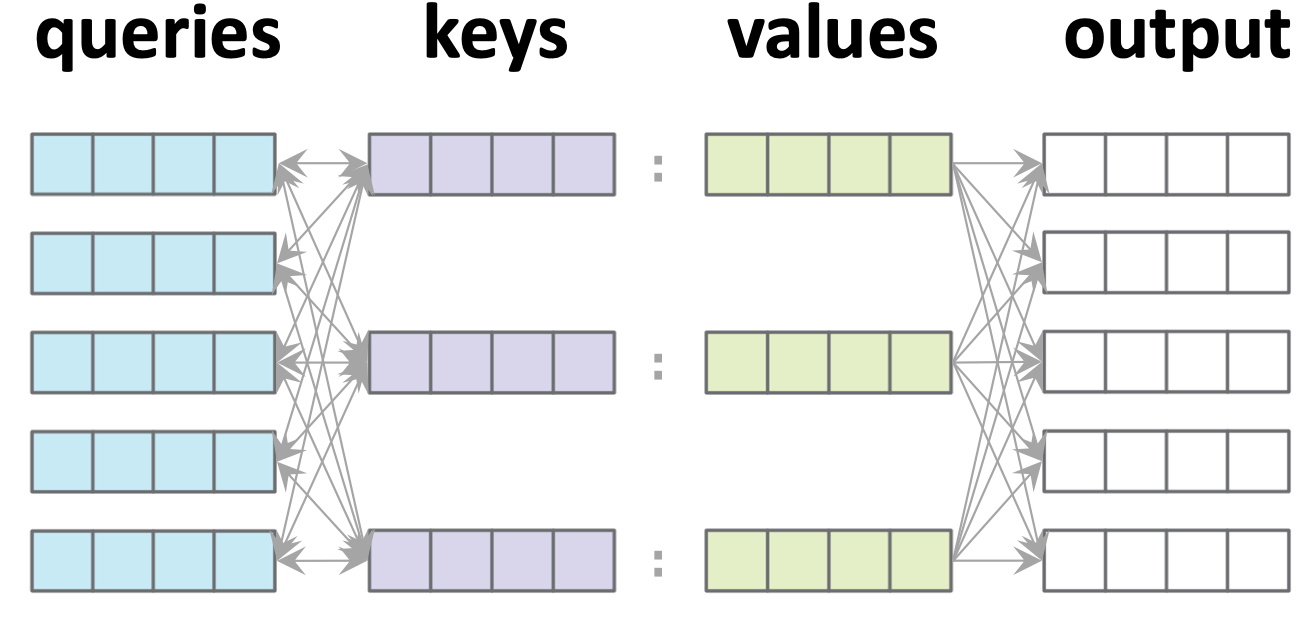
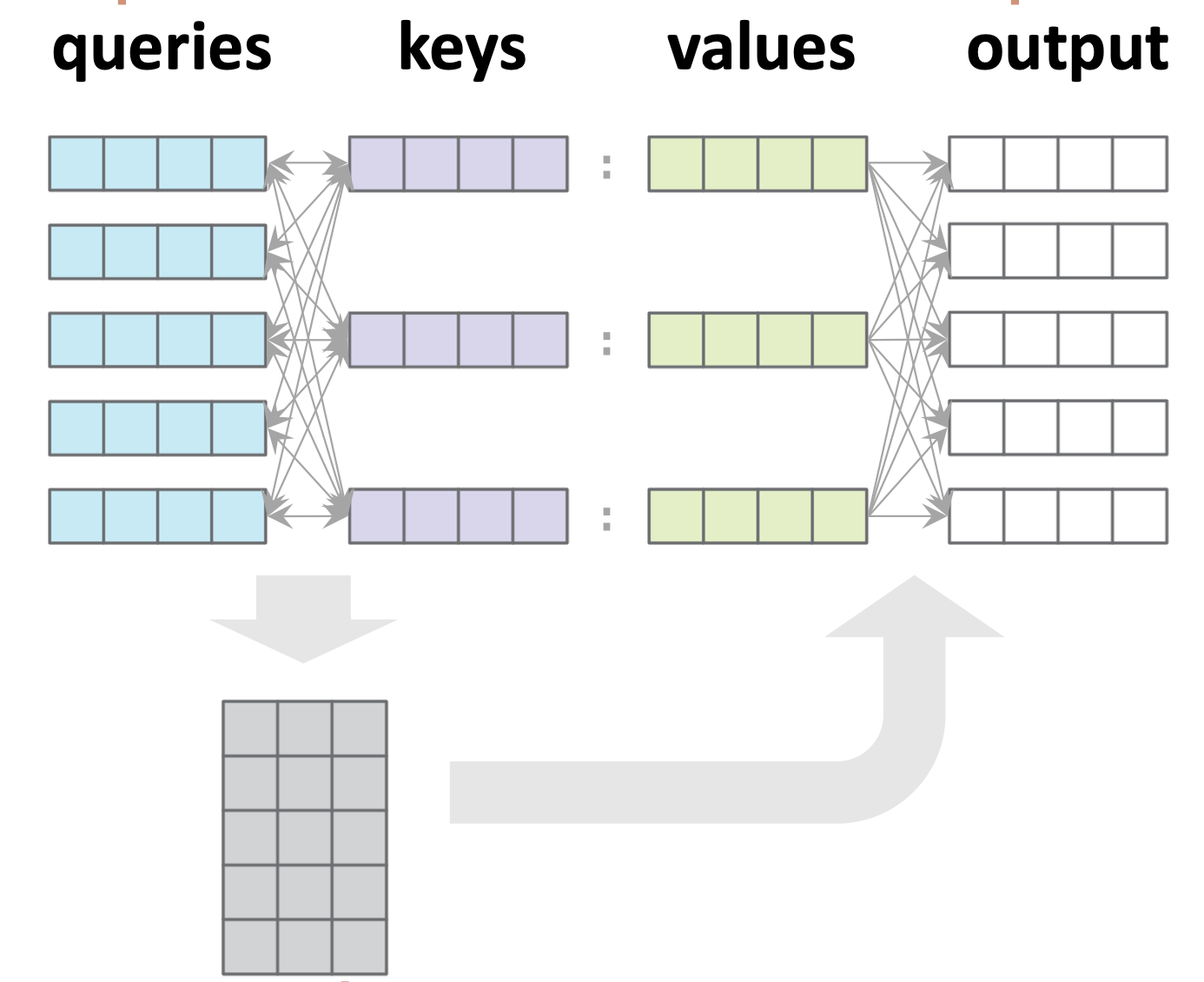
Multi-query example:
For each query \(i,\\\) \(a_i = \text{softmax}([s_{i1}, s_{i2}, s_{i3}, \ldots, s_{i n_k}])\)
Stack all such \(a_i\) vertically
y=\left[\begin{array}{c}
y_1 \\
y_2 \\
\vdots \\
y_{n q}
\end{array}\right] \in \mathbb{R}^{n_q \times d_v}
For each query \(i,\) \(y_i=\sum\nolimits_j a_{ij} v_{j}\)
Stack all such \(y_i\) vertically
A=\left[\begin{array}{c}
a_1 \\
a_2 \\
\vdots \\
a_{n q}
\end{array}\right] \in \mathbb{R}^{n_q \times n_k}
Comments:
y \in \mathbb{R}^{n_q \times d_v}
- Attention says nothing about how to get queries/keys/values.
- Attention itself is parameter-free.
- Shapewise, we only need:
- \(d_k = d_q\) (so we often omit \(d_q\))
- any other shapes need not match:
- \(n_{q}\) need not equal \(n_k\)
- \(d_v\) need not equal \(d_k\)
- Note all queries are processed in parallel.
- No cross-wiring between queries.
- Any output is connected to every value and every key, but only its corresponding query.
- This is the vanilla default attention mechanism, aka, "query-key-value dot-product cross attention".
- One such attention mechanism is called one "Head"
A \in \mathbb{R}^{n_q \times n_k}
- \(n_{q}\): number of queries
- \(n_k\): number of keys
- \(d_q\): dim(query embedding)
- \(d_k\): dim(key embedding)
- \(d_v\): dim(value embedding)
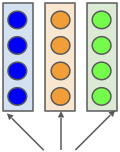
Multi-head Attention
Rather than having just one way of attending, why not have multiple?
Repeat in parallel
One head
Outline
- Recap: CNN
- Transformers
- Tokens
- Attention
- Self-attention
- Learned Embedding
- Full-stack
- (Applications and interpretation)
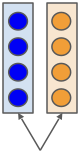
Self-attention
- query, key, value sequences: all produced by the same input sequence itself.
命
運
我
操
縱
- \(n\): number of input tokens (here \(n\)=5)
- \(d\): input token dimension (3)
- \(d_k\) = \(d_q\) = \(d_v\) (4)
tokenization
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
x^{(5)}
input token
learned projection
query, key, value token sequences
attention head
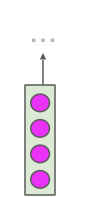
- Take the 3rd input token as example, how do we get the 3rd output token?
命
運
我
操
縱
tokenization
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
x^{(5)}
input token
learned projection
query, key, value token sequences
attention head
3rd output token
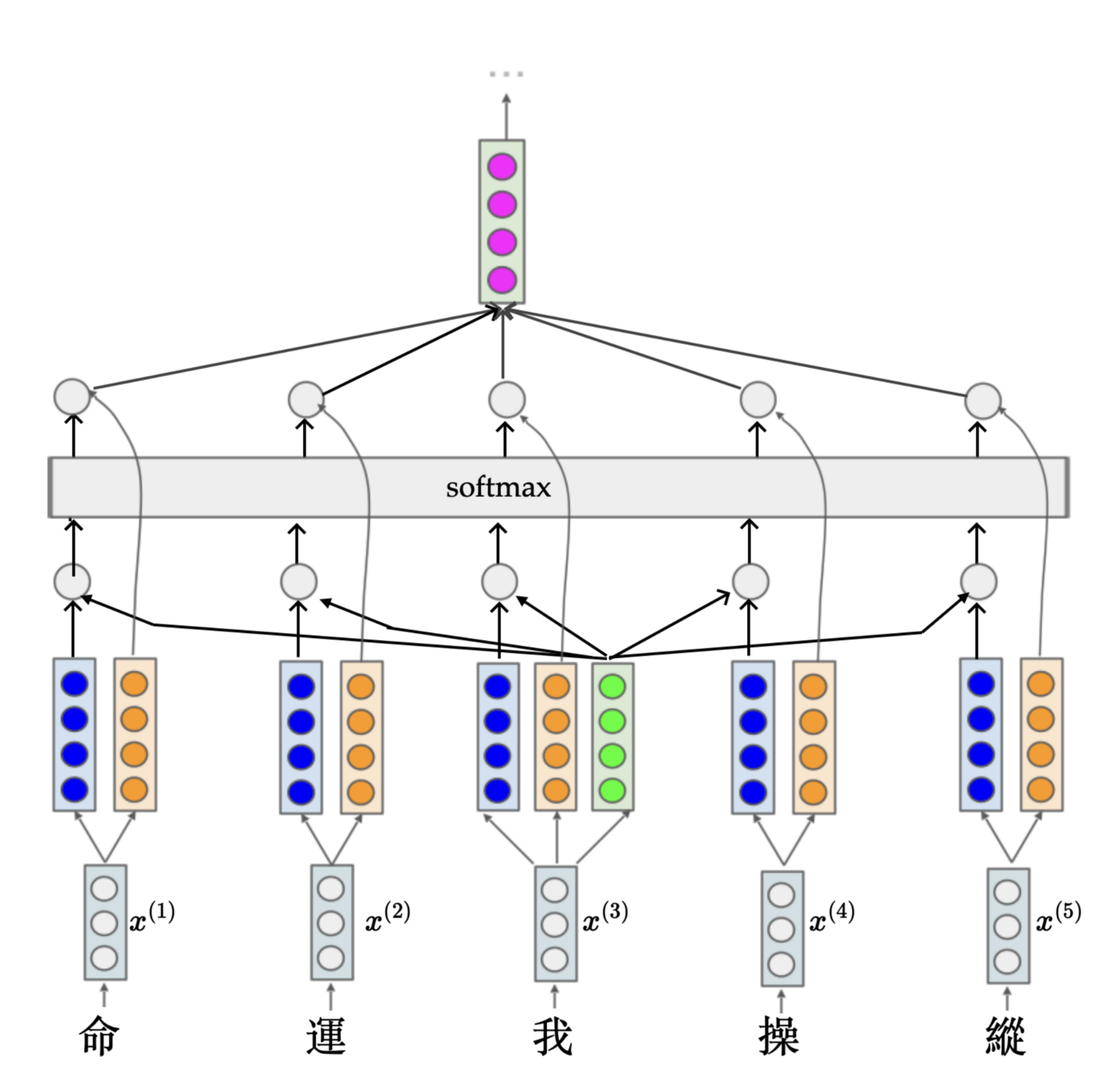
Take the 3rd input token as example, how do we get the 3rd output token?
命
運
我
操
縱
tokenization
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
x^{(5)}
input token
learned projection
query, key, value token sequences
softmax
one attention head
the 3rd output token
Outline
- Recap: CNN
- Transformers
- Tokens
- Attention
- Self-attention
- Learned Embedding
- Full-stack
- (Applications and interpretation)
x^{(i)} \in \mathbb{R}^{d}
q^{(i)} \in \mathbb{R}^{d_k}
k^{(i)} \in \mathbb{R}^{d_k}
v^{(i)} \in \mathbb{R}^{d_k}
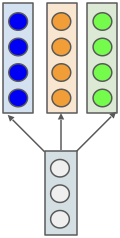
- Which color is query/key/value respectively?
- How do we go from \(x\) to \(q, k, v\)?
via learned projection weights
命
W_k
W_v
W_q
x^{(i)} \in \mathbb{R}^{d}
q^{(i)} \in \mathbb{R}^{d_k}
k^{(i)} \in \mathbb{R}^{d_k}
v^{(i)} \in \mathbb{R}^{d_k}
- Importantly, all these learned projection weights \(W\) are shared along the token sequence:
- These three weights \(W\) -- once learned -- do not change based on input token \(x.\)
- If the input sequence had been longer, we can still use the same weights in the same fashion --- just maps to a longer output sequence.
- This is yet another parallel processing (similar to convolution)
- But each \((q,k,v)\) do depend on the corresponding input \(x\) (can be interpreted as dynamically changing convolution filter weights)
x^{(1)}
x^{(2)}
x^{(3)}
x^{(4)}
x^{(5)}
命
運
我
操
縱
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
W_k
W_v
W_q
Outline
- Recap: CNN
- Transformers
- Tokens
- Attention
- Self-attention
- Learned Embedding
- Full-stack
- (Applications and interpretation)
Transformers
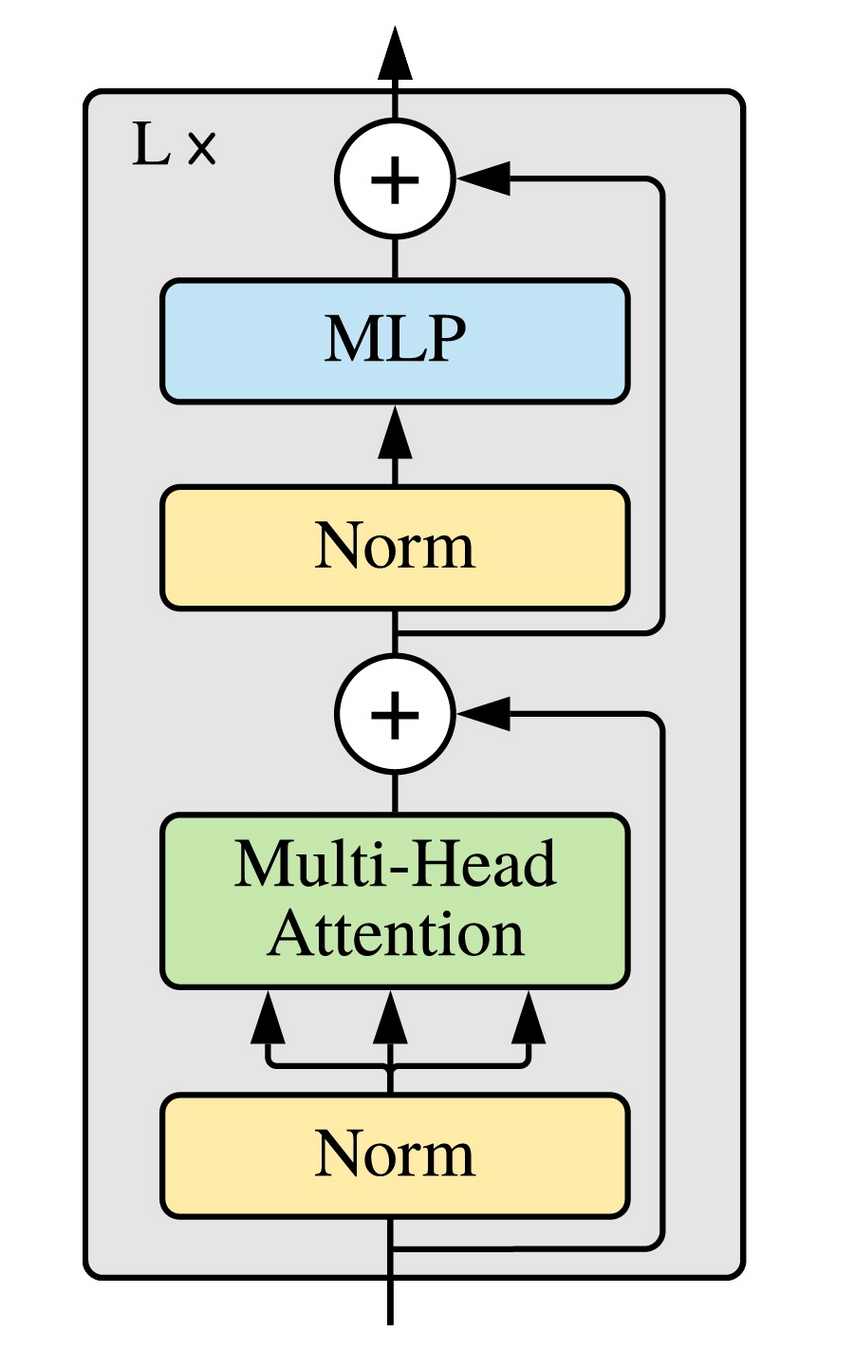
Some other ideas commonly used in practice:
- Causal attention
- Residual connection
- Layer Normalization
Causal self-attention
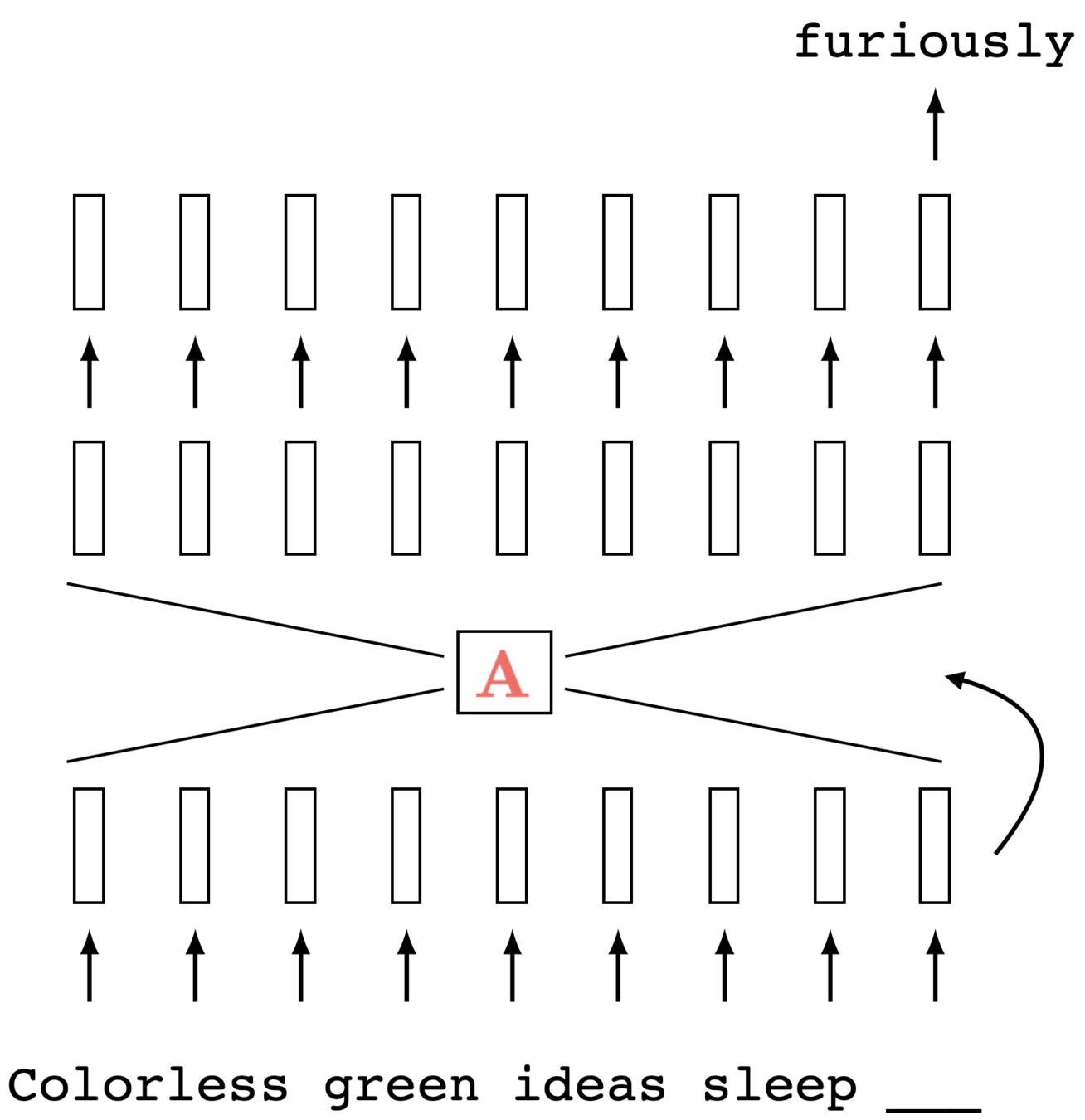
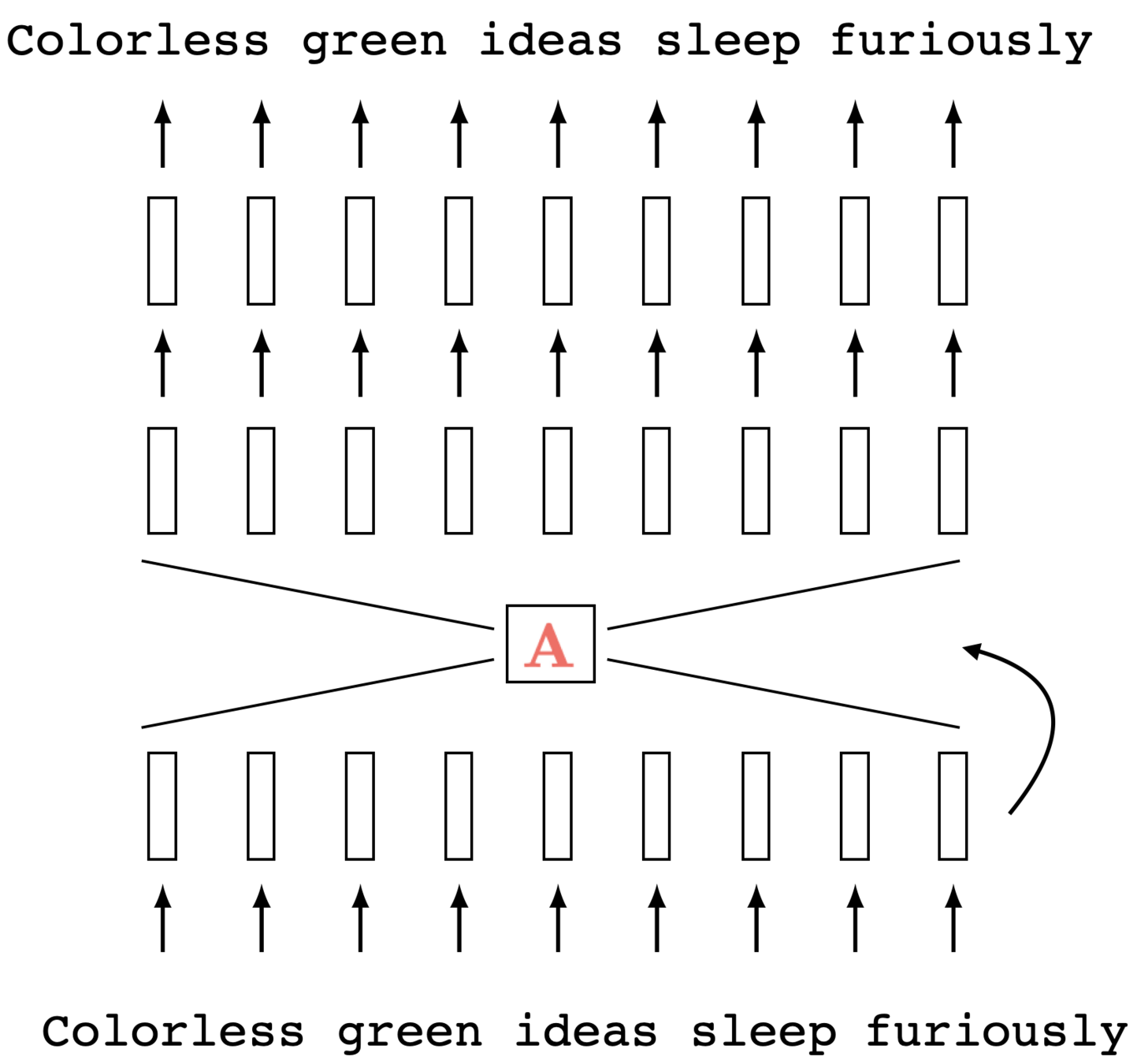
(via masking)
Transformers
All parameters are in projection
- \(W_q, W_k, W_v\) are the most specific to transforms
- MLP (i.e. fully-connected layers) could have their own weights too; same idea as week 6 NN
(
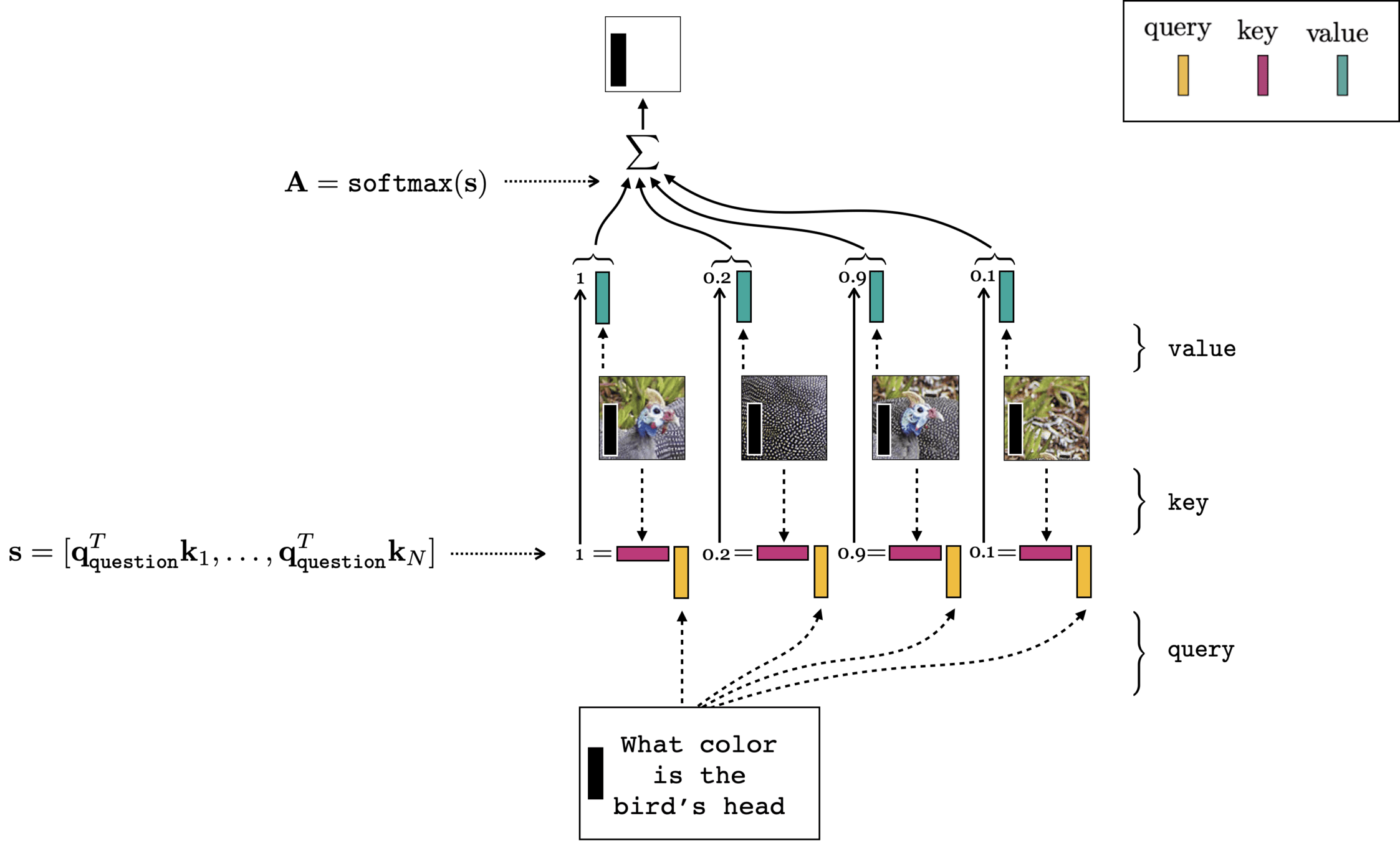
Multi-modality (text + image)
- notice how query and (keyvalue) come from different inputs?
- similar to the dictionary example
- unlike the self-attention translation example.
Success mode:
[“DINO”, Caron et all. 2021]
Failure mode:
)
Thanks
(for your attention :)!
We'd love it for you to share some lecture feedback.
introml-sp24-lec8
By Shen Shen
