Lecture 8: Representation Learning
Shen Shen
April 4, 2025
11am, Room 10-250
Intro to Machine Learning
Outline
- Neural networks are representation learners
- Auto-encoders
- Unsupervised and self-supervised learning
- Word embeddings
- (Some recent representation learning ideas)
Outline
- Neural networks are representation learners
- Auto-encoders
- Unsupervised and self-supervised learning
- Word embeddings
- (Some recent representation learning ideas)
\dots
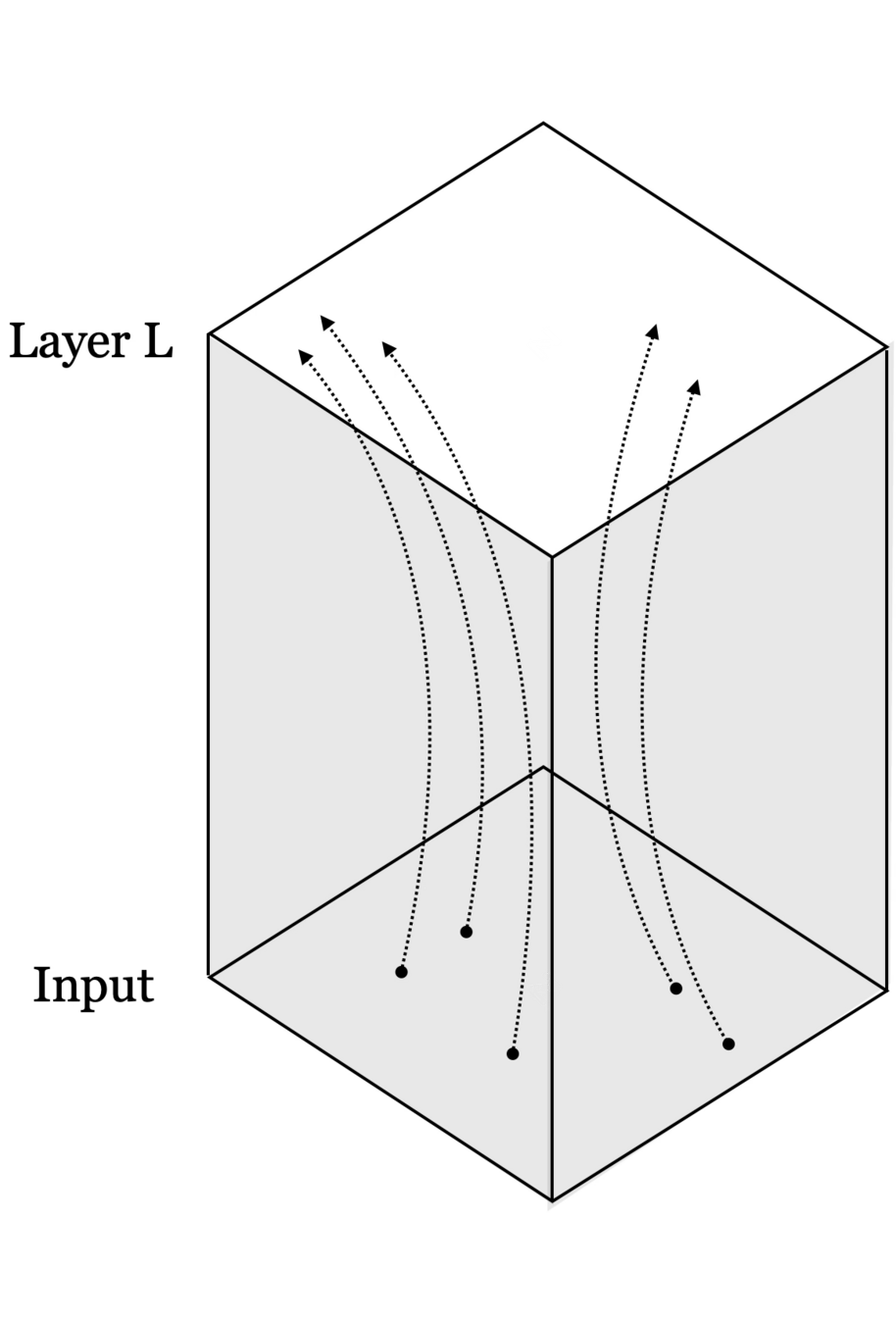
layer
linear combo
activations
Recap:
\dots
\dots
layer
\dots
x_1
x_2
x_d
input
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
\Sigma
f(\cdot)
neuron
learnable weights
hidden
output
compositions of ReLU(s) can be quite expressive
in fact, asymptotically, can approximate any function!
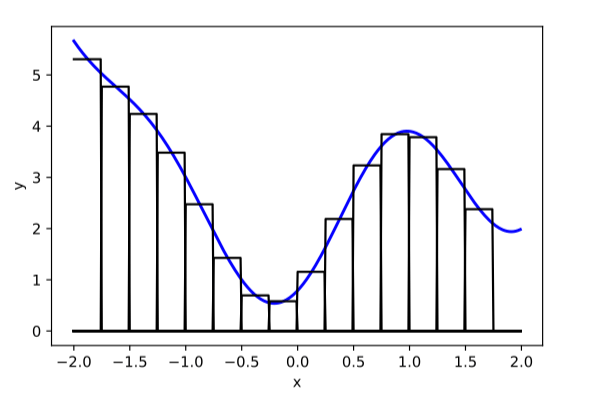
[image credit: Phillip Isola]
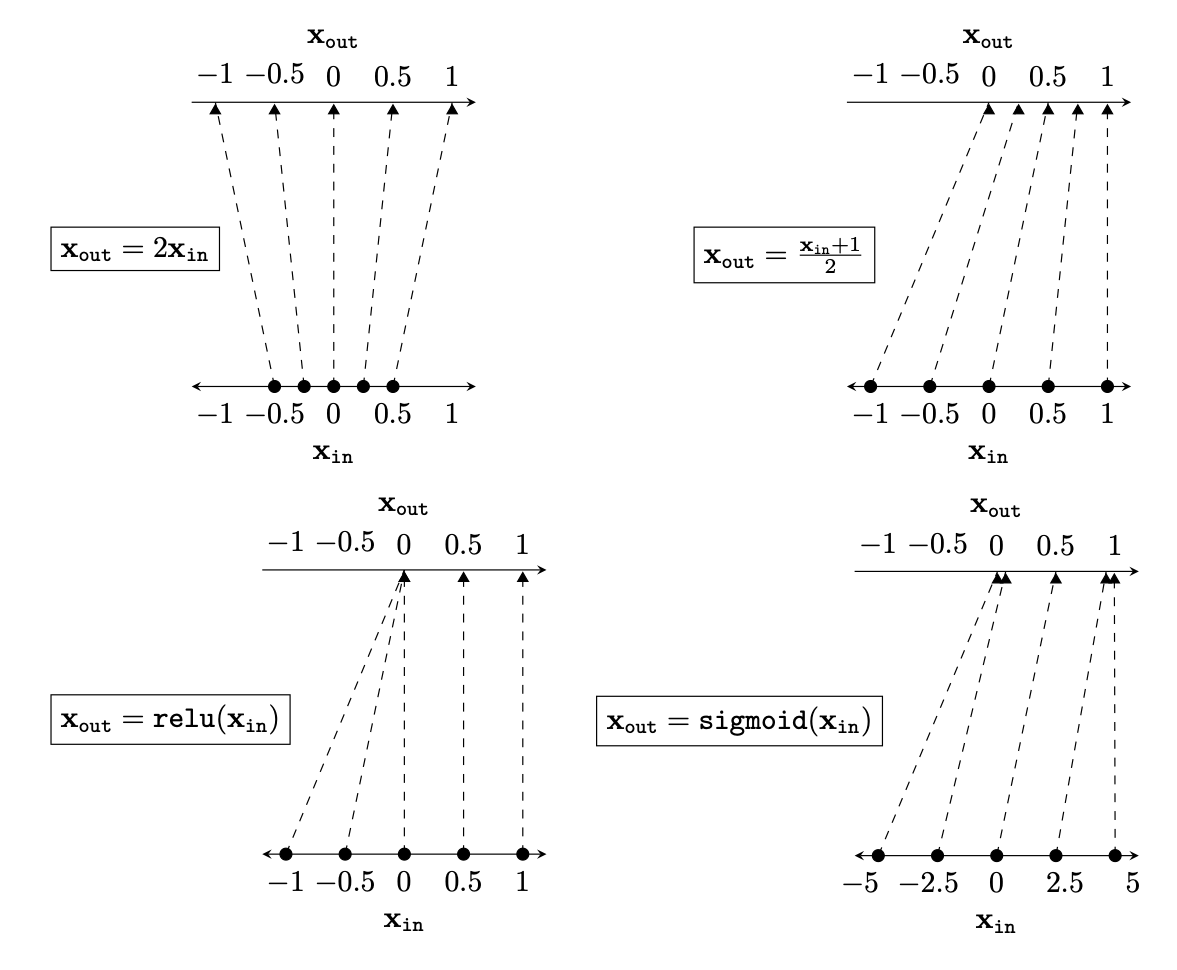
Two different ways to visualize a function
[images credit: visionbook.mit.edu]
Two different ways to visualize a function
[images credit: visionbook.mit.edu]
Representation transformations for a variety of neural net operations
[images credit: visionbook.mit.edu]
and stack of neural net operations
)
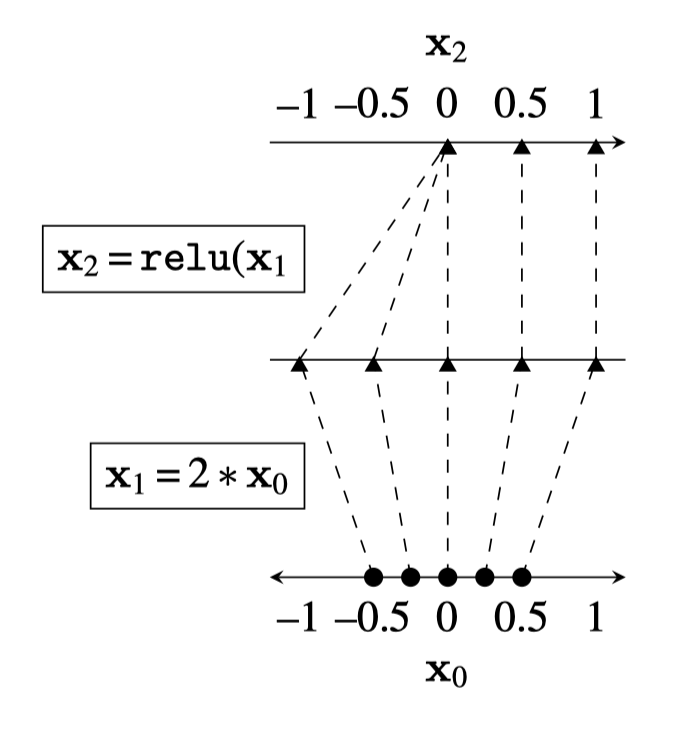
[images credit: visionbook.mit.edu]
wiring graph
equation
mapping 1D
mapping 2D
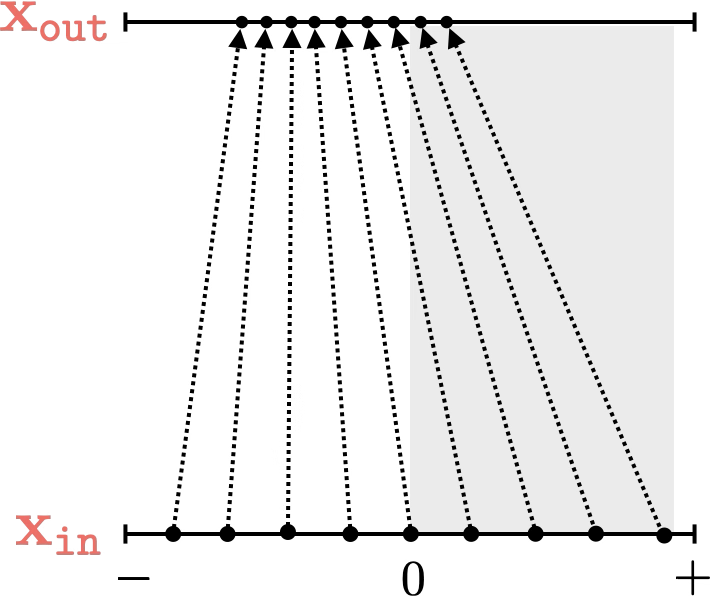
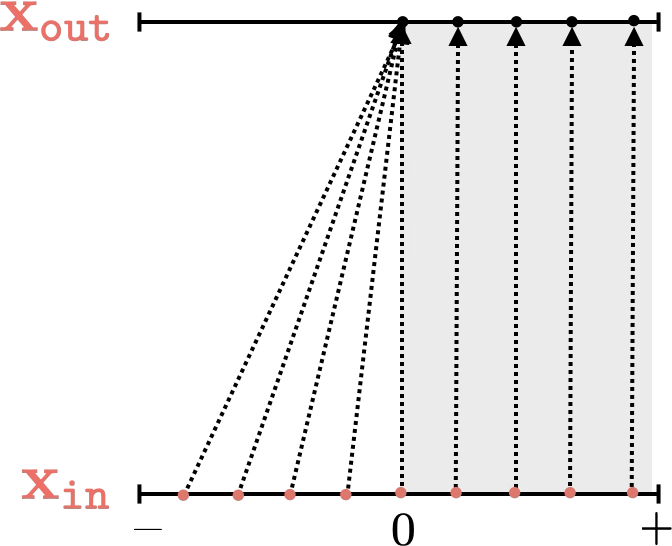
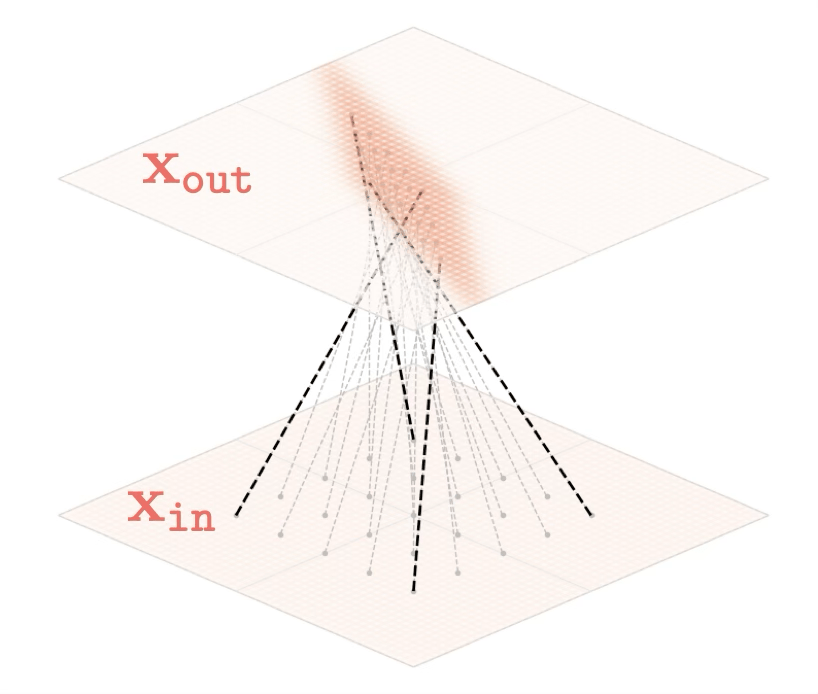
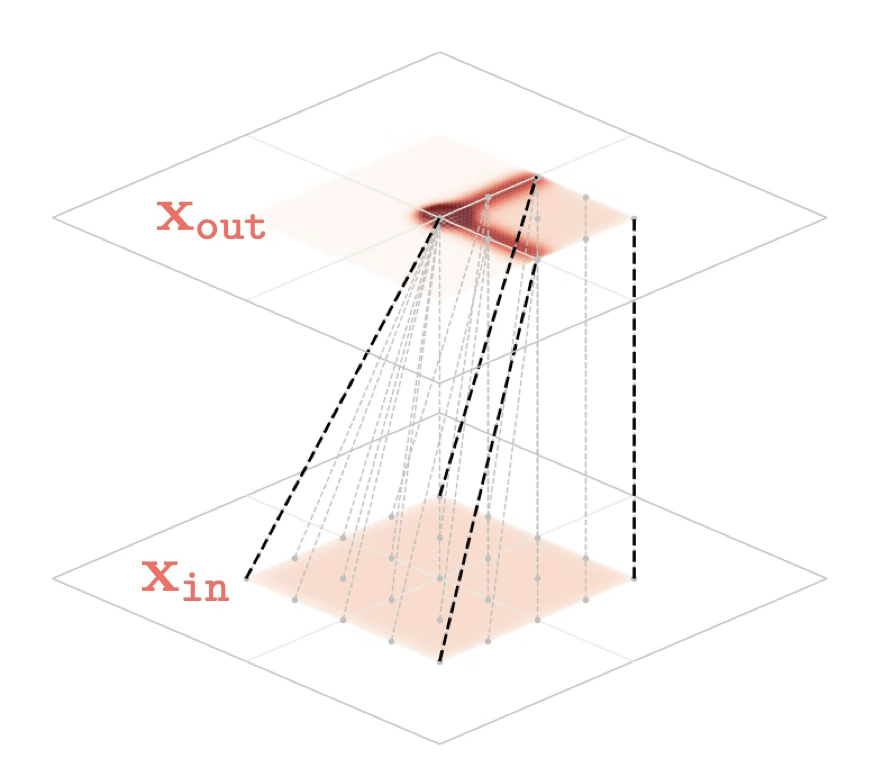
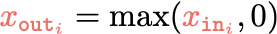
[images credit: visionbook.mit.edu]
[images credit: visionbook.mit.edu]
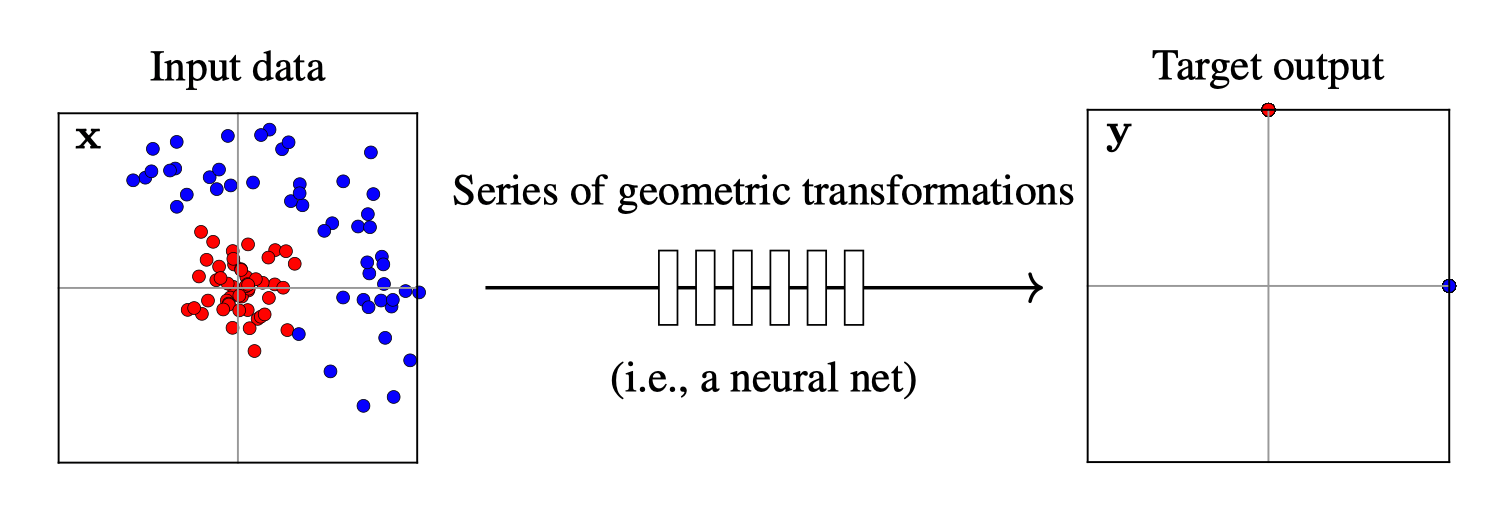
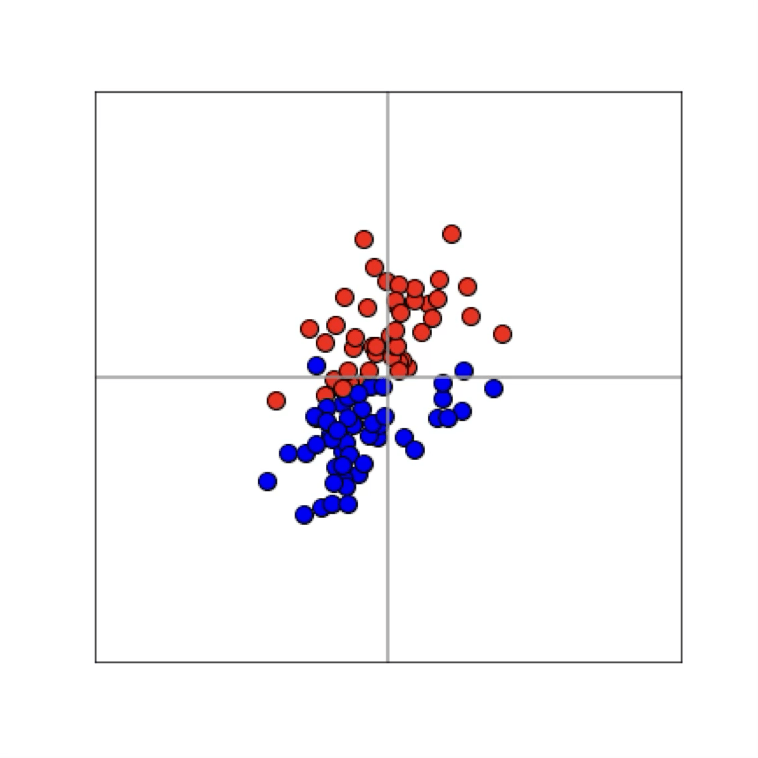
Training data
x
z_1
a_1
z_2
g
{z}_1=\text { linear }(x)
{a}_1=\text { ReLU}(z_1)
g=\text {softmax}(z_2)
{z}_2=\text { linear }(a_1)
x\in \mathbb{R^2}
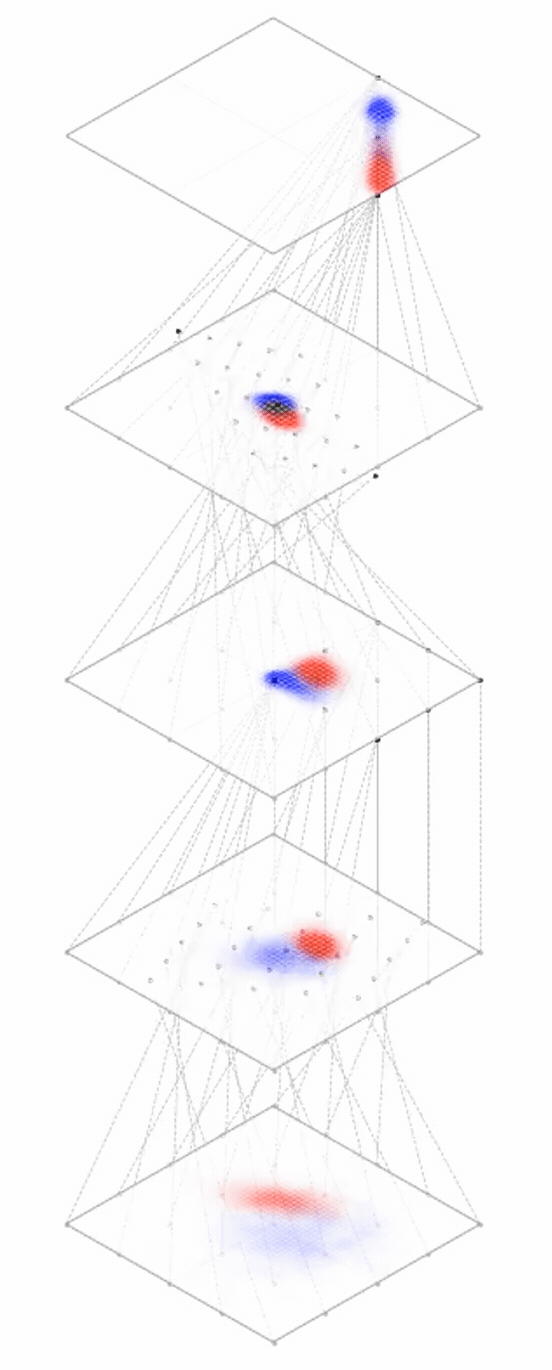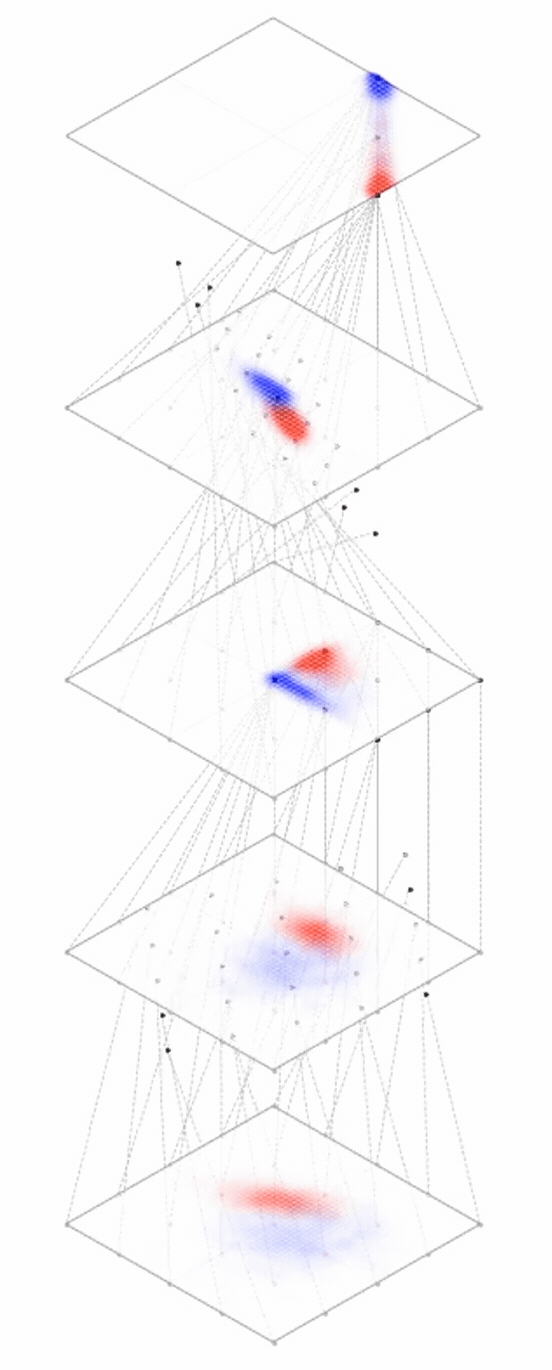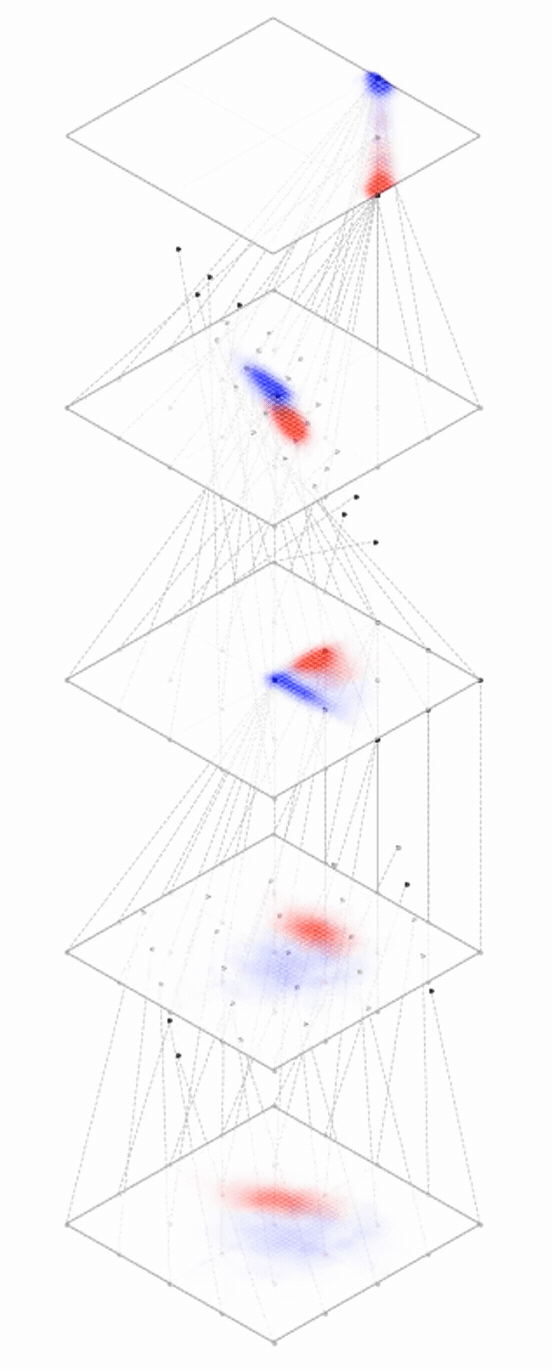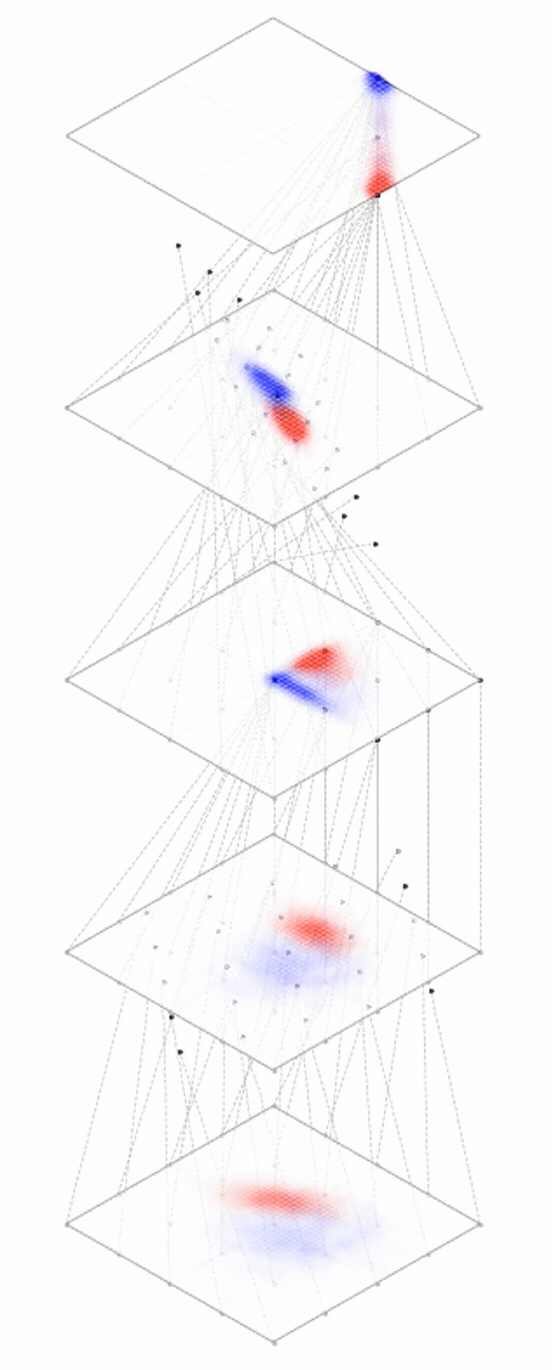
maps from complex data space to simple embedding space
[images credit: visionbook.mit.edu]
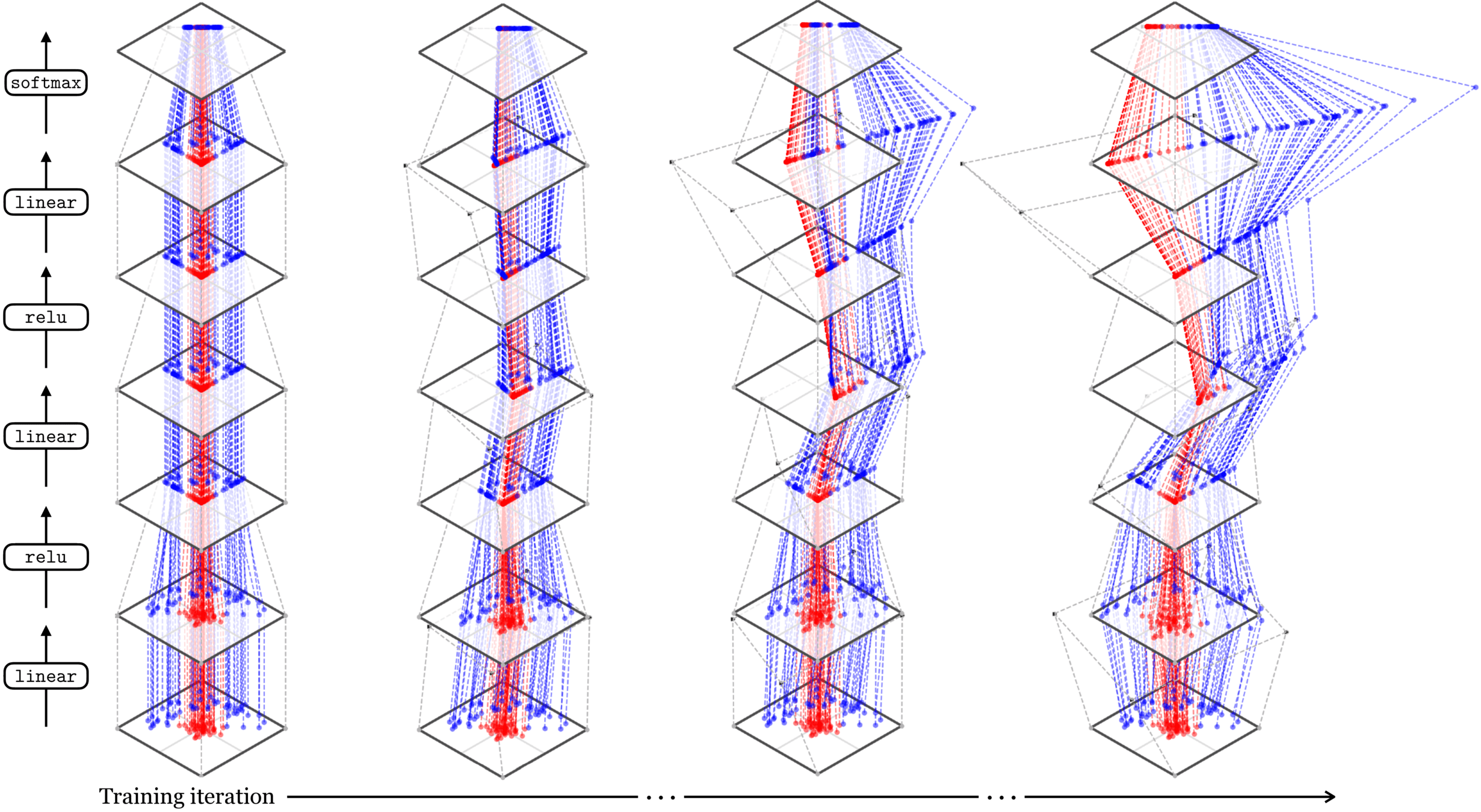
[images credit: visionbook.mit.edu]
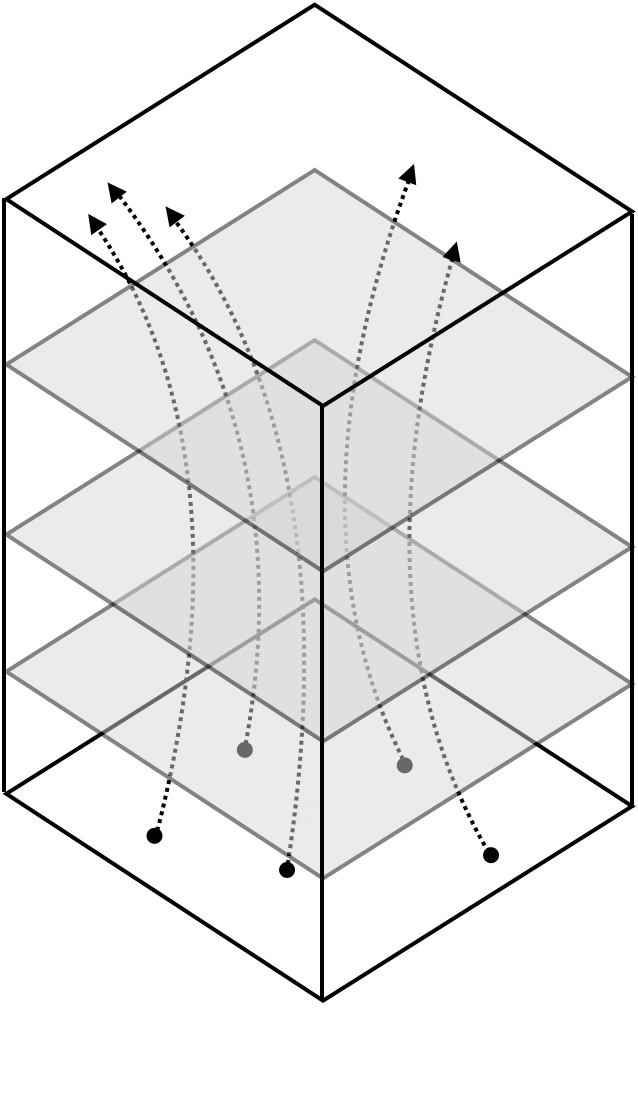
Neural networks are representation learners
Deep nets transform datapoints, layer by layer
Each layer gives a different representation (aka embedding) of the data
[images credit: visionbook.mit.edu]
Outline
- Neural networks are representation learners
- Auto-encoders
- Unsupervised and self-supervised learning
- Word embeddings
- (Some recent representation learning ideas)
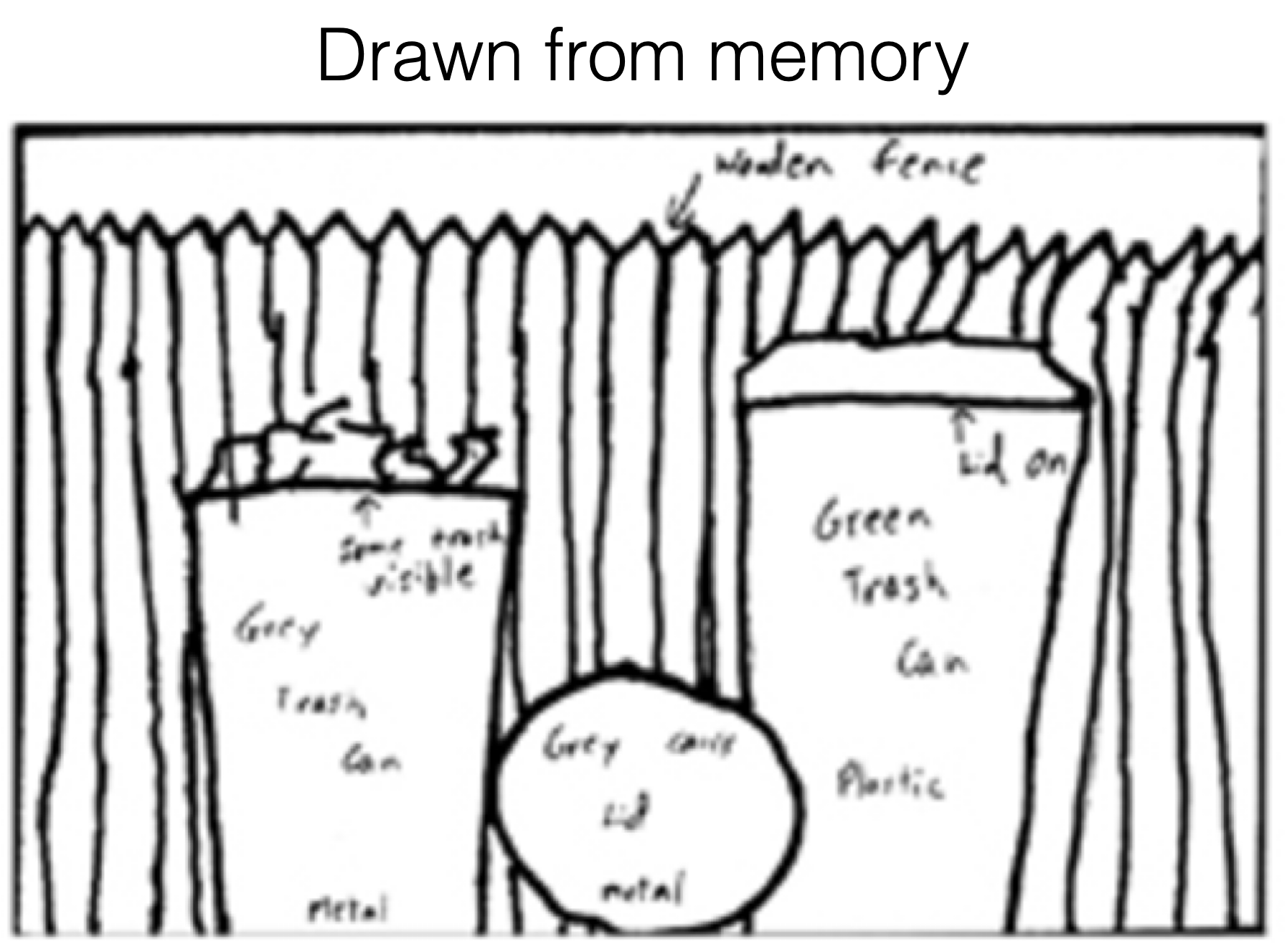
[Bartlett, 1932]
[Intraub & Richardson, 1989]
[https://www.behance.net/gallery/35437979/Velocipedia]
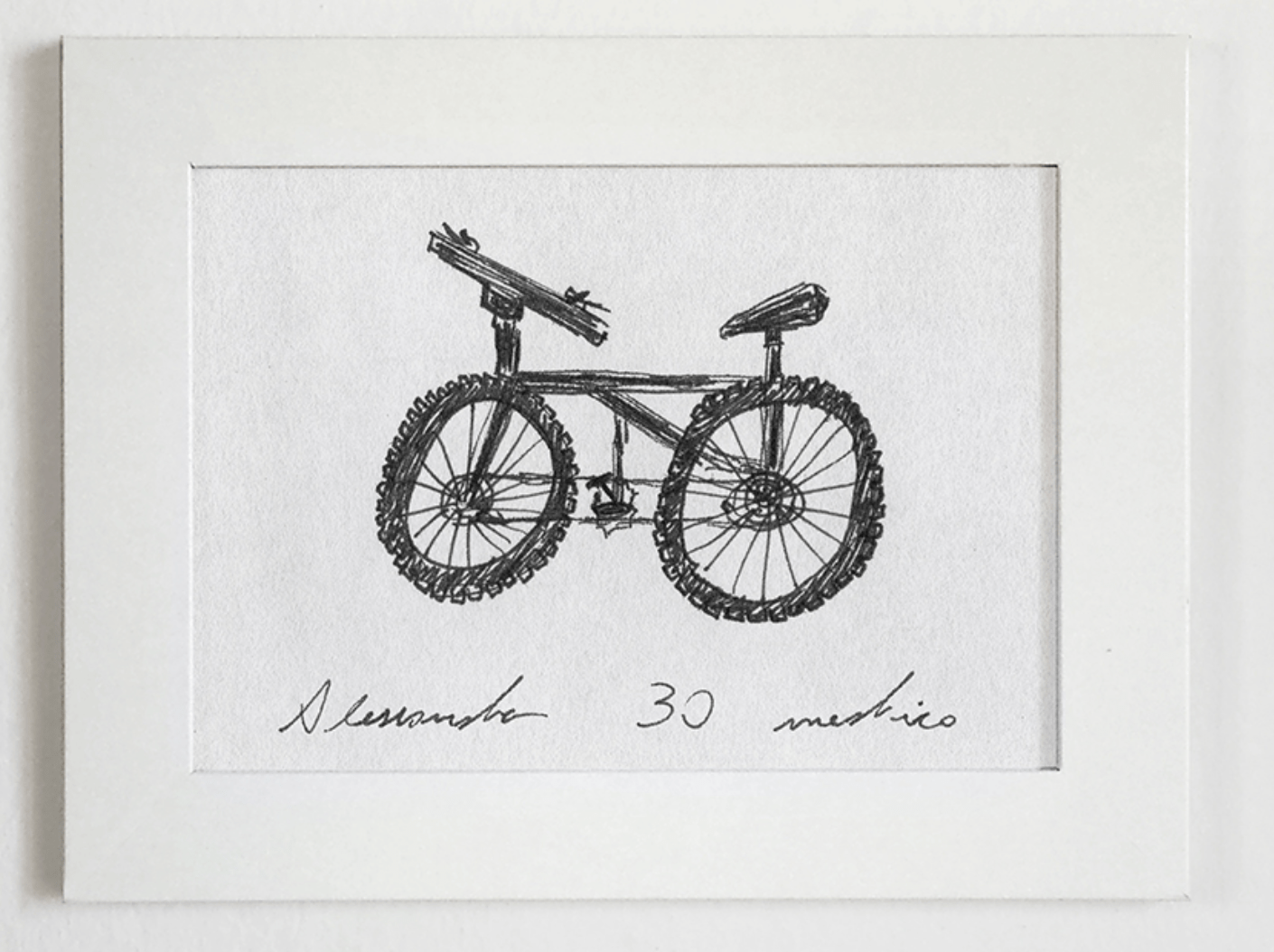
"I stand at the window and see a house, trees, sky. Theoretically I might say there were 327 brightnesses and nuances of colour. Do I have "327"? No. I have sky, house, and trees.”
— Max Wertheimer, 1923
🧠
humans also learn representations
[images credit: visionbook.mit.edu]
Good representations are:
- Compact (minimal)
- Explanatory (roughly sufficient)
[See “Representation Learning”, Bengio 2013, for more commentary]
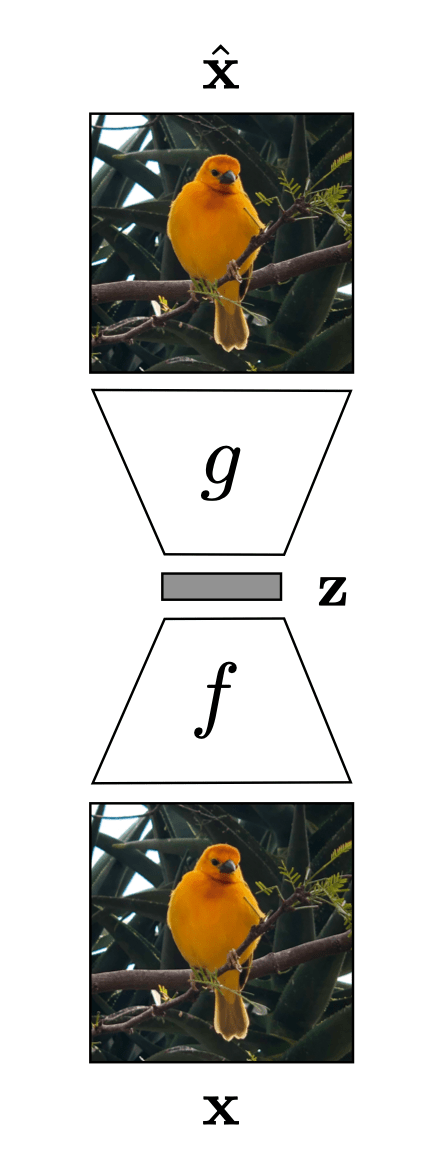
Auto-encoder
"What I cannot create, I do not understand." Feynman
[images credit: visionbook.mit.edu]
compact representation/embedding
Auto-encoder
\underbrace{\hspace{1cm}}
\underbrace{\hspace{1cm}}
encoder
decoder
bottleneck
Auto-encoder
x
\tilde{x}=\text{NN}(x;W)
\min_{W} ||x - \tilde{x}||^2
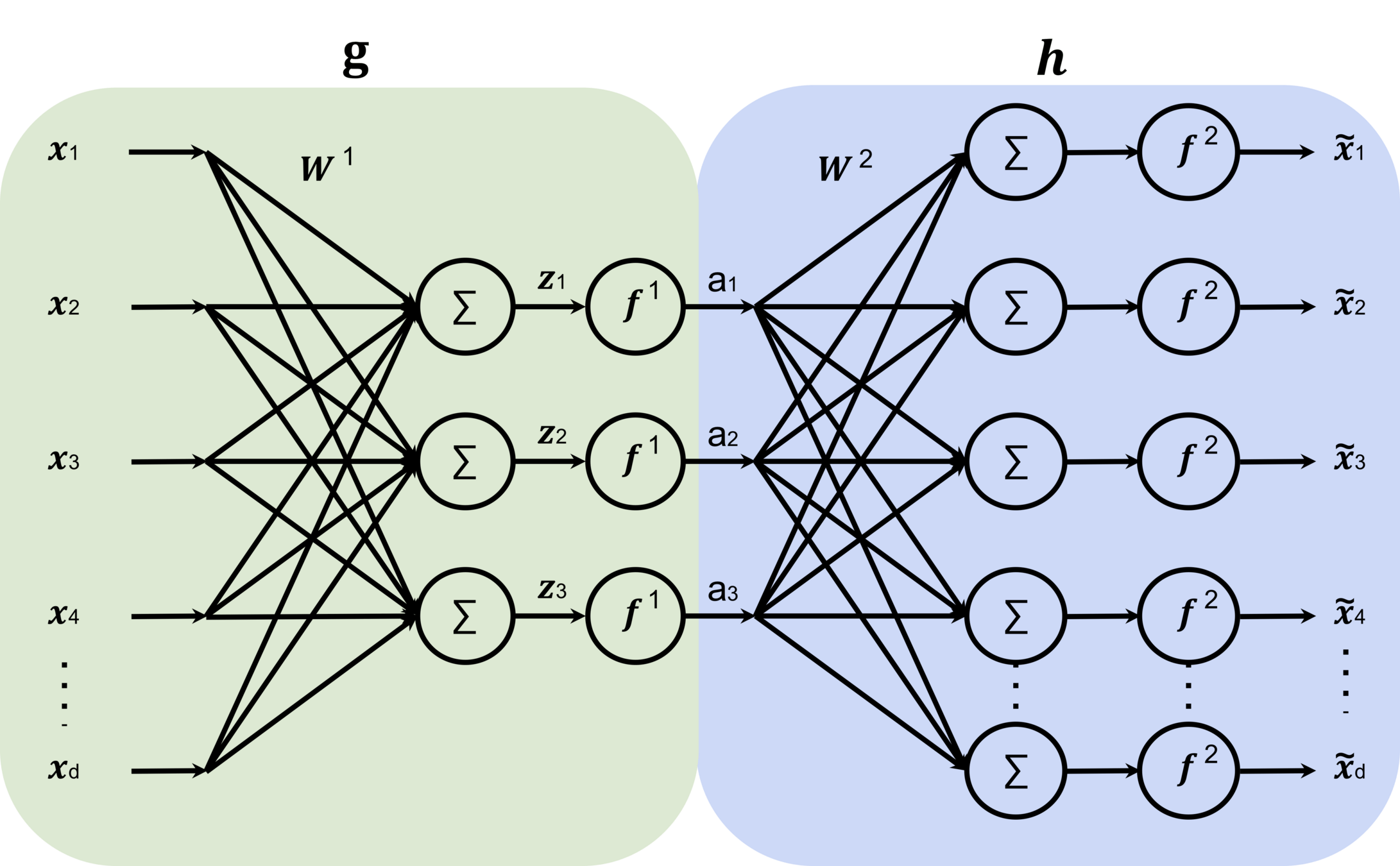
input \(x \in \mathbb{R^d}\)
output \(\tilde{x} \in \mathbb{R^d}\)
\dots
bottleneck
typically, has lower dimension than \(d\)
Auto-encoder
Training Data
\left\{{x}^{(i)}\right\}_{i=1}^n
loss/objective
\mathcal{L}(F(\mathbf{x}), \mathbf{x})=\|F(\mathbf{x})-\mathbf{x}\|^2
hypothesis class
A model
\(f\)
F= h \circ g: \mathbb{R}^d \rightarrow \mathbb{R}^m \rightarrow \mathbb{R}^d
h
g
\(m<d\)
[images credit: visionbook.mit.edu]
$$g$$
$$h$$
Data space
Encoder
Decoder
Represnetation space
[Often, encoders can be kept to get "good representations" whereas decoders can serve as "generative models"]
Outline
- Neural networks are representation learners
- Auto-encoders
- Unsupervised and self-supervised learning
- Word embeddings
- (Some recent representation learning ideas)
Supervised Learning
Training data
$$\{x^{(1)}, y^{(1)}\}$$
$$\{x^{(2)}, y^{(2)}\}$$
$$\{x^{(3)}, y^{(3)}\}$$
$$\ldots$$
Learner
$$f(x) \to y$$
"Good"
Representation
Unsupervised Learning
Training Data
$$\{x^{(1)}\}$$
$$\{x^{(2)}\}$$
$$\{x^{(3)}\}$$
$$\ldots$$
Learner
Label prediction (supervised learning)
Features
Label
$$x$$
$$y$$
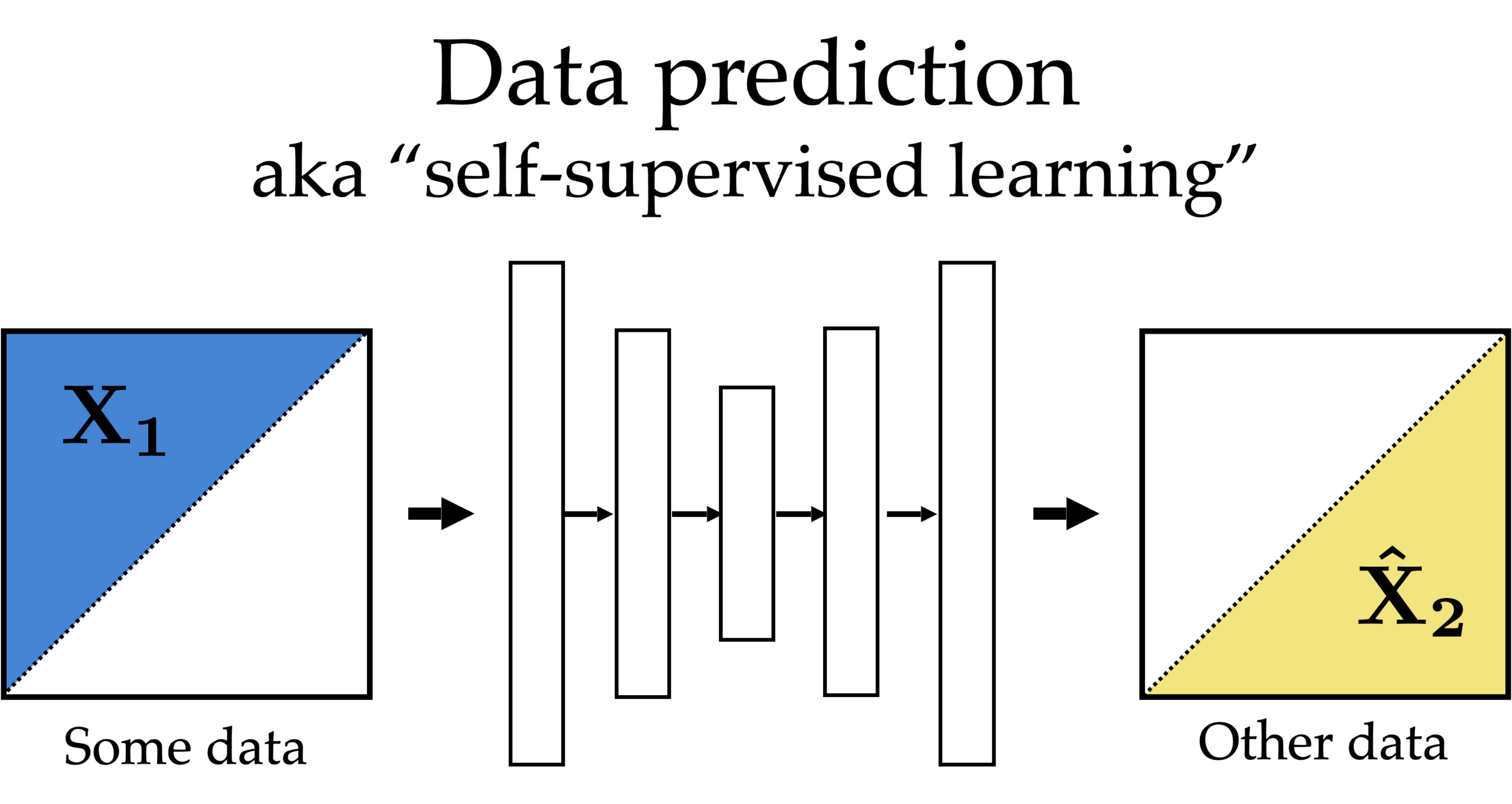
Feature reconstruction (unsupervised learning)
Features
Reconstructed Features
$$x$$
$$\hat{x}$$
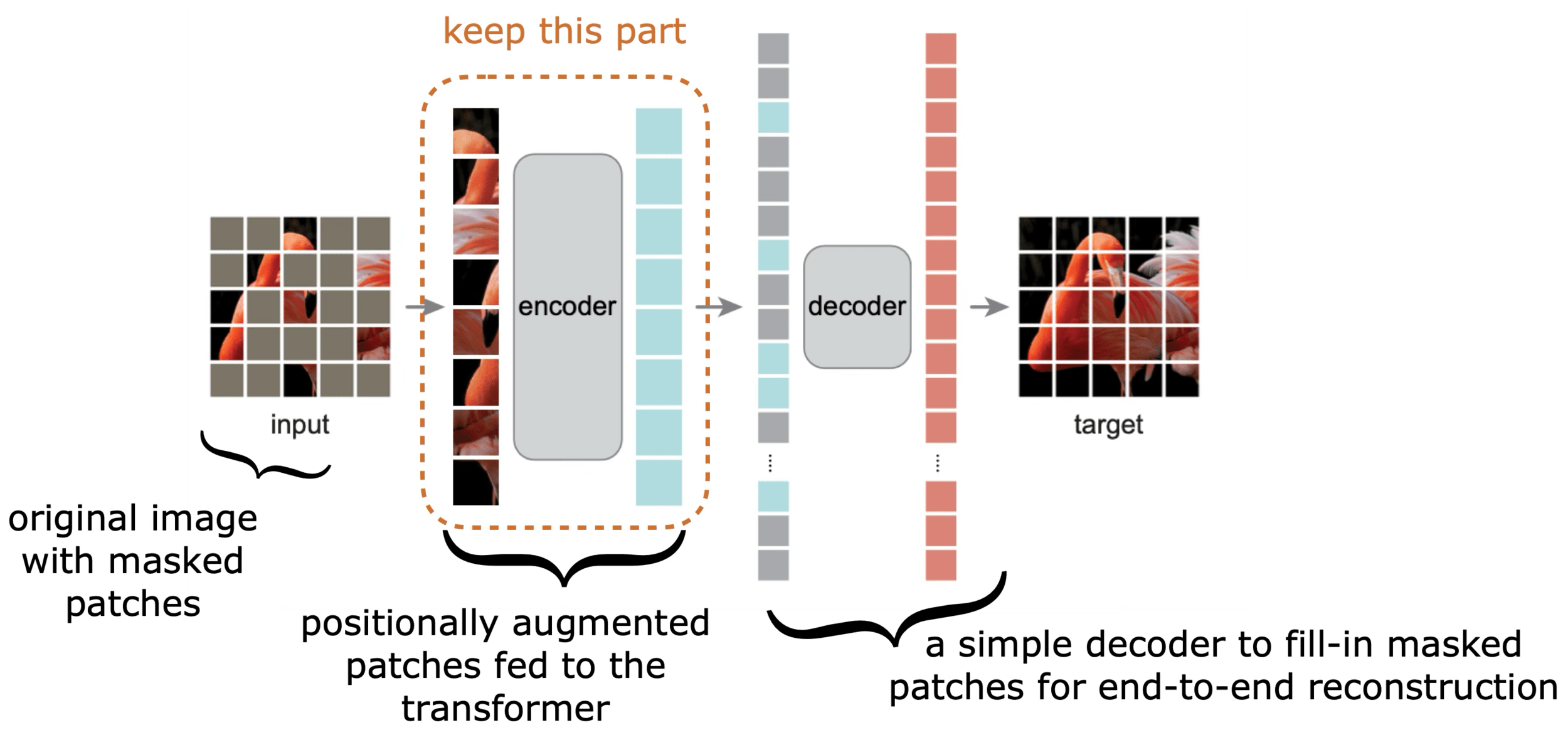
Self-supervised learning
Partial features
Other partial features
Masked Auto-encoder
[He, Chen, Xie, et al. MAE, 2021]
todo: move that better MAE plot here
[Zhang, Isola, Efros, ECCV 2016]
predict color from gray-scale
[Zhang, Isola, Efros, ECCV 2016]
Masked Auto-encoder
[Devlin, Chang, Lee, et al. 2019]
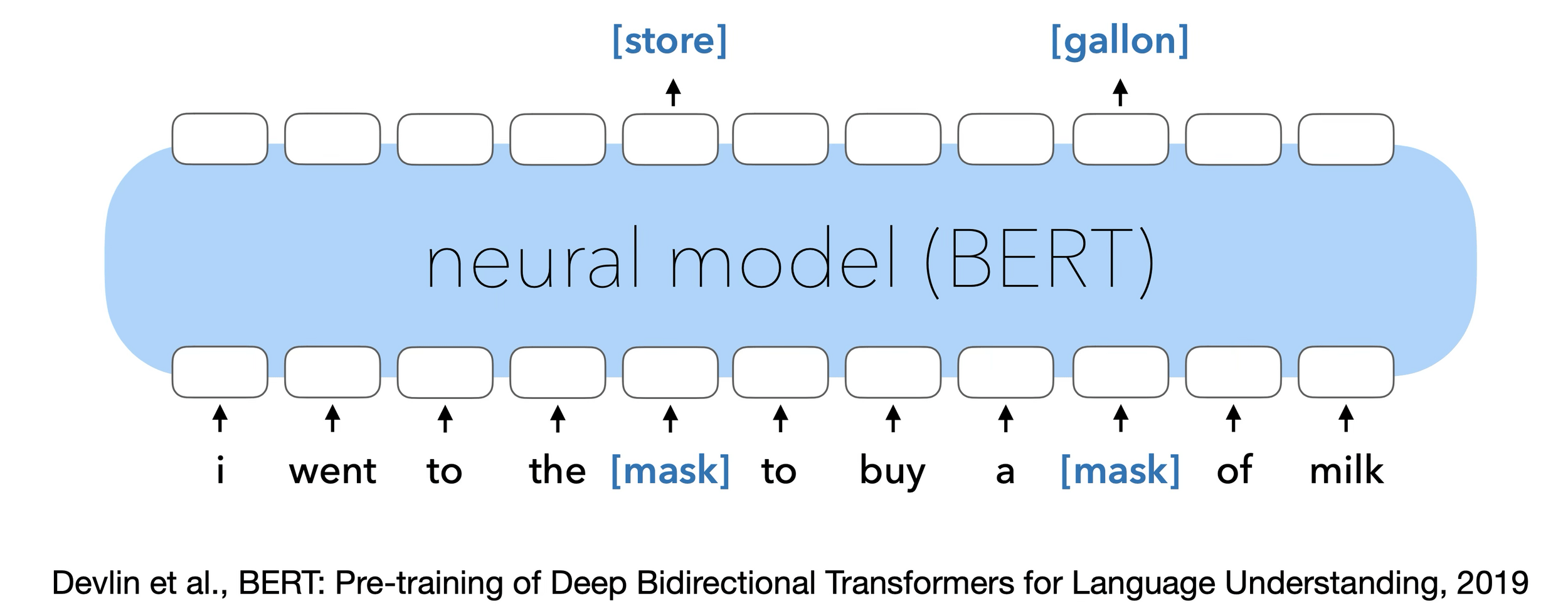
Self-supervised learning
Common trick:
- Convert “unsupervised” problem into “supervised” setup
- Do so by cooking up “labels” (prediction targets) from the raw data itself — called pretext task
Outline
- Neural networks are representation learners
- Auto-encoders
- Unsupervised and self-supervised learning
- Word embeddings
- (Some recent representation learning ideas)
Large Language Models (LLMs) are trained in a self-supervised way
- Scrape the internet for unlabeled plain texts.
- Cook up “labels” (prediction targets) from the unlabeled texts.
- Convert “unsupervised” problem into “supervised” setup.
"To date, the cleverest thinker of all time was Issac. "
feature
label
To date, the
cleverest
\dots
To date, the cleverest
thinker
To date, the cleverest thinker
was
\dots
\dots
\dots
To date, the cleverest thinker of all time was
Issac
[video edited from 3b1b]
[image edited from 3b1b]
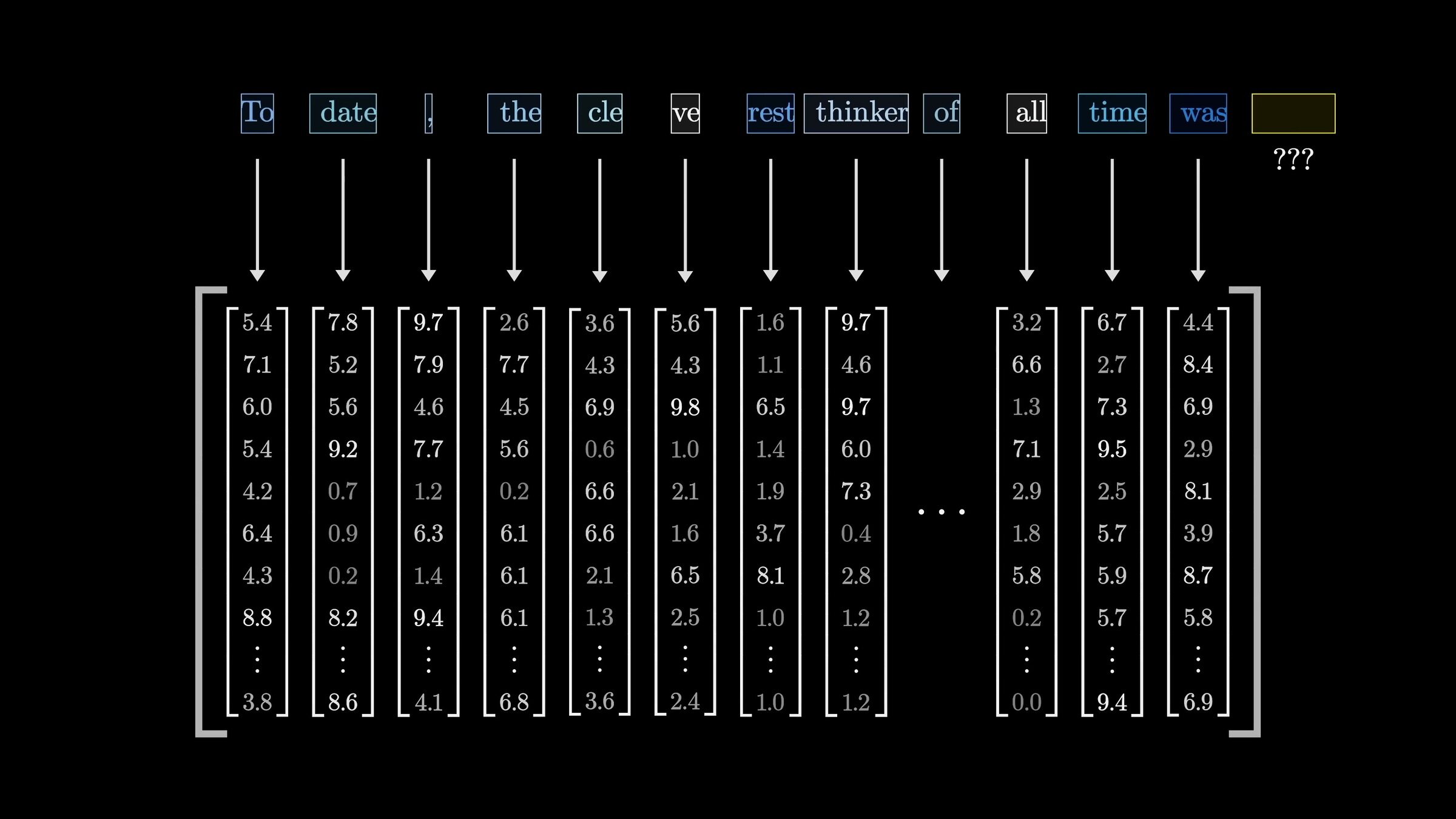
\(n\)
\underbrace{\hspace{5.98cm}}
\left\{
\begin{array}{l}
\\
\\
\\
\\
\\
\\
\\
\end{array}
\right.
\(d\)
input embedding (e.g. via a fixed encoder)
[video edited from 3b1b]
[video edited from 3b1b]
a
robot
must
obey
\left\{
\begin{array}{l}
\\
\\
\\
\end{array}
\right.
distribution over the vocabulary
Transformer
"A robot must obey the orders given it by human beings ..."
push for Prob("robot") to be high
push for Prob("must") to be high
push for Prob("obey") to be high
push for Prob("the") to be high
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
a
robot
must
obey
input embedding
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
transformer block
\left\{
\begin{array}{l}
\\
\\
\\
\\
\end{array}
\right.
\(L\) blocks
\(\dots\)
[video edited from 3b1b]
Word embedding
dot-product similarity
[video edited from 3b1b]
dot-product similarity
For now, let's think about dictionary look-up:
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}good embedding representation => sensible dot-product similarity
=> enables effective attention in transformers next week.
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "lemon"
output = dict_en2fr[query]apple
pomme
banane
citron
banana
lemon
Key
Value
lemon
\(:\)
\(:\)
\(:\)
Query
Output
citron
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]What if we run
Python would complain. 🤯
orange
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
Query
Output
???
What if we run
But we can probably see the rationale behind this:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
We implicitly assumed the (query, key, value) are represented in 'good' embeddings.
If we are to generalize this idea, we need to:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
get this sort of percentage
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.1
pomme
0.1
banane
0.8
citron
+
+
apple
banana
lemon
orange
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
apple
banana
lemon
orange
,
,
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
dot-product similarity
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
apple
banana
lemon
orange
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
pomme
banane
citron
+
+
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
0.1
0.1
0.8
=[\quad \quad \quad ]
apple
banana
lemon
orange
softmax
\Bigg(
\begin{array}{l}
\end{array}
\Bigg.
\Bigg)
\begin{array}{l}
\end{array}
\Bigg.
,
,
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.8
pomme
0.1
banane
0.1
citron
+
+
=[\quad \quad \quad ]
0.1
0.1
0.8
pomme
banane
citron
+
+
and output
weighted average over values
very roughly, the attention mechanism does exactly this kind of "soft" look-up:
Outline
- Neural networks are representation learners
- Auto-encoders
- Unsupervised and self-supervised learning
- Word embeddings
- (Some recent representation learning ideas)
- Compact (minimal)
- Explanatory (roughly sufficient)
- Disentangled (independent factors)
- Interpretable
- Make subsequent problem solving easy
[See “Representation Learning”, Bengio 2013, for more commentary]
Auto-encoders try to achieve these
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\left\{
\begin{array}{l}
\\
\\
\\
\end{array}
\right.
these may just emerge as well
Good representations are:
\left(
\begin{array}{l}
\\
\\
\\
\\
\\
\\
\end{array}
\right.
- pre-training
- contrastive
- multi-modality
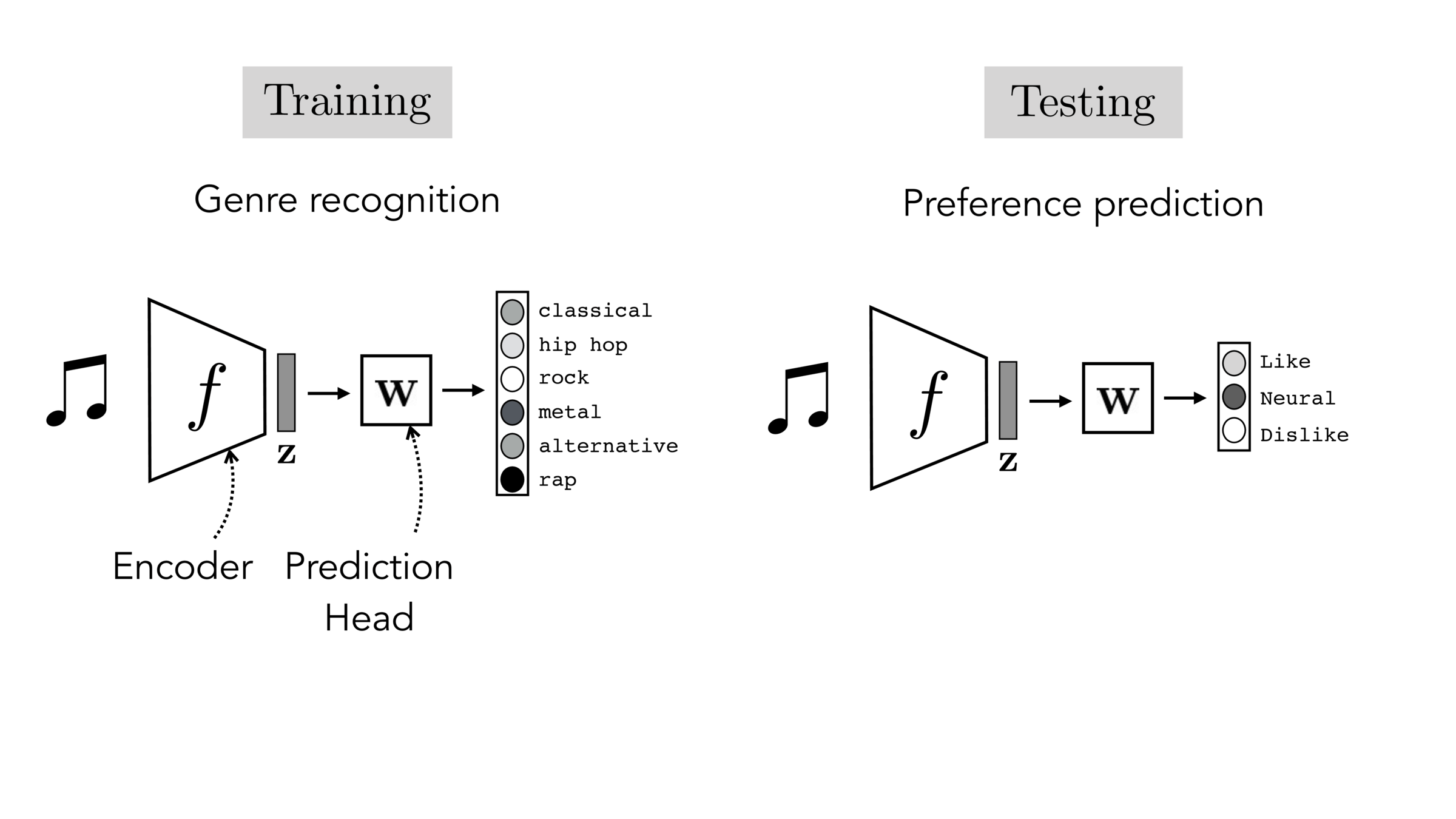
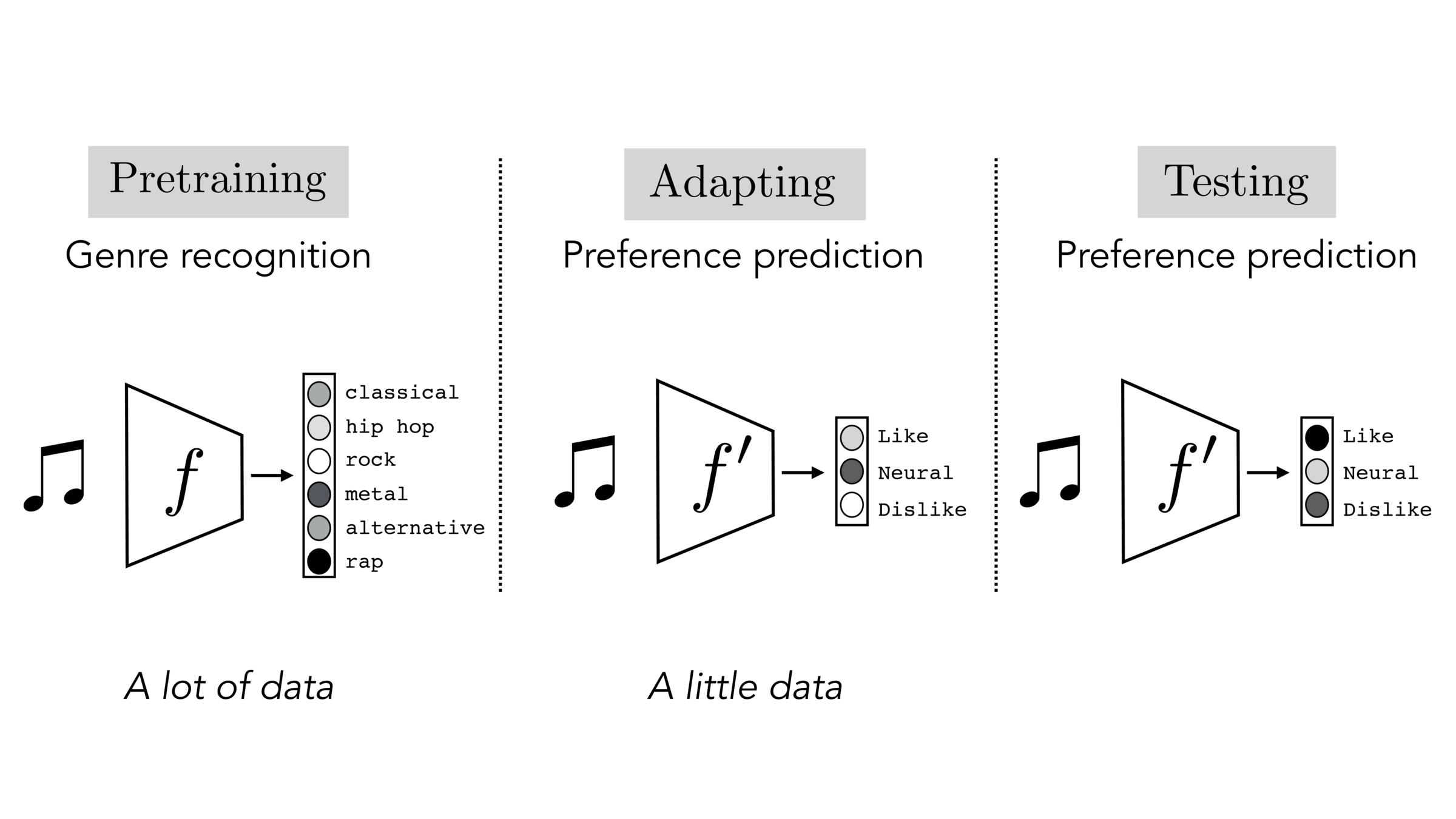
Often, what we will be “tested” on is not what we were trained on.
[images credit: visionbook.mit.edu]
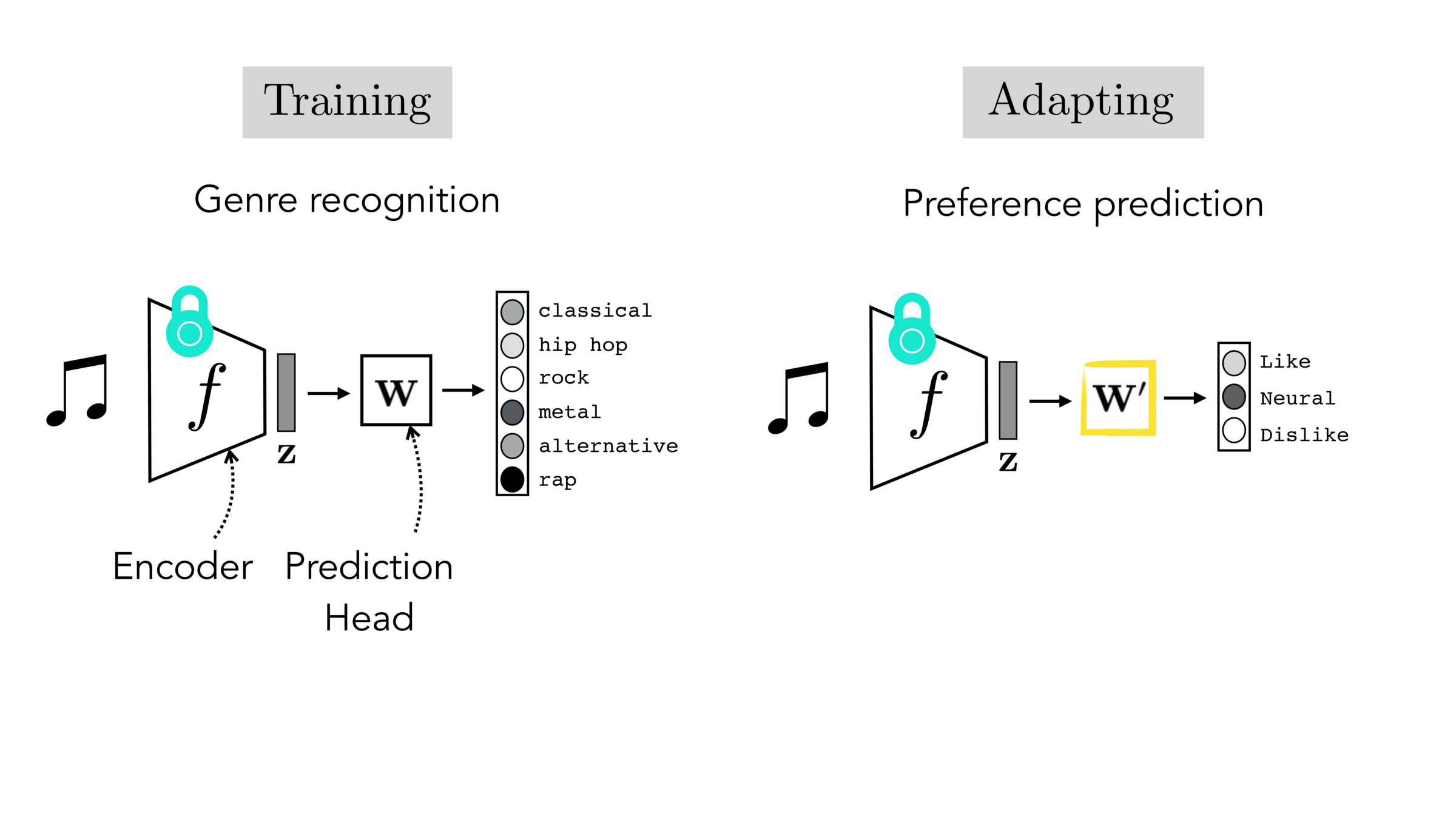
Final-layer adaptation: freeze \(f\), train a new final layer to new target data
[images credit: visionbook.mit.edu]
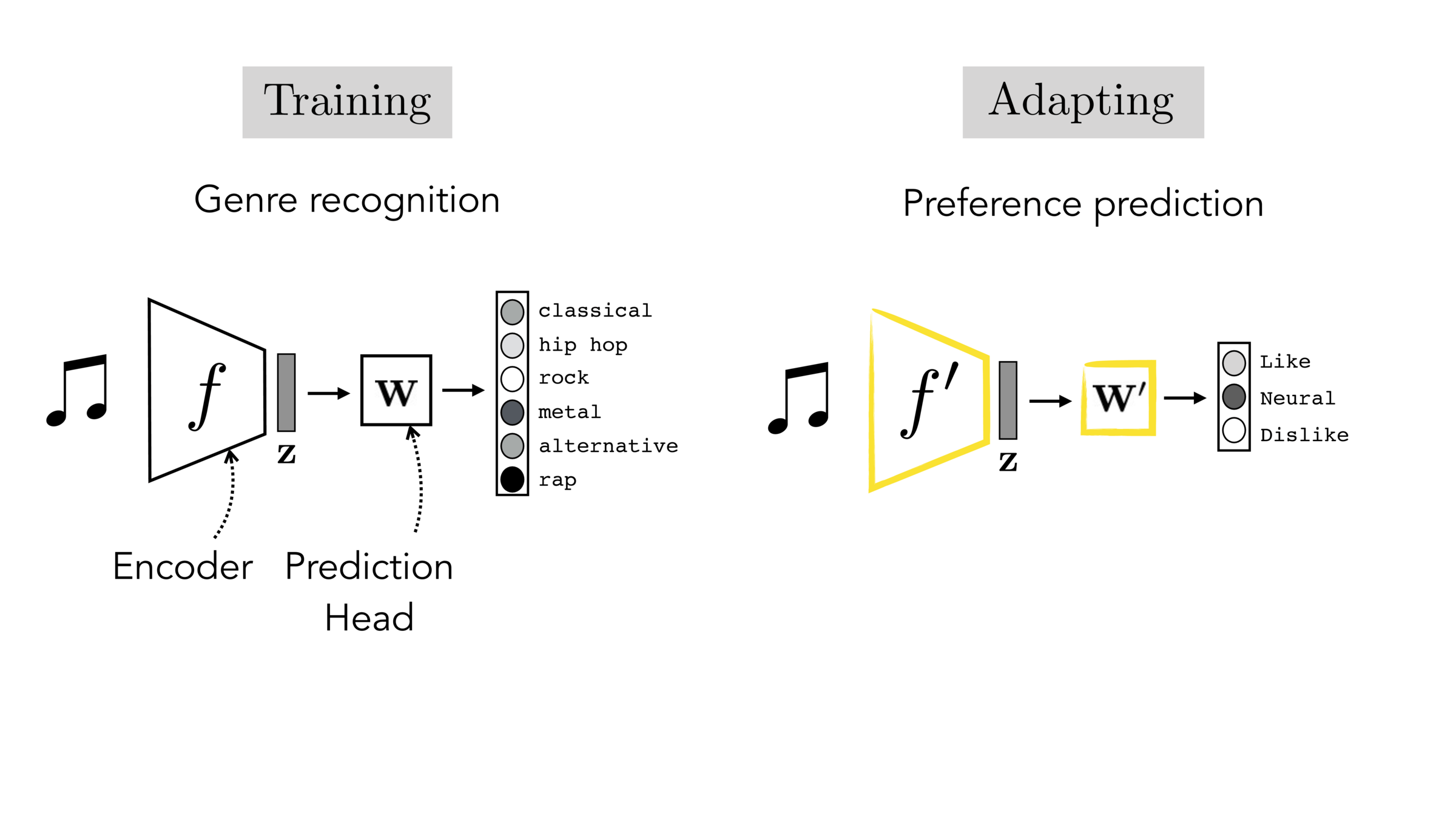
Finetuning: initialize \(f’\) as \(f\), then continue training for \(f'\) as well, on new target data
[images credit: visionbook.mit.edu]
[images credit: visionbook.mit.edu]
The allegory of the cave
[images credit: visionbook.mit.edu]
Contrastive learning
[images credit: visionbook.mit.edu]
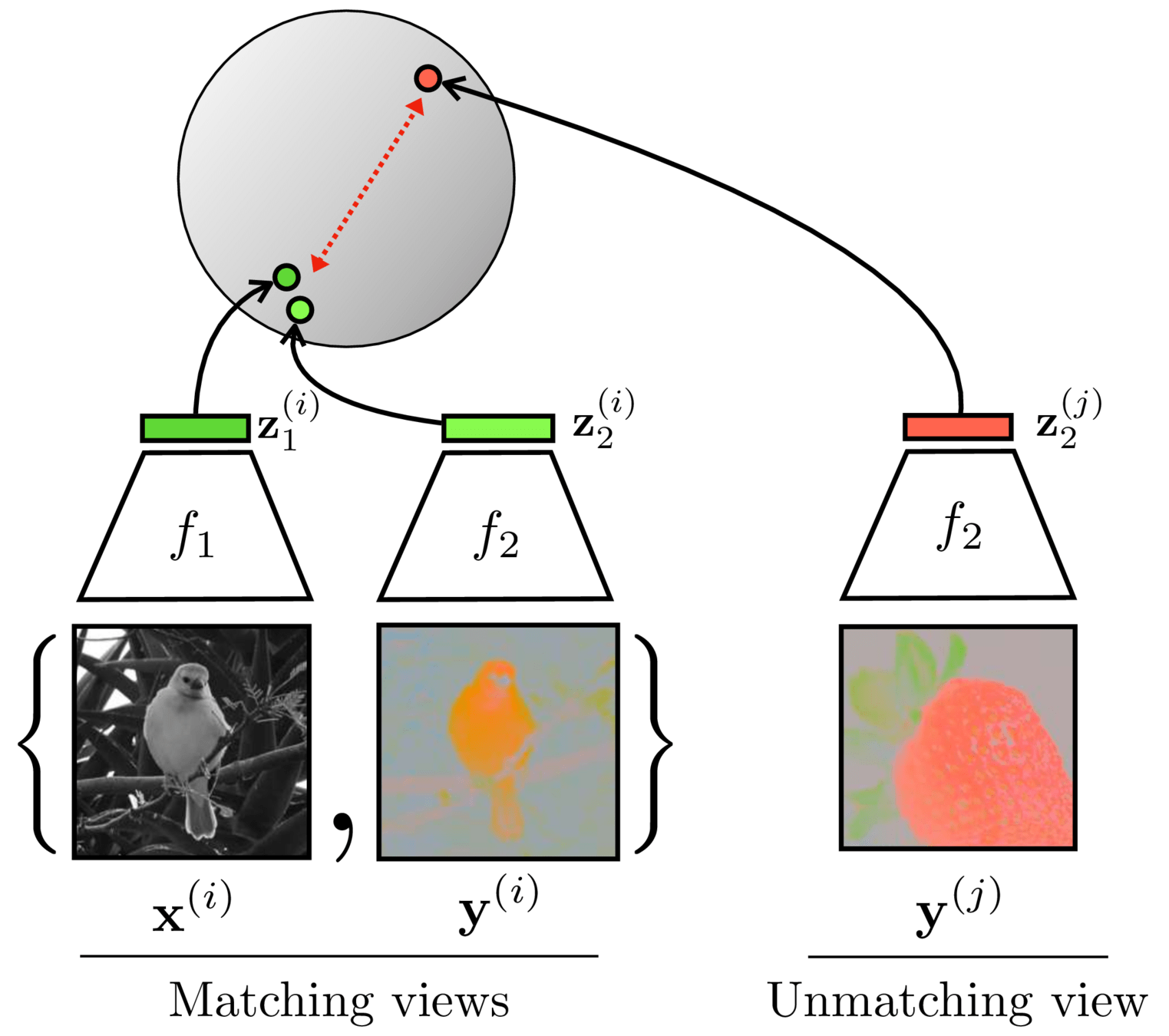
Contrastive learning
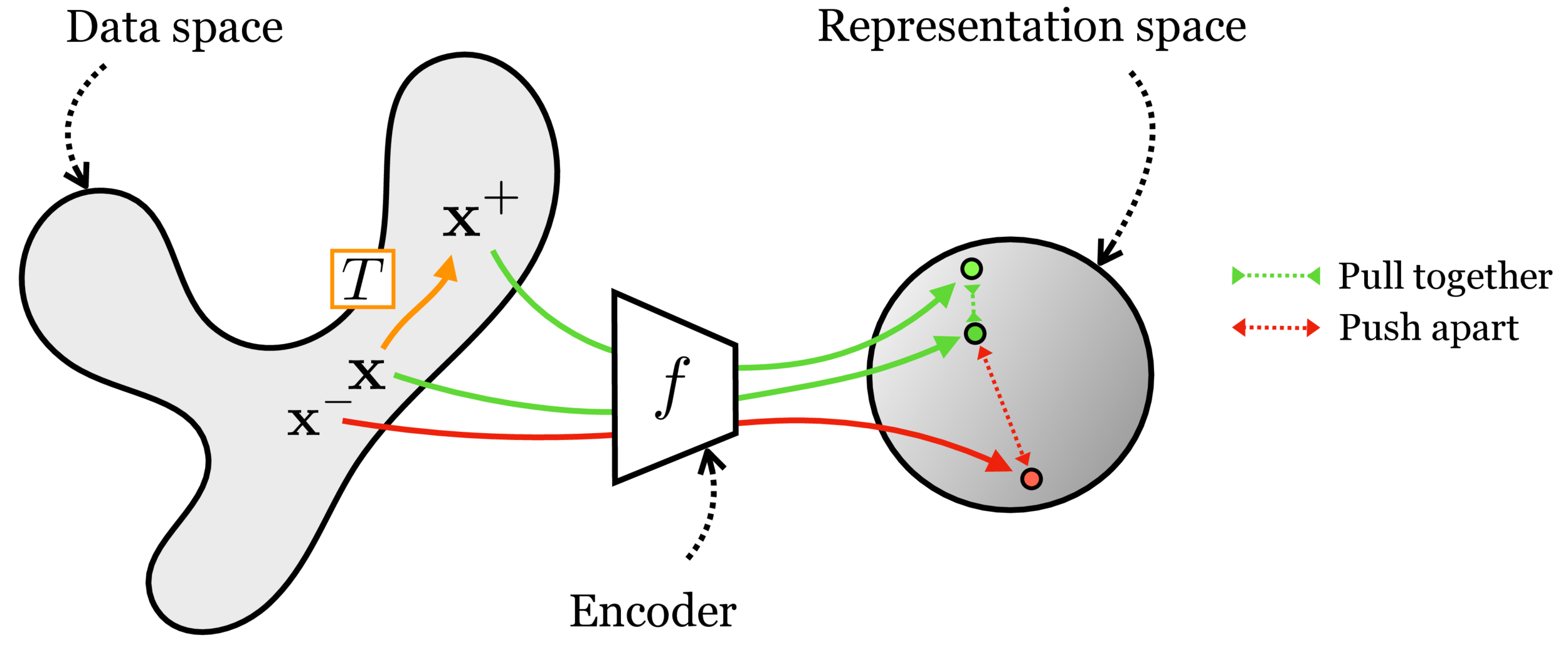
[images credit: visionbook.mit.edu]
[Chen, Kornblith, Norouzi, Hinton, ICML 2020]
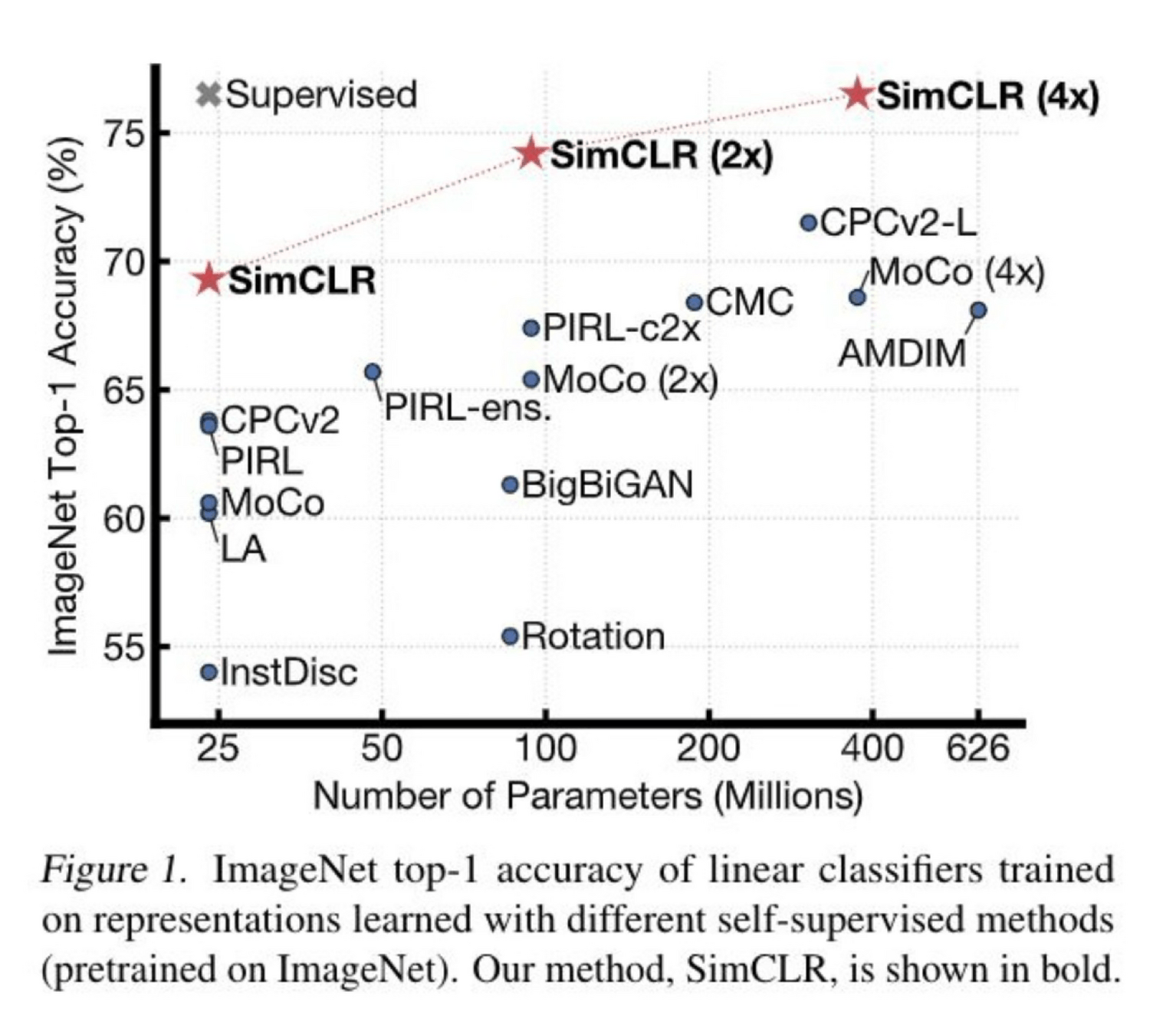
SimCLR animation
Multi-modality
[images credit: visionbook.mit.edu]
[Slide credit: Andrew Owens]
[Owens et al, Ambient Sound Provides Supervision for Visual Learning, ECCV 2016]
Video - audio
[Slide credit: Andrew Owens]
[Owens et al, Ambient Sound Provides Supervision for Visual Learning, ECCV 2016]
What did the model learn?
[Slide credit: Andrew Owens]
[Owens et al, Ambient Sound Provides Supervision for Visual Learning, ECCV 2016]
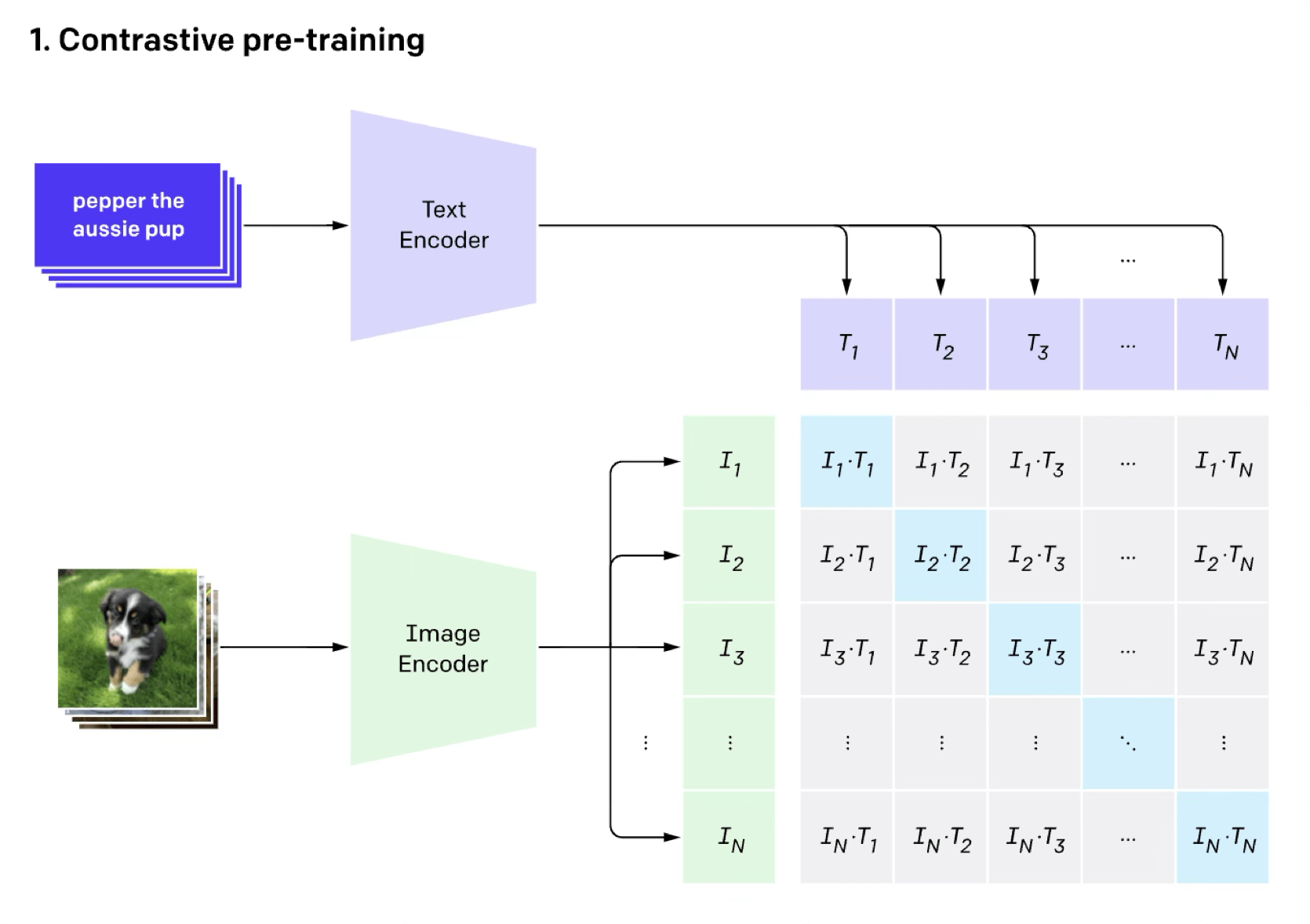
Image classification (done in the contrastive way)
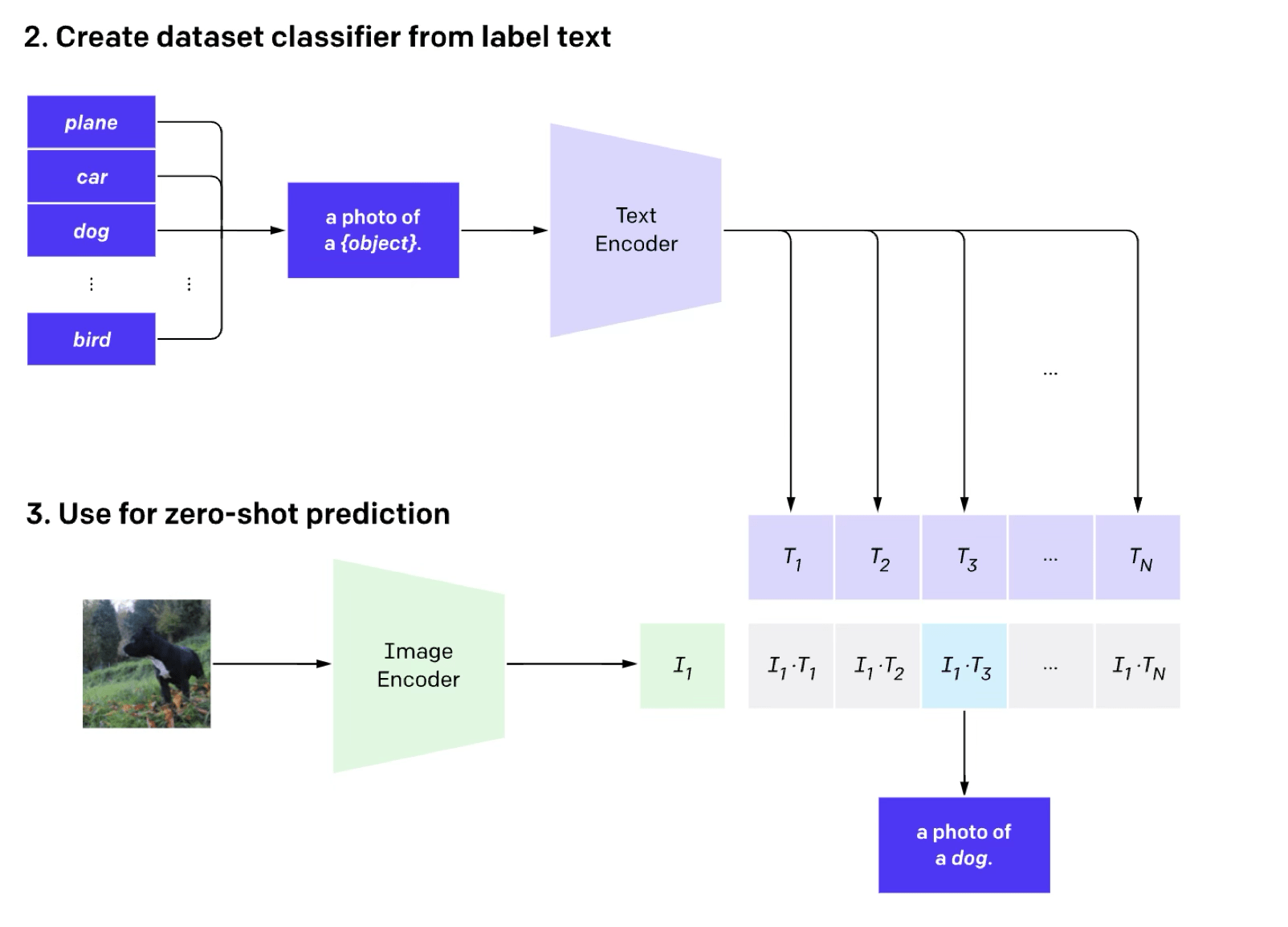
Image classification (done in the contrastive way)
[https://arxiv.org/pdf/2204.06125.pdf]
Dall-E: text-image generation
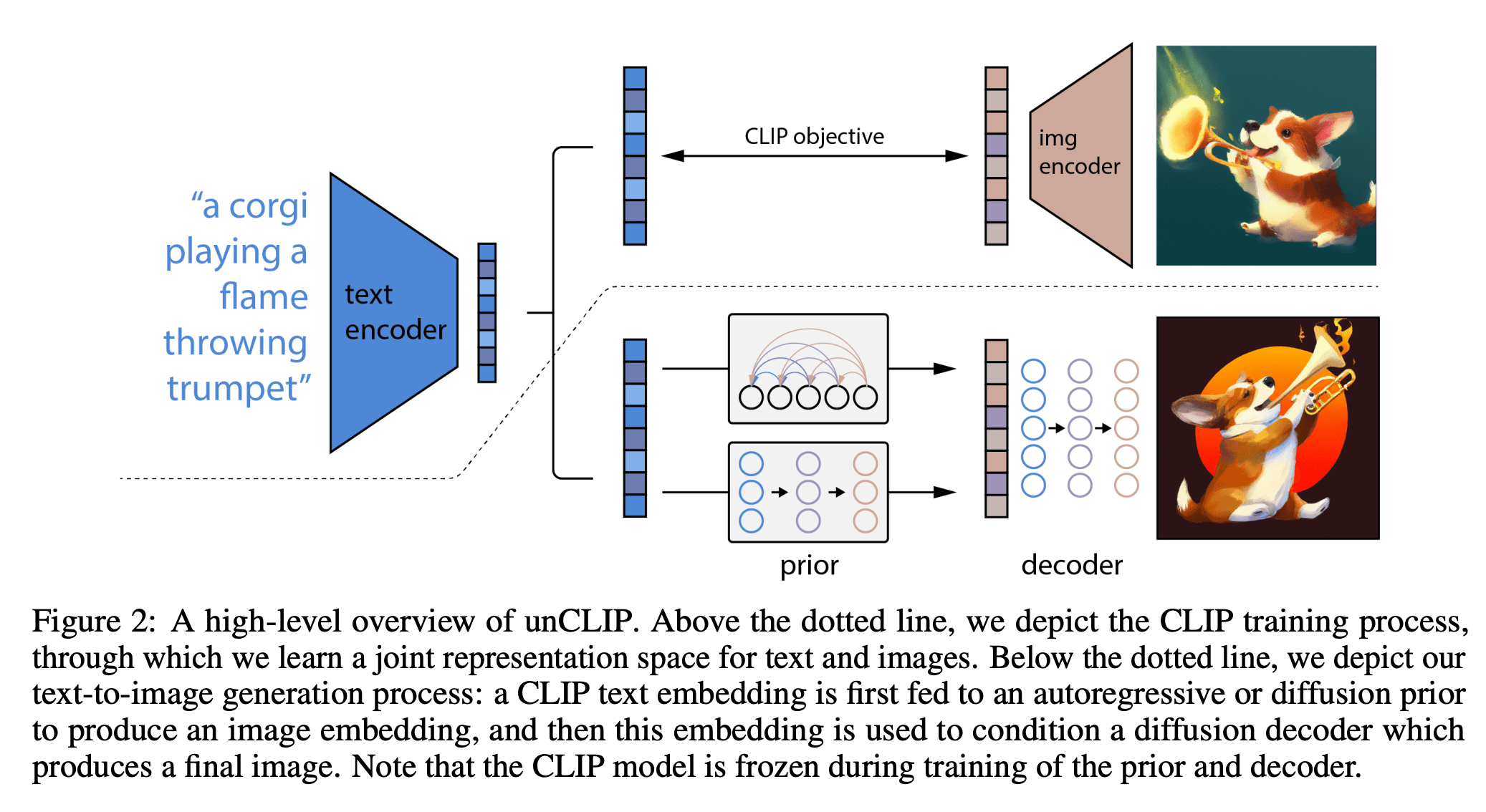
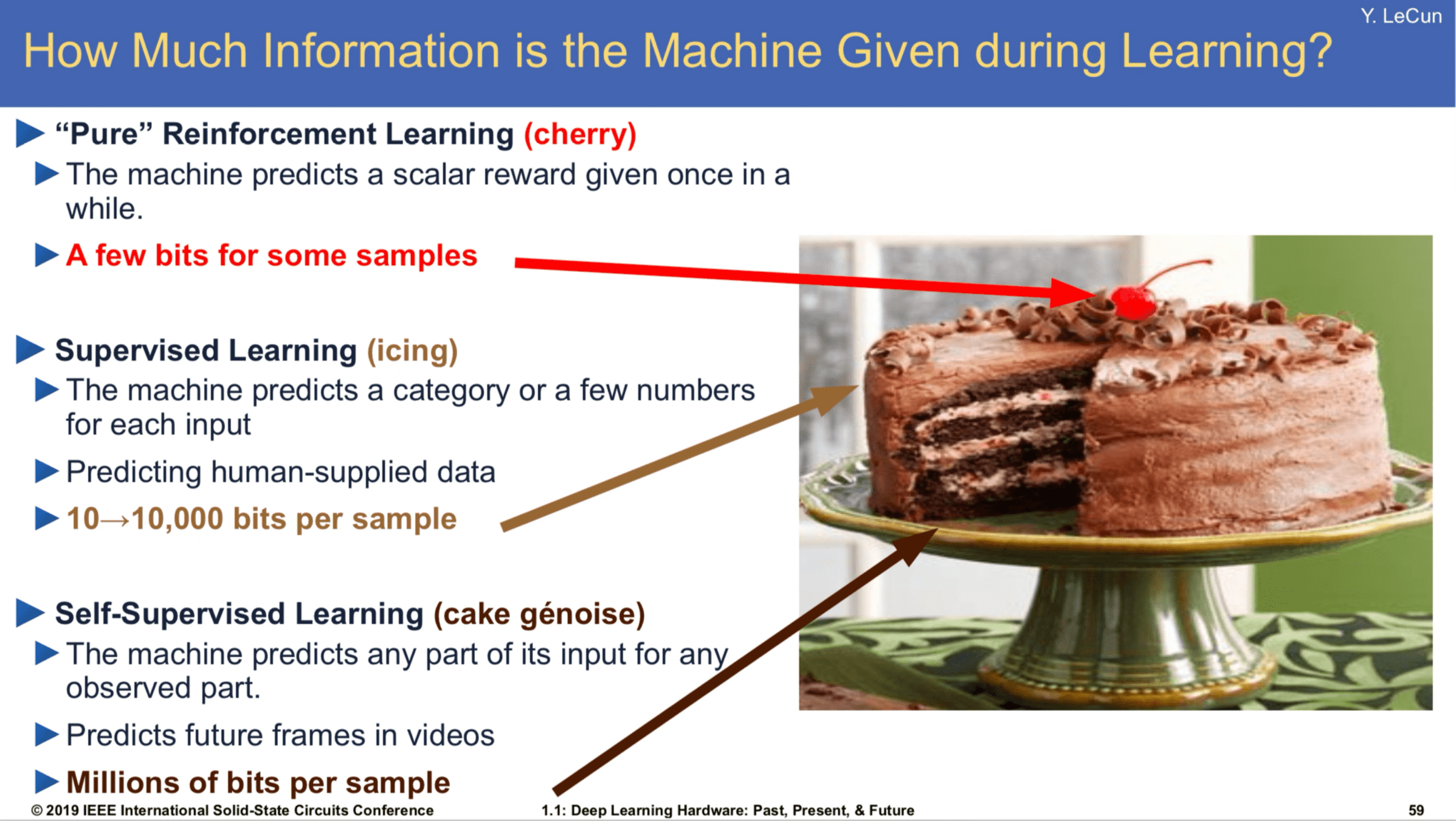
[Slide Credit: Yann LeCun]
Summary
- We looked at the mechanics of neural net. Today we see deep nets learn representations, just like our brains do.
- This is useful because representations transfer — they act as prior knowledge that enables quick learning on new tasks.
- Representations can also be learned without labels, e.g. as we do in unsupervised, or self-supervised learning. This is great since labels are expensive and limiting.
- Without labels there are many ways to learn representations. We saw today:
- representations as compressed codes, auto-encoder with bottleneck
- (representations that are predictive of their context)
- (representations that are shared across sensory modalities)
Thanks!
We'd love to hear your thoughts.
6.390 IntroML (Spring25) - Lecture 8 Representation Learning
By Shen Shen
