userFullId :: (Int, String, String) -> String
userFullId (uid, login, name) = show uid ++ ":" ++ login

ghci> userFullId (3, "pumpkin", "Ivan")
"3:pumpkin"

type BinaryIntFunction = Int -> Int -> Int
type String            = [Char]
type FilePath          = String
type TripleList a      = [(a, a, a)]
type SwapPair a b      = (a, b) -> (b, a)

userFullId :: User -> String
userFullId (uid, login, name) = show uid ++ ":" ++ login

type User = (Int, String, String)

struct user {
    int uid;
    string login;
    string pass;
};

type User = (Int, String, String)

data TrafficLight = Red | Yellow | Green | Blue

-- pattern matching with types
lightName :: TrafficLight -> String
lightName Red    = "red"
lightName Yellow = "yellow"
lightName Green  = "green"
lightName Blue   = "magenta"

ghci> map lightName [Yellow, Red, Blue, Yellow]
["yellow","red","magenta","yellow"]

data User = MkUser Int String String

      ┌─ type name
      │
      │       ┌─ constructor name (or constructor tag)
      │       │
data User = MkUser Int String String
 │                  │    │      │
 │                  └────┴──────┴── types of fields
 │
 └ "data" keyword

data User = MkUser Int String String

getUid :: User -> Int
getUid (MkUser uid _ _) = uid    -- pattern should be in ()

getName :: User -> String
getName (MkUser _ name _) = name

ghci> import Data.List (nub)
ghci> let users = [ MkUser 2 "Ivan" "123"
                  , MkUser 1 "Mark" "1"
                  , MkUser 3 "Ivan" "xxx"
                  ]
ghci> nub $ map getName users  -- unique names
["Ivan","Mark"]

ghci> :t MkUser
MkUser :: Int -> String -> String -> User

data Point2D a = Point2D a a  -- constructor name can be the same as type name

pointToList :: Point2D a -> [a]
pointToList (Point2D x y) = [x, y]

ghci> pointToList (Point2D 5 10)
[5, 10] 
ghci> doublePoint (Point2D 'a' 'b')
Point2D ('a', 'b') ('a', 'b') 
ghci> maxCoord (Point2D 5 10)
10
ghci> distFromZero (Point2D 5 10)
11.180339887498949

doublePoint :: Point2D a -> Point2D (a, a)
doublePoint (Point2D x y) = Point2D (x, y) (x, y) 

maxCoord :: Point2D Int -> Int
maxCoord (Point2D x y) = max x y

distFromZero :: Point2D Double -> Double
distFromZero (Point2D x y) = sqrt (x^2 + y^2)

ghci> :t Point2D  -- remeber, constructors are just functions
Point2D :: a -> a -> Point2D a

data IntResult = Success Int 
               | Failure String

safeDiv :: Int -> Int -> IntResult
safeDiv _ 0 = Failure "division by zero"
safeDiv x y = Success $ x `div` y

ghci> showResult $ safeDiv 7 2
"Result: 3"
ghci> showResult $ safeDiv 7 0
"Error: division by zero"

showResult :: IntResult -> String
showResult (Success n) = "Result: " ++ show n
showResult (Failure e) = "Error:  " ++ e

ghci> :t Success 
Success :: Int -> IntResult
ghci> :t Failure 
Failure :: String -> IntResult

data Vector a = Vector2D a a | Vector3D a a a

packVector :: Vector a -> [a]
packVector (Vector2D x y)   = [x, y]
packVector (Vector3D x y z) = [x, y, z]

vecLen :: Vector Double -> Double
vecLen = sqrt . sum . map (^2) . packVector

ghci> maximum $ map vecLen [Vector3D 1.1 2.2 4.5, Vector2D 3 4]
5.12835256198

ghci> sortOn vecLen [Vector3D 1.1 2.2 4.5, Vector2D 3 4]
[Vector2D 3.0 4.0, Vector3D 1.1 2.2 4.5]

ghci> :t Vector2D
Vector2D :: a -> a -> Vector a
ghci> :t Vector3D
Vector3D :: a -> a -> a -> Vector a

data Maybe a = Nothing | Just a  -- implemented in Prelude

maybeSecond :: [a] -> Maybe a
maybeSecond (_:x:_) = Just x
maybeSecond _       = Nothing

ghci> :t Nothing
Nothing :: Maybe a
ghci> :t Just
Just :: a -> Maybe a

data Either a b = Left a | Right b  -- implemented in Prelude

eitherSecond :: [a] -> Either String a
eitherSecond []      = Left "list is empty"
eitherSecond [_]     = Left "list has only single element"
eitherSecond (_:x:_) = Right x

ghci> :t Left
Left :: a -> Either a b
ghci> :t Right
Right :: b -> Either a b

data List a = Nil | Cons a (List a)

myList :: List Int
myList = Cons 2 (Cons 1 (Cons 3 Nil))

myMap :: (a -> b) -> List a -> List b
myMap _        Nil  = Nil
myMap f (Cons x xs) = Cons (f x) (myMap f xs) 

ghci> myMap (`div` 2) myList
Cons 1 (Cons 0 (Cons 1 Nil))

data [] a = [] | a : [a]

ghci> :t Nil
Nil :: List a
ghci> :t Cons
Cons :: a -> List a -> List a

data User = User 
    { uid      :: Int
    , login    :: String
    , password :: String 
    }

data User = User Int String String

uid :: User -> Int
uid (User i _ _) = i

login :: User -> String
login (User _ l _) = l

password :: User -> String
password (User _ _ p) = p

ivan :: User
ivan = User { login    = "Ivan"
            , password = "123" 
            , uid      = 1
            }

isIvan :: User -> Bool
isIvan user = login user == "Ivan"

isIvan :: User -> Bool
isIvan User{ login = userName } = userName == "Ivan"

isIvan :: User -> Bool
isIvan User{ login = "Ivan" } = True
isIvan _                      = False

cloneIvan :: User
cloneIvan = ivan { uid = 2 }  -- User 2 "Ivan" "123"

ghci> data R = R { (-->) :: Int -> Int }
ghci> let r  = R { (-->) = (+1) }
ghci> r --> 8
9

data Person 
    = User  { uid :: Int, login :: String } 
    | Admin { aid :: Int, login :: String }

login :: Person -> String  -- after desugaring
login (User  _ l) = l
login (Admin _ l) = l

ghci> uid $ Admin 0 "Vasya" 
*** Exception: No match in record selector uid

isAdmin :: Person -> Bool  -- To match just the type of the construction
isAdmin Admin{} = True     -- works even without records
isAdmin _       = False

data Man = Man { name :: String }
data Cat = Cat { name :: String }

name :: ???

data Man = Man { manName :: String }
data Cat = Cat { catName :: String }

{-# LANGUAGE DuplicateRecordFields #-}

data Man = Man { name :: String }
data Cat = Cat { name :: String }

shoutOnHumanBeing :: Man -> String
shoutOnHumanBeing man = (name :: Man -> String) man ++ "!!1!"  -- though...

isGrumpy :: Cat -> Bool
isGrumpy Cat{ name = "Grumpy" } = True
isGrumpy _                      = False

{-# LANGUAGE RecordWildCards #-}

data User = User 
    { uid      :: Int
    , login    :: String
    , password :: String 
    } deriving (Show)

toUnsafeString :: User -> String
toUnsafeString User{ uid = 0, .. } = "ROOT: " ++ login ++ ", " ++ password
toUnsafeString User{..}            = login ++ ":" ++ password

createGuest :: String -> String -> User
createGuest (read -> uid) password = User{ login = "guest", .. }

evilMagic :: Man -> Cat
evilMagic Man{..} = Cat{..}

ghci> evilMagic $ Man "Grumpy"
Cat {name = "Grumpy"}

data    Message = Message String

newtype Message = Message String

-- public key from secret key
derivePublicKey :: String -> String

checkKeyPair :: (String, String) -> Bool
checkKeyPair (secretKey, publicKey) 
    = publicKey == derivePublicKey secretKey

derivePublicKey :: SecretKey -> PublicKey

checkKeyPair :: (SecretKey, PublicKey) -> Bool
checkKeyPair (secretKey, publicKey) = publicKey == derivePublicKey secretKey

newtype PublicKey = PublicKey String
newtype SecretKey = SecretKey String

class Printable p where  -- we don't care what 'p' stores internally
    printMe :: p -> String

helloP :: Printable p => p -> String
helloP p = "Hello, " ++ printMe p ++ "!"

data Foo = Foo | Bar  -- don't care what we can do with 'Foo', care what it stores

instance Printable Foo where
    printMe Foo = "Foo"
    printMe Bar = "Bar (whatever)"

ghci> helloP Bar
"Hello, Bar (whatever)!"
ghci> helloP True
    • No instance for (Printable Bool) arising from a use of ‘helloP’
    • In the expression: helloP True

class Eq a where  
    (==) :: a -> a -> Bool  
    (/=) :: a -> a -> Bool
 
    x == y = not (x /= y)  
    x /= y = not (x == y)
    {-# MINIMAL (==) | (/=) #-}  -- minimal complete definition

{-# LANGUAGE InstanceSigs #-}

data TrafficLight = Red | Yellow | Green

instance Eq TrafficLight where
    (==) :: TrafficLight -> TrafficLight -> Bool
    Red    == Red    = True  
    Green  == Green  = True  
    Yellow == Yellow = True 
         _ == _      = False

threeSame :: Eq a => a -> a -> a -> Bool
threeSame x y z = x == y && y == z

ghci> threeSame Red Red Red
True
ghci> threeSame 'a' 'b' 'b'
False

-- simplified version of Ord class
class Eq a => Ord a where
   compare              :: a -> a -> Ordering
   (<), (<=), (>=), (>) :: a -> a -> Bool

   compare x y
        | x == y    =  EQ
        | x <= y    =  LT
        | otherwise =  GT

   x <= y           =  compare x y /= GT
   x <  y           =  compare x y == LT
   x >= y           =  compare x y /= LT
   x >  y           =  compare x y == GT

data Ordering = LT | EQ | GT

-- | Basic numeric class.
class Num a where
    {-# MINIMAL (+), (*), abs, signum, fromInteger, (negate | (-)) #-}

    (+), (-), (*)       :: a -> a -> a  -- self-explained
    negate              :: a -> a       -- unary negation
    abs                 :: a -> a       -- absolute value
    signum              :: a -> a       -- sign of number, abs x * signum x == x
    fromInteger         :: Integer -> a -- used for numeral literals polymorphism

    x - y               = x + negate y
    negate x            = 0 - x

ghci> :t 5
5 :: Num p => p
ghci> :t fromInteger 5
fromInteger 5 :: Num a => a
ghci> 5 :: Int
5
ghci> 5 :: Double
5.0

-- simplified version; used for converting things into String
class Show a where
    show :: a -> String

ghci> 5
5
ghci> show 5
"5"
ghci> "5"
"5"
ghci> show "5"
""5""

ghci> 5 :: Int
5
ghci> 5 :: Double
5.0
ghci> 5 :: Rational
5 % 1

-- simplified version; used for parsing thigs from String
class Read a where
    read :: String -> a

ghci> :t read
read :: Read a => String -> a
ghci> read "True"
*** Exception: Prelude.read: no parse
ghci> read "True" :: Bool
True

ghci> :module Text.Read  -- safe read functions are not in Prelude, unfortunately

ghci> :t readMaybe
readMaybe :: Read a => String -> Maybe a
ghci> :t readEither 
readEither :: Read a => String -> Either String a
ghci> readMaybe "5" :: Maybe Int
Just 5
ghci> readMaybe "5" :: Maybe Bool
Nothing
ghci> readEither "5" :: Either String Bool -- don't worry, convenient way exist
Left "Prelude.read: no parse"

subtract :: Num a => a -> a -> a
subtract x y = y - x

cmpSum x y = if x < y then x + y else x * y

average :: Fractional a => a -> a -> a
average x y = (x + y) / 2

ghci> :info Fractional
class Num a => Fractional a where
  (/) :: a -> a -> a
  recip :: a -> a
  fromRational :: Rational -> a
  {-# MINIMAL fromRational, (recip | (/)) #-}
  	-- Defined in ‘GHC.Real’
instance Fractional Float -- Defined in ‘GHC.Float’
instance Fractional Double -- Defined in ‘GHC.Float’

ghci> cmpSum x y = if x < y then x + y else x * y
ghci> :t cmpSum
cmpSum :: (Ord a, Num a) => a -> a -> a

foo :: (Ord a, Read a, Show b) => String -> a -> b -> b -> String
foo = undefined -- too difficult to implement

foo :: (Ord a, Read a, Show b) => String -> a -> b -> b -> String
foo = error "Function `foo` crashes your code, don't call it!" 

ghci> :t undefined
undefined :: a
ghci> undefined
*** Exception: Prelude.undefined
CallStack (from HasCallStack):
  error, called at libraries/base/GHC/Err.hs:79:14 in base:GHC.Err
  undefined, called at <interactive>:44:1 in interactive:Ghci27

ghci> :t error
error :: [Char] -> a
ghci> error "Some meaningful message"
*** Exception: Some meaningful message
CallStack (from HasCallStack):
  error, called at <interactive>:46:1 in interactive:Ghci27

data TrafficLight = Red | Yellow | Green | Blue
    deriving Eq  -- autoderiving instances

data TrafficLight = Red | Yellow | Green | Blue
    deriving (Eq, Ord, Enum, Bounded, Show, Read, Ix)

ghci> :t maxBound 
maxBound :: Bounded a => a
ghci> maxBound :: TrafficLight  -- Bounded also has 'minBound'
Blue
ghci> [Yello .. maxBound]  -- .. is from Enum instance
[Yellow, Green, Blue] 

ghci> show Blue
"Blue"
ghci> read "Blue" :: TrafficLight 
Blue

ghci> Red == Yellow  -- (==) is from Eq  class
False
ghci> Red < Yellow   -- (<)  is from Ord class
True

ghci> :t fromEnum 
fromEnum :: Enum a => a -> Int
ghci> :t toEnum 
toEnum :: Enum a => Int -> a
ghci> fromEnum Green
2
ghci> toEnum 2 :: TrafficLight 
Green

module Foo where

data Box a = Box a a deriving (Eq, Show)

==================== Derived instances ====================
Derived instances:
  instance GHC.Classes.Eq a_a1R6 =>
           GHC.Classes.Eq (Foo.Box a_a1R6) where
    (GHC.Classes.==)
      (Foo.Box a1_a1R8 a2_a1R9)
      (Foo.Box b1_a1Ra b2_a1Rb)
      = (((a1_a1R8 GHC.Classes.== b1_a1Ra))
         GHC.Classes.&& ((a2_a1R9 GHC.Classes.== b2_a1Rb)))
    (GHC.Classes./=) a_a1Rc b_a1Rd
      = GHC.Classes.not ((GHC.Classes.==) a_a1Rc b_a1Rd)
  
  instance GHC.Show.Show a_a1R7 =>
           GHC.Show.Show (Foo.Box a_a1R7) where
    GHC.Show.showsPrec a_a1Re (Foo.Box b1_a1Rf b2_a1Rg)
      = GHC.Show.showParen
          (a_a1Re GHC.Classes.>= 11)
          ((GHC.Base..)
             (GHC.Show.showString "Box ")
             ((GHC.Base..)
                (GHC.Show.showsPrec 11 b1_a1Rf)
                ((GHC.Base..) GHC.Show.showSpace (GHC.Show.showsPrec 11 b2_a1Rg))))
    GHC.Show.showList = GHC.Show.showList__ (GHC.Show.showsPrec 0)

$ ghc -ddump-deriv Foo.hs

newtype Size = Size Int
    deriving (Show, Read, Eq, Ord, Num)

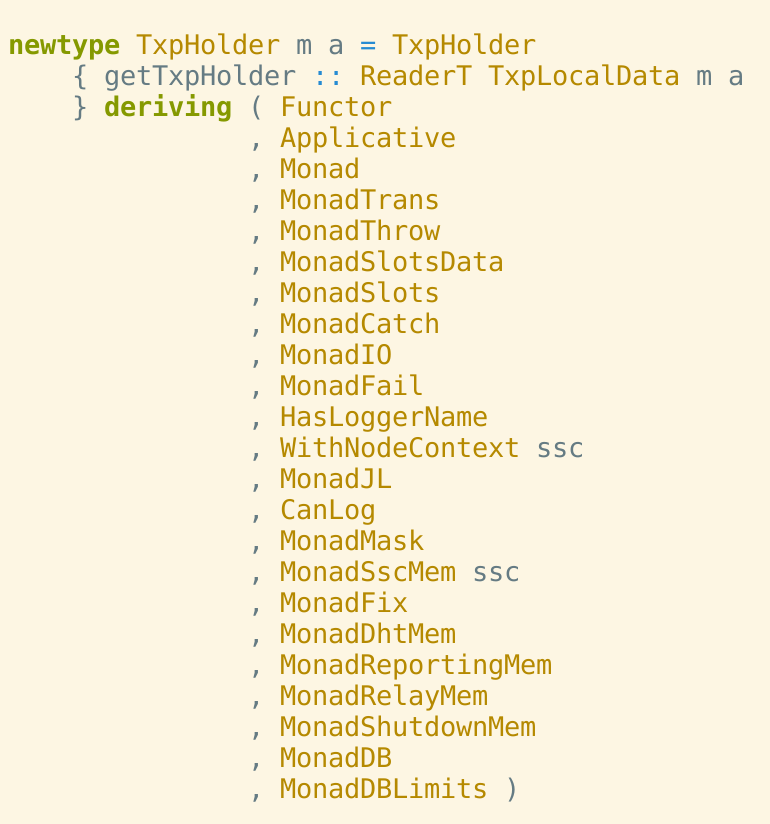
{-# LANGUAGE GeneralizedNewtypeDeriving #-}

data Doctor who = Tardis who who | Dalek Int

timeTravel :: a -> a -> String
timeTravel _ _ = "Travel through time and space!"

exterminate :: Int -> String
exterminate n = unwords $ replicate n "Exterminate!"

travel :: Doctor who -> String
travel (Tardis a b) = timeTravel a b
travel (Dalek x)    = exterminate x

ghci> travel (Tardis 0 0)
"Travel through time and space!"
ghci> travel (Dalek 3)
"Exterminate! Exterminate! Exterminate!"

data Doctor who = Tardis who who 
                | Dalek Int

ghci> :t Tardis 
Tardis :: who -> who -> Doctor who
ghci> :t Dalek 
Dalek :: Int -> Doctor who

f_Tardis :: who -> who -> (who -> who -> r) -> (Int -> r) -> r
f_Tardis a b = \tardis _dalek -> tardis a b

f_Dalek :: Int -> (who -> who -> r) -> (Int -> r) -> r
f_Dalek x = \_tardis dalek -> dalek x

f_travel :: ((who -> who -> String) -> (Int -> String) -> String) -> String
f_travel pattern = pattern timeTravel exterminate

ghci> f_travel (f_Tardis 0 0)
"Travel through time and space!"

ghci> f_travel (f_Dalek 3)
"Exterminate! Exterminate! Exterminate!"

type Doctor_f who r = (who -> who -> r) -> (Int -> r) -> r

f_Tardis :: who -> who -> Doctor_f who r
f_Tardis a b = \tardis _dalek -> tardis a b

f_Dalek :: Int -> Doctor_f who r
f_Dalek x = \_tardis dalek -> dalek x

f_travel :: Doctor_f who String -> String
f_travel pattern = pattern timeTravel exterminate

class Eq a where  
    (==) :: a -> a -> Bool  
    (/=) :: a -> a -> Bool
    x == y = not (x /= y)  
    x /= y = not (x == y)

data EqC a = EqDict
    { eq  :: a -> a -> Bool
    , neq :: a -> a -> Bool
    }

isInList :: EqC a -> a -> [a] -> Bool
isInList eqc x = any (eq eqc x)

ghci> isInList (instanceEqCWithEq (==)) 3 [2, 1, 3]
True

coerce :: Coercible a b => a -> b

ghci> newtype Size = Size { getSize :: Int } deriving (Show)
ghci> [Size 2, Size 1, Size 3]
[ Size { getSize = 2 }
, Size { getSize = 1 }
, Size { getSize = 3 }
] 

ghci> map getSize [Size 2, Size 1, Size 3]  -- O(n) time
[2, 1, 3]

ghci> :t coerce [Size 2, Size 1, Size 3]
coerce [Size 2, Size 1, Size 3] :: Coercible b [Size] => b
ghci> (coerce :: [Size] -> [Int]) [Size 2, Size 1, Size 3]  -- O(1) time
[2, 1, 3]