Network

Models

Minimal Spanning Tree

Spanning Tree:

A subgraph T of a undirected graph G = (V,E) is a spanning tree of G if it is a tree and contains every vertex of G. 

MST:

 Given a connected graph, find a spanning tree of minimum weight 

Minimal Spanning Tree

The idea is to start with an empty graph and try to add edges one at a time, always making sure that what is built remains acyclic.

And if we are sure every time the resulting graph always is a subset of some minimum spanning tree, we are done. 

MST: Algorithms

Greedy

Prim

Kruskal

MST: Prim

Start by picking any vertex to be the root of the tree.

While the tree does not contain all vertices in the graph find shortest edge leaving the tree and add it to the tree .

MST: Prim

Step 0: Choose any element  r; set S = {r} and S = .   .Take r as the root of our spanning tree.)

Step 1: Find a lightest edge such that one endpoint is in S and the other is in  V \ S . Add this edge to A and its (other) endpoint to S.

Step 2: If V \ S =    , then stop & output (minimum) spanning tree (S, A), otherwise go to Step 1

MST: Kruskal

• Let G = (V, E) be the given graph, with | V| = n
   

•  Start with a graph T = (V,) consisting of only the vertices of G and no edges. This can be viewed as n connected components, each vertex being one connected component. 
   

• Arrange E in the order of increasing costs
   

• for (i = 1, in - 1, i + +)
   

          { Select the next smallest cost edge;

          if (the edge connects two different connected components)

          add the edge to T;

          }

MST: Example

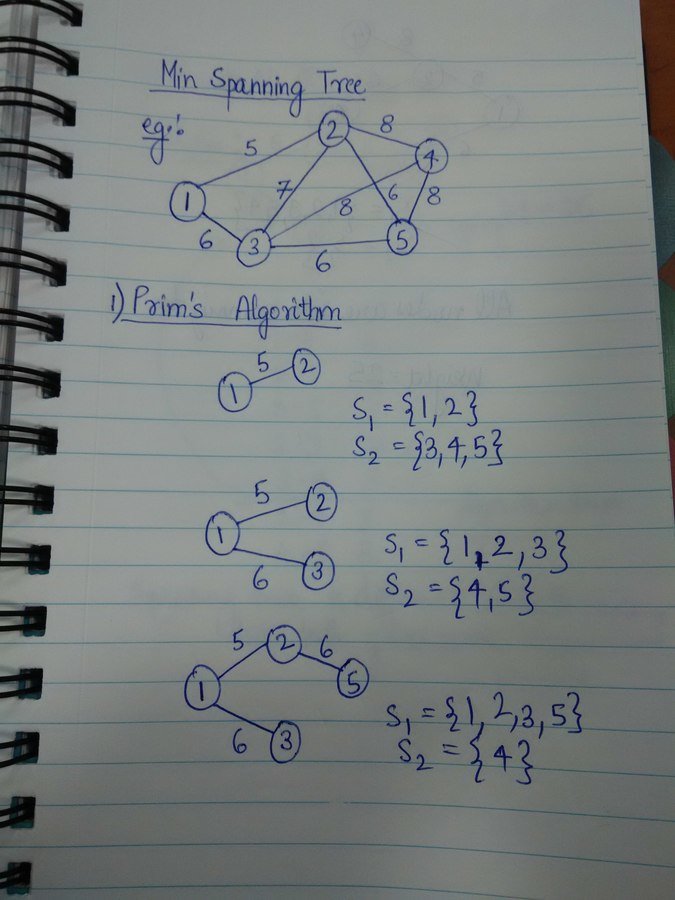
MST: Example

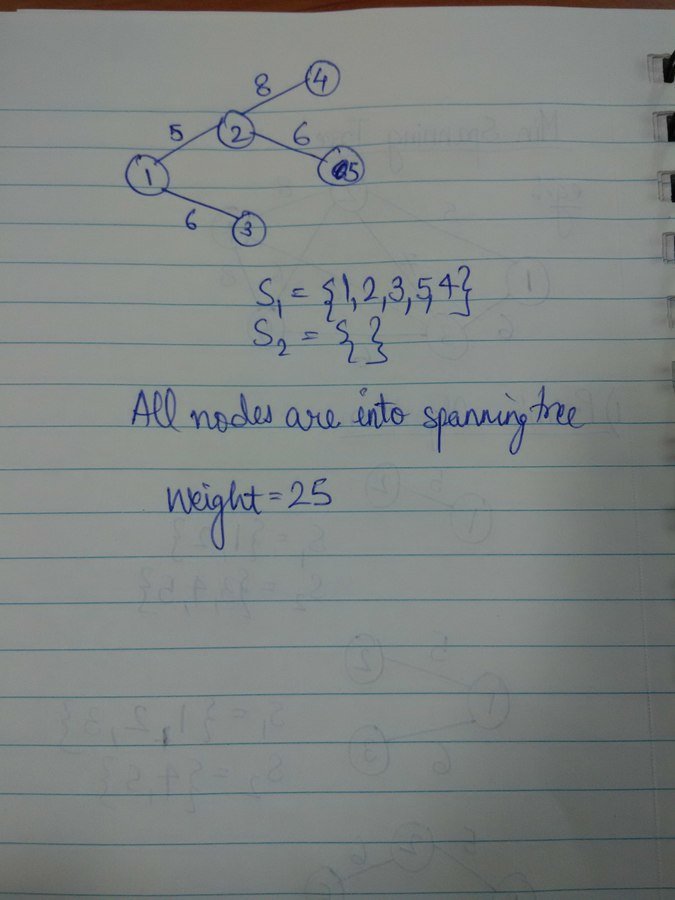
MST: Example

Maximal Flow Technique

Nodes

Arcs

Source

Sink

Capacity

Flow

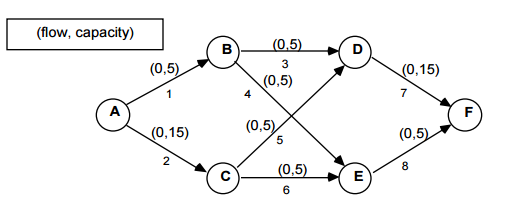
Maximum Flow Problem

 Find the maximum flow that can be sent through the arcs of the network from some specified node  called the source, to a second specified node called the sink

Exhaustion of Paths Algorithm

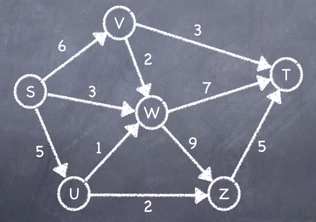
Step 1: Choose one possible route between S & T and identify the edge with the smallest capacity

Exhaustion of Paths Algorithm

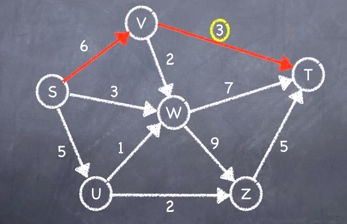
Record the smallest capacity.

Subtract this number from each capacity value on that path.

Exhaustion of Paths Algorithm

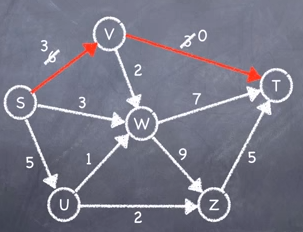
This is the updated capacity for each arc.

Exhaustion of Paths Algorithm

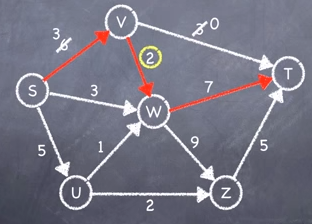
Step 2: Choose another route and repeat step 1, recording the smallest capacity again.

Exhaustion of Paths Algorithm

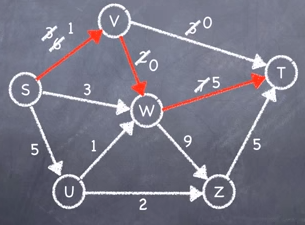
Subtracting and updating

Exhaustion of Paths Algorithm

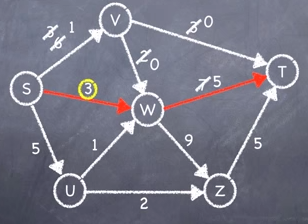
Step 3: Choose another route and repeat step 1 until all routes have been exhausted.

Exhaustion of Paths Algorithm

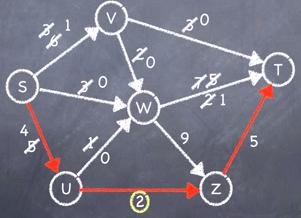
Exhaustion of Paths Algorithm

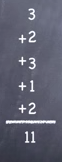
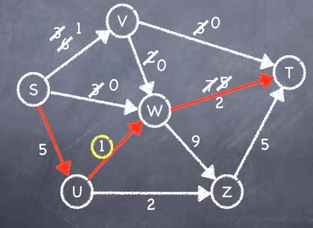
Step 4: Add all the capacities that were recorded in each step.

11 is the maximum flow of the network between S & T.

Labelling Algorithm

Node label:

( Pf , ± i) : {Pf = Potential ± flow at node i

                    {i= node

Arc label:

 ( f ,CAP) : {f = Actual flow through arc.                           {CAP=Capacity through arc

Labelling Algorithm

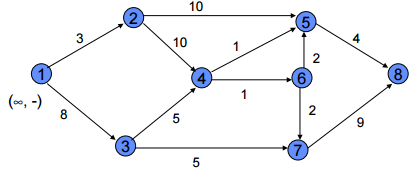
Labelling Algorithm

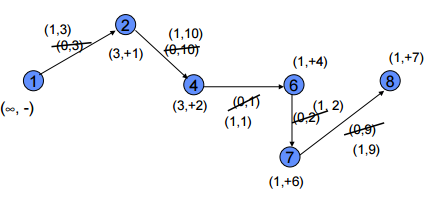
Labelling Algorithm

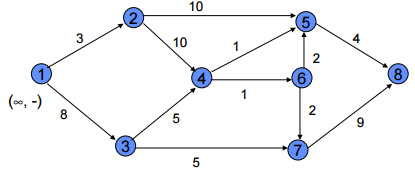
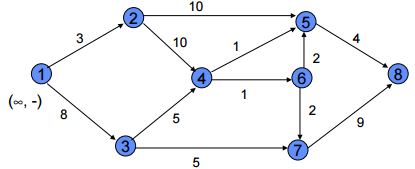
Labelling Algorithm

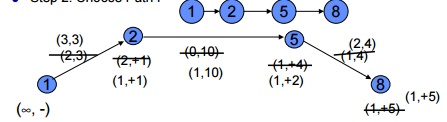
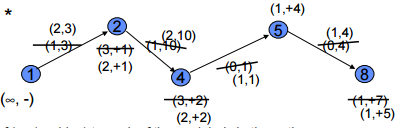
Labelling Algorithm

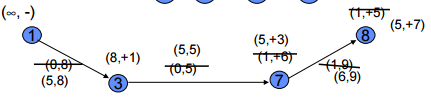
Labelling Algorithm

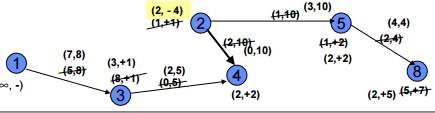
Labelling Algorithm

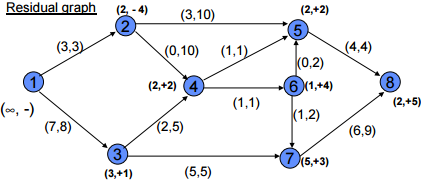
Problem Question

Max Flow-Min Cut

s-t Cut: is defined w.r.t. two distinguished nodes s and t and is a cut [S, Š] satisfying the property that s ∈ S and t ∈ Š.

A cut is a set of arcs which when deleted from the network, disconnects the source completely from the sink

Max Flow-Min Cut

Capacity of a cut

Min Cut

Theorem: The maximum value of the flow from a source node s to a sink node t in a capacitated network equals the minimum capacity among all the s-t cuts.

Operations Management Applications

Product Distribution System

Supply Chain Management

Maximum flow of orders through a job shop

References

https://www.youtube.com/watch?v=sxyCzzUuXLo

https://www.cse.ust.hk/~dekai/271/notes/L07/L07.pdf

http://www.cs.princeton.edu/courses/archive/spr04/cos226/lectures/maxflow.4up.pdf

http://www.me.utexas.edu/~jensen/methods/net.pdf/netmaxf.pdf

http://www.acsu.buffalo.edu/~nagi/courses/684/6.maxflow.pdf

Thank you!

Kamal

Karan

Natasha

Shreya

Tarun