a differentiable physics engine for robotics
Taylor Howell and Simon Le Cleac'h
Taylor Howell
Simon Le Cleac'h
team
thowell@stanford.edu
simonlc@stanford.edu
Taylor Howell
Simon Le Cleac'h
Jan Brüdigam
Zico Kolter
Mac Schwager
Zachary Manchester
team
existing physics engines
contact physics
existing physics engines
contact physics
LCP
existing physics engines
contact physics
LCP
implicit complementarity
existing physics engines
contact physics
LCP
implicit complementarity
gradients
existing physics engines
contact physics
LCP
implicit complementarity
gradients
samples
existing physics engines
contact physics
LCP
implicit complementarity
gradients
samples
subgradient
existing physics engines
Dojo key ideas
variational integrator
interior-point methods
implicit differentiation
Dojo key ideas
stability at low rates
variational integrator
interior-point methods
implicit differentiation
Dojo key ideas
stability at low rates
variational integrator
interior-point methods
accurate contact dynamics
implicit differentiation
Dojo key ideas
stability at low rates
variational integrator
interior-point methods
accurate contact dynamics
implicit differentiation
smooth gradients
variational integrator
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S=∫t1t2Ldt
S = \int_{t_1}^{t_2}{\mathcal{L} dt}
variational integrator
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S=∫t1t2Ldt
S = \int_{t_1}^{t_2}{\mathcal{L} dt}
Euler-Lagrange
F=ma
F = m a
variational integrator
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S=∫t1t2Ldt
S = \int_{t_1}^{t_2}{\mathcal{L} dt}
discretize
Euler-Lagrange
F=ma
F = m a
p+=p+h(v+mg)
p_+ = p + h (v + mg)
variational integrator
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S=∫t1t2Ldt
S = \int_{t_1}^{t_2}{\mathcal{L} dt}
SD=h∑i=1NLi
S_D = h \sum_{i=1}^{N} \mathcal{L}_i
discretize
discretize
Euler-Lagrange
F=ma
F = m a
p+=p+h(v+mg)
p_+ = p + h (v + mg)
variational integrator
m(p+−2p+p−)/h−hmg=0
m(p_+ -2p +p_-)/h - hmg = 0
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S=∫t1t2Ldt
S = \int_{t_1}^{t_2}{\mathcal{L} dt}
discretize
discretize
Euler-Lagrange
Euler-Lagrange
F=ma
F = m a
p+=p+h(v+mg)
p_+ = p + h (v + mg)
SD=h∑i=1NLi
S_D = h \sum_{i=1}^{N} \mathcal{L}_i
variational integrator
-
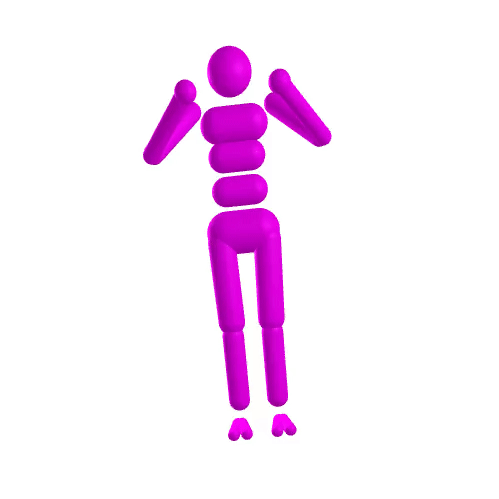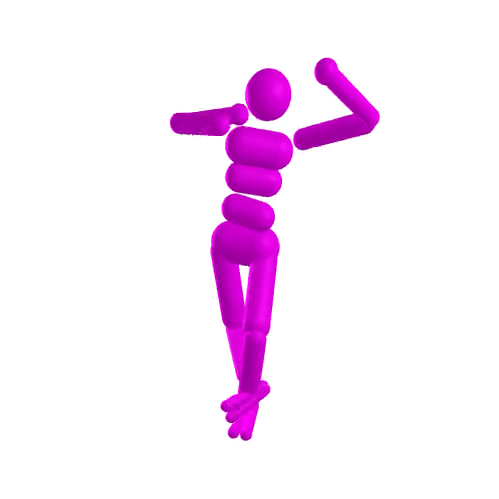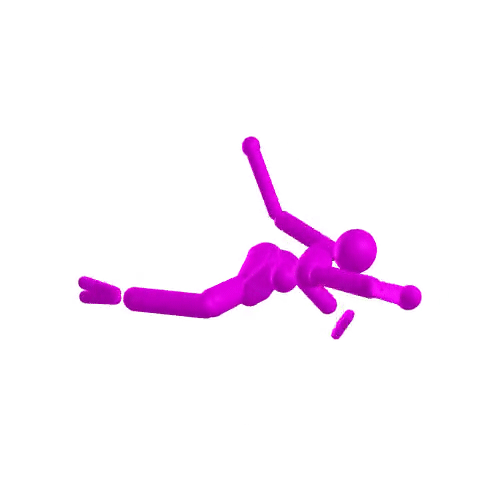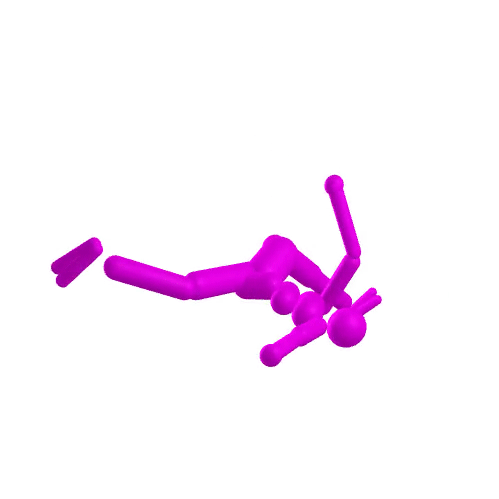
compare astronaut energy and momentum conservation to MuJoCo
variational integrator
-
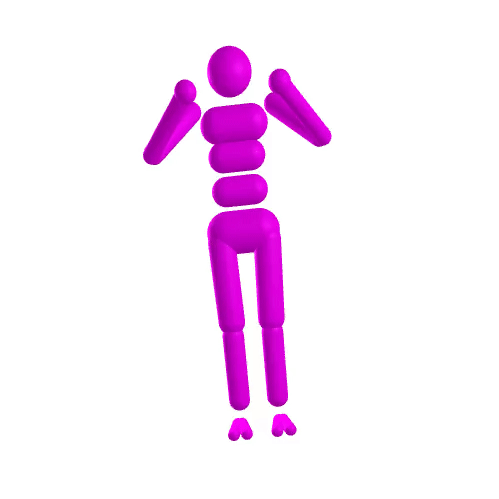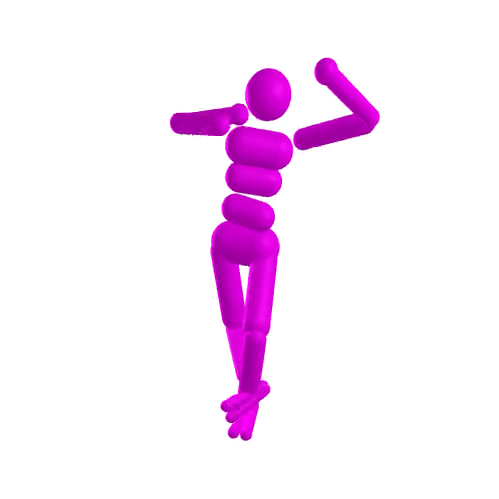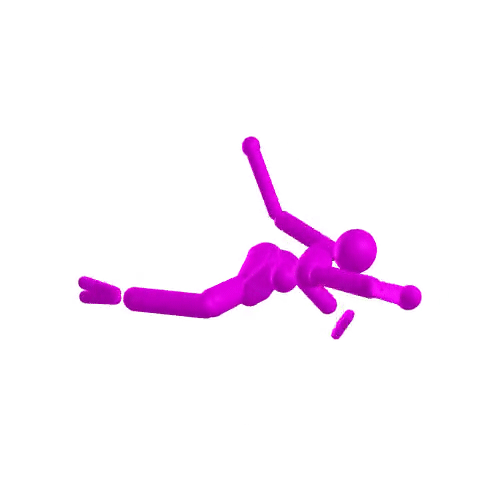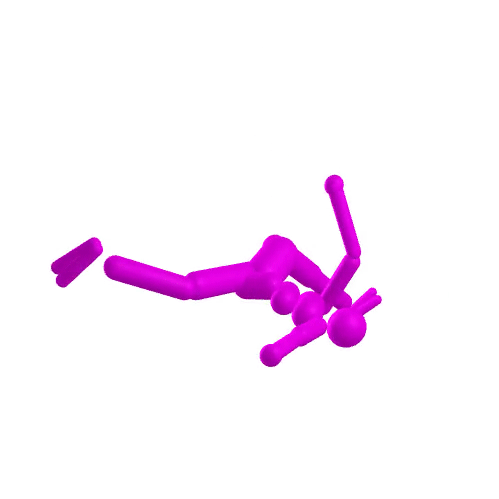
compare astronaut energy and momentum conservation to MuJoCo
- Dojo performs orders of magnitude better
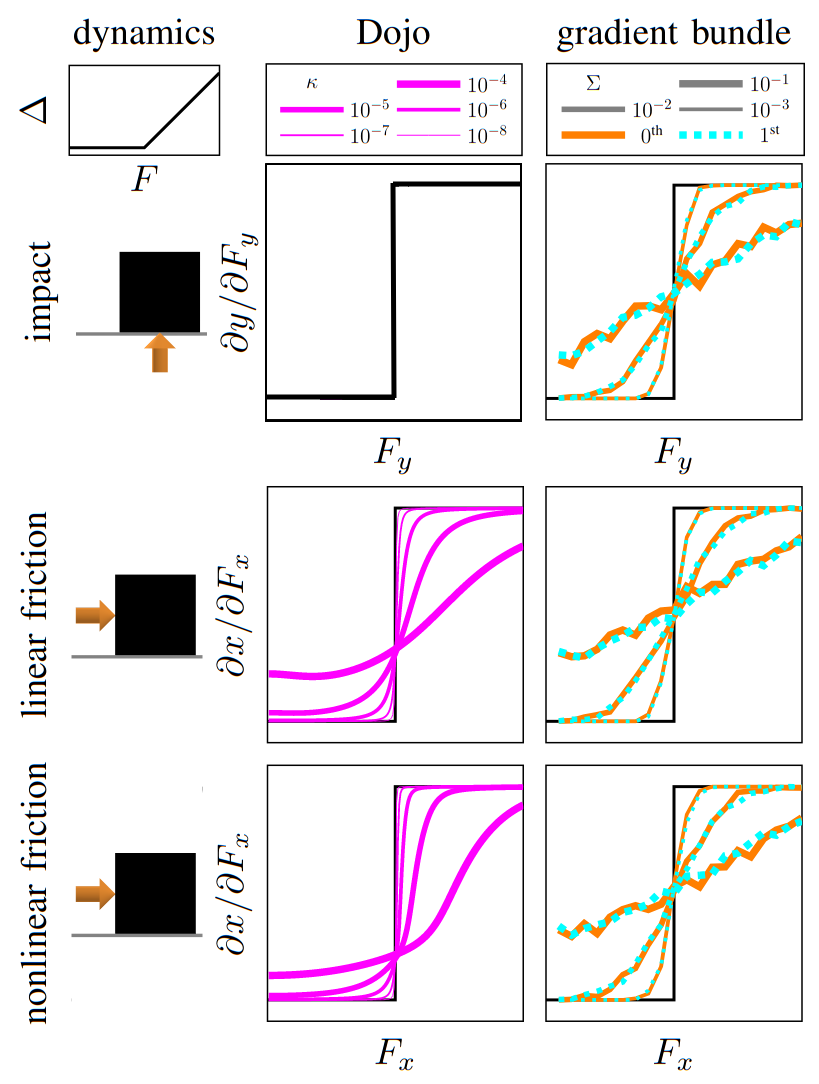
accurate contact dynamics
no collision violations
accurate contact dynamics
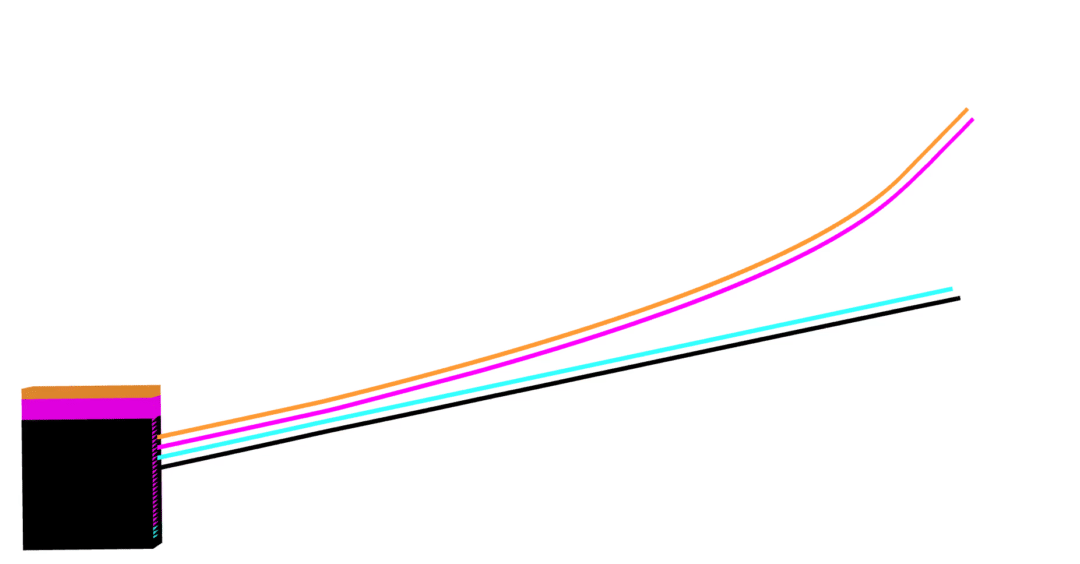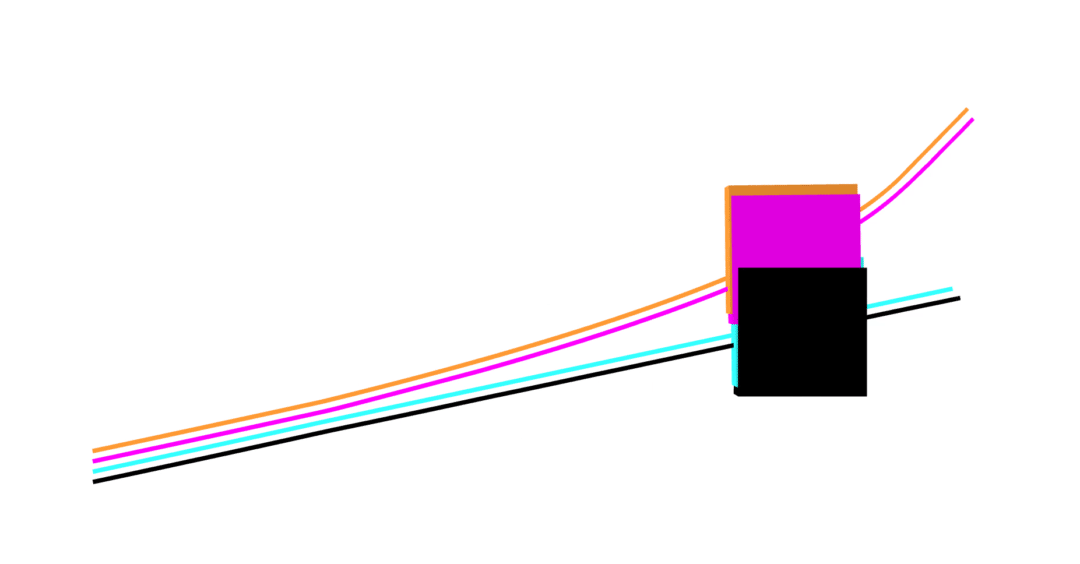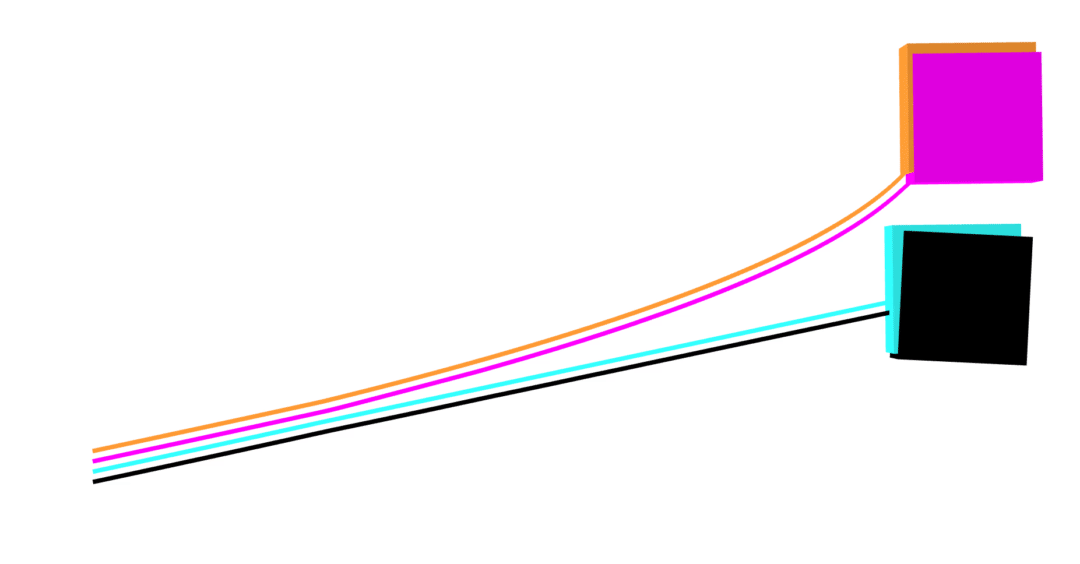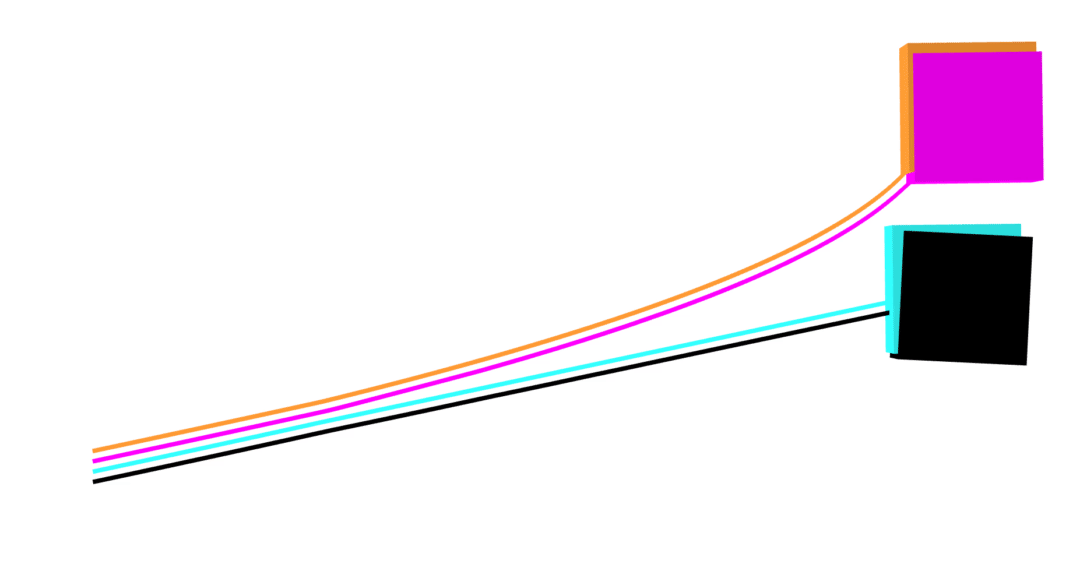
MuJoCo linear
Dojo linear
MuJoCo nonlinear
Dojo nonlinear
no collision violations
correct Coulomb friction
accurate contact dynamics
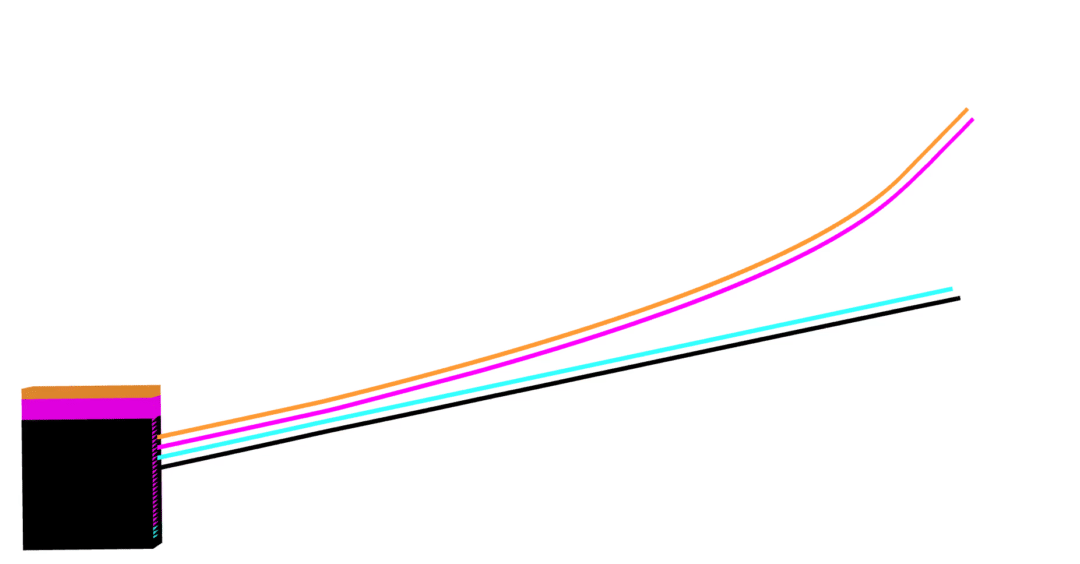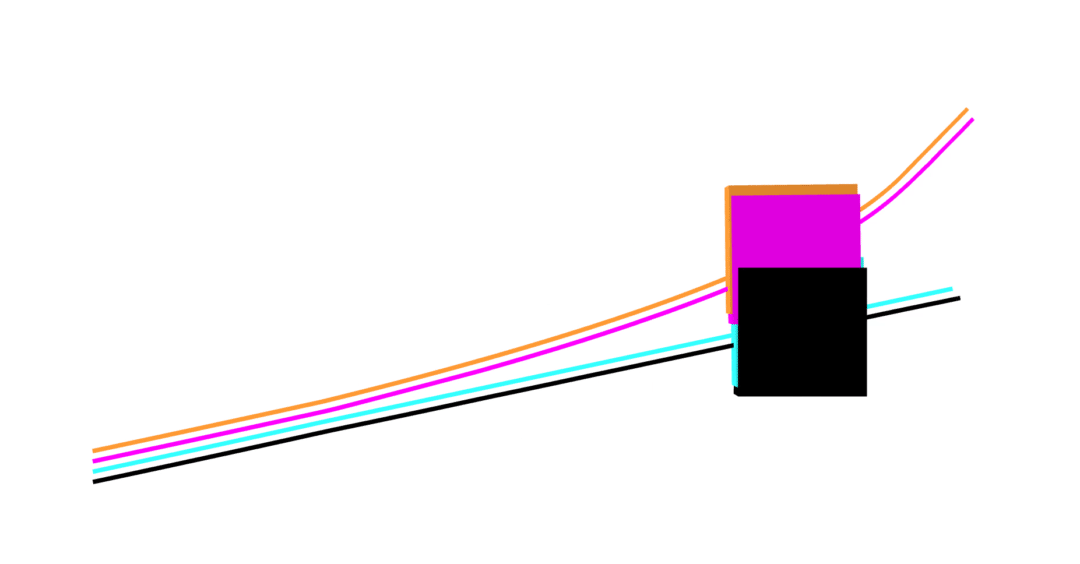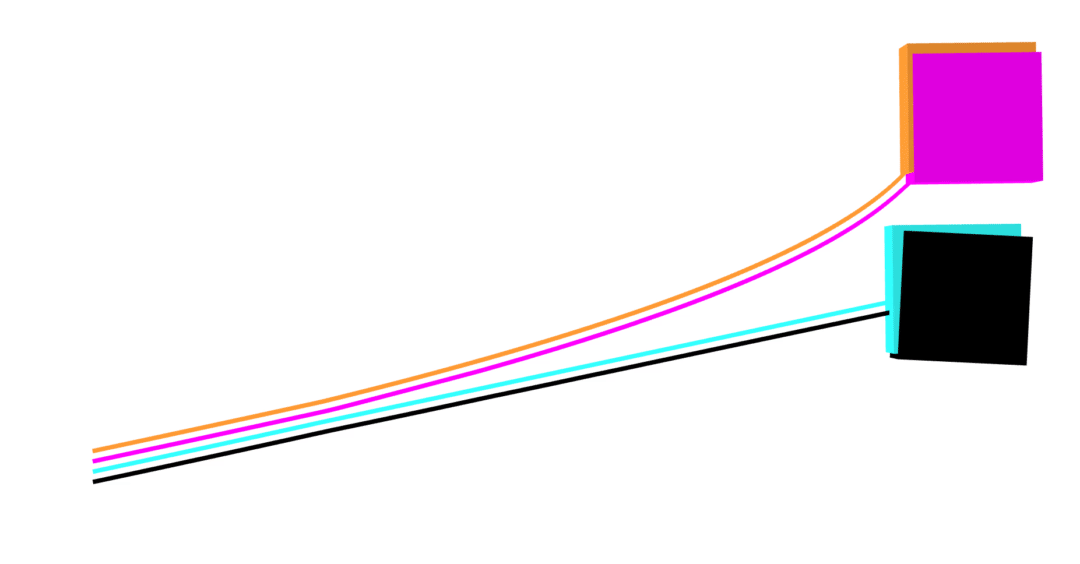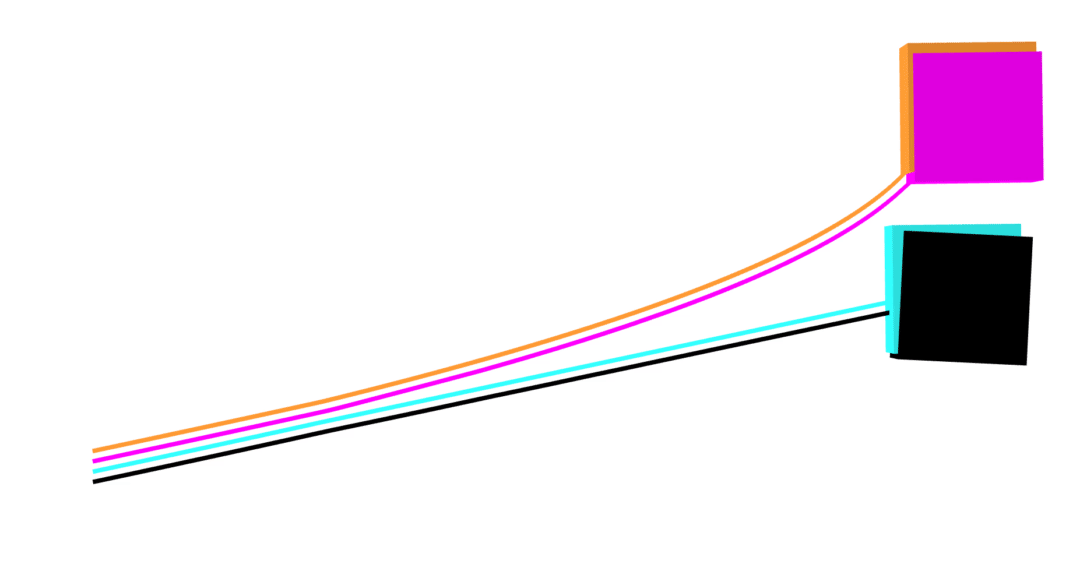
MuJoCo linear
Dojo linear
MuJoCo nonlinear
Dojo nonlinear
no collision violations
correct Coulomb friction
interior-point method
impact → inequalities
friction → second-order cone
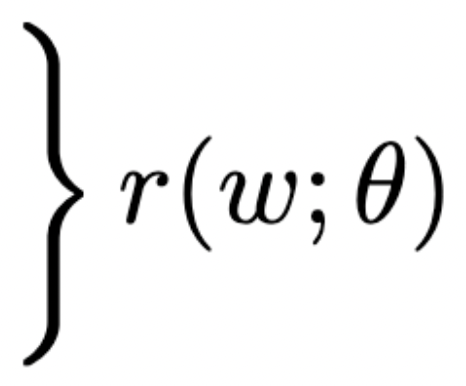
cone constraints
accurate contact dynamics
nonlinear complementarity problem
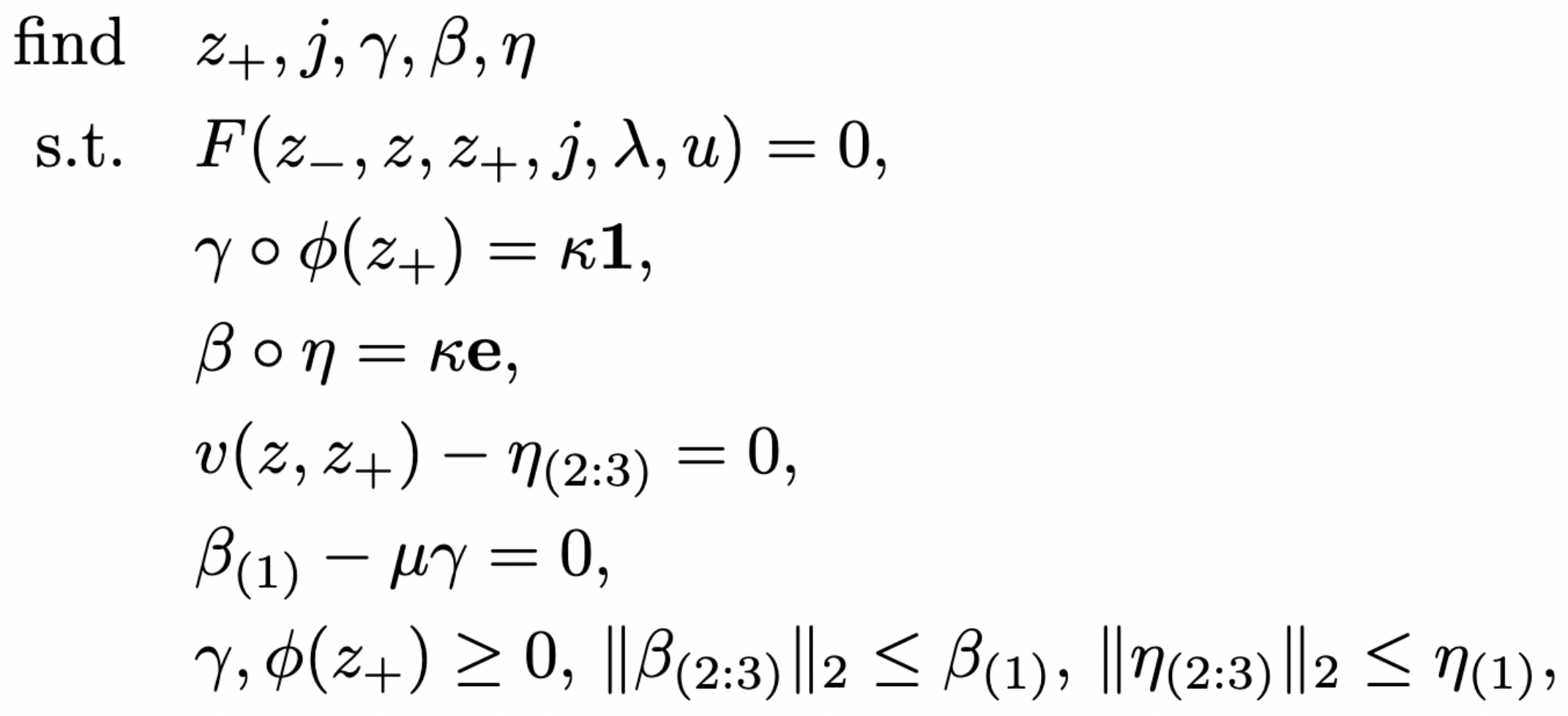
accurate contact dynamics
custom interior-point solver
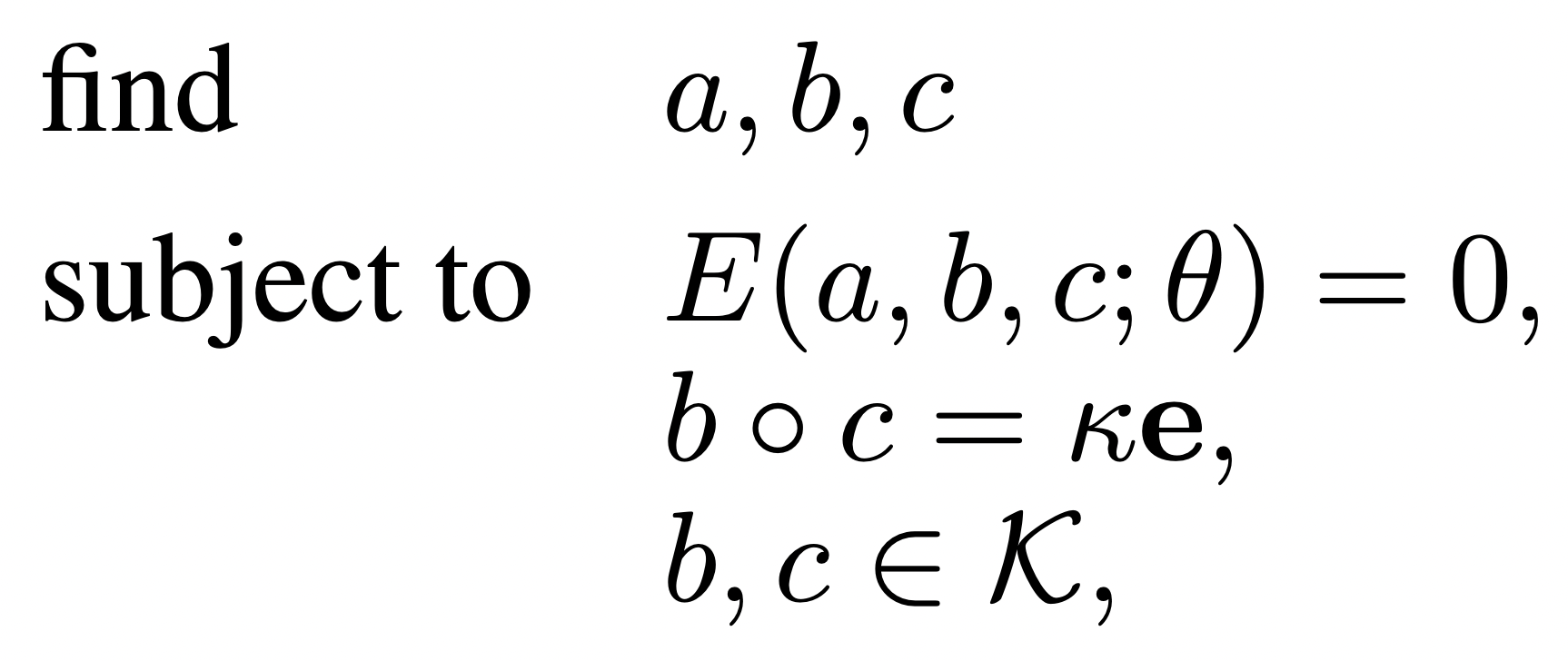
- Mehrotra predictor-corrector algorithm
- CVXOpt second-order cones
- non-Euclidean support for quaternions
smooth gradients
Lezioni di analisi infinitesimale. U. Dini.
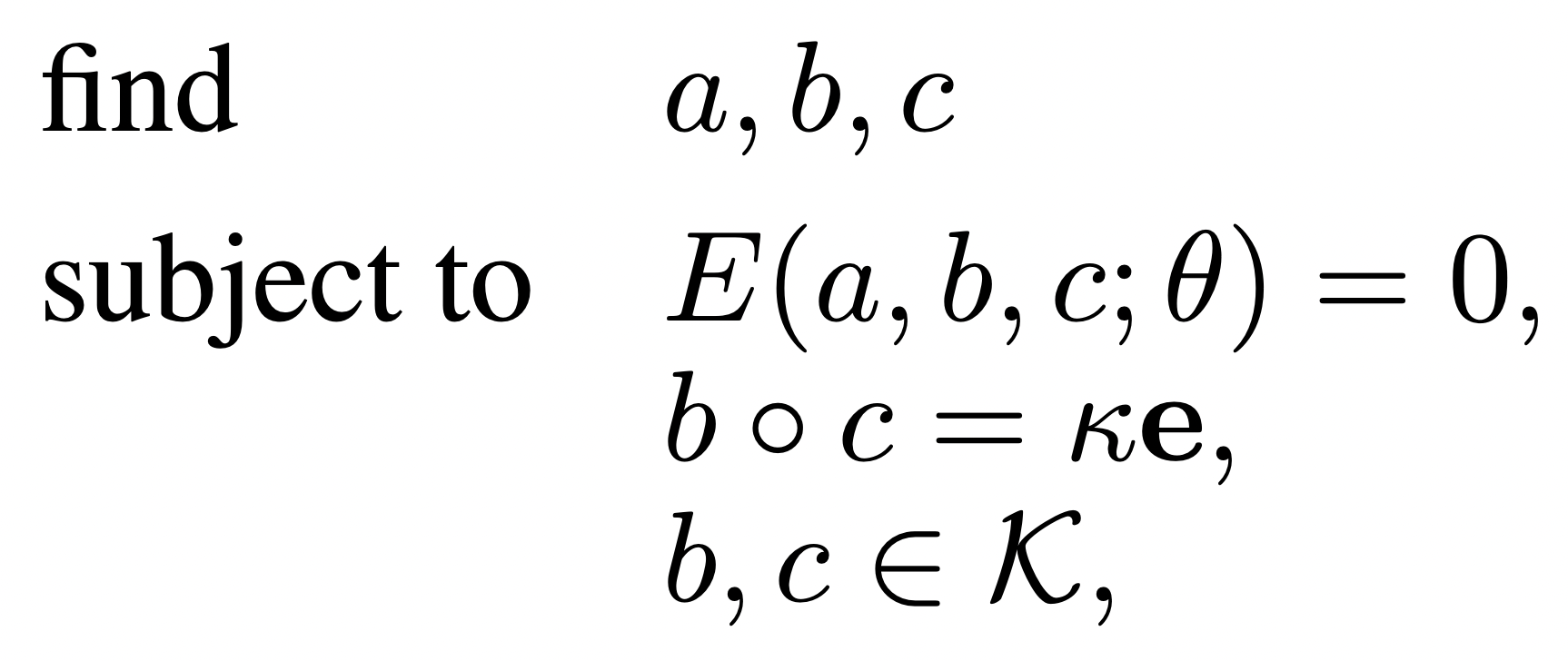
smooth gradients
implicit-function theorem
Lezioni di analisi infinitesimale. U. Dini.
r(w∗;θ)=0
r(w^*; \theta) = 0
→
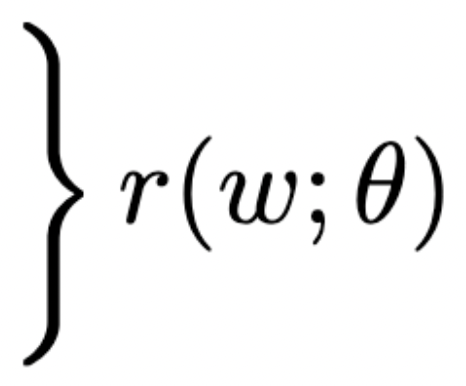
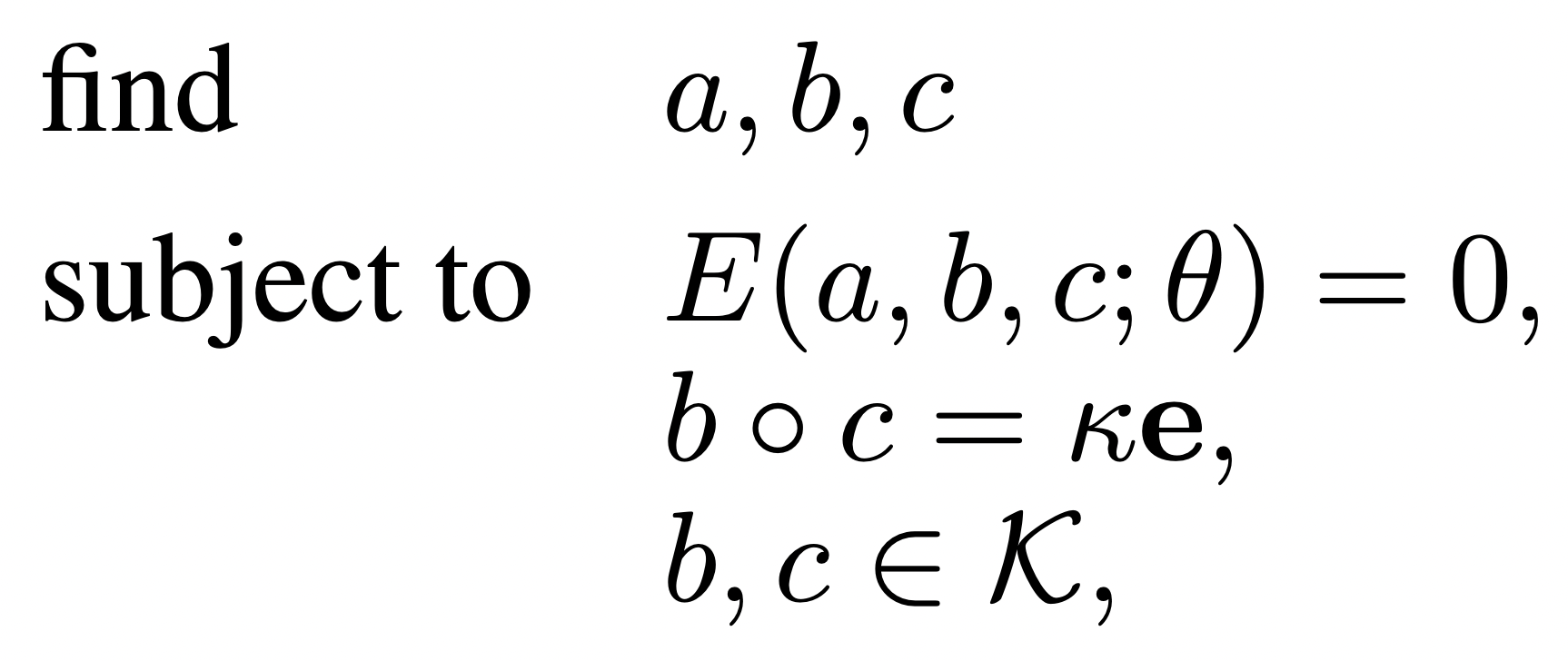
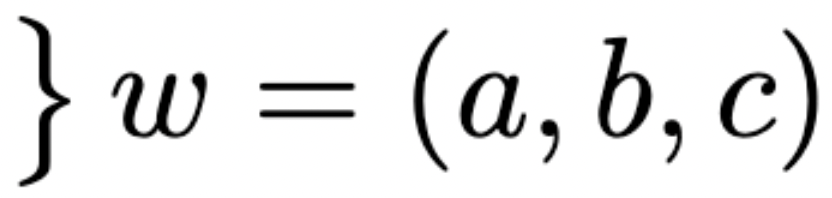
smooth gradients
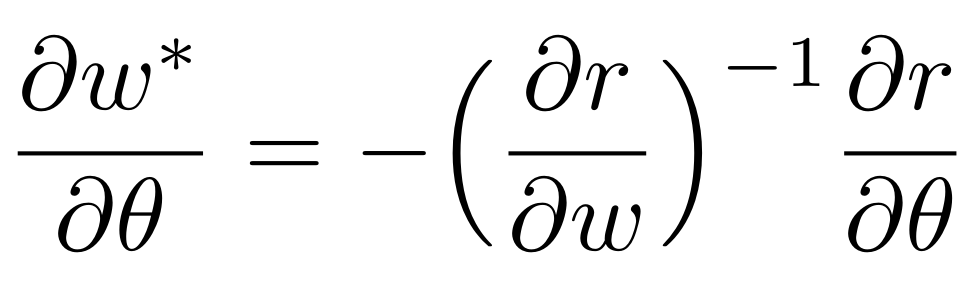
sensitivity of solution w.r.t problem data
gradients
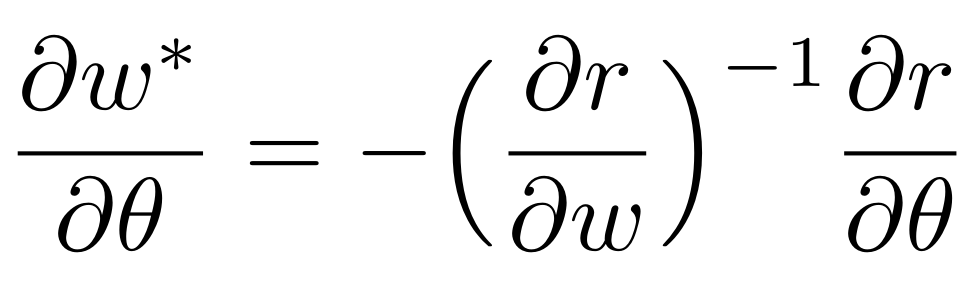
sensitivity of solution w.r.t problem data
computation cost of gradient is less than simulation step
gradients
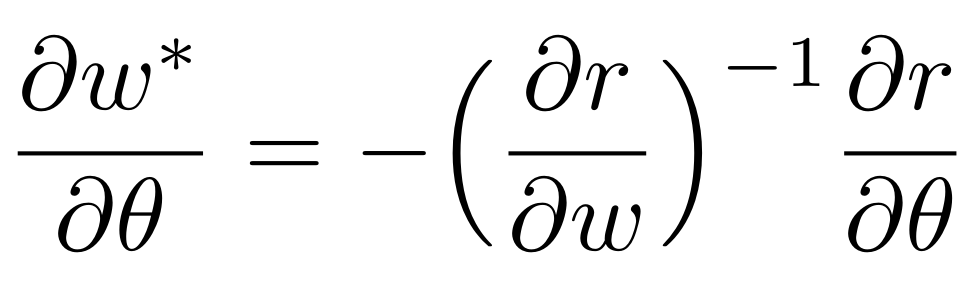
sensitivity of solution w.r.t problem data
computation cost of gradient is less than simulation step
differentiate intermediate barrier problems for smooth gradients
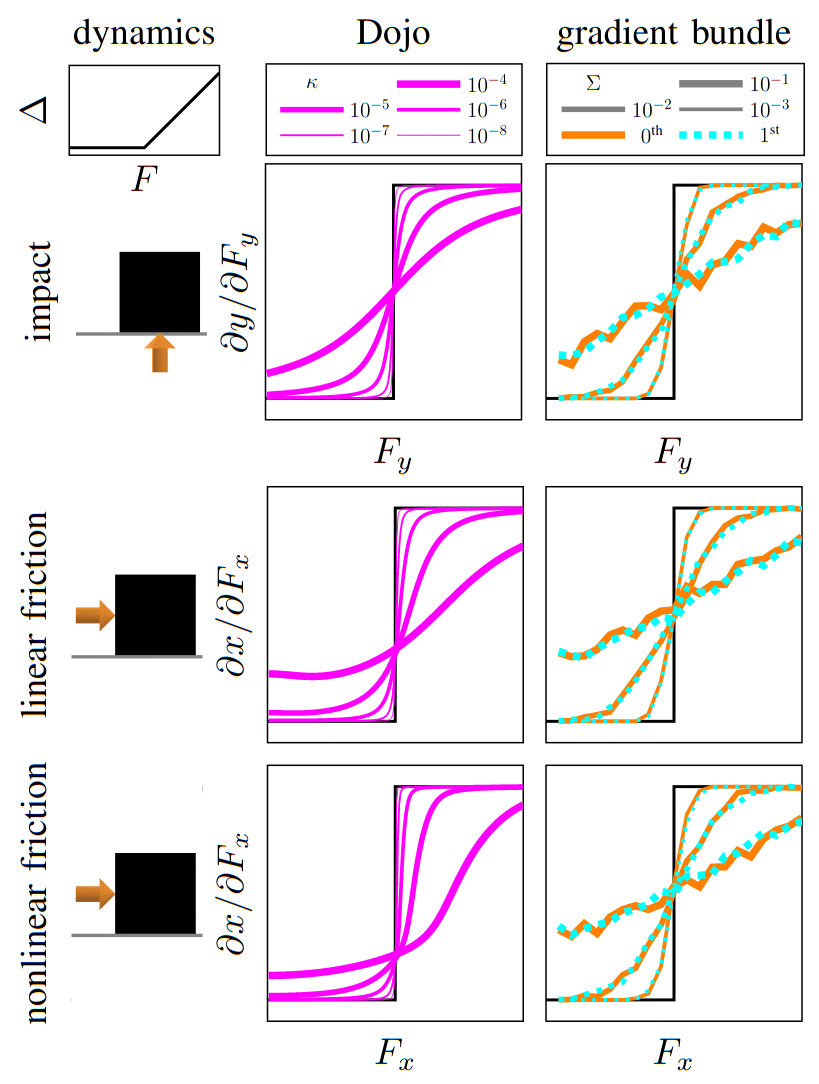
smooth gradients
box push
smooth gradients
box push
non-smooth dynamics
smooth gradients
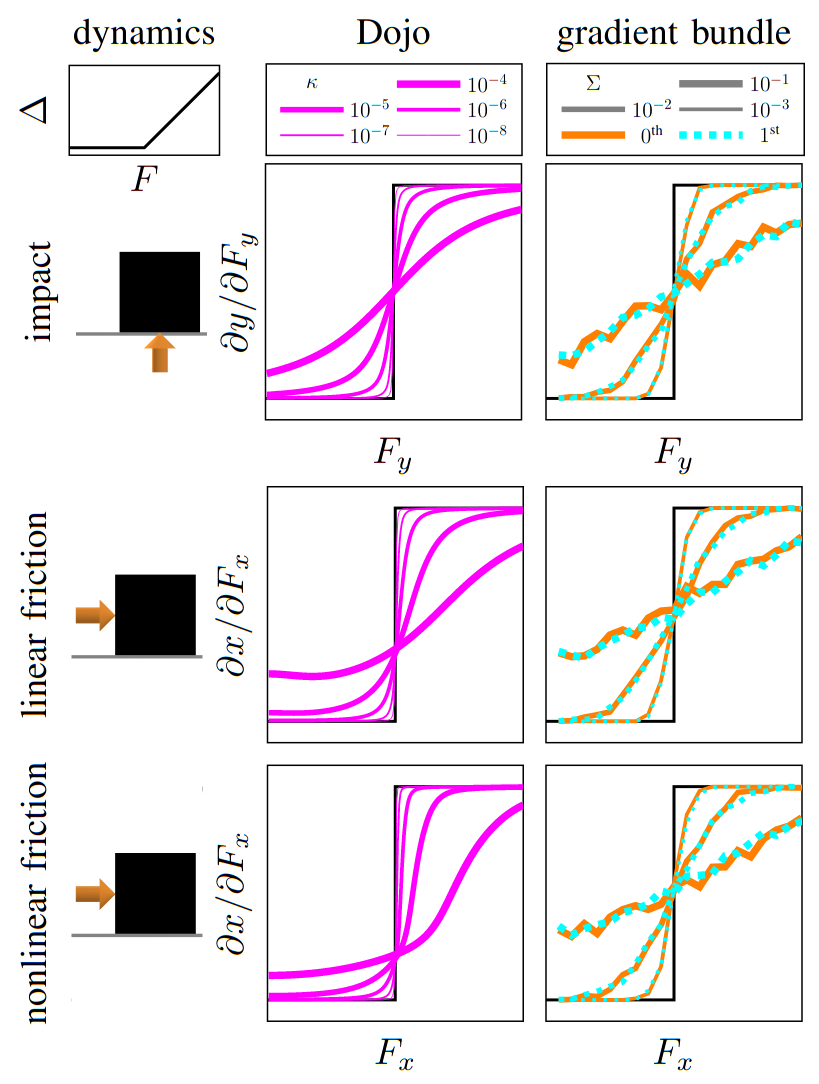
box push
non-smooth dynamics
gradient comparison
smooth gradients
box push
non-smooth dynamics
gradient comparison
less expensive to compute compared to finite-difference or stochastic sampling
github.com/dojo-sim
open-source implementation
github.com/dojo-sim
- Julia package: Dojo.jl
- gym-like environments
- Python wrapper: dojopy
- interface w/ PyTorch & JAX
open-source implementation
examples
trajectory optimization
trajectory optimization
smooth-gradient-based optimization with iterative LQR
trajectory optimization
smooth-gradient-based optimization with iterative LQR
stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
reinforcement learning
train static linear policies for locomotion
reinforcement learning
train static linear policies for locomotion
gradients enable 5-10x sample-complexity improvement over derivative-free method
reinforcement learning
train static linear policies for locomotion
gradients enable 5-10x sample-complexity improvement over derivative-free method
stability at low rates enables 2-5x sample-complexity improvement over MuJoCo
system identification
ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. S. Pfrommer, M. Halm, and M. Posa.
real-word dataset
system identification
ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. S. Pfrommer, M. Halm, and M. Posa.
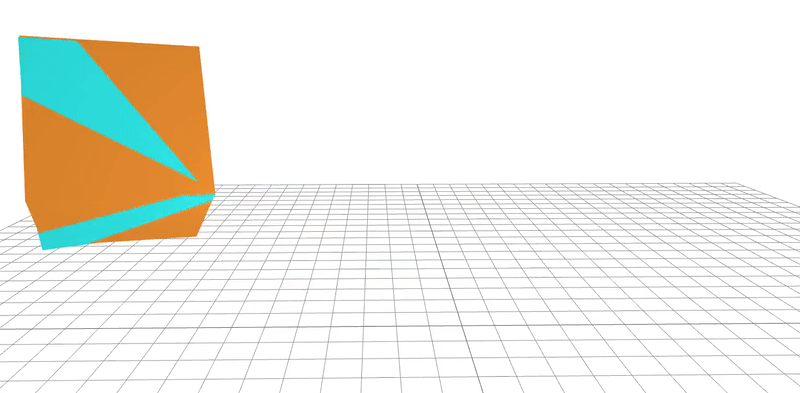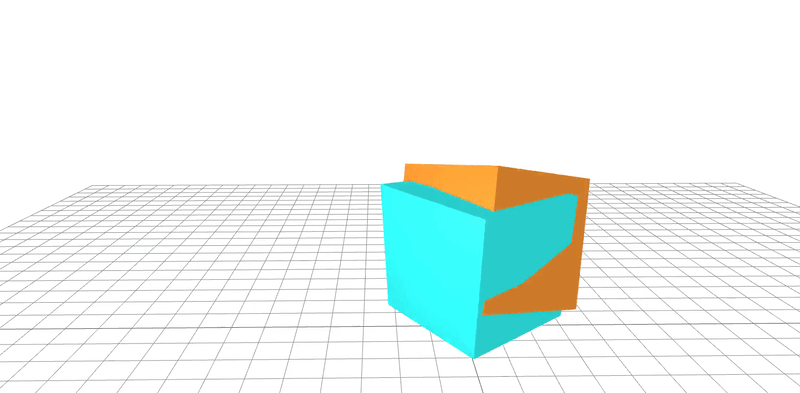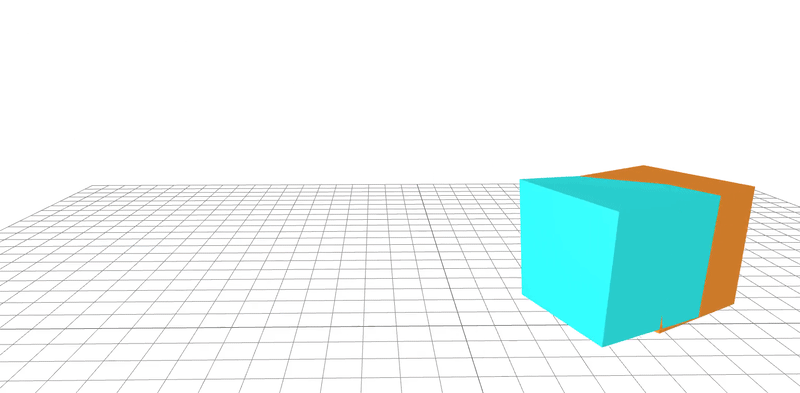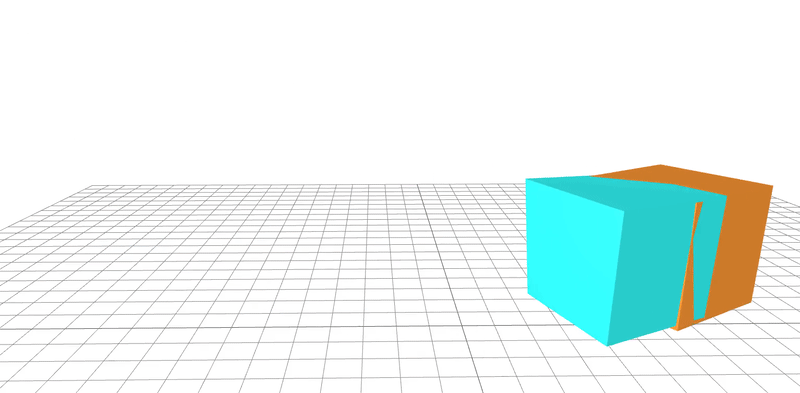
learned
ground-truth
real-word dataset
Dojo environment
system identification
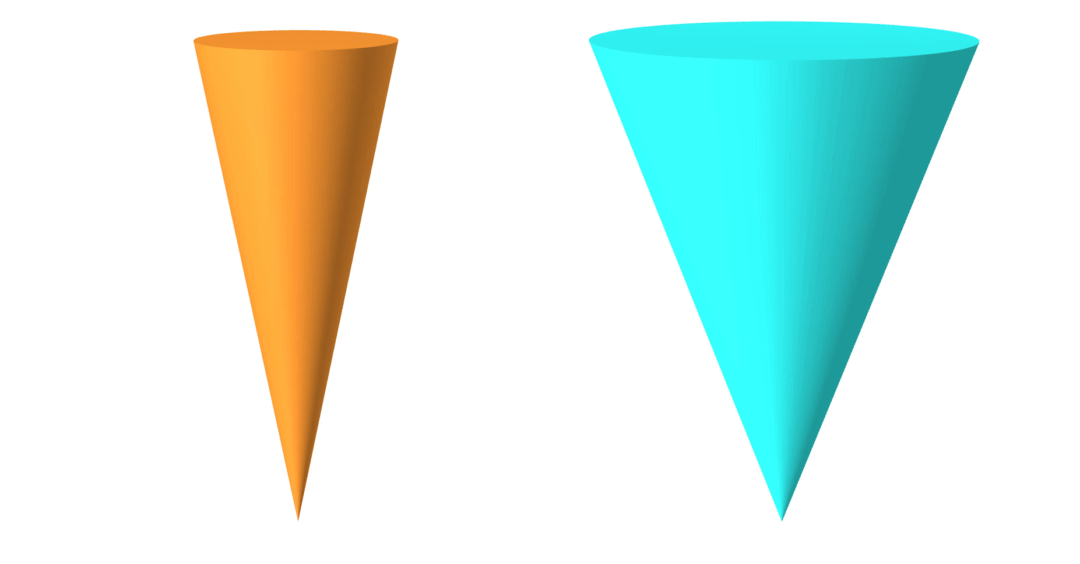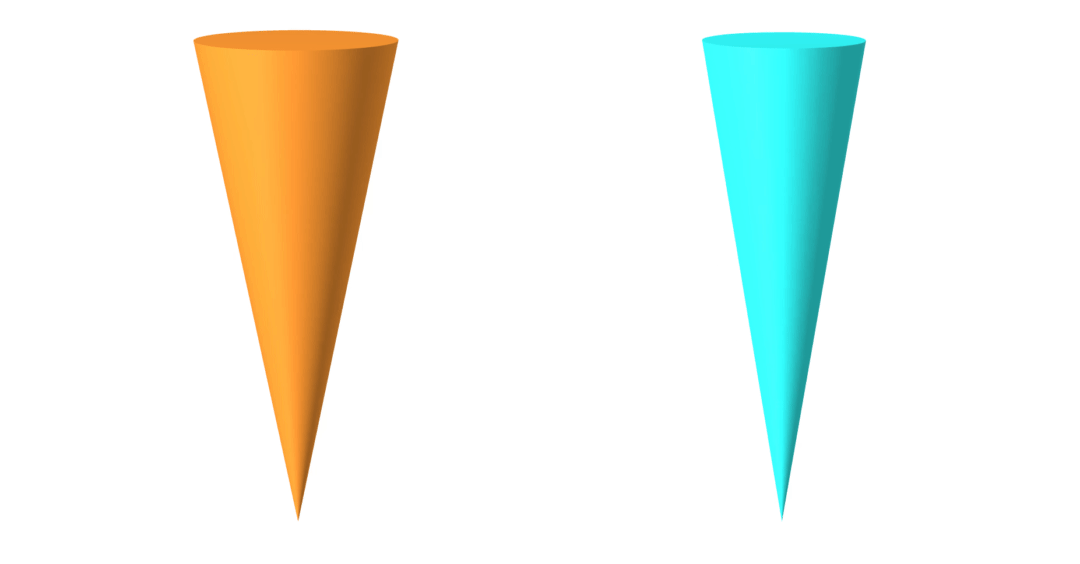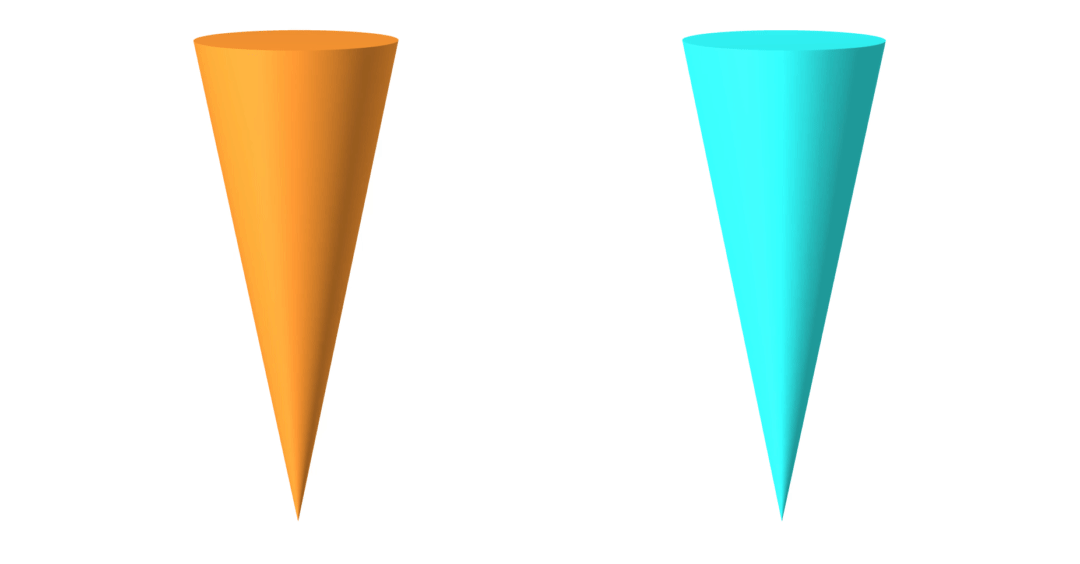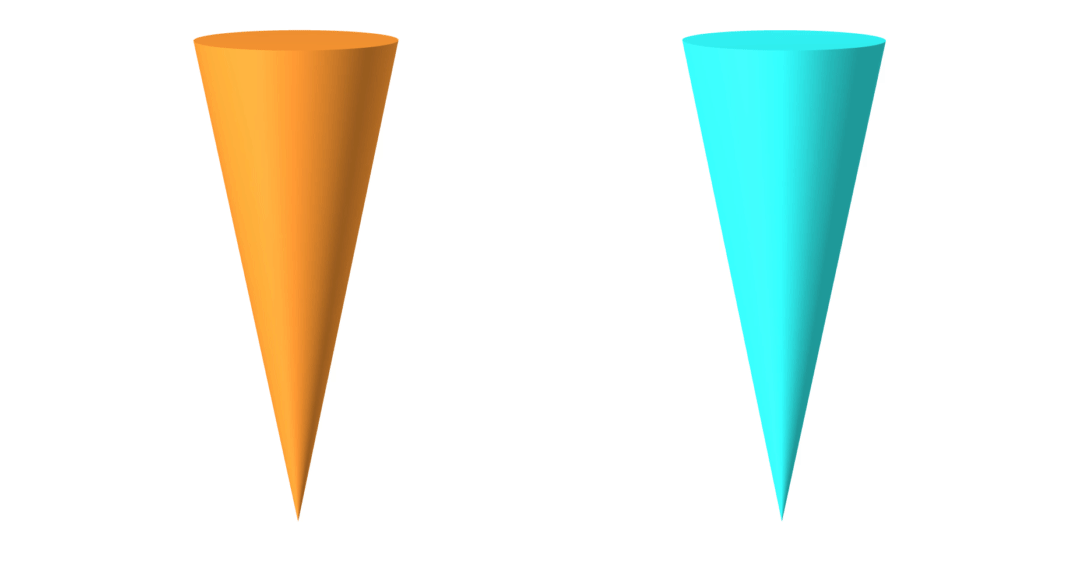
geometry
friction coefficient
ground-truth
learned
system identification
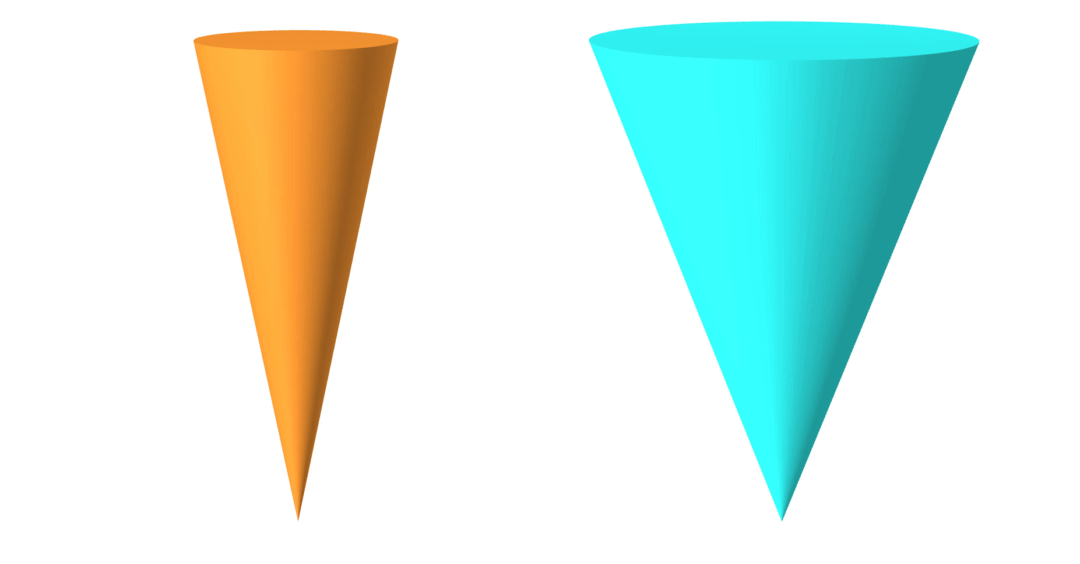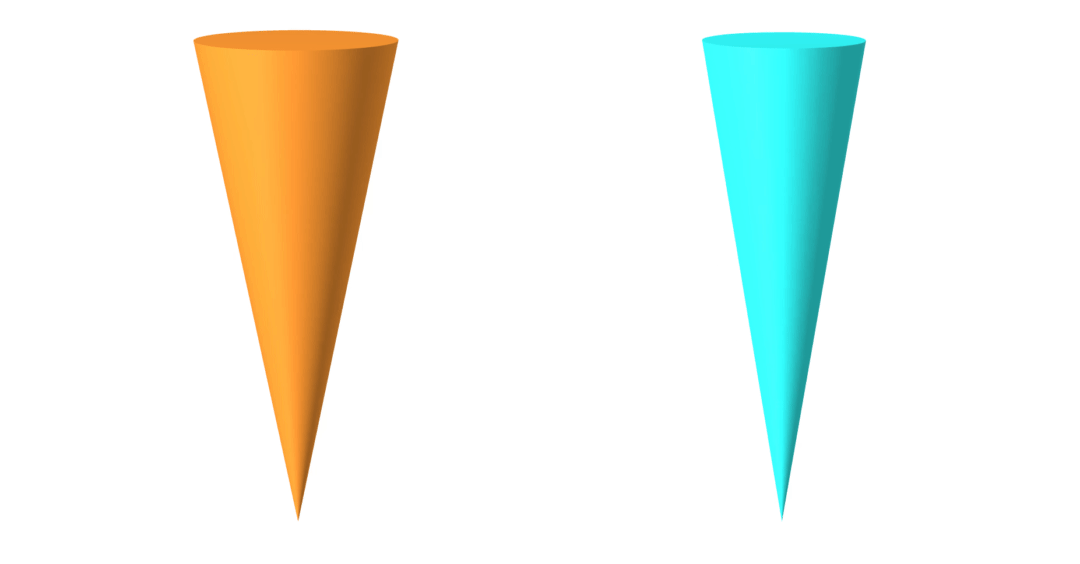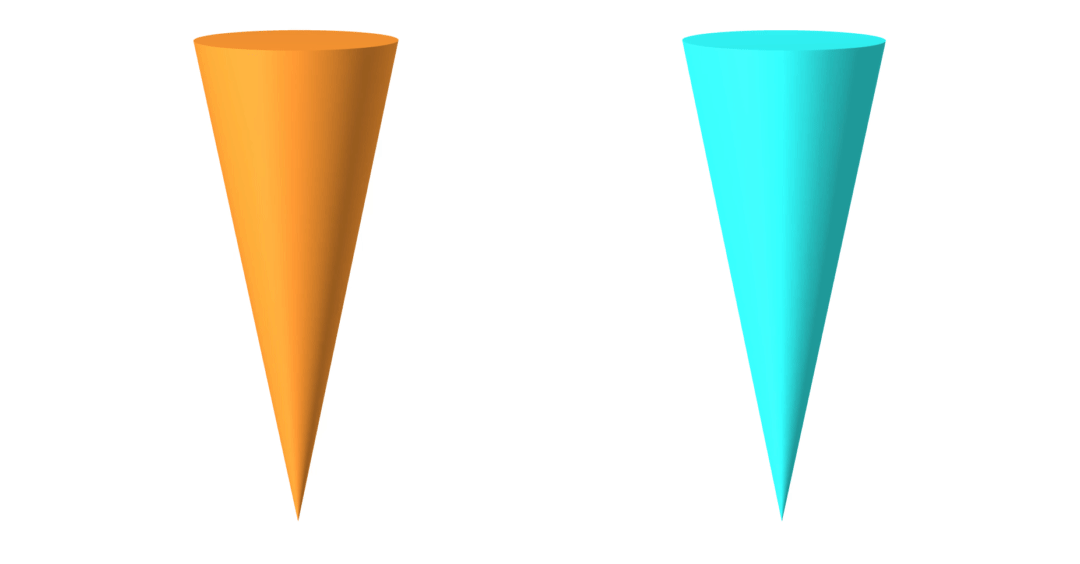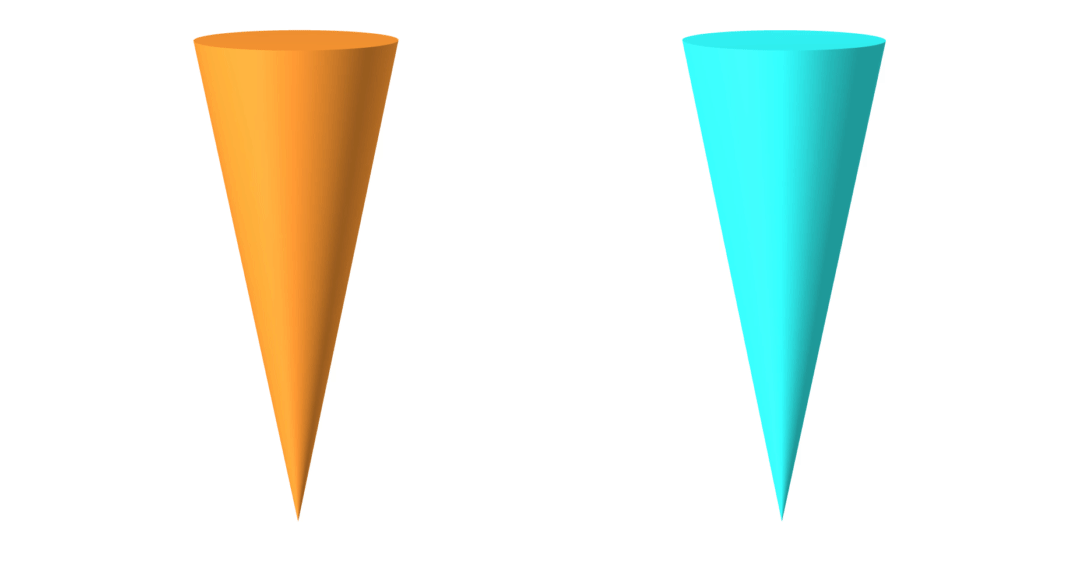
geometry
friction coefficient
ground-truth
learned
Quasi-Newton method utilizes gradients to
learn parameters to 95% accuracy in 20 steps
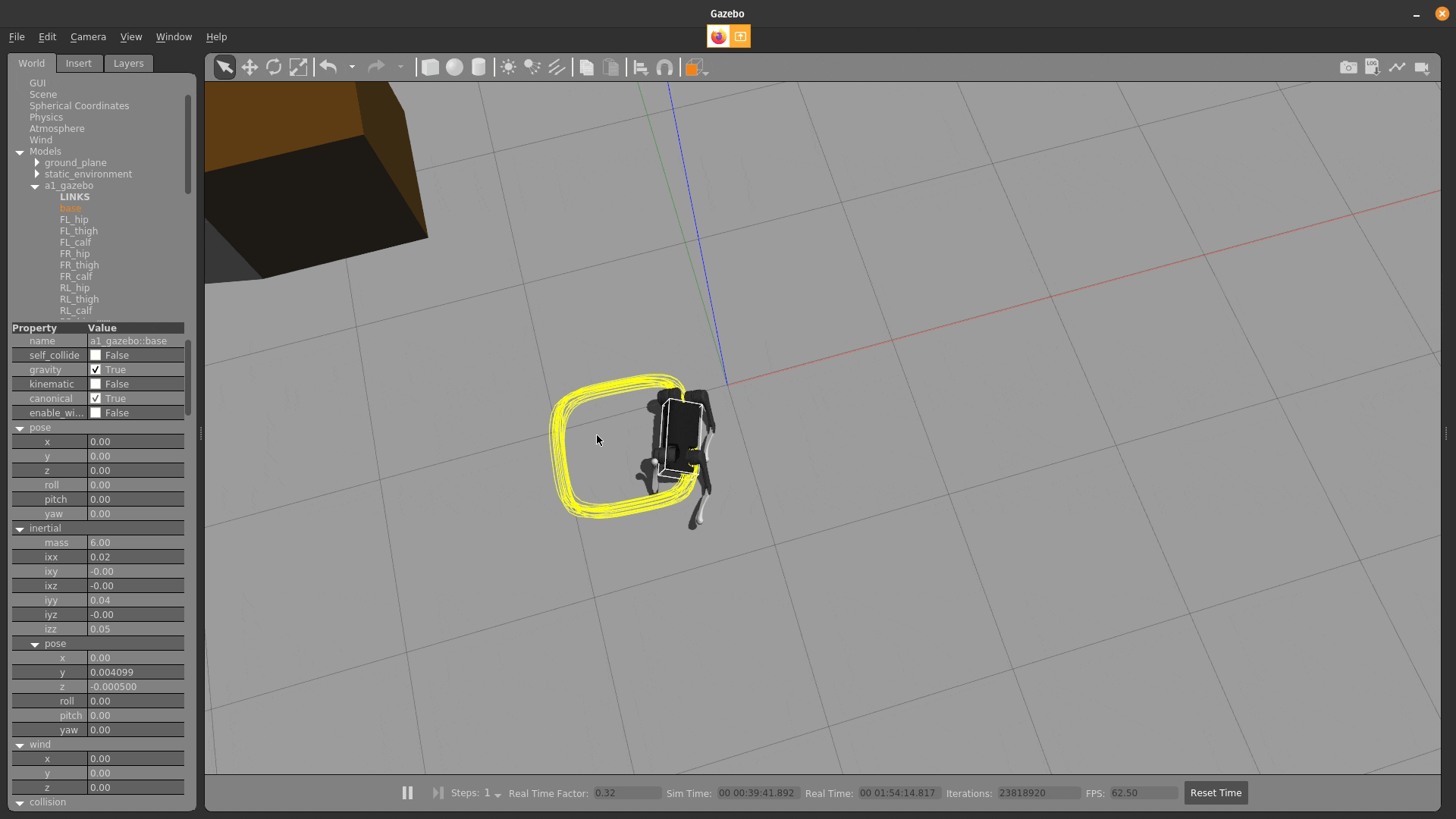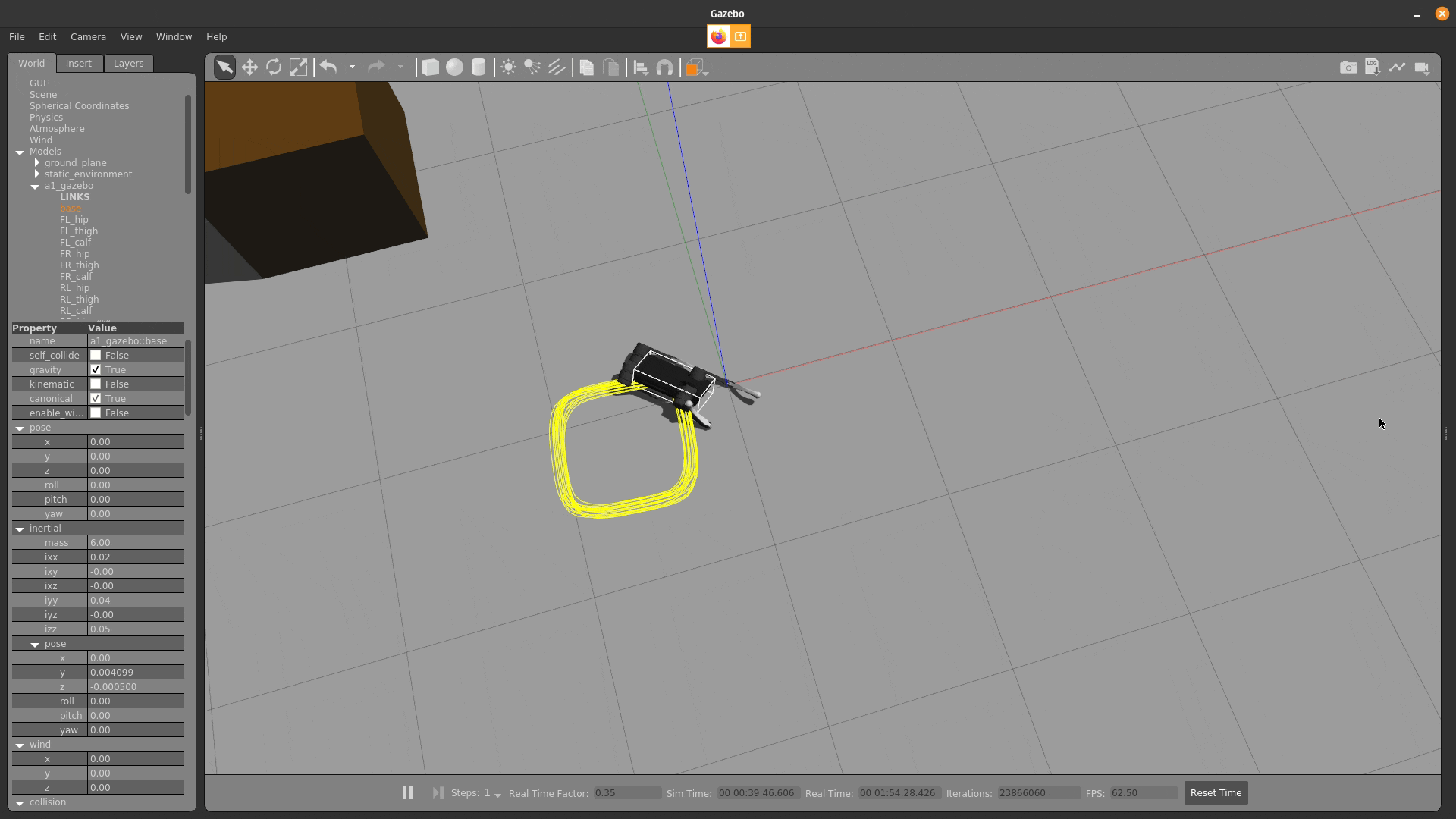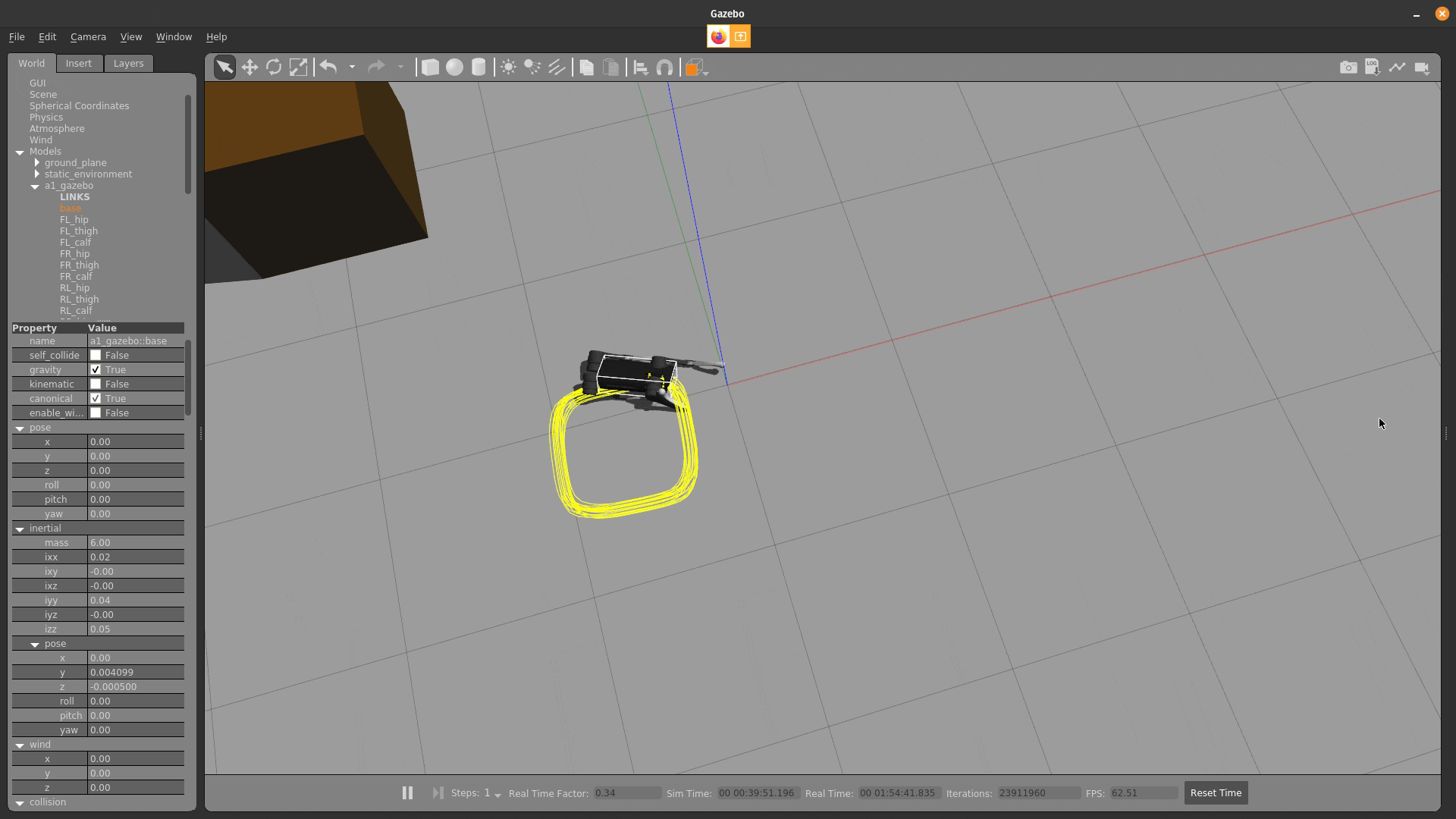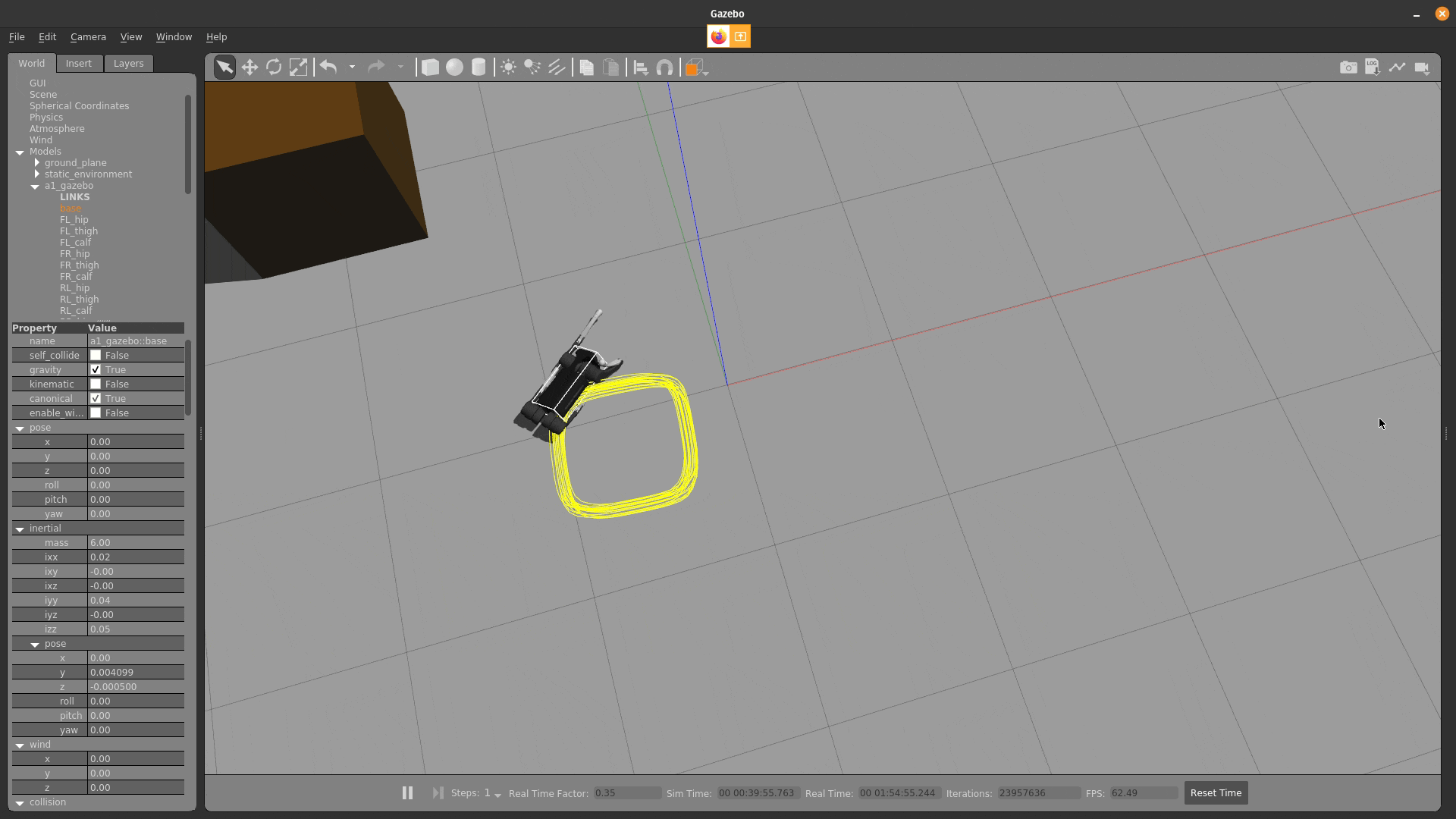
model-predictive control
Fast Contact-Implicit Model-Predictive Control.
S. Le Cleac'h & T. Howell, C. Lee, S. Yang, M. Schwager, Z. Manchester
simulation
push recovery
behavior generation
running Julia-based policy at 200-500Hz
NeRF
Differentiable Physics Simulation of Dynamics-Augmented Neural Objects. S. Le Cleac'h, HX. Yu, M. Guo, T. Howell, R. Gao, J. Wu, Z. Manchester, M. Schwager
dynamics-augmented NeRF → complex collision geometries
github.com/dojo-sim
a differentiable physics engine for robotics Taylor Howell and Simon Le Cleac'h
Dojo (RSS 2022)
By simonlc
Dojo (RSS 2022)
- 376
