Solving Rubik's Cubes
with F#

Stachu Korick | @stachudotnet | hello@stachu.net

Nov 17, 2018

Talk Inspiration

• Speed-Solving Rubik's Cubes
  • And other pattern-related hobbies
• Writing F#

A bit about me

The Plan

• [10] (this) Intro
• [10] On-Ramp Domain Knowledge
• [15] Hands-on: How to represent and "turn" a cube?
• [15] Hands-on: How to scramble a Rubik's Cube?
• [15] Show off Inefficient Solvers
  • (the Rubik's Cube is a "graph"!)
• [30] Discuss Efficient Solver Patterns
  • (sure, but it's also a "group"!)
• [10] Show off SAFE usage (Fable+Elmish+Saturn)
  • Hands-on opportunities!
• [10] Outro/Questions/Buffer
  • (probably related to the Rubik's Cube speed-solving world)

A bit about the Rubik's Cube

My Cubing Background

My Cubing Background

The Physical Structure, Pt. 1

The core structure of the Rubik's Cube does not move relative to each other, and has 6 "centers" at the end of each axis. 

The Physical Structure, Pt. 2

12 Edges surround the core and the centers.

Each of these 12 pieces has two orientations; "correct" and "flipped."

An edge cannot have opposite-side colors.

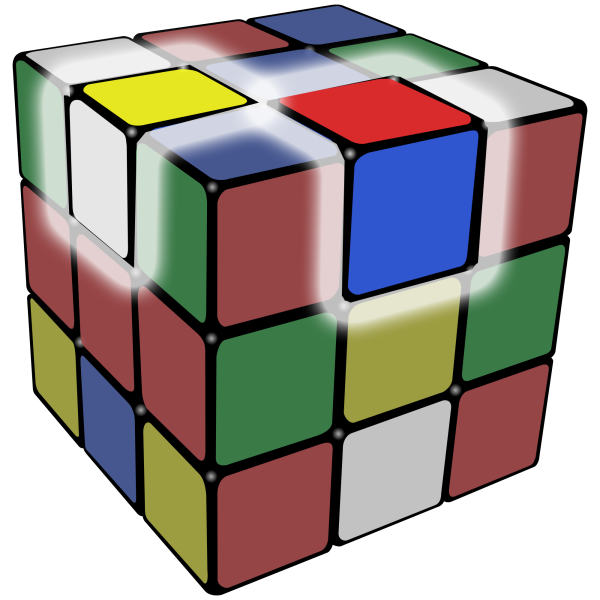
The Physical Structure, Pt. 3

8 "corner" pieces surround the core and edges.

Each of them has 3 orientations: "correct," "twisted clockwise" and "twisted counter-clockwise."

These also cannot have two "opposite" colors.

Basic 6 Moves

• R(ight)
• L(eft)
• U(p)
• D(own)
• F(ront)
• B(ack)

12 Derived Moves

An Example Algorithm

Referring to

Certain Pieces

Creating a Simple Solver

• Modeling the cube's state

• Writing a scrambler

• Transcribing the basic 18 'moves'

• Getting *some* solver running

Challenge!

How can you store the state of a Rubik's Cube?

Representing the Cube

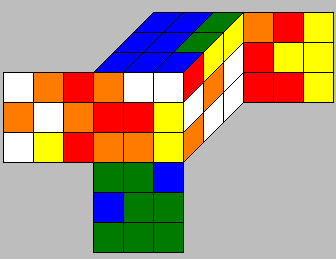
Facelet

Facelet Array

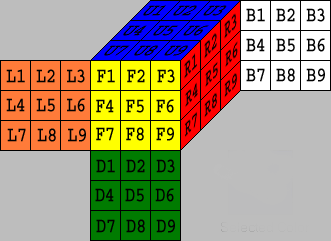
Representing the Cube

Cubie

Piece Arrays

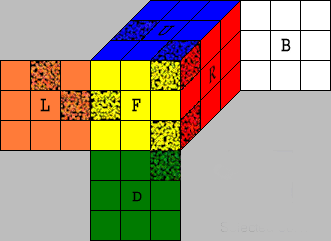
Representing the Cube

CO+CP+EO+EP

CO + CP + EO + EP

CO: 0 <= x1 < 3^7

EO: 0 <= x2< 2^11

CP: 0 <= x3< 8!

EP: 0 <= x4< 12!

Representing the Cube

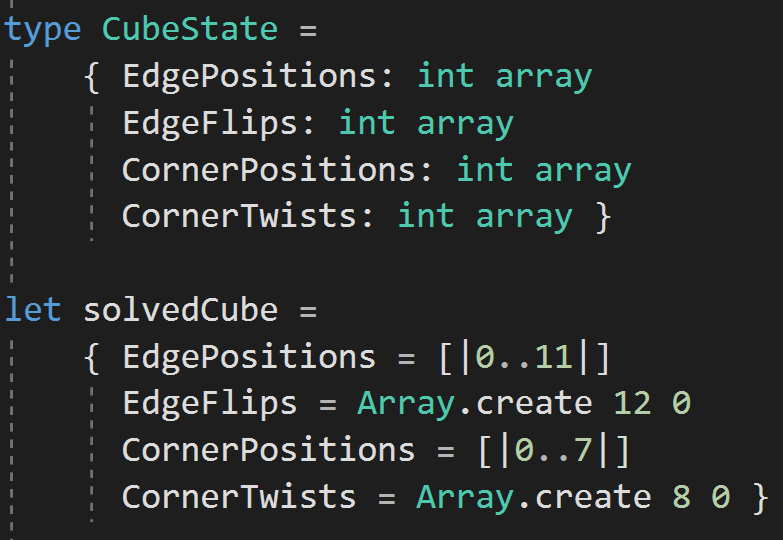
Representing the Cube

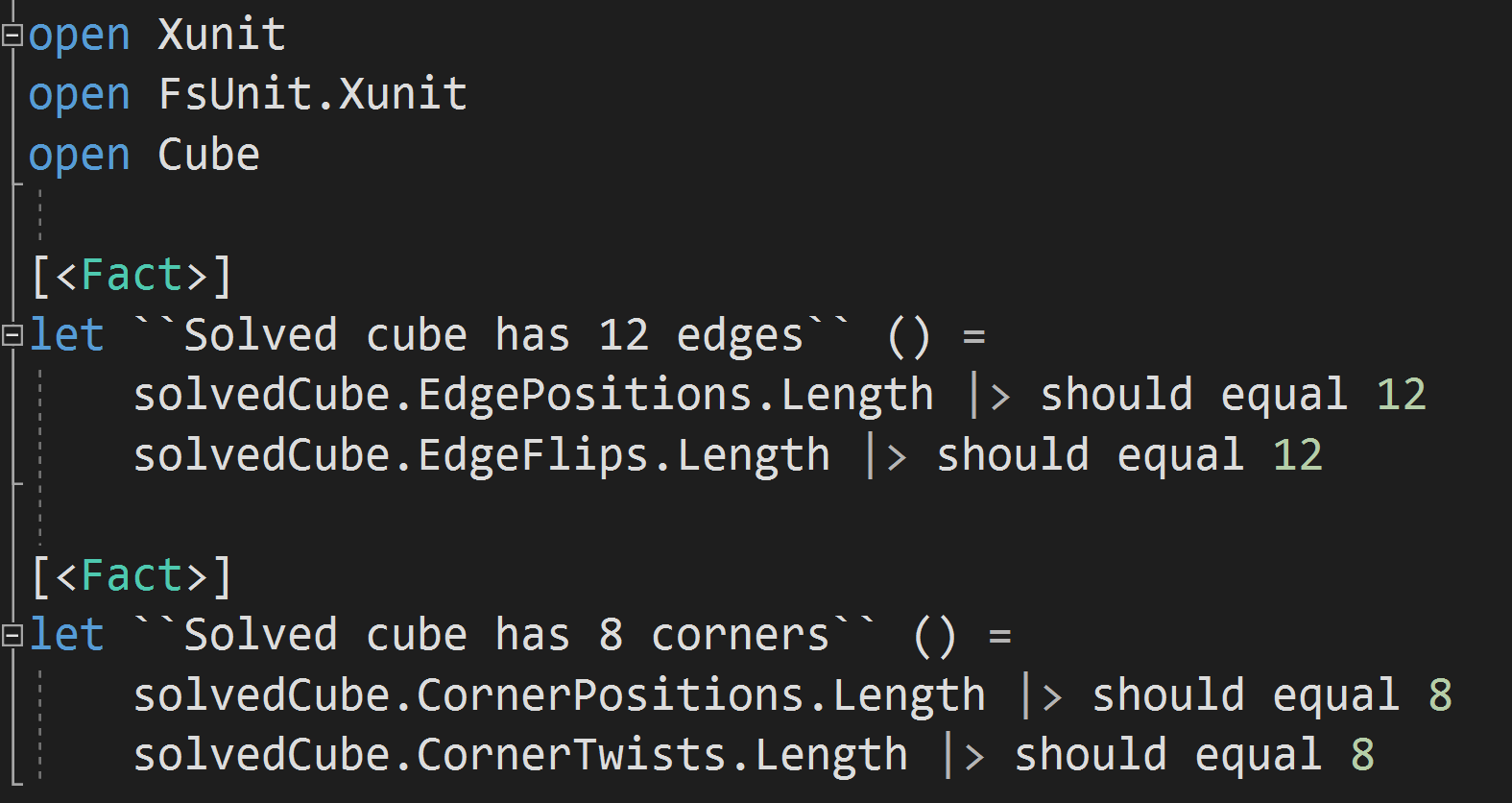
Turning the Cube

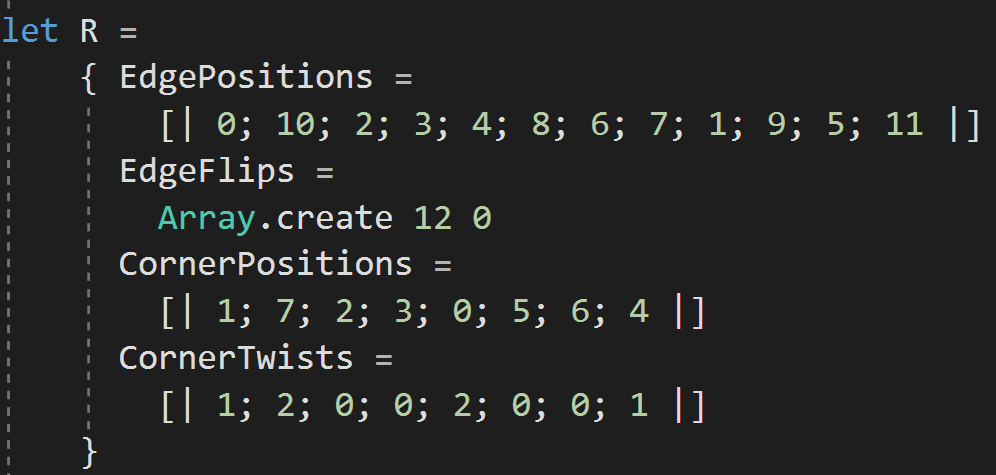
Turning the Cube

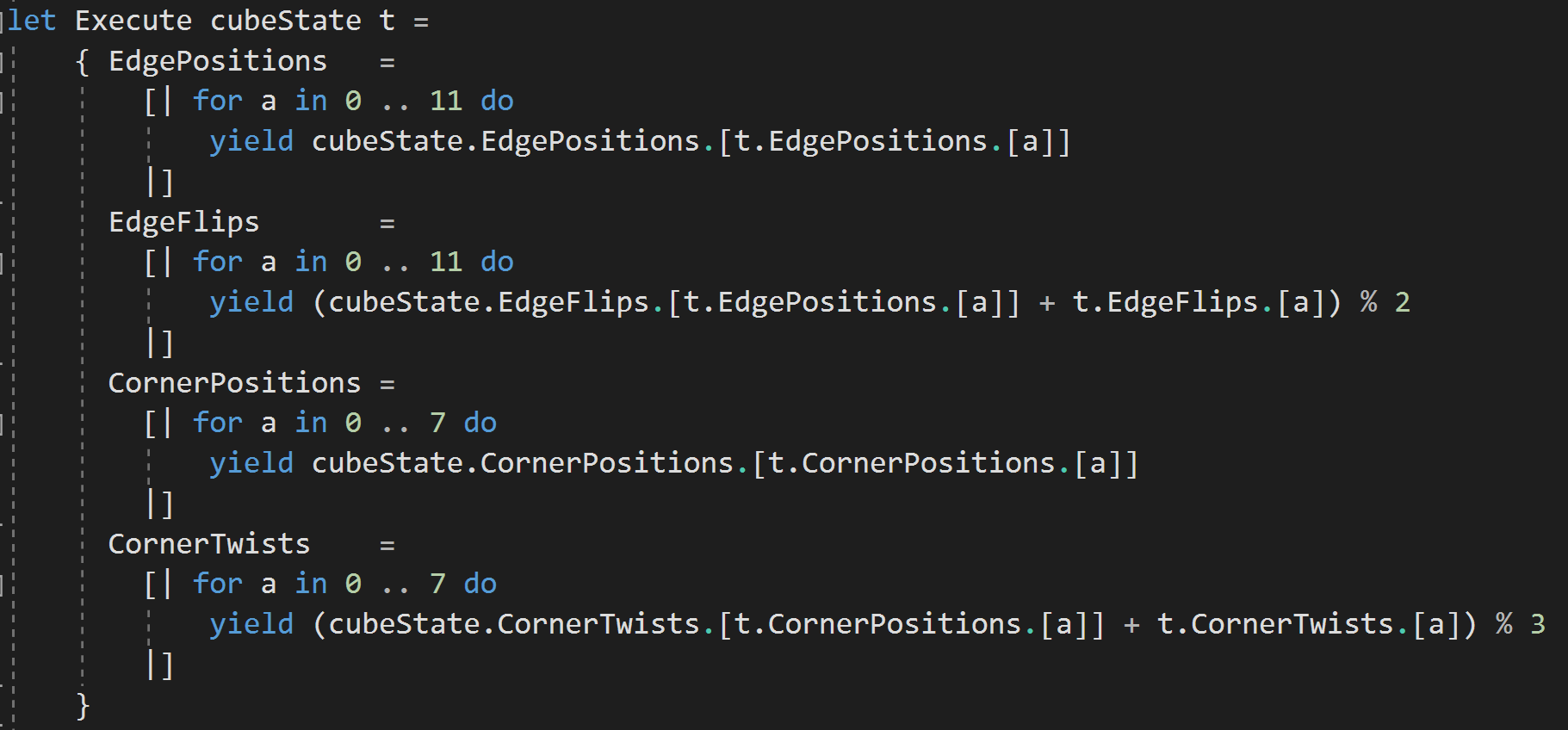
Turning the Cube

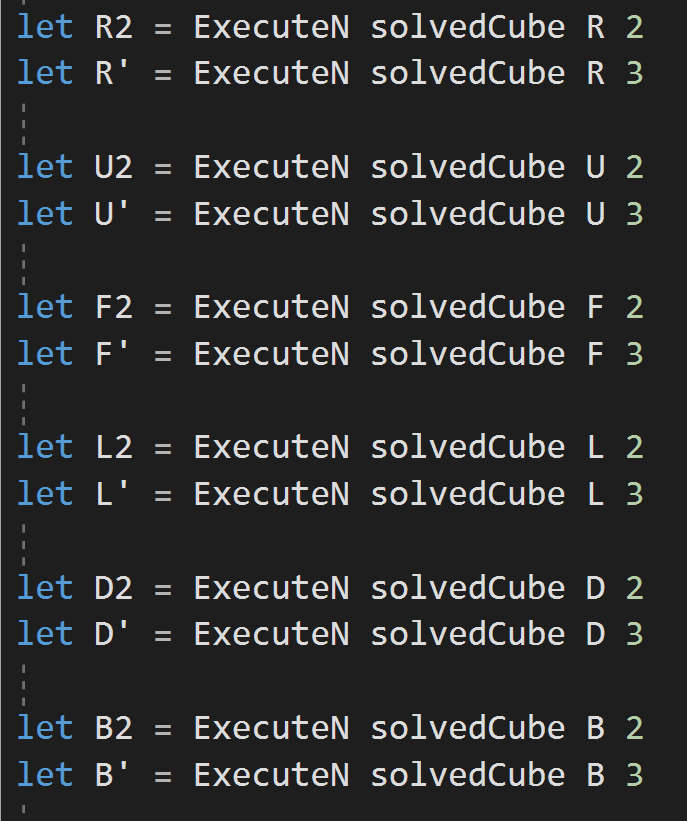
Turning the Cube

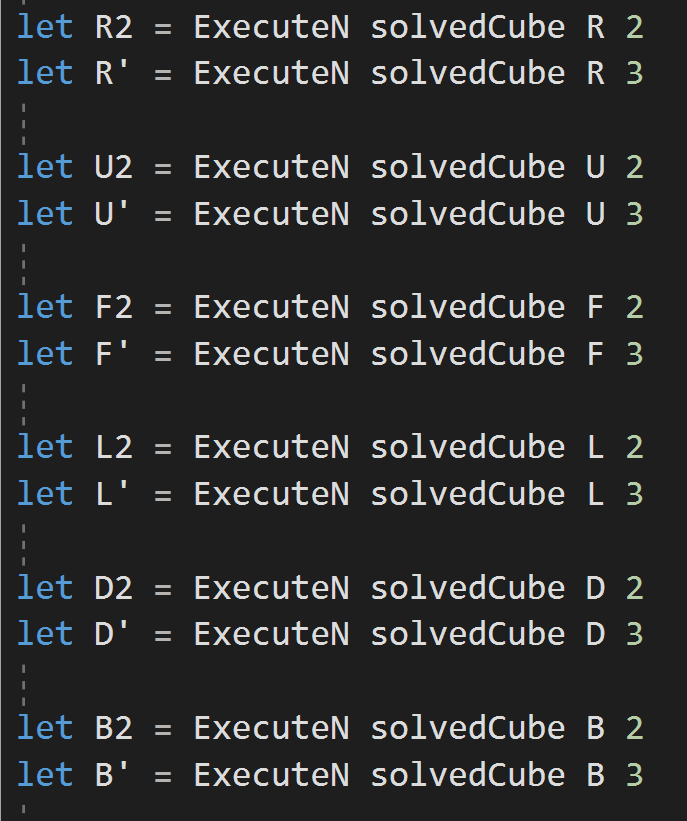
Turning the Cube

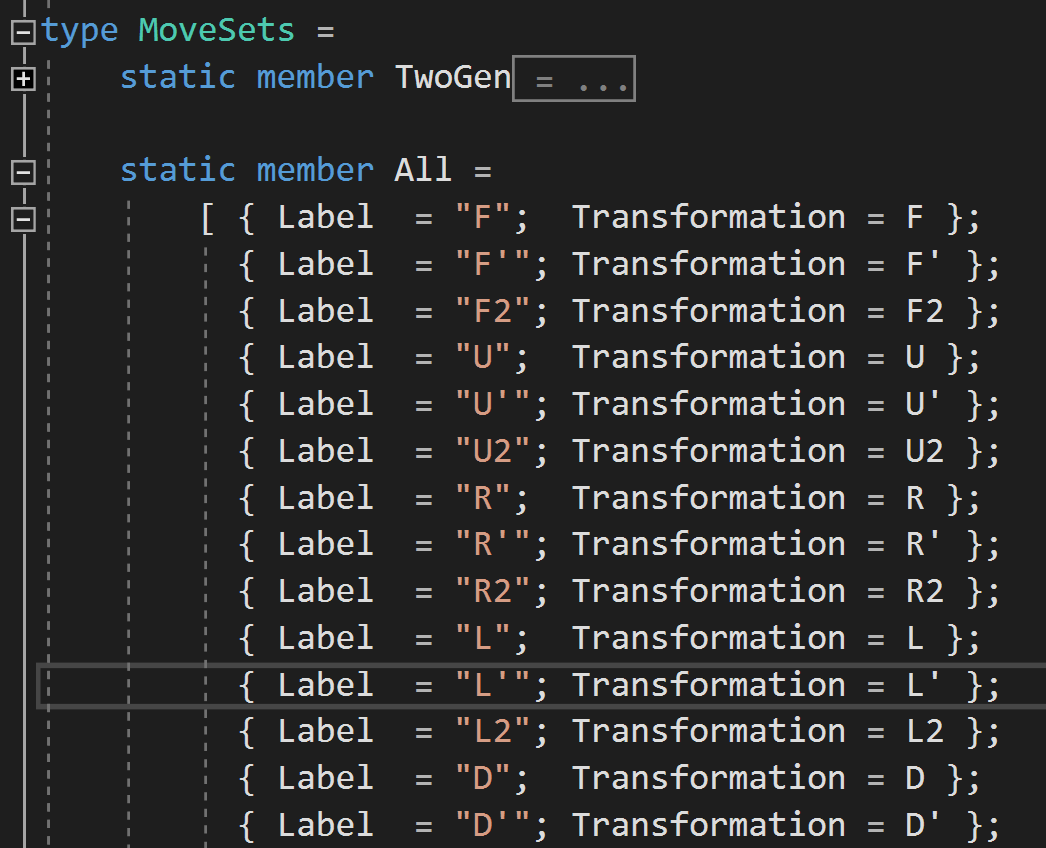
Turning the Cube

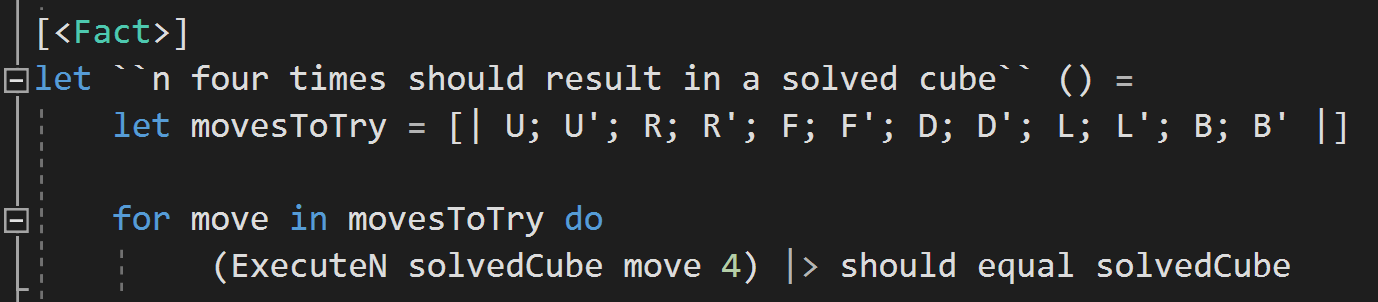
Turning the Cube

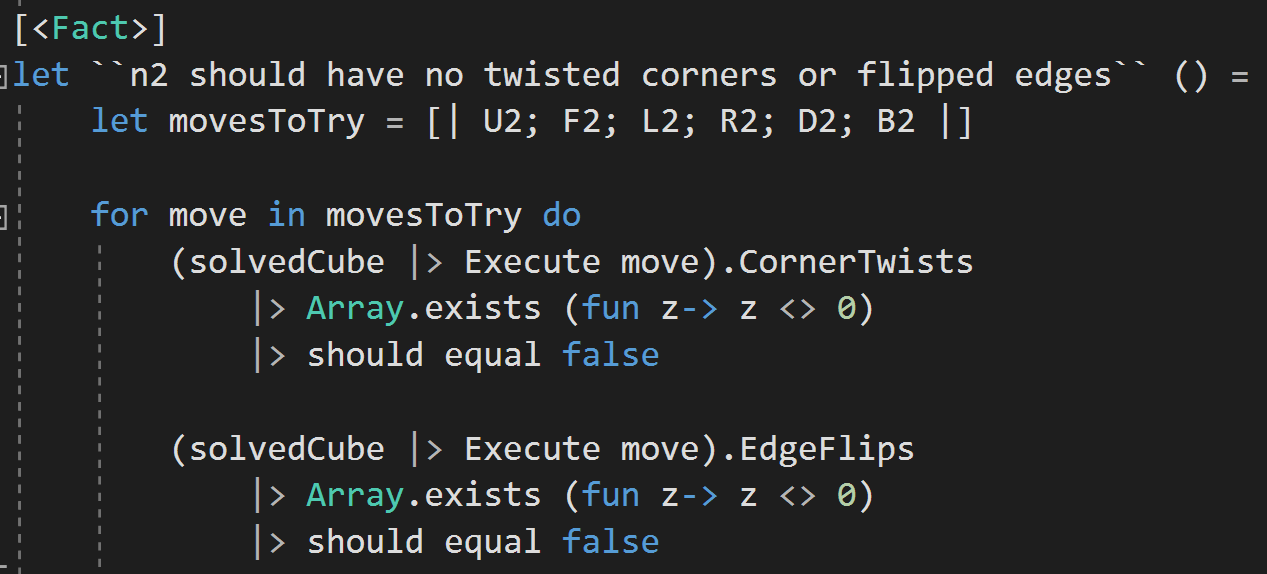
Challenge!

Scramble a Rubik's Cube

Scrambling the Cube

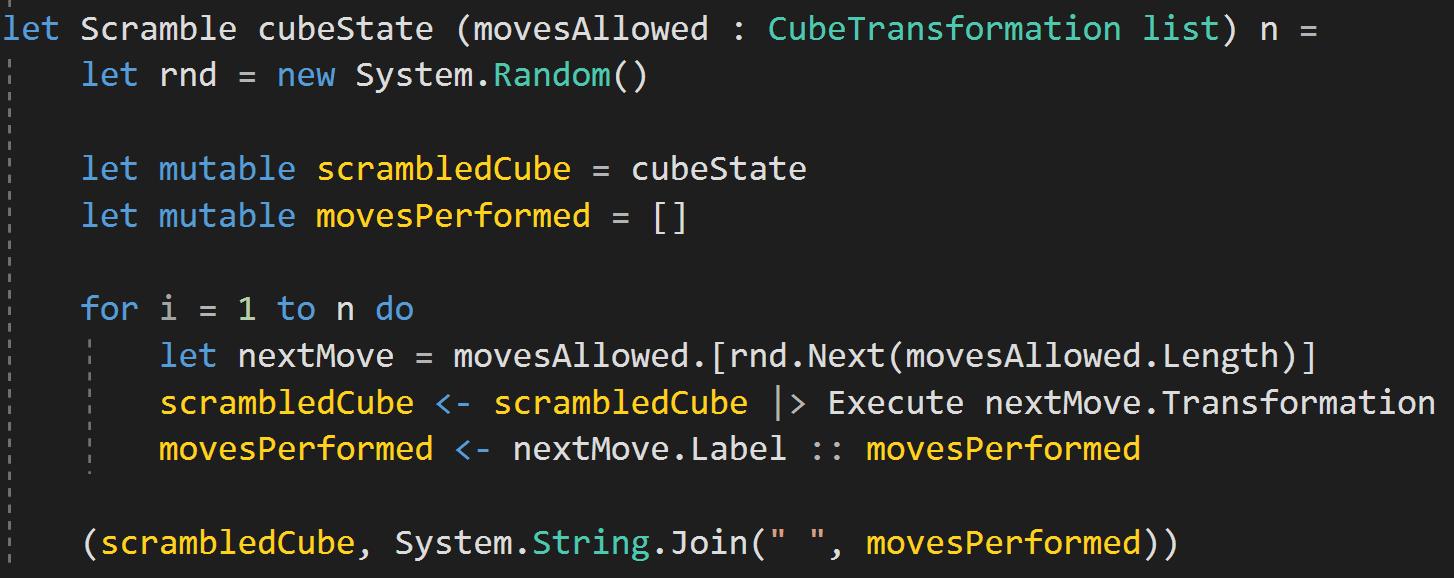
Scrambling the Cube

The Cube is a Graph

R2 U2

R2

U2

U2 R2

U2 R2 U2 R2 U2 R2

U2 R2 U2

U2 R2 U2 R2

U2 R2 U2 R2 U2

R2 U2 R2

R2 U2 R2 U2

R2 U2 R2 U2 R2

Depth-First Tree Searching

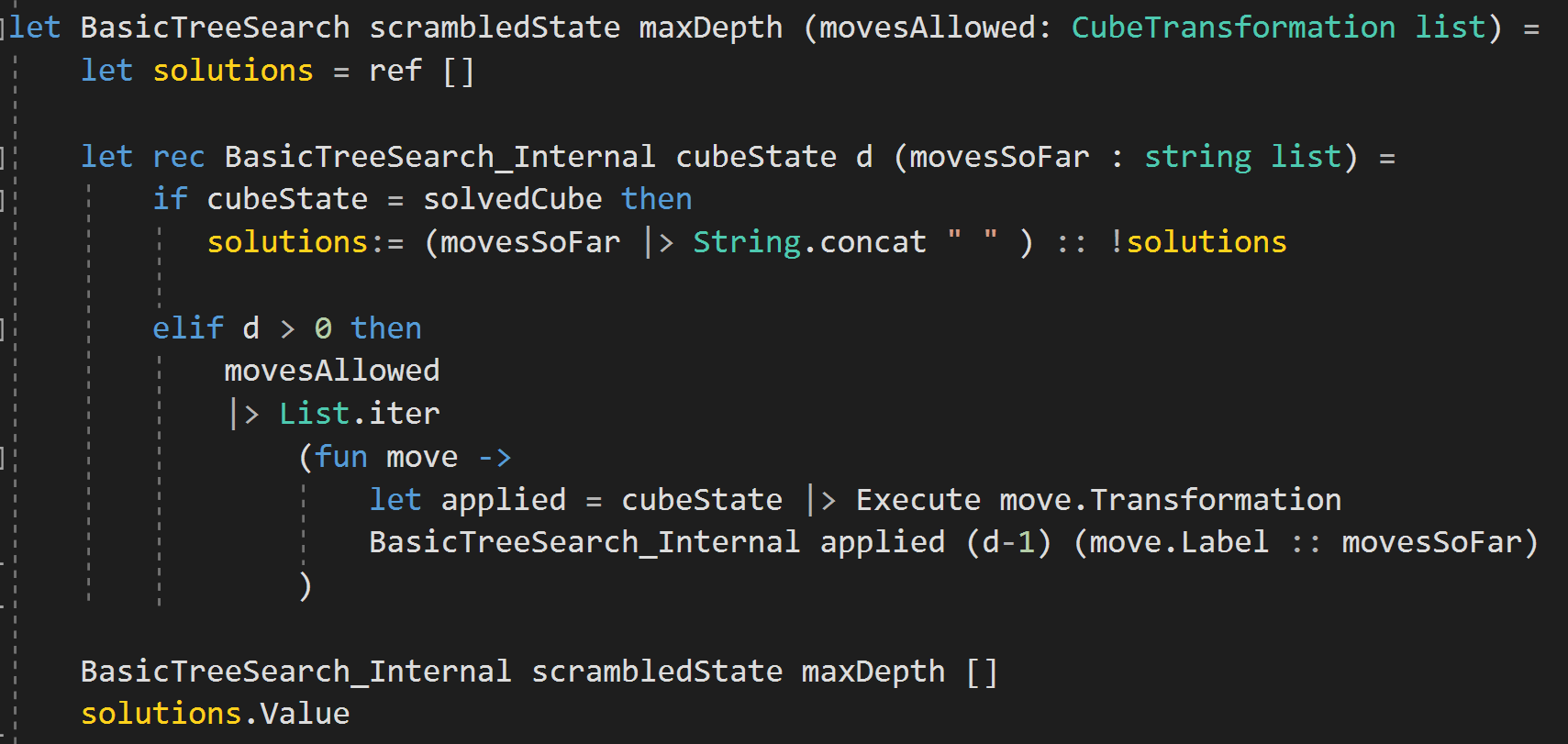
Depth-First Tree Searching

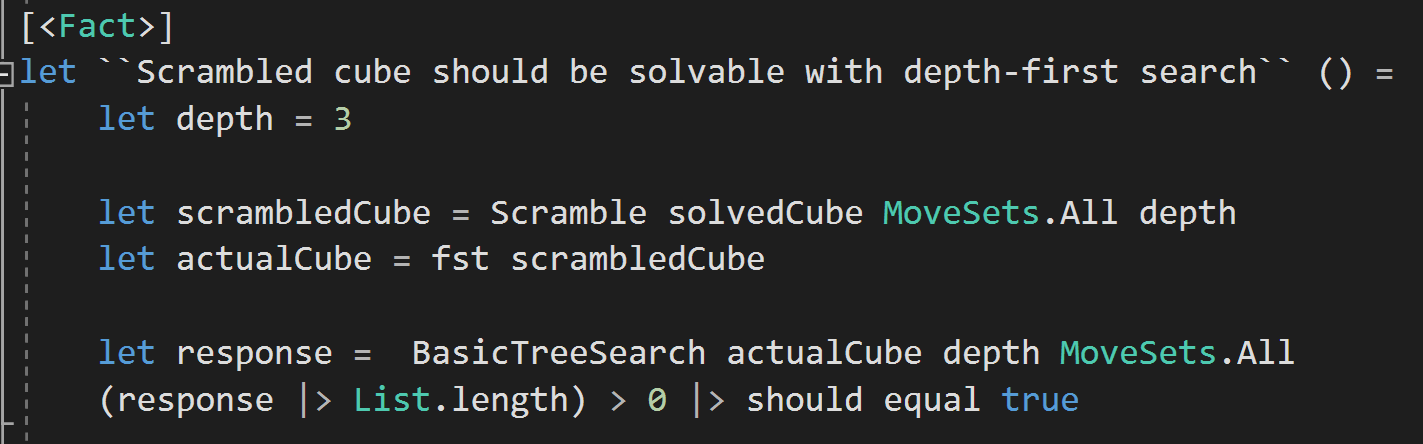
IDA Tree Searching

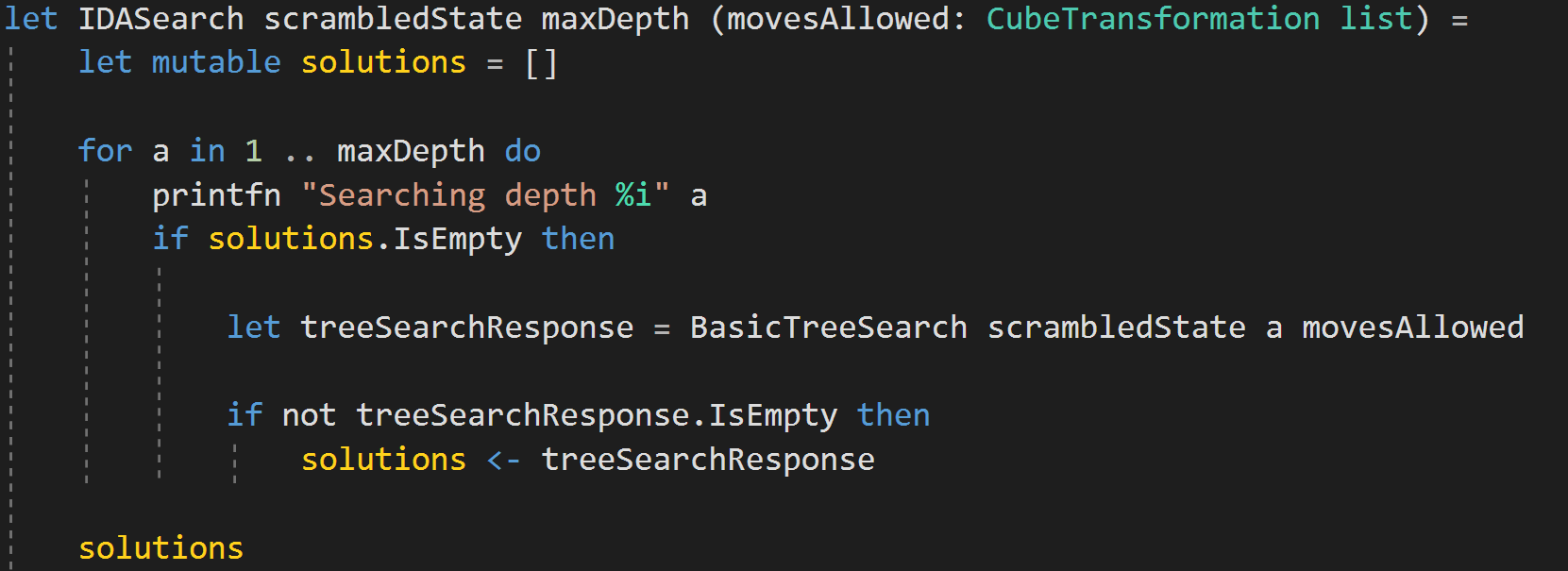
Why is this so slow?

• 43 quintillion is a big number. (really big)
• 18^20 is a big number. (even bigger)
• `Execute` takes a while to change cube state

Creating a Better Solver

Some Trade-offs for Consideration

• Human-Learnable
• Turning Ergonomics
• Support partially-defined cubes?
• Move Count
• Resource Requirements
  • CPU, RAM, Disk Storage
• Speed

Program Human Algorithms?

The "CFOP" Method

Cross

F2L

(First 2 Layers)

OLL

(Orientation of the Last Layer)

PLL

(Permutation of the Last Layer)

Creating a Complex Solver

focus: run in a reasonable amount of time

The Kociemba Algorithm

Phase 1

Phase 2

Solved:

• Edge Orientation
• Corner Orientation
• U/D Edges in U/D Layer

Solve the rest, using only <U,D,R2,L2,F2,B2>

Additional "tricks"

to Implement

• representing each of these components into simple 16-bit integers
  (16bits is a lot less than an int array!)
• move depth-caching caching
  (how many moves deep various positions are away from a 'solved' state)
• caching position-transitions
• storing the transitions between the 16bit numbers rather than computing them on the fly
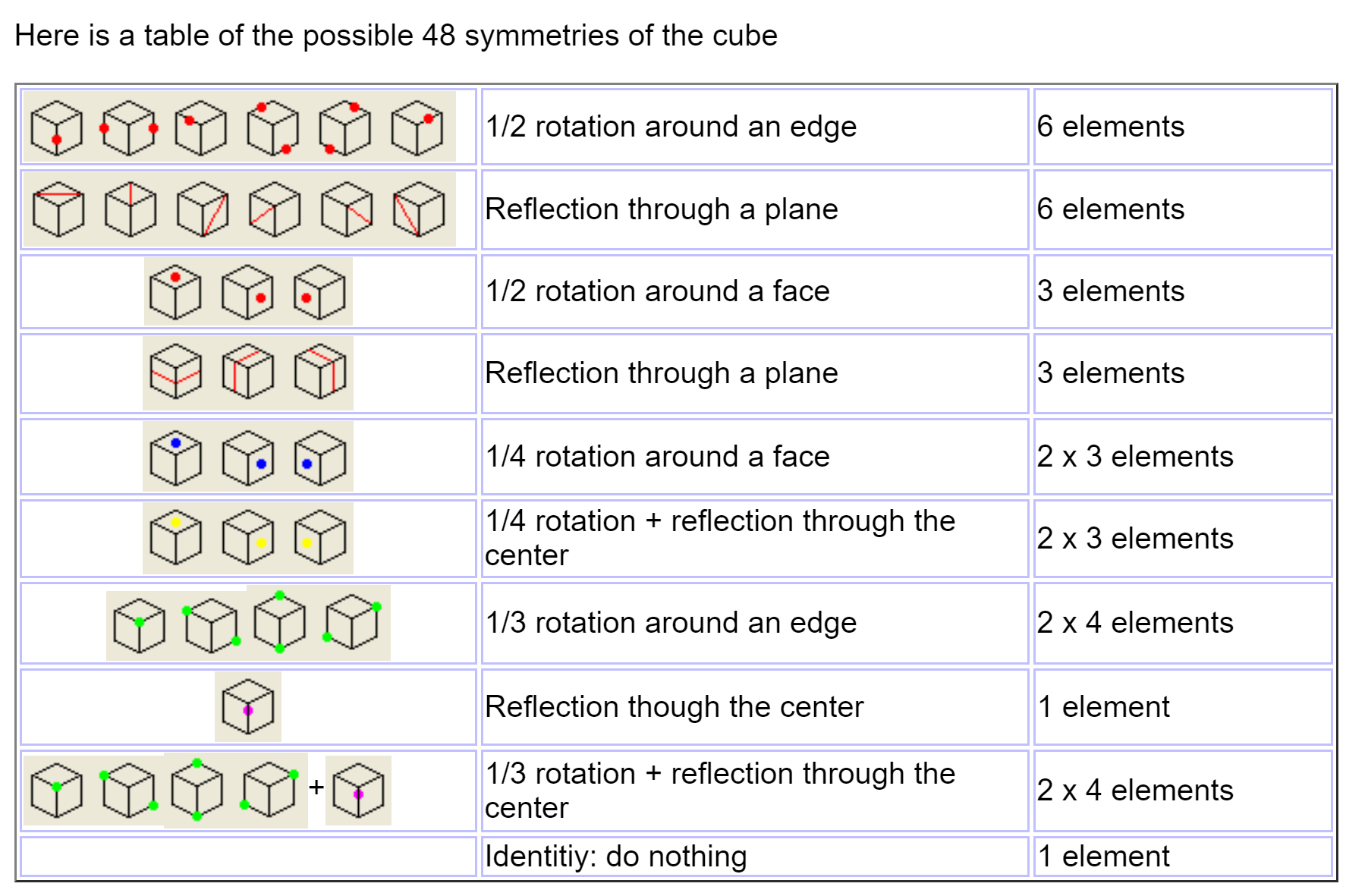
• taking advantage of symmetries
• using sub-optimal phase 1 solutions

Storing Cube State Cheaply

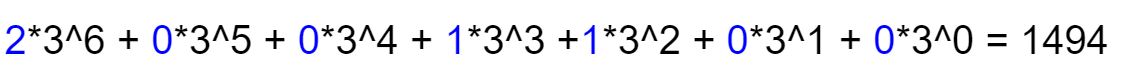
Corner Orientation

Storing Cube State Cheaply

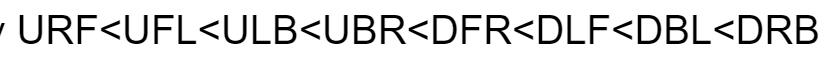
Corner Permutation

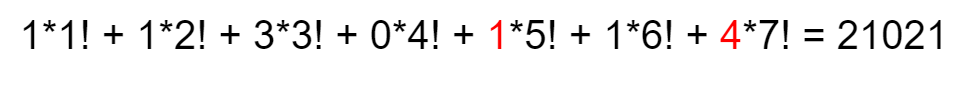
Move Tables

Symmetry Reductions

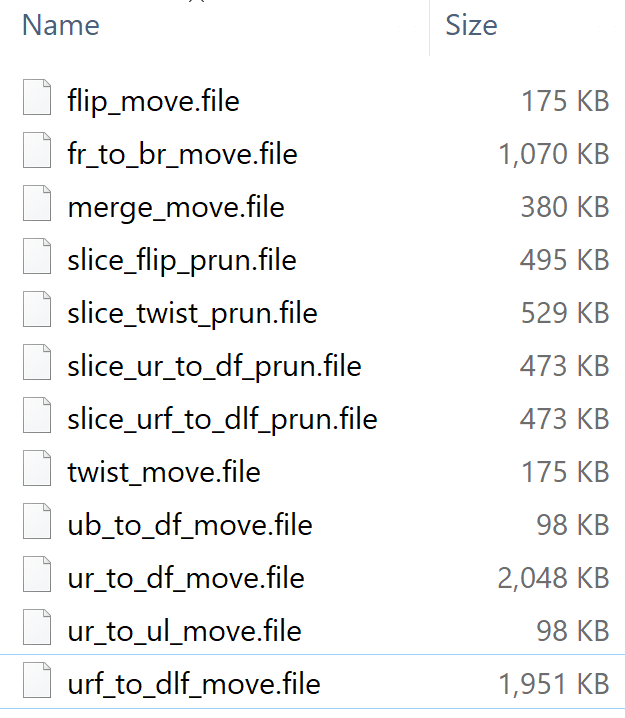
Pruning Tables

function Treesearch(position p, depth d)
  if d = 0 then 
    if p is solved then 
      Hooray! 
  else if d > 0 then 
    if prune1[p] <= d and prune2[p] <= d then
      for each available move m
        Treesearch(result of m applied to p, d-1)

Pruning Tables

Using Sub-Optimal Phase 1 Solutions

Let's See It in Action!