Suyash Bagad
Department of Electrical Engineering, IIT Bombay
As a Part of Dual Degree (B.Tech + M.Tech) Project
Prof. Saravanan Vijayakumaran
Guide
June 29, 2020
Shorter, Privacy-Enhancing
Proof of Reserves
Proof of Reserves
Outline
Log-sized Privacy-Enhancing Proofs of Reserves Protocol
Motivation and main idea
Confidentiality of Amounts in Grin
Presented at Crypto Valley Conference on Blockchain Technology, 2020
Focus on performance trade-offs and implementation
Work accepted at IEEE Security & Privacy on Blockchain, 2020
Graph-based analysis of the Grin Blockchain
Main challenge in design
Adaptability to Edwards and Ristretto curves
MimbleWimble
Monero
Revelio
\mathcal{C}_{\text{own}}
C = g^{k} \cdot h^{a}
C \in \mathcal{C}_{\text{own}} \implies k \text{ is known}
Each output in MimbleWimble is a Pedersen Commitment
For an amount \(a \in \{0,1,\dots,2^{64}-1\}\) and blinding factor \(k \in \mathbb{Z}_q\)
where \(g,h \in \mathbb{G}\) such that DL relation between them is unknown
Revelio
\mathcal{C}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13
For each \(C_i \in \mathcal{C}_{\text{anon}},\) publish the tags \((I_1, \dots, I_n) \in \mathbb{G}^n\) where \( n = |\mathcal{C}_{\text{anon}}|\)
Publish \(C_{\text{assets}} = \prod_{i \in [n]} I_i,\) and NIZK proofs \(\sigma_i \in \mathbb{Z}_q^5 \ \forall i \in [n]\)
PoK\big\{\underbrace{(\alpha,\beta,\gamma)}_{\text{secret}} \ | \ \underbrace{(C_i = g^{\alpha} \cdot h^{\beta} \ \wedge \ I_i = g_t^{\alpha} \cdot h^{\beta}) \vee (I_i = g_t^{\gamma}) }_{\text{statement}} \big\}
where \(y_i = \mathcal{H}(k_{\text{exch}}, C_i) \in \Z_q\)
I_i =
\begin{cases}
\ g_1^{k_i} \cdot h^{a_i} & \text{if } C_i \in \mathcal{C}_{\text{own}},\\
\ g_1^{y_i} & \text{if } C_i \notin \mathcal{C}_{\text{own}},
\end{cases}
Drawbacks of Revelio
Proof size linear in anonymity set size
(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q
Can we shrink proofs sizes to \(\mathcal{O}( \text{log}_2(n))\)?
Can we link the blockchain state to the proof of reserves?
Privacy of outputs depends on the anonymity set \(n\)
RevelioBP!
RevelioBP!
1
2
3
4
5
6
7
8
9
10
12
11
13
0
1
0
0
0
0
0
0
0
0
0
0
0
(
)
\textbf{e}_1 =
0
0
0
0
0
1
0
0
0
0
0
0
0
(
)
\textbf{e}_2 =
0
0
0
0
0
0
0
0
1
0
0
0
0
(
)
\textbf{e}_3 =
0
0
0
0
0
0
0
0
0
1
0
0
0
(
)
\textbf{e}_4 =
0
0
0
0
0
0
0
0
0
0
0
0
1
(
)
\textbf{e}_5 =
k_1
k_2
k_3
k_4
k_5
(
)
\textbf{k} =
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}
\ \wedge \
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
Publish tag vector \((I_1, I_2, \dots, I_s),\) \(C_{\text{assets}} = \prod_{i \in [n]} I_i\) and NIZK \(\Pi_{\text{RevBP}}\)
More on RevelioBP
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}
\ \wedge \
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
To build \(\Pi_{\text{RevBP}},\) we combine the constraints using a scalar \(u \leftarrow \mathbb{Z}_q\)
\prod_{j \in [s]} \left(g^{-k_j} \cdot g_t^{k_j} \cdot \textbf{C}^{\textbf{e}_{i_j}} \cdot I_j^{-1}\right)^{u^{j-1}} = 1,
\implies g^{- \langle \textbf{u}^s, \textbf{k} \rangle} \cdot
g_t^{\langle \textbf{u}^s, \textbf{k} \rangle} \cdot
\textbf{C}^{ \textbf{u}^s \textbf{E}} \cdot
\textbf{I}^{- \textbf{u}^s} = 1,
We then use Inner Product Argument of the form
PoK \left\{
(\textbf{a}, \textbf{b}) \in \mathbb{Z}_q^N \ | \
P = u^{c}\textbf{g}^{\textbf{a}} \textbf{h}^{\textbf{b}} \wedge c = \langle \textbf{a}, \textbf{b} \rangle \
\right\}
s + 2 \text{log}_2(sn+n+s+3) \text{ in } \mathbb{G}, \
5 \text{ in } \mathbb{Z}_q
| RevelioBP proof size | Revelio proof size |
(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q
Performance Trade-offs
| RevelioBP | Revelio | |
|---|---|---|
| Proof size | ||
| Scalability | ||
| Blockchain state | ||
| Output privacy | ||
| Inflation resistance | ||
| Own set size | ||
| Running times |
\mathcal{O}(n)
\mathcal{O}(s+\text{log}_2(sn))
\mathcal{O}(sn)
\mathcal{O}(n)
For UTXO set size \(n=1.6\times 10^5\) and \(s=10^2\)
5\text{KB}
32\text{MB}
(164,68)\\[-3pt]
\text{min}
(34,34)\\[-3pt]
\text{min}
Proof Sizes
We implemented RevelioBP in Rust over \( \mathbb{G} = \texttt{secp256k1}\) elliptic curve
n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Proof size in KB} \longrightarrow
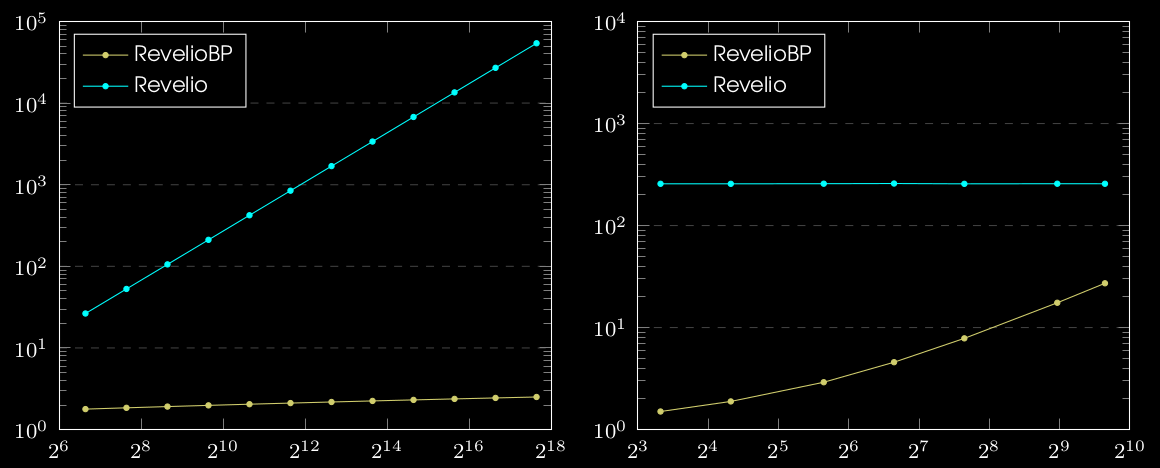
Note: All plots are in log-log scale.
RevelioBP proofs are \(\ge 10X\) shorter that that of Revelio
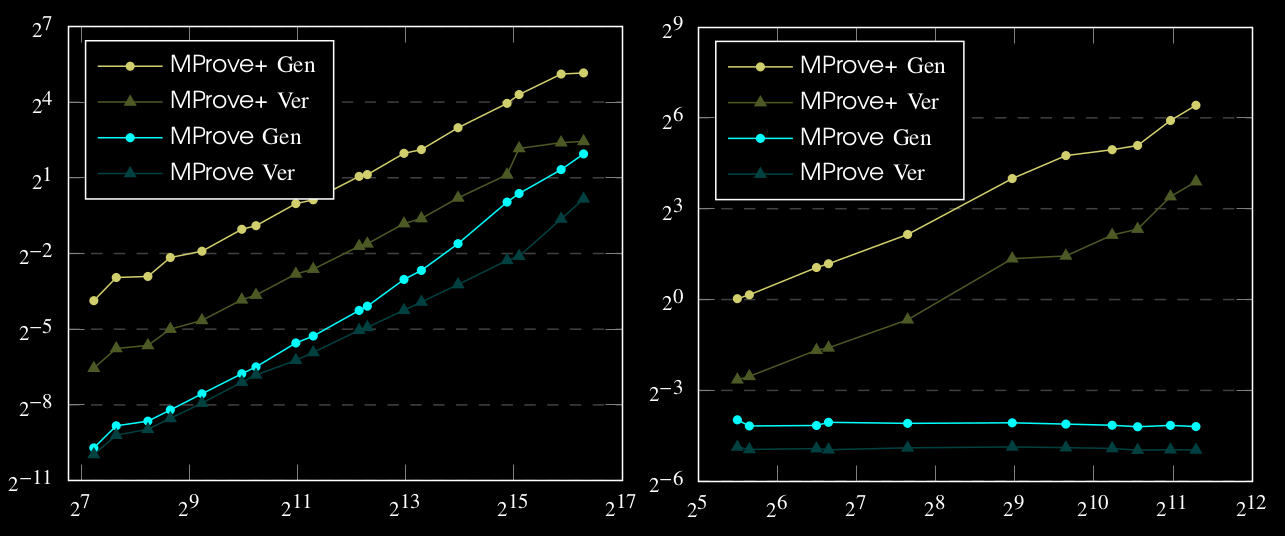
Running Times
RevelioBP proof generation is \(\approx 2X\) slower that of Revelio
n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Running time in mins} \longrightarrow
Note: All plots are in log-log scale.
RevelioBP ver. is \(\approx 3X\) faster than its gen. due to multi-exponentiation
MProve+
Key challenge: Unlinking key-images & one-time addresses in MProve
\Pi_{t_1} =
\left\{
(P_1, I_1,\alpha_1, \beta_1),
\
(P_2, I_2,\alpha_2, \beta_2),
\ \ldots \ ,
\
(P_n, I_n,\alpha_n, \beta_n),
\right\}
\textsf{Tx}_{t_2} = \{\mathcal{R}, I_{2}\}
Use an approach similar to RevelioBP
PoK\left\{ (\textbf{x}, \textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ \bigg| \
\textbf{P}^{\textbf{e}_j} = g^{x_j},
\
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j},
\
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
An MProve+ proof looks like
\Pi^{+}_{t_1} =
\{
\textbf{P},
\textbf{C}\in \mathbb{G}^n, \
\textbf{I} \in \mathbb{G}^s, \
\Pi_{\textsf{\tiny NIZK}}
\}
Implementation Challenges
Implemented MProve+ and MProve in Rust over \(\texttt{ed25519, ristretto}\)
Small subgroup attack possible in \(\texttt{ed25519}\)
Implementation Challenges
Implemented MProve+ and MProve in Rust over \(\texttt{ed25519, ristretto}\)
Small subgroup attack possible in \(\texttt{ed25519}\). For a prime \(q\)
Ristretto constructs a prime order group from an Edwards curve
MProve+ over \(\texttt{ristretto}\) allows generalisation for other Edwards curves
|\mathbb{G}_{\textsf{ed}}| = 8q,
\
|\mathbb{G}_{\textsf{ris}}| = q
We show conversion of Ristretto points to Edwards
Wrote an Elligator support over \(\texttt{ed25519}\) to generate random curve points
Running Times for \(\mathbb{G}_{\textsf{ris}}\)
n \ \longrightarrow
s \ \longrightarrow
\text{Running time in mins} \longrightarrow
Note: All plots are in log-log scale.
s=100
n=5000
n \approx 2000
Thank
Happy to answer any questions!
you!
Aztec-Suyash-Round#2
By Suyash Bagad
Aztec-Suyash-Round#2
Short Presentation of thesis project for Aztec Protocol.
