Aztec's zk\(^2\)-Rollup
Part \(1\)
UTXO vs Account
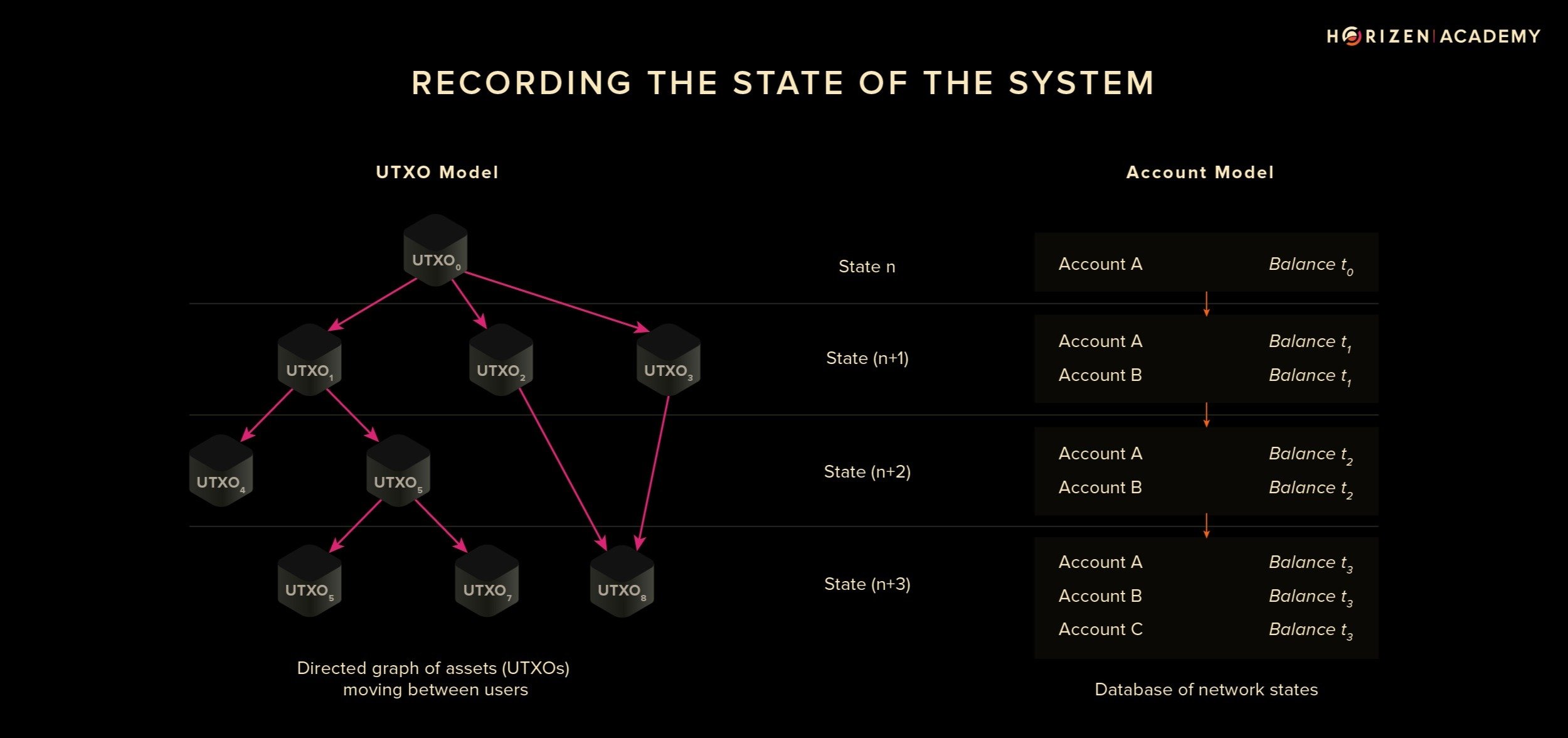
Aztec Model
20
Bob
Alice
Open account
\(\texttt{bob}\)
\(\texttt{alice}\)
8
2
10
10
0.5
1.5
18
2
10
Shield
Rollup Contract
Account UTXO
Value UTXO
\underbrace{\hspace{2.2cm}}
Private sends
\(\text{zkETH}=8.5\)
\(\text{zkDAI}=18\)
\(\text{zkETH}=1.5\)
\(\text{zkDAI}=2\)
Withdraw
\(0\)
1.5
Aztec Notes
- Account balances are calculated by adding up the available UTXOs
- UTXOs are called as notes: \(\textcolor{orange}{\textsf{Account}}\) notes and \(\textcolor{violet}{\textsf{Value}}\) notes
- State transition in UTXO model is tricky
- A user creates an account on zk.money using an alias and a nonce \(n \in \mathbb{Z}^{32}_2\)
- We compute an account identifier as:Â
- Account information is stored in account notes
Account PK
Account id
Spending PK1
\(a_{\text{id}} \ \in \ \mathbb{Z}_2^{32}\)
\(S_1 \ \in \ \mathbb{G}_1\)
\(A \ \in \ \mathbb{G}_1\)
Account PK
Account id
Spending PK2
\(a_{\text{id}} \ \in \ \mathbb{Z}_2^{32}\)
\(S_2 \ \in \ \mathbb{G}\)
\(A \ \in \ \mathbb{G}_1\)
\(a_{\text{id}} \coloneqq \left( n \ \| \ H_{B}\left(\texttt{suyashbagad}\right)[ \ 0 : 224 \ ]\right) \in \mathbb{Z}^{256}_2\)
- Spending keys are used for signing transactions
Aztec Notes
- Aztec uses value notes as a basis for private transactions on Ethereum
Value
Asset id
Nonce
Owner
Secret
\(a \ \in \ \mathbb{Z}_2^{32}\)
\(A \ \in \ \mathbb{G}_1\)
\(n \ \in \ \mathbb{Z}_2^{32}\)
\(v \ \in \ \mathbb{F}_q\)
\(s \ \in \ \mathbb{F}_q\)
- A value note is given as: \(\mathcal{V} = \{a, v, n, \mathcal{O}, s\}\)
- The nonce here is same as the one used in an account note
- A note incorporates the on-chain identity (i.e. account PK) of its owner
- The secret \(s\) is the hiding factor in computing Pedersen commitment to a note:
\mathfrak{C}(\mathcal{V}) \coloneqq
aG_0 + vG_1 + nG_2 + A_xG_3 + A_yG_4 + sG_5
Plonk Overview
Arithmetic Circuit
- A typical computational problem: find solutions to the equation (i.e. \(\textsf{stmt}\))
\(x_1^2 \cdot x_2 + x_1 + 1 = 22\)
\times
x_1
x_1
+
x_2
c
\times
- Witness: \(w \equiv (x_1=3, x_2=2)\), public inputs: \(\ell \equiv (c=1, z=22)\)
- I can convince you that I know a solution \(w\) to \(\{\textsf{stmt}, \ell\}\) without revealing \(w\)Â
- PLONK: Circuit size: \(n=4\), prover: \(\mathcal{O}(n\cdot\text{log}n)\), proof size and verifier: \(\mathcal{O}(1)\)
+
z
\iff
Plonk Arithmetisation
\textcolor{gray}{2.} a_1
\textcolor{gray}{+3.}b_1
\textcolor{gray}{-1.}c_1
\textcolor{gray}{+5} = 0
\textcolor{gray}{0.} a_3
\textcolor{gray}{+0.}b_3
\textcolor{gray}{+1.}a_3b_3
\textcolor{gray}{-1.}c_3
\textcolor{gray}{+0} = 0
(a_i,b_i) \ \textcolor{grey}{+_{\text{ecc}}} \ (c_i, d_i) = (a_{i+1},b_{i+1})
\textsf{ecc gate}:
\underbrace{\hspace{2cm}}
StandardPlonk
\underbrace{\hspace{1cm}}
TurboPlonk
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
\textsf{add gate}:
\textsf{mult gate}:
Width = \(4\)
Circuit size = \(n\)
c_1 = a_i,
d_2 = b_i,
a_{i+1} = c_{n-1},
b_{i+1} = d_{n-1},
\underbrace{\hspace{1cm}}
Copy constraints
Cell-wise permutation
Plonk Preprocessing
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
1
a_1
b_1
c_1
d_1
2
3
-1
0
5
1
0
0
0
-1
1
0
1
0
\delta_1
\delta_2
0
\delta_3
\delta_4
0
1
Constraint Selectors
2n+1
3n-1
3n+2
4n-1
Permutation Selectors
S_{\sigma_1}
S_{\sigma_2}
S_{\sigma_3}
S_{\sigma_4}
q_L
q_R
q_O
q_M
q_C
q_+
q_\textsf{ecc}
Plonk Preprocessing
2
3
-1
0
5
1
0
0
0
-1
1
0
1
0
\delta_1
\delta_2
0
\delta_3
\delta_4
0
1
Constraint Selectors
2n+1
3n-1
3n+2
4n-1
Permutation Selectors
S_{\sigma_1}
S_{\sigma_2}
S_{\sigma_3}
S_{\sigma_4}
q_L
q_R
q_O
q_M
q_C
q_+
q_\textsf{ecc}
- Compute and store coset-FFTs of selector polynomial over domain of size \(4n\)
- Verification key consists of commitments to the selector polynomials
- Selector polynomials are fixed for a given circuit/computation
- FFT: \((7+4) \times 4n\)
- MSM: \((7 + 4) \times n\)
- Memory: \((7 + 4) \times 5n\)
Plonk Prover: Round 0
- Convert wire polynomials to coefficient form
\left(a'_{1}, a'_{2}, a'_{3}, \dots, a'_{n}\right) \ \leftarrow \ \textcolor{lightgreen}{\textsf{iFFT}}\left(a_{1}, a_{2}, a_{3}, \dots, a_{n}\right)
\left(b'_{1}, b'_{2}, b'_{3}, \dots, b'_{n}\right) \ \leftarrow \ \textcolor{lightgreen}{\textsf{iFFT}}\left(b_{1}, b_{2}, b_{3}, \dots, b_{n}\right)
\left(c'_{1}, c'_{2}, c'_{3}, \dots, c'_{n}\right) \ \leftarrow \ \textcolor{lightgreen}{\textsf{iFFT}}\left(c_{1}, c_{2}, c_{3}, \dots, c_{n}\right)
\left(d'_{1}, d'_{2}, d'_{3}, \dots, d'_{n}\right) \ \leftarrow \ \textcolor{lightgreen}{\textsf{iFFT}}\left(d_{1}, d_{2}, d_{3}, \dots, d_{n}\right)
\textcolor{lightgreen}{\textsf{FFT}}
4 \times n
\textcolor{lightpink}{\textsf{MSM}}
-
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
X
\omega_1
\omega_2
\omega_3
\omega_4
\dots
\dots
\omega_{n-2}
\omega_{n-1}
\omega_{n}
a_1
a_2
a_3
a_4
\dots
a_{n-2}
\dots
a_{n-1}
a_{n}
a(X)
\textsf{Round}
0
1
2
3
4
5
Plonk Prover: Round 1
- Commit to wire polynomials
\textcolor{lightgreen}{\textsf{FFT}}
4 \times n
\textcolor{lightpink}{\textsf{MSM}}
-
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
\textsf{Round}
0
1
2
3
4
5
\textcolor{orange}{[a]} = a'_1 \textcolor{grey}{[s_1]} + a'_2 \textcolor{grey}{[s_2]} + \dots + a'_n \textcolor{grey}{[s_n]}
\textcolor{orange}{[b]} = b'_1 \textcolor{grey}{[s_1]} + b'_2 \textcolor{grey}{[s_2]} + \dots + b'_n \textcolor{grey}{[s_n]}
\textcolor{orange}{[c]} = c'_1 \textcolor{grey}{[s_1]} + c'_2 \textcolor{grey}{[s_2]} + \dots + c'_n \textcolor{grey}{[s_n]}
\textcolor{orange}{[d]} = d'_1 \textcolor{grey}{[s_1]} + d'_2 \textcolor{grey}{[s_2]} + \dots + d'_n \textcolor{grey}{[s_n]}
- Update proof: \(\pi \leftarrow (\textcolor{orange}{[a]}, \textcolor{orange}{[b]}, \textcolor{orange}{[c]}, \textcolor{orange}{[d]})\)
4 \times n
-
Plonk Prover: Round 2
- Compute permutation polynomial \(z(X)\)
\textcolor{lightgreen}{\textsf{FFT}}
4 \times n
\textcolor{lightpink}{\textsf{MSM}}
-
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
\textsf{Round}
0
1
2
3
4
5
\textcolor{orange}{[z]} = z'_1 \textcolor{grey}{[s_1]} + z'_2 \textcolor{grey}{[s_2]} + \dots + z'_n \textcolor{grey}{[s_n]}
4 \times n
-
X
\omega_1
\omega_2
\omega_3
\omega_4
\dots
\dots
\omega_{n-2}
\omega_{n-1}
\omega_{n}
z_1
z_2
z_3
z_4
\dots
z_{n-2}
\dots
z_{n-1}
z_{n}
z(X)
\small z_i =
\begin{cases}
1 & i = 1 \\
\prod_{j=1}^{i}
\frac{
(a_j \textcolor{grey}{+ \beta \omega^j + \gamma})
(b_j \textcolor{grey}{+ \beta k_1\omega^j + \gamma})
(c_j \textcolor{grey}{+ \beta k_2\omega^j + \gamma})
(d_j \textcolor{grey}{+ \beta k_3\omega^j + \gamma})}
{
(a_j \textcolor{grey}{+ \beta \sigma_1(j) + \gamma})
(b_j \textcolor{grey}{+ \beta \sigma_2(j) + \gamma})
(c_j \textcolor{grey}{+ \beta \sigma_3(j) + \gamma})
(d_j \textcolor{grey}{+ \beta \sigma_4(j) + \gamma})
} & i >1
\end{cases}
\left(z'_{1}, z'_{2}, z'_{3}, \dots, z'_{n}\right) \ \leftarrow \ \textcolor{lightgreen}{\textsf{iFFT}}\left(z_{1}, z_{2}, z_{3}, \dots, z_{n}\right)
1 \times n
1 \times n
Plonk Prover: Round 3
- Compute quotient polynomial \(t(X)\)
\begin{aligned}
t(X) =&
\left(a(X)b(X)\textcolor{gray}{q_M(X)} + a(X)\textcolor{gray}{q_L(X)} + b(X)\textcolor{gray}{q_R(X)} + c(X)\textcolor{gray}{q_O(X)} + \textcolor{gray}{q_C(X)}\right){\scriptsize \frac{1}{Z_H(X)}} + \\
&
(a(X) \textcolor{grey}{+ \beta X + \gamma})
(b(X) \textcolor{grey}{+ \beta k_1X + \gamma})
(c(X) \textcolor{grey}{+ \beta k_2X + \gamma})
(d(X) \textcolor{grey}{+ \beta k_3X + \gamma})
(z(X))
{\scriptsize\frac{\alpha}{Z_H(X)}} -\\
&
(a(X) \textcolor{grey}{+ \beta S_{\sigma_1}(X) + \gamma})
(b(X) \textcolor{grey}{+ \beta S_{\sigma_2}(X) + \gamma})
(c(X) \textcolor{grey}{+ \beta S_{\sigma_3}(X) + \gamma})
(d(X) \textcolor{grey}{+ \beta S_{\sigma_4}(X) + \gamma})
(z(X\omega))
{\scriptsize\frac{\alpha}{Z_H(X)}} +\\
&
(z(X) - 1)\textcolor{gray}{L_1(X)}
{\scriptsize\frac{\alpha^2}{Z_H(X)}}
\end{aligned}
\textsf{arith gate constraint}
\textsf{copy constraint}
- Number of wires decide the degree of \(t(X)\): \((4n-5)\)
- Lots of polynomial multiplication and division in computing \(t(X)\)
- Easier to compute in evaluation form
- But need the evaluation over a domain of size \(4n\) 😯
- Hence need all component polynomials to be in coset-fft form
Plonk Prover: Round 3
- Compute quotient polynomial \(t(X)\)
\textcolor{lightgreen}{\textsf{FFT}}
4 \times n
\textcolor{lightpink}{\textsf{MSM}}
-
\textsf{Round}
0
1
2
3
4
5
4 \times n
-
1 \times n
1 \times n
X
g\omega'_1
g\omega'_2
g\omega'_3
\dots
\dots
g\omega'_{4n}
g\omega'_{4n-1}
g\omega'_{4n-2}
\dots
\dots
\leftarrow \textcolor{olive}{\textsf{coset-FFT}}(a'_1, a'_2, \dots, a'_n)
c(X)
\vdots
\vdots
d(X)
\vdots
\vdots
a(X)
a''_1
a''_2
a''_3
\dots
\dots
\dots
a''_{4n-2}
a''_{4n-1}
z''_{4n}
b(X)
b''_1
b''_2
b''_3
\dots
b''_{4n-2}
\dots
b''_{4n-1}
b''_{4n}
\dots
z(X)
z''_1
z''_2
z''_3
\dots
z''_{4n-2}
\dots
z''_{4n-1}
z''_{4n}
\dots
\leftarrow \textcolor{olive}{\textsf{coset-FFT}}(b'_1, b'_2, \dots, b'_n)
\leftarrow \textcolor{olive}{\textsf{coset-FFT}}(z'_1, z'_2, \dots, z'_n)
\leftarrow \textcolor{olive}{\textsf{coset-FFT}}(c'_1, c'_2, \dots, c'_n)
\leftarrow \textcolor{olive}{\textsf{coset-FFT}}(d'_1, d'_2, \dots, d'_n)
5 \times 4n
Plonk Prover: Round 3
- Compute quotient polynomial \(t(X)\)
\textcolor{lightgreen}{\textsf{FFT}}
4 \times n
\textcolor{lightpink}{\textsf{MSM}}
-
\textsf{Round}
0
1
2
3
4
5
4 \times n
-
1 \times n
1 \times n
5 \times 4n
\begin{aligned}
t(X) =& \left(t_{1} + t_{2}\textcolor{gray}{X} + t_{3}\textcolor{gray}{X^2} + \dots + t_{n}\textcolor{gray}{X^{n-1}}\right) + \\
& \left(t_{n+1} + t_{n+2}\textcolor{gray}{X} + t_{n+3}\textcolor{gray}{X^2} + \dots + t_{2n}\textcolor{gray}{X^{n-1}}\right)\textcolor{gray}{X^n} + \\
& \left(t_{2n+1} + t_{2n+2}\textcolor{gray}{X} + t_{2n+3}\textcolor{gray}{X^2} + \dots + t_{3n}\textcolor{gray}{X^{n-1}}\right)\textcolor{gray}{X^{2n}} + \\
& \left(t_{3n+1} + t_{3n+2}\textcolor{gray}{X} + t_{3n+3}\textcolor{gray}{X^2} + \dots + t_{4n}\textcolor{gray}{X^{n-1}}\right)\textcolor{gray}{X^{3n}} \\
\end{aligned}
t_1(X)
t_2(X)
t_3(X)
t_4(X)
\textcolor{orange}{[t_1]} = t_1 \textcolor{grey}{[s_1]} + t_2 \textcolor{grey}{[s_2]} + \dots + t_n \textcolor{grey}{[s_n]}
\textcolor{orange}{[t_2]} = t_{n} \textcolor{grey}{[s_1]} + t_{n+1} \textcolor{grey}{[s_2]} + \dots + t_{2n}\textcolor{grey}{[s_n]}
\textcolor{orange}{[t_3]} = t_{2n} \textcolor{grey}{[s_1]} + t_{2n+1} \textcolor{grey}{[s_2]} + \dots + t_{3n}\textcolor{grey}{[s_n]}
\textcolor{orange}{[t_4]} = t_{3n} \textcolor{grey}{[s_1]} + t_{3n+1} \textcolor{grey}{[s_2]} + \dots + t_{4n}\textcolor{grey}{[s_n]}
4 \times n
Plonk Prover: Round 4, 5
- Round 4: Compute opening evaluations
\bar{a}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((a'_1, a'_2, \dots, a'_n), \ \textcolor{gray}{\mathfrak{z}})
\bar{b}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((b'_1, b'_2, \dots, b'_n), \ \textcolor{gray}{\mathfrak{z}})
\bar{c}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((c'_1, c'_2, \dots, c'_n), \ \textcolor{gray}{\mathfrak{z}})
\bar{d}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((d'_1, d'_2, \dots, d'_n), \ \textcolor{gray}{\mathfrak{z}})
\bar{s}_{\sigma_1}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((S_{\sigma_1, 1}, \dots, S_{\sigma_1, n}), \ \textcolor{gray}{\mathfrak{z}})
\bar{s}_{\sigma_2}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((S_{\sigma_2, 1}, \dots, S_{\sigma_2, n}), \ \textcolor{gray}{\mathfrak{z}})
\bar{s}_{\sigma_3}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((S_{\sigma_3, 1}, \dots, S_{\sigma_3, n}), \ \textcolor{gray}{\mathfrak{z}})
\bar{z}_{\omega}\leftarrow \textcolor{maroon}{\textsf{evaluate}}((z'_1, z'_2, \dots, z'_n), \ \textcolor{gray}{\mathfrak{z}\omega})
- Round 5: Compute linearisation polynomial \(r(X)\)
\begin{aligned}
r(X) =&
\left(\bar{a}\bar{b}\textcolor{gray}{q_M(X)} + \bar{a}\textcolor{gray}{q_L(X)} + \bar{b}\textcolor{gray}{q_R(X)} + \bar{c}\textcolor{gray}{q_O(X)} + \textcolor{gray}{q_C(X)}\right) + \\
&
\Big[
(\bar{a} \textcolor{grey}{+ \beta \mathfrak{z} + \gamma})
(\bar{b} \textcolor{grey}{+ \beta k_1\mathfrak{z} + \gamma})
(\bar{c} \textcolor{grey}{+ \beta k_2\mathfrak{z} + \gamma})
(\bar{d} \textcolor{grey}{+ \beta k_3\mathfrak{z} + \gamma})
(z(X))
\Big]
\alpha -\\
&
\Big[
(\bar{a} \textcolor{grey}{+ \beta \bar{s}_{\sigma_1} + \gamma})
(\bar{b} \textcolor{grey}{+ \beta \bar{s}_{\sigma_2} + \gamma})
(\bar{c} \textcolor{grey}{+ \beta \bar{s}_{\sigma_3} + \gamma})
(\bar{d} \textcolor{grey}{+ \beta S_{\sigma_4}(X) + \gamma})
(z_\omega)
\Big]
\alpha +\\
&
(z(X) - 1)\textcolor{gray}{L_1(\mathfrak{z})}
\alpha^2
\end{aligned}
- \(r(X)\) is a degree-\((n-1)\) polynomial
- By combining many polynomials linearly, we avoid opening them individually
Plonk Prover: Round 5
- Round 5 (contd.): Compute KZG opening proofs
W_\mathfrak{z}(X) \leftarrow \textcolor{green}{\textsf{KZG.open}}\left( \big\{r(X), a(X), b(X), c(X), d(X), S_{\sigma_1}(X), S_{\sigma_2}(X), S_{\sigma_3}(X)\big\},
\ \textcolor{grey}{\mathfrak{z}} \right)
W_{\mathfrak{z}\omega}(X) \leftarrow \textcolor{green}{\textsf{KZG.open}}\left( \big\{z(X)\big\},
\ \textcolor{grey}{\mathfrak{z}\omega} \right)
\textcolor{orange}{[W_{\mathfrak{z}}]} = w_1 \textcolor{grey}{[s_1]} + w_2 \textcolor{grey}{[s_2]} + \dots + w_n \textcolor{grey}{[s_n]}
\textcolor{orange}{[W_{\mathfrak{z}\omega}]} = w'_1 \textcolor{grey}{[s_1]} + w'_2 \textcolor{grey}{[s_2]} + \dots + w'_n \textcolor{grey}{[s_n]}
\textcolor{lightgreen}{\textsf{FFT}}
4 \times n
\textcolor{lightpink}{\textsf{MSM}}
-
\textsf{Round}
0
1
2
3
4
5
4 \times n
-
1 \times n
1 \times n
5 \times 4n
4 \times n
2 \times n
-
-
-
\(\pi = \bigg\{\underbrace{[a]_1, [b]_1, [c]_1, [d]_1, [z]_1, [t_1]_1, [t_2]_1, [t_3]_1, [t_4]_1, [W_{\mathfrak{z}}]_1, [W_{\mathfrak{z\omega}}]_1}_{\mathbb{G}_1^{2w + 3}}, \ \underbrace{\bar{a}, \bar{b}, \bar{c}, \bar{d}, \bar{z}_{\omega}, \bar{s}_{\sigma_1}, \bar{s}_{\sigma_2}, \bar{s}_{\sigma_3}}_{\mathbb{F}_p^{2w}} \bigg\}\)
Plonk Prover: Benchmarking
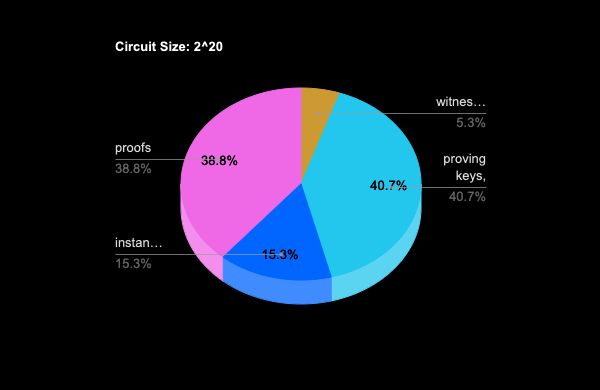
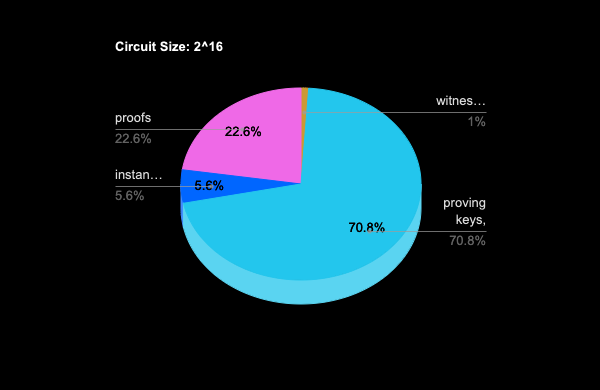
Circuit size: \(2^{16}\)
Circuit size: \(2^{20}\)
Recursion Basics
Recursive Proof Verification
- A Plonk proof \(\pi\) is verified by checking equality of polynomial evaluations
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) = F_1(x) - F_1(\mathfrak{z})\)
\(W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega) = F_2(x) - F_2(\mathfrak{z}\omega)\)
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) + u \cdot (W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega))= F_1(x) - F_1(\mathfrak{z}) + u \cdot (F_2(x) - F_2(\mathfrak{z}\omega))\)
\(\pi = \bigg\{\underbrace{[a]_1, [b]_1, [c]_1, [d]_1, [z]_1, [t_1]_1, [t_2]_1, [t_3]_1, [t_4]_1, [W_{\mathfrak{z}}]_1, [W_{\mathfrak{z\omega}}]_1}_{\mathbb{G}_1^{2w + 3}}, \ \underbrace{\bar{a}, \bar{b}, \bar{c}, \bar{d}, \bar{z}_{\omega}, \bar{s}_{\sigma_1}, \bar{s}_{\sigma_2}, \bar{s}_{\sigma_3}}_{\mathbb{F}_p^{2w}} \bigg\}\)
Recursive Proof Verification
- A Plonk proof \(\pi\) is verified by checking equality of polynomial evaluations
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) = F_1(x) - F_1(\mathfrak{z})\)
\(W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega) = F_2(x) - F_2(\mathfrak{z}\omega)\)
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) + u \cdot (W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega))= F_1(x) - F_1(\mathfrak{z}) + u \cdot (F_2(x) - F_2(\mathfrak{z}\omega))\)
\(\underbrace{\left(W_{\mathfrak{z}}(x) + uW_{\mathfrak{z\omega}}(x)\right)}_{P_0} \cdot x = \underbrace{\left(\mathfrak{z}W_{\mathfrak{z}}(x) + u\mathfrak{z}\omega W_{\mathfrak{z\omega}}(x)) + F(x) - E\right)}_{P_1}\)
\(P_0 \cdot x \stackrel{?}{=} P_1\)
\(\pi = \bigg\{\underbrace{[a]_1, [b]_1, [c]_1, [d]_1, [z]_1, [t_1]_1, [t_2]_1, [t_3]_1, [t_4]_1, [W_{\mathfrak{z}}]_1, [W_{\mathfrak{z\omega}}]_1}_{\mathbb{G}_1^{2w + 3}}, \ \underbrace{\bar{a}, \bar{b}, \bar{c}, \bar{d}, \bar{z}_{\omega}, \bar{s}_{\sigma_1}, \bar{s}_{\sigma_2}, \bar{s}_{\sigma_3}}_{\mathbb{F}_p^{2w}} \bigg\}\)
Recursive Proof Verification
- Suppose we have \(n\) Plonk proofs \((\pi_1, \pi_2, \dots, \pi_m)\) with verification equations:
\(P_0^{(i)} \cdot x \stackrel{?}{=} P_1^{(i)} \quad \forall i \in [m]\)
\(\left(P_0^{(1)} + qP_0^{(2)} + \dots +Â q^{m-1}P_0^{(m)}\right) \cdot x \stackrel{?}{=} \left(P_1^{(1)} + qP_1^{(2)} \dots + q^{m-1}P_1^{(m)}\right)\)
- A single pairing is \(\approx 300\) times costlier than a scalar multiplication
- Using recursive verification, we can verify any number of Plonk proofs using a single pairing
- Too good to be true? The circuit size presents a practical constraint on the number of proofs to be rolled up
- Failure of the recursive check implies at least one of the \(n\) proofs is wrong
Recursive Verification Circuit
- To recursively verify proofs, we only need to compute:
P_{0, \textsf{next}} = \left(P_0^{(1)} + qP_0^{(2)} + \dots + q^{m-1}P_0^{(m)}\right) \ +
\left(W_{\mathfrak{z}}(x) + uW_{\mathfrak{z\omega}}(x)\right)
P_{1, \textsf{next}} = \left(P_1^{(1)} + qP_1^{(2)} + \dots + q^{m-1}P_1^{(m)}\right) \
+ \left(\mathfrak{z}W_{\mathfrak{z}}(x) + u\mathfrak{z}\omega W_{\mathfrak{z\omega}}(x)) + F(x) - E\right)
Past \(n\) proofs
Current proof
- So this is a scalar multiplication of size \(\approx (m + 10)\)
- This involves non-native computation: i.e. computation in \(\mathbb{F}_q\) over a circuit modulo \(\mathbb{F}_p\) where \(q \gg p\).
- Performing non-native arithmetic over arithmetic circuits is very costly
- Therefore recursive verification circuits tend to be huge
Aztec Circuit Landscape
Transaction Proofs
Account Proofs
\pi^{\textsf{js}}_1 \qquad \quad
\pi^{\textsf{js}}_2 \qquad \quad
\pi^{\textsf{js}}_3 \qquad \quad
\pi^{\textsf{js}}_4
\pi^{\textsf{acc}}_1 \qquad \ \
\pi^{\textsf{acc}}_2 \qquad \ \
\pi^{\textsf{acc}}_3 \qquad \ \
\pi^{\textsf{acc}}_4
\pi^{\textsf{tx}}_1
\pi^{\textsf{tx}}_2
\pi^{\textsf{root}}_1
\pi^{\textsf{std}}_1
Root Rollup Proof:
Tx Rollup Proofs:
Root Verifier Proof:
2^{16}
2^{15}
2^{21}
2^{22}
2^{23}
\textsf{standard plonk}
\textsf{turbo plonk}
Aztec's zk-zk-Rollup Analysis
By Suyash Bagad
