A Proof of Reserves Protocol with Short Proofs and a Method to Estimate Amount Upper Bounds for MimbleWimble
Suyash Bagad
Roll Number: 15D070007
Department of Electrical Engineering, IIT Bombay
Dual Degree (B.Tech + M.Tech) Project
Prof. Saravanan Vijayakumaran
Guide
June 24, 2020
Proof of Reserves
Short Proofs
Amount Upper Bounds
MimbleWimble
Outline
Novel proof of reserves protocol with short sizes for MimbleWimble
RevelioBP vs Revelio!
Confidentiality of Amounts in Grin
Presented at Crypto Valley Conference on Blockchain Technology, 2020
Focus on performance trade-offs and implementation
Work accepted at IEEE Security & Privacy on Blockchain, 2020
Graph-based analysis of the Grin Blockchain
Part I
Novel Proof of Reserves Protocol with Short sizes for MimbleWimble
Revelio
\mathcal{C}_{\text{own}}
C = g^{k} \cdot h^{a}
C \in \mathcal{C}_{\text{own}} \implies k \text{ is known}
Each output in MimbleWimble is a Pedersen Commitment
Pedersen Commitments are homomorphic, perfectly hiding and computationally binding
For an amount \(a \in \{0,1,\dots,2^{64}-1\}\) and blinding factor \(k \in \mathbb{Z}_q\)
where \(g,h \in \mathbb{G}\) such that DL relation between them is unknown
Revelio
\mathcal{C}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13
For each \(C_i \in \mathcal{C}_{\text{anon}},\) publish the tags \((I_1, \dots, I_n) \in \mathbb{G}^n\) where \( n = |\mathcal{C}_{\text{anon}}|\)
Publish \(C_{\text{assets}} = \prod_{i \in [n]} I_i,\) and NIZK proofs \(\sigma_i \in \mathbb{Z}_q^5 \ \forall i \in [n]\)
PoK\big\{\underbrace{(\alpha,\beta,\gamma)}_{\text{secret}} \ | \ \underbrace{(C_i = g^{\alpha} \cdot h^{\beta} \ \wedge \ I_i = g_t^{\alpha} \cdot h^{\beta}) \vee (I_i = g_t^{\gamma}) }_{\text{statement}} \big\}
where \(y_i = \mathcal{H}(k_{\text{exch}}, C_i) \in \Z_q\)
I_i =
\begin{cases}
\ g_1^{k_i} \cdot h^{a_i} & \text{if } C_i \in \mathcal{C}_{\text{own}},\\
\ g_1^{y_i} & \text{if } C_i \notin \mathcal{C}_{\text{own}},
\end{cases}
\(\implies y_i \longleftrightarrow C_{i} \).
Drawbacks of Revelio
Proof size linear in anonymity set size
(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q
Can we shrink proofs sizes to \(\mathcal{O}( \text{log}_2(n))\)?
Can we link the blockchain state to the proof of reserves?
Privacy of outputs depends on the anonymity set \(n\)
RevelioBP!
RevelioBP!
1
2
3
4
5
6
7
8
9
10
12
11
13
0
1
0
0
0
0
0
0
0
0
0
0
0
(
)
\textbf{e}_1 =
0
0
0
0
0
1
0
0
0
0
0
0
0
(
)
\textbf{e}_2 =
0
0
0
0
0
0
0
0
1
0
0
0
0
(
)
\textbf{e}_3 =
0
0
0
0
0
0
0
0
0
1
0
0
0
(
)
\textbf{e}_4 =
0
0
0
0
0
0
0
0
0
0
0
0
1
(
)
\textbf{e}_5 =
k_1
k_2
k_3
k_4
k_5
(
)
\textbf{k} =
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}
\ \wedge \
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
Publish tag vector \((I_1, I_2, \dots, I_s),\) \(C_{\text{assets}} = \prod_{i \in [n]} I_i\) and NIZK \(\Pi_{\text{RevBP}}\)
More on RevelioBP
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}
\ \wedge \
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
To build \(\Pi_{\text{RevBP}},\) we combine the constraints using a scalar \(u \leftarrow \mathbb{Z}_q\)
\prod_{j \in [s]} \left(g^{-k_j} \cdot g_t^{k_j} \cdot \textbf{C}^{\textbf{e}_{i_j}} \cdot I_j^{-1}\right)^{u^{j-1}} = 1,
\implies g^{- \langle \textbf{u}^s, \textbf{k} \rangle} \cdot
g_t^{\langle \textbf{u}^s, \textbf{k} \rangle} \cdot
\textbf{C}^{ \textbf{u}^s \textbf{E}} \cdot
\textbf{I}^{- \textbf{u}^s} = 1,
We then use Inner Product Argument of the form
PoK \left\{
(\textbf{a}, \textbf{b}) \in \mathbb{Z}_q^N \ | \
P = u^{c}\textbf{g}^{\textbf{a}} \textbf{h}^{\textbf{b}} \wedge c = \langle \textbf{a}, \textbf{b} \rangle \
\right\}
s + 2 \text{log}_2(sn+n+s+3) \text{ in } \mathbb{G}, \
5 \text{ in } \mathbb{Z}_q
| RevelioBP proof size | Revelio proof size |
(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q
Performance
We implemented RevelioBP in Rust over \( \mathbb{G} = \texttt{secp256k1}\) elliptic curve
n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Proof size in KB} \longrightarrow
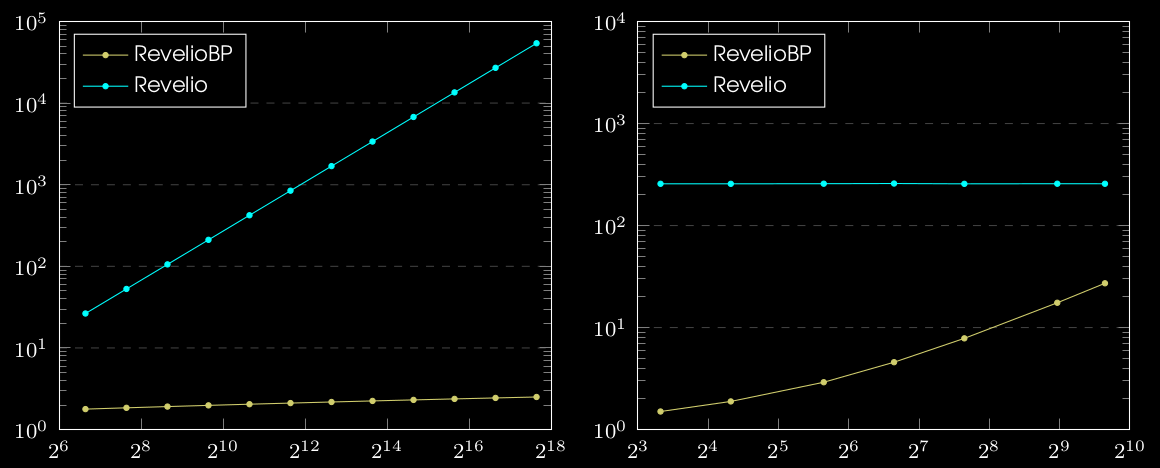
Note: All plots are in log-log scale.
RevelioBP proofs are ~10X shorter that that of Revelio
Performance
RevelioBP proof generation is ~2X slower that of Revelio
n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Running time in mins} \longrightarrow
Note: All plots are in log-log scale.
RevelioBP ver. is ~3X faster than its gen. due to multi-exponentiation
Performance Trade-offs
| RevelioBP | Revelio | |
|---|---|---|
| Proof size | ||
| Scalability | ||
| Blockchain state | ||
| Output privacy | ||
| Inflation resistance | ||
| Own set size | ||
| Running times | ||
| Parallelizable |
\mathcal{O}(n)
\mathcal{O}(s+\text{log}_2(sn))
\mathcal{O}(sn)
\mathcal{O}(n)
For UTXO set size \(n=1.6\times 10^5\) and \(s=10^2\)
5\text{KB}
32\text{MB}
(164,68)\\[-3pt]
\text{min}
(34,34)\\[-3pt]
\text{min}
Part II
On the Confidentiality of Amounts in Grin
Estimating Upper Bound on Amounts in Grin
Given an output \(P \in \mathbb{G}\) it is infeasible to find the amount it commits to!
Can the transaction rules reveal anything about amounts in Grin?
P = g^k \cdot h^a \in \mathbb{G}
A Grin Block
| Block height |
| Inputs | Outputs |
h
I_1,
O_1, O_2, O_3
| Reg. Transaction #2 |
| Inputs | Outputs |
I_3, I_4, I_5
O_4
| Reg. Transaction #1 |
| Inputs | Outputs |
| - |
O_{\text{cb}}
| Coinbase Transaction |
I_2
Dandelion
| Block height |
| Inputs | Outputs |
|
|
I_1
h
I_2
I_3
I_4
I_5
O_{\text{cb}}
O_1
O_2
O_3
O_4
Cut-through
| Block height |
| Inputs | Outputs |
|
|
I_1
h
I_2
I_3
I_4
O_{\text{cb}}
O_1
O_2
O_4
I_5 = O_3!
Block added to Blockchain!
Main Idea
| Block height |
| Inputs | Outputs |
|
|
I_1^{h_3}
h_3
I_2^{h_3}
O_{\text{cb}}^{h_3}
O_1^{h_3}
O_2^{h_3}
O_3^{h_3}
| Fees |
f_{h_3}
| Block height |
| Inputs | Outputs |
|
|
I_1^{h_2}
h_2
O_{\text{cb}}^{h_2}
O_1^{h_2}
O_2^{h_2}
| Fees |
f_{h_2}
| Block height |
| Inputs | Outputs |
|
|
I_1^{h_1}
h_1
O_{\text{cb}}^{h_1}
O_1^{h_1}
| Fees |
f_{h_1}
I_2^{h_1}
\mathcal{A}(I_{1}^{h_2}) = \mathcal{A}(O_{cb}^{h_1}) = r+f_{h_1}
\ \implies \
\mathcal{A}(O_{1}^{h_2}) + \mathcal{A}(O_{2}^{h_2}) = r+f_{h_1} - f_{h_2}
\therefore \quad
\mathcal{A}(O_{j}^{h_2}) \le r+f_{h_1}-f_{h_2} \quad \forall j=1,2
\therefore \quad
\mathcal{A}(I_{1}^{h_3}) + \mathcal{A}(I_{2}^{h_3}) \le 2r + f_{h_1}
\mathcal{A}(I_{1}^{h_3}) = \mathcal{A}(O_{\text{cb}}^{h_2}) = r+f_{h_2}, \quad
\mathcal{A}(I_{2}^{h_3}) = \mathcal{A}(O_{2}^{h_2}) \le (r+f_{h_1}-f_{h_2})
\therefore \quad
\mathcal{A}(O_{1}^{h_3}) + \mathcal{A}(O_{2}^{h_3}) + \mathcal{A}(O_{3}^{h_3}) \le 2r + f_{h_1} - f_{h_3}
\therefore \quad
\mathcal{A}(O_{j}^{h_3}) \le 2r + f_{h_1} - f_{h_3} \quad \forall j=1,2,3
General strategy: Compute number of donor coinbase outputs!
\therefore \quad
\mathcal{A}(O_{j}^{h_3}) \le (r+f_{h_1}) + (r+f_{h_2}) - (f_{h_2}+f_{h_3}) \quad \forall j=1,2,3
Grin Blockchain as a DiGraph
We define a directed graph \(G = (V,E)\) such that
Nodes \(V = V_{\text{bl}} \cup V_{\text{cb}}, \) where \( V_{\text{bl}} \) are blocks and \(V_{\text{cb}}\) are coinbase outputs
Edges \(E = E_1 \cup E_2\) where
\(E_1 = (v_1, v_2) \in V_{\text{cb}} \times V_{\text{bl}} \) if coinbase output \(v_1\) is spent in block \(v_2\)
\(E_2 = (v_1, v_2) \in V_{\text{bl}}^2 \) if at least one RTO in block \(v_1\) is spent in block \(v_2\)
\(h_1\)
\(h_1\)
\(h_2\)
\(h_2\)
\(h_3\)
\(h_3\)
Flow Upper Bounds
A vertex \(c \in V_{\text{cb}}\) in \(G\) is called a donor of a block \(b \in V_{\text{bl}}\) if there is a directed path from \(c\) to \(b\) in \(G\).
\(1499\)
\(16\)
\(1482\)
\(1469\)
\(1458\)
\(1481\)
\(1489\)
\(1495\)
\(1493\)
\(18\)
\(1479\)
\(38\)
\(33\)
\(9\)
\(5\)
\(7\)
Subgraph for \(h=1499\), \(G^{(h)} = (V^{(h)}, E^{(h)})\) where \(V^{(h)} = V^{(h)}_{\text{bl}} \cup V^{(h)}_{\text{cb}}\)
$$ \therefore \ \mathcal{A}(O^{h}) \le 7r + \sum_{b \in V_{\text{cb}}^{(h)}} f_b - \sum_{b \in V_{\text{bl}}^{(h)}} f_b $$
Results
Analysis for RTOs in 612,102 blocks (till March 17th, 2020)
\(\text{Flow ratio of RTO (FR)} = \frac{\text{Flow upper bound of RTO}}{\text{Trivial upper bound of RTO}}\)
For gauging effectiveness of flow upper bounds, we compute and plot
\(\text{Block height}\)
\(\text{Flow ratio}\)
\(88\%\) blocks have \(FR > 0.9\),
\(6.6\%\) blocks with \(h>10^5\) have \(FR < 0.5\)
Results
Unspent RTOs depict the current state of the Blockchain (Fig. 2)
\(\text{Block height}\)
\(\text{Flow ratio}\)
Jagged pattern in Flow ratio is observed in Fig. 1, Why?
\(983\) URTOs have upper bound less that \(1800\)
\(\text{Flow ratio}\)
\( \% \text{ of URTO set}\)
\(95\%\) of \(110,149\) URTOs have \(FR > 0.9\)
Figure 1
Figure 2
Conclusion
Amounts in very few RTOs found to be in a narrow range
Confidentiality of most URTOs is preserved, however...
Transaction structure could reveal some information about amounts inspite of perfectly hiding commitments
Linkability in inputs and outputs could be leveraged for tighter bounds
Would be interesting to design such analysis for Beam, Monero,...
References I
A. Poelstra, "MimbleWimble" [Online], Available:
T. P. Pedersen, "Non-Interactive and Information-Theoretic Secure Verifiable Secret Sharing", in Advances in Cryptology - CRYPTO '91, Springer, 1992, pp. 129-140.
M. Möser, et al. “An Empirical Analysis of Traceability in the Monero Blockchain”. Proceedings on Privacy Enhancing Technologies (2018)
"Linking 96% of Grin transactions" [Online], Available:
A. Kumar, C. Fischer, S. Tople and P. Saxena, "A traceability analysis of Monero’s blockchain", European Symposium on Research in Computer Security – ESORICS 2017, pp. 153-173, 2017.
References II
A. Dutta and S. Vijayakumaran, "Revelio: A MimbleWimble Proof of Peserves Protocol", in Crypto Valley Conference on Blockchain Technology (CVCBT), June 2019, pp. 7–11.
R. W. F. Lai, V. Ronge, T. Ruffing, D. Schröder, S. A. K. Thyagarajan, and J. Wang, “Omniring: Scaling private payments without trusted setup,” in Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, November 2019
"RevelioBP simulation code" [Online], Available:
B. Bünz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille, and G. Maxwell, "Bul-
letproofs: Short proofs for confidential transactions and more", in IEEE
Symposium on Security and Privacy (SP), May 2018, pp. 315–334.
Thank
Happy to answer any questions!
you!
Appendix I
Read on to dive in deeper!
Pedersen Commitment
A cryptographic tool to hide a secret \(a \in \mathbb{F}_q, \) computed as
P = \texttt{com}(a,r) = g^{r} \cdot h^{a}
where \(r \in \mathbb{F}_q, g,h \in \mathbb{G}\) and DL relation between them is unknown
Homomorphic
- Given \( P_1 = \texttt{com}(a_1, r_1), \ P_2 = \texttt{com}(a_2, r_2) \)
P_1 \cdot P_2 = \texttt{com}(a_1 + a_2, r_1+r_2)
Perfectly Hiding
- Given \( P = \texttt{com}(a,r) \in \mathbb{G} \), it is infeasible to find \(a\) or \(r\)
Computationally Binding
- Given \( P = \texttt{com}(a,r) \in \mathbb{G} \), it is infeasible for a
computationally bounded adversary to find \( (a^{\prime}, r^{\prime})\) s.t. \(P = \texttt{com}(a^{\prime}, r^{\prime})\)
Zero Knowledge Proofs
Coke from Bottle
Coke from Can
Victor
Peter
\(x\)
\(V\)
\(P\)
Zero Knowledge Proofs
Guess?
Coke from Can
Bottle!
Victor
Peter
\langle P, V \rangle (x) = \begin{cases}
1 & \text{if } V \text{ accepts} \\
0 & \text{if } V \text{ rejects}
\end{cases}
Zero Knowledge Proofs
Try again!
Coke from Can
Victor
Peter
Coke from Bottle
Zero Knowledge Proofs
Victor
Peter
Coke from Bottle
Can!
If \(P\) actually knows the taste, \( \Pr[ \langle P,V \rangle(x) = 1 ]\) = 1
If \(P\)'s claim is wrong, \( \Pr[ \langle P,V \rangle(x) = 1 ] = \left(\frac{1}{2}\right)^2 \)
\(\implies\) Completeness!
\(\implies\) Soundness!
Appendix II
Read on to dive in deeper!
More on a Grin Block
| Block height Kernel offset |
| Inputs | Outputs |
|
|
I_1
k_{\text{off}} \in \mathbb{F}_q
h
I_2
I_3
I_4
O_{\text{cb}}
O_1
O_2
O_4
| Fees |
f_{\text{cb}}, f_1,f_2
| Kernel Excesses |
X_{\text{cb}},X_1,X_2
RTO
$$ \sum_{i=1,2,4}O_i+ \left(\sum_{i=1,2} f_i\right) H - \sum_{i=1}^{4}I_i = \sum_{i=1,2}X_i + k_{\text{off}}G$$
A block contains \(n\) kernels, \(n =\) #Transactions
Each kernel contains fee and a kernel excess
Coinbase fee \(f_{\text{cb}} = 0\), mining reward \(r = 60\) grin
Each kernel also contains a Schnorr signature proving that \(X_i = x_iG\) for some \(x_i \in \mathbb{F}_q\)
Block validation check:
Related Work
Listening to ~600 peer nodes, transactions could be traced to their origin before they are aggregated
Ivan Bogatty claimed to have traced 96% of all Grin transactions
Image credits: https://github.com/bogatyy/grin-linkability
Related Work
A. Kumar et al. demonstrated 3 attacks on traceability of inputs in Monero transactions, showing that In \(87\%\) of cases, the real output being redeemed can be identified!
Idea#1: \(65\%\) transactions have 0 mix-ins as of Feb, 2017!
Idea#2: An input being spent in a ring is the one with the highest block height, where it appeared as a TXO.
Image credits: https://eprint.iacr.org/2017/338.pdf
Related Work
M\( \ddot{o} \)ser et al. presented traceability analysis of Monero similar and concurrent to that of Kumar et al's work
Proposed a novel Binned Mixin Sampling strategy as a counter-measure
Characterised Monero usage based on user-behaviour
https://arxiv.org/pdf/1704.04299.pdf
Suyash-ddp-presentation
By Suyash Bagad
Suyash-ddp-presentation
Dual Degree (B.Tech + M.Tech) Thesis presentation of Suyash Bagad at Department of Electrical Engineering, IIT Bombay.
