Price Modelling of Stablecoins
Recall - GBM & More
- Stock prices in traditional finance are modeled using GBM
\begin{aligned}
\frac{\Delta S_t}{S_t} = \mu \Delta t + \sigma \sqrt{\Delta t} \varepsilon
\end{aligned}
\begin{aligned}
\text{log}\left(\frac{ S_t}{S_0}\right) \sim \mathcal{N}\left(\left(\mu - \frac{\sigma^2}{2}\right)t , \sigma \sqrt{t}\right)
\end{aligned}
\implies
- When \(p > 0.5\), the expected growth rate of the price of the asset is
\begin{aligned}
G_{\text{HODL}} = \mu - \frac{\sigma^2}{2}
\end{aligned}
- Here the term \(-\frac{\sigma^2}{2}\) is known as the volatility drag.
- In the same case of \(p > 0.5\), if we have \(\frac{2\sqrt{\mu}}{\sqrt{3}} < \sigma < 2\sqrt{\mu},\) we have
\begin{aligned}
G_{\text{LP}} = \frac{1}{2}\left(\mu - \frac{\sigma^2}{4}\right) > G_{\text{HODL}}
\end{aligned}
Volatility
Random process
Markov process
Drift
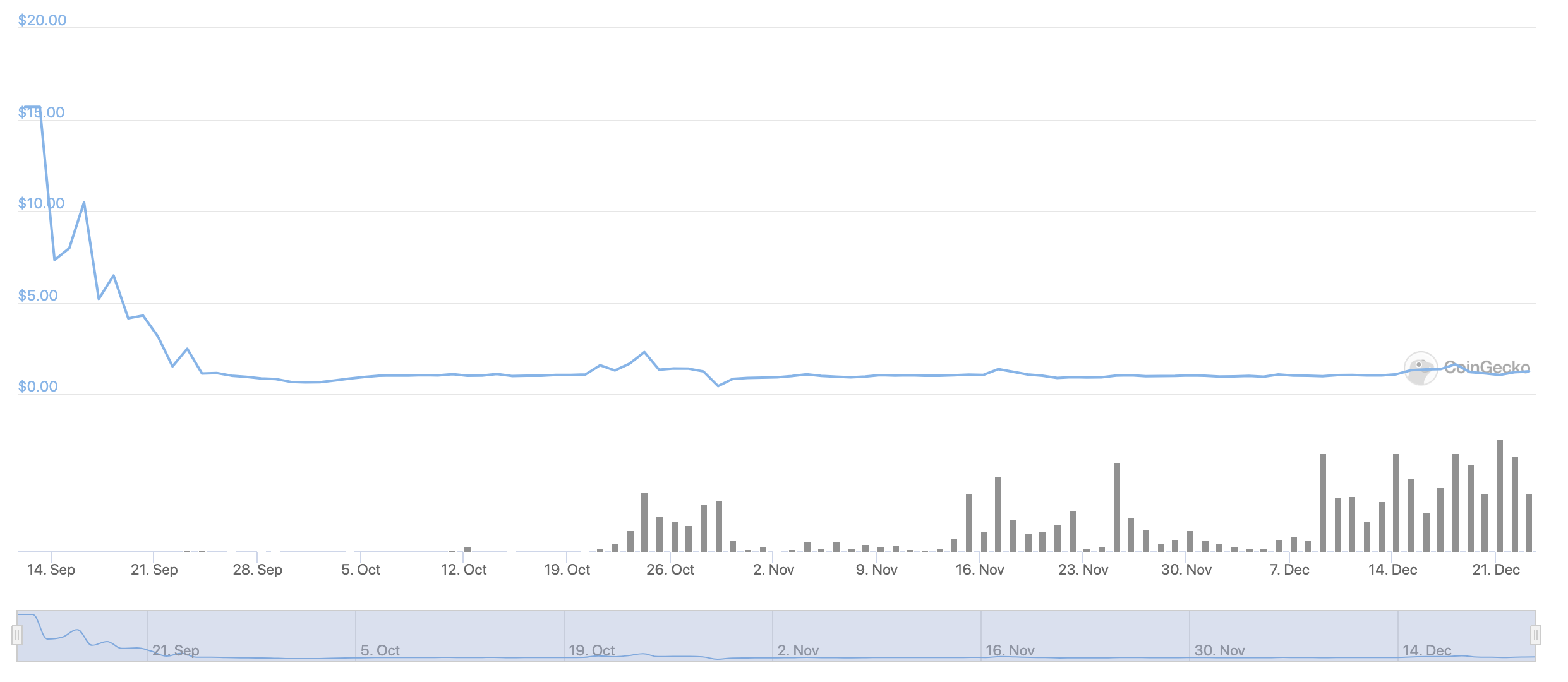
Basis Cash
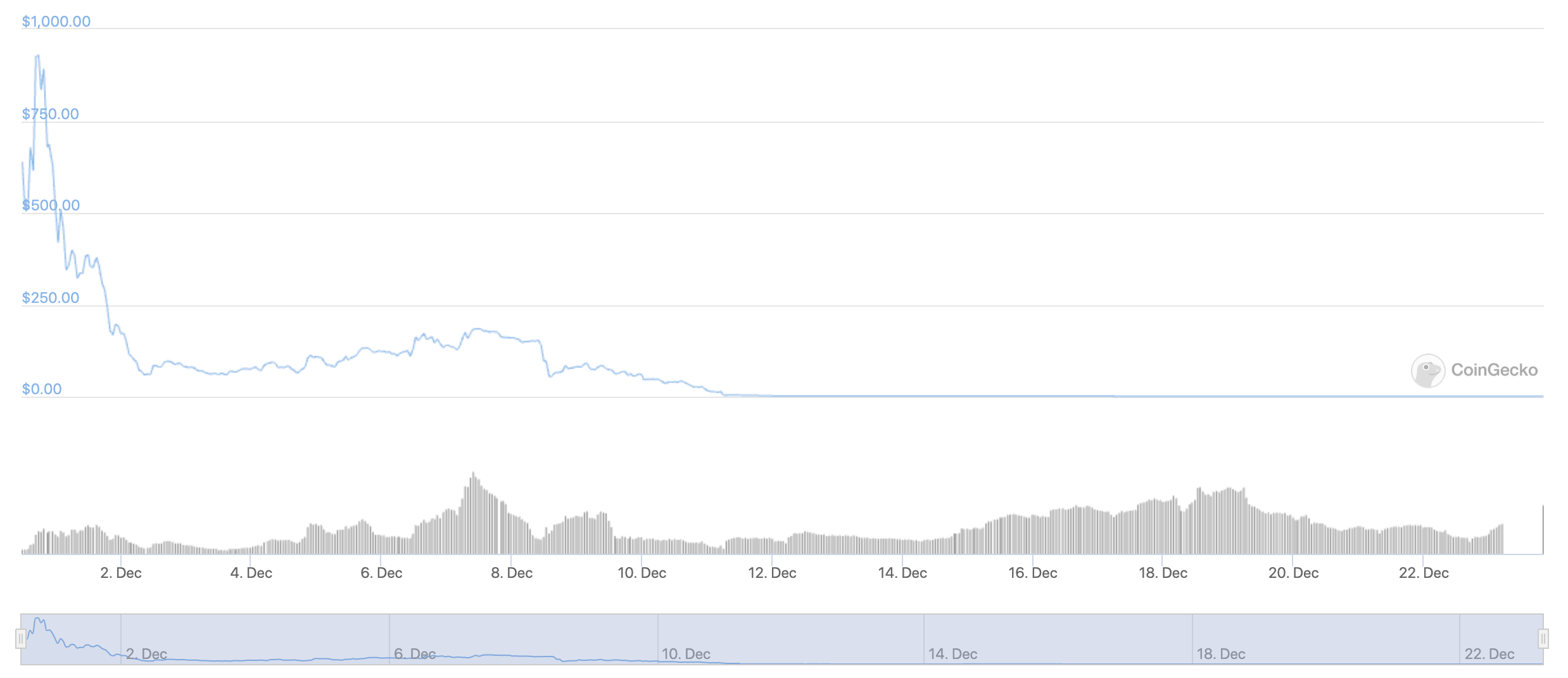
Price Profile (BAC/USD)
Stability starts
Basis Cash
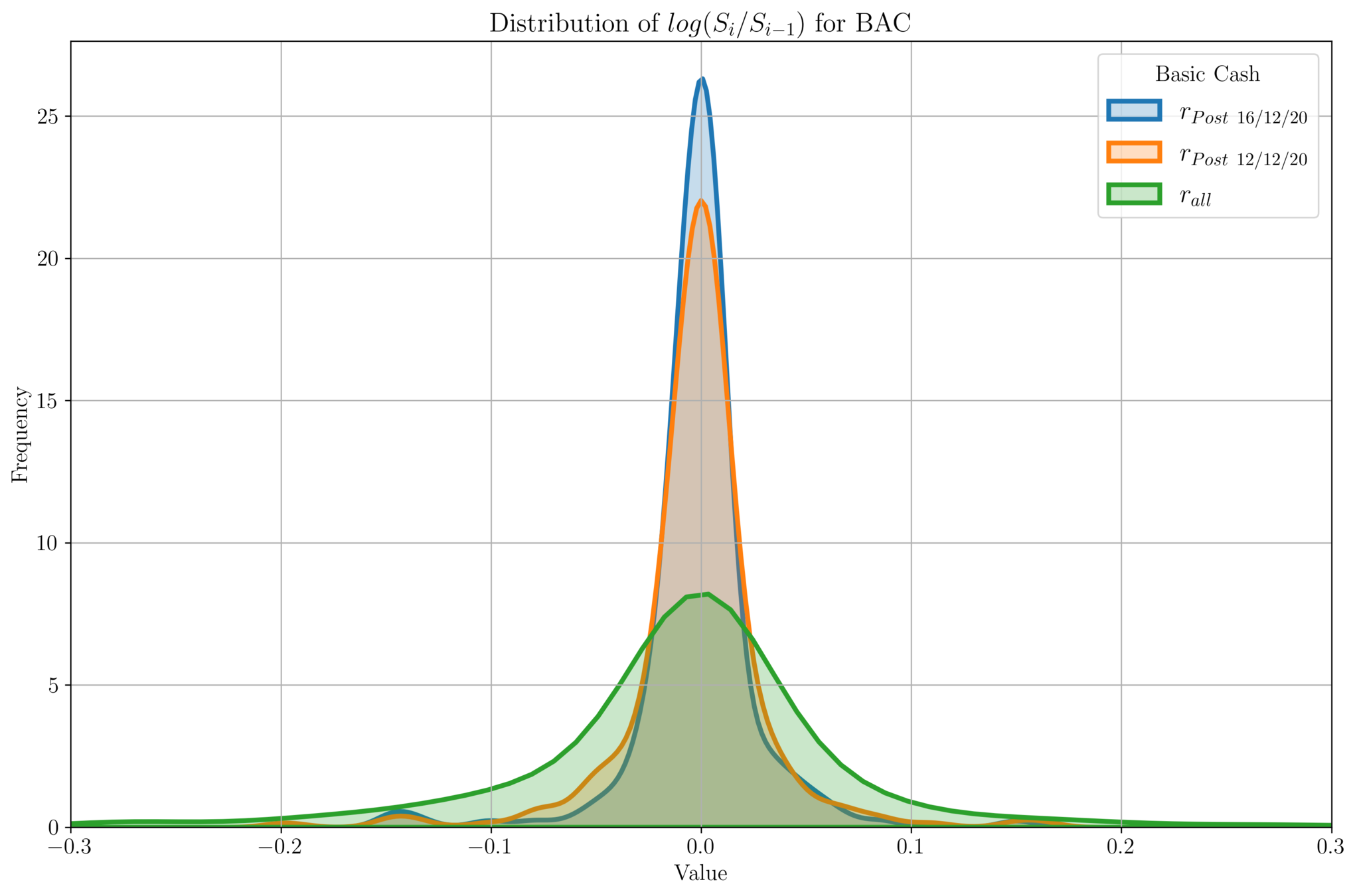
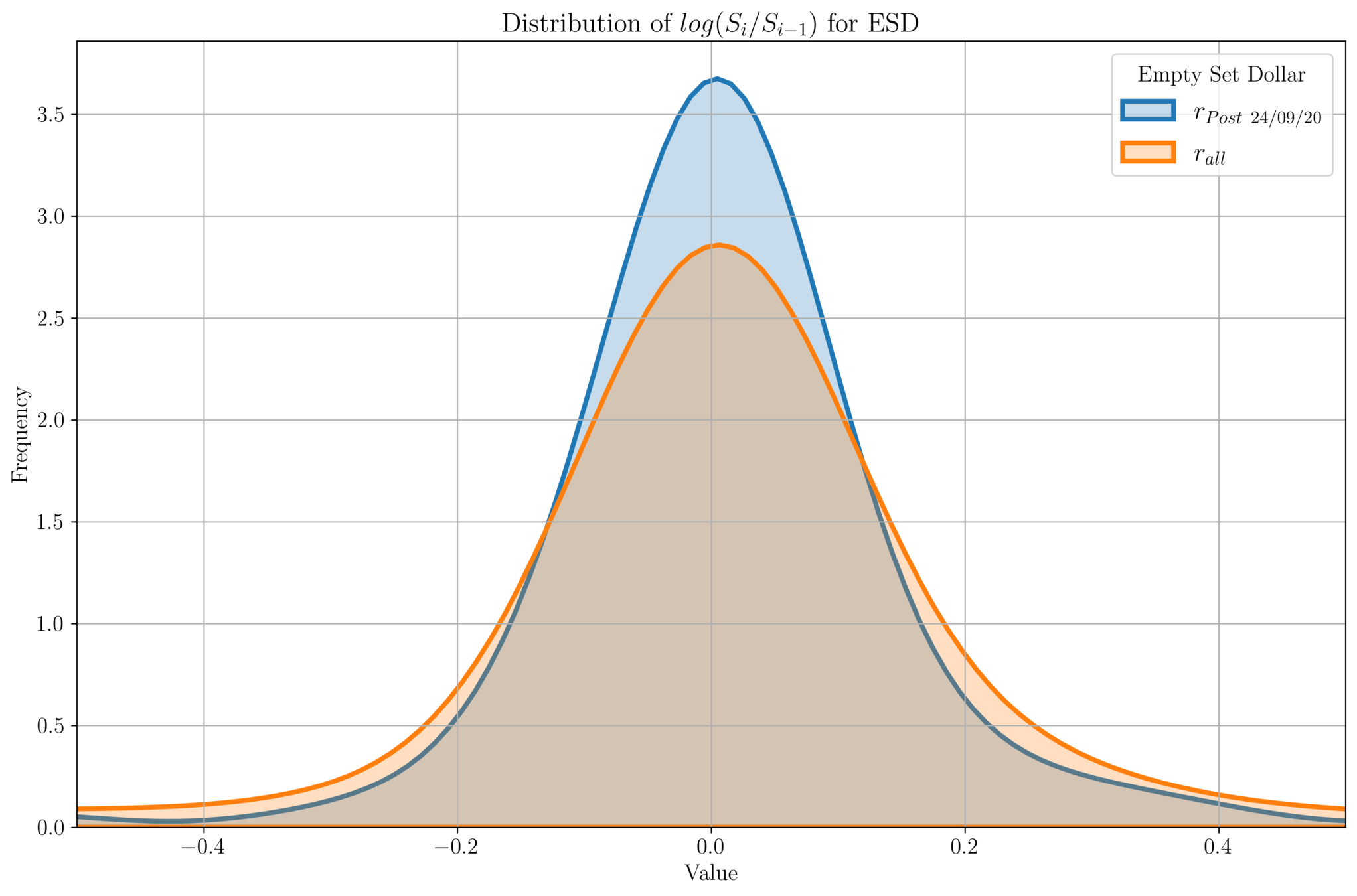
- We plot the distribution of \(\text{log}\left(\frac{S_i}{S_{i-1}}\right)\) for price data \(\{S_i\}\).
- Ideally for stablecoins, we should have a delta function at \(X = 0\).
- For all the price data, we see a Gaussian distribution centered at 0.
- For all-time price data, we see a spread around \([-0.2, 0.2]\).
- For more recent price data (which is stabilized around \(\$1\), we see the variance gets smaller.
Ampleforth
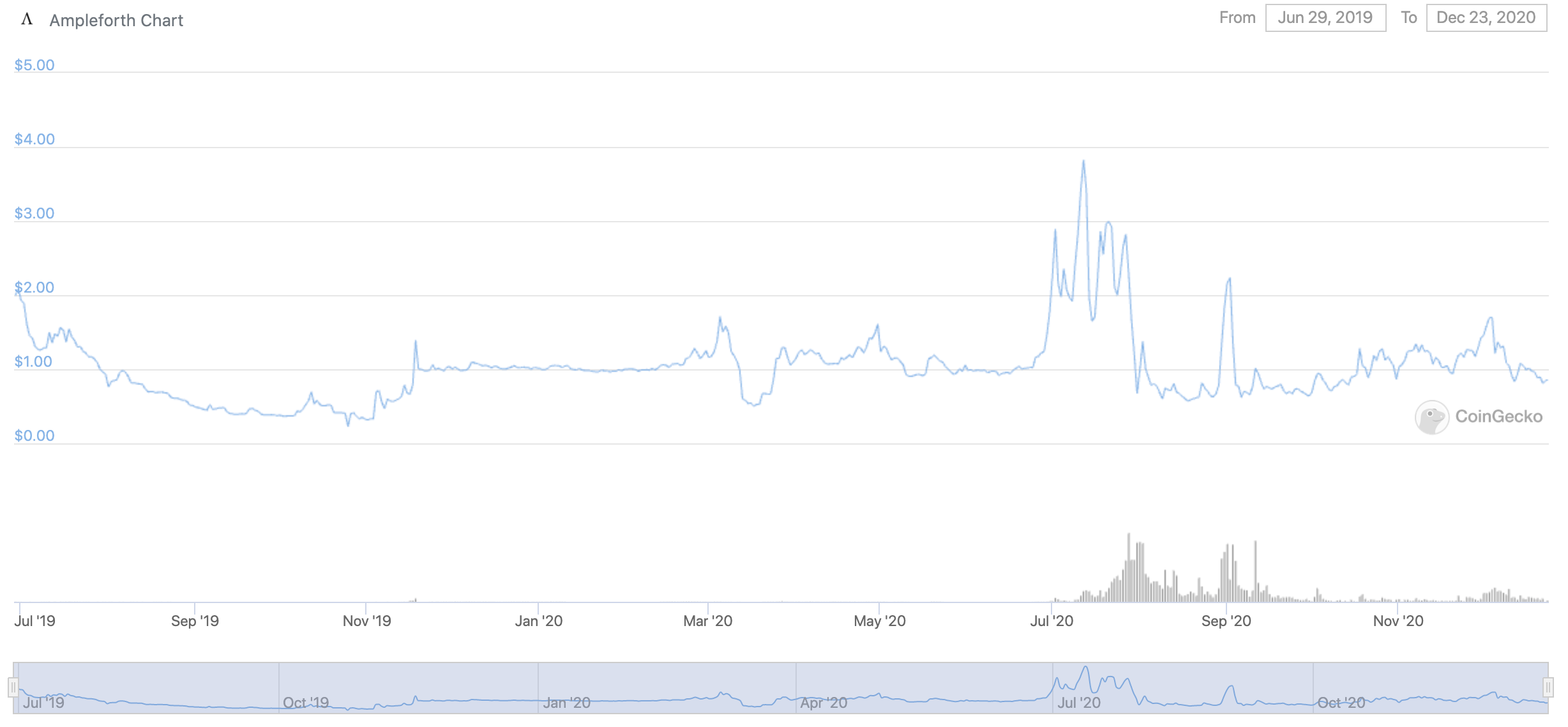

- Prices before June 26th are more stable (\(\sim \$1\)).
- Volume trade increase led to price fluctuations.
- Here too, we expect the distribution of prices to be Gaussian.
Ampleforth
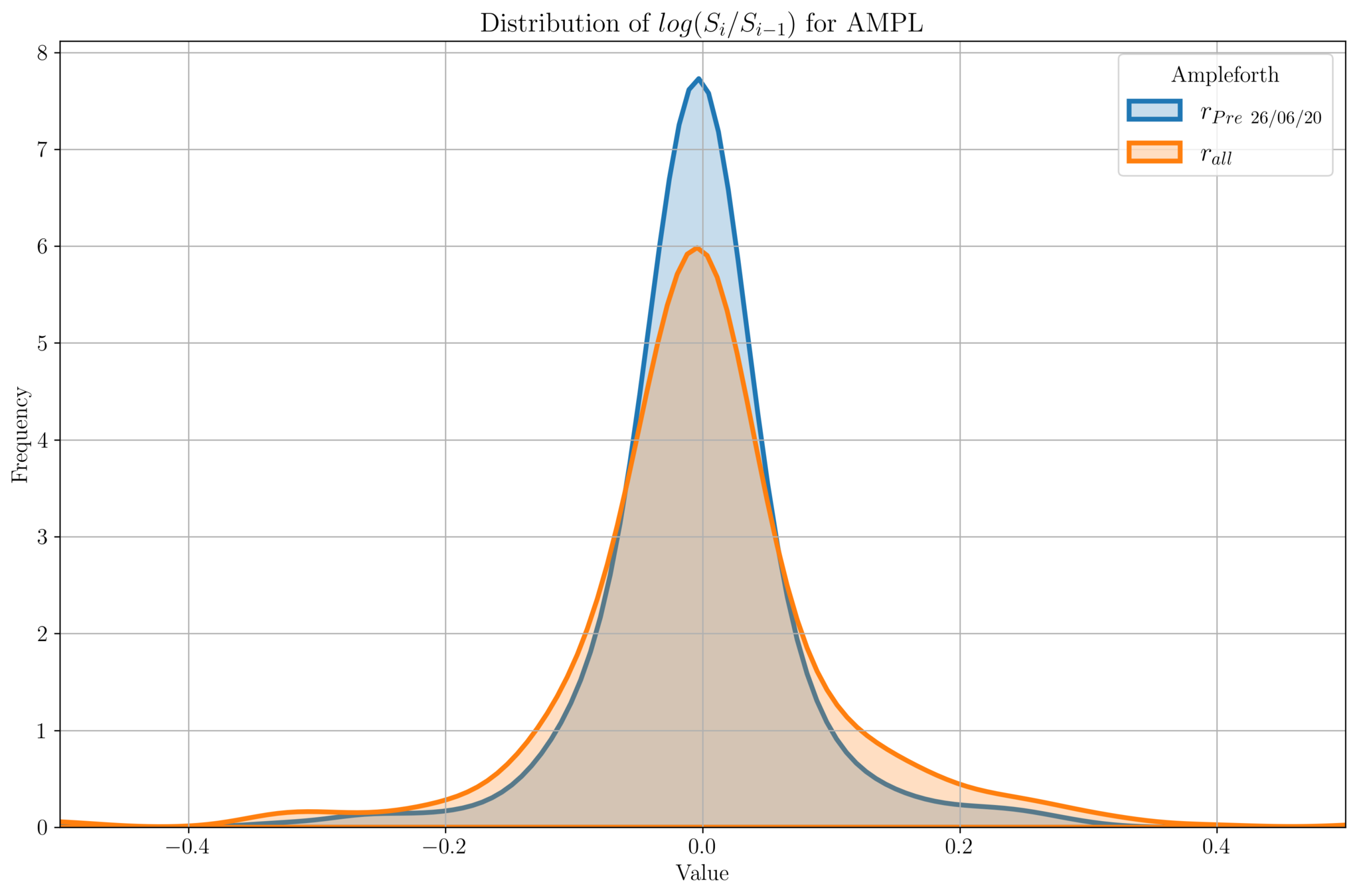
Empty Set D\(\phi\)llar
Empty Set D\(\phi\)llar
Drift & Volatility Analysis
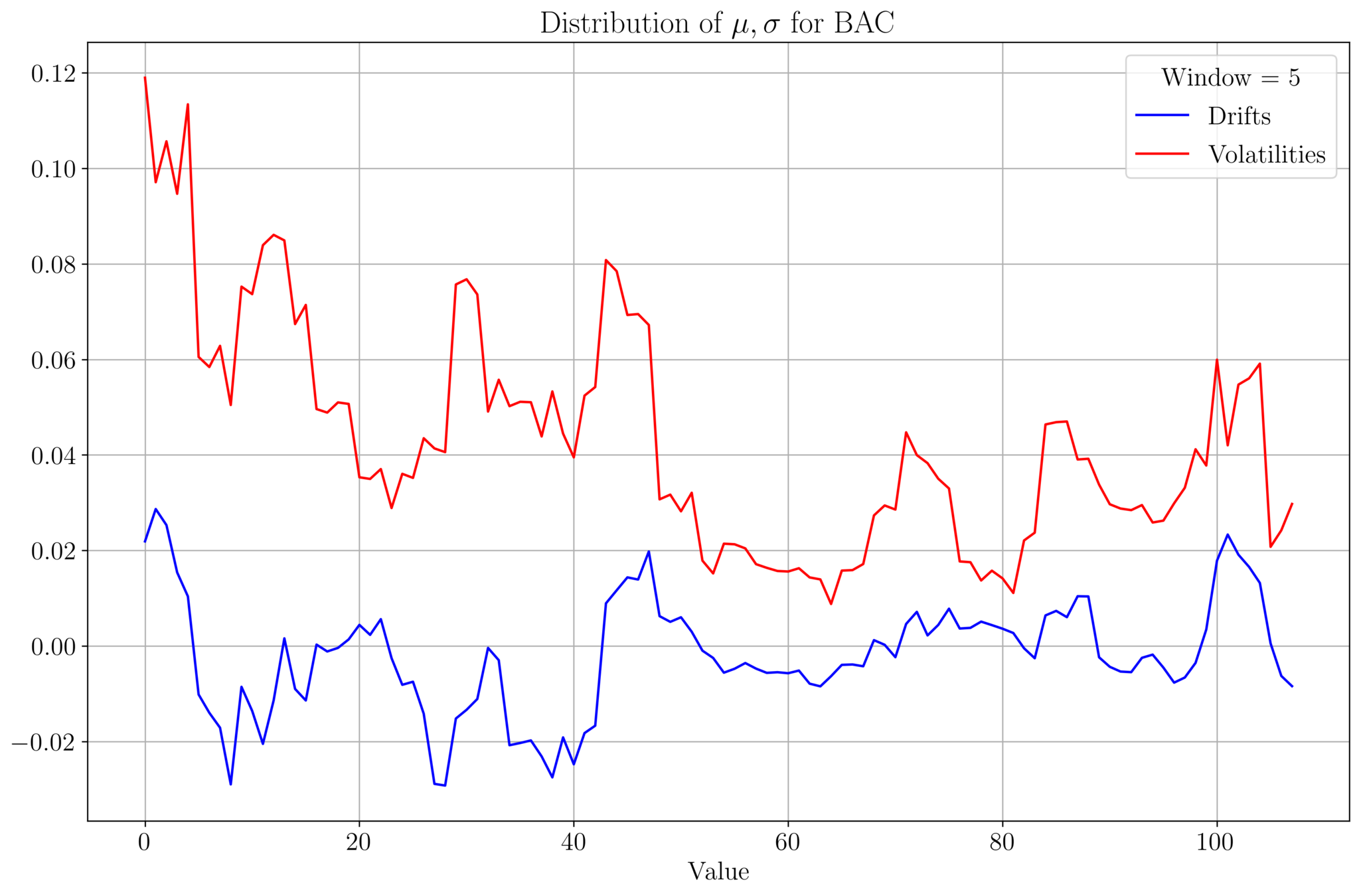
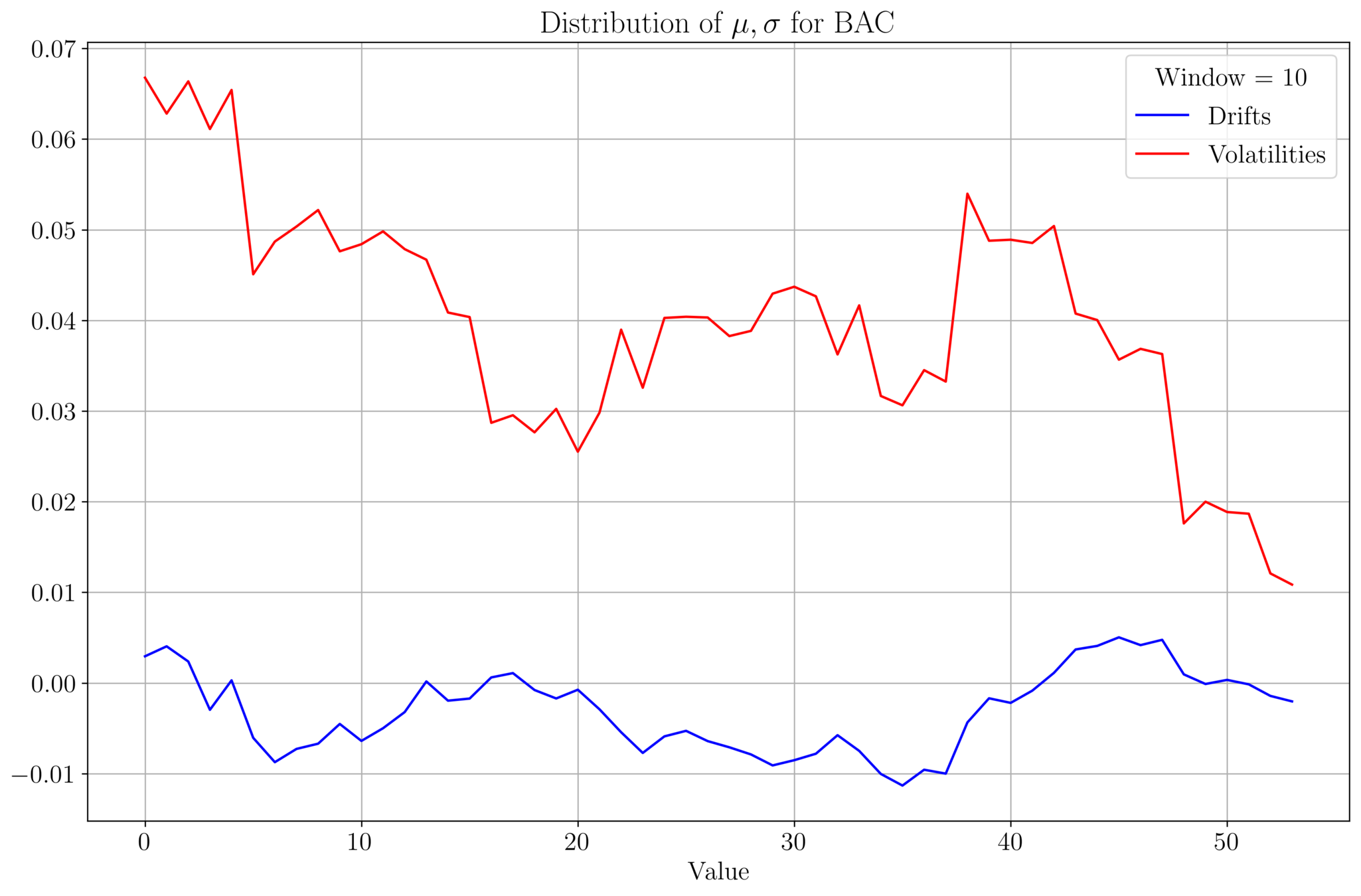
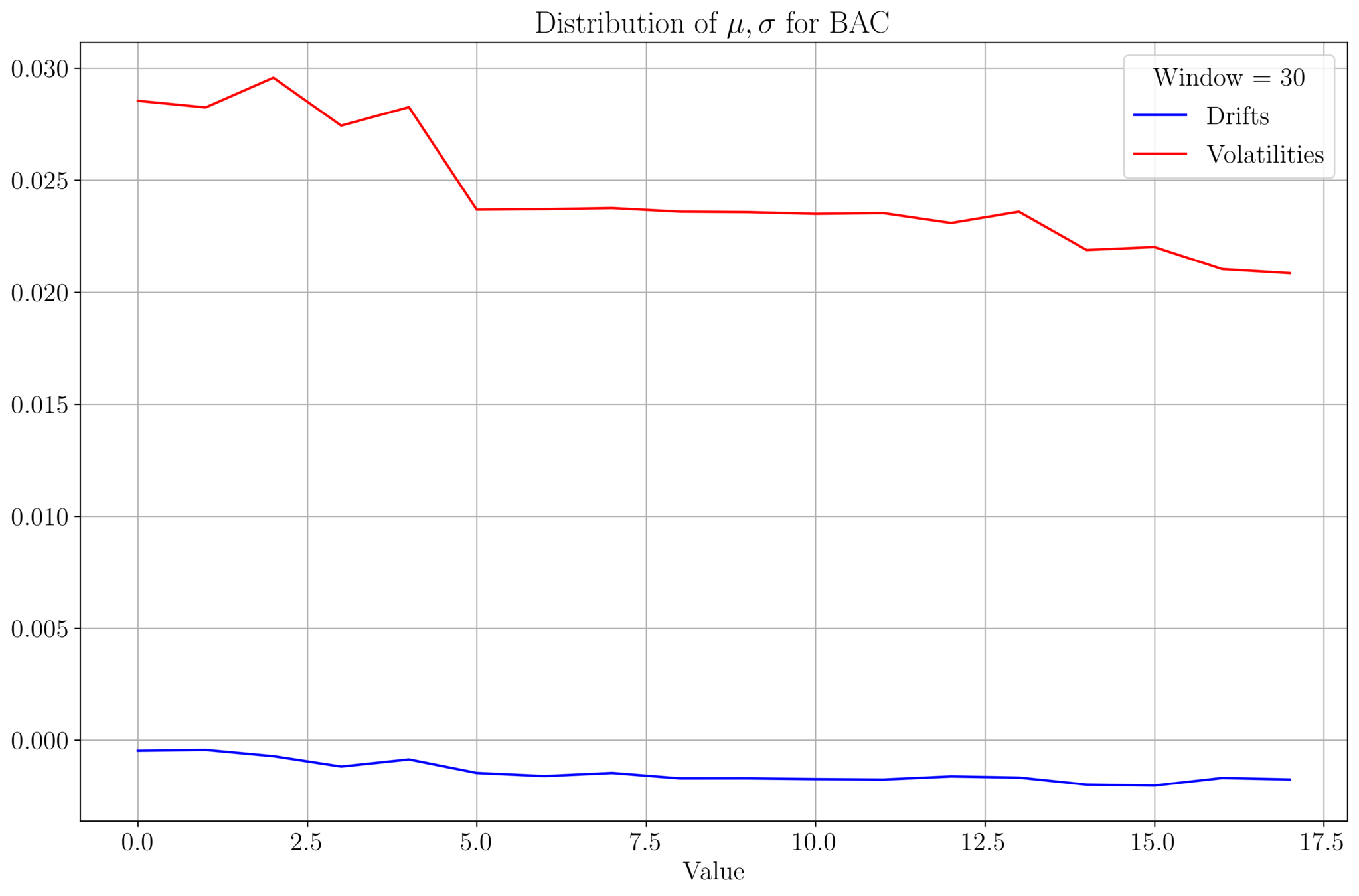
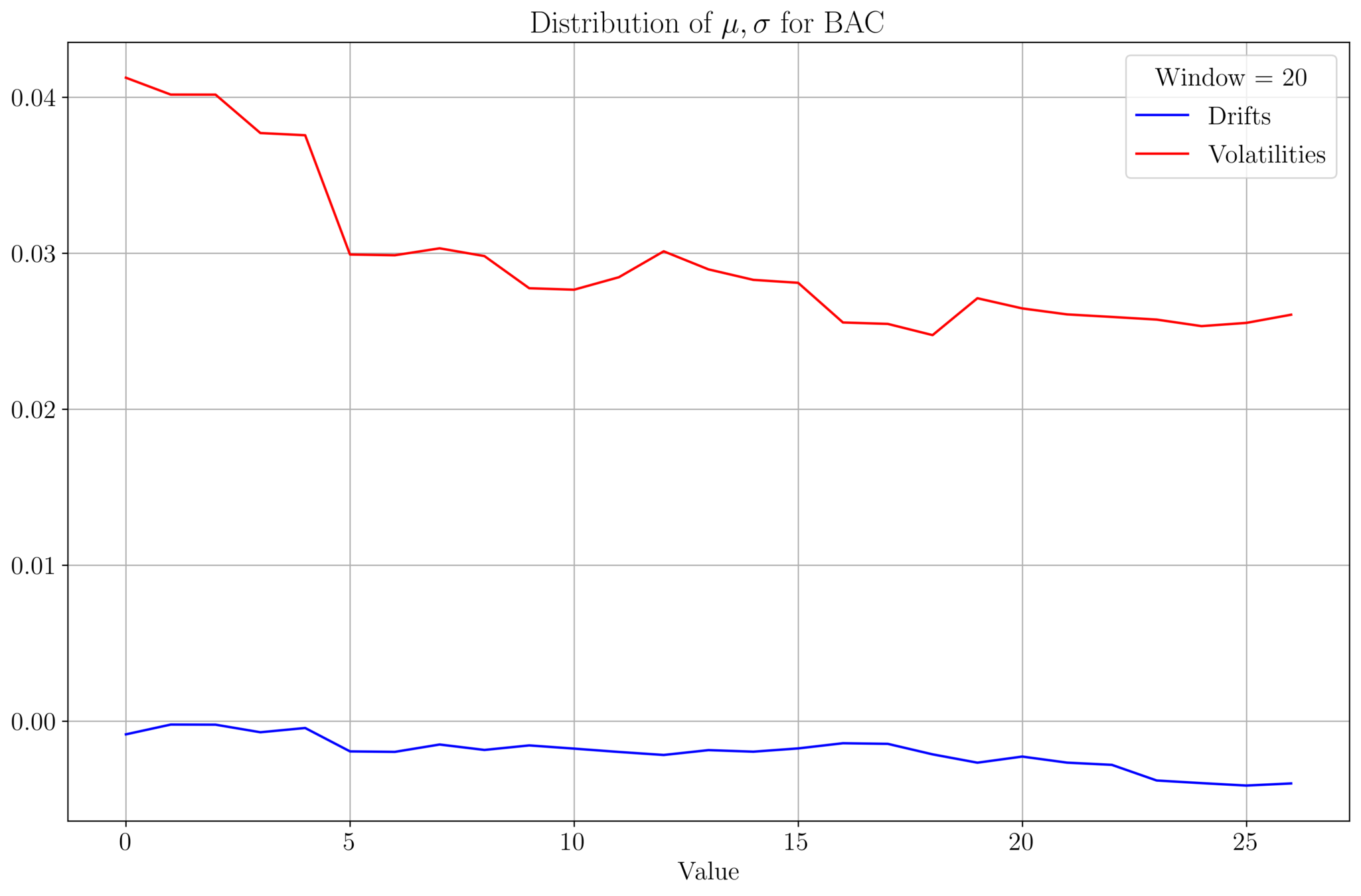
- We analyse \(\mu, \sigma\) of BAC prices for a data set of size 542.
- Plot of \((\mu, \sigma)\) values for a given window size:
Drift & Volatility Analysis




- As the window size increases, \(\mu, \sigma\) tends to stabilize
- \(\mu\) and \(\sigma\) roughly follow a similar profile
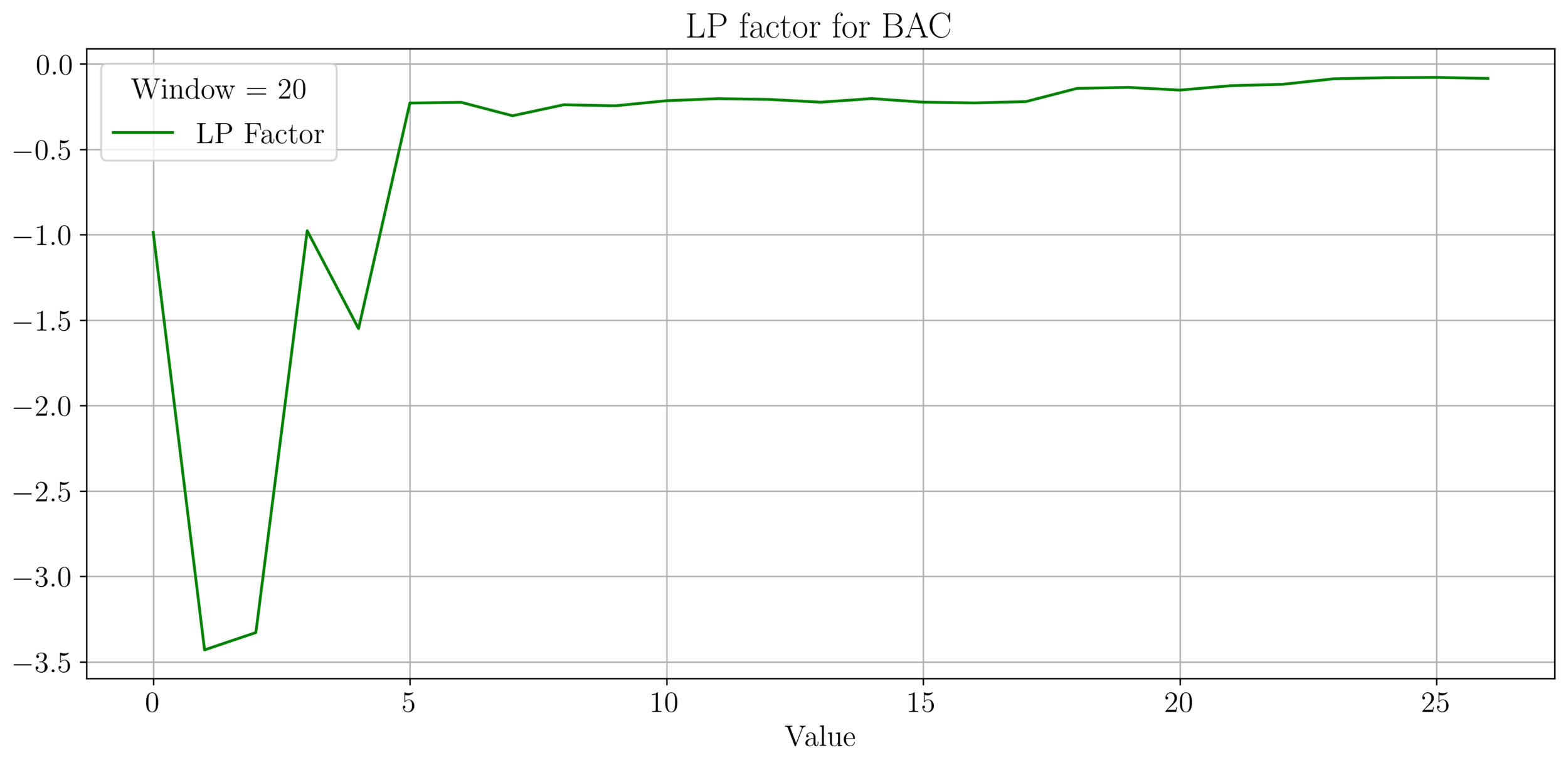
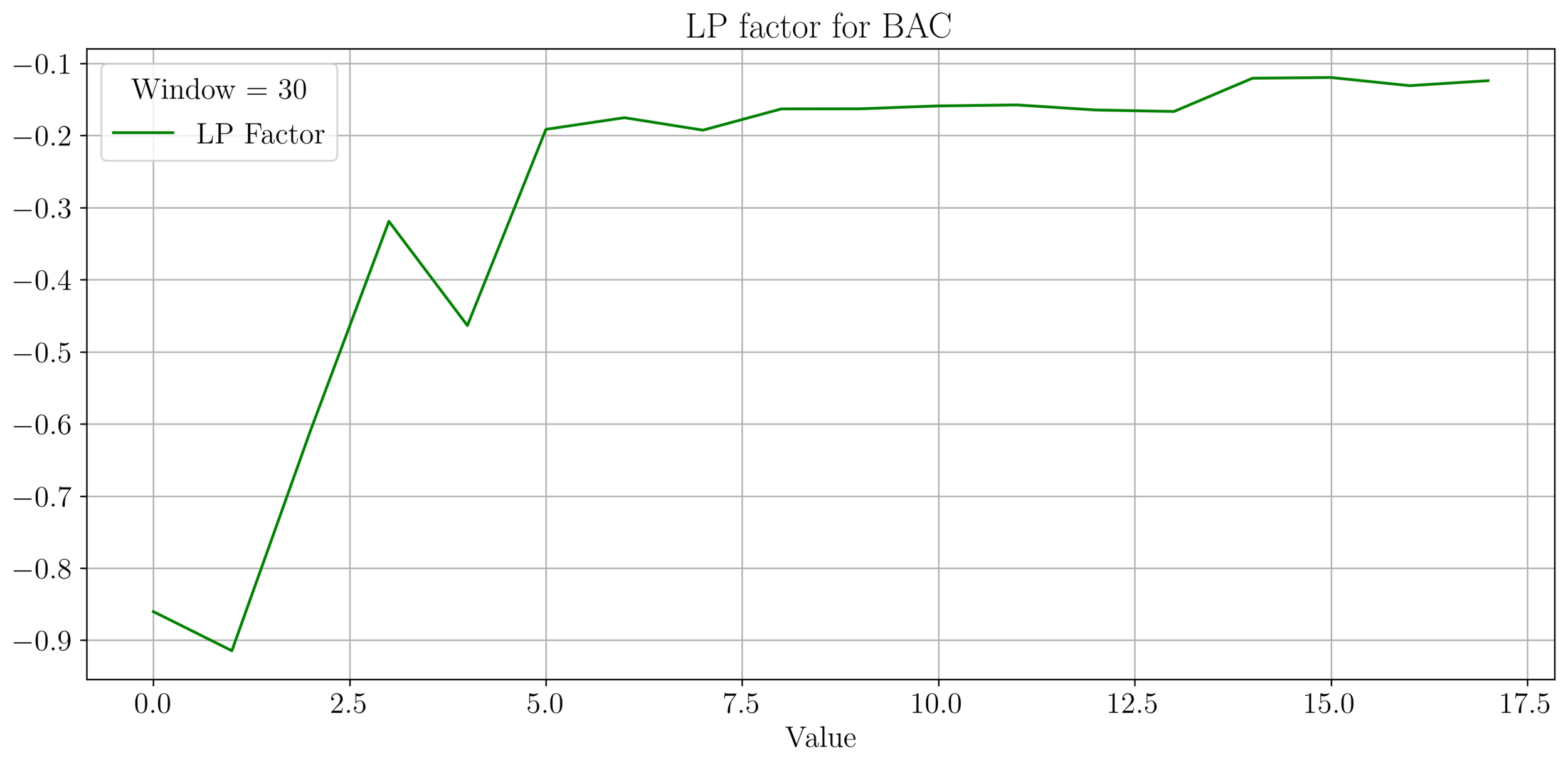
LP Wealth Factor
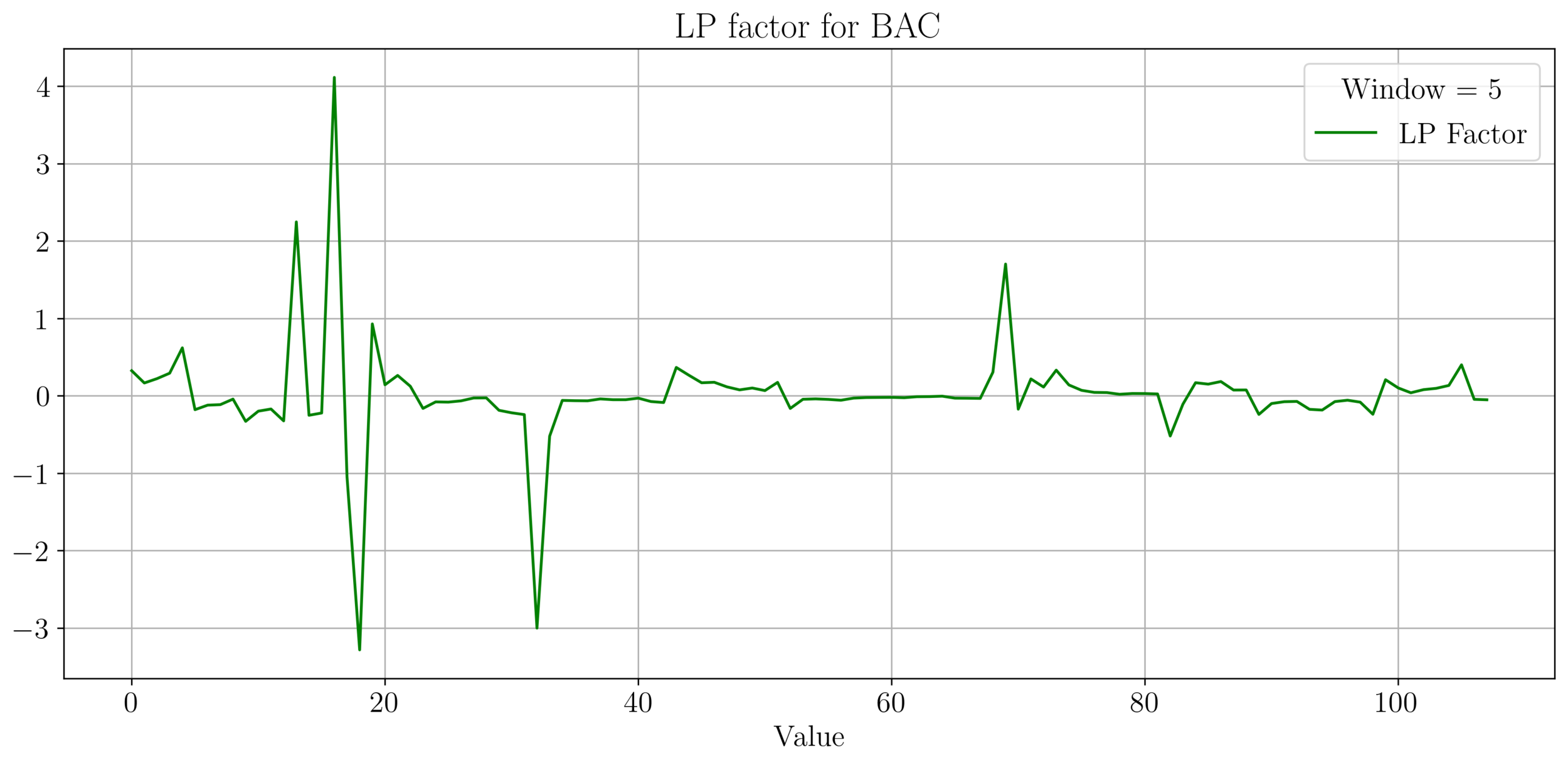
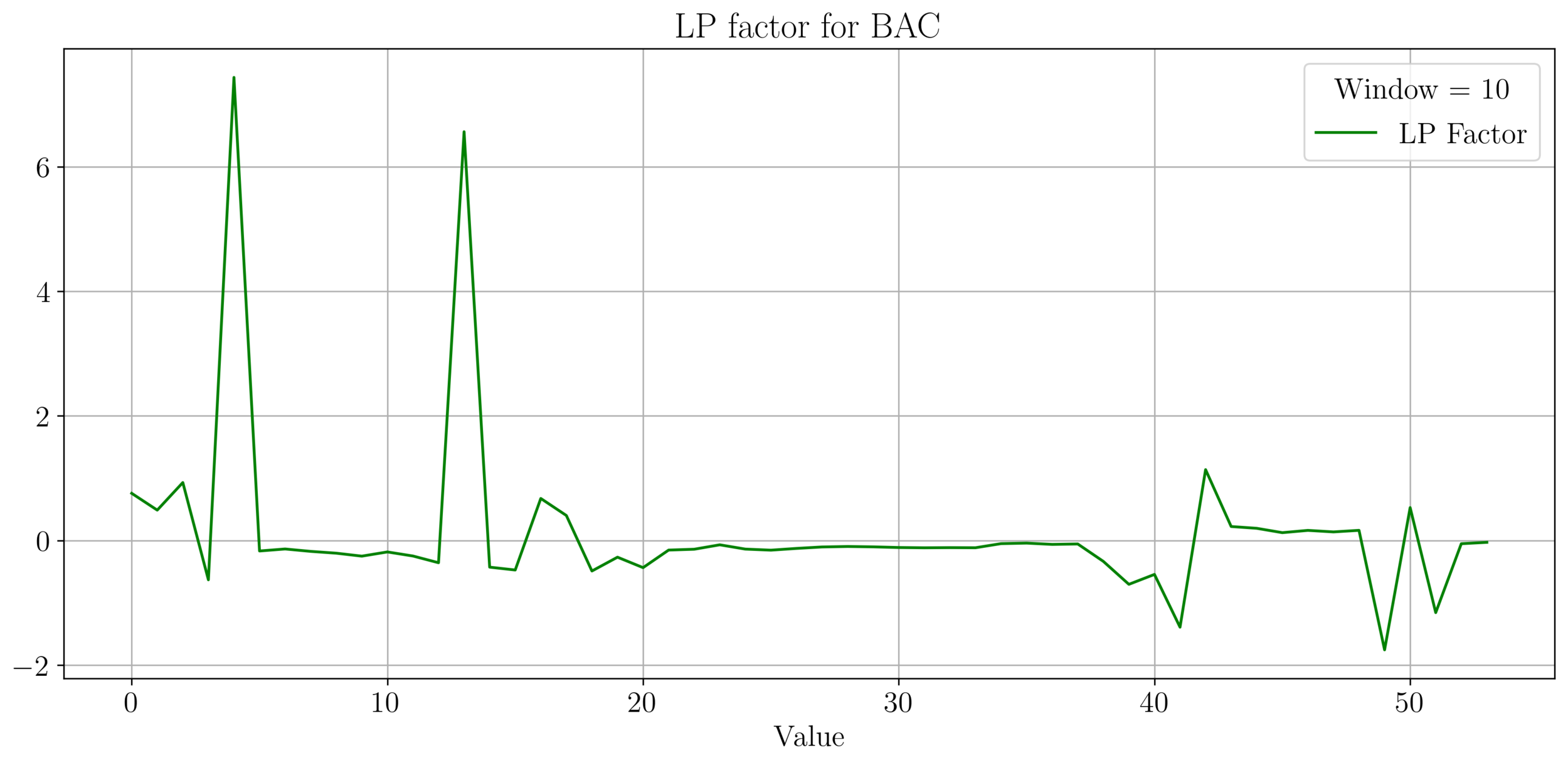
- We plot the factor \(f = \frac{\sigma^2}{2\mu}\), for max LP wealth growth, we want \(f \in (0.66, 2)\).
- We observe an irregular pattern here, need more investigation on this.
Price Analysis of BAC, ESD, AMPL
By Suyash Bagad
Price Analysis of BAC, ESD, AMPL
GBM Modelling of price processes of BAC, ESD, AMPL.
- 307



