Private Transactions on Ethereum
Suyash Bagad
Merkle Tree
- Suppose we want to store \(2^{k}\) files in a decentralized and succinct way
\(h = H\big(\)
\(\big)\)
- Here, \(h\) indeed is a succinct representation of the files \(\{f_i\}_{i \in [8]}\)
- The problem is: to check if a file in included in \(h\), you need all \(\{f_i\}_{i \in [8]}\) files
- A better way to achieve this is using Merkle trees!
\(f_1\)
\(f_2\)
\(f_3\)
\(f_4\)
\(f_5\)
\(f_6\)
\(f_7\)
\(f_8\)
Merkle Tree
- Suppose we want to store \(2^{k}\) files in a decentralized and succinct way
\(f_1\)
\(f_2\)
\(f_3\)
\(f_4\)
\(f_5\)
\(f_6\)
\(f_7\)
\(f_8\)
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
Merkle Tree
- Suppose we want to store \(2^{k}\) files in a decentralized and succinct way
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(H'(H(f_1), H(f_2))\)
\(H'(H(f_3), H(f_4))\)
\(H'(H(f_5), H(f_6))\)
\(H'(H(f_7), H(f_8))\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)
\(H'(h^1_1, h^1_2)\)
\(H'(h^1_3, h^1_4)\)
\(H'(h^2_1, h^2_2)\)
Merkle Tree
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)
- Indeed, \(h_1^3\) is succinct form of the files. How do we prove inclusion?
Merkle Tree
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)
- Indeed, \(h_1^3\) is succinct form of the files. How do we prove inclusion?
Merkle Tree
\(H(f_1)\)
\(H(f_2)\)
\(H(f_3)\)
\(H(f_4)\)
\(H(f_5)\)
\(H(f_6)\)
\(H(f_7)\)
\(H(f_8)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_1\)
- Only \(\left( H(f_6), h^1_4, h_1^2 \right)\) are enough to prove inclusion of \(f_5\)! Sister nodes!
Tornado.Cash
- Brings transaction privacy by breaking the on-chain link between the recipient and destination addresses
- Works in two stages: Deposit and Withdraw
Deposit
- Deposit: \((i)\) Generate \(k, r \leftarrow \mathbb{F}_p\) and compute \(C_1 = H(k, r)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\((ii)\) Send \(N\) ETH to contract \(\mathcal{C}\) which adds \(C_1\) to the Merkle tree
\(h^3_1\)
- Deposit: \((i)\) Generate \(k, r \leftarrow \mathbb{F}_p\) and compute \(C_1 = H(k, r)\)
\(C_1\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\((ii)\) Send \(N\) ETH to contract \(\mathcal{C}\) which adds \(C_1\) to the Merkle tree
\(h^3_1\)
Deposit
- Deposit: \((i)\) Generate \(k, r \leftarrow \mathbb{F}_p\) and compute \(C_1 = H(k, r)\)
\(C_1\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\((ii)\) Send \(N\) ETH to contract \(\mathcal{C}\) which adds \(C_1\) to the Merkle tree
\(h^3_2\)
\(h^3_1\)
Deposit
- Deposit: \((i)\) Generate \(k, r \leftarrow \mathbb{F}_p\) and compute \(C_1 = H(k, r)\)
\(C_1\)
\(C_2\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\((ii)\) Send \(N\) ETH to contract \(\mathcal{C}\) which adds \(C_1\) to the Merkle tree
\(h^3_3\)
\(h^3_1\)
\(h^3_2\)
Deposit
- Deposit: \((i)\) Generate \(k, r \leftarrow \mathbb{F}_p\) and compute \(C_1 = H(k, r)\)
\(C_1\)
\(C_2\)
\(C_3\)
\(C_4\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\((ii)\) Send \(N\) ETH to contract \(\mathcal{C}\) which adds \(C_1\) to the Merkle tree
\(h^3_5\)
\(h^3_1\)
\(h^3_2\)
\(h^3_3\)
\(h^3_4\)
Deposit
Withdraw
- To withdraw a coin \(k,r \in \mathbb{F}_p\) at position \(l \in \mathbb{Z}_{2^{16}-1}\), we do:
\((i)\) Select a withdrawal address \(A\)
\((ii)\) Select a root \(R\) among the stored ones and compute opening \(O(l)\) w.r.t \(R\)
\((iii)\) Compute nullifier hash \(h= H(k)\)
\((iv)\) Compute a proof using Groth16 proof system s.t. :
\begin{aligned}
\texttt{wit} &\leftarrow (k, r) \in \mathbb{F}_p^{2}, \ l \in \mathbb{Z}_{2}^{16}, \ O(l) \in \mathbb{Z}_p^{16} \\
\texttt{stmt} &\leftarrow h = H(k) \ \wedge \ O(l) \text{ is opening proof of } H(k, r) \text{ at position } l \text{ to } R
\end{aligned}
\((v)\) The contract verifies the proof and uniqueness of the nullifier hash.
If that succeeds, the contract transfers \(N\) ETH to \(A\).
Withdraw
- To withdraw \(C_3\), create a proof \(\pi = \mathcal{P}\left( k_3, r_3, (C_4, h_1^1, h_2^2) \right)\)
- The contract verifies \(\pi\) and checks if nullifier hash is unused.
\(C_1\)
\(C_2\)
\(C_3\)
\(C_4\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(H(0)\)
\(h^1_1\)
\(h^1_2\)
\(h^1_3\)
\(h^1_4\)
\(h^2_1\)
\(h^2_2\)
\(h^3_5\)
Comparison
| Anonymity | ||
| Non-custodial | ||
| Variable amounts | ||
| Shielded payments | ||
| ZK Rollup | ||
| Proof system |
\(^{\dagger}\) Concerns with Tornado.cash: https://lightco.in/2019/08/07/tornado-review/
Groth16
PLONK
\(^{\ddagger}\) Theoretically, ZK Rollups with Groth16 is possible. Loopring uses Groth16 with ZK Rollups.
\(\dagger\)
\(\ddagger\)
Benchmarks
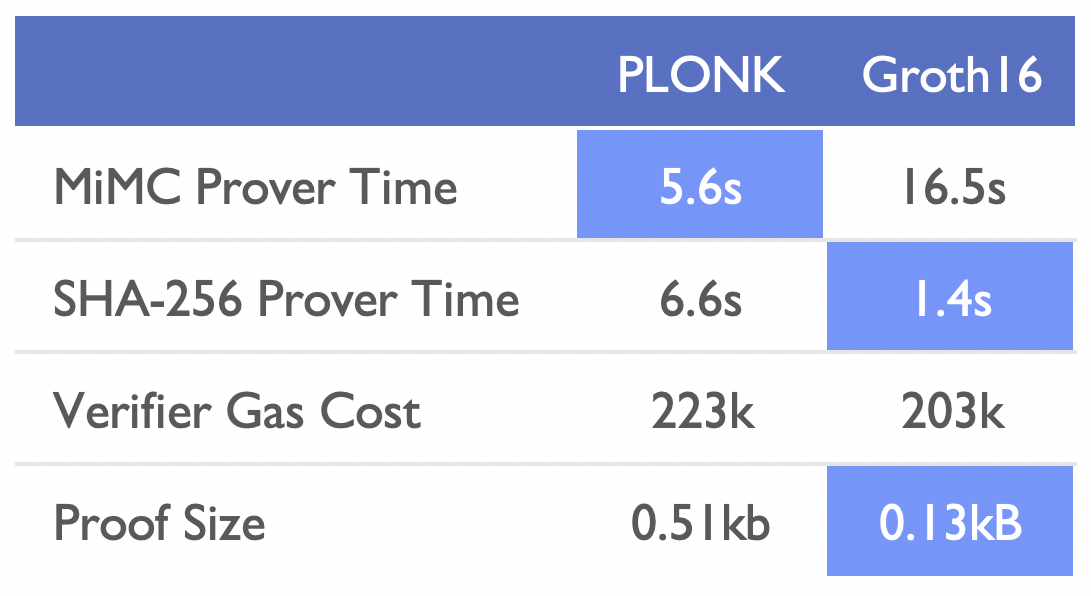
- The CRS in Groth16 is non-universal, each circuit requires a trusted setups
- TurboPLONK competes Groth16 in performance
- UltraPLONK (Q3 2021) is set be 3-4x better than TurboPLONK
Thank you!
Private Transactions on Ethereum
By Suyash Bagad
Private Transactions on Ethereum
Brief overview of projects like Hopper, Hieswap and Tornado.cash.
