LP Wealth Growth in Uniswap
Preliminaries
- \(X_t, Y_t \) are the quantities of numeraire and asset held by the LPs in the AMM
- The price process of the asset is defined as \(S_0 = 1, S_t = S_{t-1}e^{\delta U_t}\)
- \(\{U_i\}_{i \in \mathbb{N}}\) are i.i.d random variables s.t. \(\mathbb{P}[U_i = 1] = p, \ \mathbb{P}[U_i = -1] = 1-p\)
- The implicit price given by the curve at time \(t\) is given by \(S_t^{\ast} = \frac{X_t}{Y_t}\)
- Percentage fee: \((1 - \gamma)\), we constrain \(\gamma\) to be of the form \(e^{- k_{\gamma} \delta}, k_{\gamma} \in \mathbb{Z}\)
- Trading equation \((X_t + \Delta X_t)^{\gamma} (Y_t - \Delta Y_t) = X_t^{\gamma} Y_t\)
- Note that this is equivalent to \((X_t + \gamma\Delta X_t) (Y_t - \Delta Y_t) = X_t Y_t\)
\begin{aligned}
\therefore \left(1 + \frac{\Delta X_t}{X_t}\right)^{\gamma} \left(1 - \frac{\Delta Y_t}{Y_t}\right) = 1 \quad
&\implies \left(1 + \gamma\frac{\Delta X_t}{X_t}\right) \left(1 - \frac{\Delta Y_t}{Y_t}\right) = 1
\end{aligned}
\begin{aligned}
\therefore (X_t + \gamma\Delta X_t) (Y_t - \Delta Y_t) &= X_t Y_t
\end{aligned}
\begin{aligned}
(X_t + \Delta X_t)^{\gamma} (Y_t - \Delta Y_t) &= X_t^{\gamma} Y_t
\end{aligned}
Markov Chains
- A stochastic model describing a sequence of possible events in which the probability of each event depends only on the current system state.
- A discrete-time Markov chain is a sequence of random variables \(X_1, X_2, X_3, \ldots \) s.t.
\mathbb{P}\left(X_{n+1} = x \ | \ X_1 = x_1, X_2 = x_2, \dots, X_{n} = x_n\right) = \mathbb{P}\left(X_{n+1} = x \ | \ X_{n} = x_n\right)
Credits: https://setosa.io/ev/markov-chains/
Markov Chains
- State space: \(S = \{A, B\}\), Transition matrix \(P \in \mathbb{R}_{[0, 1]}^{|S| \times |S|}\)
- Stationary distribution: A probability distribution \(\pi = (p_A, p_B)\) that remains unchanged in the Markov chain as time progresses.
\pi P = \pi
- Clearly, \(\pi\) is the left eigenvector of P for the eigenvalue \(\lambda = 1\).
- For the above \(P\), we would have \(\pi = \left(\frac{5}{8}, \frac{3}{8}\right)\)
Implicit Price Manipulation
- Suppose at time \(t\), we have \(S_t = \gamma^{-1}\left(\frac{X_t}{Y_t}\right) e^{\delta} = \gamma S_t^{\ast} e^{\delta}\)
- We wish to bring the implicit price to \(S_{t+1}^{\ast} = \left(\frac{X_t}{Y_t}\right) e^{\delta}\) by trading \(\Delta Y_t\) for \(\Delta X_t\)
- Thus, we have
\begin{aligned}
\left(\frac{X_t + \Delta X_t}{Y_t - \Delta Y_t}\right) &= \left(\frac{X_t}{Y_t}\right) e^{\delta}\\[15pt]
\quad (X_t + \Delta X_t)^{\gamma} (Y_t - \Delta Y_t) &= X_t^{\gamma} Y_t
\end{aligned}
\begin{aligned}
\implies \ \left(1 + \frac{\Delta X_t}{X_t}\right) = \left(1 - \frac{\Delta Y_t}{Y_t}\right) e^{\delta}
\end{aligned}
\begin{aligned}
\implies \ \left(1 + \frac{\Delta X_t}{X_t}\right)^{\gamma} \left(1 - \frac{\Delta Y_t}{Y_t}\right) = 1
\end{aligned}
\begin{aligned}
\therefore \quad \Delta X_t = X_t\left(e^{\frac{\delta}{\gamma + 1}} - 1\right), \ \Delta Y_t = Y_t\left(1 - e^{\frac{-\gamma\delta}{\gamma + 1}}\right)
\end{aligned}
- Similarly, if \(S_t = \gamma \left(\frac{X_t}{Y_t}\right) e^{-\delta}\) and we pull the implicit price to \(S_{t+1}^{\ast} = \left(\frac{X_t}{Y_t}\right) e^{-\delta}\)
\begin{aligned}
\therefore \quad \Delta X_t = X_t\left(1 - e^{\frac{-\gamma\delta}{\gamma + 1}}\right), \ \Delta Y_t = Y_t\left(e^{\frac{\delta}{\gamma + 1}} - 1\right)
\end{aligned}
Price as Markov Process
- Recall, we traded \(\Delta Y_t\) for \(\Delta X_t\) when \(S_t = \gamma^{-1} S_t^{\ast} e^{\delta} \implies S_t > \gamma^{-1} S_t^{\ast} \)
- Similarly, we traded \(\Delta X_t\) for \(\Delta Y_t\) when \(S_t = \gamma S_t^{\ast} e^{-\delta} \implies S_t < \gamma S_t^{\ast} \)
Not profitable
Get \(\Delta Y_t\) for \(\Delta X_t\)
Get \(\Delta X_t\) for \(\Delta Y_t\)
\(0\)
\(\delta\)
\(-\delta\)
\(k_{\gamma}\delta\)
\(-k_{\gamma}\delta\)
\(\dots\)
\(\dots\)
\(k_{\gamma}\delta+\delta\)
\(-k_{\gamma}\delta-\delta\)
\text{log}\left(\frac{S_t}{S_t^{\ast}}\right)
- Thus, \(M_t = \text{log}\left(\frac{S_t}{S_t^{\ast}}\right)\) is a Markov process with \(S = \{-k_{\gamma}\delta, \dots, -1, 0, 1, \dots, k_{\gamma}\delta\}\).
- A trade occurs when \(M_t\) stays on one of the two end states.
- Let's construct the transition matrix \(P\) and find a stationary distribution \(\pi\)
Price as Markov Process
- Let's construct the transition matrix \(P\) and find a stationary distribution \(\pi\)
\(-k_{\gamma}\delta\)
\(-k_{\gamma}\delta + \delta\)
\(-k_{\gamma}\delta + \delta\)
\(-k_{\gamma}\delta\)
\(\ldots\)
\(k_{\gamma}\delta\)
\(k_{\gamma}\delta\)
\(\ldots\)
\(-k_{\gamma}\delta + 2\delta\)
\(1-p\)
\(p\)
\(0\)
\(1-p\)
\(1-p\)
\(p\)
\(1-p\)
\(p\)
\(p\)
\(0\)
\(0\)
\(p\)
\(0\)
\text{log}\left(\frac{S_t}{S_t^{\ast}}\right)
\pi =
\begin{cases}
\left[ (2k_{\gamma} + 1)^{-1}, \dots, (2k_{\gamma} + 1)^{-1} \right] & \text{if } p = 0.5 \\[5pt]
\left[ \frac{(1 - c)}{c^{-(2k_{\gamma}+1)} - 1},
\frac{(1 - c)c^{-1}}{c^{-(2k_{\gamma}+1)} - 1},
\frac{(1 - c)c^{-(2k_{\gamma} + 1)}}{c^{-(2k_{\gamma}+1)} - 1} \right] & \text{if } p \in (0.5,1], \ c = \frac{1-p}{p}
\end{cases}
Constant Growth of Invariant
\begin{aligned}
K_{\gamma} &= \frac{(X + \Delta X_t)(Y - \Delta Y_t)}{X_t Y_t} \\[5pt]
&= \left(\frac{X + \Delta X_t}{X_t}\right)^{1 - \gamma} \frac{(X + \Delta X_t)^{\gamma}(Y - \Delta Y_t)}{X_t^{\gamma} Y_t} \\[5pt]
&= \left(1 + \frac{\Delta X_t}{X_t}\right)^{1 - \gamma} = e^{\delta \frac{1 - \gamma}{1 + \gamma}}
\end{aligned}
- After each trade the product \(C_t = X_tY_t\) is increased by the same factor \(K_{\gamma}\)
- If \(N_t\) trades occur until time \(t\), the wealth in the AMM at time \(t\) in the absence of fees is
\begin{aligned}
K_{\gamma}^{-\frac{N_t}{2}} (Y_t S_t^{\ast} + X_t) &= (X_t Y_t)^{-\frac{1}{2}} (Y_t S_t^{\ast} + X_t)
= 2 (X_t Y_t)^{-\frac{1}{2}} Y_t = 2 (S_t^{\ast})^{\frac{1}{2}}
\end{aligned}
Expected Geometric Return for LPs
\begin{aligned}
\mathbb{E}(\text{log} \ W_t) &= \mathbb{E}(\text{log} (Y_tS_t + X_t)) \\
&= \mathbb{E}(\text{log} (Y_tS^{\ast}_t + X_t)) + \mathbb{E}\left(\text{log} \left(\frac{Y_tS_t + X_t}{Y_tS^{\ast}_t + X_t}\right)\right)
\end{aligned}
- The wealth of LPs at time \(t\) is given as \(W_t = Y_t S_t + X_t\). Expected wealth is
\begin{aligned}
\gamma \le \frac{S_t}{S^{\ast}_t} \le \gamma^{-1}
\implies \gamma \le \left(\frac{Y_tS_t + X_t}{Y_tS^{\ast}_t + X_t}\right) \le \gamma^{-1}
\end{aligned}
But we have,
\(m\) (constant)
\begin{aligned}
\therefore \ \mathbb{E}(\text{log} \ W_t) &= \mathbb{E}(\text{log} (Y_tS^{\ast}_t + X_t)) + m
\end{aligned}
\(\because \ K_{\gamma}^{-\frac{N_t}{2}}(Y_t S_t^{\ast} + X_t) = 2(S_t^{\ast})^{\frac{1}{2}} \)
\begin{aligned}
= \mathbb{E}\left( \text{log} K_{\gamma}^{\frac{N_t}{2}} + \frac{1}{2}\text{log} S_t^{\ast}\right) + m
\end{aligned}
\begin{aligned}
= \left(\frac{\text{log} K_{\gamma}}{2}\right) \mathbb{E}(N_t) + \frac{1}{2} \mathbb{E}(\text{log} S_t^{\ast}) + m
\end{aligned}
Asymptotic Geometric Return for LPs
\begin{aligned}
\therefore \ \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t}
\end{aligned}
\begin{aligned}
= \left(\frac{\text{log} K_{\gamma}}{2}\right) \lim_{t\to\infty} \frac{\mathbb{E}(N_t)}{t} +
\frac{1}{2} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} S_t^{\ast})}{t}
\end{aligned}
\begin{aligned}
(1 - p)(-\delta) + p\delta = \delta(2p-1)
\end{aligned}
Average number of trades during an interval of time while in the stationary distribution of the Markov chain.
Let \(\pi = \left[\pi(-k_{\gamma}\delta), \dots, \pi(-k_{\gamma}\delta) \right]\)
\(\mathbb{E}(N_t) = nt [(1 - p)\pi(-k_{\gamma}\delta) + p\pi(k_{\gamma}\delta)]\), \(\frac{1}{n}\) is the time interval
\begin{aligned}
\therefore \ \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t}
\end{aligned}
\begin{aligned}
= \left(\frac{\text{log} K_{\gamma}}{2}\right) n[(1 - p)\pi(-k_{\gamma}\delta) + p\pi(k_{\gamma}\delta)] +
\frac{n\delta(2p-1)}{2}
\end{aligned}
Therefore, we finally have a closed form expression for the wealth growth of LPs!
Understanding Volatility Drag
Geometric Brownian Motion
- Stock prices in traditional finance are modeled using GBM
\begin{aligned}
\frac{\Delta S_t}{S_t} = \mu \Delta t + \sigma \sqrt{\Delta t} \varepsilon
\end{aligned}
- \(\mu \Delta t\) - the expected returns of the stock
- \(\sigma \sqrt{\Delta t} \varepsilon\) - models the random fluctuations of the stock price
- On solving the above SDE, we note that \(S_t\) is log-normally distributed
\begin{aligned}
\text{log}\left(\frac{ S_t}{S_0}\right) \sim \mathcal{N}\left(\left(\mu - \frac{\sigma^2}{2}\right)t , \sigma \sqrt{t}\right)
\end{aligned}
Volatility
Random process
Markov process
Drift
Price Process as a GBM
- For the price process \(S_t\) of the asset \(Y_t\), we have
- Mean: \(\mathbb{E}(\text{log}(S_t)) = \delta p + (-\delta)(1 - p) = \delta(2p-1)\)
- Variance: \(\mathbb{V}(\text{log}(S_t)) = \mathbb{E}((\text{log}(S_t))^2) - (\mathbb{E}(\text{log}(S_t)))^2 = \delta^2 - \delta^2(2p-1)^2 = 4\delta^2 p(1-p)\)
- Let us assume that \(\delta\) depends on \(\Delta t = \frac{1}{n}\). For \(S_t\) to be GBM, we must have
S_t =
\begin{cases}
S_{t-1}e^{\delta} & \text{with probability } p \\
S_{t-1}e^{-\delta} & \text{with probability } (1-p)
\end{cases}
\begin{aligned}
\delta_n (2p_n - 1) &= \left(\mu - \frac{\sigma^2}{2} \right)\frac{1}{n} \\
2\delta_n \sqrt{p(1-p)} &= \frac{\sigma}{\sqrt{n}}
\end{aligned}
- Thus, we get \(\delta_n \approx \frac{\sigma}{\sqrt{n}}\) and \(p_n \approx \frac{1}{2} + \frac{d}{2\sigma \sqrt{n}} \) where \(d = \left(\mu - \frac{\sigma^2}{2} \right)\).
LP Wealth Growth
- For a time interval \(\Delta_t = \frac{1}{n}\) and let \(a = \frac{1-p}{p}\), the growth rate of LP wealth is
\begin{aligned}
\lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} =
\begin{cases}
\frac{n\delta}{2} \frac{1}{1 - 2 \frac{\text{log}\gamma}{\delta}} \left(\frac{1 - \gamma}{1 + \gamma}\right) & p = \frac{1}{2} \\[10pt]
\frac{n\delta(2p-1)}{2} \left(\frac{1 \ - \ a \gamma^{-\frac{2}{\delta}\text{log}(a)}}{1 \ + \ a \gamma^{-\frac{2}{\delta}\text{log}(a)}}
\left(\frac{1 - \gamma}{1 + \gamma}\right) + 1\right)
& p > \frac{1}{2}
\end{cases}
\end{aligned}
- The wealth of LP at time \(t\), given by \(W_t = X_t + S_t Y_t\)
- The factor by which the price \(S_t\) can change
- Fee percentage \(1 - \gamma\), note that \(\gamma \rightarrow 1\)
- Substituting \((p_n, \delta_n)\) from previous slide, we can obtain LP wealth growth for a continuous case.
- Case I: \(p = \frac{1}{2} \implies d = 0\). Substituting \(\delta_n = \frac{\sigma}{\sqrt{n}}\) for \(n \rightarrow \infty\)
Convergence to Continuity
\begin{aligned}
\lim_{n\to\infty} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} &=
\lim_{n\to\infty} \frac{\sigma\sqrt{n}}{2} \frac{1}{1 - 2 \sqrt{n} \frac{\text{log}\gamma}{\sigma}} \left(\frac{1 - \gamma}{1 + \gamma}\right)
= -\frac{\sigma^2}{4\text{log}(\gamma)} \left(\frac{1 - \gamma}{1 + \gamma}\right)
\end{aligned}
-\frac{1}{\text{log}(\gamma)} \left(\frac{1 - \gamma}{1 + \gamma}\right)
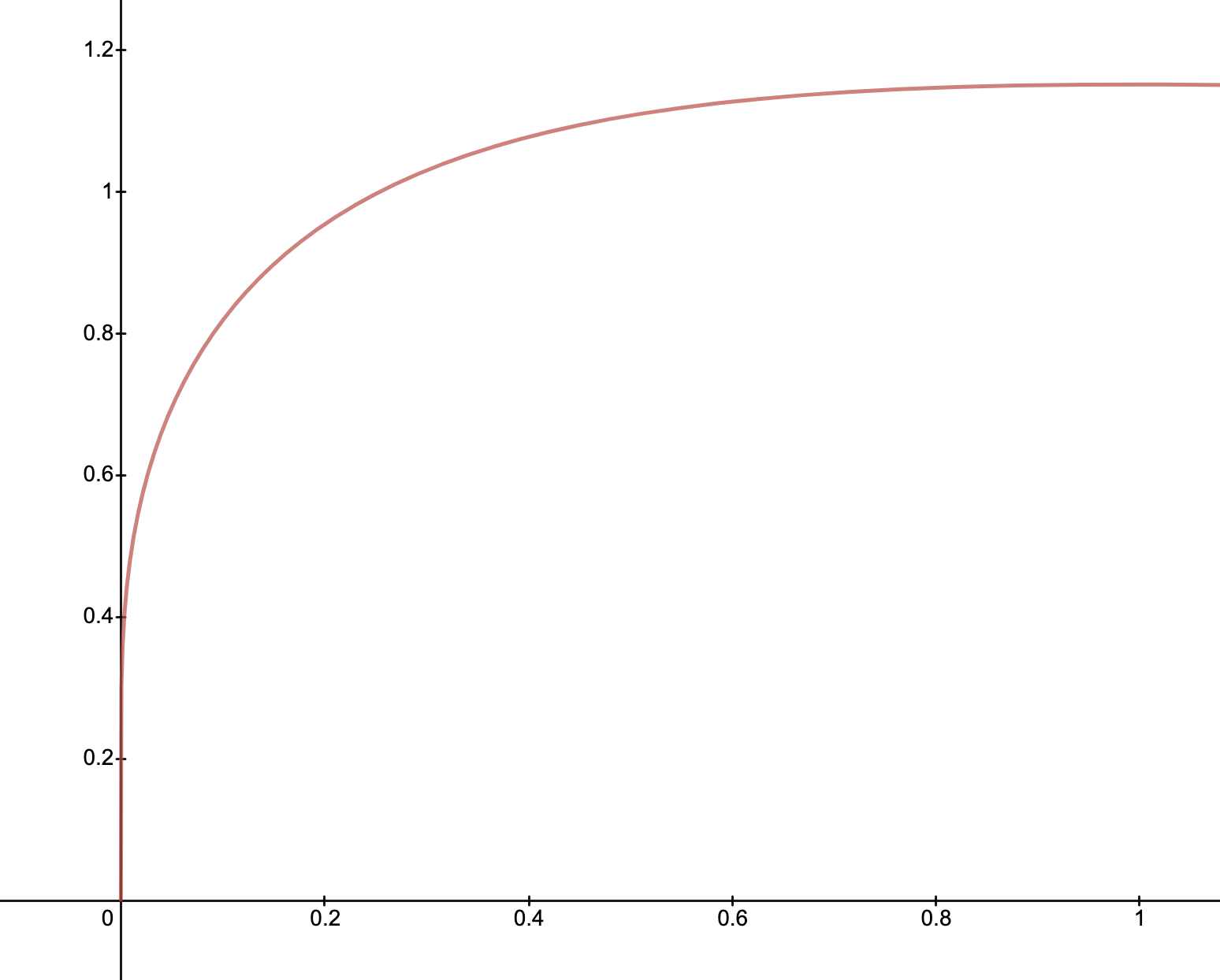
- The LP wealth increases in \(\gamma \in [0,1]\)
- For \(\gamma \rightarrow 1\), the return is
\begin{aligned}
\lim_{\gamma\to1} -\frac{\sigma^2}{4\text{log}(\gamma)} \left(\frac{1 - \gamma}{1 + \gamma}\right) = \frac{\sigma^2}{8}
\end{aligned}
- The un-rebalanced portfolio is zero!
Convergence to Continuity
\begin{aligned}
\lim_{n\to\infty} \lim_{t\to\infty} \frac{\mathbb{E}(\text{log} \ W_t)}{t} &=
\frac{d}{2}
\left(
\left( \frac{1 + \gamma^{\frac{4d}{\sigma^2}}}{1 - \gamma^{\frac{4d}{\sigma^2}}} \right)
\left(\frac{1 - \gamma}{1 + \gamma}\right)
+ 1
\right)
\end{aligned}
- Case II: \(p > \frac{1}{2}\). Substituting \(p_n\) and \(\delta_n\)
- The LP wealth decreases in \(\gamma \in [0,1]\) if \(4d > \sigma^2\). \(\gamma \rightarrow 0\) gives best possible growth \(d\).
- The wealth increases in \(\gamma \in [0,1]\) if \(4d < \sigma^2\). \(\gamma \rightarrow 1\) gives best growth \(\frac{d}{2} + \frac{\sigma^2}{8}\).
\begin{aligned}
\left( \frac{1 + \gamma^{\frac{4d}{\sigma^2}}}{1 - \gamma^{\frac{4d}{\sigma^2}}} \right)
\left(\frac{1 - \gamma}{1 + \gamma}\right)
\end{aligned}
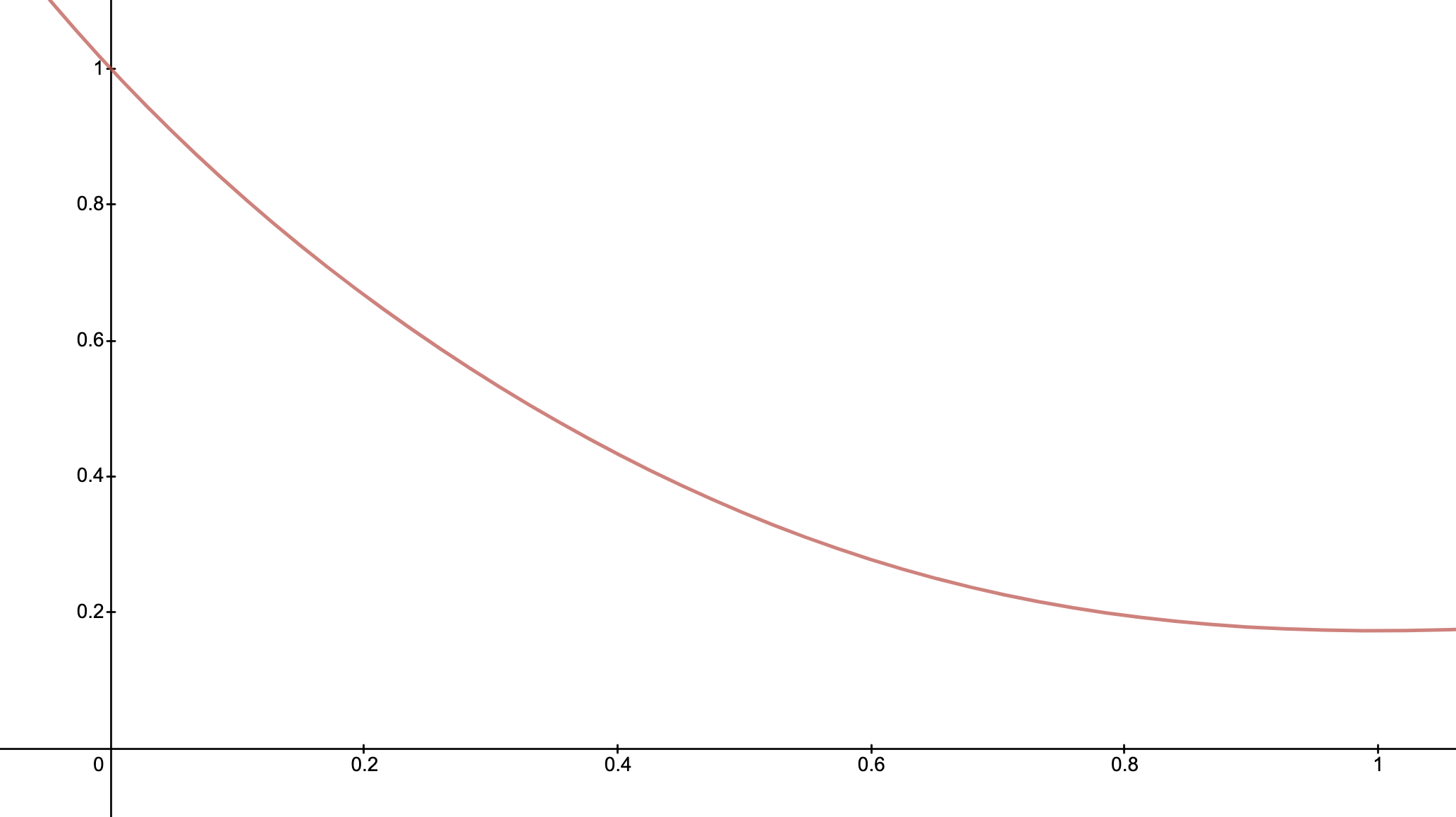
\(\frac{4d}{\sigma^2} > 1\)
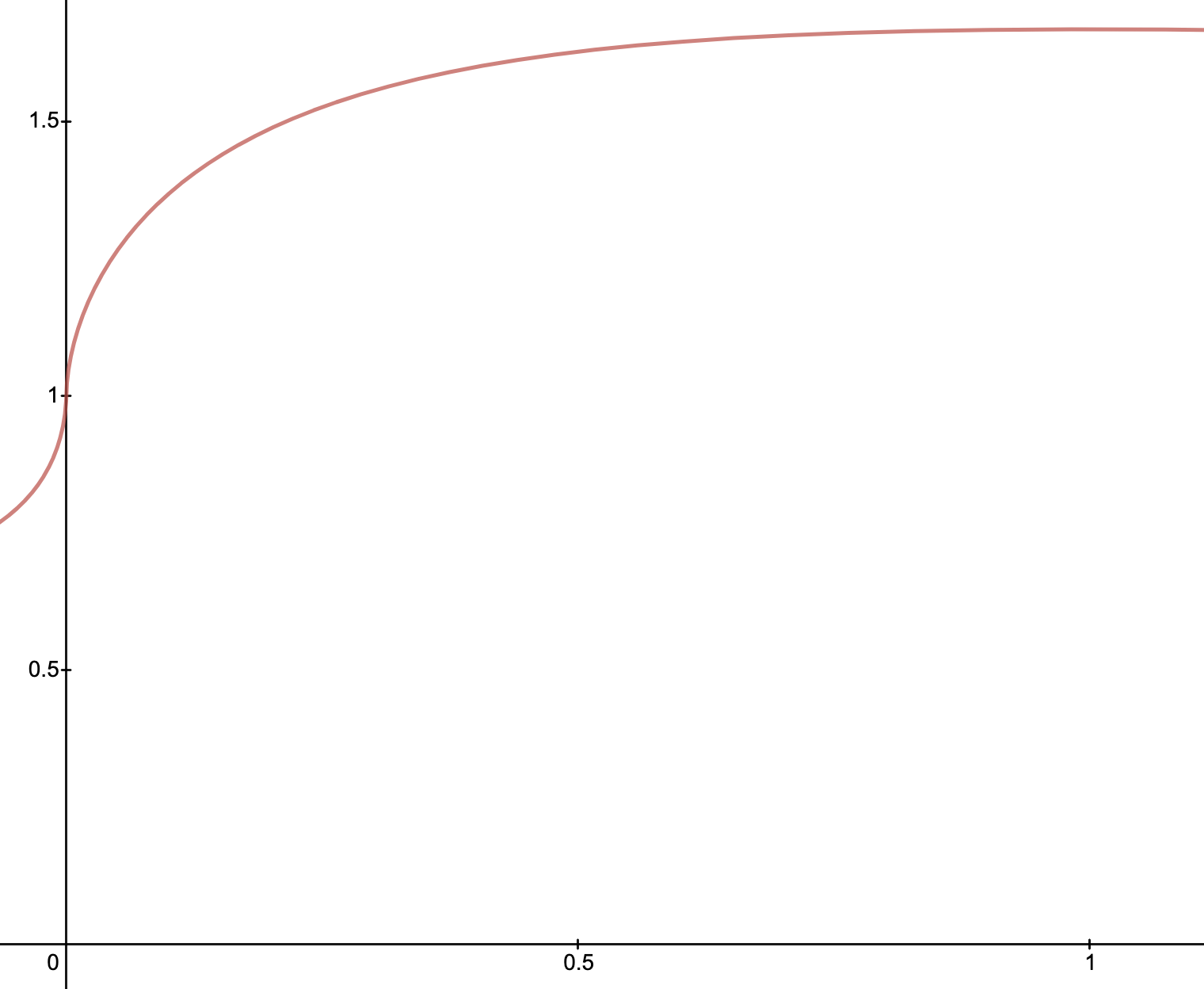
\(\frac{4d}{\sigma^2} < 1\)
Summary
\(p = \frac{1}{2}\)
\(p > \frac{1}{2}\)
HOLDers
LPs
\(0\)
\(\mu - \frac{\sigma^2}{2}\)
\(3\sigma^{2}> 4\mu\)
\(3\sigma^{2} < 4\mu\)
\(\frac{\sigma^2}{8}\)
\(\frac{1}{2}\left(\mu - \frac{\sigma^2}{4}\right)\)
\(3\sigma^{2}= 4\mu\)
\(\mu - \frac{\sigma^2}{2}\)
\(\mu - \frac{\sigma^2}{2}\)
- Therefore, LPs always do either equal or better than HODLers!
- For LPs to always do better, we must that: \(3\sigma^2 > 4\mu\) and \(\mu > \frac{\sigma^2}{4}\). Thus,
\begin{aligned}
\frac{4\mu}{3} < \sigma^2 < 4\mu \ \implies \ \frac{2}{3} < \frac{\sigma^2/2}{\mu} < 2
\end{aligned}
Volatility Drag
- When \(p > 0.5\), the expected growth rate of the price of the asset is
\begin{aligned}
G_{\text{HODL}} = \mu - \frac{\sigma^2}{2}
\end{aligned}
- Here the term \(-\frac{\sigma^2}{2}\) is known as the volatility drag.
- In the same case of \(p > 0.5\), if we have \(\frac{2\sqrt{\mu}}{\sqrt{3}} < \sigma < 2\sqrt{\mu},\) we have
\begin{aligned}
G_{\text{LP}} = \frac{1}{2}\left(\mu - \frac{\sigma^2}{4}\right) > G_{\text{HODL}}
\end{aligned}
Within that range, being a Uniswap LP will eventually make you rich, and in fact richer than you could become by holding any unrebalanced portfolio consisting of cash and the asset.
- LP Wealth paper Authors
Uniswap LP Growth and Volatility Drag
By Suyash Bagad
Uniswap LP Growth and Volatility Drag
Some deep diving about the volatility drag in prices in Uniswap.
