Data Structures

2017 TFcis Summer

By LFsWang

Binary Index Tree

樹狀樹組

前綴和問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$

前綴和問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$

暴力法：用陣列亂做！$O(N)$

前綴和問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$

使用級數和$S$來完成！

$$S_n=a_1+a_2+\cdots +a_n$$

高中數學

$$S_i=a_1+a_2+\cdots +a_n$$

$$=S_{i-1}+a_i$$

可以在$O(N)$時間預處理

$$a_i+a_{i+1}+\cdots +a_{j}$$

$$=(a_1+a_2+\cdots +a_j)-(a_1+a_2+\cdots +a_{i-1})$$

$$=S_j-S_{i-1}$$

可以在$O(1)$時間回答問題

前綴和問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$
把$a_i$的數值設定為$v$

原來的方法爆炸

	區間和	修改數值
陣列亂做	O(N)	O(1)
前綴和	O(1)	O(N)
BIT / 線段樹	O(logN)	O(logN)

二元引索樹

可以在$O(logN)$的時間查詢前綴和以及修改
花費空間與原始陣列相等$O(N)$
常數小，Code簡單
從1開始

aka 樹狀樹組、BIT

$lowbit(x)$

正整數$x$在二進位表示法下，最低位1代表的數字

$$12=1100_2,lowbit(12)=0100_2$$

$$13=1101_2,lowbit(13)=0001_2$$

Hack for lowbit

如果目前的數位系統是 二補數 ，那lowbit有快速算法

$$lowbit(x)=x\& -x$$

二補數表示法

$$x=12=1100_2$$

$$-x=\sim x+1$$

$$-12=\sim 1100_2 +1$$

$$~~~~~=0011_2+1$$

$$=0100_2$$

bit[x]

定義bit的節點$b_i$

$$b_i=\sum^i_{i-lowbit(i)+1}a_i=a_i+a_{i-1}+\cdots+a_{i-lowbit(i)+1}$$

Example

$$lowbit(12)=0100_2=4$$

$$b_{12}=a_{12}+a_{11}+a_{10}+a_{9}$$

大概的結構

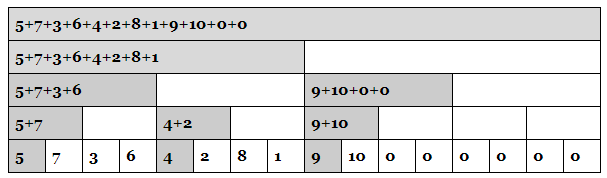
區間求和

把一個數字依據$lowbit$分解加起來

$b_x$表示了$a_x+a_{x-1}+\cdots+a_{x-lowbit(x)+1}$

因此剩下的項可由

$b_{x-lowbit(x)}=a_{x-lowbit(x)}+a_{x-lowbit(x)-1}+\cdots$取得

Cute code for sum

int sum(int i)
{
    int s=0;
    while(i)
    {
        s+=bit[i];
        i-=i&-i;
    }
    return s;
}

單點加值

更新$a_x$，首先先找bit中第一個包含$a_x$的資料：$b_x$

然後更新下一個有$a_x$的資料：$b_{x+lowbit(x)}$到超出範圍

單點加值

證明前頁方法的正確性

引理：$a_x\in b_i\Leftrightarrow i\geq x>i-lowbit(i)$

就bit點的定義

$$b_i=\sum^i_{i-lowbit(i)+1}a_i=a_i+a_{i-1}+\cdots+a_{i-lowbit(i)+1}$$

單點加值

定理1. 若$b_i$包含$a_x$，則$b_{i+lowbit(i)}$也包含$a_x$

$b_{i+lowbit(i)}$的範圍是什麼？

顯然$x$不會超過上界

$$ x \leq i+lowbit(i)$$

下界？

單點加值

定理1. 若$b_i$包含$a_x$，則$b_{i+lowbit(i)}$也包含$a_x$

因為$i+lowbit(i)$在二進位加法下會進位

$$lowbit(i+lowbit(i))\geq 2\times lowbit(i)$$

$$\begin{matrix} 12=&01100_2 \\ lowbit(12)=&00100_2 \\ 12+lowbit(12)=&10000_2 \end{matrix}$$

單點加值

定理1. 若$b_i$包含$a_x$，則$b_{i+lowbit(i)}$也包含$a_x$

$$2\times lowbit(i)\leq lowbit(i+lowbit(i))$$

$$i+lowbit(i)-lowbit(i+lowbit(i))\leq i+lowbit(i)-2\times lowbit(i)$$

$$=i-lowbit(i) < x$$

單點加值

定理1. 若$b_i$包含$a_x$，則$b_{i+lowbit(i)}$也包含$a_x$

結合上界下界，得到

$$lowbit(i+lowbit(i))\leq i-lowbit(i) < x< i+lowbit(i)$$

故$a_x \in b_{i+lowbit(i)} \square $

單點加值

定理2. 若$b_i$包含$a_x$，則$b_y$皆不包含$a_x$

$$\text{for } i<y<i+lowbit(i)$$

$$y-i \geq lowbit(y)$$

$$y-lowbit(y)+1 > i \geq x\square$$

Cute code for add

void add(int i,int v)
{
    while(i<=N)
    {
        bit[i]+=v;
        i+=i&-i;
    }
}

練習題

有數列$a_1,a_2,a_3,\cdots,a_n$，找有多少$(i,j)$滿足

$$i<j,a_i>a_j$$

Segment tree?

線段樹

最大值問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$max(a_i,a_2,\cdots,a_j)$
把$a_i$改成$v$

線段樹的概念

區間分割成許多片段，要使用時再組合起來

因此線段樹能處理的問題需要能透過「組合」答案完成

區間加法：$ (a_i+\cdots a_m)+(a_{m+1}+\cdots+a_j)$

區間最大值：$ max(a_i,\cdots ,a_m),max(a_{m+1},\cdots a_j)$

線段樹的分解

線段樹是一個二元樹，每一個節點代表區間$[L,R]$的資訊(答案)

若非葉節點，左右子樹分別為左半區間及右半區間的資訊

$$[L,R]$$

$$[L,M]$$

$$[M+1,R]$$

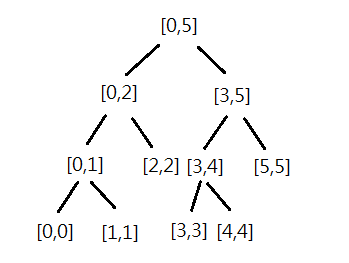
低品質示意圖

實作線段樹

區間有分成開區間以及閉區間

$$M=(L+R)/2$$

$[L,R]$的左右節點是$[L,M],[M+1,R]$，葉子是$[L,L]$

$[L,R)$的左右節點是$[L,M),[M,R)$，葉子是$[L,L+1)$

範例實作都用前者

節點定義

根據需求，會在線段樹上記錄許多不同的資訊，通常要記錄的資訊就是題目要求的資料

struct node
{
    int max;
}a[4*MAXN];

合併節點

線段樹的關鍵就是要如何透過合併節點算答案

區間最大值：$max([L,R])=max(max([L,M]),max([M+1,R]))$

node pull(const node &x,const node &y)
{
    node tmp;
    tmp.max = max( x.max , y.max );
    return tmp;
}

建構線段樹

我們可以在$O(N)$的時間初始化線段樹

#define IL(X) ((X)*2+1)
#define IR(X) ((X)*2+2)
void build(int L,int R,int id)
{
    if(L==R)
    {
        arr[id].max = a[L];
        return ;
    }
    int M = (L+R)/2;
    build(L  ,M,IL(id));
    build(M+1,R,IR(id));
    arr[id] = pull( arr[IL(id)] , arr[IR(id)] );
}

如果當前區間只有一個

直接算答案

否則遞迴左右

再合併答案

線段樹的參數

在線段樹的操作，通常會需要三個變數：L,R,id記錄節點資訊

L,R：表示點id的區間範圍

如果定義Root ID = 0，那左右子樹的ID

$$\text{Left ID}= x\times 2+1$$

$$\text{Right ID}= x\times 2+2$$

查詢線段樹

我們可以在$O(logN)$的時間查詢任意區間

node Query(int l,int r,int L,int R,int id)
{
    if( l==L && r==R ) return arr[id];
    int M = (L+R)/2;
    if( r <= M )return Query(l,r,L  ,M,IL(id));
    if( M <  l )return Query(l,r,M+1,R,IR(id));
    return pull(
        Query(l  ,M,L  ,M,IL(id)),
        Query(M+1,r,M+1,R,IR(id))
    );
}

如果要查的區塊與現在一樣

直接丟答案

否則看看在哪一邊

跨區間要合併答案

單點修改

我們可以在$O(logN)$的時間修改一個點的資料

void Modify(int i,int v,int L,int R,int id)
{
    if(L==R){//==i
        arr[id].sum = v;
        return ;
    }
    int M = (L+R)/2;
    if( i<=M )Modify(i,v,L  ,M,IL(i));
    else      Modify(i,v,M+1,M,IR(i));
    arr[id] = pull( arr[IL(id)] , arr[IR(id)] );
}

找到位置就直接改

不然就看看在哪邊

改完要pull重算答案

練習題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求區間連續最大和$a_i+a_2+\cdots+a_j,L\leq i\leq j \leq R$
求區間兩兩乘積和 (只有一個數字值為0 )
把$a_i$改成$v$

Lazy Flag

懶惰標記

區間和問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$
把$a_i,a_2,\cdots,a_j$都加$v$

區間和問題

線段樹單點修改$O(NlogN)$比暴力修改$O(N)$慘烈

透過增加標記來解決問題！

如果一個節點上有標記：表示整個區間要做某件事，但沒做

有標記的節點

有多重標記要注意優先順序

struct node
{
    int size;// = Range size
    int sum;
    int lazy_add;
    bool real_sum()
    {
        return sum + lazy_add*size;
    }
    bool islazy()
    {
        return lazy_add != 0;
    }
};

雖然不做事，但是可以由操作推出答案的話就能用懶惰標記

用懶惰標記求取目前區間正確的答案

下推標記

要存取下方區間資料前，要先讓區間真的做事

void push(int id)
{
    arr[IL(id)].lazy_add += arr[id].lazy;
    arr[IR(id)].lazy_add += arr[id].lazy;
    //重算答案
    arr[id] = pull(arr[IL(id)],arr[IR(id)]);
}
node pull(node x,node y)
{
    node tmp;
    tmp.size = x.size + y.size;
    tmp.sum = x.real_sum() + y.real_sum();
    //use real_sum not sum!
    tmp.lazy_add = 0;
    return tmp;
}

把懶惰標記送下去

送完要更新自己的答案！

怕忘記可以寫在push裡面

練習題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$
把$a_i,a_2,\cdots,a_j$都加$v$
把$a_i,a_2,\cdots,a_j$都乘$v$

永久化標記

如果標記是可以互相抵銷的，而且處理push太麻煩或是無法操作，就不推標記了

取而代之的，在通過標記時修正答案！

區間加值問題

除了下推標記，我們也可以在回傳答案時加上此區間的影響

int query(int l,int r,int L,int R,int id)
{
    int effect = (r-l+1)*a[id].lazy_sum;
    if(l==L&&r==R) return a[id].sum + effect;
    int M = (L+R)/2;

    if( r<=M )return query(l,r,L  ,M,IL(id)) + effect;
    if( M< l )return query(l,r,M+1,R,IR(id)) + effect;
    return 
        (query(l  ,M,L  ,M,IL(id))+
        query(M+1,r,M+1,R,IR(id))+ effect )%mod;
}

區間加值問題

因為加法的標記可以拆分後疊加，滿足要點，同理乘法也可以，但務必要注意如何維護標記及答案！。

[L,R] add 50

[c] add 12

total : $50+ (c +12)$

[L,R] mul 2

[c] mul 3

total : $2\times(c\times 3 )$

區間根號問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$
把$a_i,a_2,\cdots,a_j$都開根號，取整

懶惰標記

怪怪的？

區間根號沒有簡單標記可以處裡！

暴力完成！

區間根號

如果把一個數字反覆開根號，最後會停留在1

一個數字至多進行$\log\log N$次的根號操作就會回到1

$$N=2^{\log N}$$

$$\frac{\log N}{2^p}=1,p=\log\log N$$

區間根號

我們紀錄一個區間是否全部為1

如果是就不開根號

否則就暴力慢慢改

時間複雜度？

區間根號

每一次的更新一個數字是$O(\log N)$

每一次的修改是$O(K\log N)$, K是非1的數字數量

所有的詢問中有多少數字非1？

$$O(Q+N)$$

區間根號

$O(Q+N)$個數字在$O(\log\log V)$次之後會變成$1$

總計花費$O((Q+N)\log\log V)$

總時間複雜度

$$\sum \text{Query+Modify} = O( Q\log N+(Q+N)\log\log V)$$

Excellent!

區間根號

如果數字會快速的停留在定值，可以考慮暴力亂做！

樹堆

Treap

線段樹的弱點

線段樹的區間建立時就固定了，難以做元素搬移的動作

部分題目可以用時光倒流補空位解決

樹堆

分裂合併式樹堆分析

✔可以做元素區間搬移

✔可以打標記

✔實作簡單

✘常數有夠肥

✘初學Debug不易

樹堆的定義

樹堆同時滿足二元搜尋樹以及堆積的性質

一個樹堆的節點由兩個資料組成$(key,pri)$

二元搜尋樹key

左子樹 < 根 < 右子樹

樹堆的定義

樹堆同時滿足二元搜尋樹以及堆積的性質

一個樹堆的節點由兩個資料組成$(key,pri)$

堆積pri

根 < 左子樹 , 右子樹

Treap node

struct treap{
    int key;
    int pri;
    treap *l,*r;
    treap(int v)
    {
        key=v;
        l=r=nullptr;
        pri=rand();
    }
};
using ptreap = treap*;

Treap的基本操作

merge：把兩個樹堆合併成一個樹堆
spilt：把一個樹堆分成兩個

Treap使用隨機權重，使操作平均複雜度為$O(\log N)$

Treap的基本操作

merge：把兩個樹堆合併成一個樹堆

merge(a,b)需要保證：

a裡面key的都小於b的key

Merge

傳入兩棵樹，回傳合併過後的結果

Step 1.

如果a,b有一個是空的

直接丟回非空的Treap

ptreap merge(ptreap a,ptreap b)
{
    if(!a||!b) return a?a:b;
}

Merge

傳入兩棵樹，回傳合併過後的結果

Step 2.

根據堆性質

pri小的當根

ptreap merge(ptreap a,ptreap b)
{
    if(!a||!b) return a?a:b;
    if( a->pri < b->pri )
    {
        
        return a;
    }
    else
    {
        
        return b;
    }
}

Merge

假設a是根，要讓剩下的樹滿足二元樹的性質

因為b的元素都大於a，因此b要與a的右半邊合併

Merge

傳入兩棵樹，回傳合併過後的結果

Step 3.

b當根的時候同理

變成b的左邊與a合併

merge的過程沒有用到key的資料

ptreap merge(ptreap a,ptreap b)
{
    if(!a||!b) return a?a:b;
    if( a->pri < b->pri )
    {
        a->r = merge( a->r,b );
        return a;
    }
    else
    {
        b->l = merge( a,b->l );
        return b;
    }
}

Spilt

將一個Treap分成key小於等於以及大於K的部份

void spilt(int k,ptreap root,ptreap &a,ptreap &b)

Spilt

將一個Treap分成key小於等於以及大於K的部份

Step 1.

root是空的

就都是空的

void spilt(int k,ptreap root,ptreap &a,ptreap &b){
    if( root == nullptr ){
        a=b=nullptr;
        return ;
    }
}

Spilt

將一個Treap分成key小於等於以及大於K的部份

Step 2.

如果root <= K

那root就給a

否則給b

void spilt(int k,ptreap root,ptreap &a,ptreap &b){
    if( root == nullptr ){
        a=b=nullptr;
        return ;
    }
    if( root->key <= k ){
        a = root;

    }
    else{
        b = root;

    }
}

Spilt

將一個Treap分成key小於等於以及大於K的部份

<=K

因為$root\leq K$

左半邊也小於K

把右半邊$\leq K$的部分切回來放到root的右邊

Spilt

將一個Treap分成key小於等於以及大於K的部份

Step 3.

如果root給b同理

把屬於b的部分切回來

void spilt(int k,ptreap root,ptreap &a,ptreap &b){
    if( root == nullptr ){
        a=b=nullptr;
        return ;
    }
    if( root->key <= k ){
        a = root;
        spilt(k,root->r,a->r,b);
    }
    else{
        b = root;
        spilt(k,root->l,a,b->l);
    }
}

樹堆

把數列安裝到樹堆上

目標：讓Treap的中序走訪是原來的數列

$a_i$

$a_1,\cdots a_{i-1}$

$a_{i+1},\cdots a_n$

改造Treap

使用size(節點數量)取代key

利用數列的項$1,2,3,\cdots N$當作key

而這一資訊可以透過size求到

化絕對為相對

Size based Treap

左邊有K個點

Root編號就是K+1

Treap node

struct treap{
    int size;
    int key;
    int pri;
    treap *l,*r;
    treap(int v)
    {
        size = 1;
        key=v;
        l=r=nullptr;
        pri=rand();
    }
};
using ptreap = treap*;
typedef treap * ptreap;

原來的key就來放$a_i$的數值了

pull

現在的Treap跟線段樹一樣，要從兒子合併資訊(size)

因此需要使用pull來更新節點

nullptr protect

因為樹堆的操作會遇到空指標，透過一些技巧來避免RE

inline int size(ptreap s)
{
    return s==nullptr ? 0 : s->size ;
}

存取size/節點元素時透過專門函數存取

pull

更新的資料是

左邊+自己+右邊

inline ptreap pull(ptreap p)
{
    p->size = 1 + size(p->l) + size(p->r);
    return p;
}

merge

把兩個樹堆按照中序順序合併

這裡完全不關key的事

只要加上pull即可

ptreap merge(ptreap a,ptreap b)
{
    if(!a||!b) return a?a:b;
    if( a->pri > b->pri )
    {
        a->r = merge( a->r,b );
        return pull(a);
    }
    else
    {
        b->l = merge( a,b->l );
        return pull(b);
    }
}

Spilt

將一個Treap中序前K個元素剪下來

如果root 編號$\leq K$

那root就給a

否則給b

記得pull

注意K是數量

void spilt(int k,ptreap root,ptreap &a,ptreap &b){
    if( root == nullptr ){
        a=b=nullptr;
        return ;
    }
    if( size(root->l)+1 <= k ){
        a = root;
        spilt( k-1-size(root->l) ,root->r , a->r , b );
        pull(a);
    }
    else{
        b = root;
        spilt(k,root->l,a,b->l);
        pull(b);
    }
}

Treap

數列剪剪樂工具完成!

任意問題=

用spilt把需要的部分剪出來

在用merge裝回去

區間最大值問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$\max(a_i,a_2,\cdots,a_j)$
把$a_i$改成$v$

在node裡記錄左右子樹+自己的最大值pull

把第i個數字剪出來改再黏回去

區間旋轉問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$\max(a_i,a_2,\cdots,a_j)$
把$\{a_i,a_{i+1},\cdots a_j\}$改成$\{a_{i+1},\cdots a_j,a_i\}$

在node裡記錄左右子樹+自己的最大值pull

把整段剪下來，再把第一個黏到後面去

區間反轉問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$[L,R]$區間連續最大和
把$\{a_i,a_{i+1},\cdots a_j\}$改成$\{a_j,\cdots a_{i+1},a_i\}$

在node打懶惰標記! (線段樹做不到 Why?)

大榕樹的咒語

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

把$c_1,c_2\cdots c_i$插入到第$p$個數字後
從第$p$個數字後刪掉$K$個數字
求$[L,R]$區間連續最大和
求$[L,R]$區間連續和
把$\{a_i,a_{i+1},\cdots a_j\}$改成$\{a_j,\cdots a_{i+1},a_i\}$

持久化

Persistent

區間第K大數

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$[L,R]$的第$K$大數是什麼

持久化資料結構

可以查詢歷史版本的資料結構

持久化資料結構：資料結構+Copy on write

Copy on write

為了維護歷史版本，新增/修改資料的時候不對原始資料做操作

而是複製一份新的資料

複製一棵樹：$O(N)$ ?

空間複雜度：$O(N)$ ?

Copy on Write

複製出的節點，對於相同的資訊可以共用，遇到修改時再複製

時間複雜度：與原來一樣

空間複雜度：$O(\log N)$

Copy on Write

進行所有修改操作時，先複製一份root，只對複製的資料操作

ptreap copy(ptreap p)
{
    return new treap(*p);
}

每完成一次操作，就會多一個root

持久化Treap

ptreap merge(ptreap a,ptreap b)
{
    if(!a||!b) return a?a:b;
    ptreap r;
    if( a->pri > b->pri )
    {
        r = copy(a);
        r->r = merge( a->r,b );
    }
    else
    {
        r = copy(b);
        r->l = merge( a,b->l );
    }
    return pull(r);
}

持久化線段樹

pnode Modify(int i,int v,int L,int R,pnode r)
{
    pnode cpr = copy(r);
    if(L==R){//==i
        cpr->sum = v;
        return cpr;
    }
    int M = (L+R)/2;
    if( i<=M )Modify(i,v,L  ,M,r->l);
    else      Modify(i,v,M+1,M,r->r);
    return pull( cpr );
}

區間第K大

我們可以嘗試使用持久化線段樹來解決！
使用線段樹節點$a_k$表示數字$k$出現的次數

使用第$i$個線段樹表示$a_1$到$a_i$區間的資料！

可以離散化就離散化

區間第K大

數列$<A>=\{1,2,1,4,3\}$

$$\text{RMQ}_0=\{0,0,0,0\}$$

$$\text{RMQ}_1=\{1,0,0,0\}$$

$$\text{RMQ}_2=\{1,1,0,0\}$$

$$\text{RMQ}_3=\{2,1,0,0\}$$

$$\text{RMQ}_4=\{2,1,0,1\}$$

$$\text{RMQ}_5=\{2,1,1,1\}$$

區間第K大

求區間$[L,R]$有幾個數字$\leq v$？

查詢線段樹

$$\text{RMQ}_R-\text{RMQ}_{L-1}$$

區間第K大

求區間$[L,R]$第$K$大的數字？

線段樹上二分搜$v$

$$\text{RMQ}_R-\text{RMQ}_{L-1}$$

\text{Query :} O(\log N)

\text{Build :} O(N\log N)

樹套樹

Tree in Tree

樹套樹

樹中有樹

就是把學過的所有樹加以堆疊應用！

BIT+線段樹
線段樹+線段樹
Treap+線段樹
一般的樹+線段樹

區間第K大數

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$[L,R]$的第$K$大數是什麼
把$a_i$改成$v$

持久化線段樹

把$a_i$改掉就要修正$\text{RMQ}_i \sim \text{RMQ}_N$
複雜度$O(N\log N)$

大爆炸

前綴和問題

有數列$a_1,a_2,a_3,\cdots,a_n$，想要做一些事

求$a_i+a_2+\cdots+a_j$

可以用$S_j-S_{i-1}$求出來

可是修改$O(N)$

前綴和問題

可以用$S_j-S_{i-1}$求出來

可是修改$O(N)$

區間第K大數

可以用$\text{RMQ}_j-\text{RMQ}_{i-1}$求出來

可是修改$O(N)$

改用BIT維護區間和！

可修改區間第K大數

使用BIT維護區間

$\text{BIT}_i$表示區間$a_i$到$a_{i-lowbit(i)+1}$的線段樹資料

$<A>=\{1,2,1,4,3\}$

$$\text{BIT}_1={1,0,0,0}$$

$$\text{BIT}_2={1,1,0,0}$$

$$\text{BIT}_3={1,0,0,0}$$

$$\text{BIT}_4={2,1,0,1}$$

$$\text{BIT}_5={0,0,1,0}$$

可修改區間第K大數

對於每一個$a_i$要在$log N$個線段樹上修改

每一個線段樹花費$O(\log N)$

總花費

$$O(\log^2 N)$$

可修改區間第K大數

查詢區間第$K$大數：要在區間$[L,R]$二分搜

每一次二分搜要把$\log N$個線段樹加起來

$O(\log^3 N)$

BIT紀錄區間元素數量

$O(\log^2 N)$

可修改區間第K大數

修改：把BIT的$\log N$個線段樹都改掉

$O(\log^2 N)$

我們可以在

$O(N\log^2 N+Q\log^2 N)$

完成可修改區間第K大數！

資料結構

By sylveon

資料結構

1,784

Data Structures

Binary Index Tree

樹狀樹組

前綴和問題

前綴和問題

前綴和問題

前綴和問題

二元引索樹

\(lowbit(x)\)

Hack for lowbit

二補數表示法

bit[x]

大概的結構

區間求和

Cute code for sum

單點加值

單點加值

單點加值

單點加值

單點加值

單點加值

單點加值

Cute code for add

練習題

Segment tree?

線段樹

最大值問題

線段樹的概念

線段樹的分解

實作線段樹

節點定義

合併節點

建構線段樹

線段樹的參數

查詢線段樹

單點修改

練習題

Lazy Flag

懶惰標記

區間和問題

區間和問題

有標記的節點

下推標記

練習題

永久化標記

區間加值問題

區間加值問題

區間根號問題

懶惰標記

區間根號

區間根號

區間根號

區間根號

區間根號

樹堆

線段樹的弱點

樹堆

樹堆的定義

樹堆的定義

Treap node

Treap的基本操作

Treap的基本操作

Merge

Merge

Merge

Merge

Spilt

Spilt

Spilt

Spilt

Spilt

樹堆

改造Treap

Size based Treap

Treap node

pull

nullptr protect

pull

merge

Spilt