Intern Meeting
2023/08/17
Formalizing the Contact-Sampling Problem
While True:
find u s.t.
periodically:
What are we really trying to do here?
What about here?
Formalizing the Contact-Sampling Problem
While True:
find u s.t.
periodically:
Solve optimal control problem
Choose a state that would have a minimum value function.
The Optimal Control Problem
First, spent a long time thinking about this from an optimization p.o.v.
Minimize some measure of distance
Dynamics constraint
Torque limit / step limit
Joint limits
The Greedy Controller
Greedy Controller
Minimize distance between the next object state and the goal object state.
Torque limit / step limit
Joint limits
This is a constrained optimization, and I have 3 ways to offer how to solve it.
Comparable performances
Greedy Controller
1. Pass it to SNOPT with custom gradients.
3. Write my own constrained optimizer with Augmented Lagrangian
2. Random sampling within bounds and choosing best.
Discussion on solvers
Greedy Controller
1. Pass it to SNOPT with custom gradients.
3. Write my own constrained optimizer with Augmented Lagrangian
2. Random sampling within bounds and choosing best.
Finds an good solution, but with constraint violation within the iter. limit.
Perhaps best performing for this problem. Not sure if it will scale.
Found it to be more robust than SNOPT.
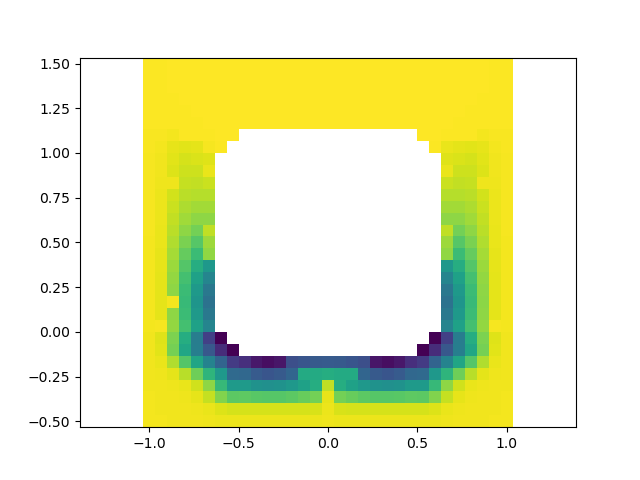
Solving the contact sampling problem.
The "dynamics" formulation - jointly minimize over state-action pair.
(i.e. minimize the Q function)
This problem is a lot harder for multiple reasons. Let's try passing it on to the augmented Lagrangian multiplier.
Solving the contact sampling problem.
The "dynamics" formulation - jointly minimize over state-action pair.
(i.e. minimize the Q function)
Important: qa should be non-penetrating!
The Kinematic Formulation
Instead of jointly optimizing over qa and u, is there something that qa tells us about the likely location of places that we can actuate the object in?
Step 1. If we are allowed to put any actuator on the surface of the object, how would the object move in response to the forces?
Locally, for quasi-dynamic systems, this relation is described by a Jacobian.
The Kinematic Formulation
Instead of jointly optimizing over qa and u, is there something that qa tells us about the likely location of places that we can actuate the object in?
Step 2. But we need to take into consideration that this impulse was produced by a robot (e.g. cannot be produced in the null-space)
Locally, for quasi-dynamic systems, this relation is described by a Jacobian.
Contact as a Joint
In the absence of any contact constraints, this imposes a "joint Jacobian" that maps actuator torques to motion of the objects.
So locally, contact can be thought of as a joint.
Contact as a Joint
Note that this is intimately connected to the "Bu matrix" of the dynamics, the sensitivity of object position w.r.t. the torques.
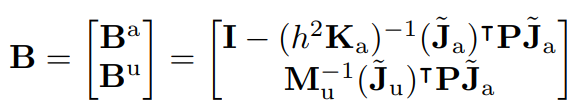
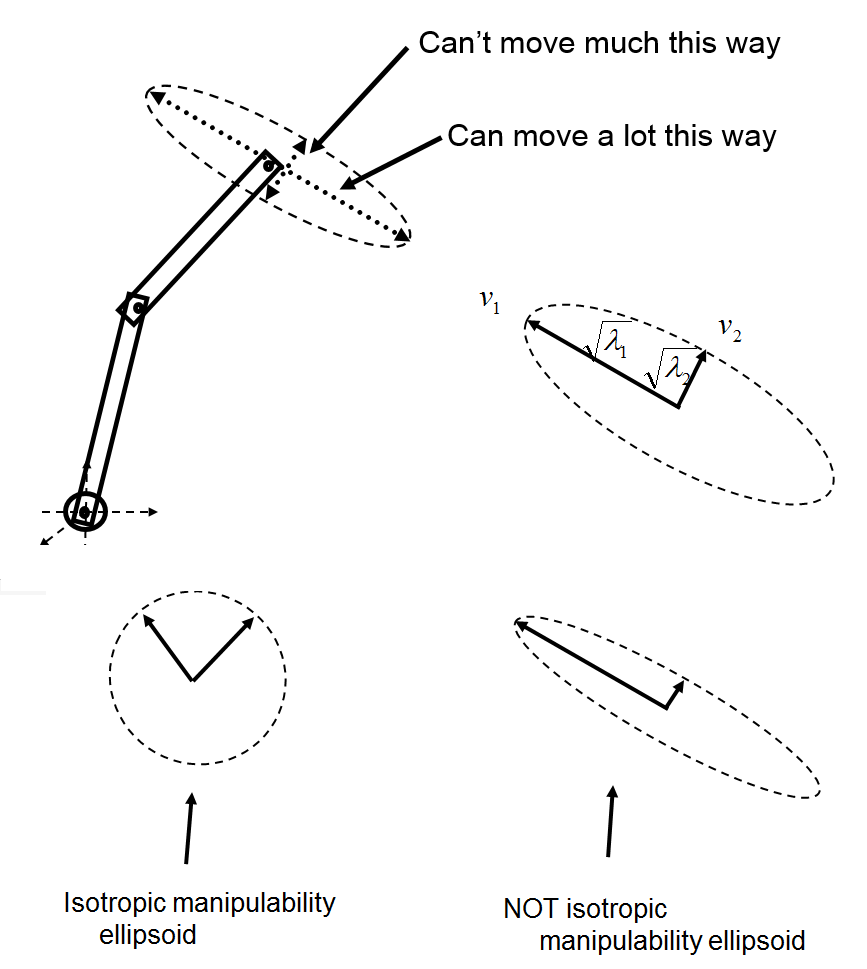
If we inject a norm-ball in tau, the Bu matrix maps the norm ball to the "manipulability ellipsoid" of the object.
Contact Placement as Mechanism Design
The problem of contact placement can be thought of as "mechanism design" that maximizes the manipulability ellipsoid along a certain direction.
The Unilateral nature of contact
Step 3. We are still missing one important nature of contact!
We can only push, but not pull. This introduces additional constraints on the "contact joint" that often differs from other kind of joints.
The Unilateral nature of contact
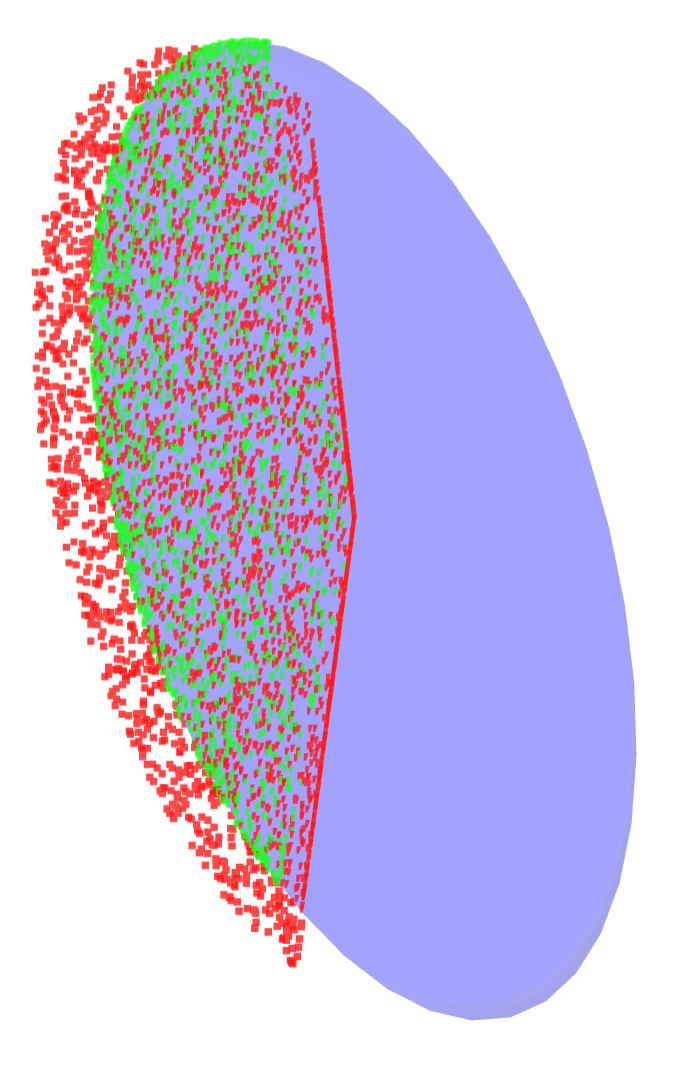
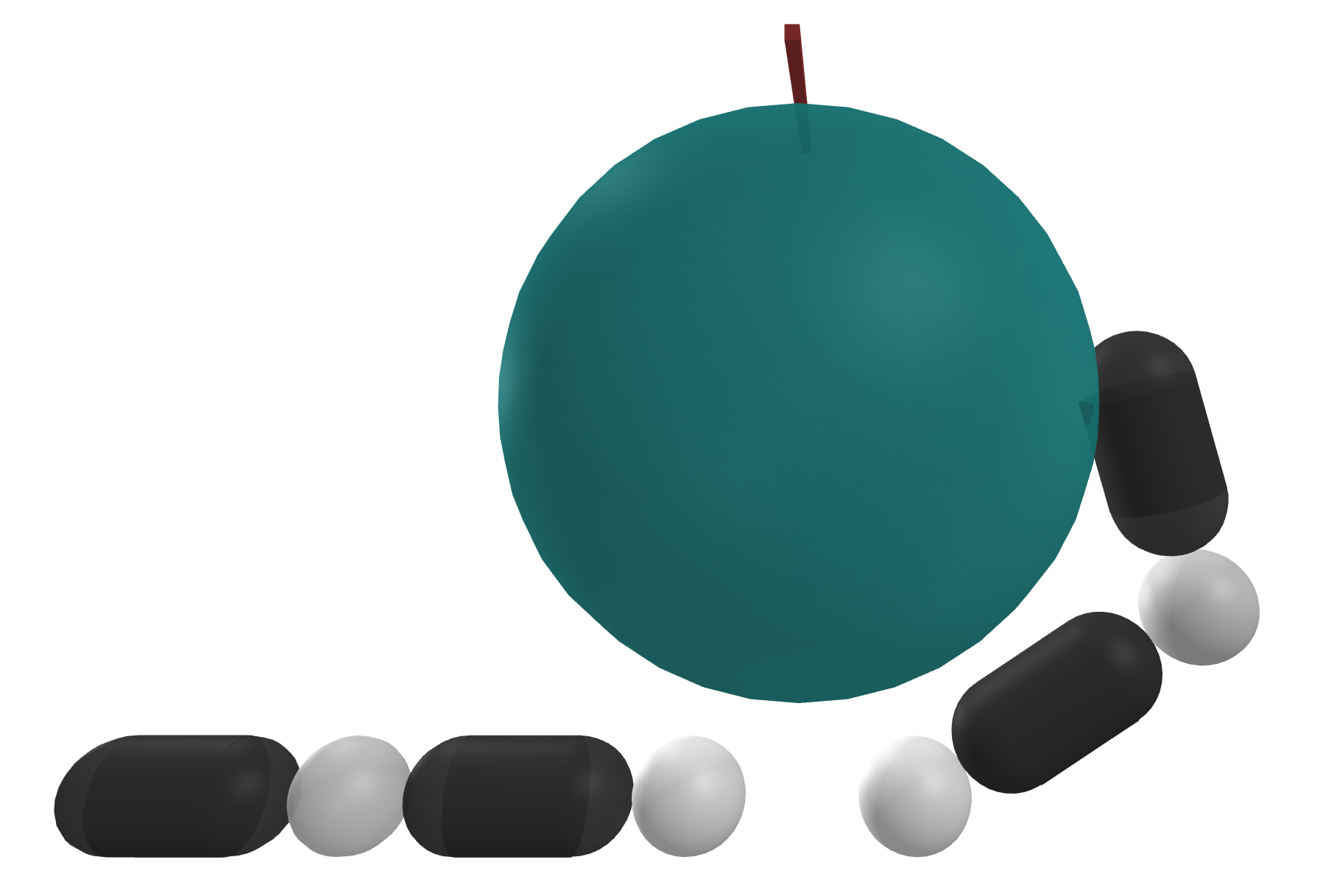
Points computed from this set
Simulator rollouts of a action norm-ball
Ellipsoid informed by the local
B matrix
The Unilateral nature of contact

Points computed from this set
Simulator rollouts of a action norm-ball
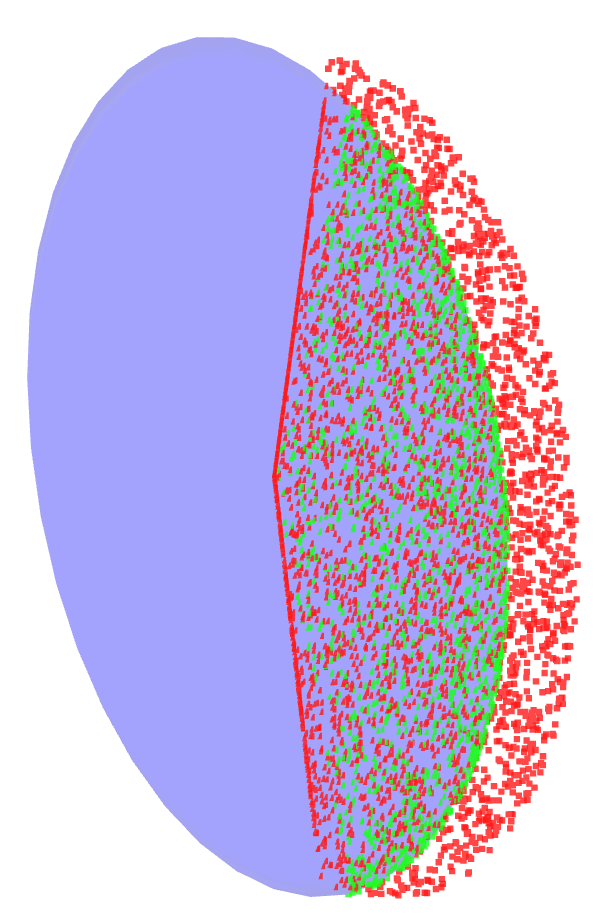
Ellipsoid informed by the local
B matrix
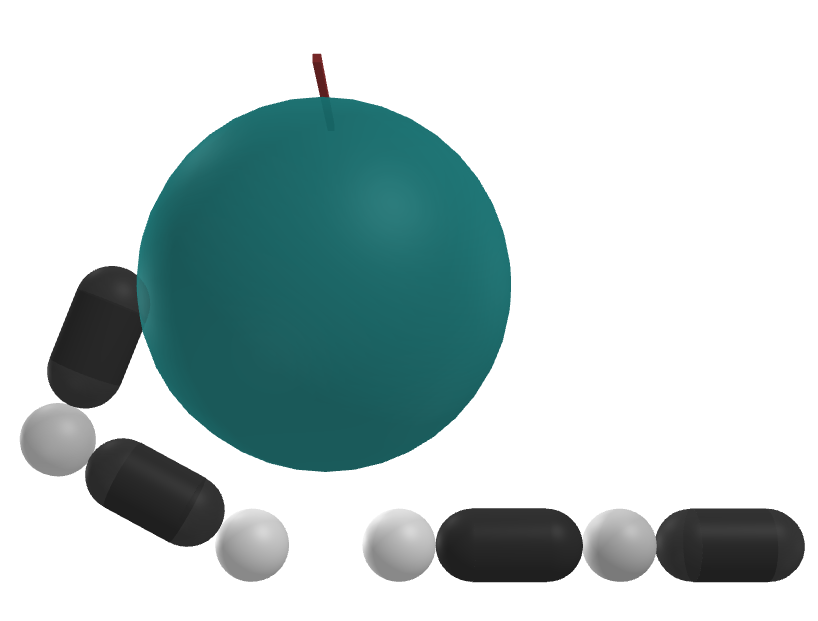
The Unilateral nature of contact
Points computed from this set
Simulator rollouts of a action norm-ball
Ellipsoid informed by the local
B matrix
The Smoothed Contact Joint
Step 4. The contact point and the point qa are connected by an inverse kinematics constraint, which is awkward to deal with.
We can relax this constraint by considering a "smoothed contact" relaxation that allows body to exert force from a distance.
Copy of CLF
By Terry Suh
Copy of CLF
- 361



