Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models
Tao Pang*, H.J. Terry Suh*, Lujie Yang, Russ Tedrake
MIT CSAIL, Robot Locomotion Group
Published in T-RO 2023
ICRA 2024 Presentation



The Software Bottleneck in Robotics


A
B
Do not make contact
Make contact
Today's robots are not fully leveraging its hardware capabilities

Larger objects = Larger Robots?
Contact-Rich Manipulation Enables Same Hardware to do More Things
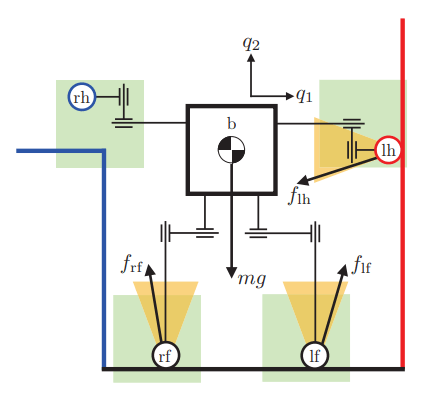
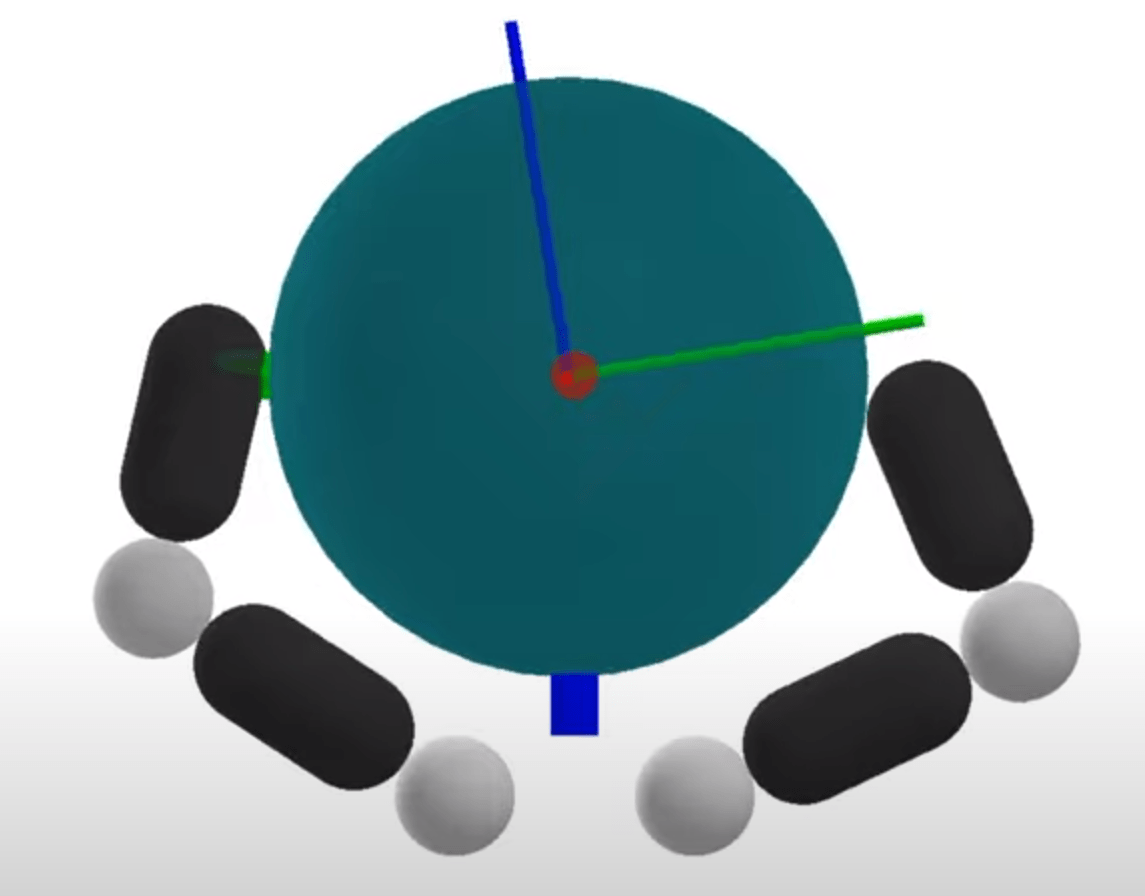
Case Study 1. Whole-body Manipulation

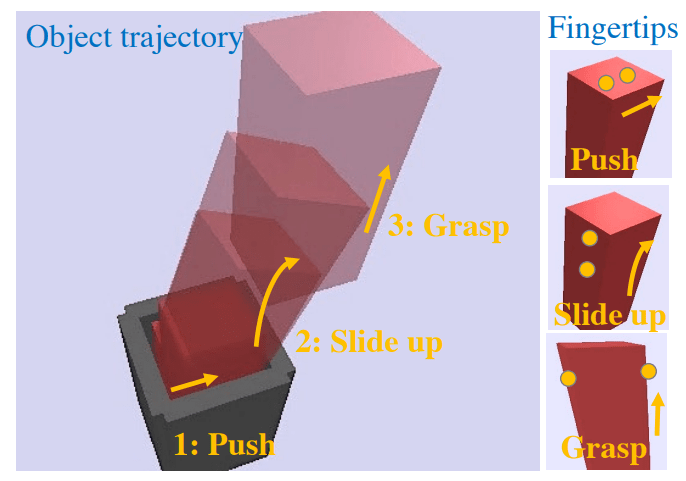
What is Contact-Rich Manipulation?
What is Contact-rich Manipulation?
Case Study 2. Dexterous Hands
OpenAI
What our paper is about
1. Why is RL succeeding where model-based methods struggle?
2. Can we do better by understanding?
What our paper is about
1. Why is RL succeeding where model-based methods struggle?
2. Can we do better by understanding?
- RL Regularizes Landscapes using stochasticity
- Allows Monte-Carlo Abstraction of Contact Modes
- Global optimization with stochasticity
What our paper is about
1. Why is RL succeeding where model-based methods struggle?
2. Can we do better by understanding?
- RL Regularizes Landscapes using stochasticity
- Allows Monte-Carlo Abstraction of Contact Modes
- Global optimization with stochasticity
- interior-point smoothing of contact dynamics
- Efficient gradient computation using sensitivity analysis
- Use of RRT to perform fast online global planning
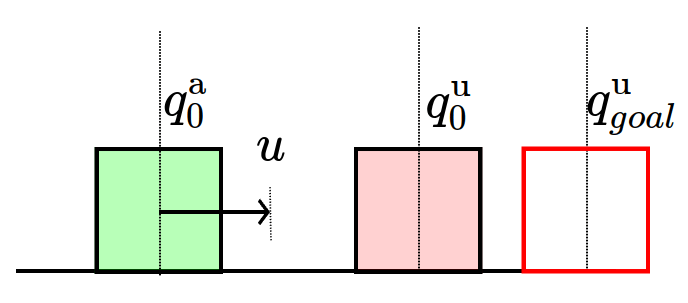
Toy Problem
Simplified Problem
Given initial and goal ,
which action minimizes distance to the goal?
Toy Problem
Simplified Problem
Consider simple gradient descent,

Dynamics of the system
No Contact
Contact
The gradient is zero if there is no contact!
The gradient is zero if there is no contact!
Local gradient-based methods get stuck due to the flat / non-smooth landscapes
Previous Approaches to Tackling the Problem

[MDGBT 2017]
[HR 2016]
[CHHM 2022]
[AP 2022]
Contact
No Contact
Cost
Mixed Integer Programming
Mode Enumeration
Active Set Approach
Why don't we search more globally for each contact mode?
In no-contact, run gradient descent.
In contact, run gradient descent.
Problems with Mode Enumeration
System
Number of Modes
The number of modes scales terribly with system complexity
No Contact
Sticking Contact
Sliding Contact
Number of potential active contacts
How does RL power through these problems?
Reinforcement Learning fundamentally considers a stochastic objective
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost
How does RL power through these problems?
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost
How does RL power through these problems?
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost
Contact
No Contact
Averaged
Randomized smoothing
regularizes landscapes
Cost
How does RL power through these problems?
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost

Contact
No Contact
Averaged
Randomized smoothing
regularizes landscapes
Cost
But leads to high variance,
low sample-efficiency.

Non-smooth Contact Dynamics
Smooth Surrogate Dynamics

No Contact
Contact
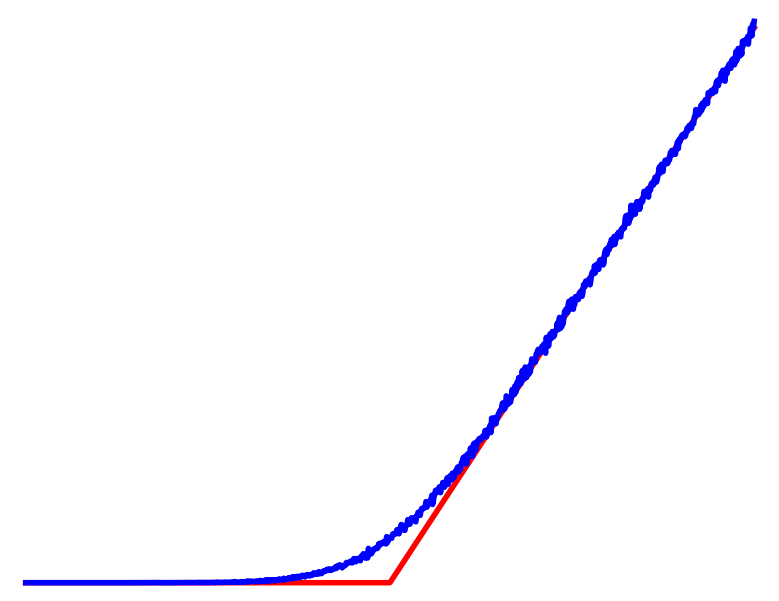
Averaged
Dynamic Smoothing
What if we had smoothed dynamics instead of the overall cost?
Effects of Dynamic Smoothing
Reinforcement Learning

Cost
Contact
No Contact
Averaged
Dynamic Smoothing
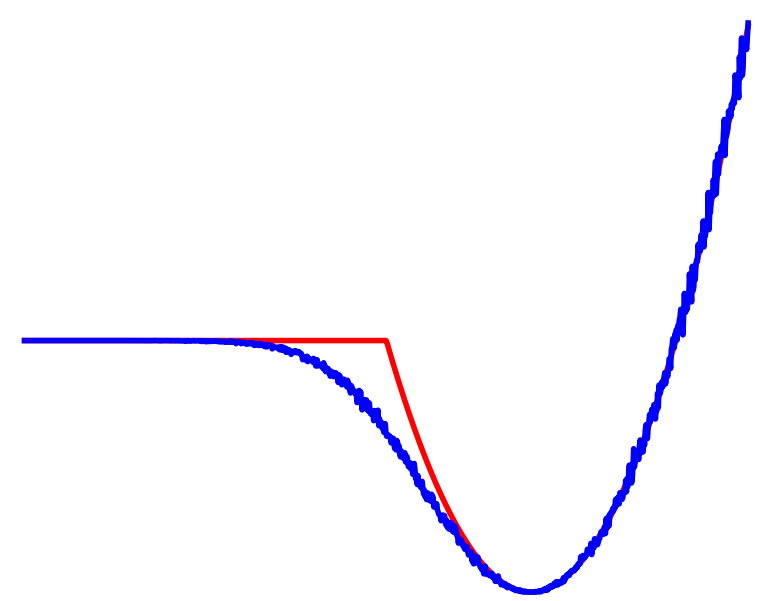
Averaged
Contact
No Contact
No Contact
Can still claim benefits of averaging multiple modes leading to better landscapes
Importantly, we know structure for these dynamics!
Can often acquire smoothed dynamics & gradients without Monte-Carlo.
Example: Box vs. wall
Commanded next position
Actual next position
Cannot penetrate into the wall
Implicit Time-stepping simulation
No Contact
Contact
Structured Smoothing: An Example
Importantly, we know structure for these dynamics!
Can often acquire smoothed dynamics & gradients without Monte-Carlo.
Example: Box vs. wall
Implicit Time-stepping simulation
Commanded next position
Actual next position
Cannot penetrate into the wall
Log-Barrier Relaxation
Structured Smoothing: An Example
Differentiating with Sensitivity Analysis
How do we obtain the gradients from an optimization problem?


Differentiating with Sensitivity Analysis
How do we obtain the gradients from an optimization problem?


Differentiate through the optimality conditions!
Stationarity Condition
Implicit Function Theorem

Differentiate by u
Quasi-dynamic Simulator
Quasidynamic Equations of Motion
Object Dynamics
Impedance-Controlled Actuator Dynamics
Non-Penetration
Friction Cone Constraints
Conic Complementarity
Quasi-dynamic Simulator
Quasidynamic Equations of Motion
Object Dynamics
Impedance-Controlled Actuator Dynamics
Non-Penetration
Friction Cone Constraints
Conic Complementarity
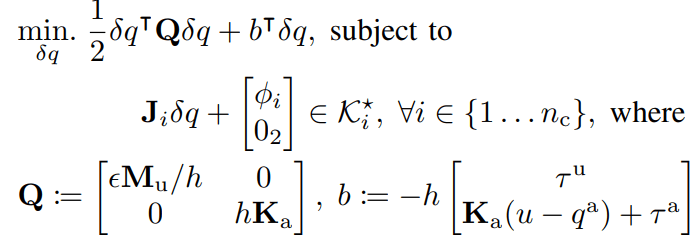
KKT Optimality
Conditions of SOCP
Quasi-dynamic Simulator
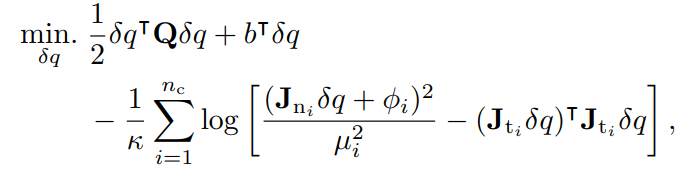
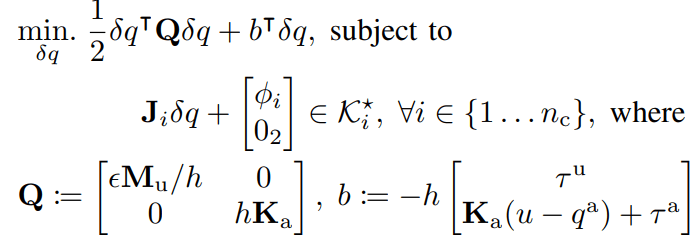
Original SOCP Problem
Interior-Point Relaxation
Example: Box vs. wall
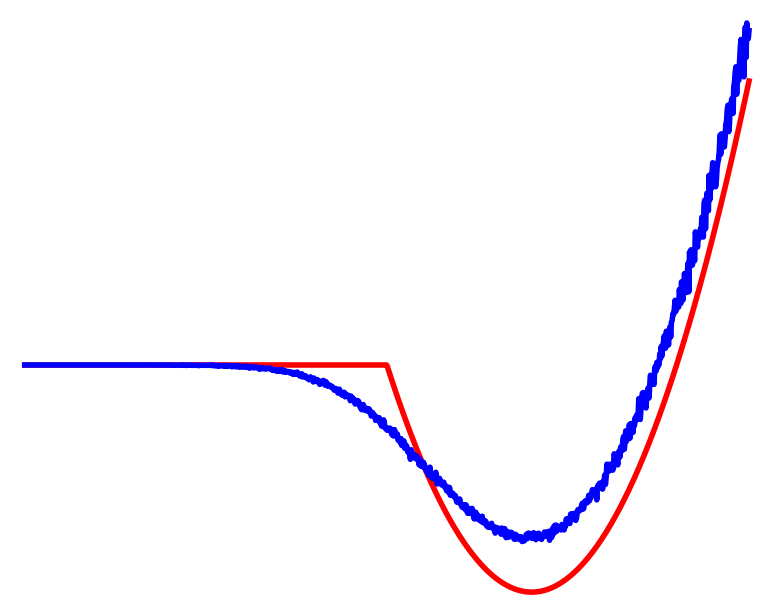
Randomized smoothing
Barrier smoothing
Randomized smoothing distribution that results in barrier smoothing
Barrier vs. Randomized Smoothing
Barrier & Randomized Smoothing are Equivalent
Gradient-based Optimization with Dynamics Smoothing
Scales extremely well in highly-rich contact
Efficient solutions in ~10s.
Single Horizon
Single Horizon
Multi-Horizon
Fundamental Limitations with Local Search


How do we push in this direction?
How do we rotate further in presence of joint limits?
Highly non-local movements are required to solve these problems

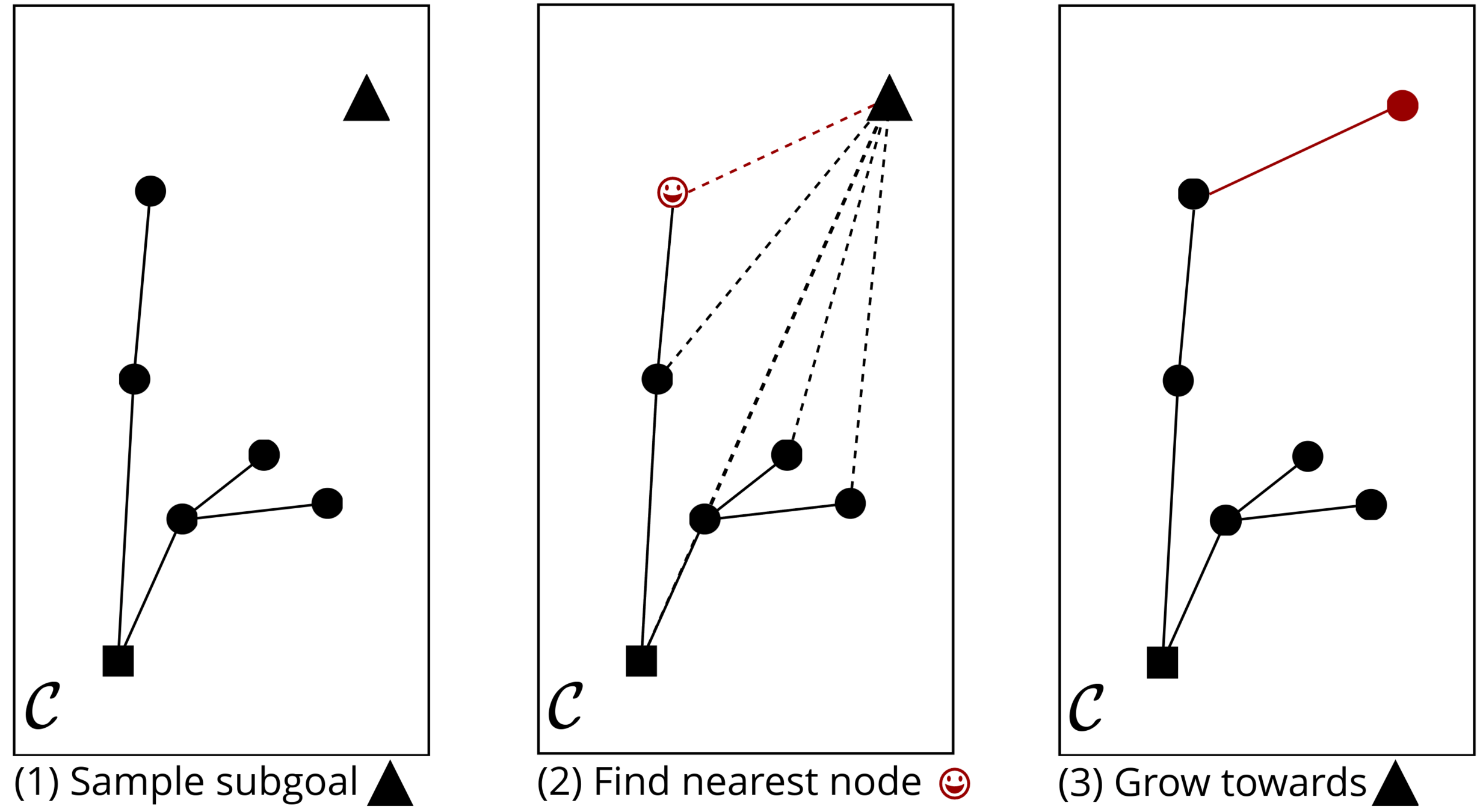
Rapidly Exploring Random Tree (RRT) Algorithm
[10] Figure Adopted from Tao Pang's Thesis Defense, MIT, 2023
(1) Sample subgoal
(2) Find nearest node
(3) Grow towards
RRT for Dynamics
Works well for Euclidean spaces. Why is it hard to use for dynamical systems?

What is "Nearest" in a dynamical system?
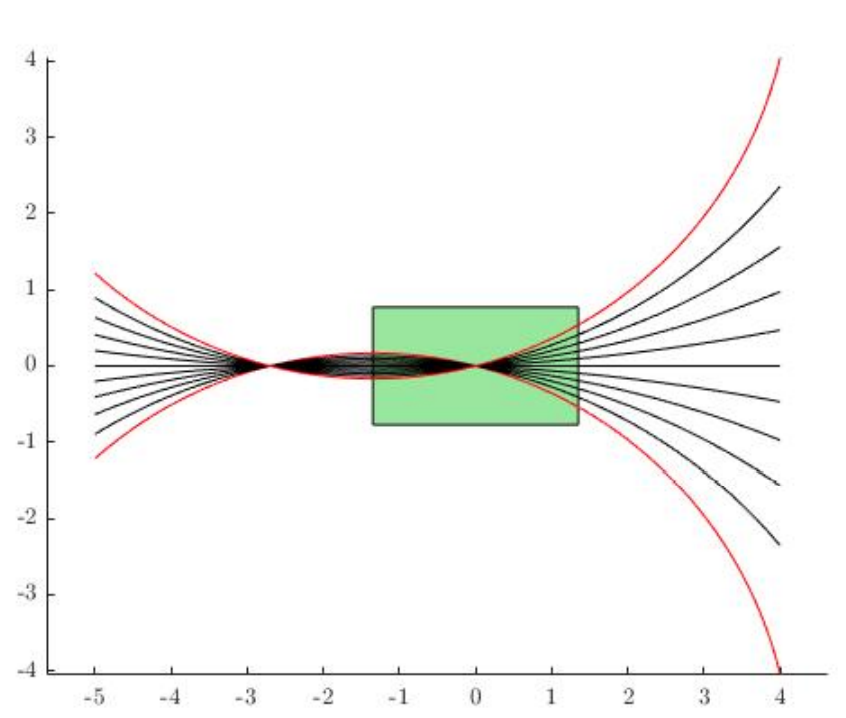
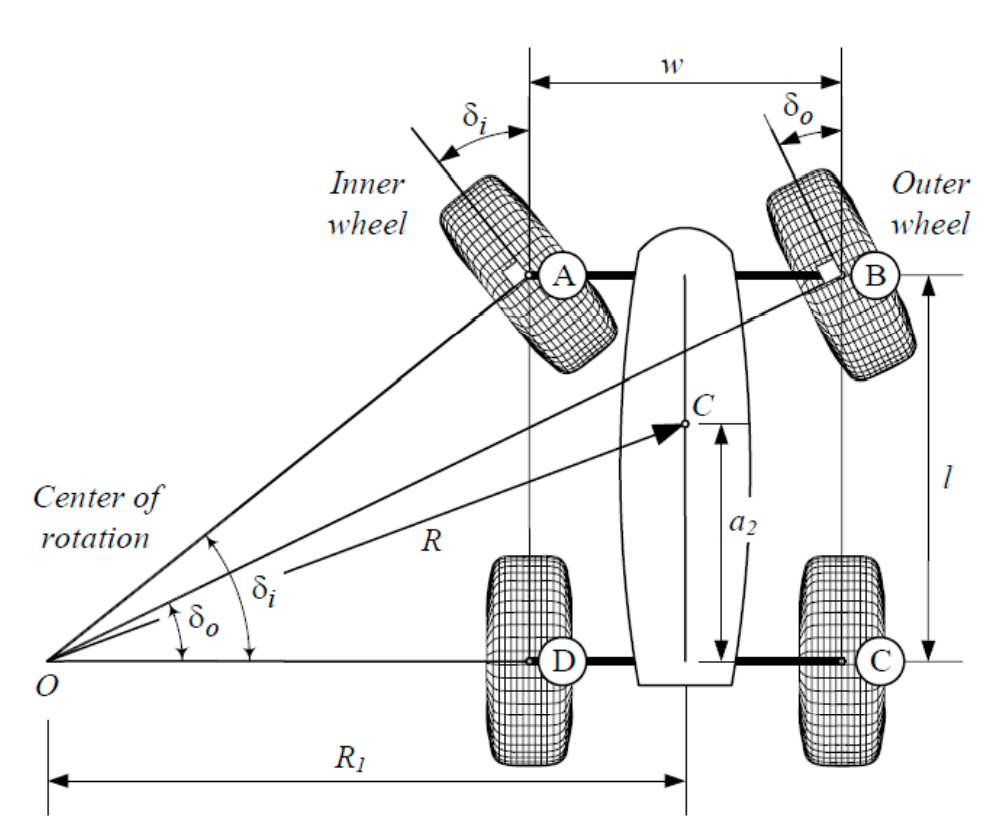
Rajamani et al., "Vehicle Dynamics", Springer Mechanical Engineering Series, 2011
Suh et al., "A Fast PRM Planner for Car-like Vehicles", self-hosted, 2018.
Closest in Euclidean space might not be closest for dynamics.
A Dynamically Consistent Distance Metric
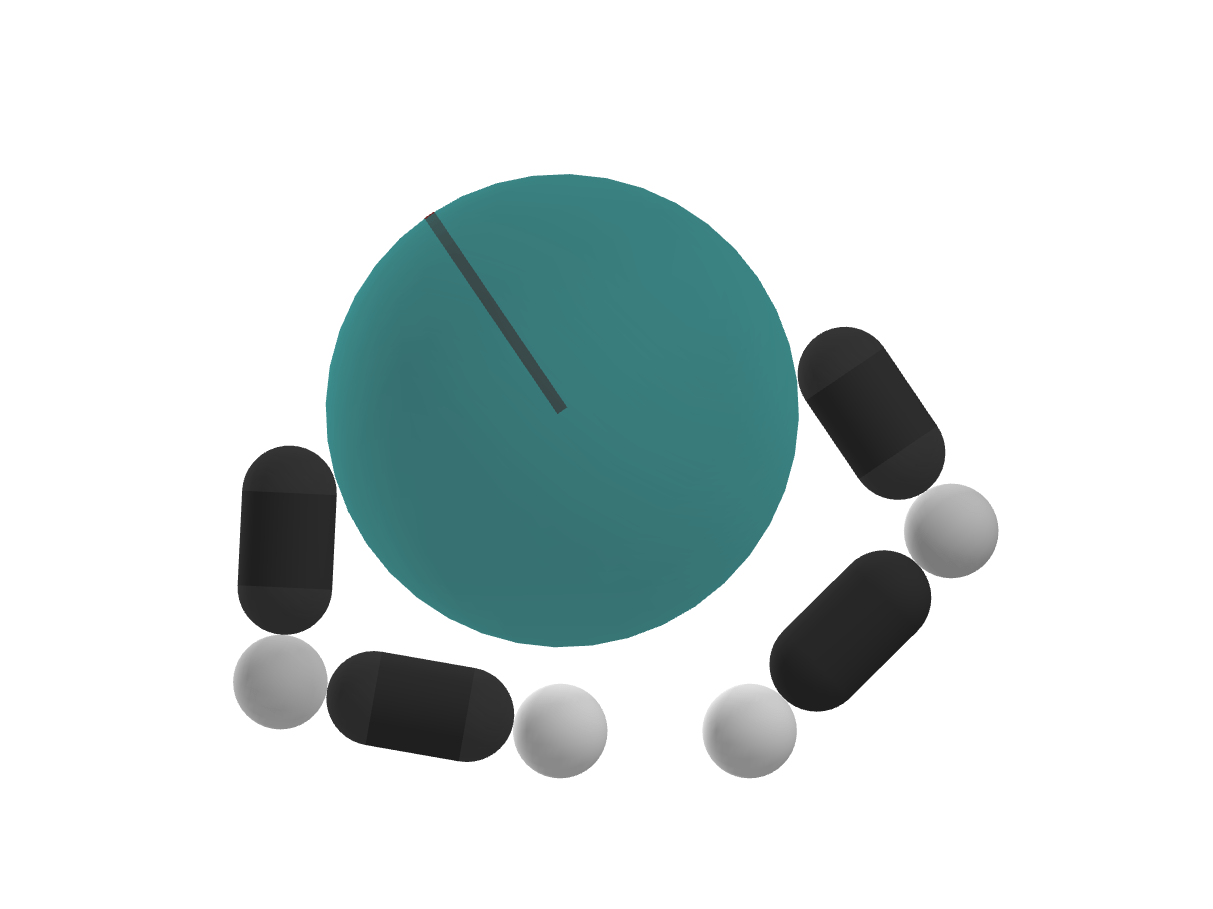
What is the right distance metric
What is the right distance metric
Fix some nominal values for ,
How far is from ?
The least amount of "Effort"
to reach the goal
A Dynamically Consistent Distance Metric
We can derive a closed-form solution under linearization of dynamics
Mahalanobis Distance induced by the Jacobian

Linearize around (no movement)
Jacobian of dynamics
A Dynamically Consistent Distance Metric
Mahalanobis Distance induced by the Jacobian


Locally, dynamics are:
Large Singular Values,
Less Required Input
A Dynamically Consistent Distance Metric


Locally, dynamics are:
(In practice, requires regularization)
Mahalanobis Distance induced by the Jacobian
Zero Singular Values,
Requires Infinite Input
A Dynamically Consistent Distance Metric
Contact problem strikes again.
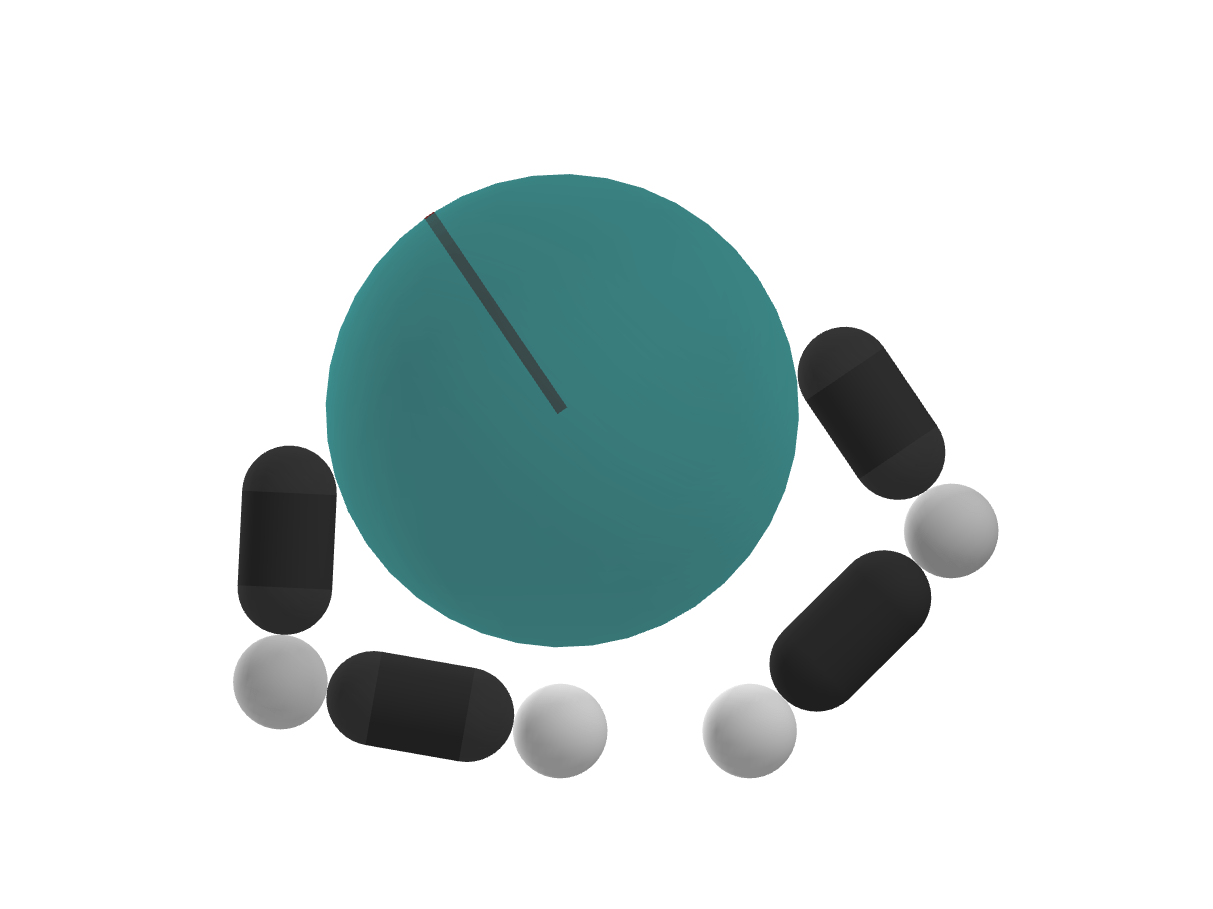
According to this metric, infinite distance if no contact is made!
What if there is no contact?
Mahalanobis Distance induced by the Jacobian
A Dynamically Consistent Distance Metric
Mahalanobis Distance induced by the Jacobian
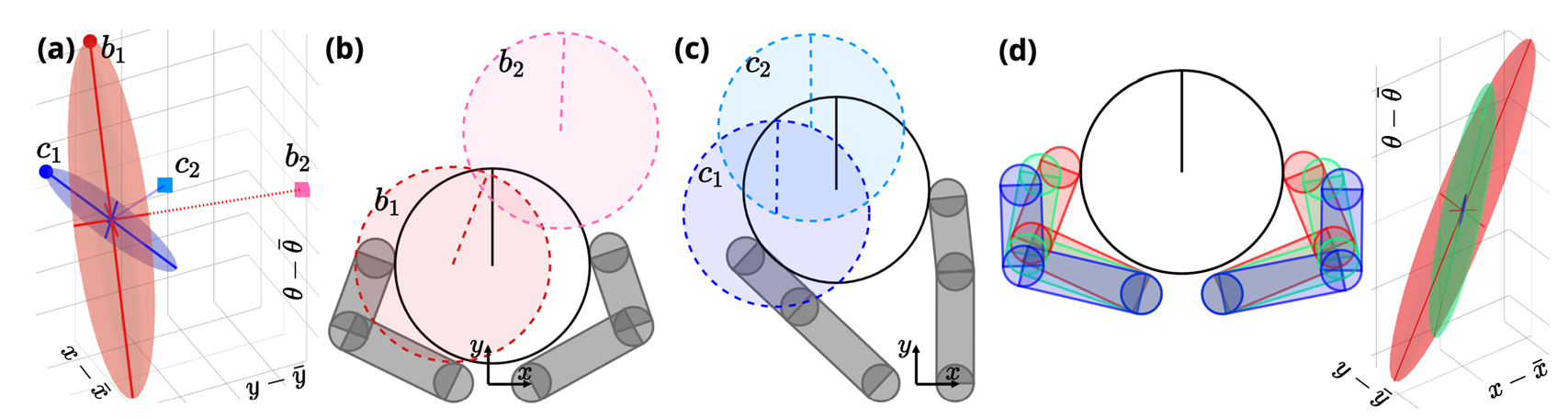
Again, dynamic smoothing comes to the rescue!
A Dynamically Consistent Distance Metric



Now we can apply RRT to contact-rich systems!


However, these still require lots of random extensions!
With some chance, place the actuated object in a different configuration.
(Regrasping / Contact-Sampling)
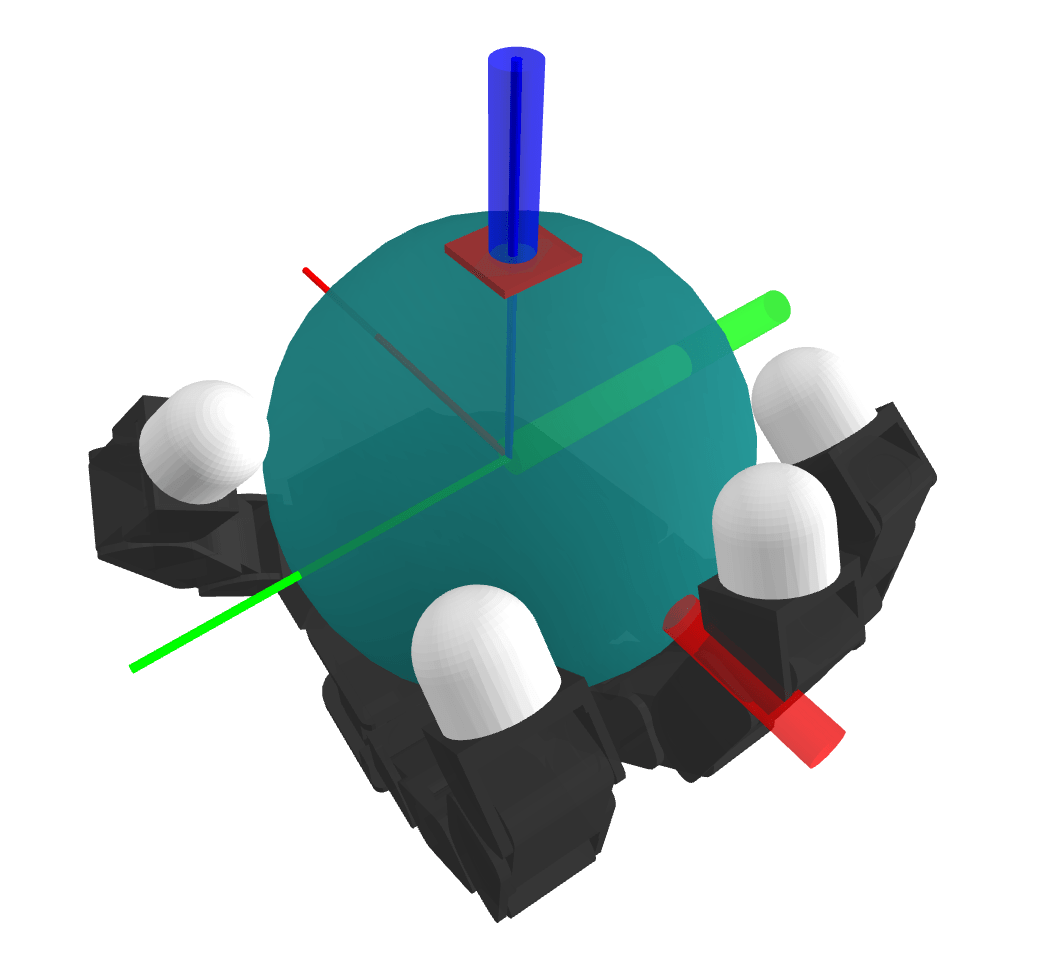
Contact-Rich RRT with Dynamic Smoothing
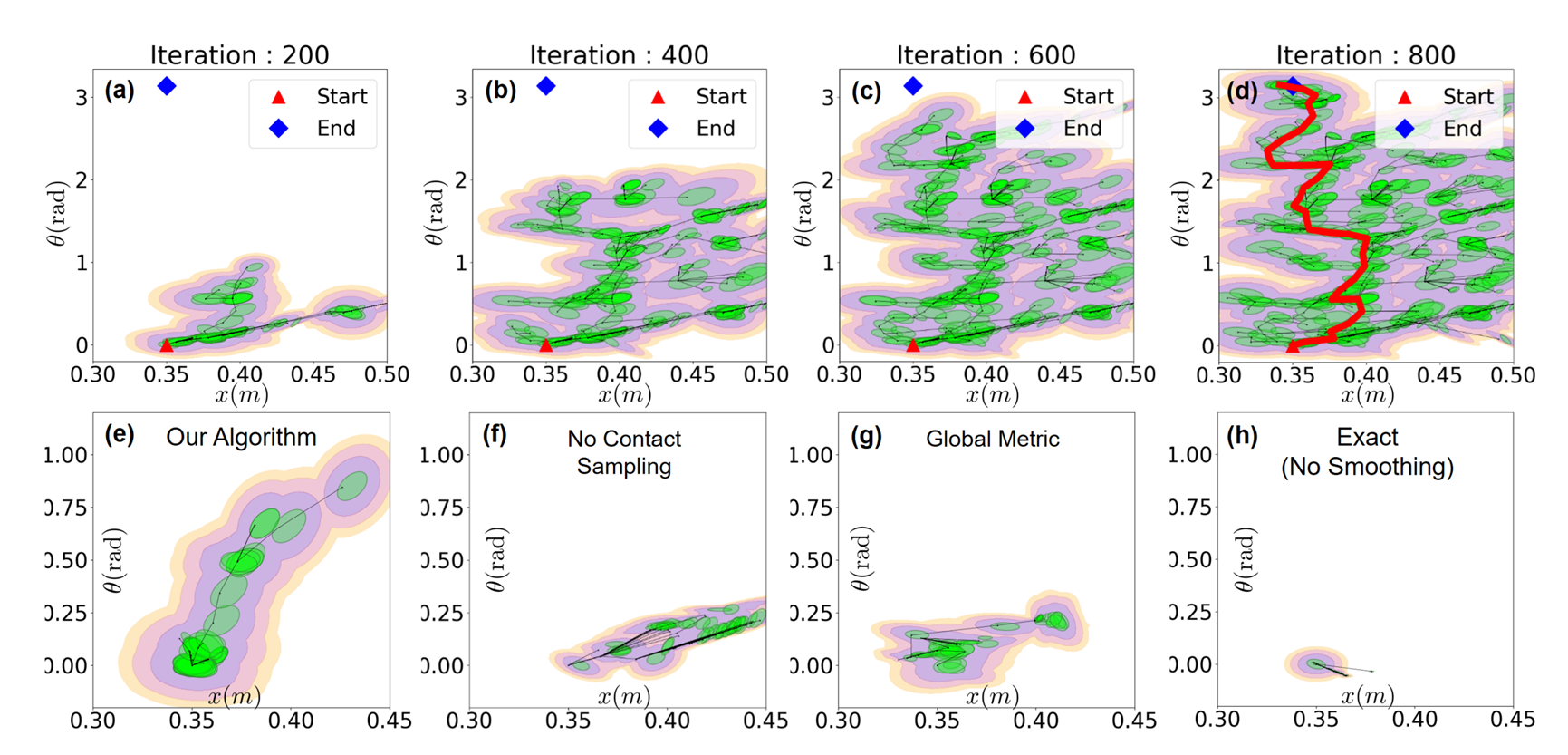
Our method can find solutions through contact-rich systems in few iterations! (~ 1 minute)
What our paper is about
1. Why is RL succeeding where model-based methods struggle?
2. Can we do better by understanding?
- RL Regularizes Landscapes using stochasticity
- Allows Monte-Carlo Abstraction of Contact Modes
- Global optimization with stochasticity
- interior-point smoothing of contact dynamics
- Efficient gradient computation using sensitivity analysis
- Use of RRT to perform fast online global planning
Much to Learn & Improve on from RL's success
Teaser
Meet us at Posters!




Tao Pang*
H.J. Terry Suh*
Lujie Yang
Russ Tedrake
ThBT 27.07

Paper
Code

Poster


ICRA Presentation
By Terry Suh
ICRA Presentation
- 332



