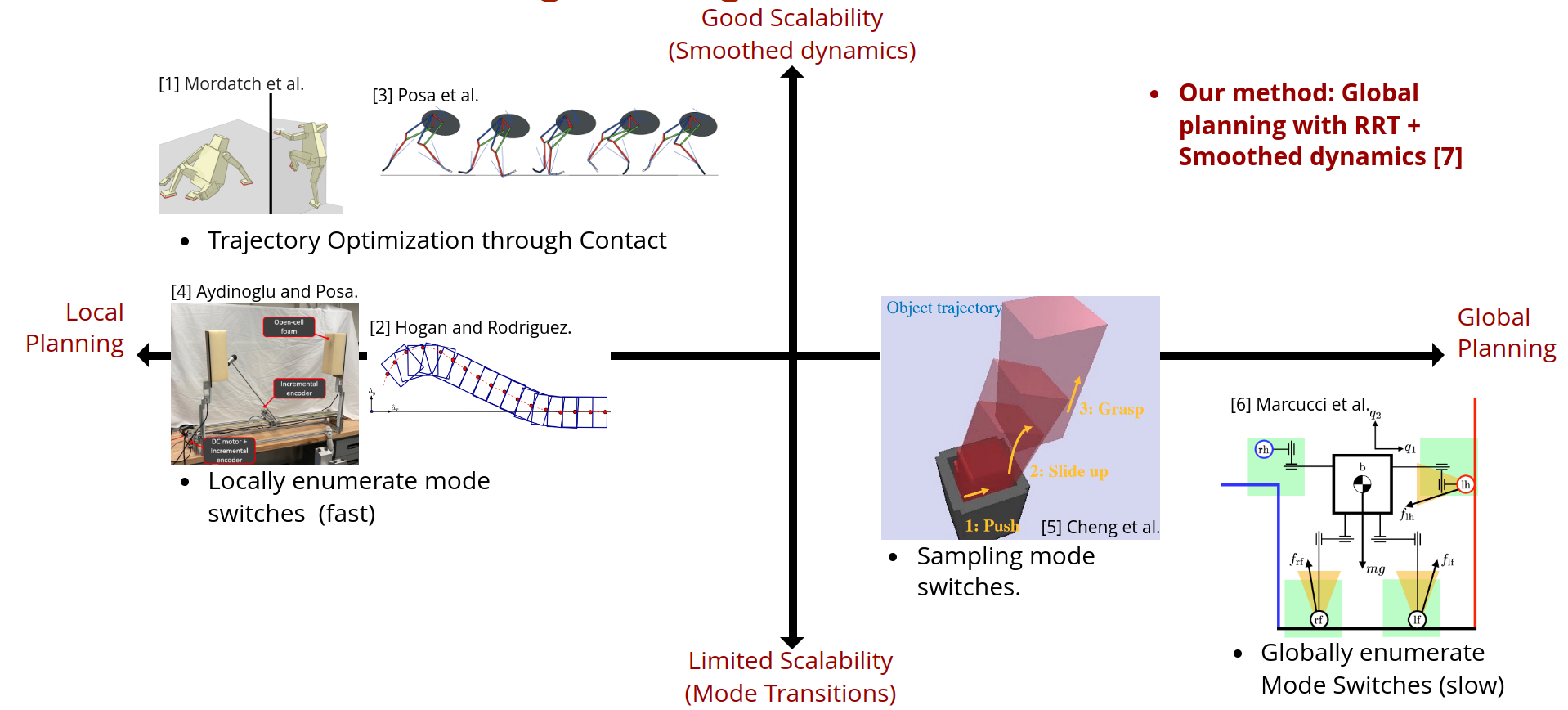
Exposing the Real Difficulties of
Contact-Rich Manipulation
H.J. Terry Suh, MIT
UIUC Robotics Seminar
Spring 2024
The Software Bottleneck in Robotics


A
B
Do not make contact
Make contact
Today's robots are not fully leveraging its hardware capabilities

Larger objects = Larger Robots?
Contact-Rich Manipulation Enables Same Hardware to do More Things
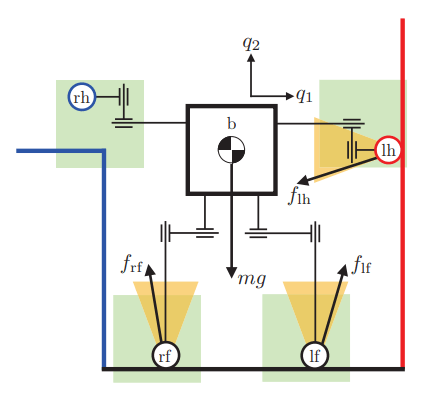
Case Study 1. Whole-body Manipulation

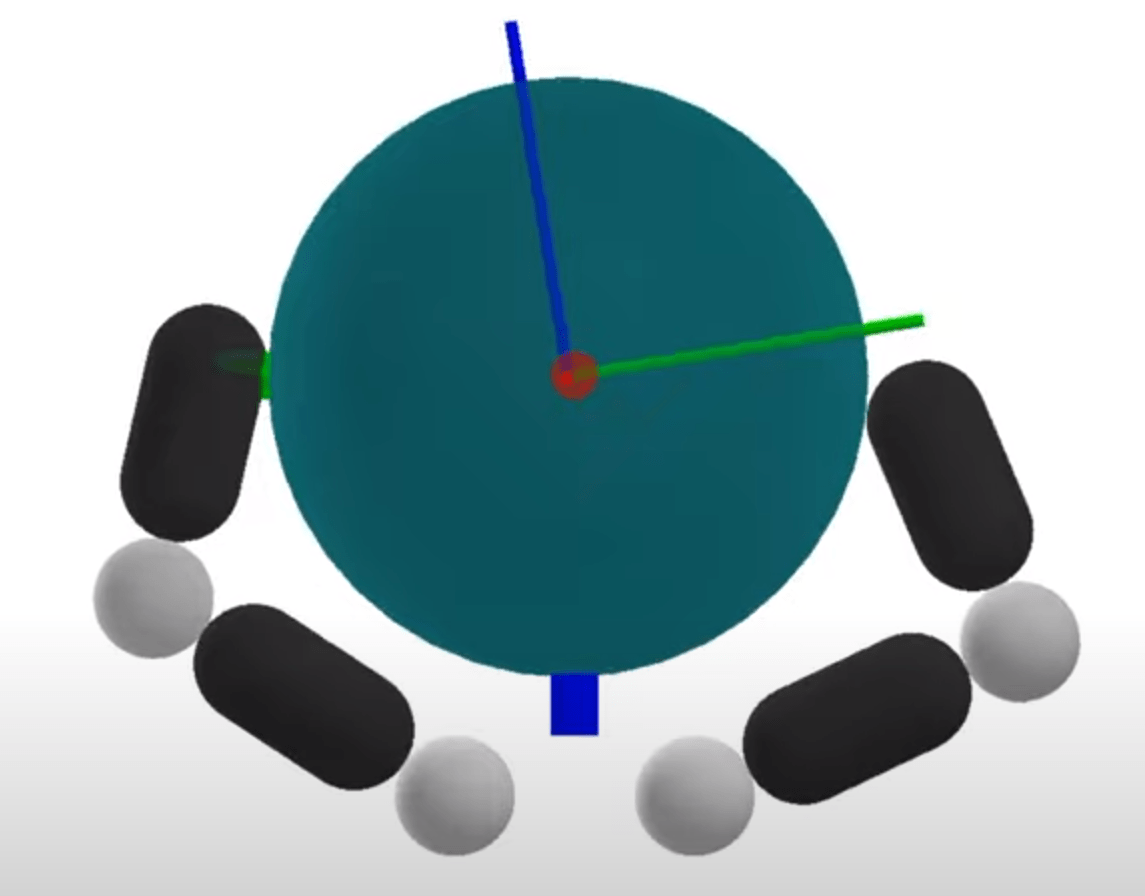
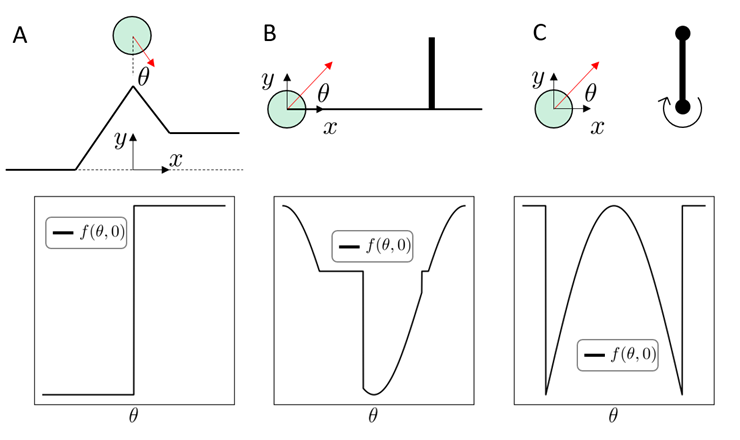
What is Contact-Rich Manipulation?
What is Contact-Rich Manipulation?



Morgan et al., RA-L 2022
Kandate et al., RSS 2023
Wonik Allegro Hand
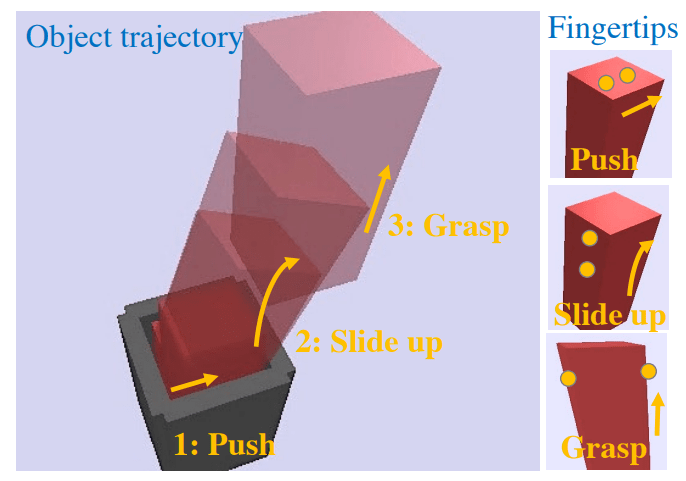
Case Study 2. Dexterous Hands
What is Contact-rich Manipulation?
Case Study 2. Dexterous Hands
OpenAI
What this talk is about
1. What are the fundamental difficulties of contact-rich manipulation?
2. Why did RL succeed in this domain?
3. Can we do better by understanding?
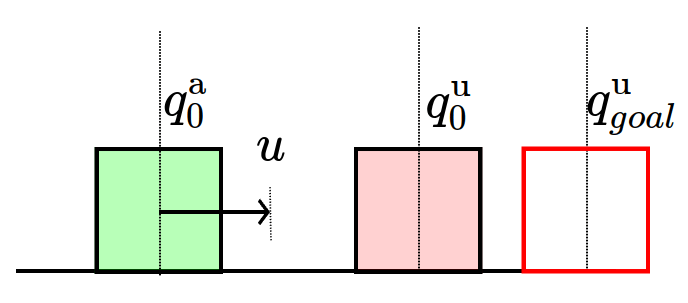
Toy Problem
Simplified Problem
Given initial and goal ,
which action minimizes distance to the goal?
Toy Problem
Simplified Problem
Consider simple gradient descent,
Toy Problem
Simplified Problem
Consider simple gradient descent,

Dynamics of the system
No Contact
Contact
Toy Problem
Simplified Problem
Consider simple gradient descent,

Dynamics of the system
No Contact
Contact
The gradient is zero if there is no contact!
The gradient is zero if there is no contact!
Toy Problem
Simplified Problem
Consider simple gradient descent,

Dynamics of the system
No Contact
Contact
The gradient is zero if there is no contact!
The gradient is zero if there is no contact!
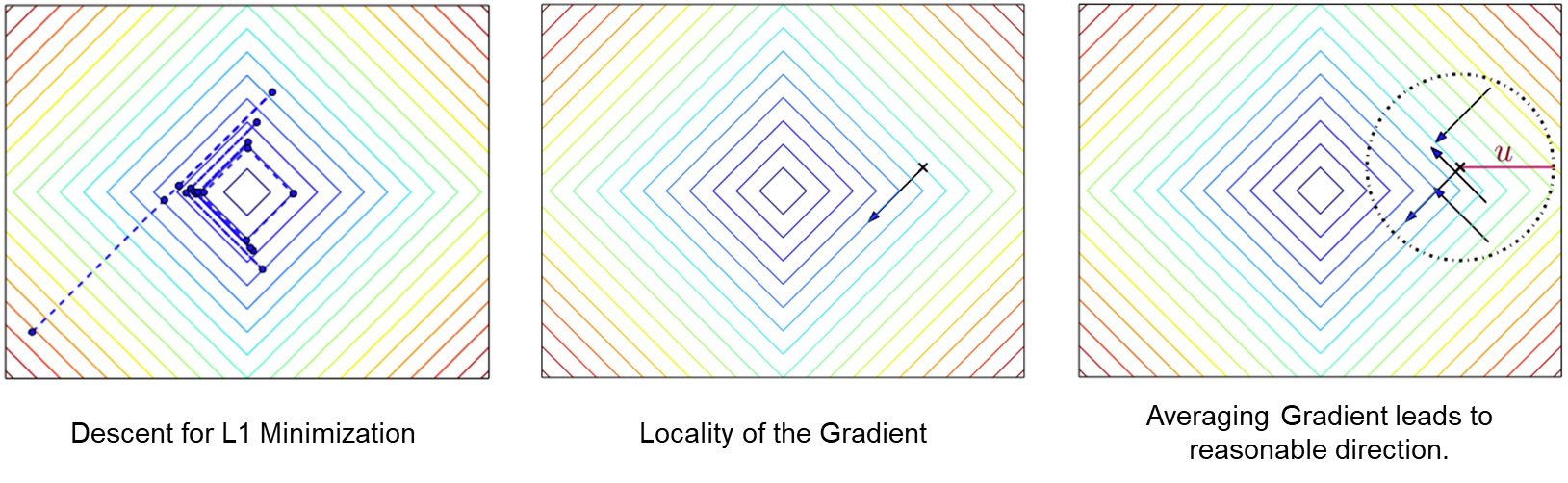
Local gradient-based methods get stuck due to the flat / non-smooth landscapes
Previous Approaches to Tackling the Problem
Why don't we search more globally for each contact mode?
In no-contact, run gradient descent.
In contact, run gradient descent.
Contact
No Contact
Cost
Previous Approaches to Tackling the Problem
Mixed Integer Programming
Mode Enumeration
Active Set Approach

Contact
No Contact
Cost
Why don't we search more globally for each contact mode?
In no-contact, run gradient descent.
In contact, run gradient descent.
Previous Approaches to Tackling the Problem

[MDGBT 2017]
[HR 2016]
[CHHM 2022]
[AP 2022]

Contact
No Contact
Cost
Mixed Integer Programming
Mode Enumeration
Active Set Approach
Why don't we search more globally for each contact mode?
In no-contact, run gradient descent.
In contact, run gradient descent.
Problems with Mode Enumeration
System
Number of Modes
No Contact
Sticking Contact
Sliding Contact
Number of potential active contacts
Problems with Mode Enumeration


System
Number of Modes
The number of modes scales terribly with system complexity
No Contact
Sticking Contact
Sliding Contact
Number of potential active contacts
How does RL power through these problems?
Reinforcement Learning fundamentally considers a stochastic objective
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost
How does RL power through these problems?
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost
How does RL power through these problems?
Previous Formulations
Reinforcement Learning

Contact
No Contact
Cost
Contact
No Contact
Averaged
Randomized smoothing
regularizes landscapes
Cost
How does RL power through these problems?
Previous Formulations
Reinforcement Learning

Contact
No Contact
Averaged
Cost
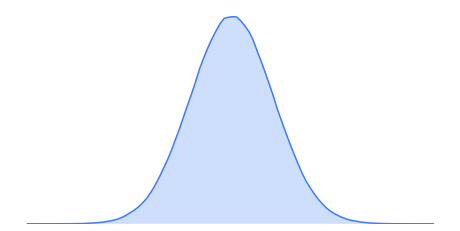
Some samples end up in contact, some samples do not!
No consideration of modes.
Randomized smoothing
regularizes landscapes
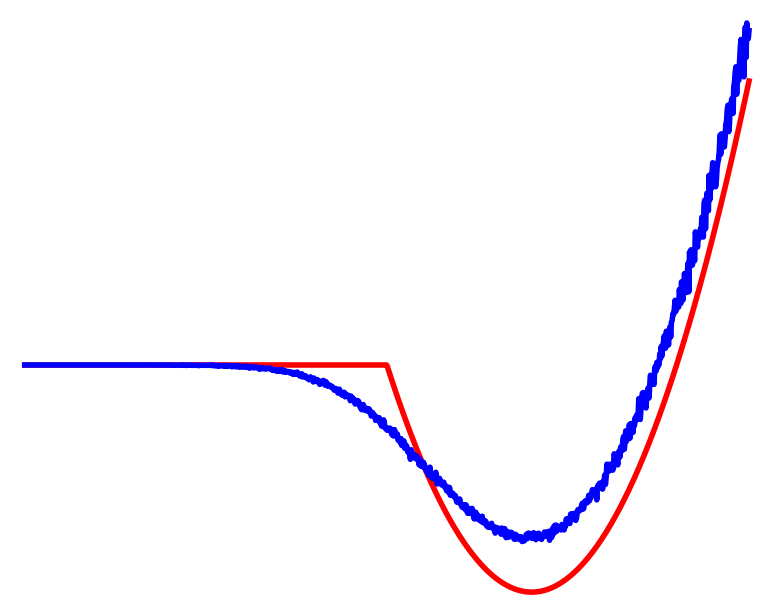
Original Problem
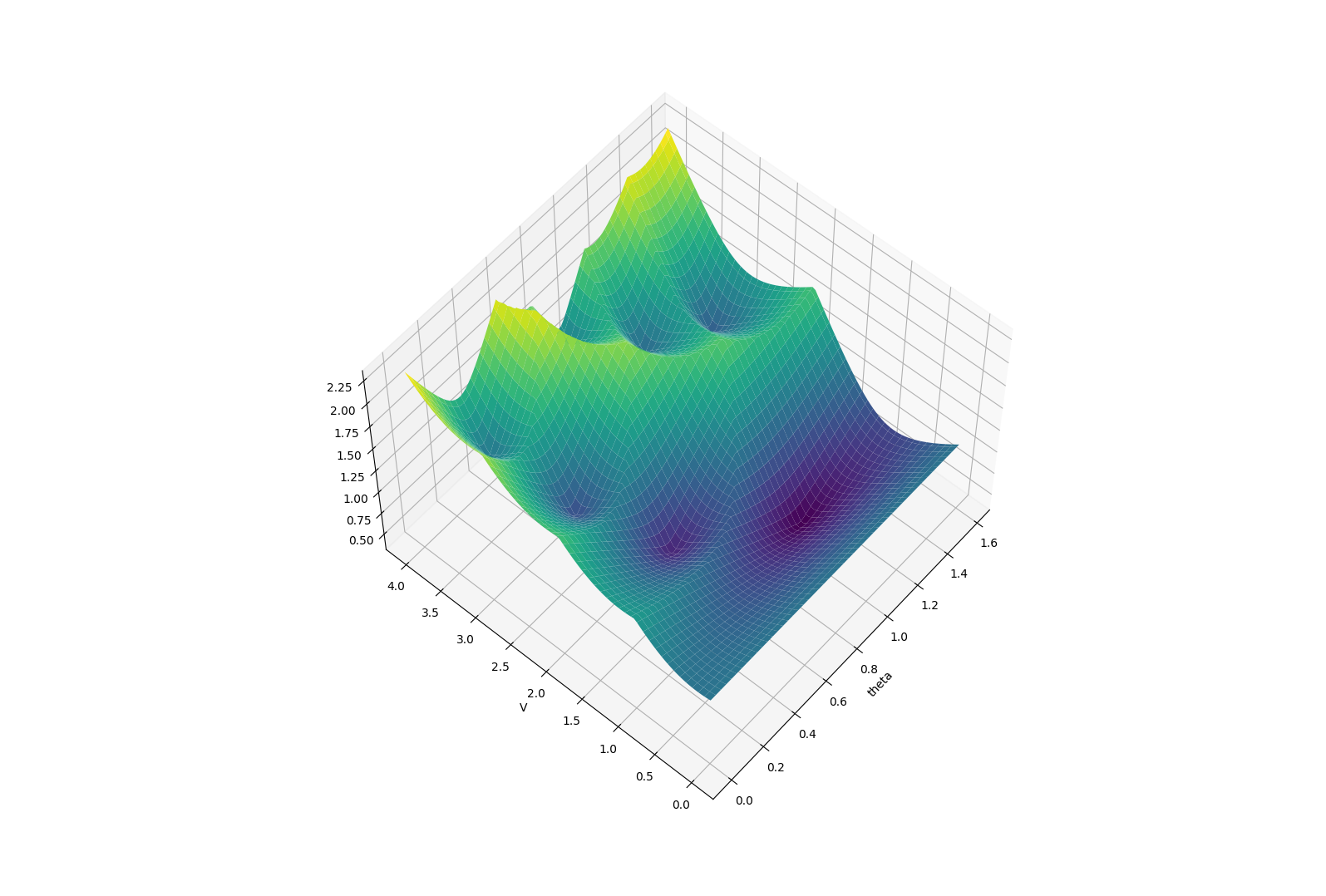
Long-horizon problems involving contact can have terrible landscapes.
How does RL power through these problems?
[SSZT 2022]
Smoothing of Value Functions.
Smooth Surrogate
The benefits of smoothing are much more pronounced in the value smoothing case.
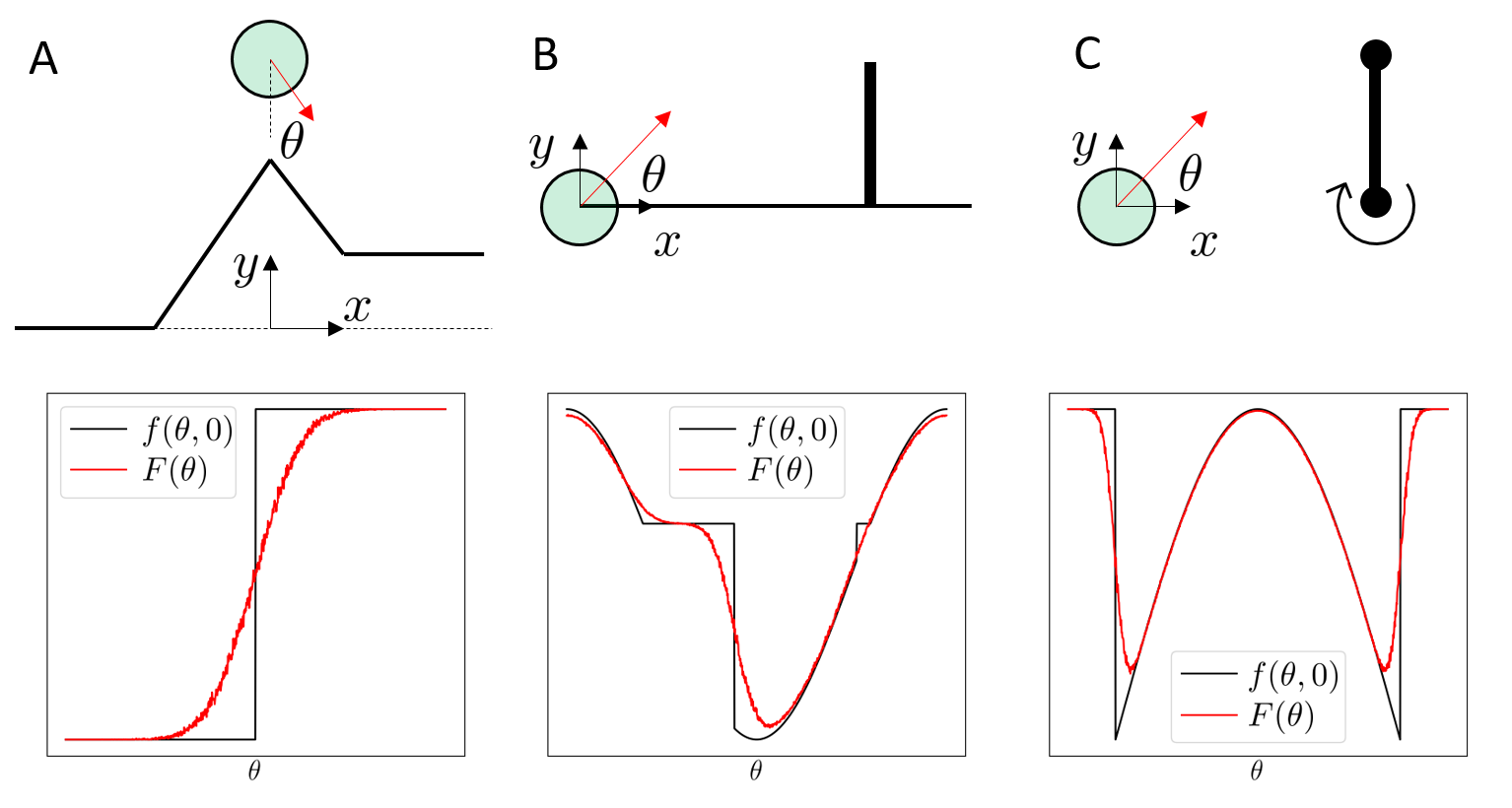
Beautiful story - noise sometimes regularizes the problem, developing into helpful bias.
[SSZT 2022]
Gradient Estimation in RL
But how do we take gradients through a stochastic objective?
Zeroth-Order Gradient Estimator
REINFORCE
Score Function Gradient
Likelihood Ratio Gradient
Stein Gradient Estimator
Gradient Estimation in RL
But how do we take gradients through a stochastic objective?
Zeroth-Order Gradient Estimator
REINFORCE
Score Function Gradient
Likelihood Ratio Gradient
Stein Gradient Estimator
Variance scales with number of decision variables...
Can we do better?
Gradient Estimation in RL
But how do we take gradients through a stochastic objective?
Zeroth-Order Gradient Estimator
REINFORCE
Score Function Gradient
Likelihood Ratio Gradient
Stein Gradient Estimator
First-Order Gradient Estimator
Reparametrization Gradient
Gradient Sampling
What if we have gradients?
Gradient Estimation in RL
But how do we take gradients through a stochastic objective?
Zeroth-Order Gradient Estimator
REINFORCE
Score Function Gradient
Likelihood Ratio Gradient
Stein Gradient Estimator
First-Order Gradient Estimator
Reparametrization Gradient
Gradient Sampling
What if we have gradients?
First-Order Gradient Estimator
Reparametrization Gradient
Gradient Sampling
Surprisingly, naive use of gradients cannot do better!
Do Differentiable Simulators Give Better Policy Gradients?
- "Empirical Bias" from discontinuities that frequently occur in contact.
- Higher variance than zeroth-order due to long-horizon chaotic / stiff dynamics

Non-smooth Contact Dynamics
Smooth Surrogate Dynamics

No Contact
Contact
Averaged
Dynamic Smoothing
What if we had smoothed dynamics instead of the overall cost?
Effects of Dynamic Smoothing
Reinforcement Learning

Cost
Contact
No Contact
Averaged
Dynamic Smoothing
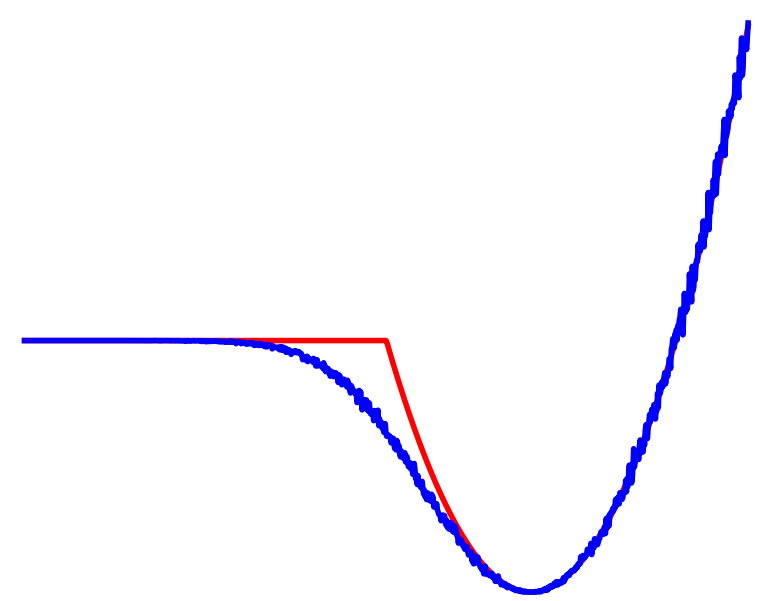
Averaged
Contact
No Contact
No Contact
Can still claim benefits of averaging multiple modes leading to better landscapes
Importantly, we know structure for these dynamics!
Can often acquire smoothed dynamics & gradients without Monte-Carlo.
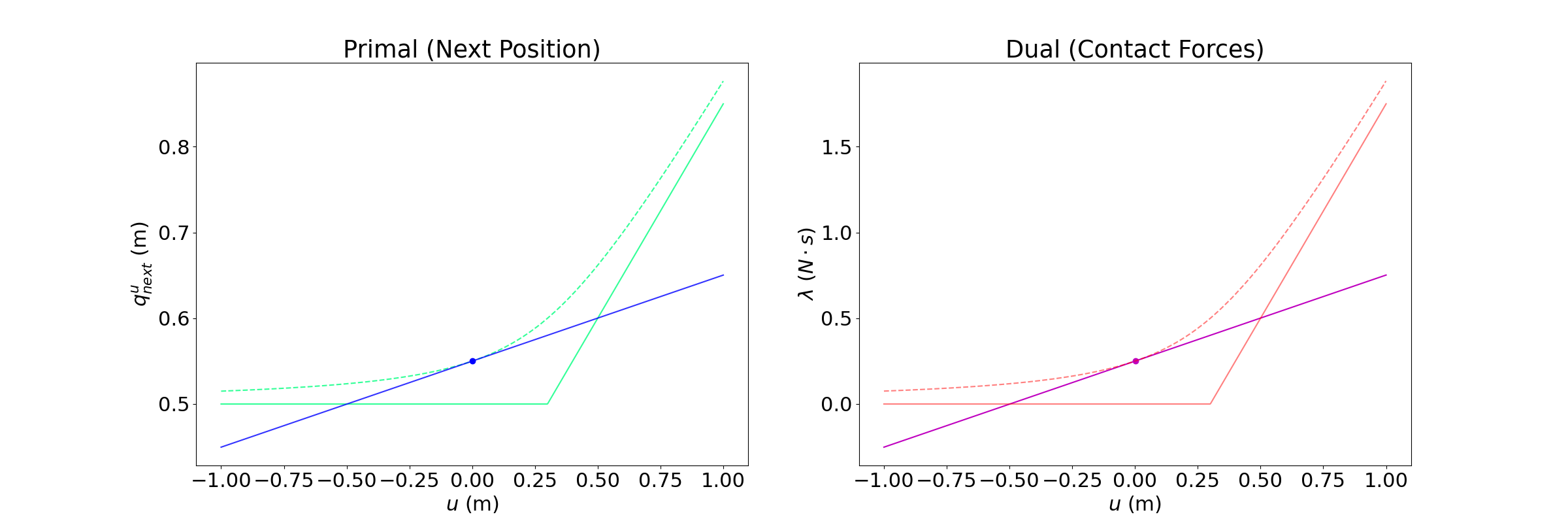
Example: Box vs. wall
Commanded next position
Actual next position
Cannot penetrate into the wall
Implicit Time-stepping simulation
No Contact
Contact
Structured Smoothing: An Example
Importantly, we know structure for these dynamics!
Can often acquire smoothed dynamics & gradients without Monte-Carlo.
Example: Box vs. wall
Implicit Time-stepping simulation
Commanded next position
Actual next position
Cannot penetrate into the wall
Log-Barrier Relaxation
Structured Smoothing: An Example
Importantly, we know structure for these dynamics!
Can often acquire smoothed dynamics & gradients without Monte-Carlo.
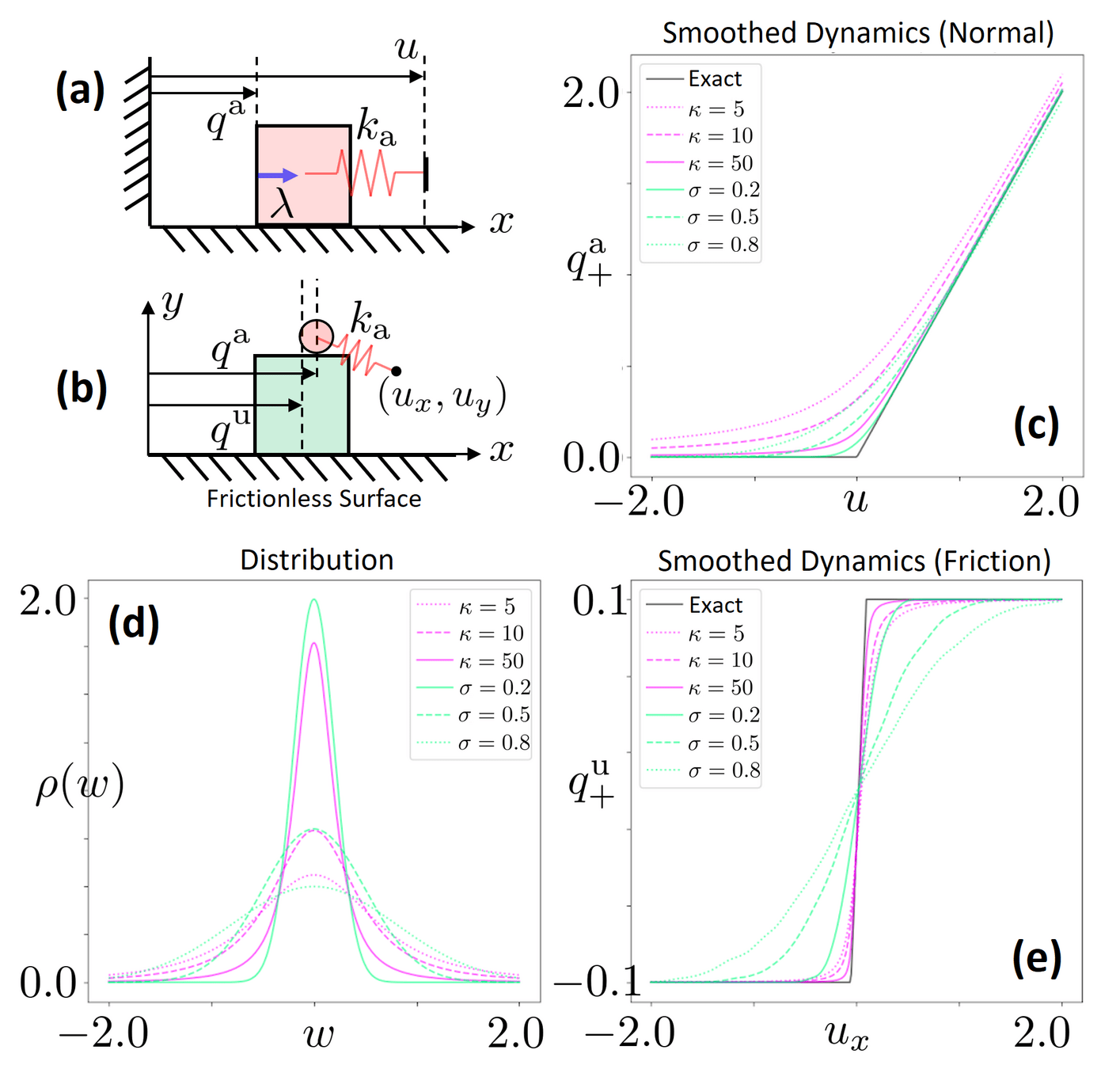
Example: Box vs. wall
Randomized smoothing
Barrier smoothing
Randomized smoothing distribution that results in barrier smoothing
Barrier vs. Randomized Smoothing
Differentiating with Sensitivity Analysis
How do we obtain the gradients from an optimization problem?


Differentiating with Sensitivity Analysis
How do we obtain the gradients from an optimization problem?


Differentiate through the optimality conditions!
Stationarity Condition
Implicit Function Theorem

Differentiate by u
Differentiating with Sensitivity Analysis

[HLBKSM 2023]

[MBMSHNCRVM 2020]
[PSYT 2023]
How do we obtain the gradients from an optimization problem?


Differentiate through the optimality conditions!
Stationarity Condition
Implicit Function Theorem

Differentiate by u
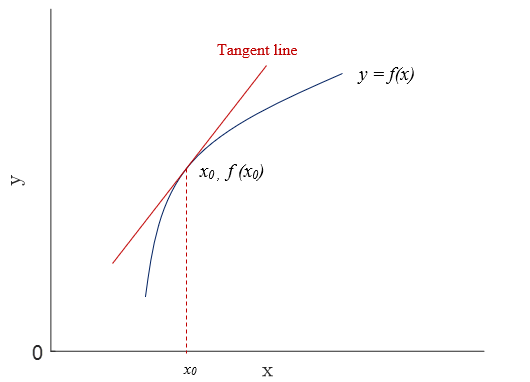
Using Gradients for Planning & Control
Optimization
Find minimum step subject to Taylor approximation
Leads to Gradient Descent
Using Gradients for Planning & Control
Optimization
Find minimum step subject to Taylor approximation
Leads to Gradient Descent
Optimal Control (1-step)
Find minimum step subject to Taylor approximation
Linearization
Can we follow the same recipe for contact?
What does it mean to linearize contact dynamics?
Is the typical Taylor approximation sufficient for characterizing contact locally?
Linearization
What does it mean to linearize contact dynamics?
Is the typical Taylor approximation sufficient for characterizing contact locally?
Linearization

No Contact
Contact
What does it mean to linearize contact dynamics?
Is the typical Taylor approximation sufficient for characterizing contact locally?
Linearization

No Contact
Contact
Taylor Approximation
Taylor Approximation doesn't fundamentally respect unilateral nature of contact! (Can't pull)
What are we missing?
Dynamics Linearization
Contact Force Linearization
Contact Constraints
Optimal control algorithms for contact
have to take contact constraints into account!
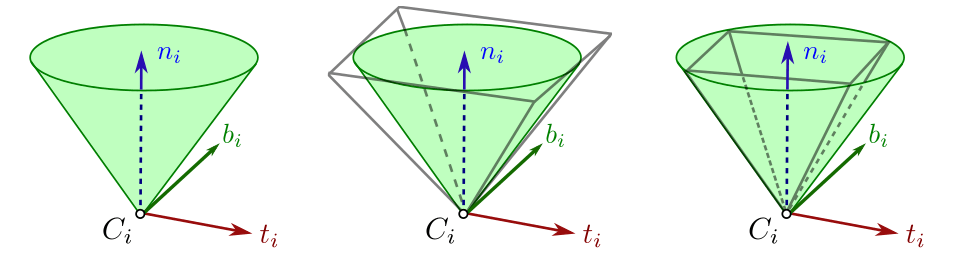
*image taken from Stephane Caron's blog
Taylor Approximation for Contact Dynamics
Dynamics Linearization
Contact Force Linearization
Contact Constraints
Input Limit
Motion Sets: Local Approximation to Allowable Motion (1-step Reachable Set)
Contact-Aware Taylor Approximation
Naive Taylor Approximation
Samples
Naive Taylor Approximation
Samples
Contact-Aware Taylor Approximation

Contact-Aware Taylor Approximation
Naive Taylor Approximation
Samples
Inverse Dynamics Control for Contact
Dynamics Linearization
Contact Force Linearization
Contact Constraints
Input Limit
Find best input within the allowable set that minimizes distance to goal.
Gradient-Based Inverse Dynamics
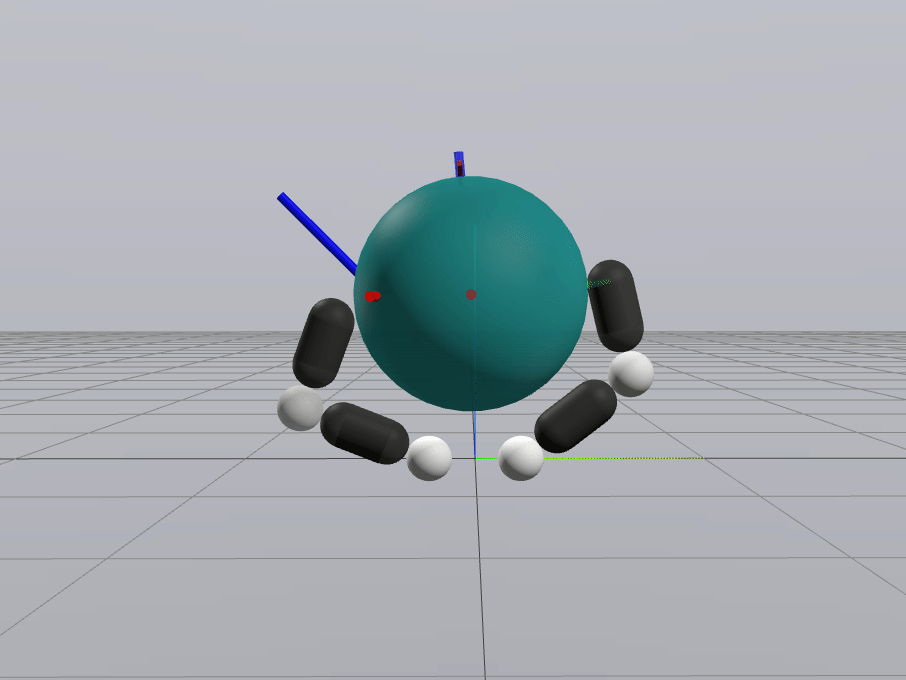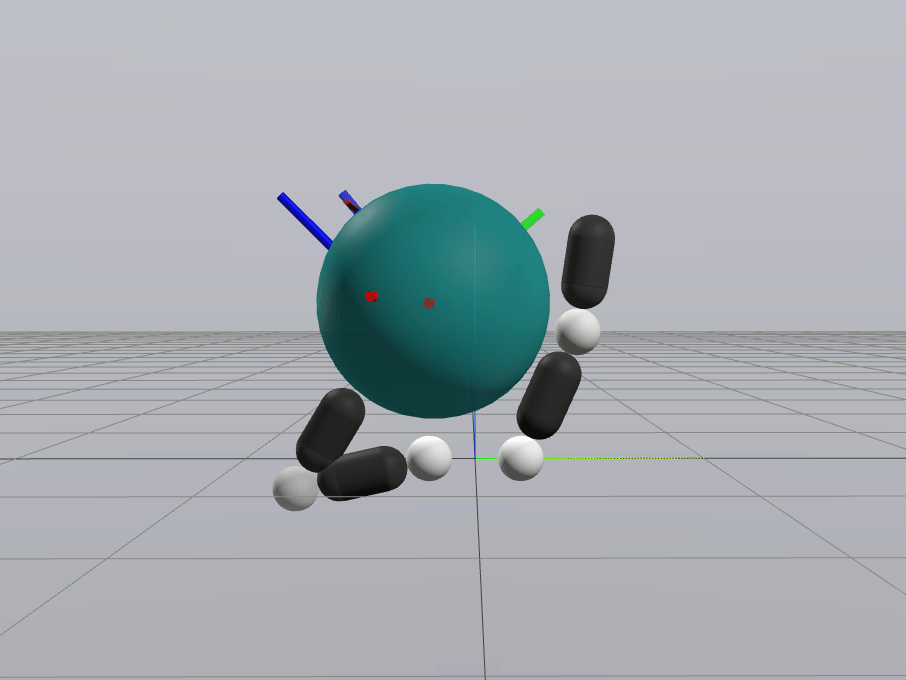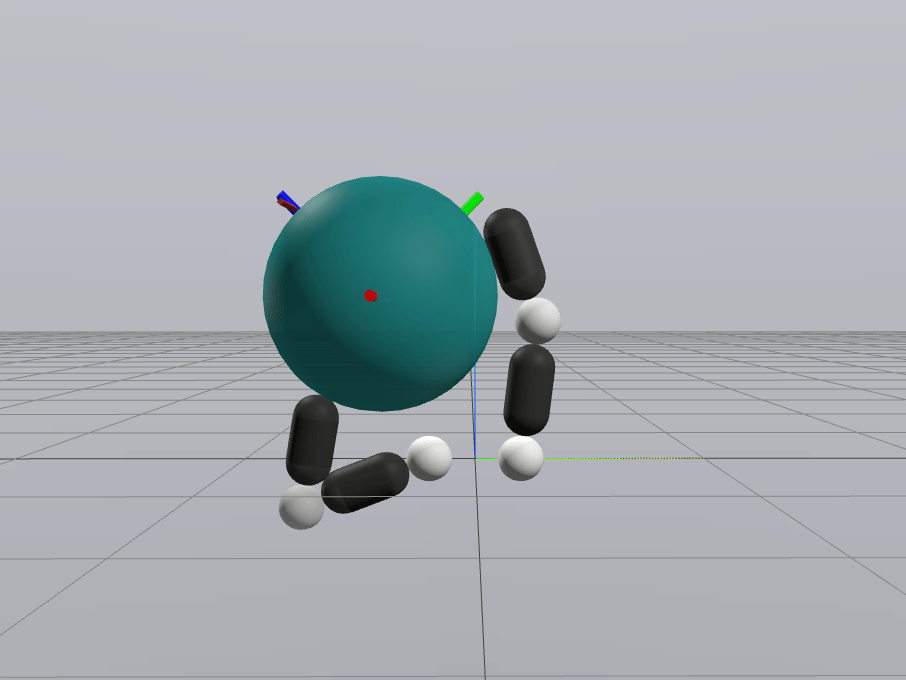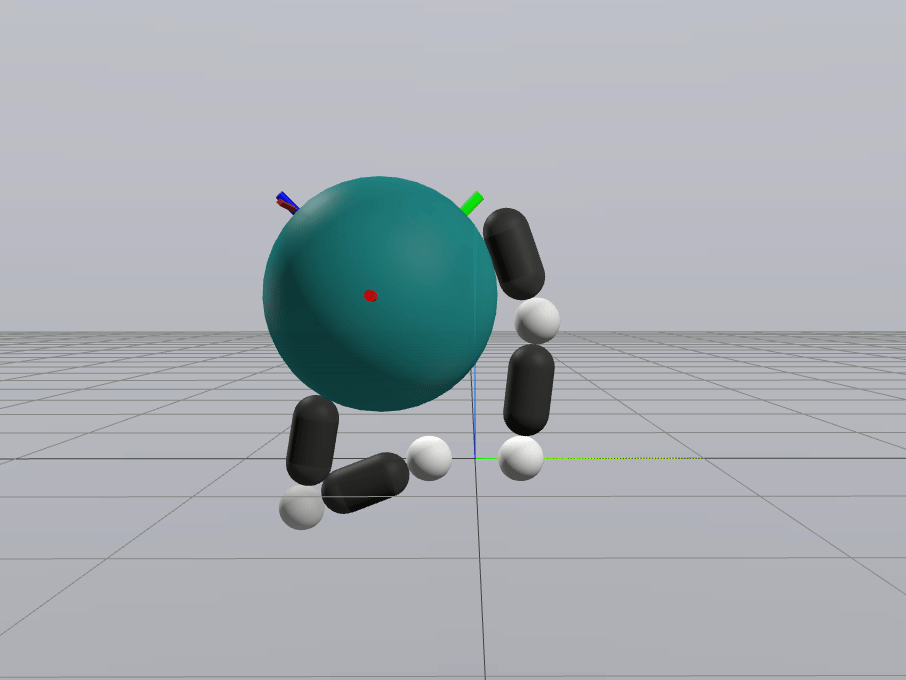
Naive Linearization
Contact-Aware Linearization
Greedy Control Goes Surprisingly Far
Gradient-Based Inverse Dynamics
Greedy Control Goes Surprisingly Far

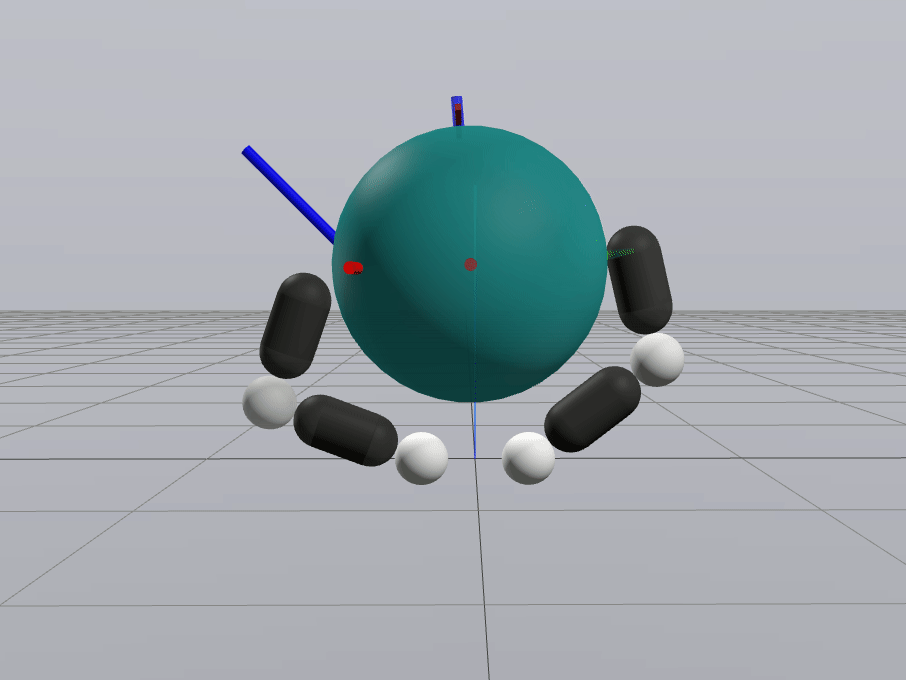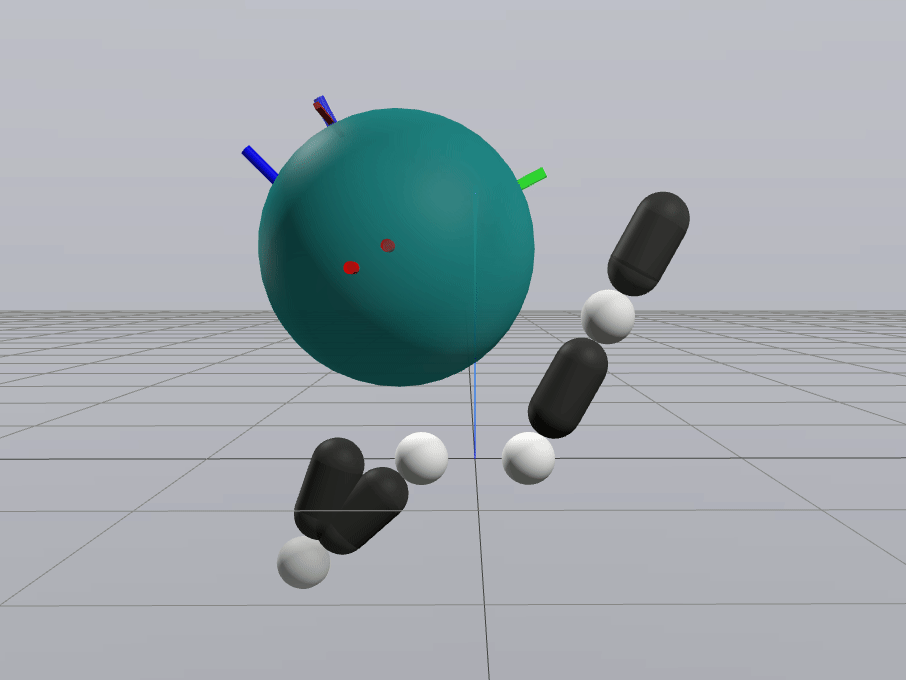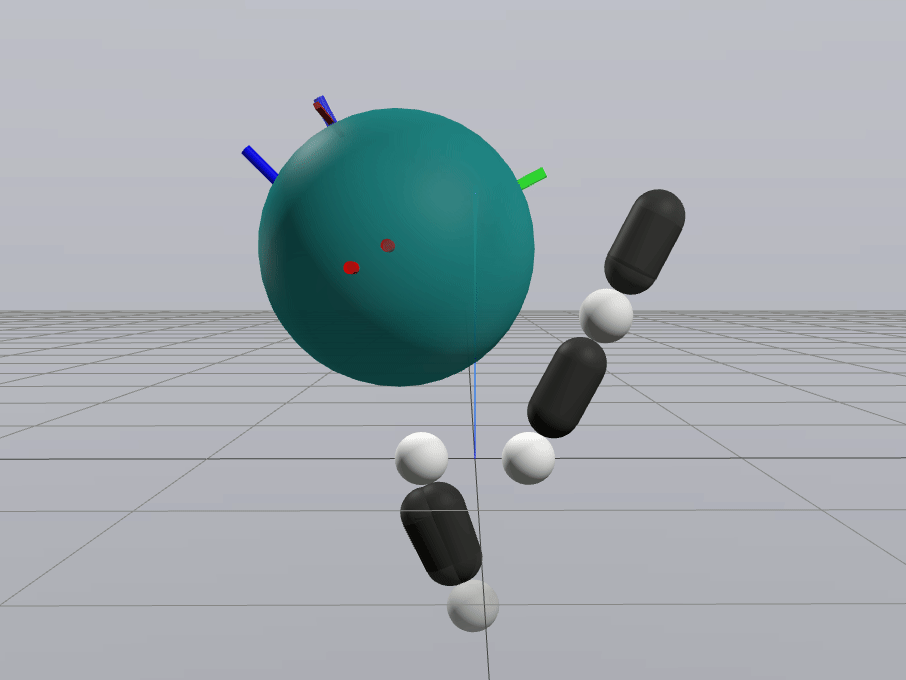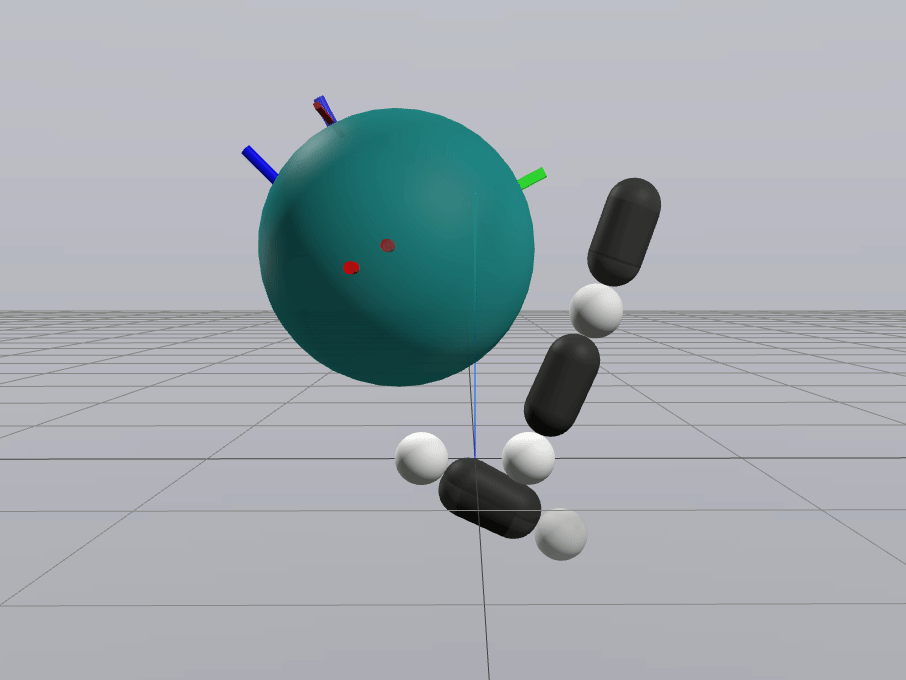
What is hard about manipulation?
Can achieve local movements along the motion set.


What is hard about manipulation?

Can achieve local movements along the motion set.
But what if we want to move towards the opposite direction?


What is hard about manipulation?
Can achieve local movements along the motion set.

But what if we want to move towards the opposite direction?
Contact constraints force us to make a seemingly non-local decision
in response to different goals / disturbances.
What is hard about manipulation?
Attempting to achieve a 180 degree rotation goes out of bounds!
What is hard about manipulation?
Attempting to achieve a 180 degree rotation goes out of bounds!
Joint Limit Constraints
Give Rise to "Gaits" in order to achieve continuous motion.
And gaits are highly non-local!
Fundamental Limitations with Local Search


How do we push in this direction?
How do we rotate further in presence of joint limits?

Highly non-local movements are required to solve these problems
Motivating the Hybrid Action Space
Local Control
(Inverse Dynamics)
Actuator Placement if feasible
What if we gave the robot a decision to move to a different configuration?
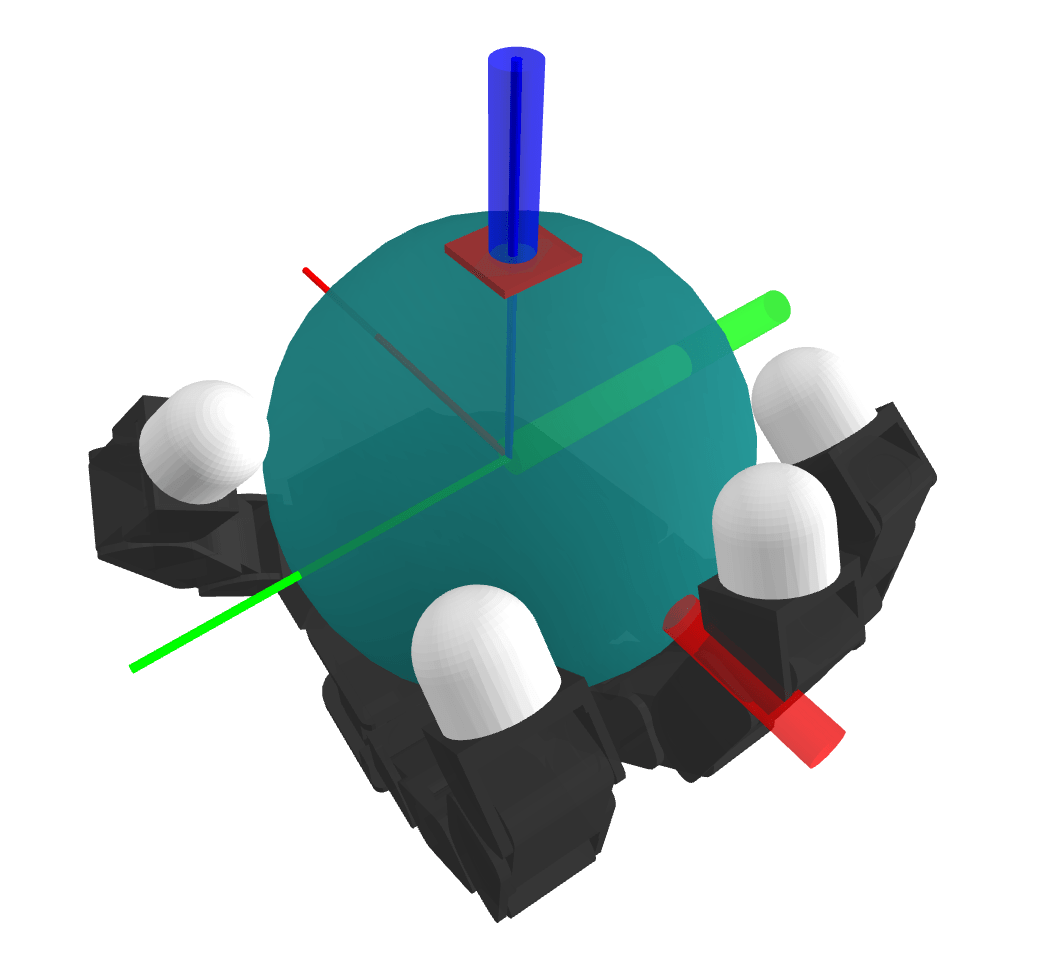
T-Pusher Problem

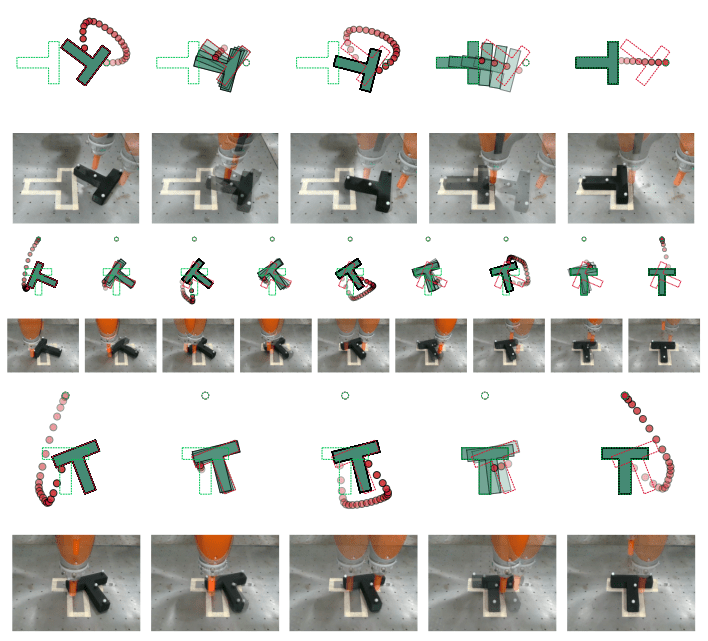
[GCMMAPT 2024]
[CXFCDBTS 2024]
T-Pusher Problem


[GCMMAPT 2024]
[CXFCDBTS 2024]
Motion Sets help decide
where we should make contact
The Fundamental Difficulty of Manipulation
How do we need know we need to open the gripper before we grasp the object?
The Fundamental Difficulty of Manipulation

How do we need know we need to open the gripper before we grasp the object?
We need to have knowledge that grasping the box is beneficial
The Fundamental Difficulty of Manipulation

D. Povinelli, "Folks Physics for Apes: The Chimpanzee's Theory of How The World Works"
Takeaways.
1. Contact-Rich Manipulation is not harder than Contact-Poor manipulation.
2. Discrete logical-looking decisions induced by contact / embodiment constraints make manipulation difficult.
3. Learn, understand, and improve upon RL.
-
H.J. Terry Suh*, Tao Pang*, Russ Tedrake,
"Bundled Gradients through Contact via Randomized Smoothing",
RA-L 2022, Presented at ICRA 2022

Thank You





Tao
Pang
Max
Simchowitz
Kaiqing
Zhang
Lujie
Yang
Russ
Tedrake
Tong
Zhao
James (Xinpei)
Ni
Jiuguang
Wang

Yuki
Shirai
-
H.J. Terry Suh, Max Simchowitz, Kaiqing Zhang, Russ Tedrake,
"Do Differentiable Simulators Give Better Policy Gradients?",
ICML 2022, Outstanding Paper Award
- Tao Pang*, H.J. Terry Suh*, Lujie Yang, Russ Tedrake,
"Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasidynamic Contact Models"
TRO 2023

Chapter 5. Efficient Global Search
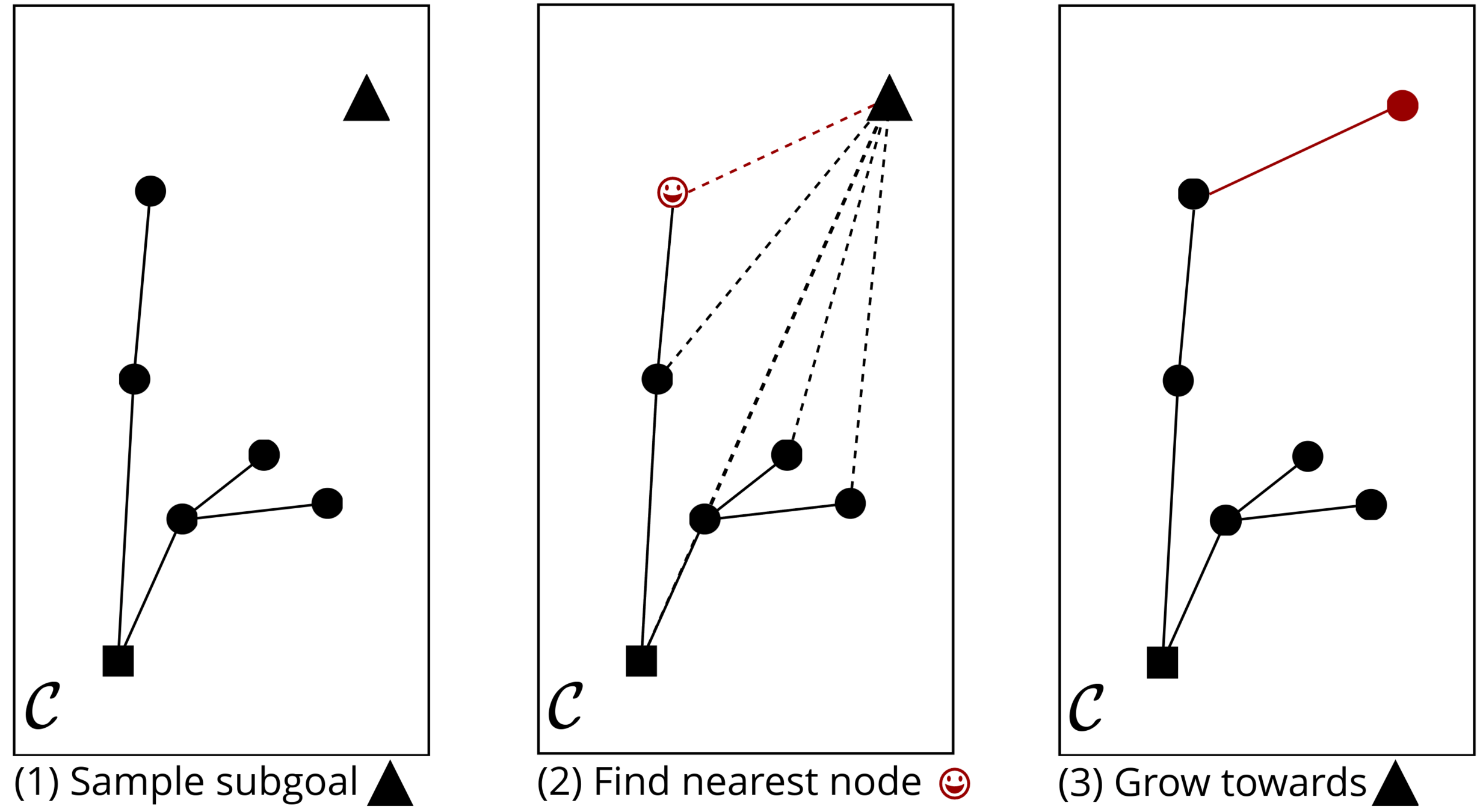
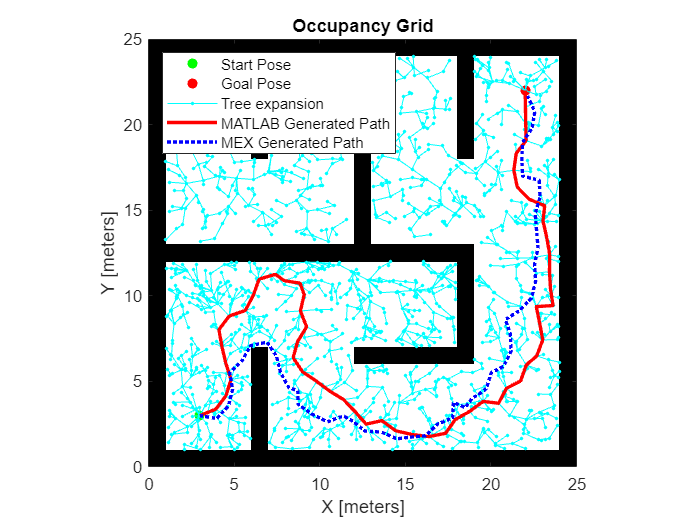
Rapidly Exploring Random Tree (RRT) Algorithm
Figure Adopted from Tao Pang's Thesis Defense, MIT, 2023
(1) Sample subgoal
(2) Find nearest node
(3) Grow towards
Rapidly Exploring Random Tree (RRT) Algorithm
Steven M. LaValle, "Planning Algorithms", Cambridge University Press , 2006.
RRT for Dynamics
Works well for Euclidean spaces. Why is it hard to use for dynamical systems?

RRT for Dynamics

Works well for Euclidean spaces. Why is it hard to use for dynamical systems?

What is "Nearest" in a dynamical system?
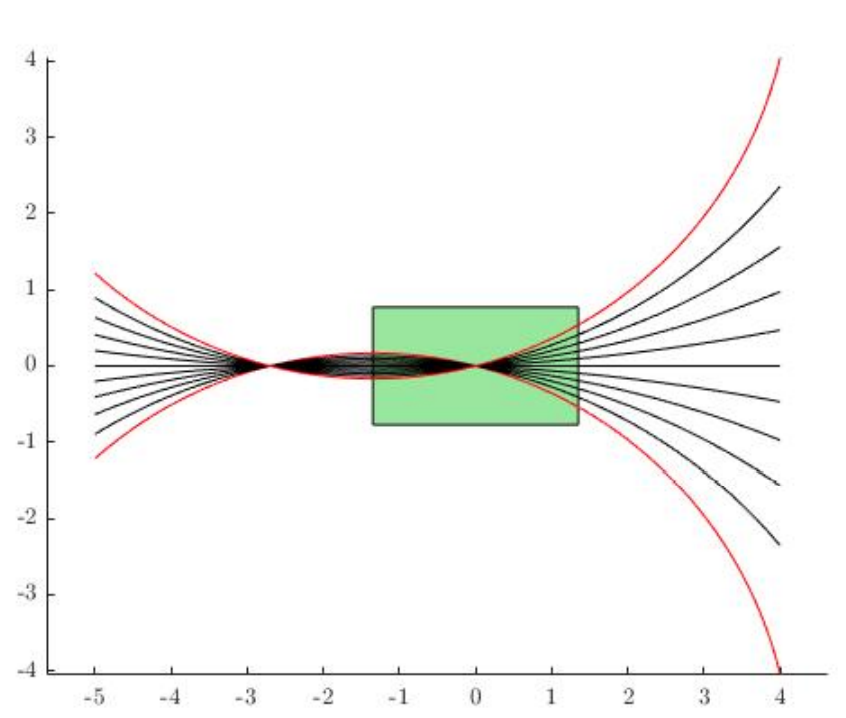
Closest in Euclidean space might not be closest for dynamics.
Rajamani et al., "Vehicle Dynamics"
SDW 2018

RRT for Dynamics
Works well for Euclidean spaces. Why is it hard to use for dynamical systems?
How do we "grow towards" a chosen subgoal?


Need to find actions (inputs) that would drive the system to the chosen subgoal.



Rajamani et al., "Vehicle Dynamics"
SDW 2018

RRT for Dynamics
Works well for Euclidean spaces. Why is it hard to use for dynamical systems?
How do we "grow towards" a chosen subgoal?


Note that these decisions are coupled



SDW 2018
Rajamani et al., "Vehicle Dynamics"

RRT for Dynamics
How do we "grow towards" a chosen subgoal?

We already know how to do this!
Inverse Dynamics



A Dynamically Consistent Distance Metric
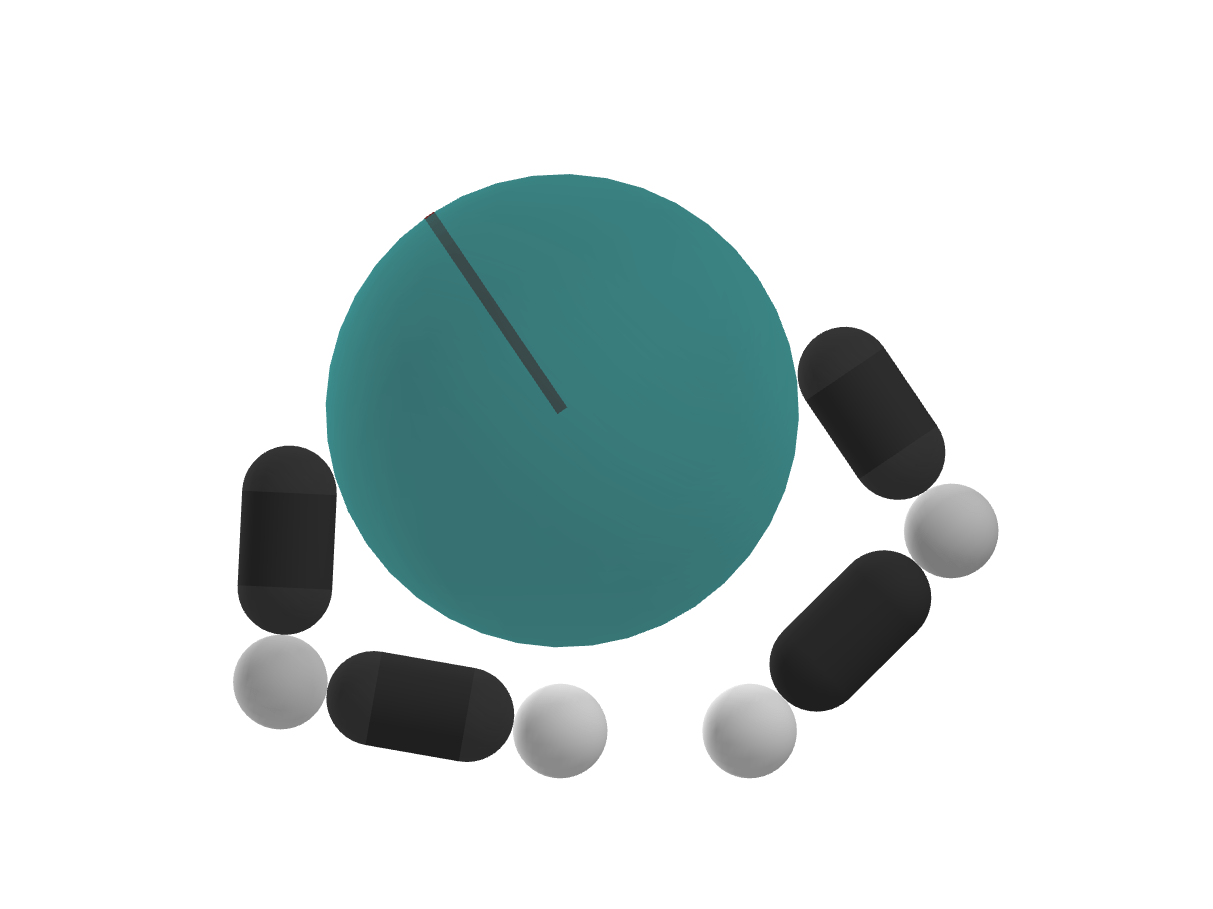
What is the right distance metric
Fix some nominal values for ,
How far is from ?
A Dynamically Consistent Distance Metric
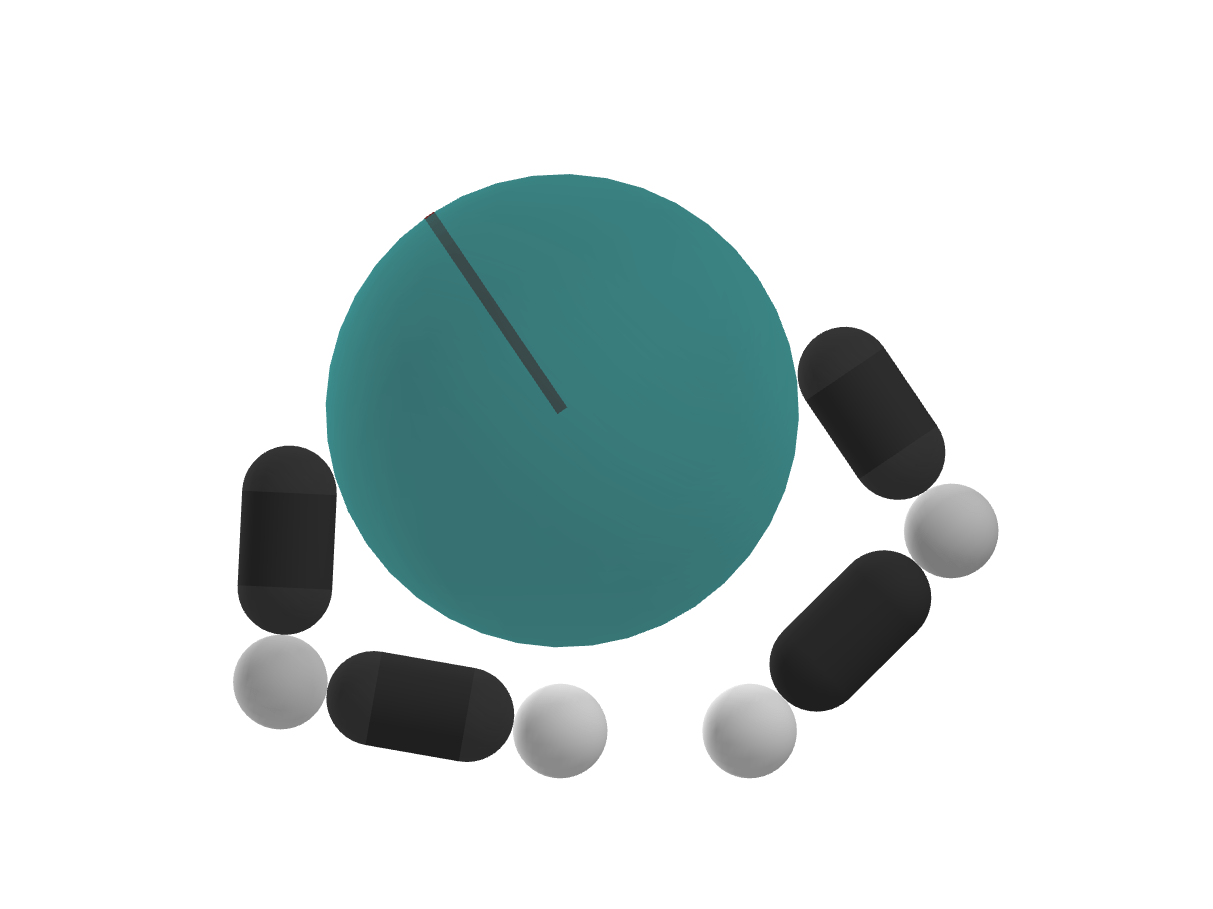
What is the right distance metric
The least amount of "Effort"
to reach the goal
Fix some nominal values for ,
How far is from ?
A Dynamically Consistent Distance Metric
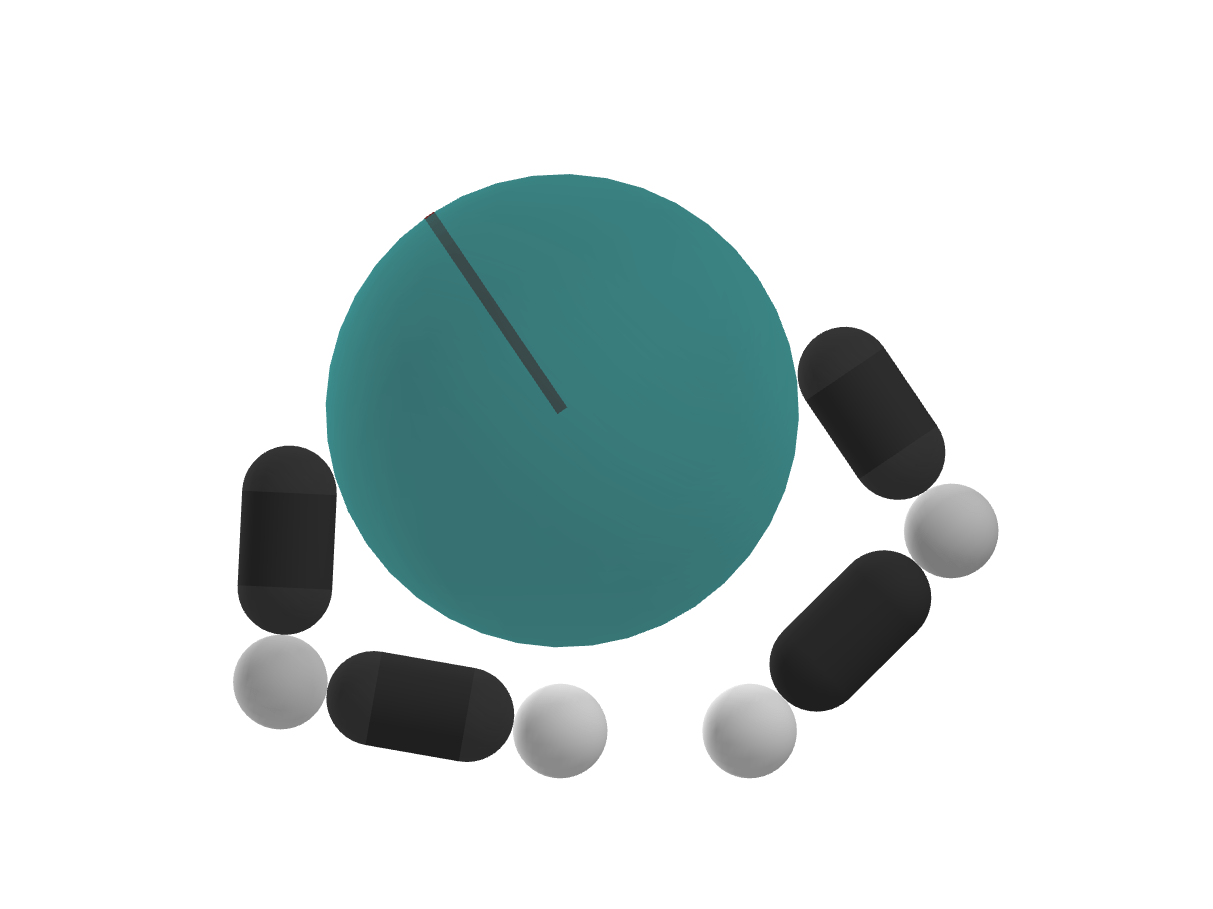
What is the right distance metric
What is the right distance metric
Fix some nominal values for ,
How far is from ?
The least amount of "Effort"
to reach the goal
A Dynamically Consistent Distance Metric
We can derive a closed-form solution under linearization of dynamics

Linearize around (no movement)
Jacobian of dynamics
A Dynamically Consistent Distance Metric
We can derive a closed-form solution under linearization of dynamics
Mahalanobis Distance induced by the Jacobian

Linearize around (no movement)
Jacobian of dynamics
A Dynamically Consistent Distance Metric
Mahalanobis Distance induced by the Jacobian


Locally, dynamics are:
Mahalanobis Distance induced by the Jacobian
A Dynamically Consistent Distance Metric
Mahalanobis Distance induced by the Jacobian


Locally, dynamics are:
Large Singular Values,
Less Required Input
A Dynamically Consistent Distance Metric


Locally, dynamics are:
(In practice, requires regularization)
Mahalanobis Distance induced by the Jacobian
Zero Singular Values,
Requires Infinite Input
A Dynamically Consistent Distance Metric
Contact problem strikes again.
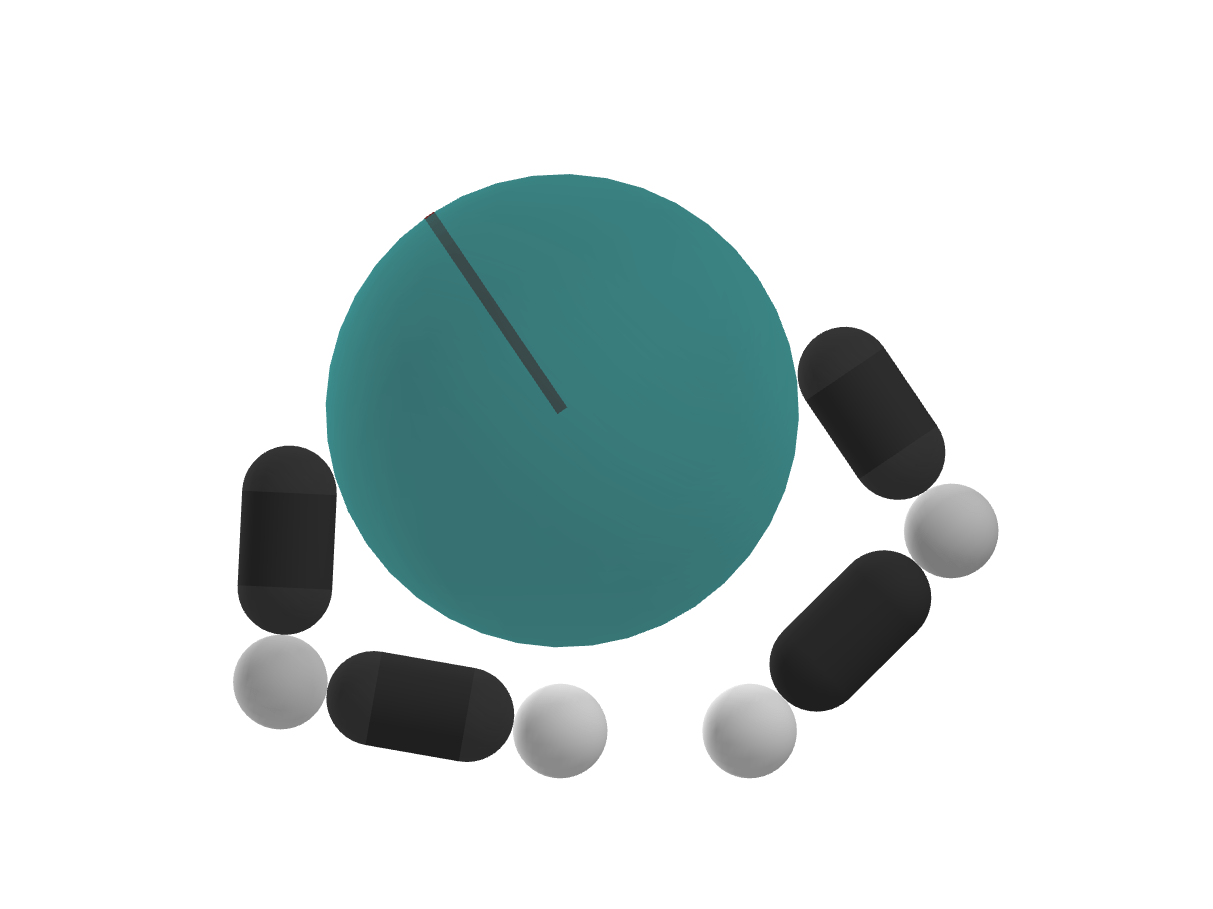
According to this metric, infinite distance if no contact is made!
What if there is no contact?
Mahalanobis Distance induced by the Jacobian
A Dynamically Consistent Distance Metric
Again, smoothing comes to the rescue!
Mahalanobis Distance induced by the Jacobian
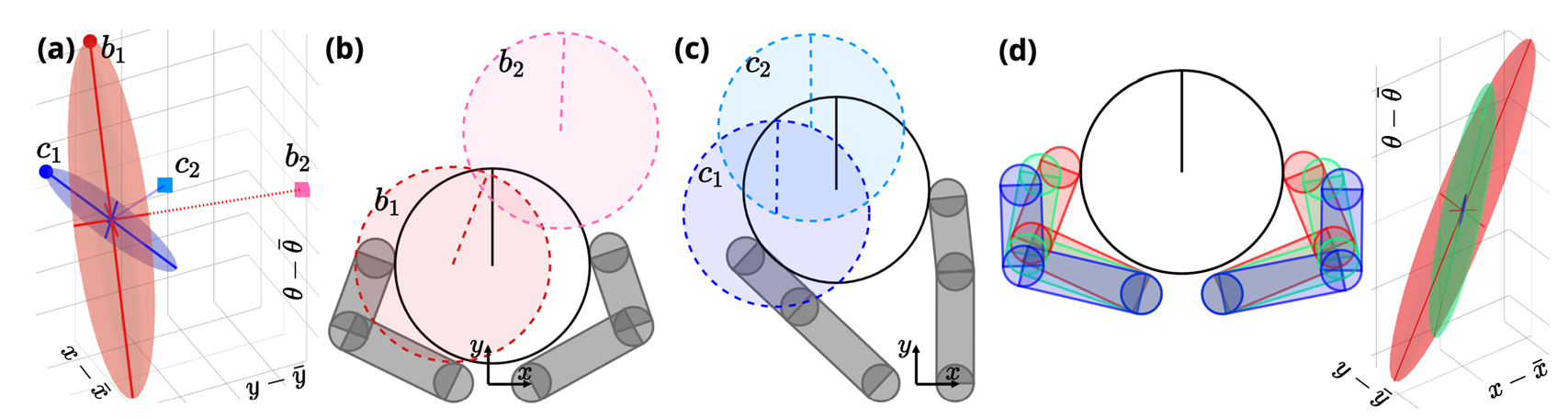
A Dynamically Consistent Distance Metric



Now we can apply RRT to contact-rich systems!

A Dynamically Consistent Distance Metric



Now we can apply RRT to contact-rich systems!



However, these still require lots of random extensions!

A Dynamically Consistent Distance Metric



Now we can apply RRT to contact-rich systems!



However, these still require lots of random extensions!
With some chance, place the actuated object in a different configuration.
(Regrasping / Contact-Sampling)

Contact-Rich RRT with Dynamic Smoothing
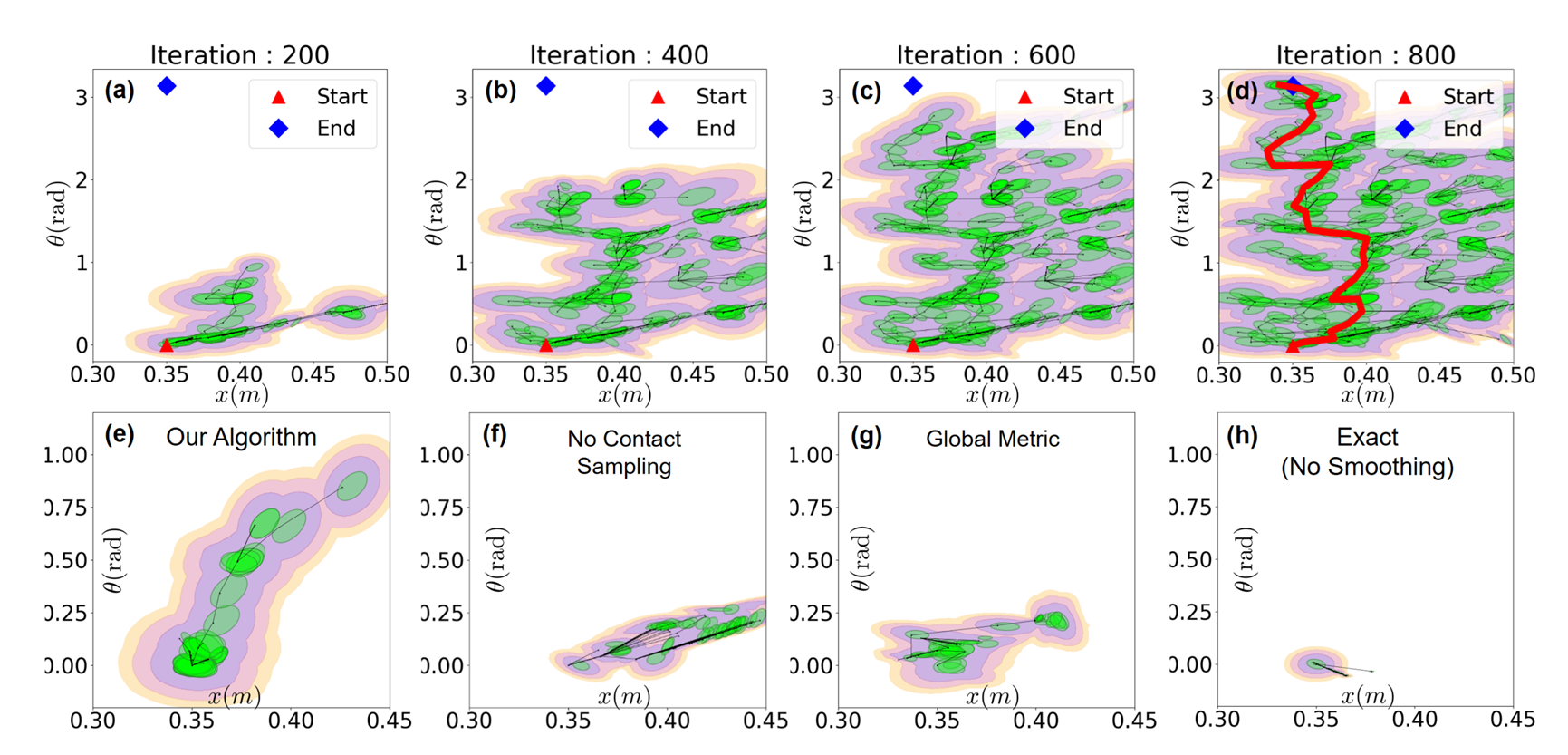
Our method can find solutions through contact-rich systems in few iterations! (~ 1 minute)
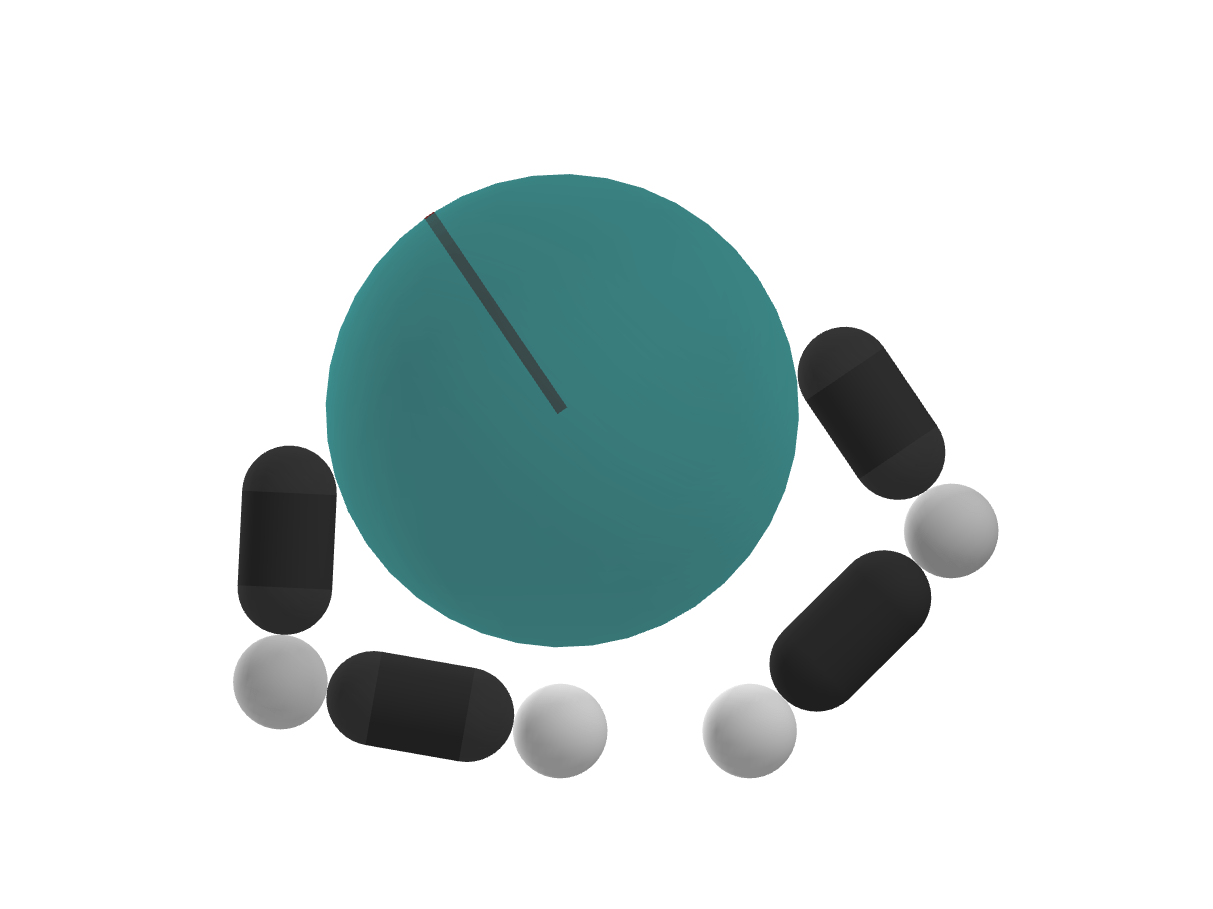
Contact-Rich RRT with Dynamic Smoothing

Without regrasping, the tree grows slowly.
Contact-Rich RRT with Dynamic Smoothing

Using a global Euclidean metric hinders the growth of the tree.
Contact-Rich RRT with Dynamic Smoothing

No dynamic smoothing gets completely stuck.
Efficient Global Planning for
Highly Contact-Rich Systems



Fast Solution Time
Beyond Local Solutions


Contact Scalability
RRT with Dynamics Smoothing

Smoothing Techniques for Non-Smooth Problems
Some non-smooth problems are successfully tackled by smooth approximations without sacrificing much from bias.
Is contact one of these problems?
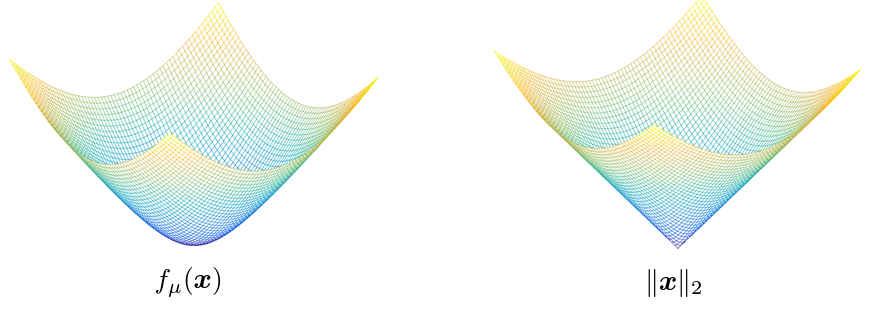

*Figures taken from Yuxin Chen's slides on "Smoothing for Non-smooth Optimization"
Smoothing in Optimization
We can formally define smoothing as a process of convolution with a smooth kernel,
In addition, for purposes of optimization, we are interested in methods that provide easy access to the derivative of the smooth surrogate.
Original Function
Smooth Surrogate
Derivative of the Smooth Surrogate:
These provide linearization Jacobians in the setting when f is dynamics, and policy gradients in the setting when f is a value function.
Taxonomy of Smoothing
Case 1. Analytic Smoothing
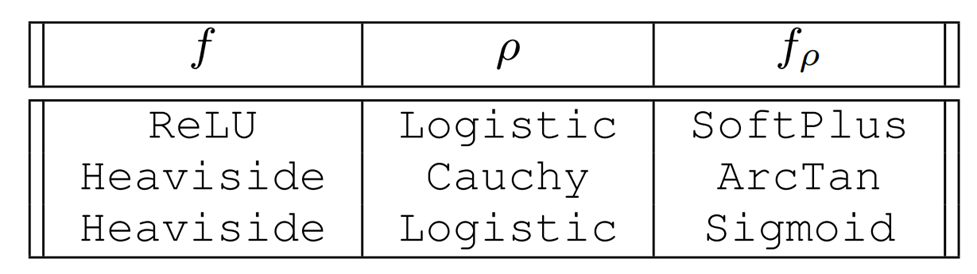
- If the original function f and the distribution rho is sufficiently structured, we can also evaluate the smooth surrogate in closed form by computing the integral.
- This can be analytically differentiated to give the derivative.
- Commonly used in ML as smooth nonlinearities.
Taxonomy of Smoothing
Case 2. Randomized Smoothing, First Order
- When we write convolution as an expectation, it motivates Monte-Carlo sampling methods that can estimate the value of the smooth surrogate.
- In order to obtain the derivative, we can use the Leibniz integral rule to exchange the expectation and the derivative.
- This means we can sample derivatives to approximate the derivative of the sampled function.
- Requires access to the derivative of the original function f.
- Also known as the Reparametrization (RP) gradient.
Taxonomy of Smoothing
Case 2. Randomized Smoothing, First Order
*Figures taken from John Duchi's slides on Randomized Smoothing
Taxonomy of Smoothing
Case 2. Randomized Smoothing, Zeroth-Order
- Interestingly, we can obtain the derivative of the randomized smoothing objective WITHOUT having access to the gradients of f.
- This gradient is derived from Stein's lemma
- Known by many names: Likelihood Ratio gradient, Score Function gradient, REINFORCE gradient.
This seems like it came out of nowhere? How can this be true?
Taxonomy of Smoothing
Rethinking Linearization as a Minimizer.
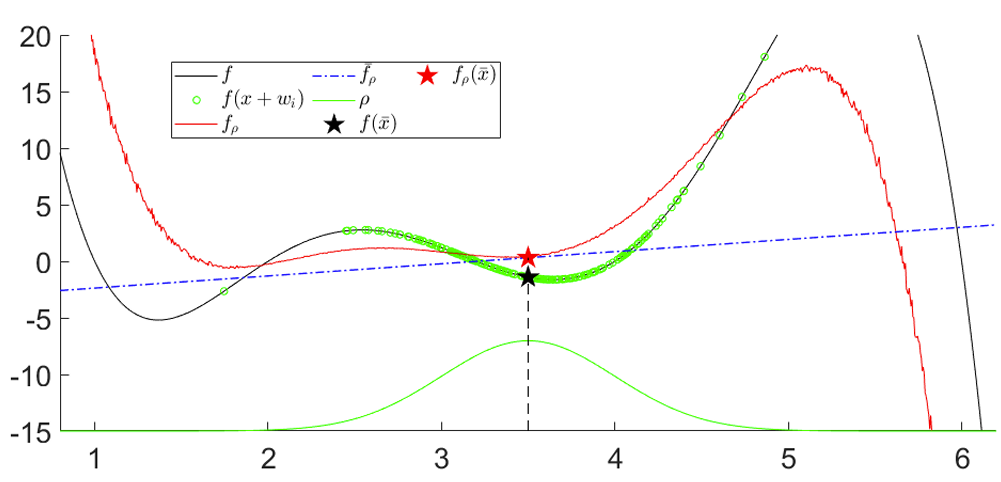
- The linearization of a function provides the best linear model (i.e. up to first order) to approximate the function locally.
- We could use the same principle for a stochastic function.
- Fix a point xbar. If we were to sample bunch of f(xbar + w_i) and run a least-squares procedure to find the best linear model, this converges to the linearization of the smooth surrogate.
Also provides a convenient way to compute the gradient in zeroth-order. Just sample and run least-squares!
Tradeoffs between structure and performance.
The generally accepted wisdom: more structure gives more performance.
Analytic smoothing
Randomized Smoothing
First-Order
Randomized Smoothing
Zeroth-Order
- Requires closed-form evaluation of the integral.
- No sampling required.
- Requires access to first-order oracle (derivative of f).
- Generally less variance than zeroth-order.
- Only requires zeroth-order oracle (value of f)
- High variance.
Structure Requirements
Performance / Efficiency
Smoothing of Optimal Control Problems
Optimal Control thorugh Non-smooth Dynamics
Policy Optimization
Cumulative Cost
Dynamics
Policy (can be open-loop)
Dynamics Smoothing
Value Smoothing
Smoothing of Optimal Control Problems
Dynamics Smoothing
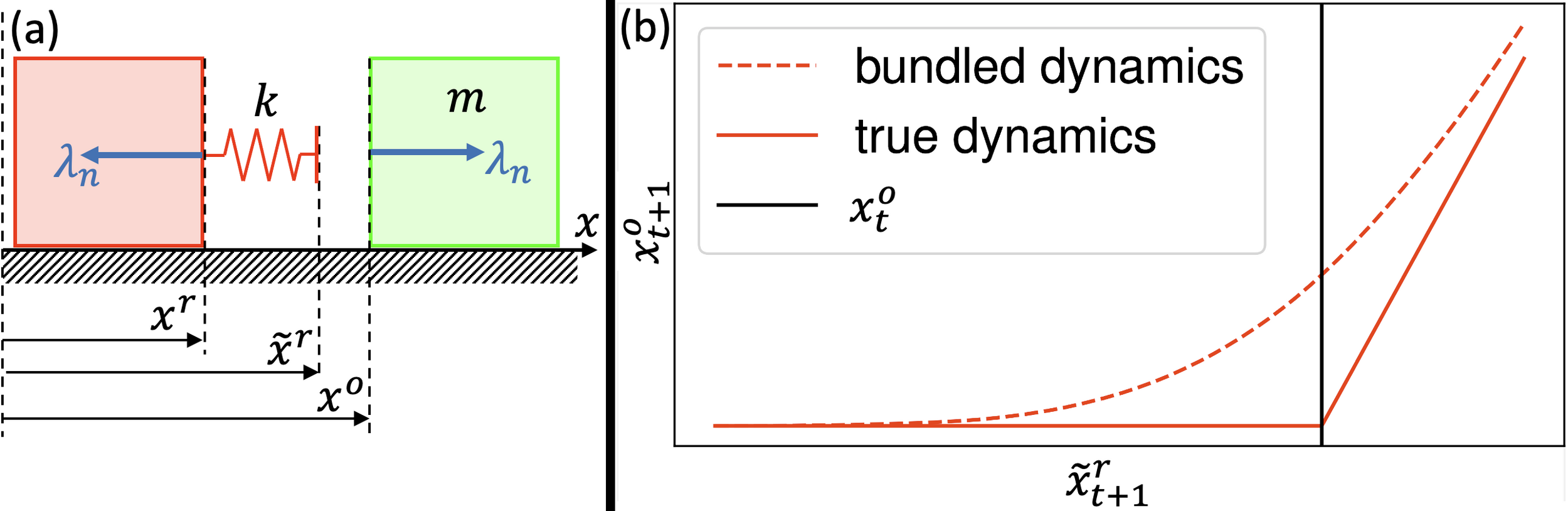
What does it mean to smooth contact dynamics stochastically?
Since some samples make contact and others do not, averaging these "discrete modes" creates force from a distance.
Smoothing of Optimal Control Problems
Dynamics Smoothing
Quadratic Programming
To numerically solve this problem, we rely on the fact that we have a known dynamic programming solution to linear dynamics with quadratic cost.
Until convergence:
- Rollout current iterate of input sequence.
- Linearize dynamics around the trajectory
- Solve for the optimal input under linearized dynamics
Sequential Quadratic Programming
Sequential Quadratic Programming
Importantly, the linearization utilizes stochastic gradient estimation techniques.
Optimal Control with Dynamics Smoothing
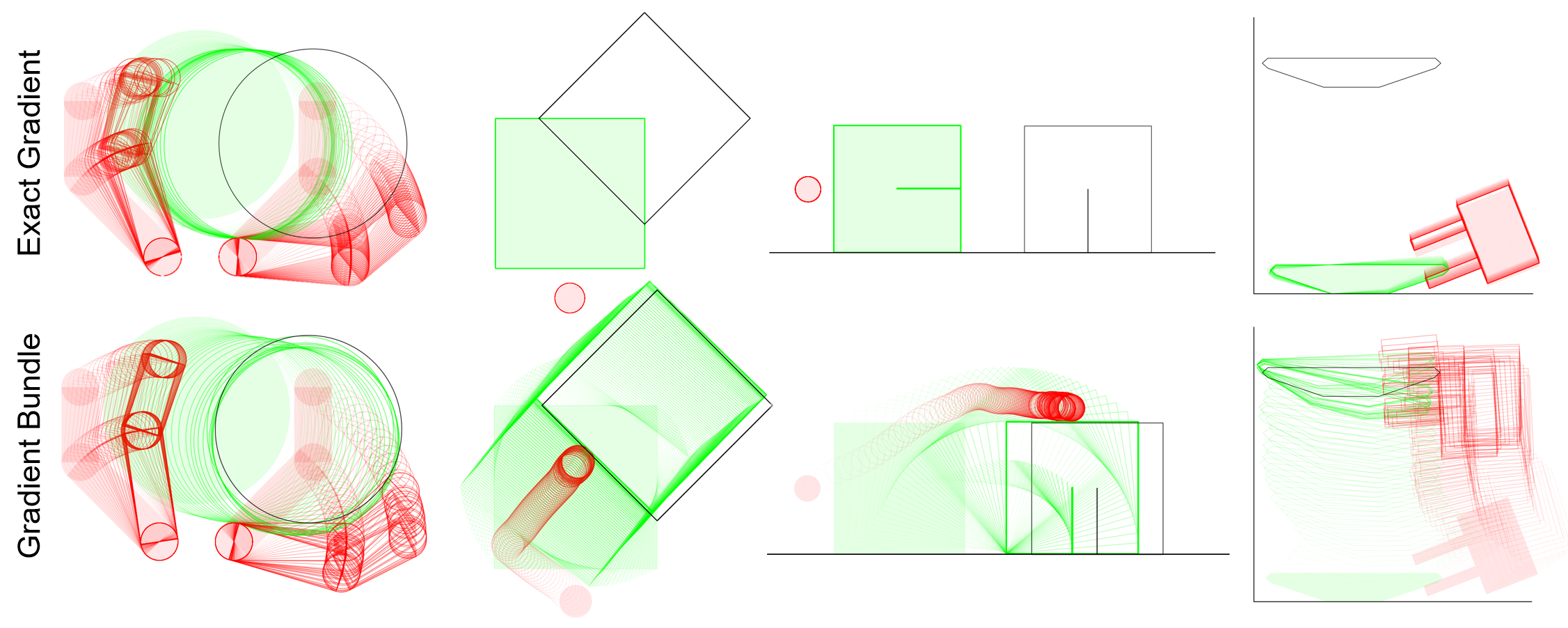
Exact
Smoothed
Smoothing of Value Functions.
Optimal Control thorugh Non-smooth Dynamics
Policy Optimization
Cumulative Cost
Dynamics
Policy (can be open-loop)
Dynamics Smoothing
Value Smoothing
Recall that smoothing turns into .
Why not just smooth the value function directly and run policy optimization?
Smoothing of Value Functions.
Original Problem

Long-horizon problems involving contact can have terrible landscapes.
Smoothing of Value Functions.
Smooth Surrogate
The benefits of smoothing are much more pronounced in the value smoothing case.

Beautiful story - noise sometimes regularizes the problem, developing into helpful bias.
How do we take gradients of smoothed value function?
Analytic smoothing
Randomized Smoothing
First-Order
Randomized Smoothing
Zeroth-Order
- Requires differentiability over dynamics, reward, policy.
- Generally lower variance.
- Only requires zeroth-order oracle (value of f)
- High variance.
Structure Requirements
Performance / Efficiency
Pretty much not possible.
How do we take gradients of smoothed value function?
First-Order Policy Search with Differentiable Simulation
Policy Gradient Methods in RL (REINFORCE / TRPO / PPO)
- Requires differentiability over dynamics, reward, policy.
- Generally lower variance.
- Only requires zeroth-order oracle (value of f)
- High variance.
Structure Requirements
Performance / Efficiency
Turns out there is an important question hidden here regarding the utility of differentiable simulators.
Do Differentiable Simulators Give Better Policy Gradients?



Very important question for RL, as it promises lower variance, faster convergence rates, and more sample efficiency.
What do we mean by "better"?
Consider a simple stochastic optimization problem
First-Order Gradient Estimator
Zeroth-Order Gradient Estimator
Then, we can define two different gradient estimators.
What do we mean by "better"?
First-Order Gradient Estimator
Zeroth-Order Gradient Estimator
Bias
Variance
Common lesson from stochastic optimization:
1. Both are unbiased under sufficient regularity conditions
2. First-order generally has less variance than zeroth order.
What happens in Contact-Rich Scenarios?
Bias
Variance
Common lesson from stochastic optimization:
1. Both are unbiased under sufficient regularity conditions
2. First-order generally has less variance than zeroth order.
Bias
Variance
Bias
Variance
We show two cases where the commonly accepted wisdom is not true.
1st Pathology: First-Order Estimators CAN be biased.
2nd Pathology: First-Order Estimators can have MORE
variance than zeroth-order.
Bias from Discontinuities
1st Pathology: First-Order Estimators CAN be biased.
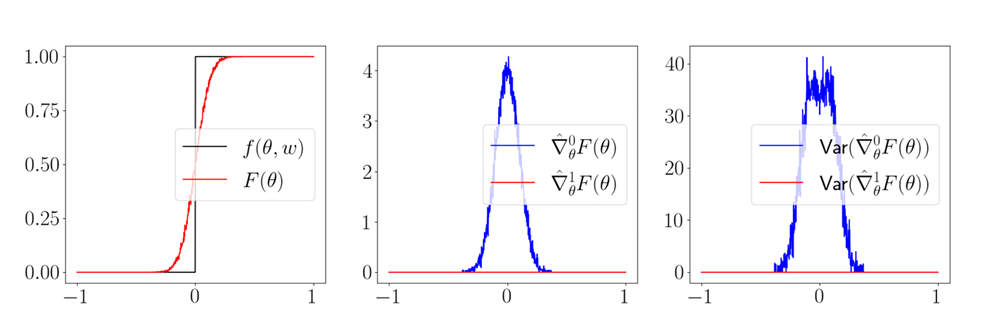
What's worse: the empirical variance is also zero!
(The estimator is absolutely sure about an estimate that is wrong)
Not just a pathology, could happen quite often in contact.
Empirical Bias leads to High Variance
Perhaps it's a modeling artifact? Contact can be softened.
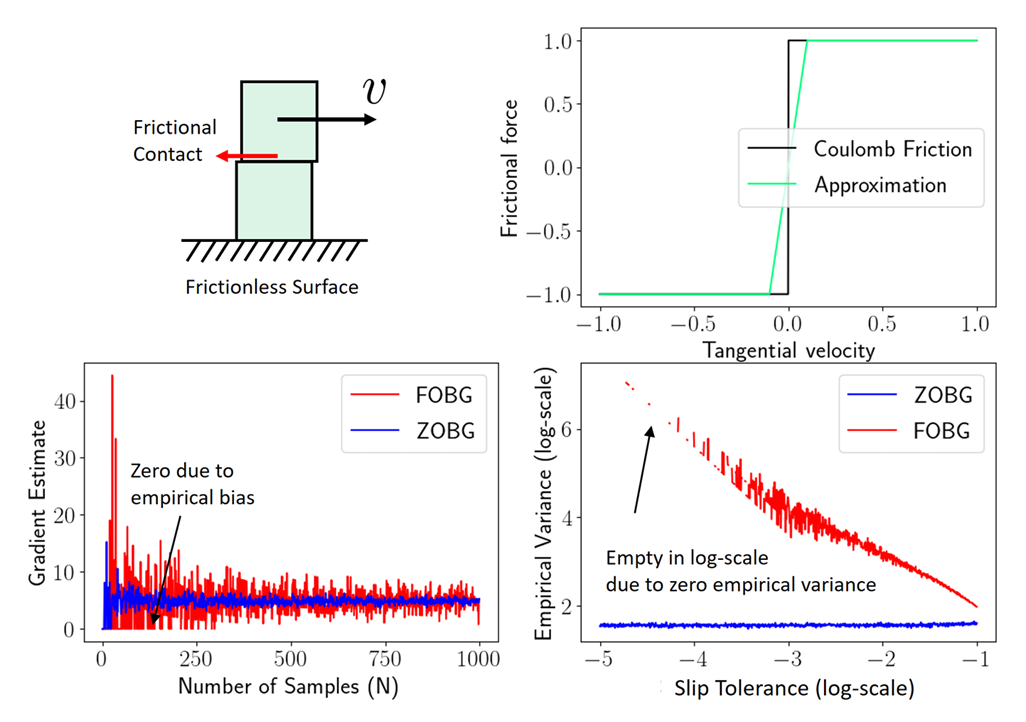
- From a low-sample regime, no statistical way to distinguish between an actual discontinuity and a very stiff function.
- Generally, stiff relaxations lead to high variance. As relaxation converges to true discontinuity, variance blows up to infinity, and suddenly turns into bias!
- Zeroth-order escapes by always thinking about the cumulative effect over some finite interval.
Variance of First-Order Estimators
2nd Pathology: First-order Estimators CAN have more variance than zeroth-order ones.
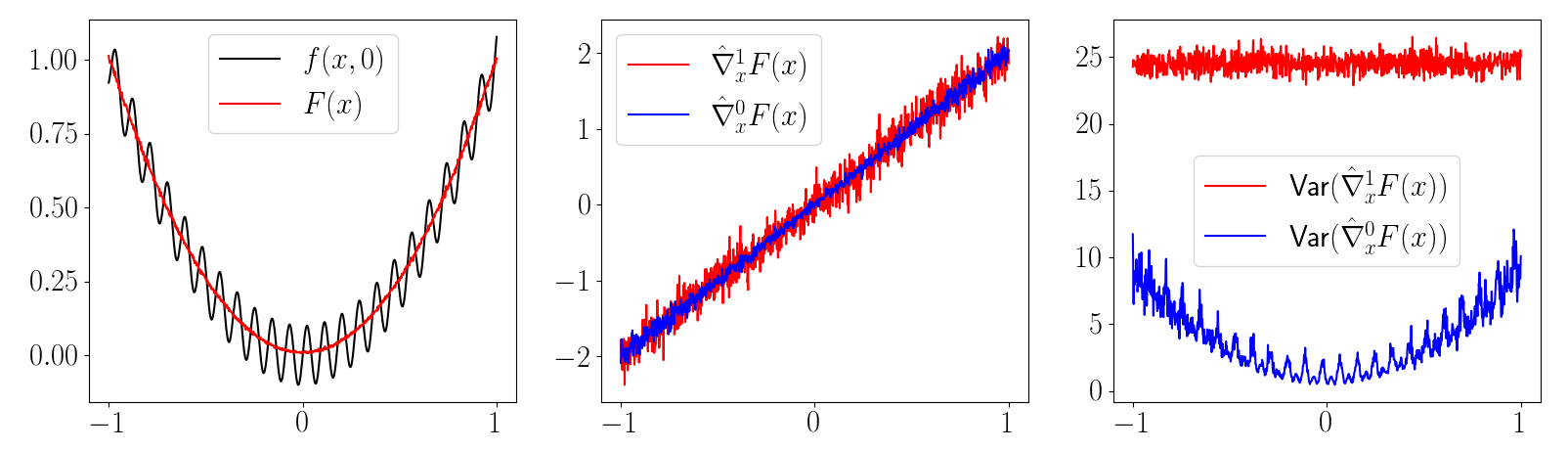
Scales with Gradient
Scales with Function Value
Scales with dimension of decision variables.
High-Variance Events
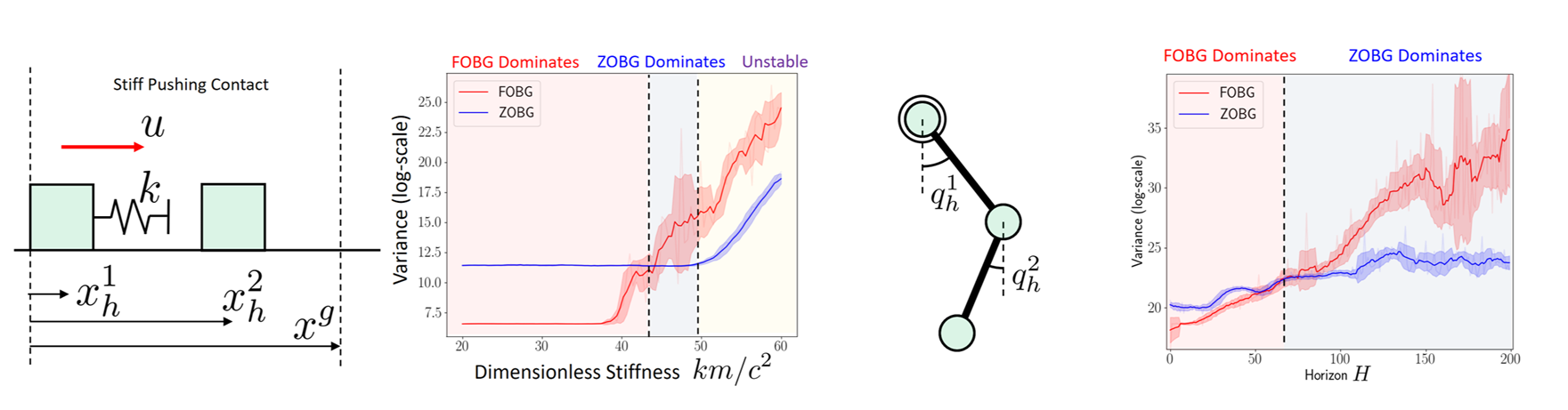
Case 1. Persistent Stiffness
Case 2. Chaotic
- Contact modeling using penalty method is a bad idea for differentiable policy search
- Gradients always has the spring stiffness value!
- High variance depending on initial condition
- Zeroth-order always bounded in value, but the gradients can be very high.
Motivating Contact-rich RRT
How do we overcome local minima of local gradient-based methods?
Our ideal solution
The RRT Algorithm
Global Search with Smoothing: Contact-Rich RRT

Motivating Contact-Rich RRT
Sampling-Based Motion Planning is a popular solution in robotics for complex non-convex motion planning
How do we define notions of nearest?
How do we extend (steer)?
- Nearest states in Euclidean space are not necessarily reachable according to system dynamics (Dubin's car)
- Typically, kinodynamic RRT solves trajopt
- Potentially a bit costly.
Reachability-Consistent Distance Metric
Reachability-based Mahalanobis Distance
How do we come up with a distance metric between q and qbar in a dynamically consistent manner?
Reachability-Consistent Distance Metric
Reachability-based Mahalanobis Distance
How do we come up with a distance metric between q and qbar in a dynamically consistent manner?

Consider a one-step input linearization of the system.
Then we could consider a "reachability ellipsoid" under this linearized dynamics,
Note: For quasidynamic formulations, ubar is a position command, which we set as the actuated part of qbar.
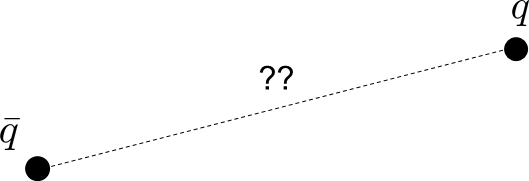
Reachability Ellipsoid
Reachability Ellipsoid
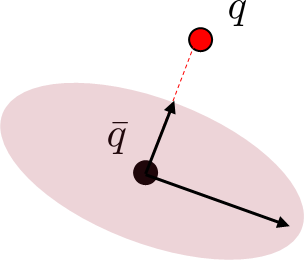
Intuitively, if B lengthens the direction towards q from a uniform ball, q is easier to reach.
On the other hand, if B decreases the direction towards q, q is hard to reach.
Mahalanobis Distance of an Ellipsoid
Reachability Ellipsoid
The B matrix induces a natural quadratic form for an ellipsoid,
Mahalanobis Distance using 1-Step Reachability
Note: if BBT is not invertible, we need to regularize to property define a quadratic distance metric numerically.
Smoothed Distance Metric

For Contact:
Don't use the exact linearization, but the smooth linearization.
Global Search with Smoothing
Dynamically consistent extension
Theoretically, it is possible to use long-horizon trajopt algorithms such as iLQR / DDP.
Here we simply do one-step trajopt and solve least-squares.
Importantly, the actuation matrix for least-squares is smoothed, but we rollout the actual dynamics with the found action.
Dynamically consistent extension
Contact Sampling
With some probability, we execute a regrasp (sample another valid contact configuration) in order to encourage further exploration.

Global Search with Smoothing

Smoothing of Contact Dynamics
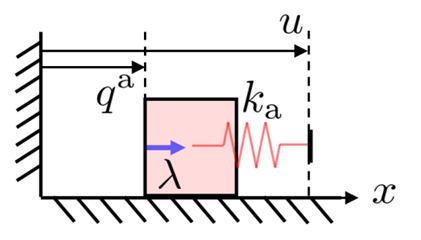
Without going too much into details of multibody contact dynamics, we will use time-stepping, quasidynamic formulation of contact.
- We assume that velocities die out instantly
- Inputs to the system are defined by position commands to actuated bodies.
- The actuated body and the commanded position is connected through an impedance source k.
Equations of Motion (KKT Conditions)
Non-penetration
(Primal feasibility)
Complementary slackness
Dual feasibility
Force Balance
(Stationarity)
Quasistatic QP Dynamics
We can randomize smooth this with first order methods using sensitivity analysis or use zeroth-order randomized smoothing.
But can we smooth this analytically?
Barrier (Interior-Point) Smoothing
Quasistatic QP Dynamics
Equations of Motion (KKT Conditions)
Interior-Point Relaxation of the QP
Equations of Motion (Stationarity)

Impulse
Relaxation of complementarity
"Force from a distance"
What does smoothing do to contact dynamics?

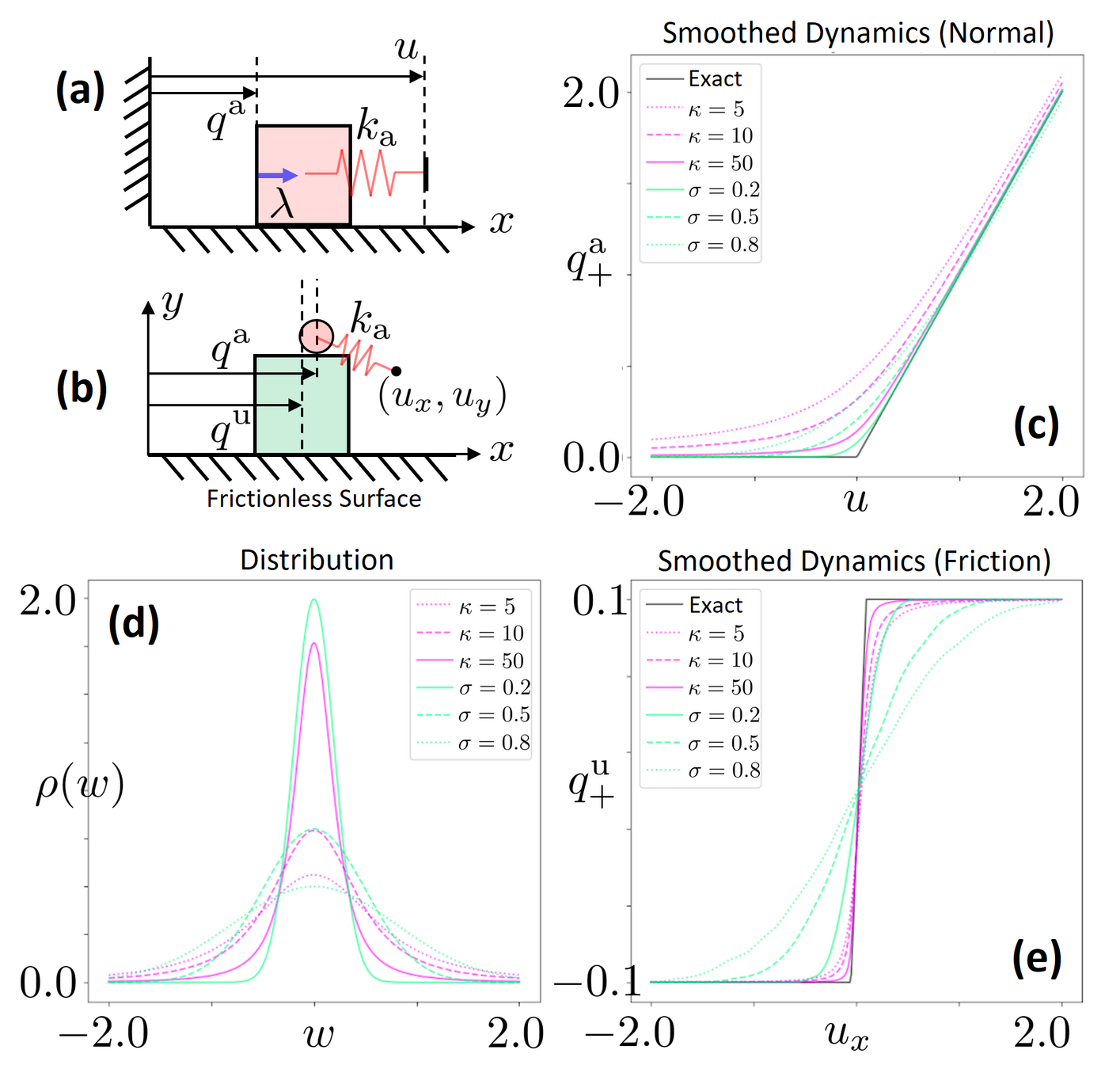


- Both schemes (randomized smoothing and barrier smoothing) provides "force from a distance effects" where the exerted force increases with distance.
- Provides gradient information from a distance.
- In contrast, without smoothing, zero gradients and flat landscapes cause problems for gradient-based optimization.
Is barrier smoothing a form of convolution?
Equivalence of Randomized and Barrier Smoothing.
- For the simple 1D pusher system, it turns out that one can show that barrier smoothing also implements a convolution with the original function and a kernel.
- This is an elliptical distribution with a "fatter tail" compared to a Gaussian".

Later result shows that there always exists such a kernel for Linear Complementary Systems (LCS).
Limitations of Smoothing
Contact is non-smooth. But Is it truly "discrete"?
The core thesis of this talk:
The local decisions of where to make contact are better modeled as continuous decisions with some smooth approximations.
My viewpoint so far:
Limitations of Smoothing
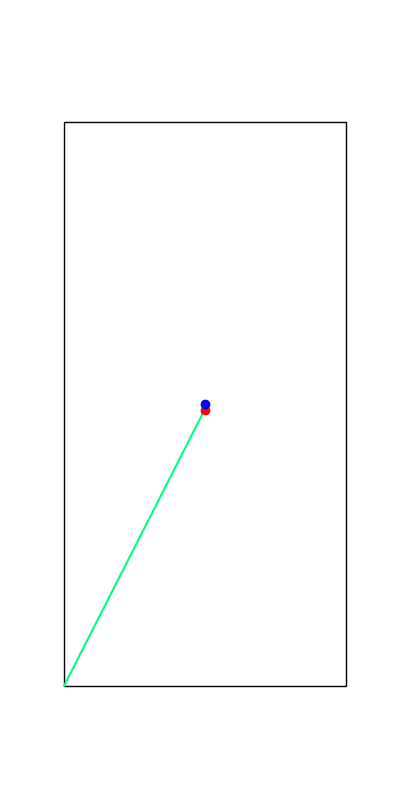
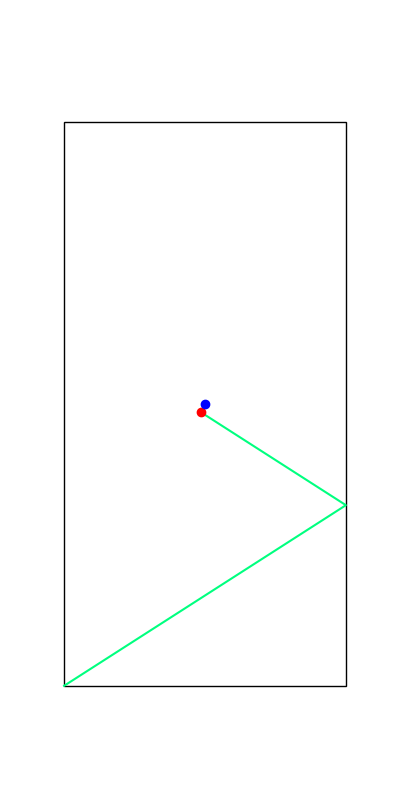
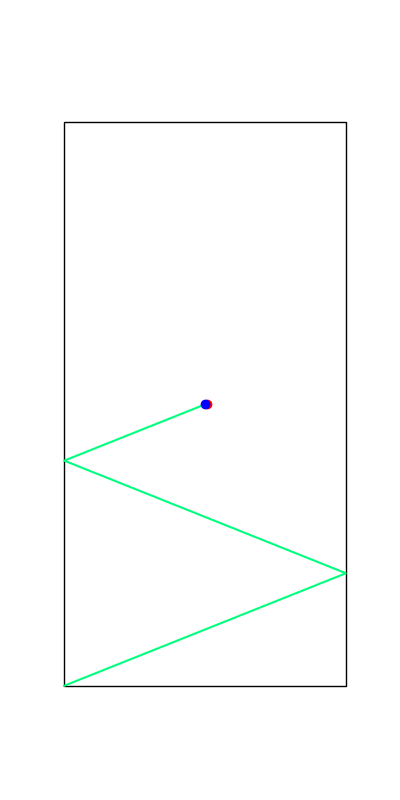
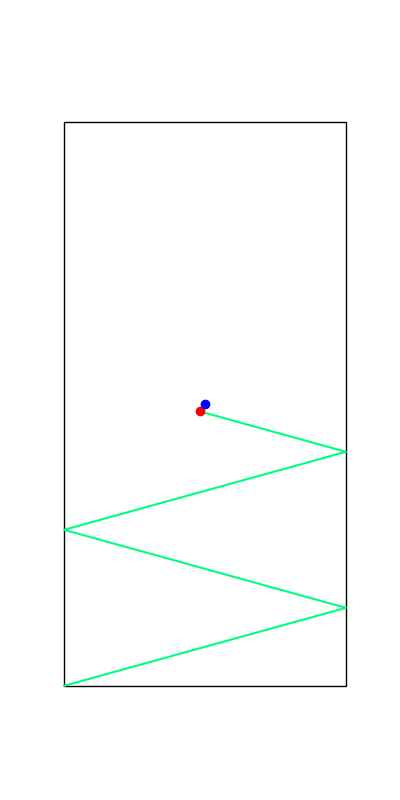
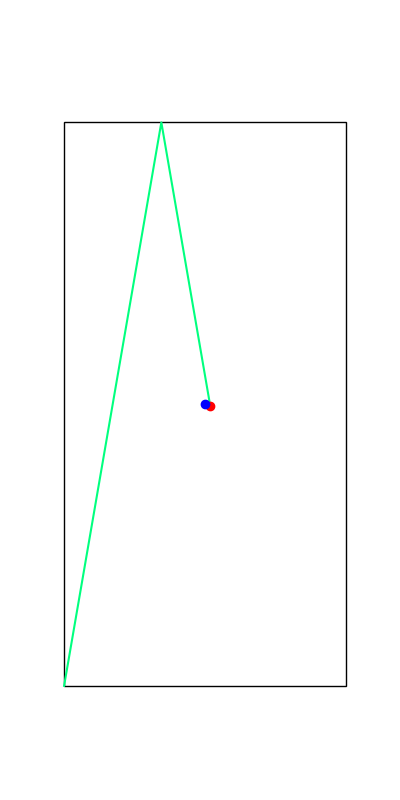
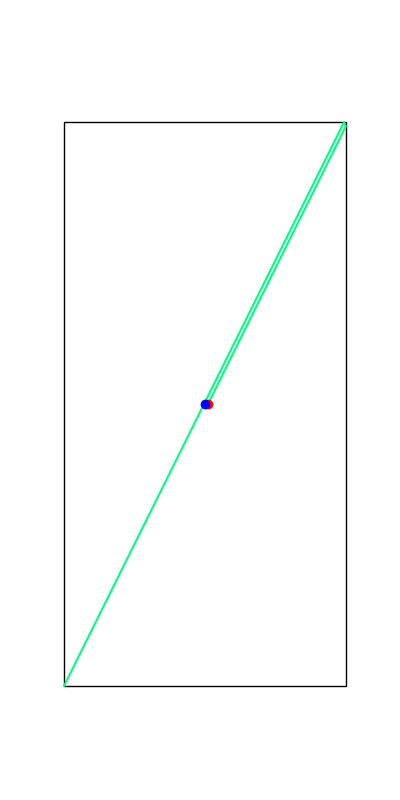
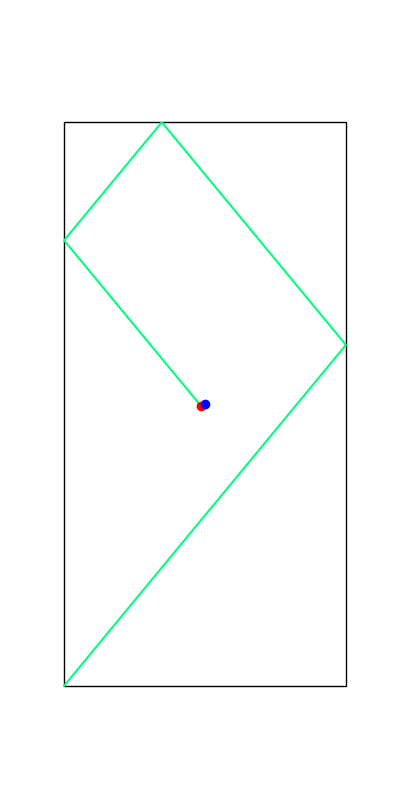
These reveal true discrete "modes" of the decision making process.
Limitations of Smoothing
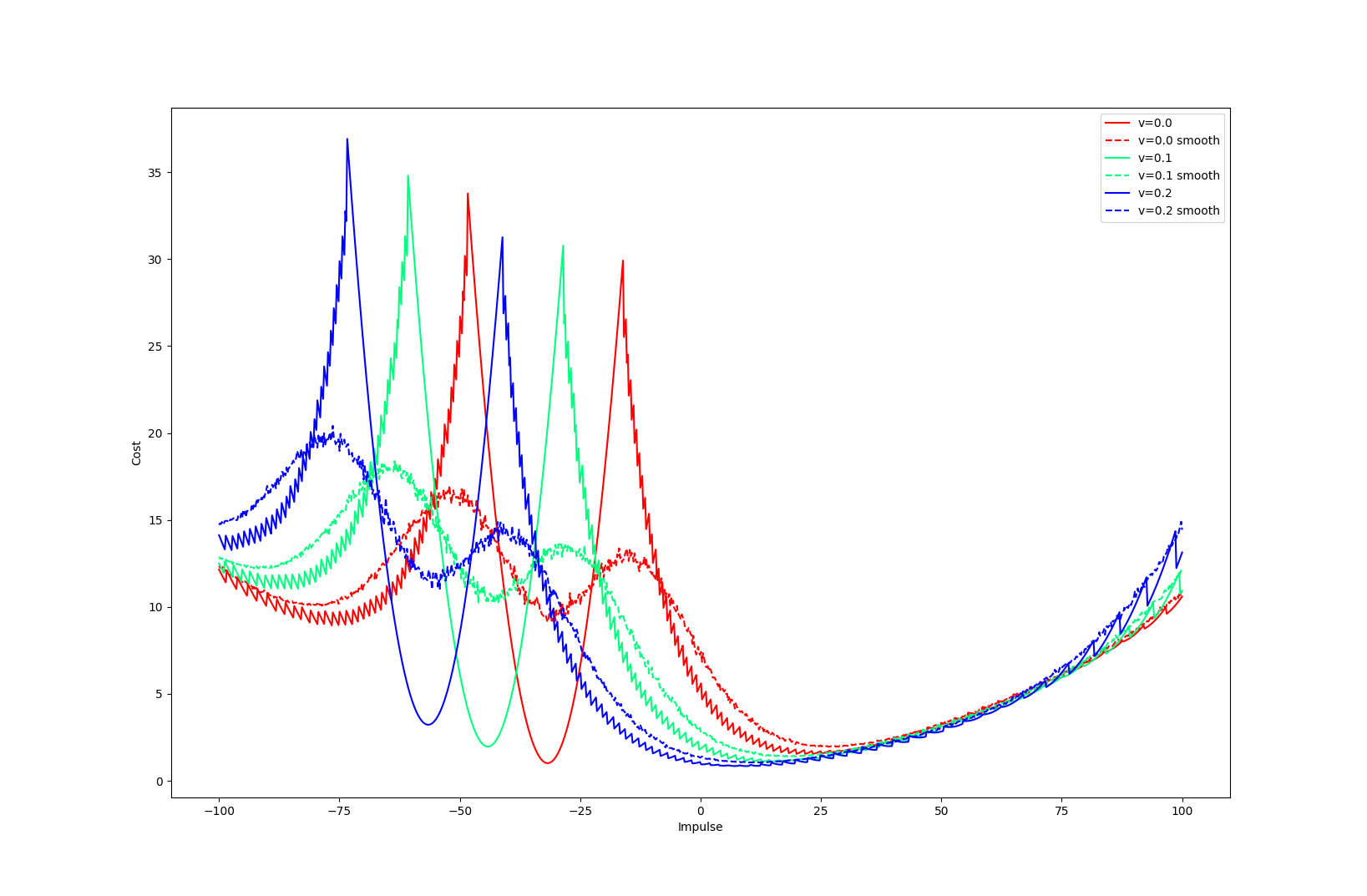
Apply negative impulse
to stand up.
Apply positive impulse to bounce on the wall.
Bias of Smoothing
rho subscript denotes smoothing
We have linearized the smoothened dynamics around u = qa.
Depending on where we set the goal to be, we see three distinct regions.
Bias of Smoothing
rho subscript denotes smoothing

0.5m
0.0m
Region 1. Beneficial Bias
Goal = 0.61m
Optimal input
The linearized model provides helpful bias, as the optimal input moves the actuated body towards making contact.
Bias of Smoothing
rho subscript denotes smoothing

0.5m
0.0m
Region 2. Hurtful Bias
Goal = 0.52m
Optimal input
If you command the actuated body to hold position, the unactuated body will be pushed away due to smoothing.
The actuated body wants to go backwards in order to decrease this effect if the goal is not too in front of the unactuated body.
Bias of Smoothing
rho subscript denotes smoothing

0.5m
0.0m
Region 3. Violation of unilateral contact
Goal = 0.45m
Optimal input
If you set the goal to behind the unactuated body, the linear model thinks that it can pull, and will move backwards.
Motivating Gradient Interpolation
Bias
Variance
Common lesson from stochastic optimization:
1. Both are unbiased under sufficient regularity conditions
2. First-order generally has less variance than zeroth order.
Bias
Variance
Bias
Variance
1st Pathology: First-Order Estimators CAN be biased.
2nd Pathology: First-Order Estimators can have MORE
variance than zeroth-order.
Can we automatically decide which of these categories we fall into based on statistical data?
The Alpha-Ordered Gradient Estimator
Perhaps we can do some interpolation of the two gradients based on some criteria.
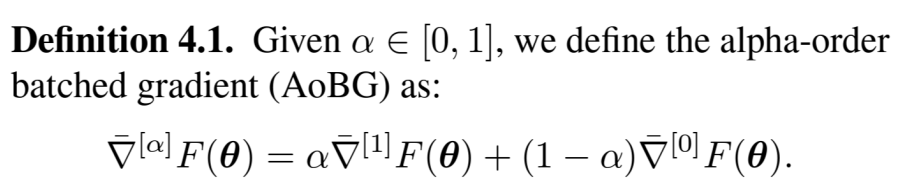
Previous works attempt to minimize the variance of the interpolated estimator using empirical variance.
Robust Interpolation
Thus, we propose a robust interpolation criteria that also restricts the bias of the interpolated estimator.

Robust Interpolation
Robust Interpolation
Implementation
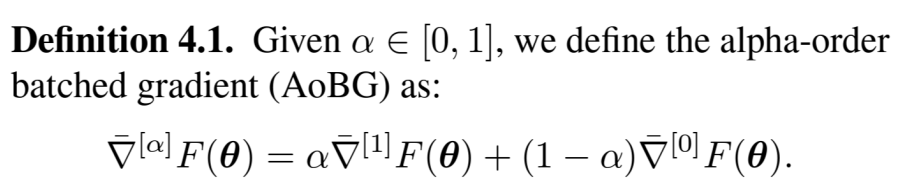
Confidence Interval on the zeroth-order gradient.
Difference between the gradients.
Key idea: Unit-test the first-order estimate against the unbiased zeroth-order estimate to guarantee correctness probabilistically. .
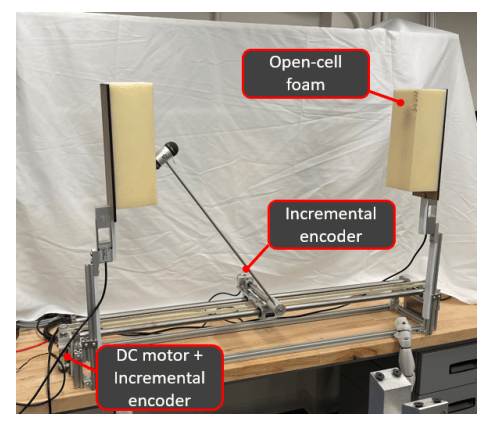
Results: Ball throwing on Wall
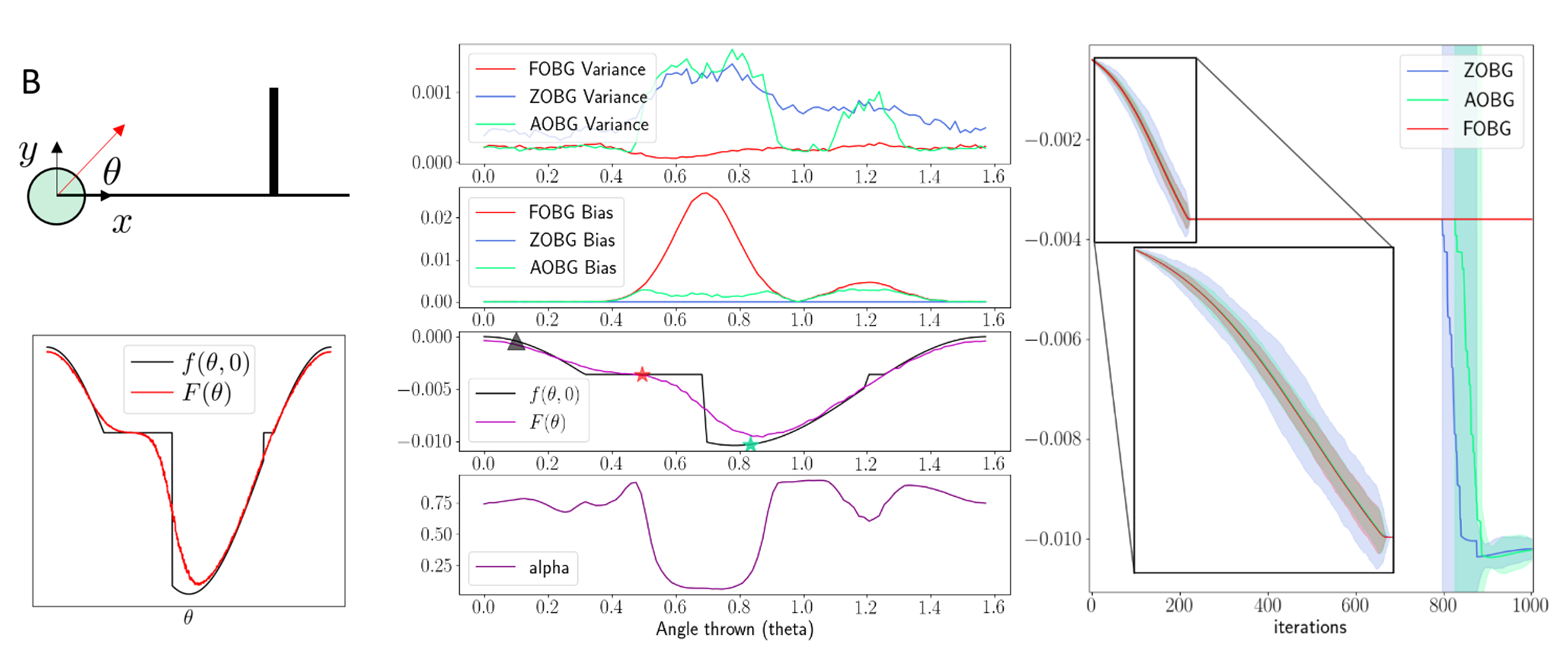
Key idea: Do not commit to zeroth or first uniformly,
but decide coordinate-wise which one to trust more.
Results: Policy Optimization
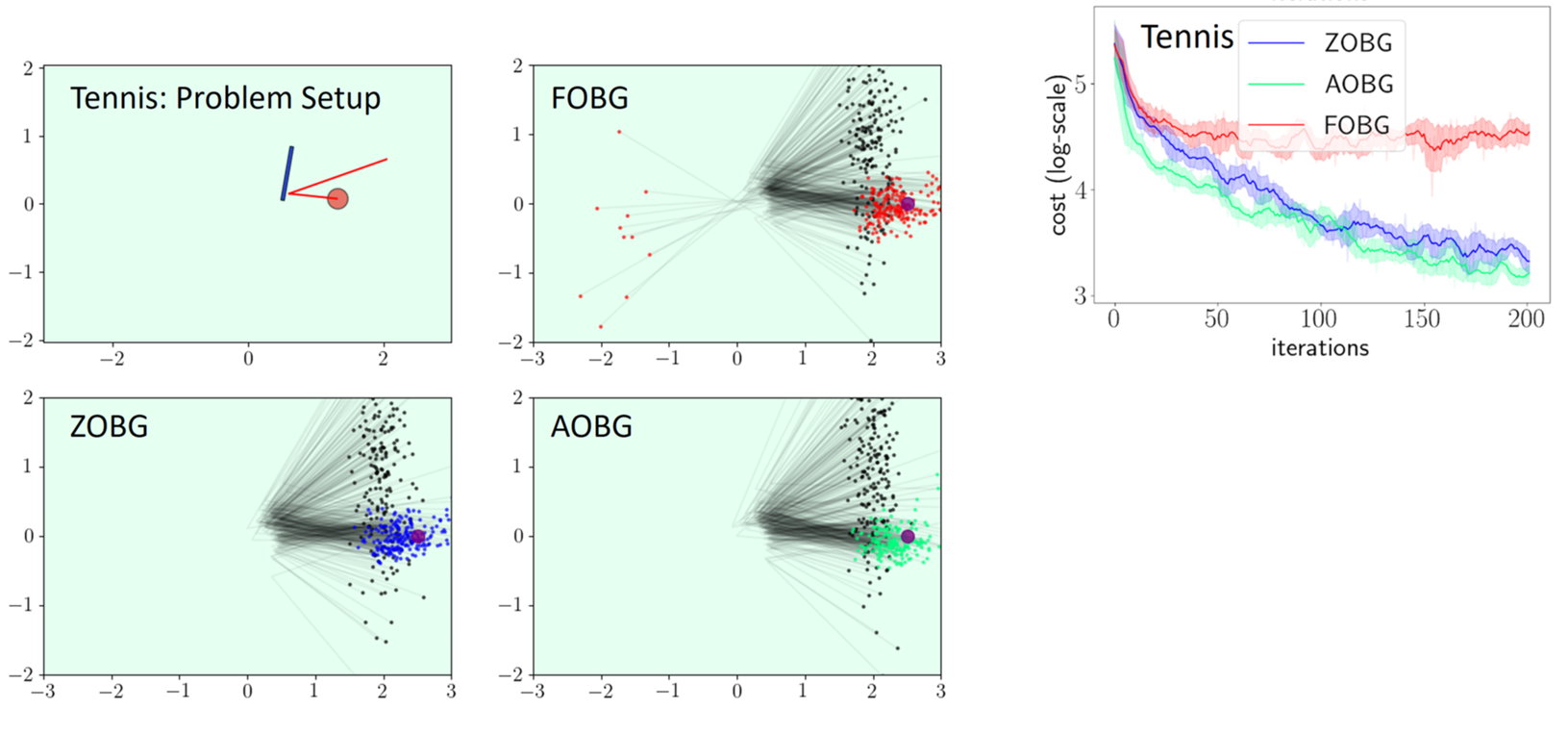
Able to capitalize on better convergence of first-order methods while being robust to their pitfalls.
Exposing the Real Difficulties of Contact-Rich Manipulation
By Terry Suh
Exposing the Real Difficulties of Contact-Rich Manipulation
- 338



