Organizing Thoughts....
Doing this on slides.com since lab doesn't have powerpoint.
Why is non-smooth optimization harder?
Should we take expectation over the value function or the dynamics?
When should we prefer first-order gradients vs. zero-order gradients?
Should we inject noise in parameters or output of the policy?
Why are stochastic objectives better?
How do we take gradients of stochastic objectives when the inner objective is discontinuous?
What do we really want to achieve in terms of robotics?
Can we deploy trajopt / controllers that assume smooth dynamics on actual non-smooth systems?
ReLU networks are non-smooth. Why aren't we having problems?
Lit. says non-smooth fails to converge only with "steepest descent". Seems more like a convergence rate argument?
Value function is a higher variance objective.
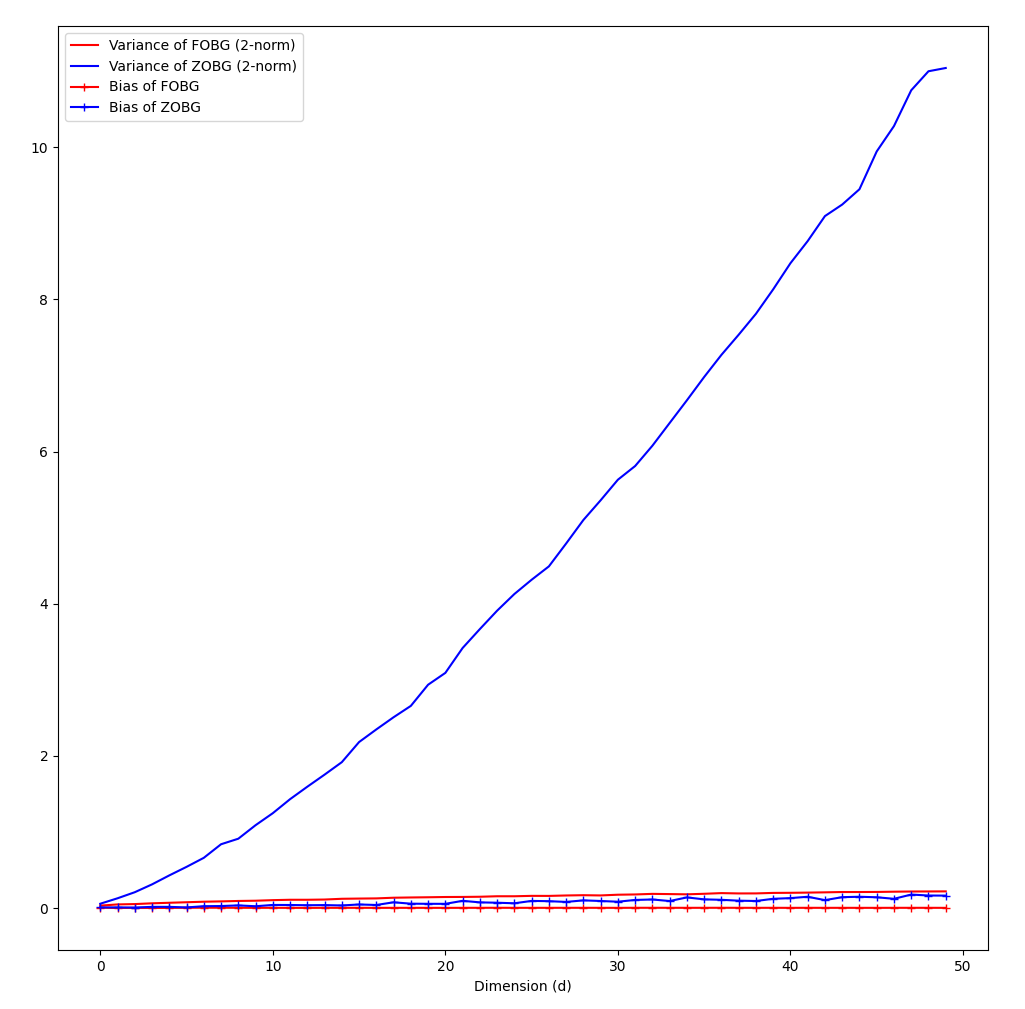
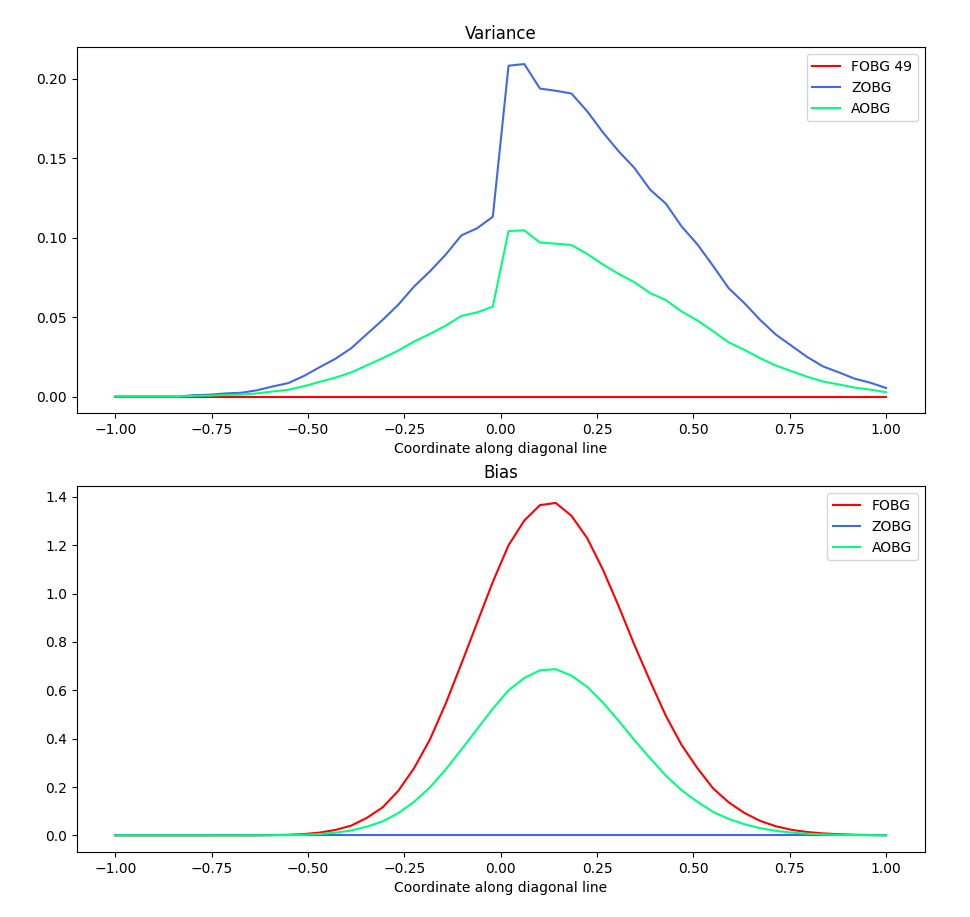
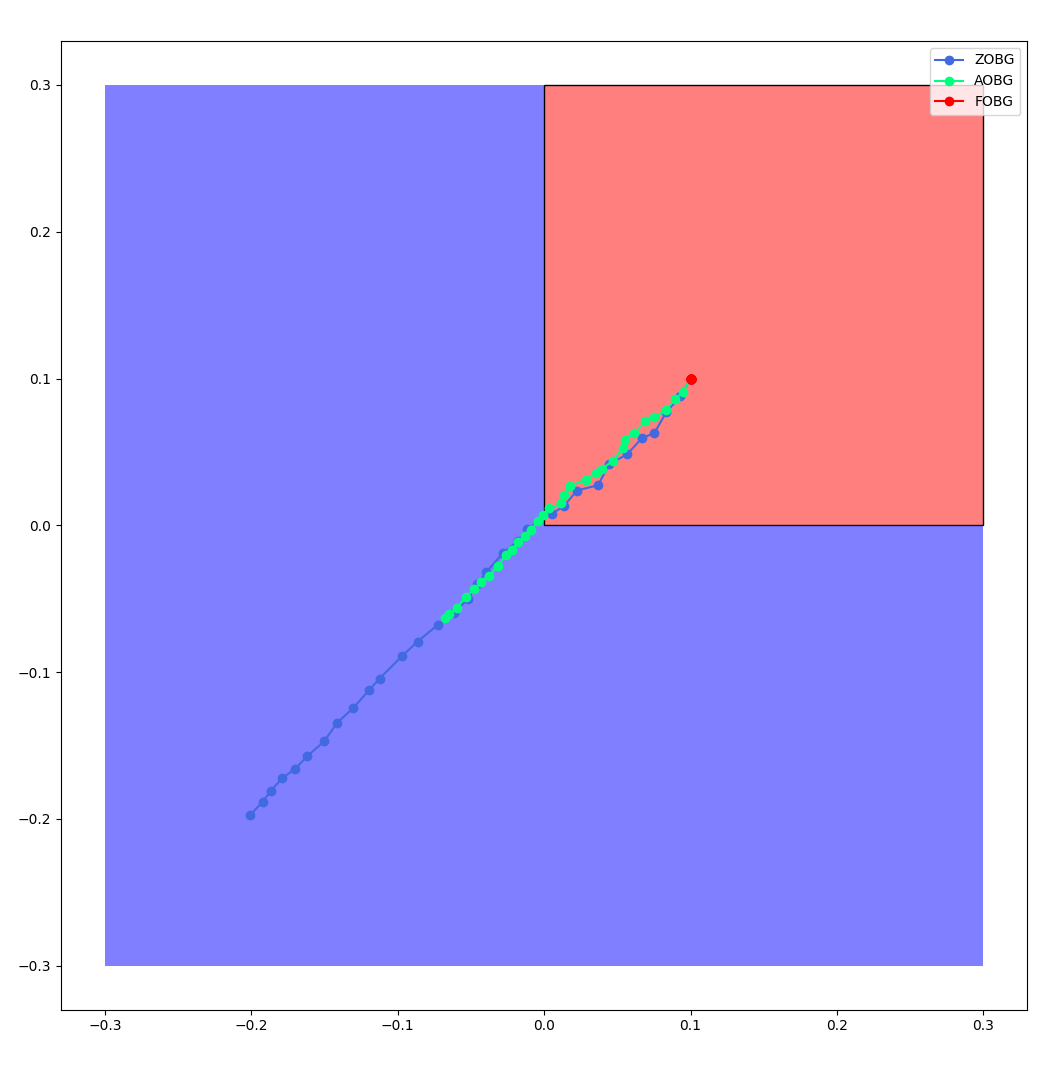
Variance vs. dimension. Effect on convergence rate.
Variance vs. dimension. Effect on convergence rate.
Needle in a haystack
Output is more interpretable
How does output affect the landscape? Still have the same effect?
Robustness
Smooth
Filtering
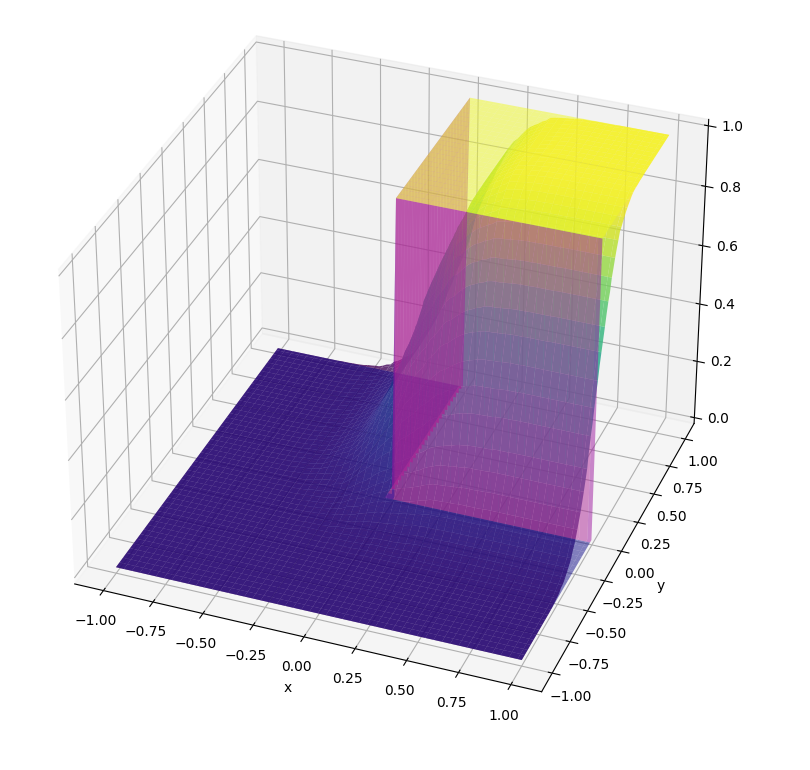
Is it really discontinuous? In what setting?
Aren't value functions always continuous?
Analysis on Systems with Complementarity Constraints / QP systems
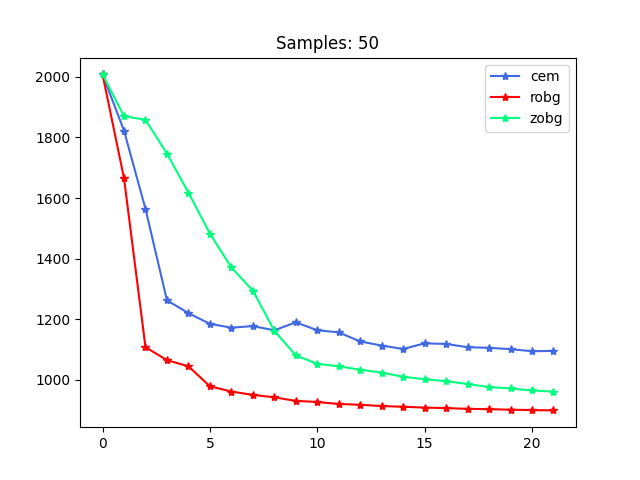
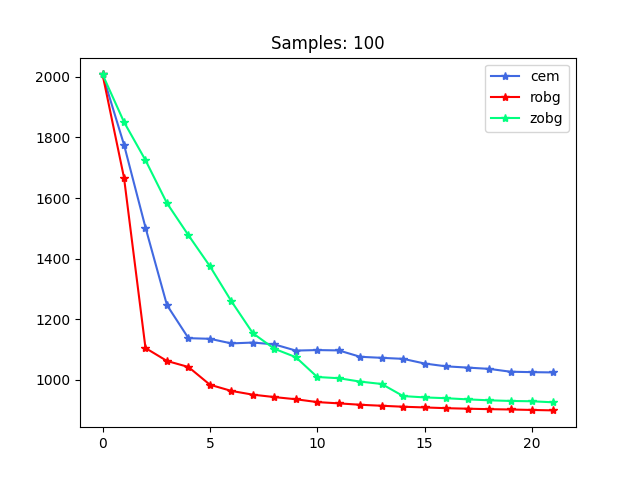
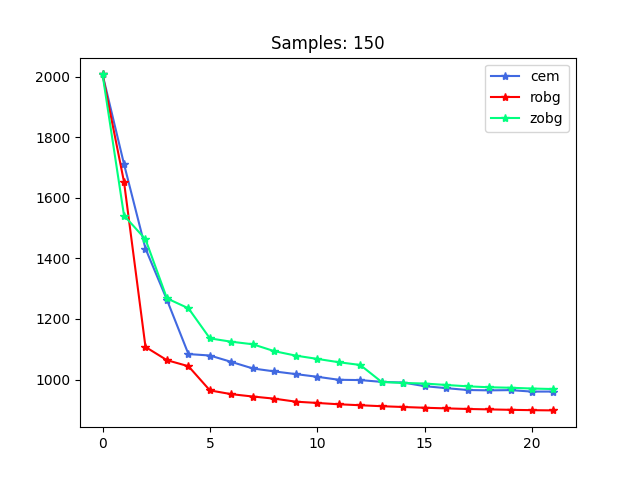
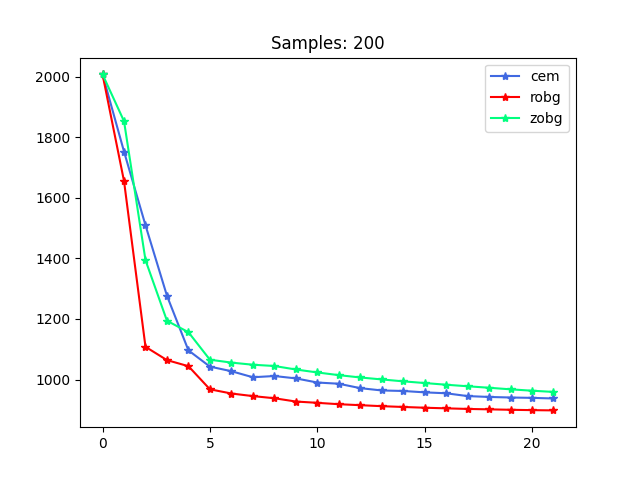




Summary of Conv. with Yunzhu
1. Gradient will always be better, but the cost is not that great.
2. May want to find problems where it's clear that gradient is more beneficial. Long horizon / high-dim.
3. Smoothing dynamics may be more surprising then smoothing value function.
Summary of Meeting with Max, Kaiqing
1. Need to normalize input / coordinates for dimension to correctly account for output.
2. p-schatten norms
3. Repeat test for discontinuous functions
4. Enumerate actual examples
5. Exploration is more interesting then analyzing rates for convex functions?
Summary of Conv. with Yunzhu
1. Gradient will always be better, but the cost is not that great.
2. May want to find problems where it's clear that gradient is more beneficial. Long horizon / high-dim.
3. Smoothing dynamics may be more surprising then smoothing value function.
Summary of Meeting with Max, Kaiqing
1. Need to normalize input / coordinates for dimension to correctly account for output.
2. p-schatten norms
3. Repeat test for discontinuous functions
4. Enumerate actual examples
5. Exploration is more interesting then analyzing rates for convex functions?

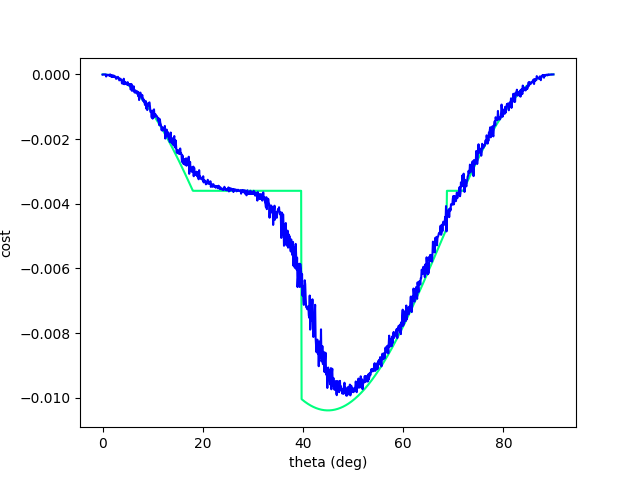
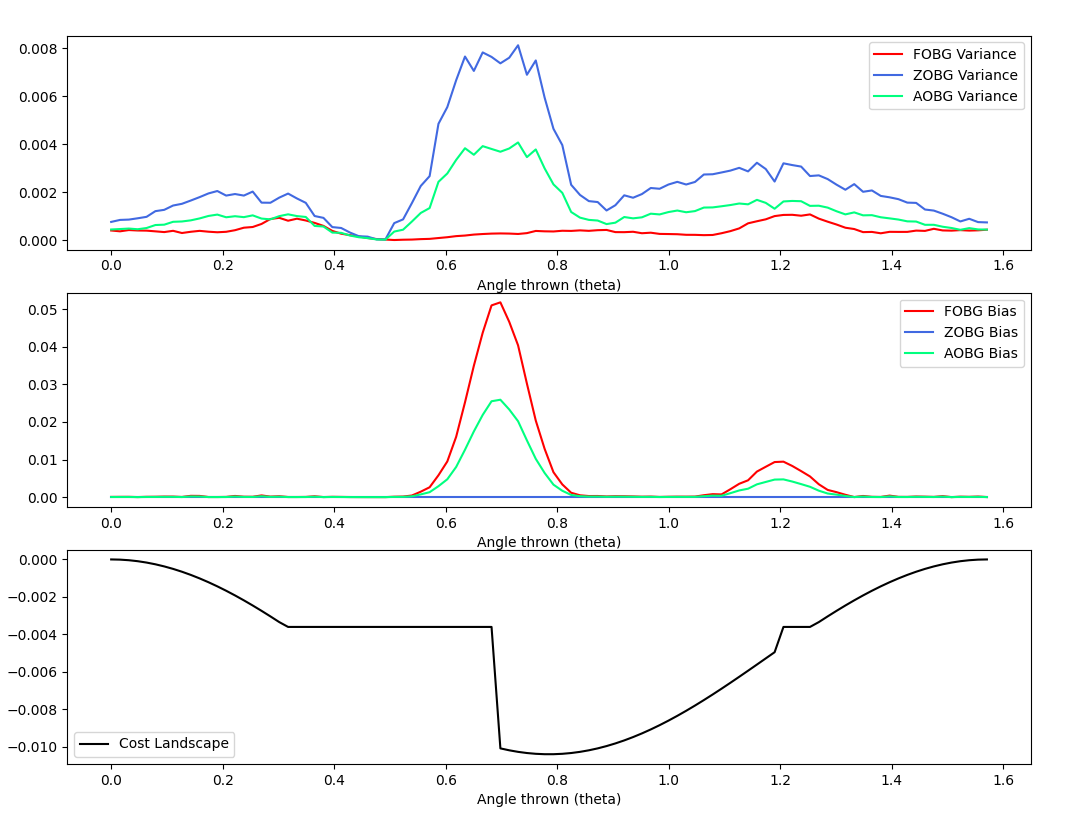
Discontinuity and
High-Lipschitz Phenomena
Impact / Stiffness
Geometry
Constraints
Stability
Pendulum w/ bouncing walls
Impacts in Locomotion
Articulated Kneed Walker
SLIP
Box Flipping
Billiard
Box Stacking (Cairn)
Russ_Update_11_21
By Terry Suh
Russ_Update_11_21
- 315



