Onion Problem Updates
AIS Setup for Carrots
Assuming quasi-static behavior, compression takes in a single image and outputs the compressed variable.
Then there is a reward function and a dynamics function that we need to learn. (Assume action abstraction is identity map)
z_t = \sigma_\alpha(\mathbf{I}_t)
r_t = r_\gamma(z_t,a_t)
z_{t+1} = \psi_\beta(z_t,a_t)
a_t = \mu_\delta(u_t)
\mathcal{L}_{\alpha,\beta,\gamma} = \lambda\big|\bar{r}_t - r_\gamma(\underbrace{\sigma_\alpha(\mathbf{I}_t)}_{z_t},u_t)\big| + (1-\lambda)\big\|\underbrace{\sigma_\alpha(\mathbf{I}_{t+1})}_{z_{t+1}} - \psi_\beta(\underbrace{\sigma_\alpha(\mathbf{I}_t)}_{z_t},u_t)\big\|
Now, minimize the loss, from samples (lambda=0.9)
With the original reward being, given a Lyapunov function,
\bar{r}(\mathbf{I}_t,u_t)=V(\mathbf{I}_{t+1})-V(\mathbf{I}_t)=V(f(\mathbf{I}_t,u_t))-V(\mathbf{I}_t)
(\mathbf{I}_t,\mathbf{I}_{t+1},u_t)
Parametrizations
Which class of functions to use for these?
z_t = \sigma_\alpha(\mathbf{I}_t)
r_t = r_\gamma(z_t,a_t)
z_{t+1} = \psi_\beta(z_t,a_t)
Linear
MLP
Convolutional
Linear
MLP
Quadratic
Linear
MLP
Need to solidify notion of "models that are better for control techniques."
- Linear dynamics + Quadratic Objective: can solve the optimal control problem efficiently and optimally, but the problem itself is approximate due to limited model capacity.
- Fully MLP: cannot solve the optimal control problem (NP-hard), but it tackles a more "exact" problem due to better model capacity.
- Which choice of functions (especially dynamics and reward) gives necessary conditions for the optimal control problem to be "gradient dominant" for online gradient descent? what about dynamic programming?
- How do we encode in robustness? (you don't get this for free by asking for optimality)
Data Collection
Now we need to collect data of the form:
(\mathbf{I}_t,\mathbf{I}_{t+1},u_t)
After refactoring the simulator code (it was badly written......), collected 20,000 samples according to the following distribution.
- Collect samples along a trajectory according to a random uniform policy.
- 20 trajectories in, reset the sim to initial.
- After 1000 samples, decrease number of onions.
Training
MLP Comp + MLP Dynamics
MLP Comp + Linear Dynamics
Conv Comp + MLP Dynamics
Conv Comp + Linear Dynamics
Linear Comp + Linear Dynamics
Linear Comp + MLP Dynamics
Model capacity seems very influenced by expressiveness of compression, and almost unaffected by expressiveness of dynamics.
Testing (Simulation error)
Best criteria is to look at simulation error of how good the reward trajectory is predicted.
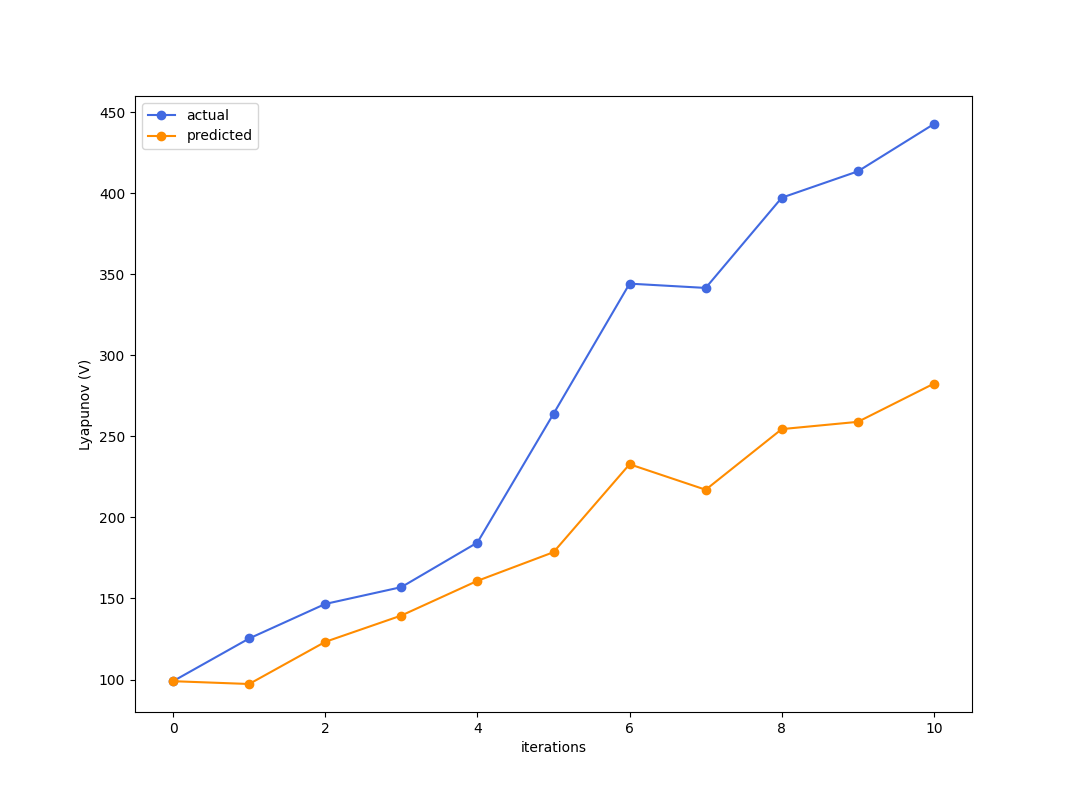
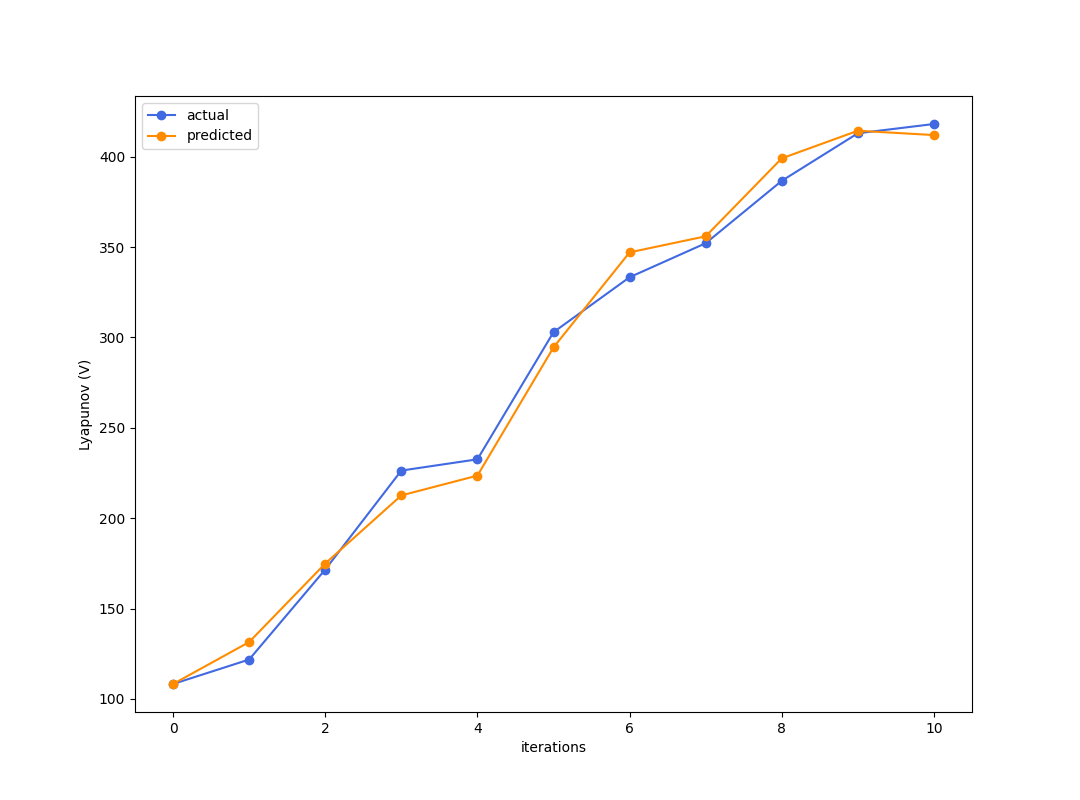
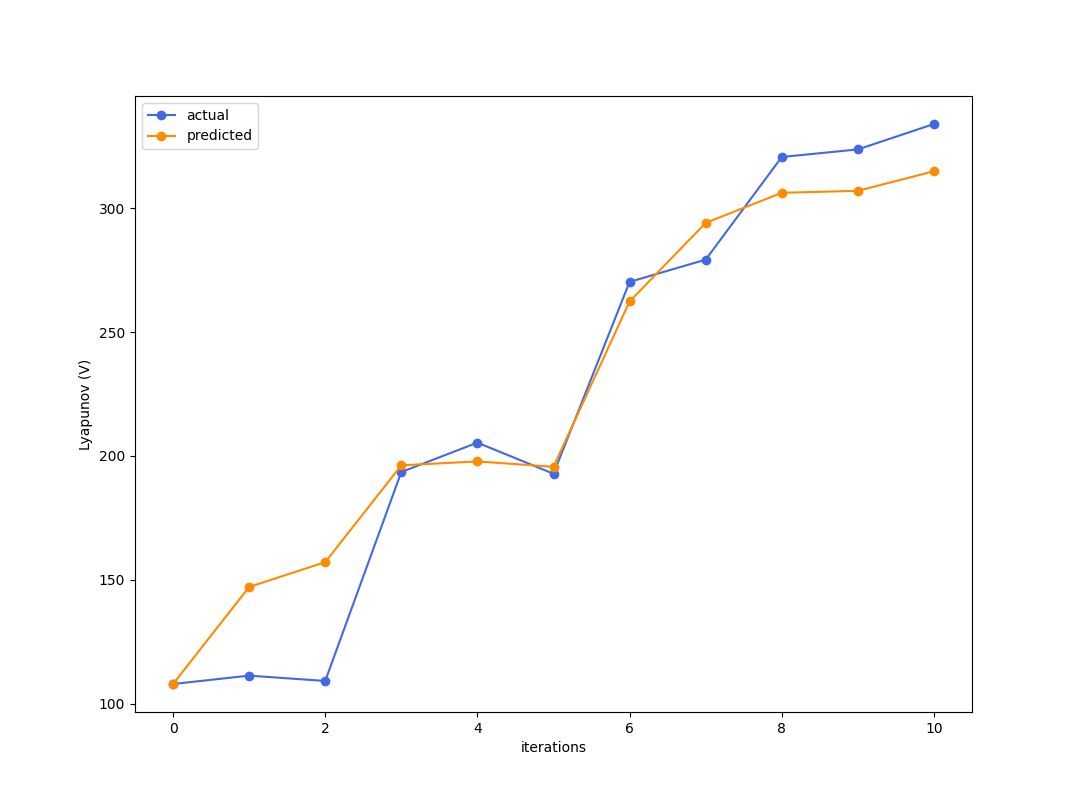
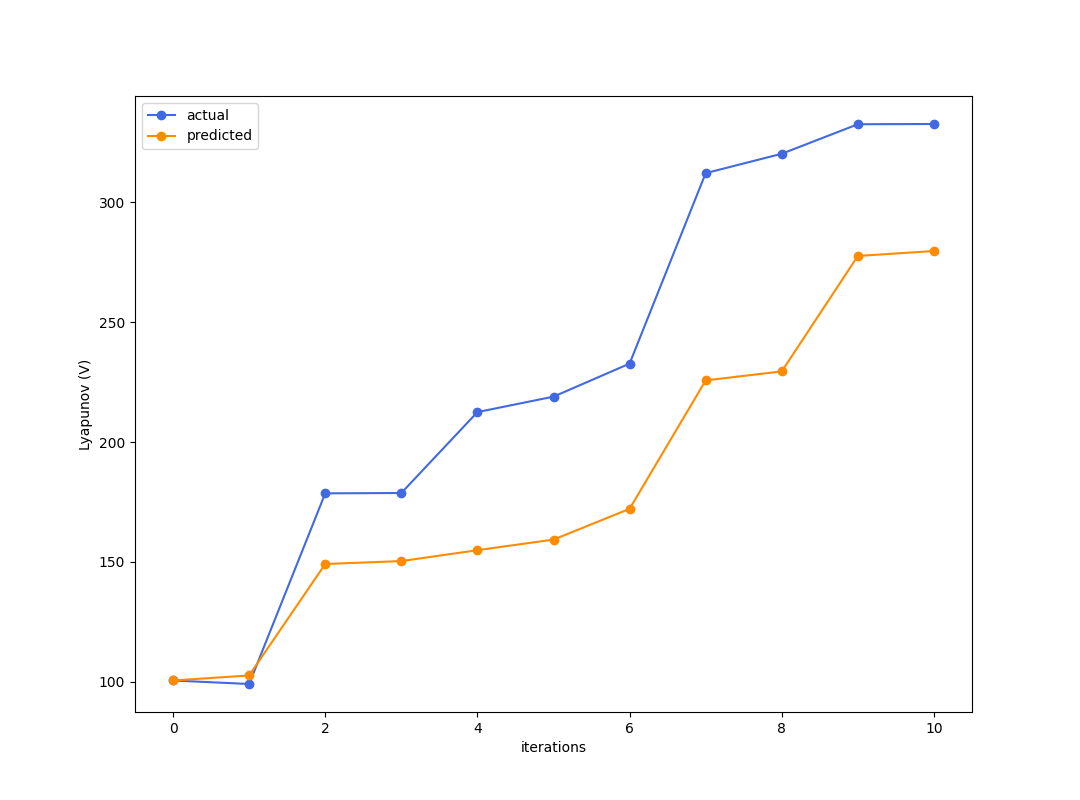
Enough to get kind of excited....?
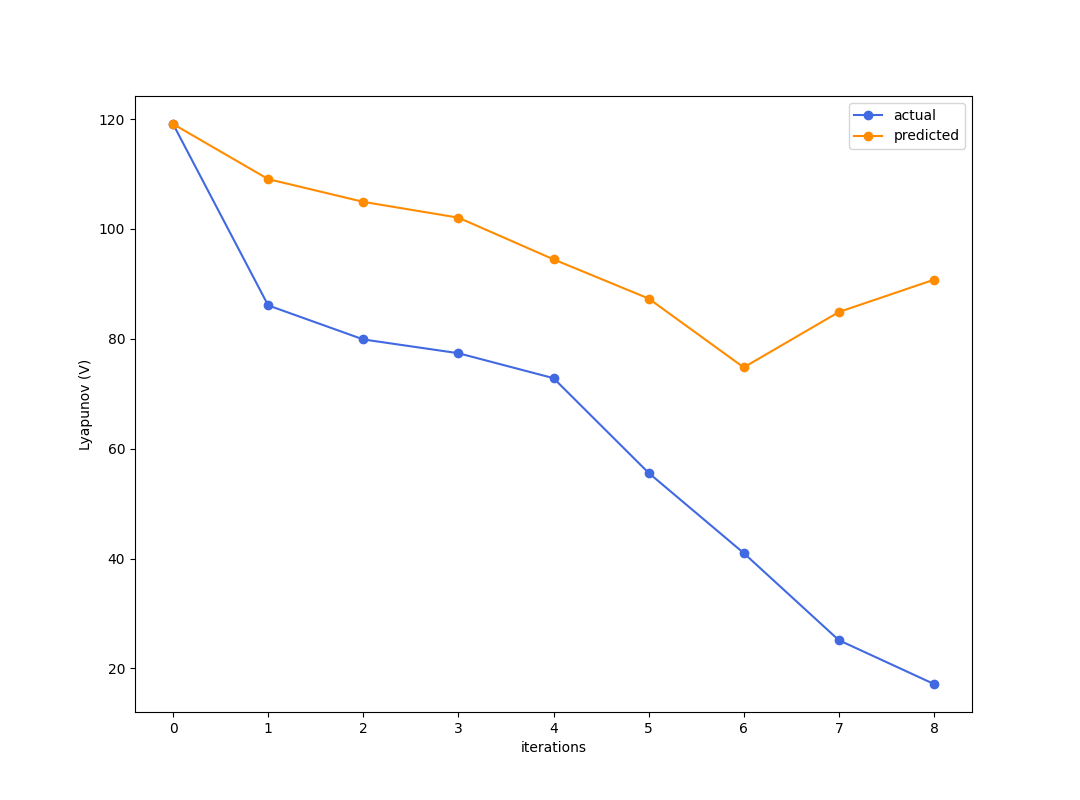
Testing (Simulation error)
Once you hand-code some optimal policy, the prediction isn't too great and we might be seeing a typical case of distribution shift.
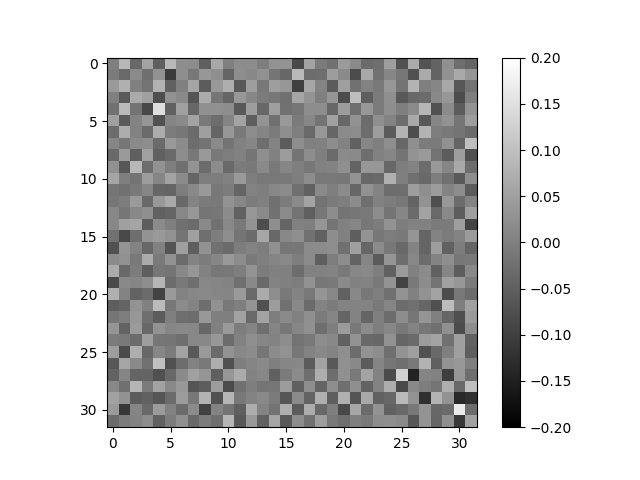
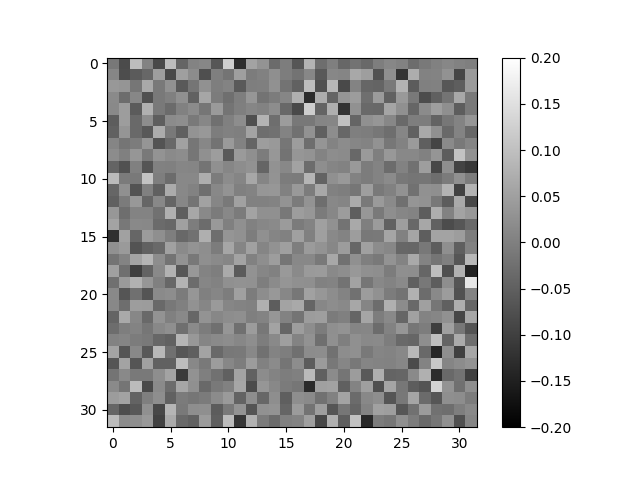
Visualizing Information States
Assuming a linear map (without bias) from image to AIS, one can visualize each row of the map as a "kernel". But this isn't too successful.
The Arrow Test
Randomly sample actions, only visualize those estimated to have negative reward.
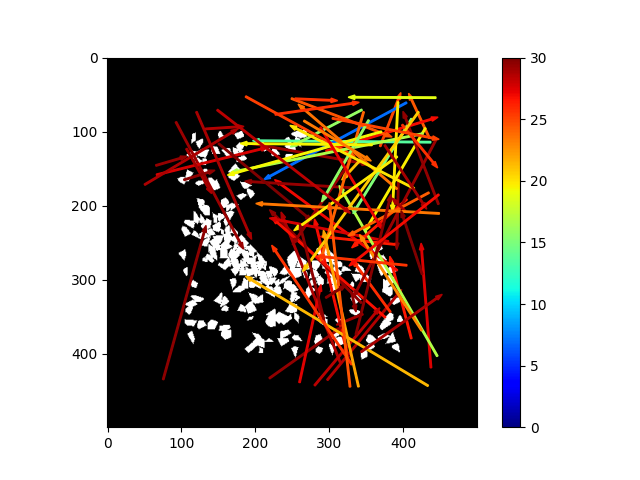
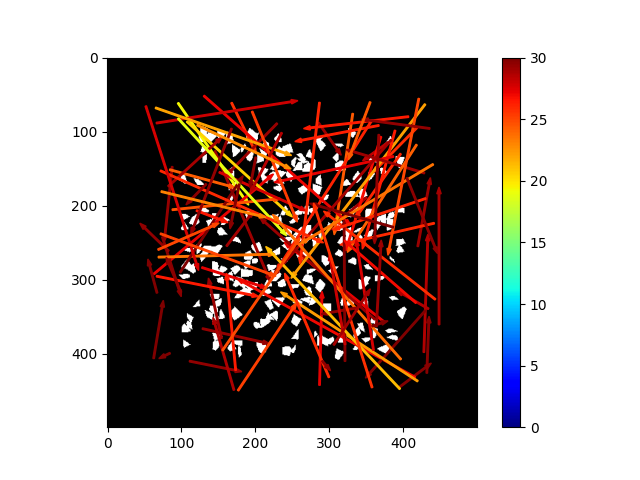
It's doing something!
Trying out Closed-loop Controllers
u^*_t=\pi(\mathbf{I_t})=\text{argmin } r(\sigma(\mathbf{I_t}),u_t)
Recall definition of our reward....
\begin{aligned}
\bar{r}(\mathbf{I}_t,u_t) &= V(\mathbf{I}_{t+1}) - V(\mathbf{I}_t) \\
&= V(f(\mathbf{I}_t,u_t)) - V(\mathbf{I}_t)
\end{aligned}
\begin{aligned}
r(z_t,u_t) = r(\sigma(\mathbf{I}_t), u_t) \approx \bar{r}(\mathbf{I}_t,u_t)
\end{aligned}
Random CLF
u_t \sim \mathcal{U}\big[\{u_t | r(\sigma(\mathbf{I}_t),u_t) < 0\}\big]
(NOTE: none of these controllers actually use the dynamics function. Not necessary for one-step lookup as this is encoded in the reward already. )
Greedy Descent
To test out the models in closed-loop, let's propose two simple controllers.
Greedy Descent
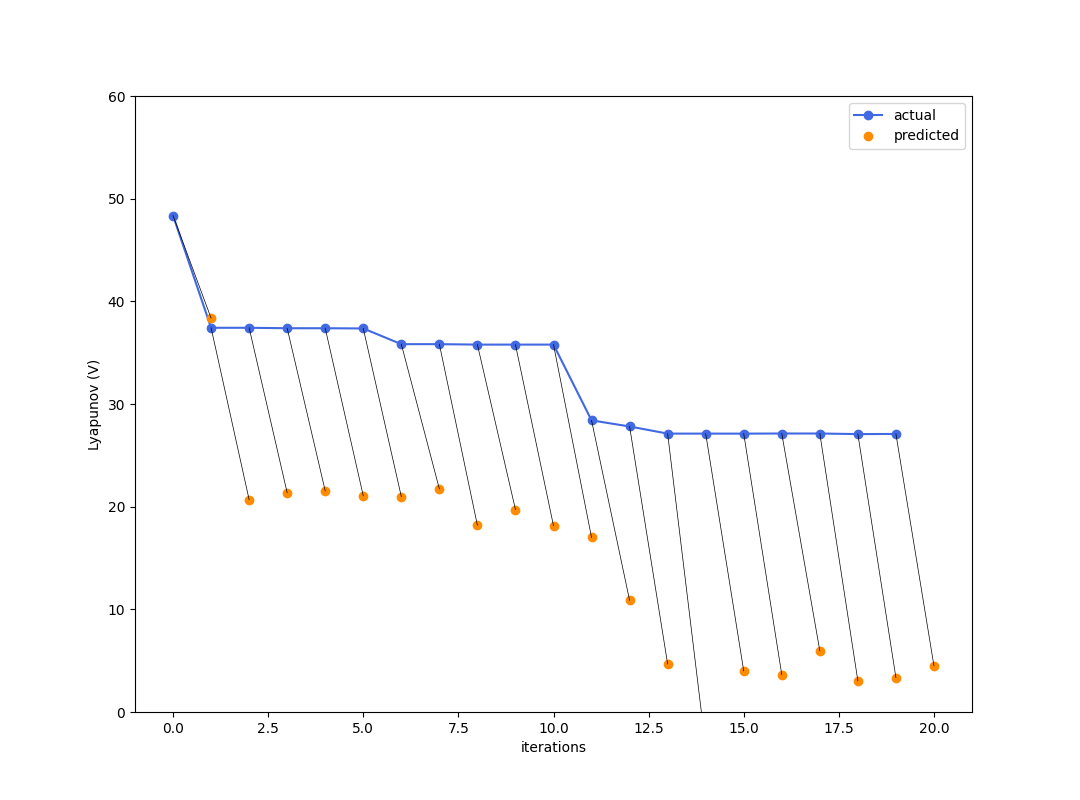
Even here, acting optimally (in a greedy sense) hurts you because you trusted your model too much.
Random CLF
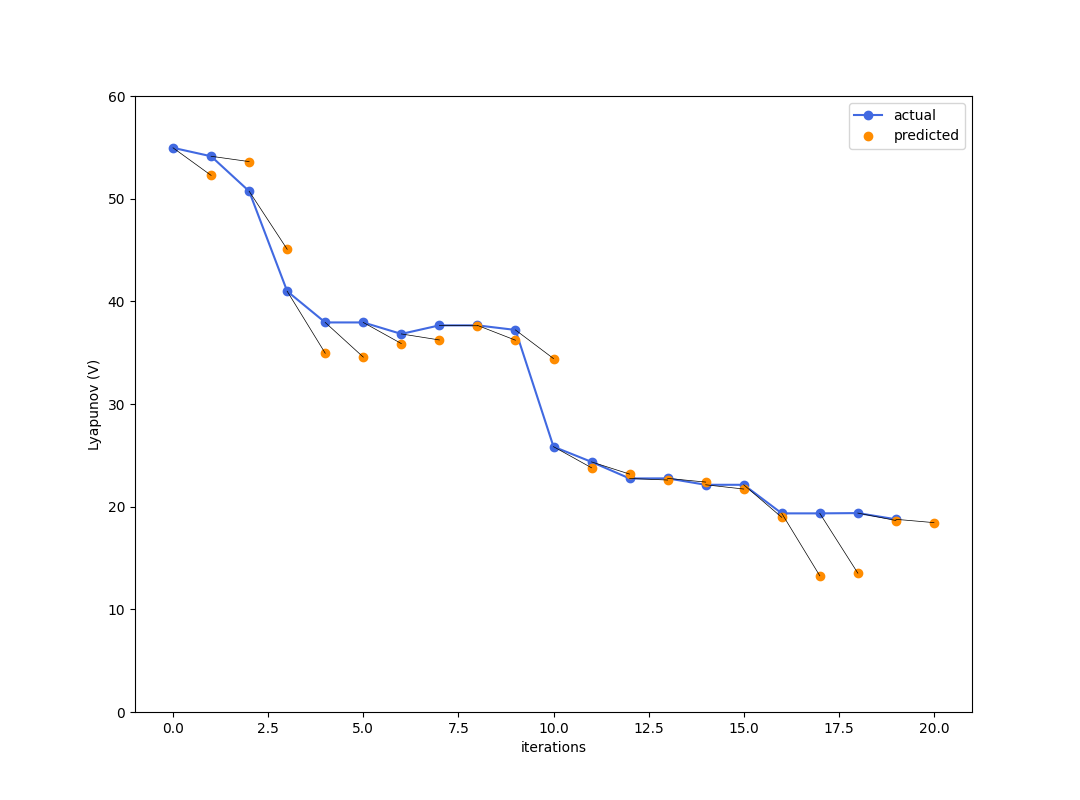
Here, you are at least getting somewhere by introducing randomness. But not good enough yet.
Addressing the Failure
1. Our model is not accurate enough due to distribution shift.
2. Controller is not robust enough to model uncertainty.
Simple solution to the first one is to run on-policy RL with the current model.
1. Run policy online to collect some SARS samples. The policy used was a slightly different version of epsilon-greedy.
2. Update parameters of AIS using these SARS samples.
3. Keep iterating with a mixed batch of offline samples (the original samples that were used to train random policy) and online samples (the new SARS samples)
On-policy RL
Unsure if the actual performance improved....
Prediction Accuracy
But prediction certainly seems better.
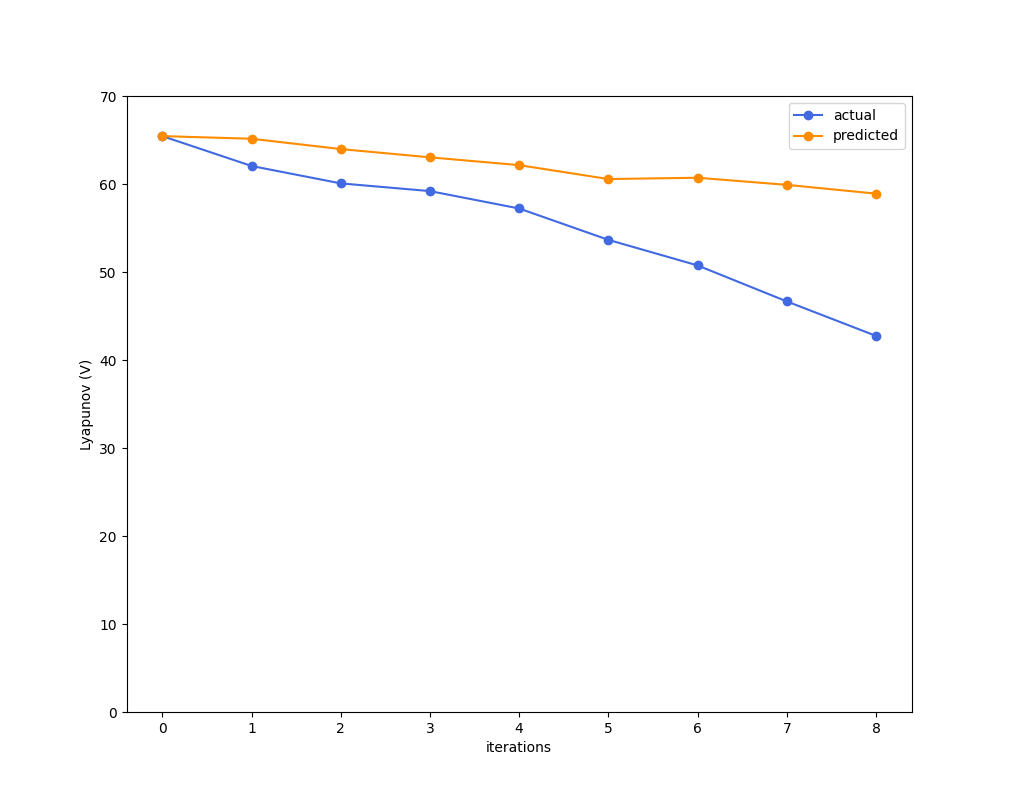
Model Accuracy doesn't solve it.
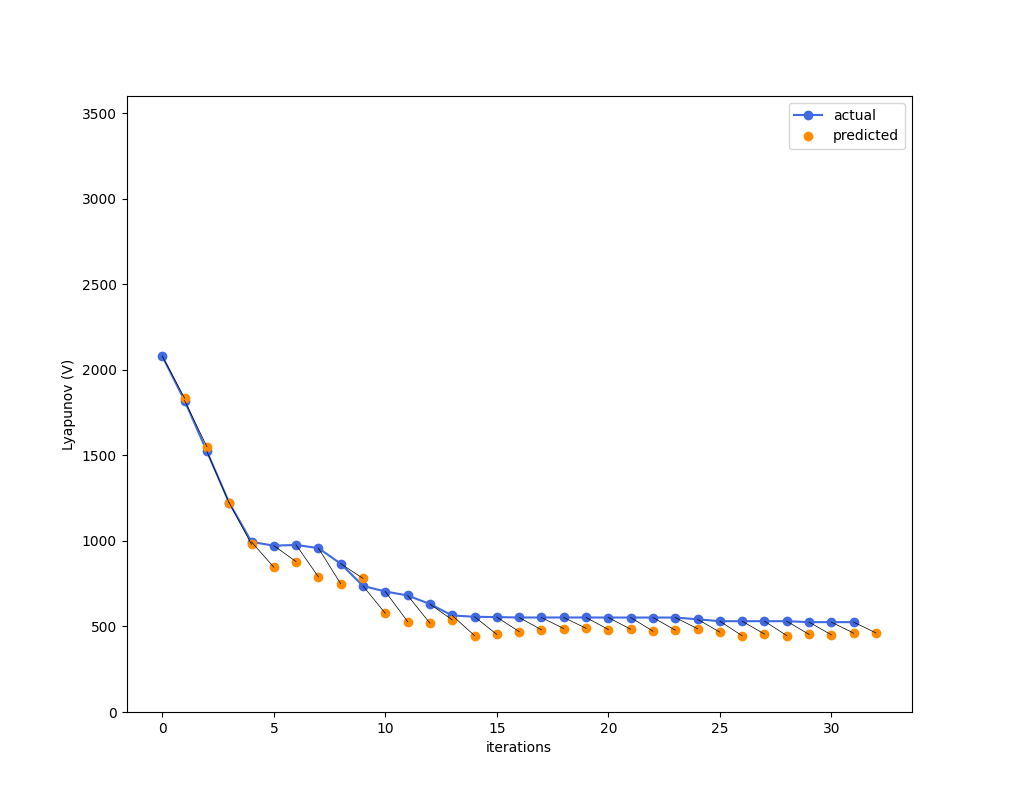
Steepest descent
Model Accuracy doesn't solve it.
random clf
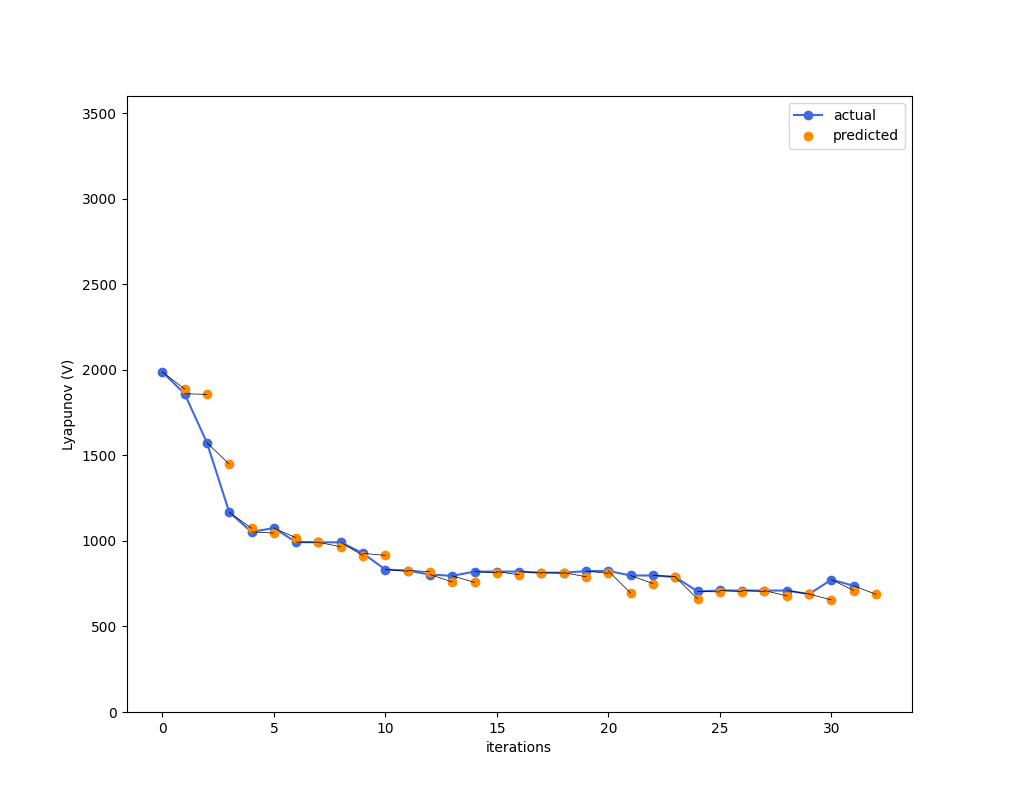
Model Accuracy doesn't solve it.
Sampling-based MPC
(3 timesteps)
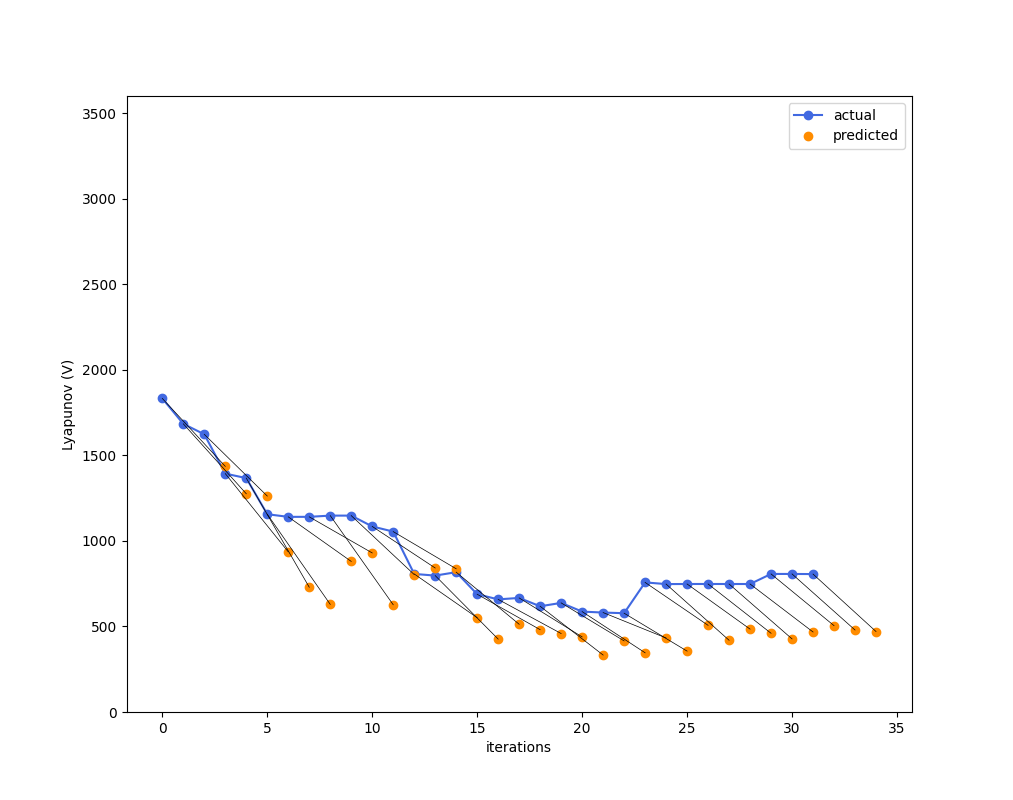
Big Lessons & Plans
Asking for optimality HURTS when your model is uncertain because it will exploit uncertainty, and we have to face the fact that the model will never be perfect. So....
Important to do the following things:
1. Characterize uncertainty on reward prediction.
2. Use this uncertainty to develop a robust (and optimal) policy.
Big Question:
Is there a class of models for dynamics / reward that permits easy synthesis of robust controllers....?
Next Question
What are models that are better for control?
Onion Problem Updates
By Terry Suh
