What Model of Contact Dynamics Do Deep Networks Learn?
Terry
The Big Questions / Positioning
-
Is there something about learning dynamics that makes planning easier?
-
How do deep networks deal with lack of data within the penetration regime?
-
Establish equivalence between MBRL and randomized smoothing? (complete the story since randomized smoothing equiv. to analytic smoothing).
-
Previous works (ContactNets, Alberto's group) have focused on accuracy of dynamics, but we really care about how good the model is for purposes of planning. Lessons from smoothing tell us that smooth models ARE in fact better for planning. So are deep models learning these things?
-
Workshop double submission?
Analyzing Asymptotics
Taking a step back, it's amazing that we can answer the following question: if we had infinite data, infinite capacity, what function are we asking the network to learn?
Take an example of standard MSE Loss.
\min_g \mathbb{E}_{x,u\sim \rho}[\|g(x,u) - f(x,u)\|^2_2]
If the distribution of data has infinite support, then
g^* = f
Data Augmentation Leads to Smoothness
Often, we only have finite data. Common trick in MBRL is to do data augmentation to produce a more robust model to the training data.
Consider 'Yunzhu's trick' of adding noise to the training data. (Keypoints into the Future)
Motivation: even if we deviate away from the data, we want to stabilize to points we've seen before.
x_t
u_t
x_{t+1}
x_t+w_t
Yunzhu's picture.
Full picture.
x_{t+1}
x_t
u_t
x_{t+1}
x_t+w_t
x_{t+1}
x_t
u_t
x_{t+1}
Data Augmentation Leads to Smoothness
\min_g \mathbb{E}_{w,v\sim \mu}\bigg[\mathbb{E}_{x,u\sim \rho}[\|g(x,u) - f(x+w,u+v)\|^2_2]\bigg]
Again in the limit of infinite data and infinite compute,
This scheme can be mathematically analyzed to give a more insightful form.
g^* = \mathbb{E}_{w,v\sim \mu}[f(x+w,u+v)]
Big Interesting Statement: By asking the model to be more robust (i.e. by doing data augmentation), we ask the model to learn a smooth, force-from-a-distance model of contact dynamics.
(Note that this really establishes equivalence of randomized smoothing and MBRL,
with the difference being offline vs. online).
No Data during Penetration
\text{dom}_x f = \{\phi(x) \geq 0\}
Something special about contact dynamics: we never get to see configurations that are in contact, such that
But rollouts of learned dynamics will, which leads to bad prediction.
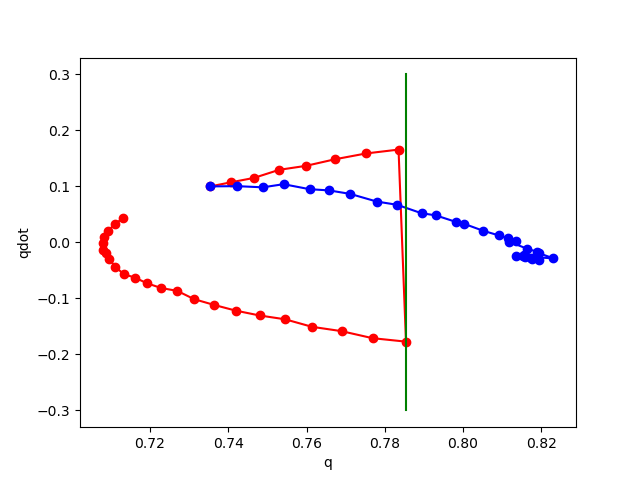
Phase plot of pendulum with impact on wall.
Red: rollout of true dynamics.
Blue: rollout of learned dynamics.
Right of Green: Penetration region.
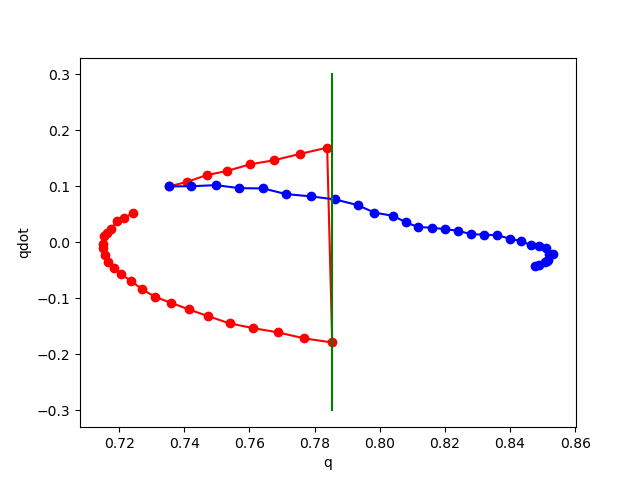
Data Augmentation
Here's what happens when we add noise at training time.
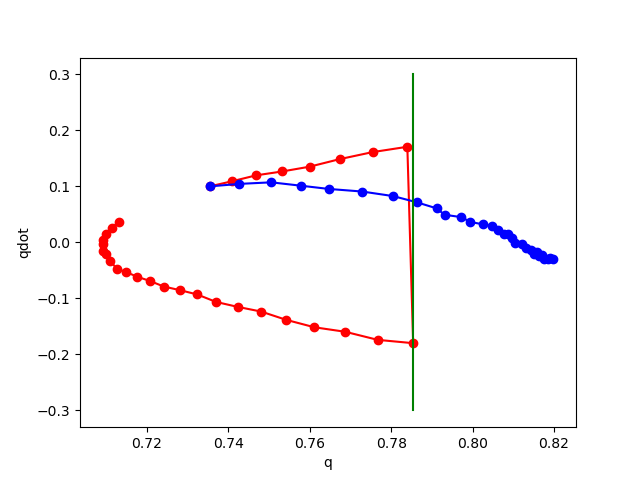
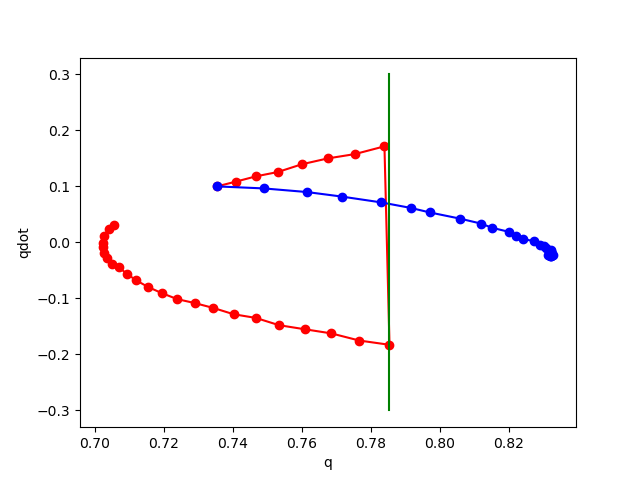
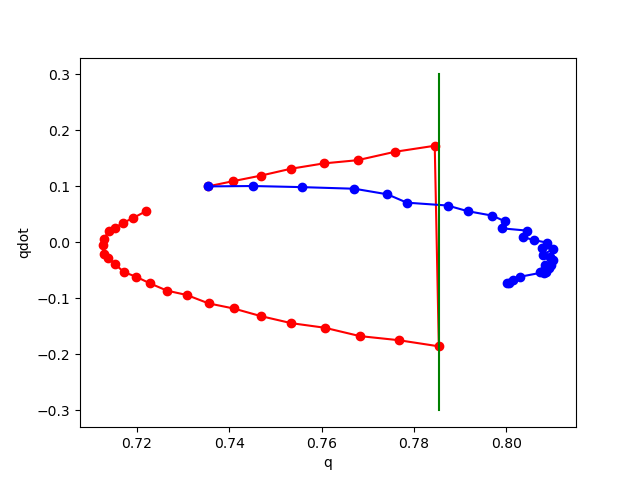
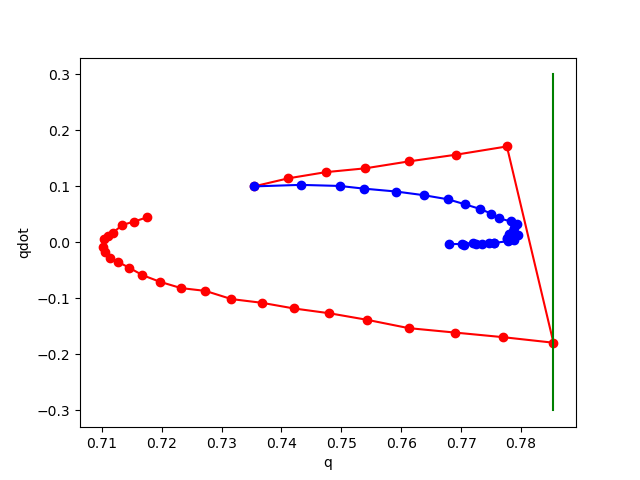
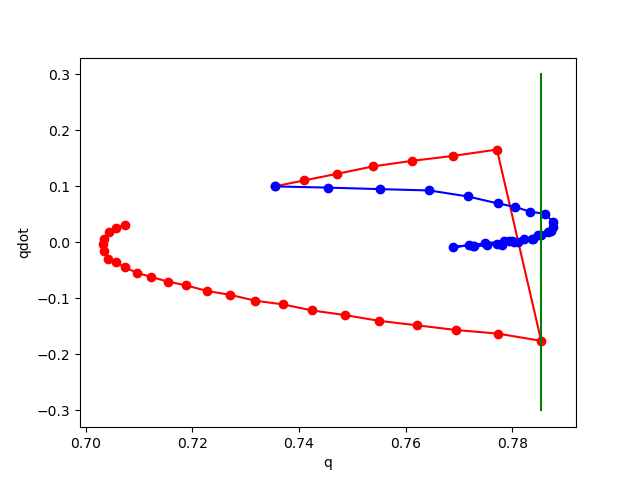
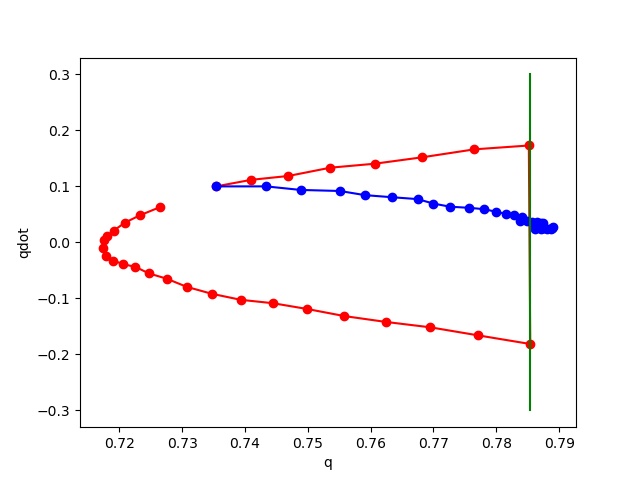
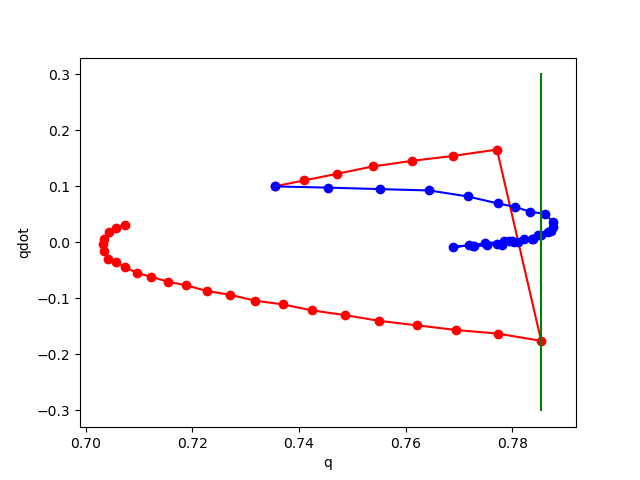
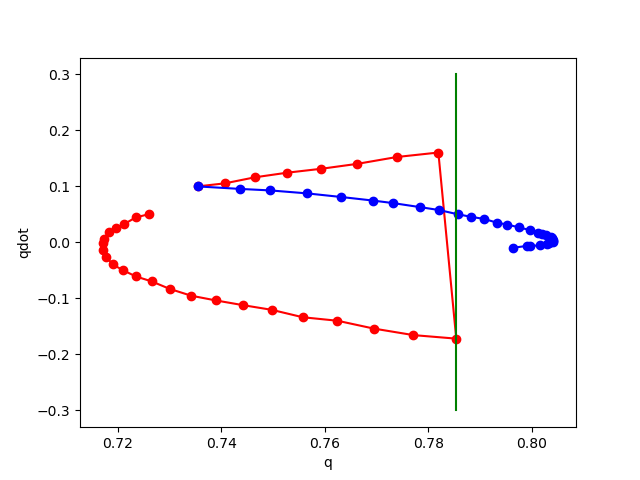
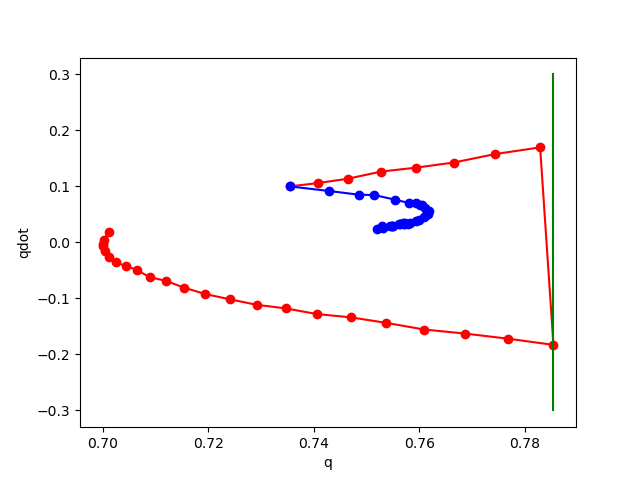
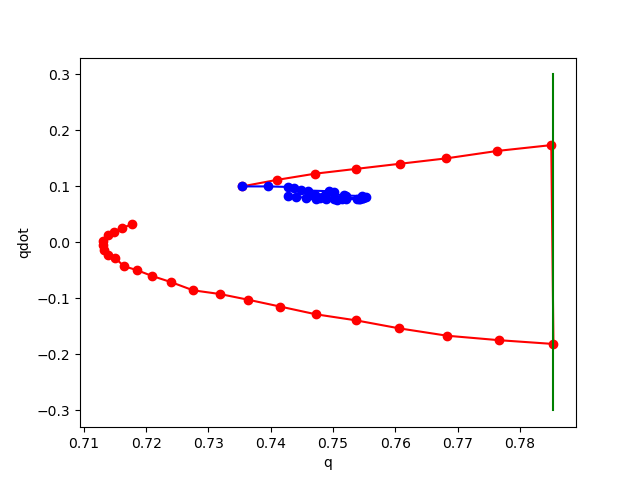
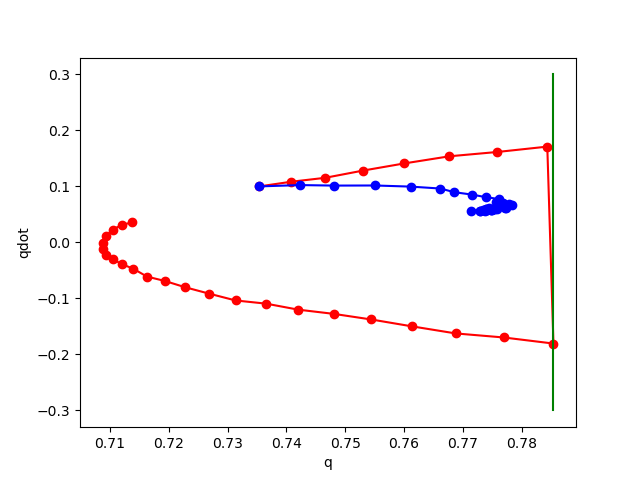
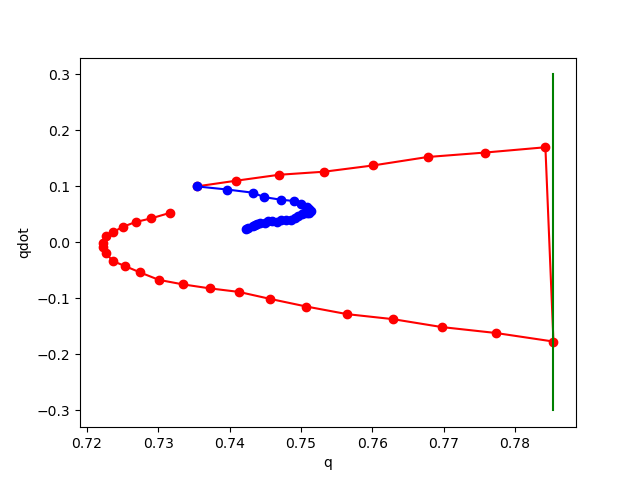
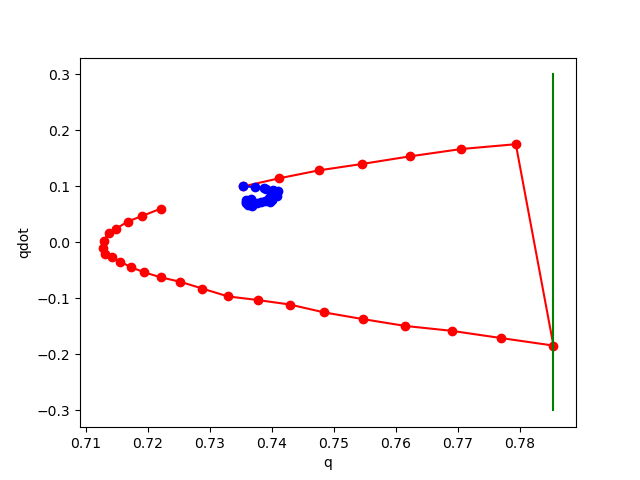
No noise
noise std 0.01
noise std 0.02
An interesting question:
g(x,u) = \begin{cases}
\mathbb{E}_{w,v}[f(x+w,u+v)] & x\in \text{dom}_x f \\
h(x,u) & \text{else }
\end{cases}
Asymptotically, the data augmentation scheme must be asking the network to learn the following function,
Which hypothetically has the following properties:
1. It's okay to go into penetration during rollouts, because you will be pushed away.
2. You get to apply force from a distance.
The next big question.
Does this give you models that are not necessarily "accurate", but better for planning?
- does data augmentation give you better gradients? (MPPI vs. Gradient-based)
- how does the injected variance affect performance of different planning methods?
- how does the injected variance affect prediction error on the test set?
DeepContactDynamics
By Terry Suh
