Quasi-resonant collisions:
a kinetic setting for bi-temperature modeling
WASCOM
June 12, 2025
\(\phantom{x}^*\)CERMICS, École des Ponts, France
\underline{\text{T. Borsoni}}^*, \text{ L. Boudin, J. Mathiaud, F. Salvarani}
a peculiar polyatomic Boltzmann model
(\partial_t + v \cdot \nabla_x) f_{t,x}(v,I) = Q(f_{t,x})(v,I)
\(f \equiv f_{t,x}(v, I)\) density of molecules
+
x
the polyatomic Boltzmann equation
with internal energy levels description
v
Boltzmann equation:
v,I
v_*,I_*
v',I'
v'_*,I'_*
\begin{align*}
v+v_*&=v'+v'_* \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &= \frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_* \\
\end{align*}
Conservation laws
I
Collision operator:
\newcommand{\dd}{\mathrm{d}}
Q(f)(v,I) = \iint_{\R^3 \times \mathbb{S}^2} \iiint_{(\R_+)^3}
[f(v',I') f(v'_*,I'_*) -
f(v,I) f(v_*,I_*)] \;
\textcolor{green}{B} \; \dd \mu^{\otimes 3}(I_*,I',I'_*) \, \dd v_* \, \dd \sigma
\begin{align*}
v' = \frac{v+v_*}{2} + \sqrt{\Delta} \; \sigma, \\
v'_* = \frac{v+v_*}{2} - \sqrt{\Delta} \; \sigma,\\
\end{align*}
\newcommand{\Sb}{\mathbb{S}}
\sigma \in \Sb^2,
\begin{align*}\Delta := \frac14 |v-v_*|^2 + I + I_* - I' - I'_*
\end{align*}
\implies
(momentum)
(total energy)
\(\textcolor{green}{B \equiv B(v,v_*, \sigma,I,I_*, I',I'_*)} > 0 \iff \) the collision is possible \(\iff \Delta \geq 0\)
Collision kernel:
total energy
= \frac12|v|^2 + I
\partial_t f_{t}(v,I) = Q(f_{t})(v,I)
\(f \equiv f_{t}(v, I)\) density of molecules
the space-homogeneous
polyatomic Boltzmann equation
Boltzmann equation:
v,I
v_*,I_*
v',I'
v'_*,I'_*
\mathcal{M}(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T}} - \frac{I}{\textcolor{blue}{T}} \right)
Equilibrium distribution :
(momentum)
(total energy)
+
x
v
I
total energy
= \frac12|v|^2 + I
\begin{align*}
v+v_*&=v'+v'_* \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &= \frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_* \\
\end{align*}
Conservation laws
quasi-resonant collisions
\(\bullet\) What and why
\(\bullet\) How
\(\bullet\) Characteristics
Conservation laws
(momentum)
(internal energy)
(kinetic energy)
(total energy)
separately
kinetic + internal
exactly
resonant
collision
approximately
quasi-resonant
collision
Observed experimentally, e.g. \(\mathrm{CO}_2\)
Polyatomic Boltzmann model with a collision kernel with restricted support
to select only quasi-resonant collisions
- Boltzmann model where at "all times'' the solution is close to a two-temperature Maxwellian
- Derivation of an ODE system on the two temperatures: Landau-Teller relaxation system
explicit computations
unique feature of quasi-resonant
resonant
possible collisions
The model of resonant collisions as singular restriction of the support of the collision kernel \(B\)
\mathcal{M}(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)
Equilibrium:
two distinct temperatures
v,I
v_*,I_*
v',I'
v'_*,I'_*
\begin{align*}
I+I_* &= I' + I'_*,
\end{align*}
\begin{align*}
v+v_*&=v'+v'_*, \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*,
\end{align*}
(separation kinetic/internal)
kinetic
temperature
internal
temperature
\(\equiv\) support of the collision kernel \(B\)
\varepsilon
Our model for quasi-resonant collisions as tight restriction of the support OF THE COLLISION KERNEL \(B\)
v,I
v_*,I_*
v',I'
v'_*,I'_*
\mathcal{M}(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T}} - \frac{I}{\textcolor{blue}{T}} \right)
Equilibrium:
two distinct temperatures
same
temperature
one single temperature
\begin{align*}
I+I_* &\approx I' + I'_*,
\end{align*}
\begin{align*}
v+v_*&=v'+v'_*, \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*,
\end{align*}
quasi-resonant
possible collisions
\(\equiv\) support of the collision kernel \(B\)
Expected behaviour of the quasi-resonant dynamics
time
short time
long time
relaxation towards a
two-temperature
Maxwellian
\propto \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)
\partial_t f_{t} = Q_\varepsilon(f_{t})
- the solution (almost) remains of two-temperature Mawellian shape
- the kinetic (\(\textcolor{blue}{T_k}\)) and internal (\(\textcolor{blue}{T_i}\)) temperatures relax towards each other, (almost) following Landau-Teller ODE system \((LT)\)
(T_i(t), \, T_k(t)) \approx (\overline{T}_i(t), \, \overline{T}_k(t))
\newcommand{\dd}{\mathrm{d}}
\newcommand{\e}{\varepsilon}
\begin{equation*}
\begin{cases}
&\overline{T}_k'(t) = \e^2 \, P[\overline{T}_k, \overline{T}_i] (\overline{T}_i - \overline{T}_k),\\
&\overline{T}_i'(t) = \e^2 \; \widetilde{P}[\overline{T}_k, \overline{T}_i] (\overline{T}_k - \overline{T}_i),
\end{cases} \quad {\small(\overline{T}_i(0),\overline{T}_k(0)) = (T_i(0),T_k(0))}.
\end{equation*}
(LT)
(1)
(2)
(2)
Long-time behaviour: Landau-Teller relaxation of (\(\textcolor{blue}{T_k}\)) and (\(\textcolor{blue}{T_i}\)) towards each other
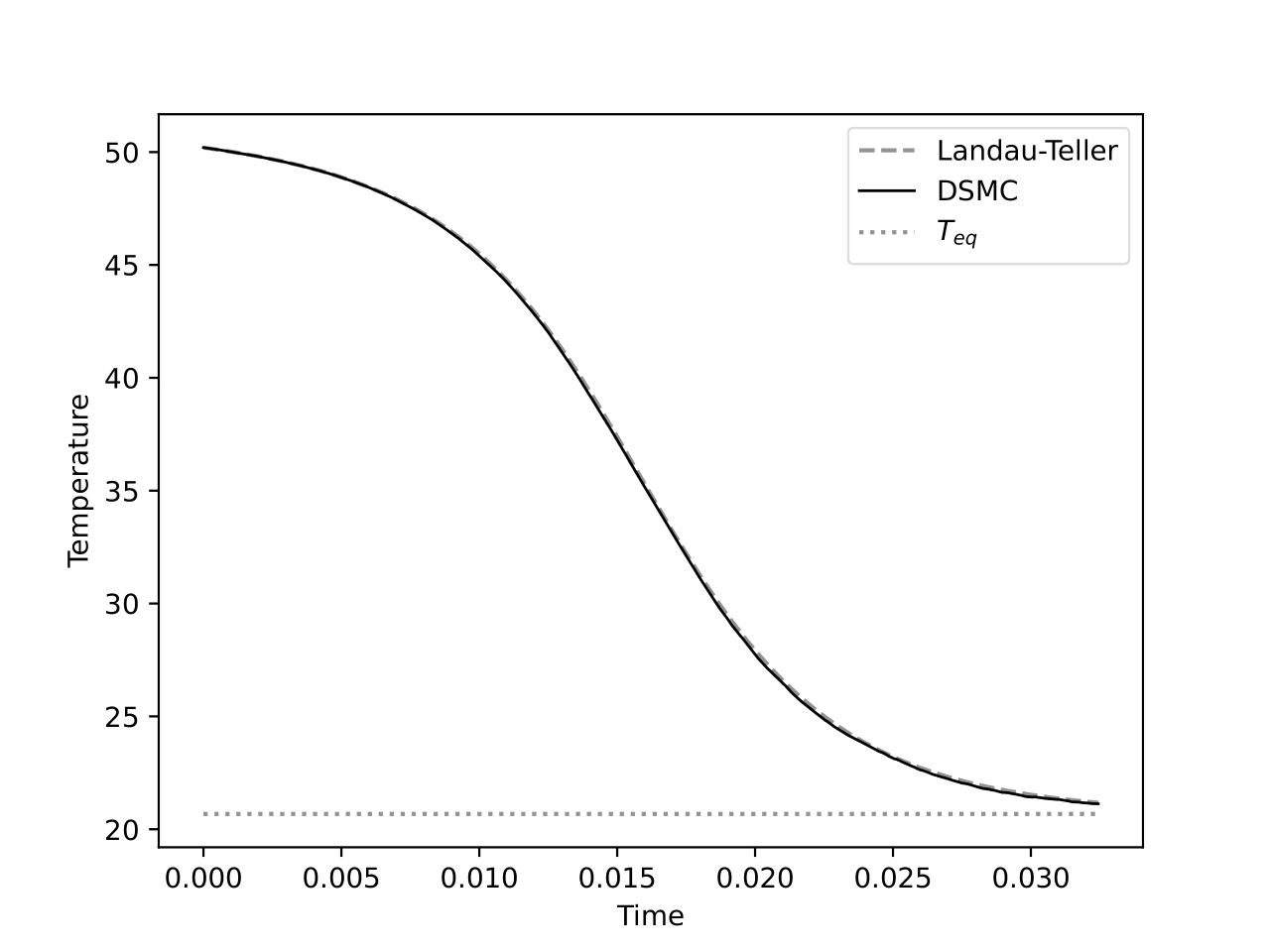
Numerical experiment
\bullet \; T_k^0 = 1, \quad T_i^0 = 50, \quad T_{eq} = 20.6,
- Simulation of quasi-resonant Boltzmann with DSMC
- Solving of Landau-Teller ODE system
\partial_t f_{t} = Q_\varepsilon(f_{t})
\newcommand{\dd}{\mathrm{d}}
\newcommand{\e}{\varepsilon}
\begin{equation*}
\begin{cases}
&\overline{T}_k'(t) = \e^2 \; P[\overline{T}_k, \overline{T}_i] (\overline{T}_i - \overline{T}_k),\\
&\overline{T}_i'(t) = \e^2 \; \widetilde{P}[\overline{T}_k, \overline{T}_i] (\overline{T}_k - \overline{T}_i),
\end{cases} \quad {\small(\overline{T}_i(0),\overline{T}_k(0)) = (T_i(0),T_k(0))}.
\end{equation*}
- Comparison of \(T_i\) and \(\overline{T}_i\) to check if indeed
(T_i(t), \, T_k(t)) \approx (\overline{T}_i(t), \, \overline{T}_k(t))
get \(T_k\) and \(T_i\)
Parameters
\varepsilon = 10^{-1},
\mathrm{d} \mu(I) = \mathrm{d} I,
\textcolor{black}{\bullet \; B_\varepsilon(v,v_*,\sigma,I,I_*,I',I'_*) = \frac{\mathbf{1}_{[I'+I'_* \leqslant E]}}{2 \pi}
\times \frac{E^3}{E_i \, E_i' \, \sqrt{E_k}} \times }
\frac{\mathbf{1}_{[|\log(E_k/E_i) - \log(E_k' / E_i')| \leqslant \varepsilon]}}{\varepsilon}\textcolor{black}{,}
E_k = \frac14|v-v_*|^2, \quad E_i = I+I_*, \quad E_k' = \frac14|v'-v'_*|^2, \quad E'_i = I'+I'_*, \quad E = E_k + E_i = E_k'+ E_i'.
N_{\mathrm{DSMC}} = 10^5.
Thank you for your attention!
TB, Boudin, Mathiaud, Salvarani: A kinetic model for polyatomic gas with quasi-resonant collisions leading to bi-temperature relaxation processes, preprint (2025).
- Rigorous proof that \(f_t\) close to two-temperature maxwellian at all times
- Obtention of Landau-Teller-type equation for general kernels
Perspectives
Presentation Wascom
By Thomas Borsoni
