Contributions around the Boltzmann equation and some of its variants
Thomas Borsoni
supervised by
Laurent Boudin & Laurent Desvillettes
1/27
Mesoscopic
Microscopic
Macroscopic
(statistical)
description of gases
2/27
Density of molecules: \(f \equiv f_{t,x}(v)\)
The original Boltzmann equation
Statistical description of a monoatomic gas
[A. Greg: Kinetic theory of gases, wikipedia.]
\partial_t f_{t,x}(v) + v \cdot \nabla_x f_{t,x}(v) = Q(f_{t,x})(v)
v
x
+
advection
collisions
(e.g. \(\mathrm{Ar} \) )
3.1/27
[A. Greg: Kinetic theory of gases, wikipedia.]
Focus on collisions
the Homogeneous Boltzmann equation
Density of molecules: \(f_t(v)\)
\partial_t f_t(v) = Q(f_t)(v)
\(x \)
advection
\(+ \, v \cdot \nabla_x f\)
3.2/27
the collision operator
v
v_*
v'
v'_*
x
\begin{align*}
v' = \frac{v+v_*}{2} + \frac{|v-v_*|}{2} \sigma \\
v'_* = \frac{v+v_*}{2} - \frac{|v-v_*|}{2} \sigma\\
\end{align*}
\newcommand{\Sb}{\mathbb{S}}
\sigma \in \Sb^2
\newcommand{\dd}{\mathrm{d}}
\textcolor{black}{Q(f)(v) = }\iint_{\R^3 \times \mathbb{S}^2} \textcolor{black}{\big( f(v') f(v'_*) - f(v) f(v_*) \big)} \, B(v,v_*,\sigma)
\, \dd \sigma \, \dd v_*
\begin{align*}
v+v_*&=v'+v'_* \\
|v|^2 + |v_*|^2 &= |v'|^2 + |v'_*|^2 \\
\end{align*}
Conservation of
mass, momentum, energy
\implies
3.3/27
Entropy and equilibrium
v
f^{\rm in}
f_t \underset{t \to \infty}{\longrightarrow} c \, e^{-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} }
v
\textcolor{blue}{u}
The Boltzmann entropy:
\newcommand{\dd}{\mathrm{d}}
H (f) := \int_{\R^3} (f \log f - f)(v) \, \dd v
2. \(D(g) = 0 \iff g =M \) a Maxwellian:
characterization of equilibria
M(v) \propto \exp\left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} \right)
\partial_t f_t(v) = Q(f_t)(v), \\
f_0 = f^{\rm in},
Boltzmann's H Theorem
1. If \(f \equiv f_t(v)\) solves
\(2^{nd}\) principle of thermodynamics
\((HB)\)
then
\newcommand{\dd}{\mathrm{d}}
\frac{\dd}{\dd t}H (f_t) =: - D(f_t) \leq 0.
Illustration of the expected behaviour
4/27
\textcolor{blue}{\sqrt{T}}
original
monoatomic molecules
polyatomic
molecules
Part \(\mathrm{I}.1\)
Part \(\mathrm{ I}.2\)
polyatomic molecules
resonant collisions
fermions
Part \(\mathrm{II}\)
e.g. \(\mathrm{Ar}\)
e.g. \(\mathrm{N_2}\)
e.g. \(\mathrm{CO_2}\)
e.g. \(\mathrm{e^-}\)
5/27
Contributions
\(\mathrm{I}.1\). Boltzmann equation for polyatomic gases
\(\mathrm{I}.2\). Boltzmann equation for polyatomic gases with (quasi-)resonant collisions
\(\mathrm{II}\). Boltzmann-Fermi-Dirac equation
Bonus: general weighted \(L^p\) Csiszar-Kullback-Pinsker inequalities
- General modelling framework for single gas & mixtures with chemical reactions
- Compactness result in resonant setting
- Develop & study quasi-resonant Boltzmann model
- Entropy/entropy production inequalities via a transfer method
- Relaxation to equilibrium with explicit rate
w/ Lods
w/ Bisi, Groppi
w/ Boudin, Mathiaud, Salvarani
[1,2]
[4]
[5]
[3]
[1] TB, M. Bisi, M. Groppi, Commun. Math. Phys., 2022.
[3] TB, L. Boudin, F. Salvarani, J. Mat. Anal. Appl., 2023.
[4] TB, J. Stat. Phys., 2024.
[2] M. Bisi, TB, M. Groppi, Kinet. Relat. Models, 2024.
[5] TB, B. Lods, preprint, 2024.
6/27
w/ Bisi, Groppi
[1] TB, M. Bisi, M. Groppi: "A general framework for the kinetic modelling of polyatomic gases", Commun. Math. Phys., 2022.
[2] M. Bisi, TB, M. Groppi: "An internal state kinetic model for chemically reacting mixtures of monatomic and polyatomic gases", Kinet. Relat. Models, 2024.
Part \(\mathrm{I}\). Boltzmann equation for polyatomic gases
[1]
[3] TB, L. Boudin, F. Salvarani: "Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions", J. Mat. Anal. Appl., 2023.
w/ Boudin, Mathiaud, Salvarani
[3]
\(\mathrm{I}.1\). Boltzmann equation for polyatomic gases
\(\mathrm{I}.2\). Boltzmann equation for polyatomic gases with (quasi-)resonant collisions
General modelling framework for single gas & mixtures with chemical reactions
[2]
Compactness result in resonant setting
Develop & study quasi-resonant Boltzmann model
7/27
\(\R^3 \times \textcolor{orange}{\R^3 \times \N \times \N \times \N}\)
\(\mathrm{I}.1\). internal structure of polyatomic molecules: rotation, vibration,...
v
\omega
n_1
n_2
n_3
(v,\textcolor{orange}{\omega, n_1, n_2, n_3})
\in
state of the molecule
space of states
energy of the molecule
\frac12 |v|^2 + \textcolor{orange}{\frac12 |\omega|^2 + n_1 E_1 + n_2 E_2 + n_3 E_3 + E_{pot}}
An example:
8.1/27
\(\R^3 \times \textcolor{orange}{\mathcal{E}}\)
\(\mathrm{I}.1\). internal structure of polyatomic molecules: general setting
v
(v,\textcolor{orange}{\zeta})
\in
state of the molecule
space of states
energy of the molecule
\frac12 |v|^2 + \textcolor{orange}{\varepsilon(\zeta)}
\newcommand{\E}{\mathcal{E}}
\zeta
\((\mathcal{E}, \mu)\)
\(\varepsilon : \mathcal{E} \to \R\)
2. Internal energy function:
existence of fundamental energy level
finiteness of the partition function
\(\bar{\varepsilon} := \varepsilon - \inf_{\mu} {\varepsilon}\) (\( : \mathcal{E} \to \R_+\))
1. Space of internal states:
[TB, Bisi, Groppi]
8.2/27
a parallel with probability theory
polyatomic internal structure
probability theory setting
\( (\Omega, \; \mathbb{P}) \) space of events
\( X : \Omega \to \R \) real random var.
\( (\mathcal{E}, \; \mu) \) space of internal states
\( \bar{\varepsilon} : \mathcal{E} \to \R_+ \) energy function
\( (\R, \, \mathbb{P}_X)\) space of outcomes
\( \mathbb{P}_X\) on \(\R\) law of \(X\)
\( (\R_+, \, \mu_{\bar{\varepsilon}}) \) space of energy levels
\( \mu_{\bar{\varepsilon}}\) on \(\R_+\) energy law
model with continuous energy levels
[Borgnakke, Larsen 75]
[Desvillettes 97]...
model with discrete energy levels
[Groppi, Spiga 99]
[Giovangigli 99]...
generalization
and pre-existing models
9/27
Resonant collision
conservations
\(\mathrm{I}.2\). A model for quasi-resonant collisions
v
\textcolor{olive}{I}
\mathcal{M}(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T_k}} - \frac{I}{\textcolor{blue}{T_i}} \right)
Equilibrium:
two temperatures
f \equiv f_{t,x}(v,I)
v,I
v_*,I_*
v',I'
v'_*,I'_*
\begin{align*}
I+I_* &= I' + I'_*
\end{align*}
\begin{align*}
v+v_*&=v'+v'_* \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*
\end{align*}
(separation kinetic/internal)
10.1/27
\lambda
Quasi-resonant collision
conservations
\(\mathrm{I}.2\). A model for quasi-resonant collisions
v,I
v_*,I_*
v',I'
v'_*,I'_*
\begin{align*}
v+v_*&=v'+v'_* \\
\frac12|v|^2 + I + \frac12|v_*|^2 + I_* &=\frac12|v'|^2 + I' + \frac12|v'_*|^2 + I'_*
\end{align*}
\begin{align*}
I+I_* &\approx I' + I'_*
\end{align*}
v
\textcolor{olive}{I}
f \equiv f_{t,x}(v,I)
Equilibrium:
\mathcal{M}(v,I) \propto\, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \textcolor{blue}{T}} - \frac{I}{\textcolor{blue}{T}} \right)
one temperature
(TB, Boudin, Mathiaud, Salvarani)
10.2/27
model for quasi-resonant collisions
\newcommand{\dd}{\mathrm{d}}
Q^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}}(f)(v,I) = \iint_{\R^3 \times \mathbb{S}^2} \iiint_{(\R_+)^3}
\big[ f' f'_* - f f_* \big] \times
B^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}} \times \varphi(I'_*) \, \dd I'_* \, \varphi(I') \, \dd I' \, \varphi(I_*) \, \dd I_* \, \dd v_* \, \dd \sigma
B^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}} = B^{\rm \textcolor{grey}{standard}} \times
c(\cdot) \frac{\mathbf{1_{\textcolor{red}{\mathcal{V}_{\lambda}}}}}{\textcolor{red}{\lambda}}
Family of collision kernels:
Family of collision operators:
\textcolor{black}{\forall} \lambda \textcolor{black}{> 0,}
Resonant asymptotics
Q^{\textcolor{red}{\text{quasi-res}}}_{\textcolor{red}{\lambda}}(f) \underset{\textcolor{red}{\lambda} \to 0}{\longrightarrow}
Q^{\rm \textcolor{green}{res}} (f),
Q^{\rm \textcolor{green}{res}} (f)(v,I) = \iint_{\R^3 \times \mathbb{S}^2} \iint_{(\R_+)^{\textcolor{green}{2}}}
\big[ f' f'_* - f f_* \big] \times B^{\rm \textcolor{green}{res}} \times
\textcolor{green}{\varphi(I+I_* - I')\,\varphi(I') \, \mathrm{d} I'} \, \varphi(I_*) \, \mathrm{d} I_*
\, \mathrm{d} v_* \, \mathrm{d} \sigma,
B^{\rm \textcolor{green}{res}} = B^{\rm \textcolor{grey}{standard}} (I'_* = I+I_* - I') E
\(\mathcal{V}_{\lambda}\)
\textcolor{black}{\forall} \lambda \textcolor{black}{> 0,}
11/27
quasi-resonant dynamic
Homogeneous quasi-resonant Boltzmann dynamic's expected behaviour
time
\(T_i\) & \(T_k\) relax towards each other
\(f\) (almost) stays a two-temperature Maxwellian (\(T_i\) & \(T_k\))
\(f\) relaxes to a two-temperature Maxwellian
short-time
long-time
Landau-Teller
ODE system
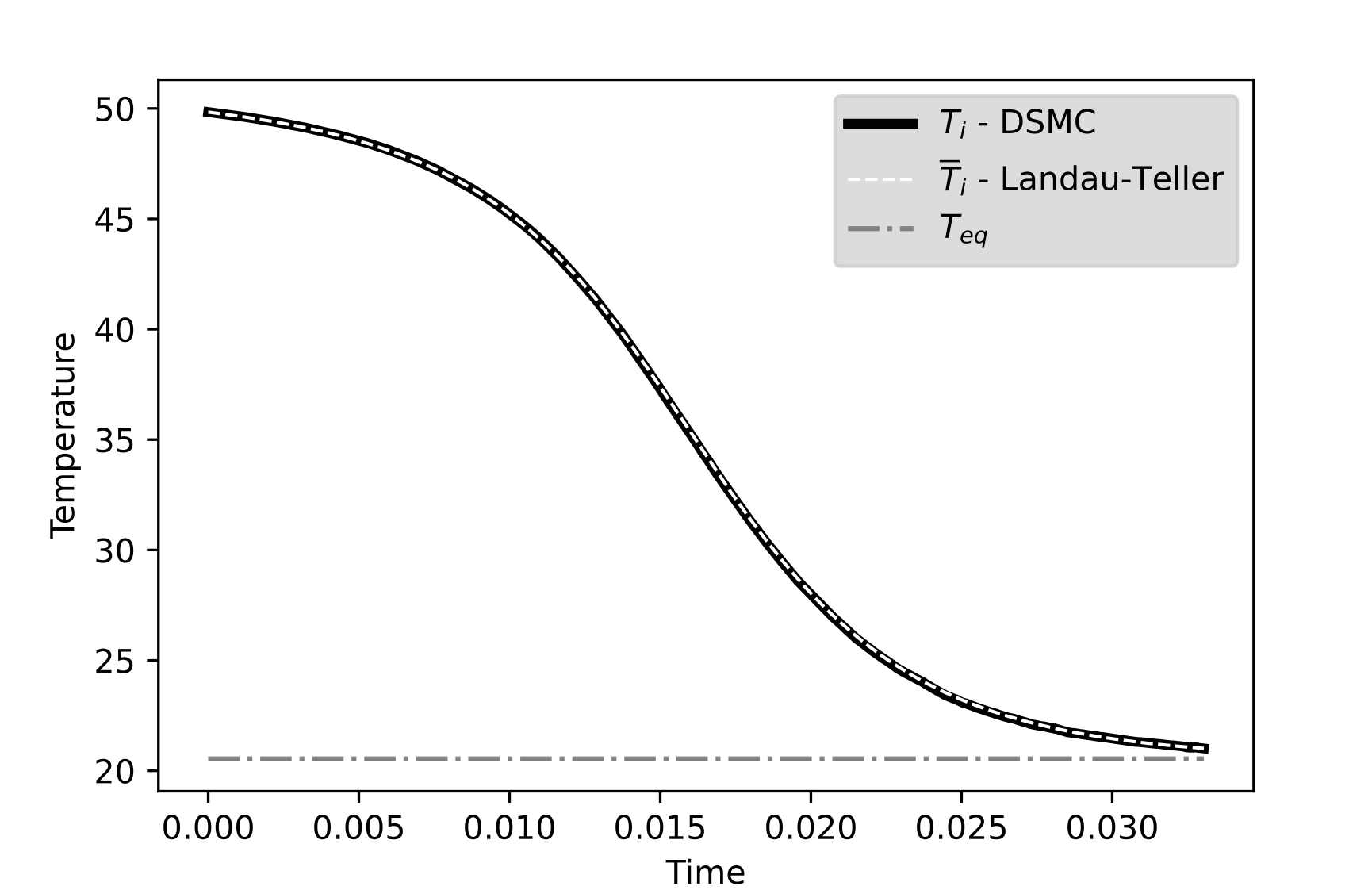
parameters: \(\lambda = 0.1\), \(T_i^0 = 50\), \(T_k^0 = 1\), \(T_{eq} = 20.6\)
Numerical experiment for validation
- Simulate quasi-resonant Boltzmann with DSMC
- Solve Landau-Teller
12/27
internal state
internal energy level
internal energy quantile
Perspectives Part \(\mathrm{I}\)
\(\mathrm{I}.1\). Explore links between paradigms and their use
- Physical modeling
- General proofs
Technical computations
Numerical simulations
(particle-based)
\(\mathrm{I}.2\). Idea of an Asymptotic-Preserving scheme for quasi-resonant Boltmzann (param. \(\lambda\))
time
Get the temperatures via Landau-Teller system
Take the solution to be a two-temperature Maxwellian
Simulate the corresponding resonant Boltzmann equation
\(\mathcal{O}(1)\)
\(\textcolor{black}{\mathcal{O}(} \lambda^{-2} \textcolor{black}{)} \)
13/27
Tool
Entropy method: functional inequalities
Goal
Explicit rate of relaxation to equilibrium for solutions to the Boltzmann-Fermi-Dirac equation
[4] TB: "Extending Cercignani's conjecture results from Boltzmann to Boltzmann-Fermi-Dirac equation", J. Stat. Phys., 2024.
[5] TB, B. Lods: "Quantitative relaxation towards equilibrium for solutions to the Boltzmann-Fermi-Dirac equation with cutoff hard potentials", preprint, 2024.
Part \(\mathrm{II}\). Boltzmann-fermi-Dirac equation
with B. Lods
Main result
Transfer of functional inequalities Boltzmann Boltzmann-Fermi-Dirac
[4]
[5]
14/27
\partial_t f_t(v) = Q_{\textcolor{purple}{\delta}}(f_t)(v)
\(f \equiv f_{t,x}(v)\)
+
x
v
homogeneous BFD equation:
the Boltzmann-Fermi-Dirac equation
Q_{\color{purple} \delta}(f)(v) = \iint_{\R^3 \times \mathbb{S}^2}
\left[f' f'_* \textcolor{purple}{(1 - \delta f) (1-\delta f_*)} - f f_* \textcolor{purple}{(1 - \delta f')(1-\delta f'_*)} \right]
B \; \mathrm{d} v_* \, \mathrm{d} \sigma
Collision operator:
0 \leq f_{t,x} \leq \frac{1}{\textcolor{purple}{\delta}}
v
v_*
v'
v'_*
Fermions -> Pauli exclusion principle -> quantum parameter \(\delta>0\)
1. Dissipation of the Fermi-Dirac entropy
2. Equilibria: Fermi-Dirac statistics
H Theorem:
(+ saturated state)
\frac{1}{\textcolor{purple}{\delta}}
v
Conservation of mass, momentum, energy
\begin{align*}
v+v_*&=v'+v'_* \\
|v|^2 + |v_*|^2 &= |v'|^2 + |v'_*|^2 \\
\end{align*}
15/27
Fermi-Dirac entropy
Boltzmann entropy
H_{\textcolor{green}{0}}(g) = \int g \log g - g
H_{\textcolor{purple}{\delta}}(f) = \int f \log f + {\textcolor{purple}{\delta}}^{-1} (1 - {\textcolor{purple}{\delta}} f)
\log (1-{\textcolor{purple}{\delta}} f)
M_{\textcolor{green}{0}}(v) = e^{a - b|v-u|^2}
\displaystyle M_{\textcolor{purple}{\delta}}(v) = \frac{e^{a - b|v-u|^2}}{1 + \textcolor{purple}{\delta} e^{a - b|v-u|^2}}
Equilibrium: Fermi-Dirac statistics
Equilibrium: Maxwellian
entropies and equilibria
Boltzmann
Boltzmann-Fermi-Dirac
16.1/27
Fermi-Dirac entropy
H_{\textcolor{green}{0}}(g) = \int \Phi_{\textcolor{green}{0}}(g)
H_{\textcolor{purple}{\delta}}(f) = \int \Phi_{\textcolor{purple}{\delta}}(f)
M_{\textcolor{green}{0}}(v) = (\Phi_{\textcolor{green}{0}}')^{-1} \left(\alpha + \beta \cdot v + \gamma |v|^2 \right)
\displaystyle M_{\textcolor{purple}{\delta}}(v) = (\Phi_{\textcolor{purple}{\delta}}')^{-1} \left(\alpha + \beta \cdot v + \gamma |v|^2 \right)
Equilibrium: Fermi-Dirac statistics
Equilibrium: Maxwellian
entropies and equilibria
Boltzmann
Boltzmann-Fermi-Dirac
\Phi_{\textcolor{purple}{\delta}}'(x) = \log \left(\frac{x}{1 - \textcolor{purple}{\delta} x} \right)
\Phi_{\textcolor{green}{0}}' = \log
entropy \(\displaystyle H : h \mapsto \int \Phi(h)\) \(\Phi\) \(\mathcal{C}^2\) st. convex
equilibrium
M = (\Phi')^{-1} (\alpha \, \textcolor{blue}{\text{mass}} + \beta \cdot \textcolor{blue}{\text{momentum}} + \gamma \, \textcolor{blue}{\text{energy}})
Boltzmann entropy
16.2/27
- Existence & stability of solutions to homogeneous BFD for cut-off hard potentials
Lu, Wennberg
Existence and uniqueness of solutions to inhomogeneous BFD for cut-off kernels
Dolbeault
- Relaxation to equilibrium of such solutions:
either \(f_0 =\) or \(f_t \; \underset{t \to \infty}{\rightarrow}\)
Derivation of the equation from particles system (partially formal)
Benedetto, Castella, Esposito, Pulvirenti
at which rate?
some results on bfd
saturated state
Fermi-Dirac stat.
17/27
\partial_t f_t = Q(f_t)
\(D(g) \gtrsim {H(g|M^g)}^{1+\alpha}\)
\displaystyle \frac{\mathrm{d}}{\mathrm{d} t} H(f_t|M^{f_0}) = - D(f_t)
\(D(g) \geqslant C H(g|M^g)\)
the entropy method
Relative entropy to equilibrium:
\(H(f_t|M^{f_0}) \lesssim t^{-1/\alpha}\)
\(H(f_t|M^{f_0}) \lesssim e^{-Ct} \)
Csiszár-Kullback-Pinsker
\|f_t - M^{f_0}\|_{L^1}^2 \lesssim H(f_t|M^{f_0})
H(g|M^g) := H(g) - H(M^g) \geq 0
18/27
D_{\textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)^{1 \textcolor{grey}{+ \alpha}}
Boltzmann
Toscani, Villani
Landau
D_{\textcolor{purple}{\delta}}(f) \gtrsim H_{\textcolor{purple}{\delta}}(f
|M_{\textcolor{purple}{\delta}}^f)^{1 \textcolor{grey}{+ \alpha}}
LAndau-Fermi-Dirac
Desvillettes, Villani
Alonso, Bagland Desvillettes, Lods
D_{\textcolor{purple}{\delta}}(f) \gtrsim H_{\textcolor{purple}{\delta}}(f|M_{\textcolor{purple}{\delta}}^f)^{1 \textcolor{grey}{+ \alpha}}
Boltzmann-FERMI-DIRAC
?
known entropy inequalities
\(D_{\textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)^{1 + \textcolor{grey}{\alpha}}\)
19/27
transfer of inequalities
D_{\textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)^{1 + \alpha}
We know:
\gtrsim \; \; D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right)
entropy inequality for Boltzmann
\gtrsim \; \; H_{\textcolor{green}{0}} \left(\frac{f}{1- \textcolor{purple}{\delta} f} \left| M_{\textcolor{green}{0}}^{\frac{f}{1- \textcolor{purple}{\delta} f}} \right. \right)^{1 + \alpha}
entropy inequality for Boltzmann-Fermi-Dirac
We want:
Toscani, Villani
D_{\textcolor{purple}{\delta}}(f) \gtrsim D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right)
Fermi-Dirac dissipation of \(f\)
Boltzmann dissipation of \( \displaystyle \frac{f}{1-\textcolor{purple}{\delta} f} \)
\( \gtrsim\)
D_{\textcolor{purple}{\delta}}(f) \textcolor{red} \qquad \qquad \qquad \qquad \qquad \qquad \qquad
\qquad \qquad \quad \textcolor{red}{\gtrsim} \;H_{\textcolor{purple}{\delta}}(f|M_{\textcolor{purple}{\delta}}^f)^{1 + \alpha}
?
20/27
H_{\textcolor{green}{0}}\left(\left.\frac{f}{1 - \textcolor{purple}{\delta} f}\right|M^{\frac{f}{1 - \textcolor{purple}{\delta} f}}_{\textcolor{green}{0}}\right)
\geqslant H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}).
(as soon as all terms make sense)
Boltzmann relative entropy to equilibrium of \(\displaystyle \frac{f}{1-\textcolor{purple}{\delta} f}\)
Fermi-Dirac relative entropy to equilibrium of \(f\)
Theorem.
[TB]
f \in L^1_2(\R^3)
\frac{f}{1 - \delta f} \in L^1_2(\R^3) \cap L \log L(\R^3),
\displaystyle 0 \leqslant f < \frac{1}{\delta}
For all
such that
and
\delta > 0
and
comparison of relative entropies
21.1/27
R_g : \delta \in \R_+ \mapsto H_{\delta}\left( \frac{g}{1 + \delta g} \left|M^{\frac{g}{1 + \delta g}}_{\delta} \right. \right).
Let
Then \(R_g\) is decreasing on \(\R_+\).
Proposition.
0 \leq g \in L^1_2(\R^3) \cap L \log L(\R^3)
and
Proof of the theorem
proof of the proposition
Key elements:
- Taylor representation of the relative entropy to eq.
- general link between entropy and equilibrium
- fact that \(x \mapsto -\left(\frac{x}{1+\delta x} \right)^2\) is decreasing
Other technicalities:
- differentiability on \(\R_+^*\)
- continuity at \(\delta = 0\)
general considerations
specific use of Fermi-Dirac features
Show \(R_g' \leq 0\) on \(\R_+^*\) and \(R_g\) \(\mathcal{C}^0\) on \(\R_+ \)
21.2/27
Proposition.
0\leqslant f \in L^1_2(\R^3)
\displaystyle \textcolor{black}{ 1 - \textcolor{purple}{\delta} f \geqslant} \kappa,
For all
such that
\textcolor{purple}{\delta} \textcolor{black}{> 0}, \;\; \kappa \textcolor{black}{\in (0,1)}
and
Classical / Fermi-Dirac equivalence
\textcolor{black}{H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}) \leqslant
H_{\textcolor{green}{0}}\left(\left.\frac{f}{1 - \textcolor{purple}{\delta} f}\right|M^{\frac{f}{1 - \textcolor{purple}{\delta} f}}_{\textcolor{green}{0}}\right)
\leqslant} \textcolor{black}{e}^{ \textcolor{black}{16} \, { \textcolor{black}{(}\kappa^{\textcolor{black}{-1}} \textcolor{black}{- 1)} } } \textcolor{black}{\cdot H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}})}
\phantom{\frac{1-\kappa}{\kappa}}
\textcolor{black}{D_{\textcolor{purple}{\delta}}(f) \leqslant
D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right)
\leqslant} \kappa^{\textcolor{black}{-4}} \textcolor{black}{ \cdot D_{\textcolor{purple}{\delta}}(f)}
For Boltzmann/BFD (& Landau/LFD) dissipations:
entropy inequality for Boltzmann
entropy inequality for Boltzmann-Fermi-Dirac
1 - \delta f \geq \kappa
\iff
1
\textcolor{purple}{\delta} f
\kappa
[TB]
\implies
22/27
\|f^{\delta}_t-M_{\delta}\|_{L^p_k} \leq C \, (1+t)^{- \eta/p},
\(p \in [1,\infty), \, k \geq 0\).
Relaxation to equilibrium for Boltzmann-fermi-dirac
Theorem 2.
[TB, Lods]
Let \(0\leqslant f^{\rm in} \in L^1_3(\R^3)\). Then \(\exists \delta^{\rm in} > 0\) such that \(\forall \delta \in (0,\delta^{\rm in})\), if \(f^{\delta} \) sol. to homogeneous Boltzmann-Fermi-Dirac w/ cut-off hard potentials,
then
\sup_{t \geq 0}\|f^{\delta}_t\|_{L^\infty} \leq \mathbf{C}^{\rm in}
Proposition.
[TB, Lods]
Let \(0\leqslant f^{\rm in} \in L^1_3(\R^3)\). Then \(\exists \,\mathbf{C}^{\rm in} > 0\) such that \(\forall \delta> 0\), if \(f^{\delta} \) sol. to homogeneous Boltzmann-Fermi-Dirac with cut-off hard potentials,
then
D_{\textcolor{purple}{\delta}}(f) \gtrsim H_{\textcolor{purple}{\delta}}(f|M_{\textcolor{purple}{\delta}})^{1 + \alpha}
\|f^{\delta}_t-M_{\delta}\|^2_{L^1_k} \lesssim\, H_{\delta}(f_t^{\delta}|M_{\delta})
23/27
\Phi_0'' \circ \psi \geqslant \Phi_1'',
H_0 \left(\psi (f)|M_0^{\psi(f)} \right) \leqslant H_1 \left(f|M_1^{f} \right)
If
then
Let \(\displaystyle H_0(f) = \int \Phi_0(f) \), \(\displaystyle H_1(f) = \int \Phi_1(f) \) with \(\Phi_0,\Phi_1\) \(\mathcal{C}^2\) s.t. convex, and
\psi = (\Phi_0')^{-1} \circ \Phi'_1.
1. Conjecture:
Comparison of relative entropies to equilibrium in general setting
Perspectives Part \(\mathrm{II}\)
2. Rate of relaxation to equilibrium for homogeneous Boltzmann-Fermi-Dirac without cut-off
24/27
BONUS: general weighted \(L^p\) Csiszár-Kullback-Pinsker inequalities
25/27
General weighted \(L^p\) Csiszár-Kullback-Pinsker
\|f-M^f\|^2_{L^p_{\varpi}} \leqslant {\small C_{\Phi, \varpi, p, f, M^f}} \; H(f|M^f),
Proposition.
(general entropy)
\(\displaystyle H(f) = \int\Phi(f)\), \(\Phi \; \; \mathcal{C}^2\) st. convex, \(M^f\) equilibrium, and
C_{\Phi, \varpi, p,f,M^f} = \left(\int_0^1 (1-\tau) \left\| \Phi''((1-\tau)M^f + \tau f)^{-1} \right\|_{L^{\frac{p}{2-p}}_{\varpi^2}}^{-1} \, \mathrm{d} \tau \right)^{-1}
For any \(f\), any \(p \in [1,2]\) and \(\varpi\) weight,
\|f-M_0^f\|^2_{L^p_{\varpi}} \leqslant 2 \max \left(\|f\|_{L^{\frac{p}{2-p}}_{\varpi^2}}, \|M_0^f\|_{L^{\frac{p}{2-p}}_{\varpi^2}} \right)\, H_{0}(f|M_0^f),
Corollary.
For any \(0\leq f \in L^1_2\cap L \log L(\R^3)\), \(p \in [1,2]\) and \(\varpi : \R^3 \to \R_+\),
(Boltzmann entropy)
\(\displaystyle H_0\) Boltzmann entropy and \(M_0^f\) Maxwellian.
[simplified]
[TB]
26/27
\(\mathrm{I}.1\). Boltzmann equation for polyatomic gases
\(\mathrm{I}.2\). Boltzmann equation for polyatomic gases with (quasi-)resonant collisions
\(\mathrm{II}\). Boltzmann-Fermi-Dirac equation
Bonus: general weighted \(L^p\) Csiszar-Kullback-Pinsker inequalities
- General modelling framework for single gas & mixtures with chemical reactions
- Compactness result in resonant setting
- Modelling & study of quasi-resonant Boltzmann
- Entropy/entropy production inequalities via a transfer method
- Relaxation to equilibrium with explicit rate
w/ Lods
w/ Bisi, Groppi
w/ Boudin, Mathiaud, Salvarani
Thank you for your attention!
[1] TB, M. Bisi, M. Groppi: "A general framework for the kinetic modelling of polyatomic gases", Commun. Math. Phys., 2022.
[2] M. Bisi, TB, M. Groppi: "An internal state kinetic model for chemically reacting mixtures of monatomic and polyatomic gases", Kinet. Relat. Models, 2024.
[3] TB, L. Boudin, F. Salvarani: "Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions", J. Mat. Anal. Appl., 2023.
[4] TB: "Extending Cercignani's conjecture results from Boltzmann to Boltzmann-Fermi-Dirac equation", J. Stat. Phys., 2024.
[5] TB, B. Lods: "Quantitative relaxation towards equilibrium for solutions to the Boltzmann-Fermi-Dirac equation with cutoff hard potentials", preprint, 2024.
[1,2]
[4]
[5]
[3]
27/27
(\partial_t + v \cdot \nabla_x) f_{t,x}(v,\textcolor{orange}{\zeta}) = Q(f_{t,x})(v,\textcolor{orange}{\zeta})
\(f \equiv f_{t,x}(v, \textcolor{orange}{\zeta})\) density of molecules
\textcolor{orange}{\zeta}
+
x
the polyatomic Boltzmann equation
v
Boltzmann equation:
v,\textcolor{orange}{\zeta}
v_*,\textcolor{orange}{\zeta_*}
v',\textcolor{orange}{\zeta'}
v'_*,\textcolor{orange}{\zeta'_*}
Collision operator:
\newcommand{\dd}{\mathrm{d}}
Q(f)(v,\textcolor{orange}{\zeta}) = \iint_{\R^3 \times \mathbb{S}^2} \textcolor{orange}{\iiint_{\mathcal{E}^3}}
\left[f(v',\textcolor{orange}{\zeta'}) f(v'_*,\textcolor{orange}{\zeta'_*}) - f(v,\textcolor{orange}{\zeta}) f(v_*,\textcolor{orange}{\zeta_*}) \right]
B \; \textcolor{orange}{\dd \mu^{\otimes 3}(\zeta_*,\zeta',\zeta'_*)} \, \dd v_* \, \dd \sigma
\begin{align*}
v' = \frac{v+v_*}{2} + \textcolor{orange}{\sqrt{\Delta}} \; \sigma, \\
v'_* = \frac{v+v_*}{2} - \textcolor{orange}{\sqrt{\Delta}} \; \sigma,\\
\end{align*}
\newcommand{\Sb}{\mathbb{S}}
\sigma \in \Sb^2
Conserved quantities
mass, momentum & energy
\begin{align*}
v+v_*&=v'+v'_* \\
\frac12|v|^2 + \textcolor{orange}{\varepsilon(\zeta)} + \frac12|v_*|^2 + \textcolor{orange}{\varepsilon(\zeta_*)} &= \frac12|v'|^2 + \textcolor{orange}{\varepsilon(\zeta')} + \frac12|v'_*|^2 + \textcolor{orange}{\varepsilon(\zeta'_*)} \\
\end{align*}
\textcolor{orange}{\Delta} := \frac14 |v-v_*|^2 + \textcolor{orange}{\varepsilon(\zeta) + \varepsilon(\zeta_*) - \varepsilon(\zeta') - \varepsilon(\zeta'_*)}
2. Characterization of equilibria
H Theorem
1. \(2^{nd}\) principle of thermodynamics
3. Mass-action law
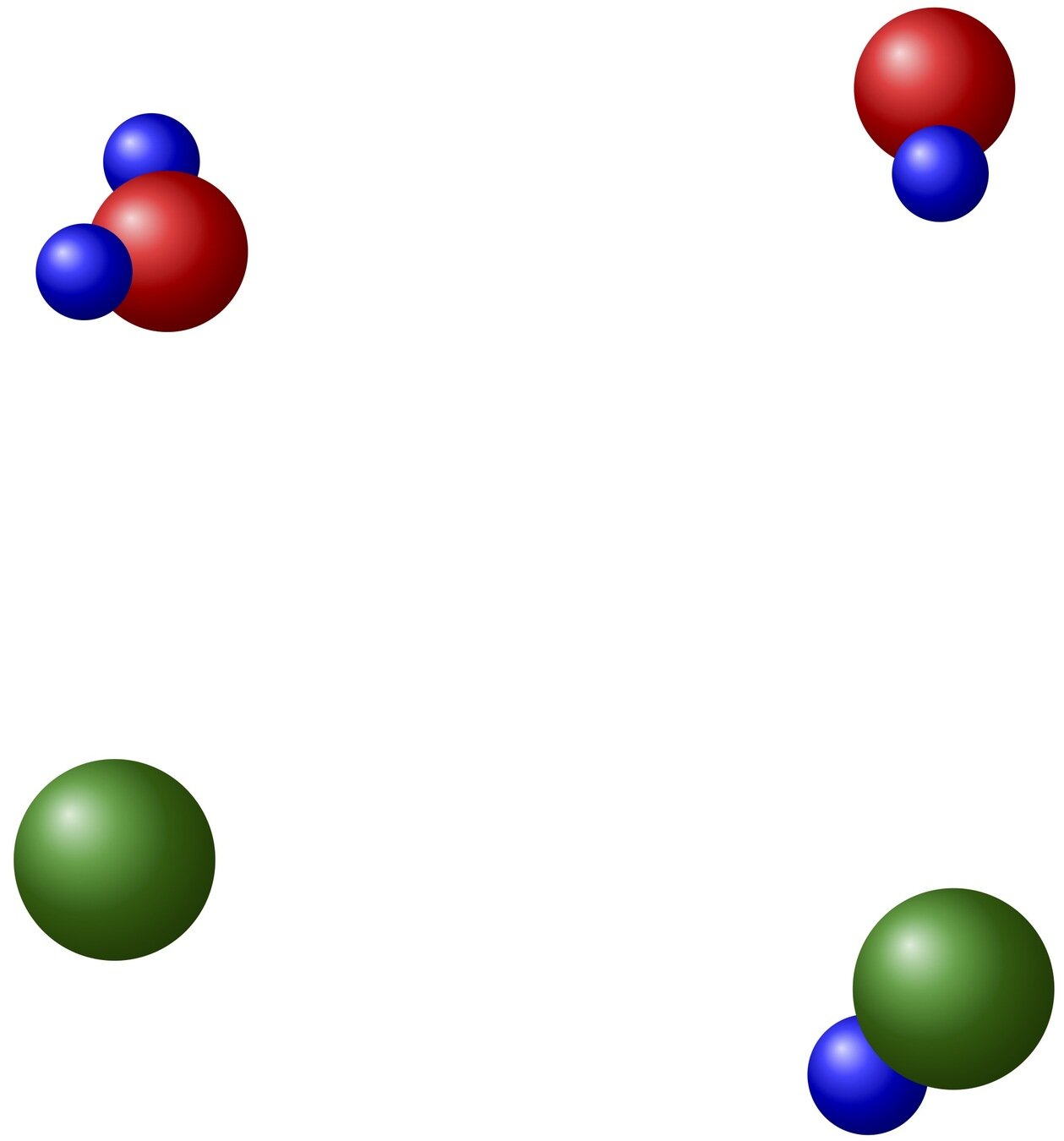
extension to mixtures with chemical reactions
\(\bullet\) models \((\mathcal{E_i},\mu_i)\) and \(\varepsilon_i\) for \(i = 1, \dots, N \)
\(\bullet\) study \(f \equiv (f_i)_i\), with \( f_i : \R^3 \times \mathcal{E}_i \to \R_+ \)
\(\bullet\) system of Boltzmann equations
\partial_t f_i + v \cdot \nabla_x f_i = Q(f)
\forall \, i,
collisions &
chemical reactions
Energy of reaction:
\Delta E = \varepsilon^0_k + \varepsilon^0_{\ell} - \varepsilon^0_i - \varepsilon^0_j
i
j
k
\ell
v \; \, \; \; \; \; \zeta
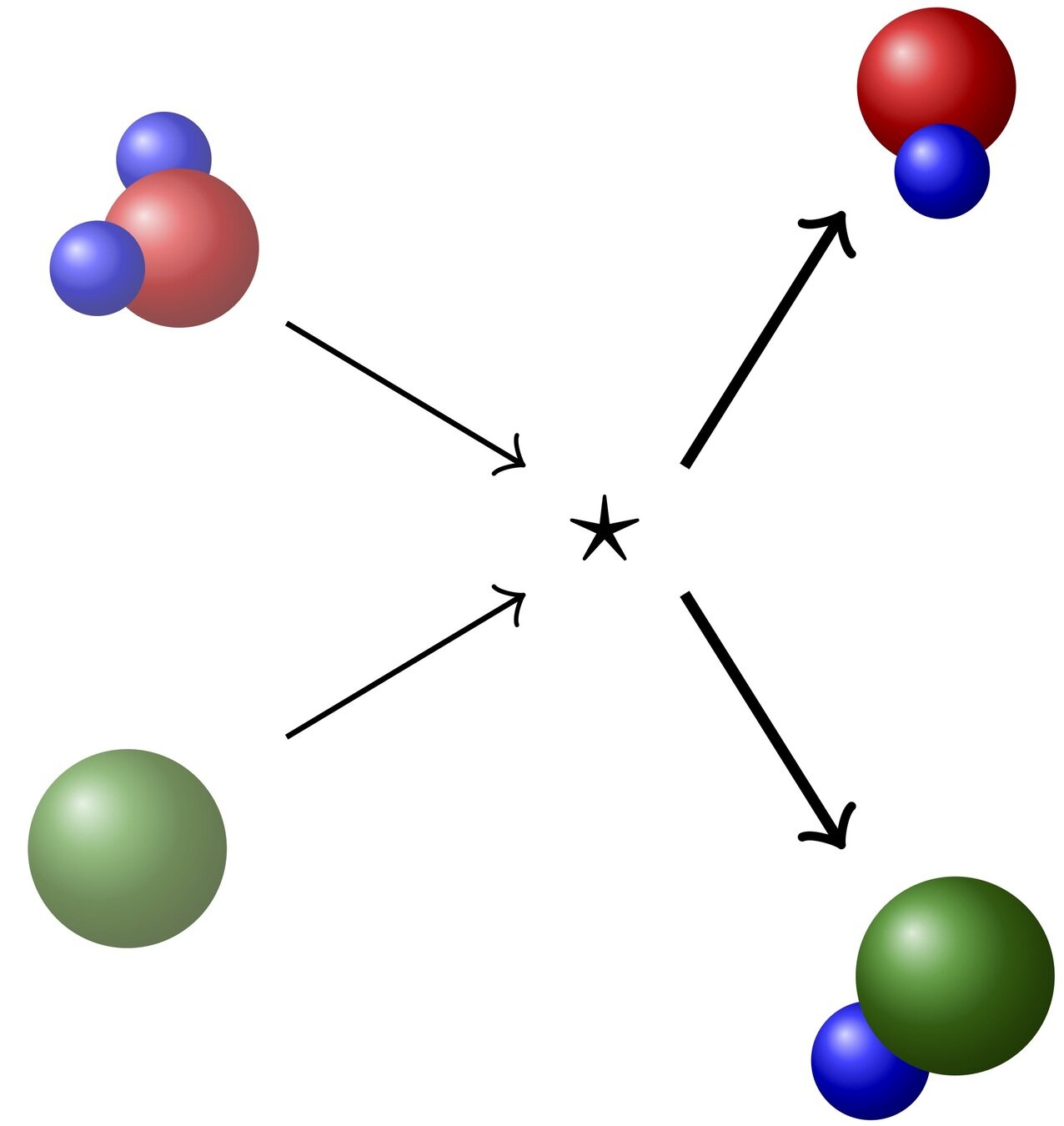
[Bisi, B., Groppi]
\(\varepsilon^0 := \text{inf ess}_{\mu} \;\varepsilon\)
compactness result of the linearized resonant Boltzmann operator
resonant collision operator \(Q(f)\)
linearize around equilibrium
resonant linearized operator \(\mathcal{L}f\)
\mathcal{L} = K - \nu \mathrm{Id}
[T.B., Boudin, Salvarani]
Theorem. \(K\) compact operator of \(L^2(\R^3 \times \R_+, \mathrm{d} v \, \varphi(I) \, \mathrm{d}I)\)
useful for
- existence & uniqueness close-to-equilibrium
- study of the spectrum
Proof strategy:
- split the study into kinetic & internal parts
- kinetic part \(\leftrightarrow\) monoatomic (+improvement)
BONUS: a nice change of variables in the sphere (variant to Grad's proof / compactness monoatomic)
\newcommand{\Sb}{\mathbb{S}}
(\sigma_1, \sigma_2) \; \in \Sb^2 \times \Sb^2 \quad \mapsto \quad \left(z = \frac{\sigma_1 + \sigma_2}{2} , \; A \right) \; \in \mathcal{B}_{\R^3}(0,1) \times \Sb^1
\newcommand{\Sb}{\mathbb{S}}
\newcommand{\dd}{\mathrm{d}}
\iint_{\Sb^2 \times \Sb^2} \varphi \left( \frac{\sigma_1 + \sigma_2}{2} \right) \, \dd \sigma_1 \, \dd \sigma_2
= \iint_{\mathcal{B}_{\R^3}(0,1) \times \Sb^1} \varphi(z) \, \textcolor{brown}{4|z|^{-1}} \, \dd z \, \dd A
\newcommand{\Sb}{\mathbb{S}}
\displaystyle = \int_0^1 (1-\tau) \int(f - M^f)^2 \, \Phi''(M^f + \tau (f-M^f)) \, \mathrm{d} v \, \mathrm{d} \tau
\displaystyle H(f|M^f) = \int \, \int_{M^f(v)}^{f(v)} \, (f(v) - x) \, \Phi''(x) \, \mathrm{d} x \, \mathrm{d} v
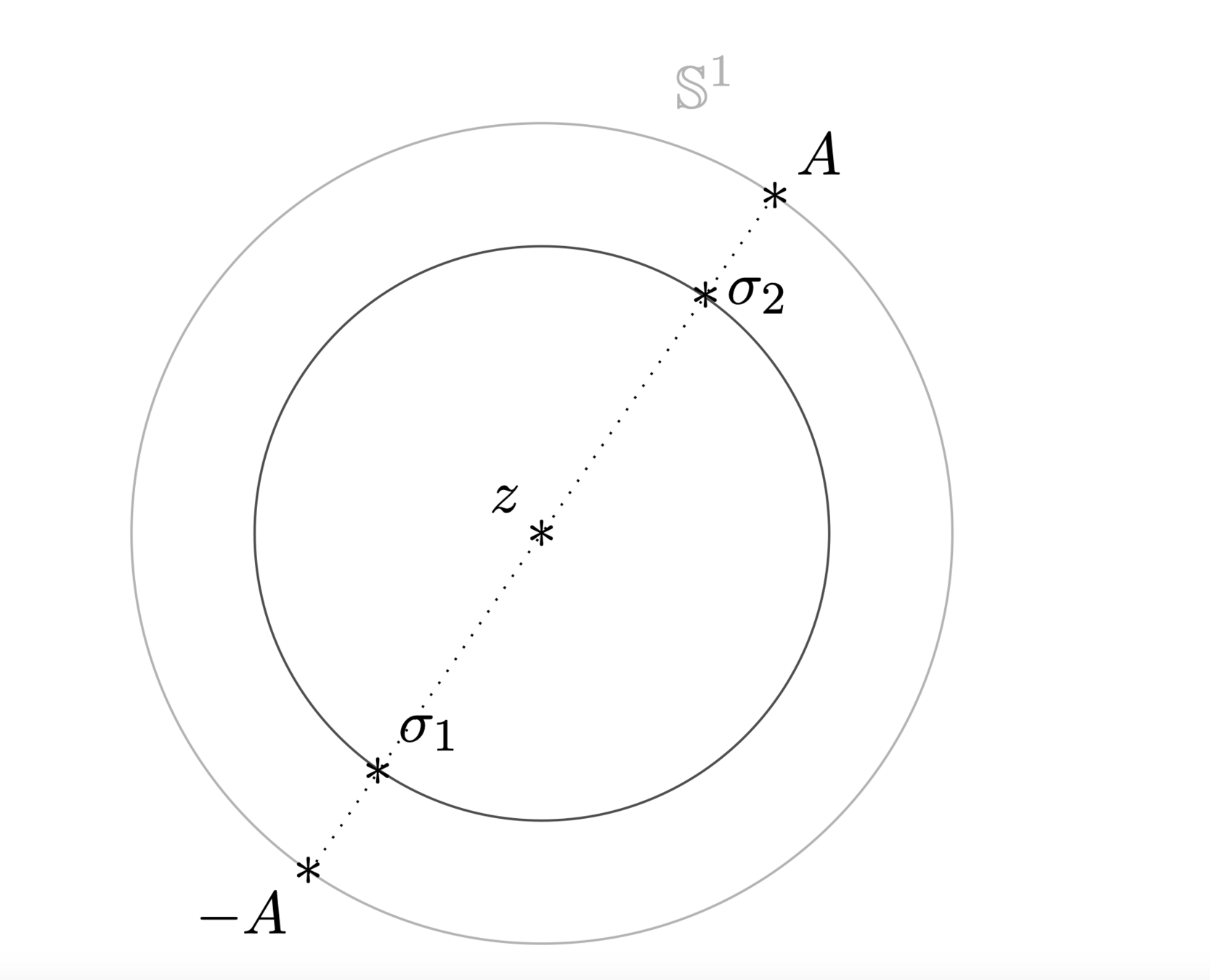
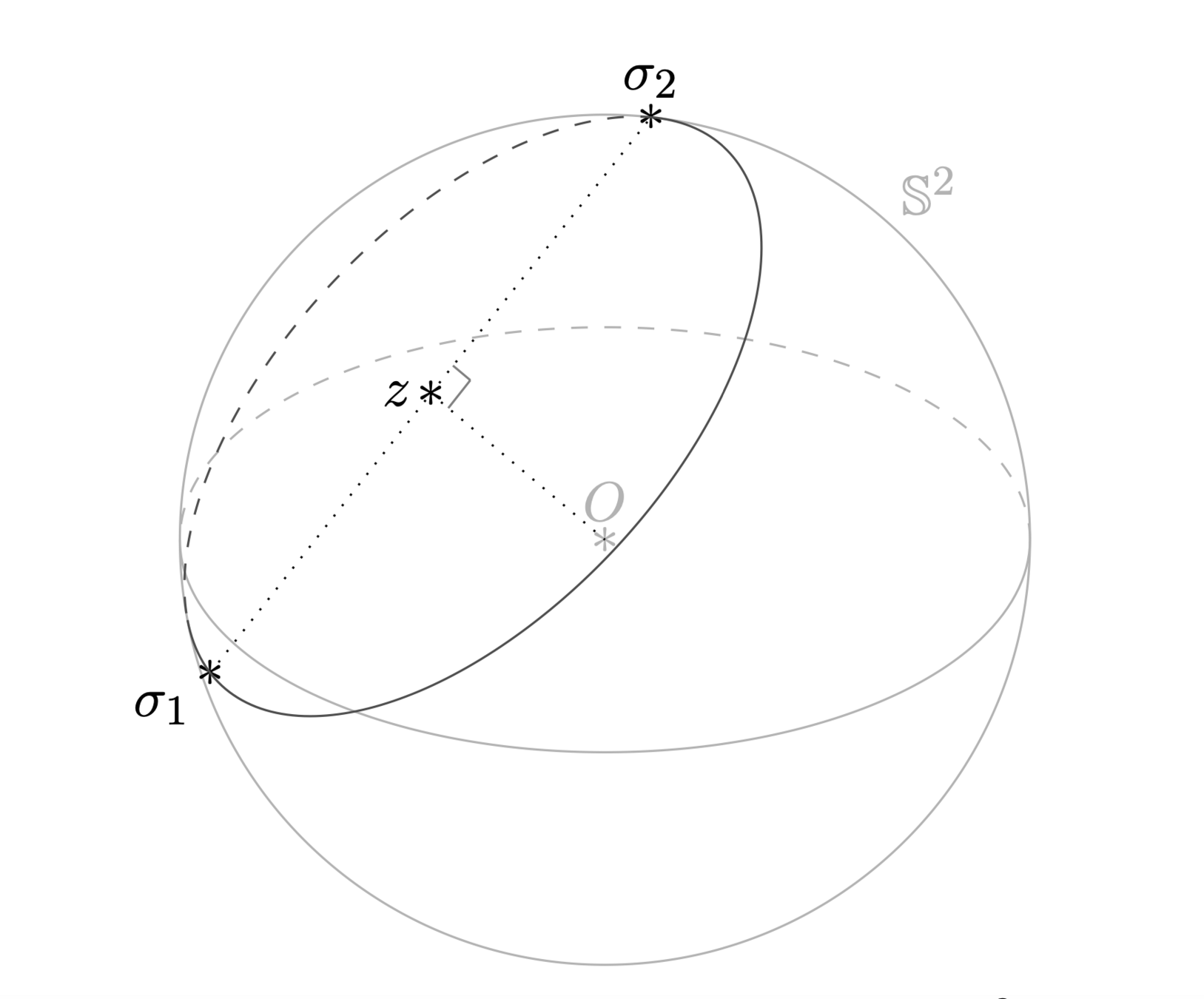
Taylor representation of relative entropy to equilibrium
\(\displaystyle H(f) = \int \Phi(f) \, \mathrm{d} v\) with \(\Phi\) \(\mathcal{C}^2\) s.t. convex
entropy:
M^f = (\Phi')^{-1} (\textcolor{blue}{\text{something conserved}})
Link between entropy and equilibrium
\psi_1, \psi_2, \dots, \psi_n
M = (\Phi')^{-1} \left( \sum_{i=1}^n \textcolor{blue}{\alpha_i} \, \psi_i \right)
Entropy
Equilibrium
Conserved quantities
\newcommand{\dd}{\mathrm{d}}
H(f) = \int \Phi(f)
\newcommand{\dd}{\mathrm{d}}
\Phi \; \; \mathcal{C}^2
st. convex
general link
Lagrange multipliers
Functional to minimize
constraints
Minimizer
\|f^{\delta}_t-M_{\delta}\|_{L^p_k} \leq C \, (1+t)^{- \eta/p},
\(p \in [1,\infty), \, k \geq 0\), and with \(C,\eta\) explicit and uniform in \(\delta\).
Relaxation to equilibrium for Boltzmann-fermi-dirac
Theorem 2.
[B., Lods]
Let \(0\leqslant f^{\rm in} \in L^1_3(\R^3)\). Then \(\exists \delta^{\rm in} > 0\) such that \(\forall \delta \in (0,\delta^{\rm in})\), if \(f^{\delta} \) sol. to Boltzmann-Fermi-Dirac w/ cut-off hard potentials,
(\(\delta\) is the quantum parameter)
Proof's core ingredients:
- \(L^{\infty}\)-bound on \(f^{\delta}\) independent of \(\delta\)
- Entropy/entropy production inequality
- Control of moments
- Maxwellian lower-bound
- Csiszar-Kullback-Pinsker inequality
1 - \delta f^{\delta} \geq \kappa
D_{\delta}(f_t^{\delta}) \geqslant C_t \; H_{\delta}(f_t^{\delta}|M_{\delta})^{1 + \alpha}
C_t \geqslant \widetilde{C}
\|f^{\delta}_t-M_{\delta}\|^2_{L^1_k} \leqslant C'\, H_{\delta}(f_t^{\delta}|M_{\delta})
\partial_t f_t^{\delta} = Q_{\delta} (f_t^{\delta}), \; \; f_0^{\delta} = f^{\rm in},
then
Proof's strategy:
\sup_{t \geq 0}\|f^{\delta}_t\|_{L^\infty} \leq \mathbf{C}^{\rm in}
the \(L^{\infty}\)-bound
Proposition.
[B., Lods]
Let \(0\leqslant f^{\rm in} \in L^1_3(\R^3)\). Then \(\exists \,\mathbf{C}^{\rm in} > 0\) such that \(\forall \delta> 0\), if \(f^{\delta} \) sol. to Boltzmann-Fermi-Dirac with cut-off hard potentials,
\delta \in (0, (1-\kappa) \mathbf{C}^{\rm in}) \; \; \implies \; \; 1 - \delta f^{\delta} \geq \kappa
Q_{\delta} \leqslant Q^+_0 + \widetilde{Q}^+_0 - Q^-_0
Q_{0} = Q^+_0 - Q^-_0
independent of \(\delta \)
\(f_t^{\delta}\) "sub-solution" to an eq. resembling classical Boltzmann
\(\widetilde{Q}^+_0\) "adjoint" to \(Q^+_0\)
(almost) copycat proof of same fact for classical Boltzmann
[Alonso, Gamba]
then
\partial_t f_t^{\delta} = Q_{\delta} (f_t^{\delta}), \; \; f_0^{\delta} = f^{\rm in},
Soutenance
By Thomas Borsoni
