Introduction

Dynamic Traffic Assignment

• Dynamically adjust routes for all vehicles based on traffic condition
• Input: origin-destination pairs
• Output: best route for each O-D pair

Why Dynamic Traffic Assignment?

• Advanced application of connected vehicle
• Mitigate traffic congestion
• Improve traffic & energy efficiency

Preliminary

Wardrop equilibrium

• Based on Nash equilibrium
• Wardrop's first principle (User Equilibrium)
  • \(cost(\text{used route}) \leq cost(\text{unused route})\) for every O-D pair
  • ​No one can lower his cost through unilateral action
• Wardrop's second principle
  • At equilibrium state, average travel time is at a minimum

solving User Equilibrium \(\iff\) optimizing Traffic Assignment

 Heuristic Approach

Gawron, C. (1998). An iterative algorithm to determine the dynamic user equilibrium in a traffic simulation model. International Journal of Modern Physics C, 9(03), 393-407.

Traffic Flow Model

• Traditional: NaSc
• Proposed: Queuing Model
  • ​Model network as directed graph \(G(E, V)\)
  • Each \(e \in E\) has capacity \(q\), length \(l\) and number of lanes \(\lambda\)
  • Vehicles queue when ingoing traffic exceeds the constraints of \(\lambda\) or \(q\)
• Faster simulation of traffic condition with Queuing Model
  • \(O((\sum |r|)\log N)\) ?

to simulate real-world traffic

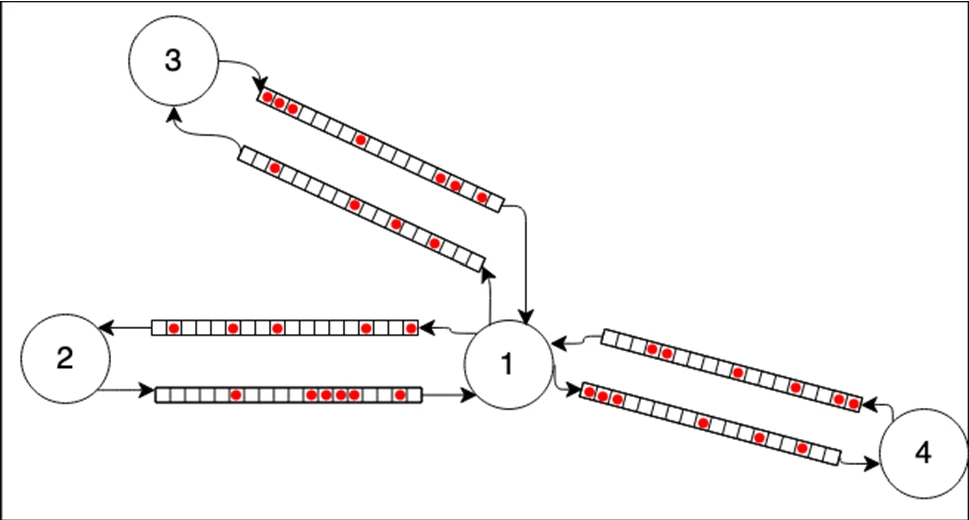
NaSc

Queuing Model

Naive

1. Initially assign shortest path to each O-D pair 
2. Simulate and update traffic condition
3. Update shortest path based on last simulation
4. Repeat 2~4

Issues

• Route choice may oscillate (convergence is not guaranteed)

Probability-based

• Each driver \(d\) has:
  • Departure time \(t_d\), origin \(O_d\), destination \(D_d\)
  • A set of candidate routes \(R_d\) (\(=k\) shortest paths)
  • Probability distribution \(p_d\) on route set \(R_d\), i.e., \(\sum\limits_{r \in R_d}p_d(r) = 1\)
  • Cost function \(c_d\) on route set \(R_d\) (regarding travel time)

Probability-based

1. Simulate (based on \(p_d\))
   • Each driver \(d\) choose its route based on \(p_d\)
2. Update \(p_d\) and \(c_d\)
   • Update cost function: (\(c_s(r)\) is based on simulation)
     • \(c_d'(r) = c_s(r)\) if \(r\) is chosen by \(d\)
     • \(c_d'(r) = \mu c_s(r) + (1 - \mu)c_d(r)\) if \(r\) is not chosen by \(d\)
   • Update probability distribution \(p_d\)
3. Take smallest \(c_d\) route

• Every user choose his best route

• Better approach to Wardrop equilibrium

Advantages

Mathematical formulation

• \(v_a\): traffic volume of link \(a\)
• \(S_a(x)\): link \(a\)'s average travel time at traffic volume \(x\)
• \(\alpha_{ij}^{ar}\): (binary) whether link \(a\) is on route \(r\) from \(i\) to \(j\)
• \(x_{ij}^r\): traffic of route \(r\) from \(i\) to \(j\)
• \(T_{ij}\): traffic demand from \(i\) to \(j\)

Definition

Minimize

• total travel time
  • \(\sum\limits_a\int^{v_a}_0S_a(x)dx\)

Subject to

• link volume = total route traffic containing the link
  • ​\(v_a = \sum\limits_i\sum\limits_j\sum\limits_r\alpha_{ij}^{ar}x_{ij}^r\)
• ​O-D pair traffic = total traffic of all O-D route
  • ​\(T_{ij} = \sum\limits_rx^r_{ij}\)
• ​basics
  • ​\(v_a \geq 0,\ x^r_{ij} \geq 0\)

Nonlinear Programming

• \(v_a\): traffic volume of link \(a\)
• \(S_a(x)\): link \(a\)'s average travel time at traffic volume \(x\)
• \(\alpha_{ij}^{ar}\): (binary) whether link \(a\) is on route \(r\) from \(i\) to \(j\)
• \(x_{ij}^r\): traffic of route \(r\) from \(i\) to \(j\)
• \(T_{ij}\): traffic demand from \(i\) to \(j\)

• Frank-Wolfe algorithm (constrained convex optimization)

Nonlinear Programming

• Low convergence rate

• For static traffic assignment only

Issues

Future work

• Study state-of-the-art algorithm

• Comparison between different approaches

• Implementation & Evaulation ?