Kongruenssi
Päivämäärältään 1, 8, 15, 22 ja 29 ovat kaikki perjantaipäiviä toukokuussa 2020. Mikä on näiden lukujen matemaattinen yhteys?
Luvut ovat aina yhden tai useamman viikon eli 7pv:n päässä toisistaan
Esim. \(15-1 = 14 = 7\cdot 2\)
\(29-8 = 21 = 7\cdot 3\)
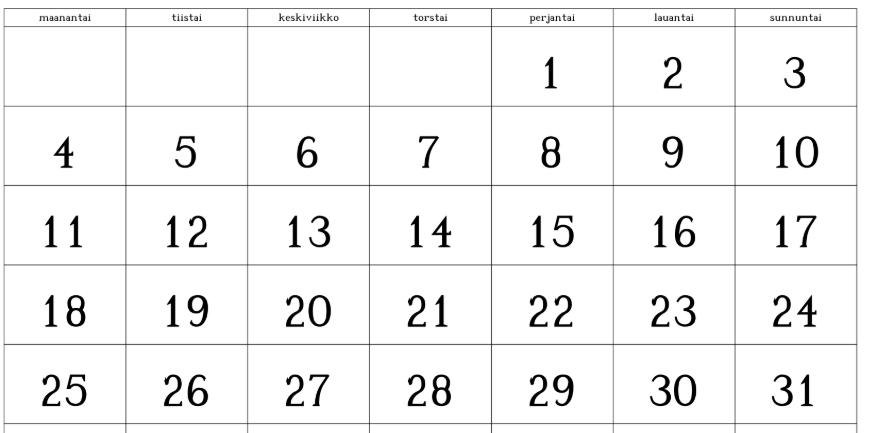
Ts. lukujen erotus on aina 7:llä jaollinen!
- Jos kokonaislukujen \(a\) ja \(b\) erotus on jaollinen luvulla \(n>1\), niin \(a\) ja \(b\) ovat kongruentit modulo \(n\)
- Merkitään \(a\equiv b \pmod{n}\)
- Esim. \(45 \equiv 3 \pmod{7}\), koska \(45-3=42=7\cdot 6\)
Määritelmä
Lauseita
-
Lause: Pos. kok.luvut \(a\) ja \(b\) ovat kongruentit modulo \(n\), jos ja vain jos luvuilla \(a\) ja \(b\) on sama jakojäännös, kun ne jaetaan luvulla \(n\)
- Esim. jakolaskuilla \(45:7\) ja \(3:7\) täytyy olla sama jakojäännös (3), koska aiemmin huomattiin, että ne ovat kongruentit modulo 7.
- Toistepäin: koska molempien jakolaskujen \(22:5\) ja \(12:5\) jakojäännös on 2, niin \(22\equiv 12\pmod{5}\)
-
Lause: Jos \(r\) on jakolaskun \(a:n\) jakojäännös, niin
\(a\equiv r \pmod{n}\)- Esim. koska jakolaskun \(10:4\) jakojäännös on \(2\), niin \(10 \equiv 2\pmod{4}\)
- Huom! Ei päde yleisesti toistepäin! (Jakojäännös on aina pienempi kuin jakaja)
Summan, tulon ja potenssin kongruenssi
Lause Olkoon \(a\equiv b \pmod{n}\), \(c\equiv d \pmod{n}\) ja \(k\) pos. kok.luku.
- Kongruenttien lukujen summat ovat kongruentteja
\(a+c\equiv b+d \pmod{n}\) - Kongruenttien lukujen tulot ovat kongruentteja
\(ac\equiv bd \pmod{n}\) - Kongruenttien lukujen potenssit ovat kongruentteja
\(a^k\equiv b^k \pmod{n}\)
Jäännösluokat
- Kongruenssi modulo n jakaa luvut n:ään jäännösluokkaan
- Ensimmäisen jäännösluokan muodostavat ne luvut x, joille pätee \(x\equiv 0\pmod{n}\) (eli n:llä jaolliset luvut)
- Toisen ne, joille pätee \(x\equiv 1 \pmod{n}\)
- \(\vdots\)
- Viimeisen ne, joille pätee \(x\equiv n-1\pmod{n}\)
- Hyödyllistä todistaessa väitteitä kaikille kokonaisluvuille: voidaan jakautua eri jäännösluokkiin
- Sama idea kuin parittomiin ja parillisiin lukuihin jakauduttaessa, jossa kyse oikeastaan kongruenssin modulo 2 jäännösluokista!
09 Kongruenssi
By Timo Pelkola
09 Kongruenssi
- 244



