Alkuluvut
Alkuluvut
- Kokonaisluku \(p>1\) on alkuluku, jos se on jaollinen vain itsellään ja luvulla \(1\)
- Esim. 2, 3, 5 ja 7 ovat alkulukuja
- Alkulukujen joukkoa merkitään \(\mathbb{P}\)
- Alkulukuja on äärettömän paljon (Euklideen lause)
- Sen sijaan luku 4 ei ole alkuluku, koska se on jaollinen 4:n ja 1:n lisäksi 2:lla
- Lukuja, jotka eivät ole alkulukuja, kutsutaan joskus yhdistetyiksi luvuiksi (myös äärettömän paljon)
Alkuluvuksi osoittaminen
- Luvun alkuluvuksi osoittaminen ja alkulukujen löytäminen on lähtökohtaisesti työlästä
- Suurin tunnettu alkuluku tällä hetkellä on \(2^{82\,589\,933}-1\), jossa on 24 862 048 numeroa
- Pelkän määritelmän avulla pos. kok.luvun \(n\) alkuluvuksi osoittaminen vaatisi, että tarkistettaisiin luvun \(n\) jaollisuus kaikilla lukua \(n\) pienemmillä pos. kok.luvuilla
- Alkuluvun osoittamisen ja löytämisen helpottamiseksi on kuitenkin joitakin tuloksia ja menetelmiä
-
Lause: Luku \(a\) on alkuluku, jos se ei ole jaollinen millään alkuluvulla, joka on enintään \(\sqrt{a}\)
- Eli voimme ainakin aloittaa tarkistamisen \(\sqrt{a}\):sta alaspäin, ja hypätä kaikkien ennestään yhdistetyiksi tiedettyjen lukujen yli
Osoita, että 19 on alkuluku
\(\sqrt{19}\approx 4{,}4\)
\(\sqrt{19}\) pienempiä lukuja on 4, 3 ja 2, joista 3 ja 2 ovat alkulukuja (4 ei ole, koska 2|4)
\(19:3=6{,}33...\) ja \(19:2=9{,}5\), joten 19 ei ole jaollinen 3:lla eikä 2:lla. Siis 19 on alkuluku.
Eratostheneen seula
- Eräs klassinen menetelmä enintään luvun \(n\) suuruisten alkulukujen löytämiseksi on ns. Eratostheneen seula
- Taulukoidaan luvut 2, 3, ...., n
- Poistetaan kaikki luvun 2 moninkerrat
- Poistetaan kaikki luvun 3 moninkerrat
- Luku 4 on jo poistettu vaiheessa 2. Poistetaan seuraavan jäljellä olevan luvun, eli luvun 5, kaikki moninkerrat
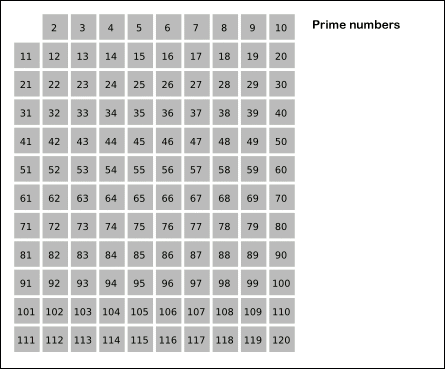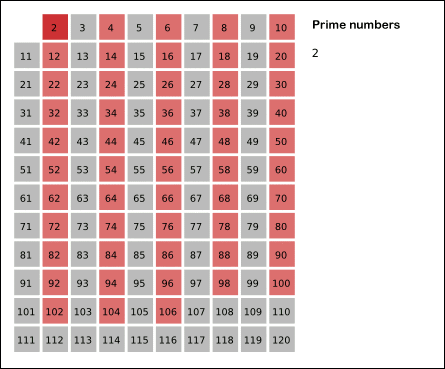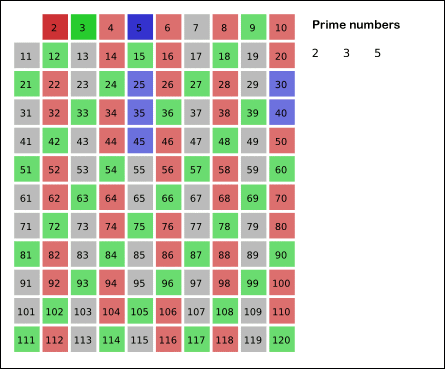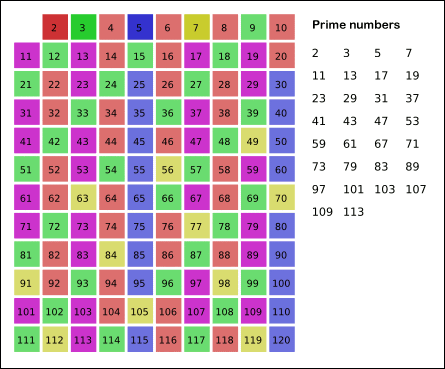
- Jatketaan...
- Kun ollaan poistettu kaikki enintään \(\sqrt{n}\):n moninkerrat, niin jäljelle jäävät luvut ovat alkulukuja
Eratostheneen seula
Alkulukuhajotelma
-
Aritmetiikan peruslause: Jokainen lukua 1 suurempi kokonaisluku voidaan esittää yksikäsitteisesti alkulukujen tulona
- Yksikäsitteisyydellä tarkoitetaan tässä sitä, että tulontekijät ovat aina samoja, vaikka niiden järjestys voi olla mikä tahansa
- Luvun esittämistä alkulukujen tulona kutsutaan alkulukuhajotelmaksi
- Esim. \(10=5\cdot 2\)
- Suurempien lukujen kanssa on helpompaa jakaa tekijöihin vaiheittain
- Esim. \(24 = 2\cdot 12 = 2\cdot 2\cdot 6 = 2\cdot 2\cdot 2\cdot 3 = 2^3 \cdot 3 \)
- Nspiressä luvun \(n\) alkulukuhajotelman saa komennolla
factor(n), GeogebrassaAlkutekijät(n)
07 Alkuluvut
By Timo Pelkola
07 Alkuluvut
- 270



