Pisteen etäisyys suorasta
Etäisyys suorasta
- Etäisyys tasossa on määritelty pisteiden välille:
\(d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) - Täytyy siis valita suoralta piste, jonka suhteen etäisyys lasketaan
- Jos voisi valita minkä tahansa pisteen suoralta, etäisyys voisi olla kuinka suuri tahansa
- Etäisyys ei kuitenkaan voi olla kuinka pieni tahansa
- Valitaan se suoran piste, jolla etäisyys on mahdollisimman pieni, eli kohtisuora etäisyys
- Valittu suoran piste on siis suoran ja tutkittavan pisteen kautta kulkevan normaalin leikkauspiste
◻
●
●
●
Etäisyyden laskeminen
Pisteen etäisyyden suorasta voisi laskea etsimällä normaalin ja suoran leikkauspisteen ja laskemalla näiden pisteiden välisen etäisyyden, mutta elämää helpottamaan on myös keksitty kaava (todistus kirjassa)
Lause: Pisteen \((x_0,y_0)\) etäisyys \(d\) suorasta \(ax+by+c=0\) lasketaan
\(d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
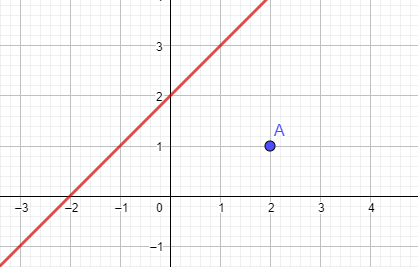
Esim 1
Laske suoran \(y=x+2\) ja pisteen \(A=(2,1)\) välinen etäisyys

Muutetaan suoran yhtälö ensiksi normaalimuotoon siirtämällä kaikki termit vasemmalle ja järjestämällä termit
\(-x+y-2=0\)
\(d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
Nähdään, että \(a=-1\), \(b=1\) ja \(c=-2\).
Sij. kaavaan: \(d=\frac{|-1\cdot2+1\cdot1+(-2)|}{\sqrt{(-1)^2+1^2}}=\frac{|-3|}{\sqrt{2}}=\frac{3}{\sqrt{2}}\)
Esim 2
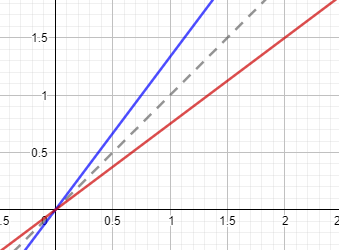
Määritä suorien \(3x-4y=0\) ja \(4x-3y=0\) välisen kulman (\(\leq 90^\circ\)) kulmanpuolittajan yhtälö
Kulmanpuolittajan muodostavat pisteet, jotka ovat yhtä kaukana kummastakin kulman kyljestä
Merkitään pistettä kulmanpuolittajalla \((x,y)\)
Etäisyys suorasta \(3x-4y=0\): \(d_1=\frac{|3x+(-4y)+0|}{\sqrt{3^2+(-4)^2}}=\frac{|3x-4y|}{5}\)
Etäisyys suorasta \(4x-3y=0\): \(d_2=\frac{|4x+(-3y)+0|}{\sqrt{4^2+(-3)^2}}=\frac{|4x-3y|}{5}\)
Etäisyyksien pitää olla sama, eli ratkaistaan \(y\) yhtälöstä \(d_1=d_2\)
\(d_1=d_2\)
\(\dfrac{|3x-4y|}{5}=\dfrac{|4x-3y|}{5}\)
\(|3x-4y|=|4x-3y|\)
\(y = x\) (tai \(y=-x\))
Toinen suora on myös kulmanpuolittaja, mutta suuremman suorien muodostamista kulmista. Tämän voi päätellä kuvaajasta tai kulmakertoimista.
\(3x-4y=4x-3y\)
\(3x-4y=-(4x-3y)\)
tai
\(-y=x\)
\(y=-x\)
\(3x-4y=-4x+3y\)
\(y=x\)
09 Pisteen etäisyys suorasta
By Timo Pelkola
09 Pisteen etäisyys suorasta
- 29



