Uma Introdução Sucinta a Differential Privacy
Victor Sanches Portella
Outubro 2022
cs.ubc.ca/~victorsp
Por que DP?
(Ou por que usar matemática em privacidade)
Análise de Dados com Privacidade
Publicar análise estatística
Objetivo:
Tomar decisões com base em dados
Usar um modelo de machine learning
Sem revelar informação privada de ninguém
Exemplos
Publicar anualmente estatisticas sobre salários
Mas o que eu quero dizer com "informação privada"?
Treinar modelos de ML
Liberar informação histórica
O Que é Informação Privada
Pergunta:
O que é informação privada?
Dados com informações médicas de fumantes e não fumantes
Análise revela fumantes tem mais chance de ter câncer
Participantes fumantes podem ter problemas com seguro
Descobrir pessoa é fumante sem ela ter revelado essa info
Informação privada foi vazada nesse caso?
Conclusão não depende de uma pessoa específica
NÃO
Objetivo:
Aprender sobre a população sem aprender sobre qualquer pessoa em específico
Anonimizar os Dados Não Basta
O caso do Prêmio Netflix
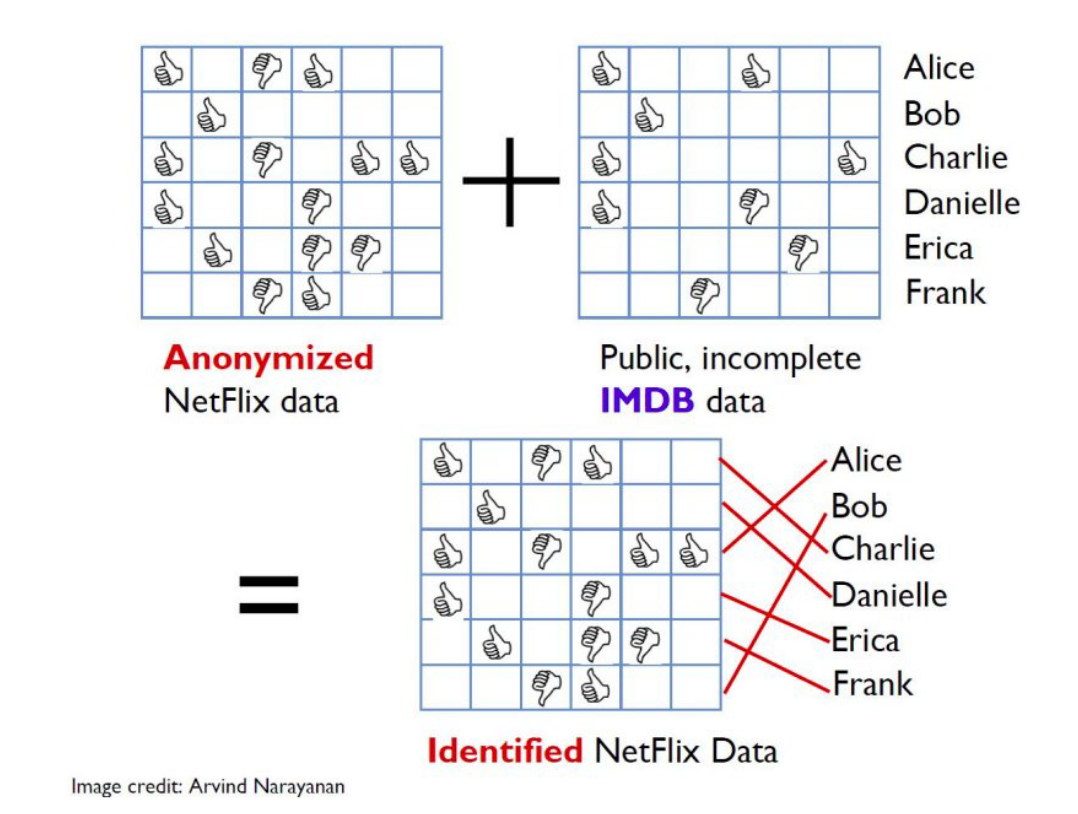
Anonimizar os Dados Não Basta 2
NYC Taxi Driver Dataset
Campos (anonimizados):
medallion, hack license
Campos (anonimizados):
Reddit percebeu um padrão...
Esse usuário aqui faz MUITAS corridas
cfcd208495d565ef66e7dff9f98764da
Taxi "NULL"
md5 0
Anonimizar os Dados Não Basta 3
Onde DP é Usada
https://desfontain.es/privacy/real-world-differential-privacy.html
US Census, Facebook, Microsoft, Google, Apple, Linkedin
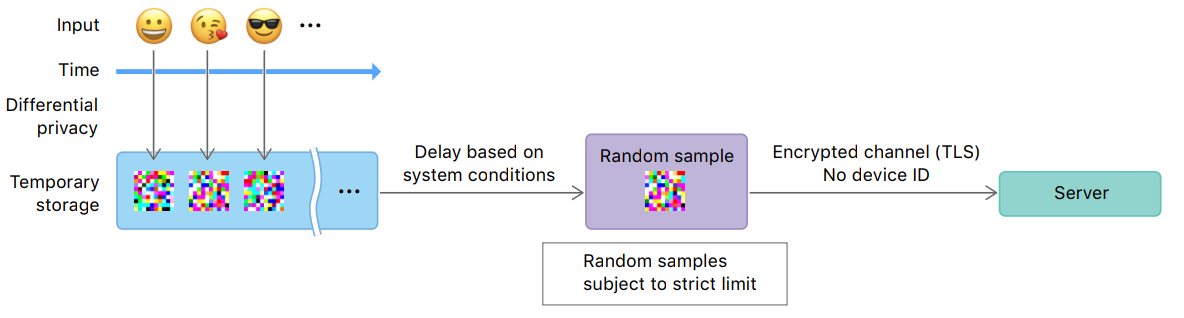
O Que é DP?
Modelo de Computação
Servidor Confiável
Limite de Confiança
Local
Differential Privacy
Adversário
Differential Privacy - Ideia
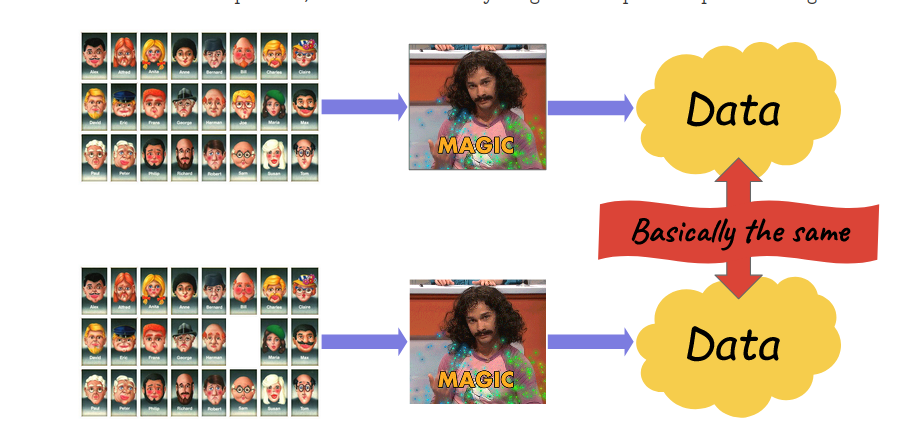
Ted's blog: https://desfontain.es/privacy/differential-privacy-in-more-detail.html
O Que É Differential Privacy
Algoritmo (média, mediana, fit de modelo de ML)
\mathcal{M}
D, D'
Bancos de dados diferindo em uma entrada
\mathbb{P}(\mathcal{M(D)} \in A) \leq e^{\varepsilon} \cdot
\mathbb{P}(\mathcal{M(D')} \in A)
\(\mathcal{M}\) é \(\varepsilon\)-DP se, para qualquer conjunto de possiveis resultados \(A\),
\varepsilon
"Privacy budget"
(menor = mais privado)
"Mudar só um usuário não muda muito o resultado"
"Um usuário participar não afeta a chance de algo ruim acontecer"
Análise de pior caso
O Que É Differential Privacy
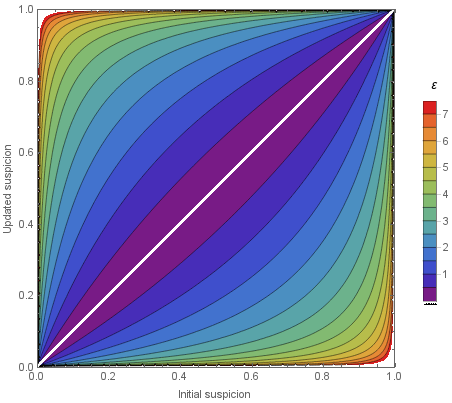
Ted's blog: https://desfontain.es/privacy/differential-privacy-in-more-detail.html
Exemplo - Randomized Response
Cada usuário
Cada usuário tem uma resposta binária: SIM ou NÃO
Responde Verdade
com probabilidade 3/4
Responde Mentira
com probabilidade 1/4
\displaystyle \Bigg \{
\mathcal{M(D)} =
% de usuários com resposta SIM
\(\log 3\)-Differentially Private
Local
Propriedades - Pós-processamento
Nenhum tipo de pós-processamento (sem acesso a dados) pode destruir a garantia de privacidade
f(\mathcal{M(D)})
\(\varepsilon\)-DP
Impossível extrair mais informação só do resultado de um algoritmo DP
\mathcal{M(D)}
\(\varepsilon\)-DP
f
Função de pós-proc.
\displaystyle \Bigg\}
Propriedades - Composição
Se mais informação privada é liberada de forma DP, as garantias degradam de forma graciosa
\mathcal{M}_2(\mathcal{M}_1(D),D)
\((\varepsilon_1 + \varepsilon_2)\)-DP
Mesmo se um mesmo usuário tem mais de uma entrada nos dados, ainda temos garantias de privacidade
\mathcal{M}_1(D)
\(\varepsilon_1\)-DP
\displaystyle \Bigg\}
\mathcal{M}_2(\textrm{aux}, D)
\(\varepsilon_2\)-DP
Differential Privacy Aproximada
As vezes \(\varepsilon\)-DP pode ser muito estringente
\(0.1\)-DP quase sempre, mas raramente acontece de ser \(15\)-DP
D, D'
Bancos de dados diferindo em uma entrada
\mathbb{P}(\mathcal{M(D)} \in A) \leq e^{\varepsilon} \cdot
\mathbb{P}(\mathcal{M(D')} \in A)
\(\mathcal{M}\) é \((\varepsilon, \delta)\)-DP se, para qualquer conjunto de possiveis resultados \(A\),
+~~ \delta
Com probabilidade \(\delta\), o alg. \(\mathcal{M}\) é \(\varepsilon\)-DP.
\(\varepsilon \approx 0.1, 1, 8\)
\(O(1)\)
\(\delta \ll 1/n\)
\(O(1/n^{\omega(1)})\)
Differential Privacy Aproximada
Differential Privacy aproximada é mais fácil de garantir
mas pode ser muito fraca!
Um algoritmo que revela todos os dados com
probabilidade \(\delta\) é \((0, \delta)\)-DP
Um exemplo mais natural:
Cada usuário tem probabilidade \(\delta\) de vazar informação privada
\(n \) usuários \(\implies\) \(\approx \delta \cdot n\) probabilidade de dados vazarem
\(\delta \approx 1/n\) significa alta chance de dados vazarem
\((0, \delta)\)-DP
\(\delta > 1/n\) não garante muita coisa
Como é DP?
('return result + rand(10)' )
Exemplo Corrente - Média
x_1, \dotsc, x_n
vetores com \(d\) dimensões de um conj.
\(d = 1\) são números, o suficiente para entender quase tudo
\(d = 1\) são números, o suficiente para entender quase tudo
Impossível calcular média DP de números de tamanho arbitrário
\mathcal{X}
\displaystyle \Bigg \}
D
Queremos calcular
f(D) = \displaystyle \frac{1}{n}\sum_{i = 1}^n x_i
de forma privada
Os algoritmos vão depender da sensibilidade da média
\displaystyle \Delta_1 = \max_{D,D' \in \mathcal{X}^n} \lVert{f(D) - f(D')}\rVert_1
vizinhos
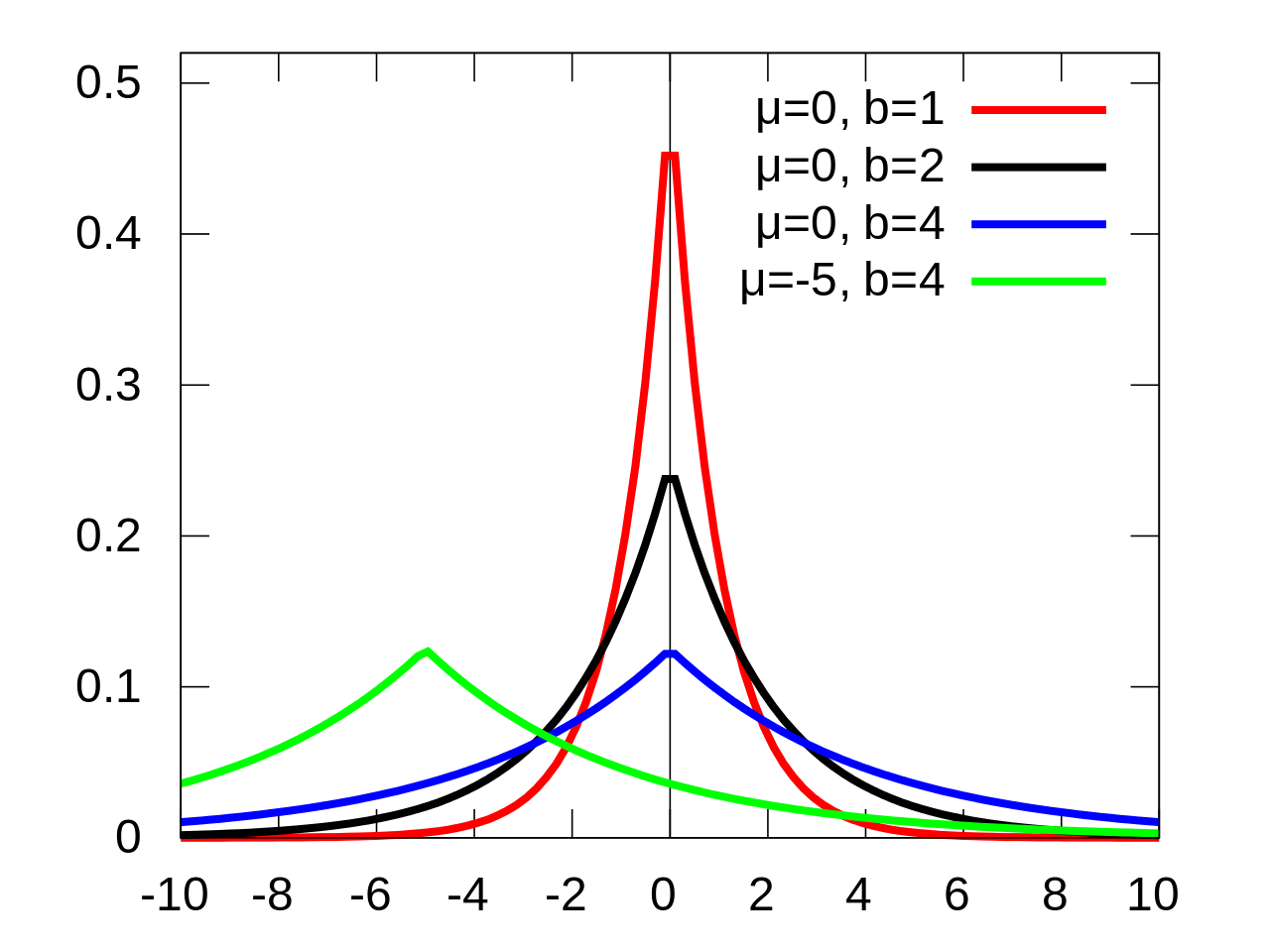
Mecanismo Laplace
x_1, \dotsc, x_n
\displaystyle \Bigg \}
D
\in \mathcal{X}
Queremos calcular
f(D) = \displaystyle \frac{1}{n}\sum_{i = 1}^n x_i
de forma privada
\displaystyle \Delta_1 = \max_{D,D' \in \mathcal{X}^n} \lVert{f(D) - f(D')}\rVert_1
vizinhos
Algoritmo \(\varepsilon\)-DP:
\displaystyle
\mathcal{M}(D) = \frac{1}{n} \sum_{i = 1}^n x_i + \mathrm{Lap}\Big(\frac{\Delta_1}{\varepsilon}\Big)
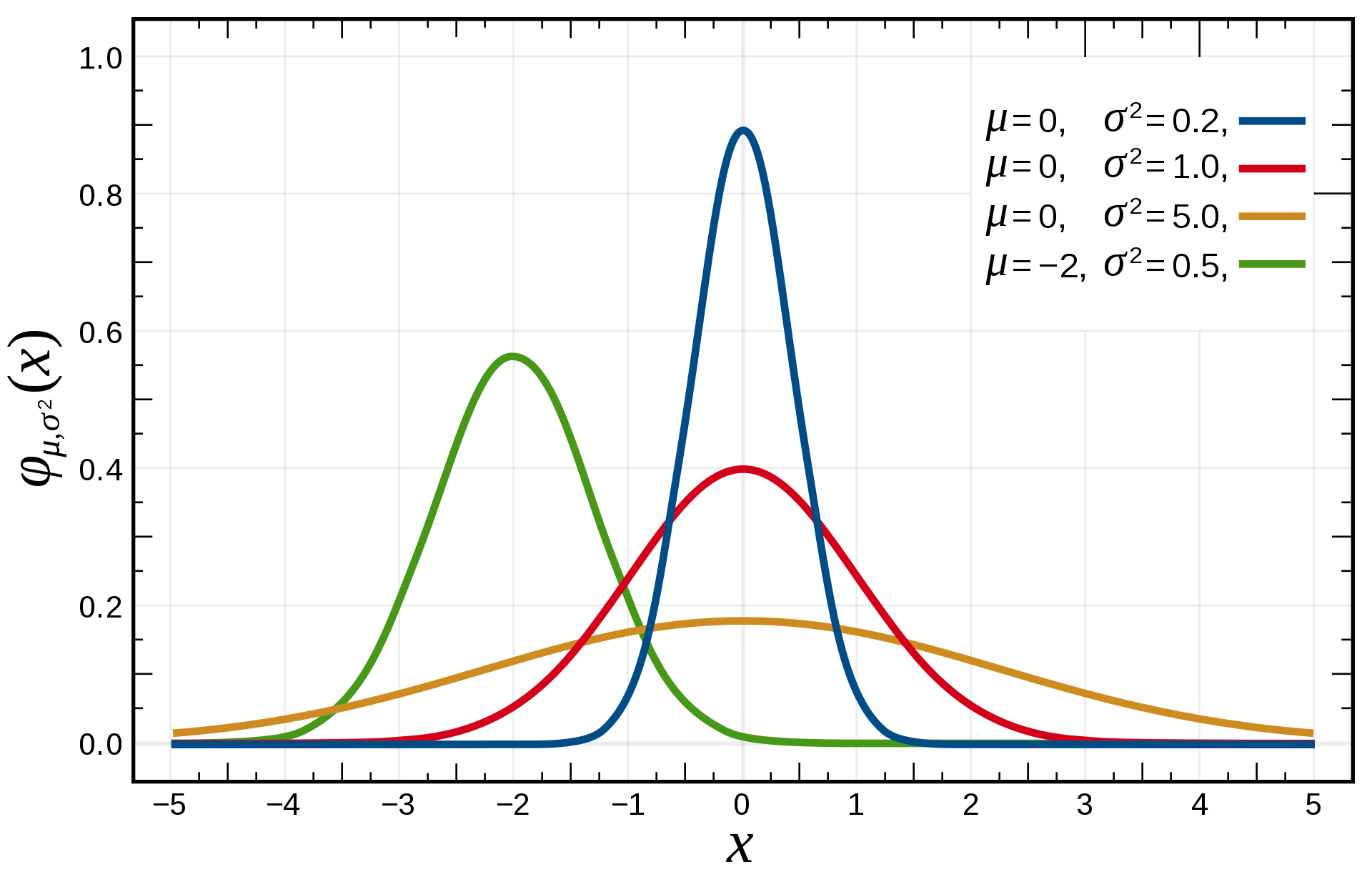
Mecanismo Gaussiano
\displaystyle \Delta_1 = \max_{D,D' \in \mathcal{X}^n} \lVert{f(D) - f(D')}\rVert_1
vizinhos
Algoritmo \((\varepsilon, \delta)\)-DP:
\displaystyle
\mathcal{M}(D) = \frac{1}{n} \sum_{i = 1}^n x_i + \mathcal{N}\Bigg(0, O\Big(\log\Big(\frac{1}{\delta}\Big)\frac{\Delta_2^2}{\varepsilon^2} \Big)\Bigg)
Sensibilidade \(\ell_2\)
\displaystyle
\Delta_2 \leq \Delta_1 \leq \sqrt{d} \cdot \Delta_2
Dependencia na dimensão pode ser muito melhor
\displaystyle \Delta_2 = \max_{D,D' \in \mathcal{X}^n} \lVert{f(D) - f(D')}\rVert_2
vizinhos
Machine Learning - Exemplos
Alguns exemplos de como treinar modelos de ML com DP
Use dados tratados com DP na fonte
Output perturbation
Adiciona ruido no modelo
Objective perturbation
Adiciona ruido na loss function
Algumas técnicas mais "famosas"
Stochastic Gradient Descent com (mais) ruido
DP-SGD
Private fine-tuning
Private aggregation
PATE
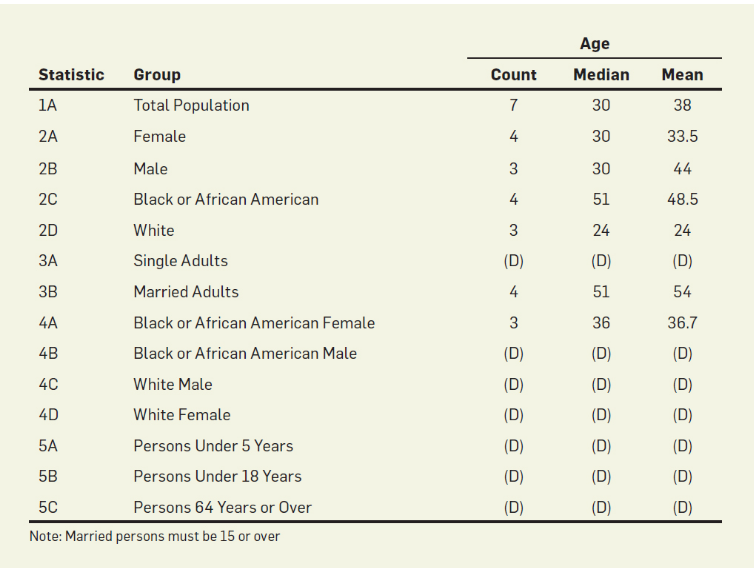
Além do Básico de DP
Controle Fino de Privacidade
\displaystyle \mathcal{L}_{D, D'} = \log \Bigg( \frac{\mathbb{P}(\mathcal{M}(D) = o)}{\mathbb{P}(\mathcal{M}(D') = o)}\Bigg)
Privacy Loss Random Variable
o \sim \mathcal{M}(D)
onde
Mas \(\mathcal{L}_{D, D'}\) tem uma distribuição, as definições acima são bem simplistas
Concentrated DP, zero Concentrated DP, Renyi DP, etc...
\(\varepsilon\)-DP
\displaystyle \mathcal{L}_{D, D'} \leq \varepsilon
\iff
com probabilidade 1
\((\varepsilon, \delta)\)-DP
\iff
\displaystyle \mathcal{L}_{D, D'} \leq \varepsilon
com probabilidade \(1 - \delta\)
Catadão de Tópicos
Exponential Mechanism
Sanitização de Banco de Dados - Histogramas e Queries
Private Multiplicative Weights Update
"Local" Sensitivity
Adaptive Data Analysis
Composição Avançada
Catadão de Fontes
Livro/Survey: Aaron Roth & Cynthia Dwork
Curso Online de Waterloo: Gautam Kamath - Fall 2020
Ted's Blog: https://desfontain.es/privacy/
Uma Introdução Sucinta a Differential Privacy
Victor Sanches Portella
Outubro 2022
cs.ubc.ca/~victorsp
Elo7 - Introd. a DP
By Victor Sanches Portella
